Transformation Properties under the Operations of the Molecular Symmetry Groups G36 and G36(EM) of Ethane H3CCH3
Abstract
1. Introduction
2. The Structure of the G36 Group
3. Irreducible Representations of G36
4. Representation Matrices for the Irreducible Representations of G
5. Representation Matrices for the G Irreducible Representation of G36
6. Generation of a Symmetry Adapted Basis Set for Ethane
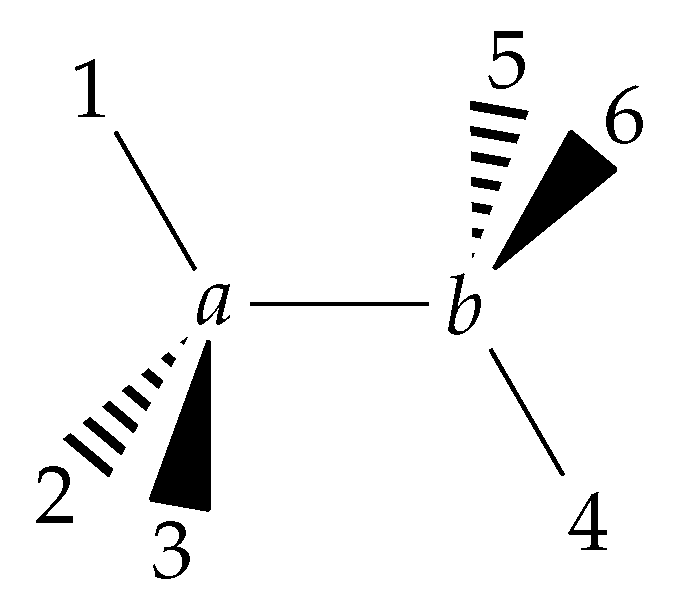
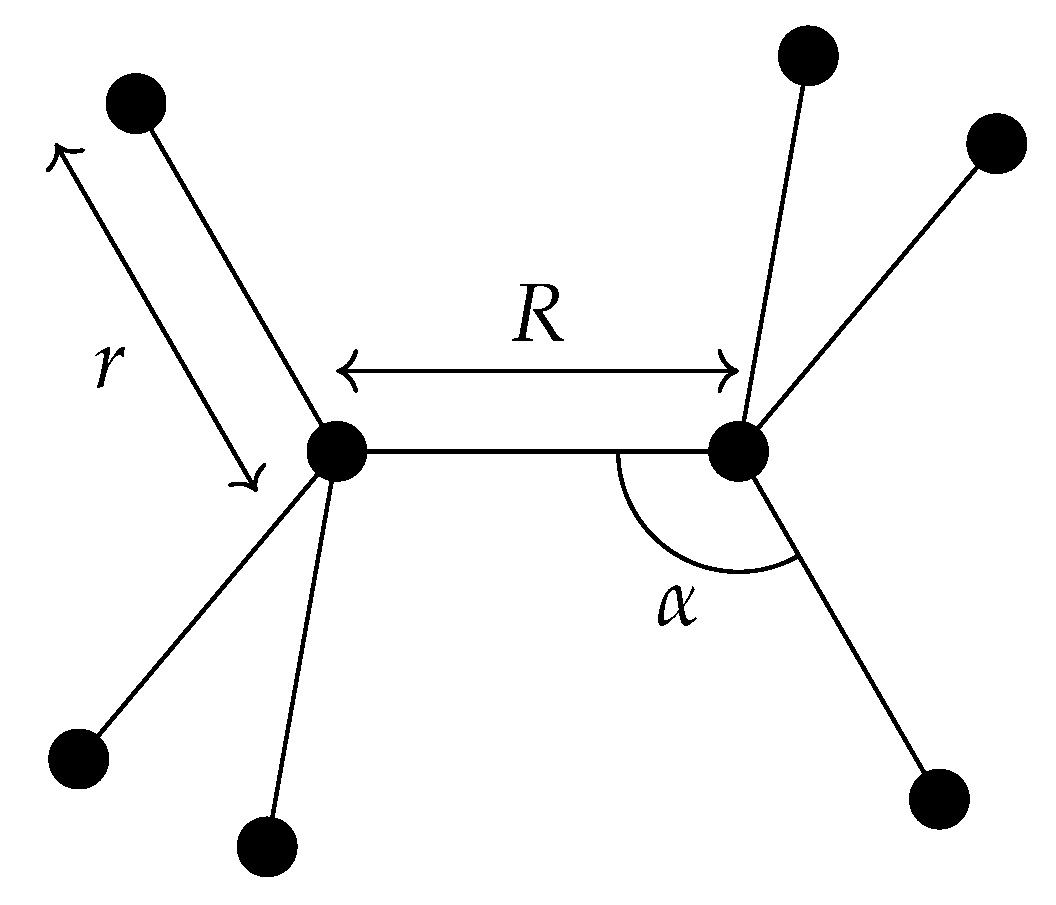
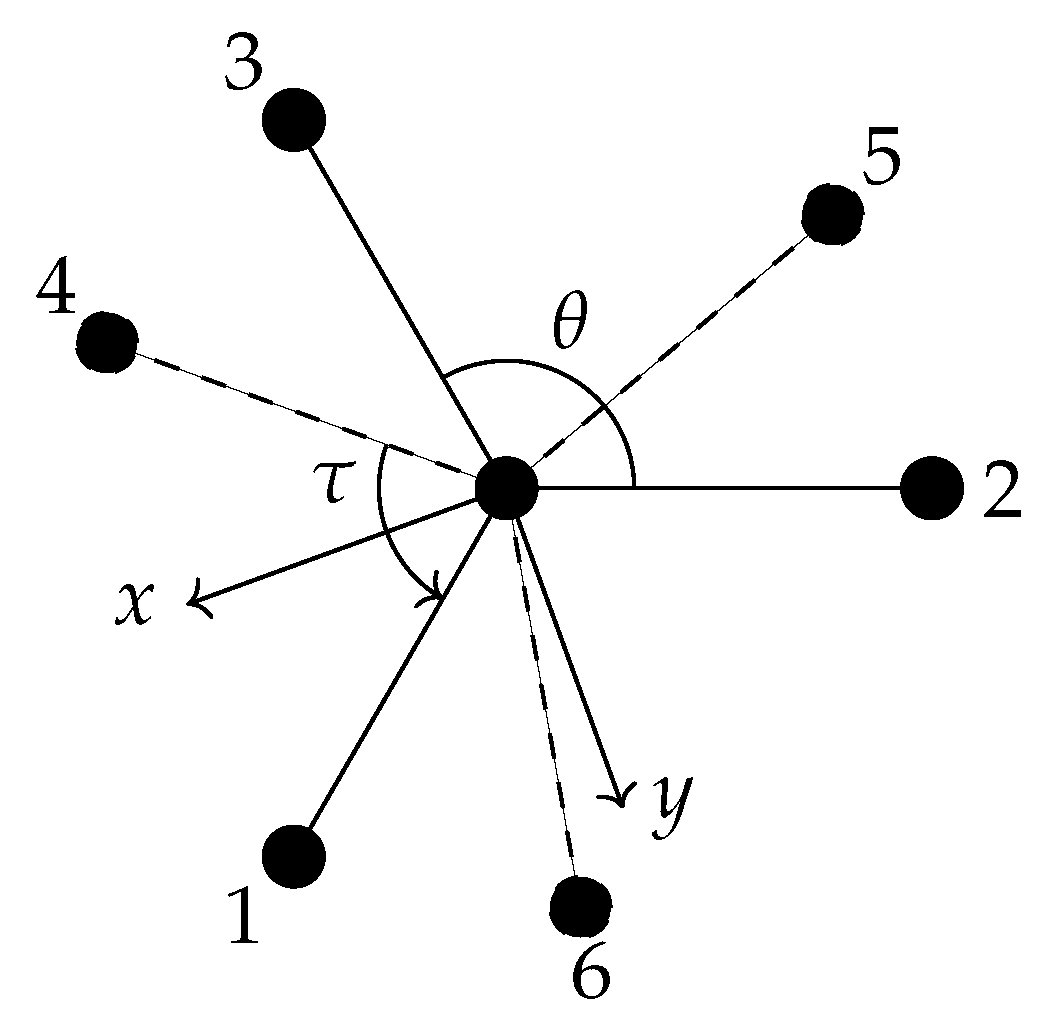
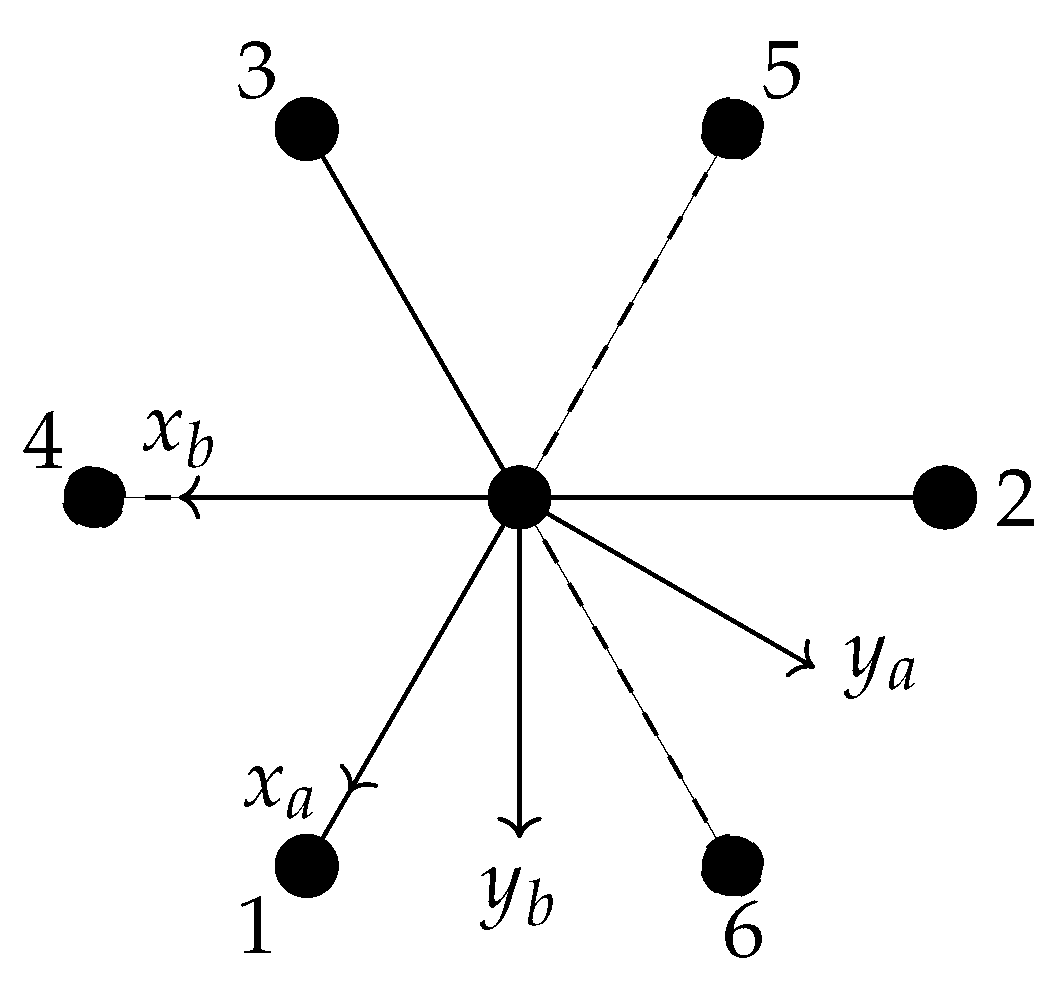
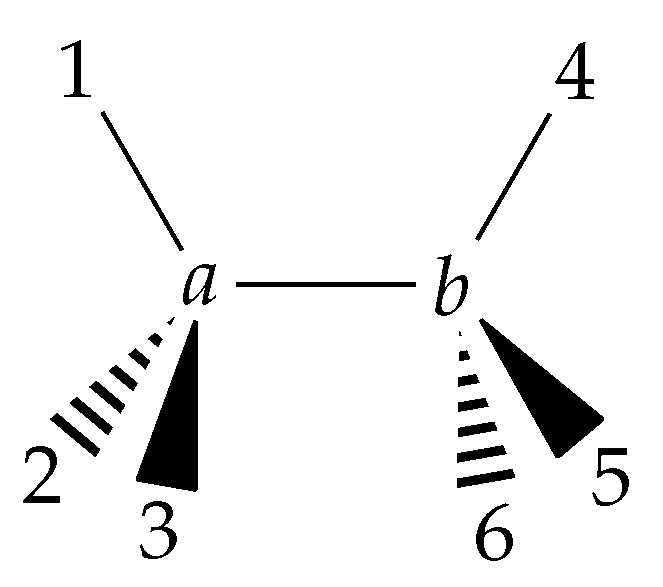
6.1. Definition of the Internal Coordinates Used for Ethane
- the C−C bond length R;
- six C−H bond lengths , k = 1, 2, …, 6;
- six bond angles ∠(H-C-C) = , k = 1, 2, …, 6;
- four dihedral-angle coordinates , , , and ,
- the torsional angle ; and
- the three rotational angles .
6.2. Transformation of the Vibrational Coordinates under G36
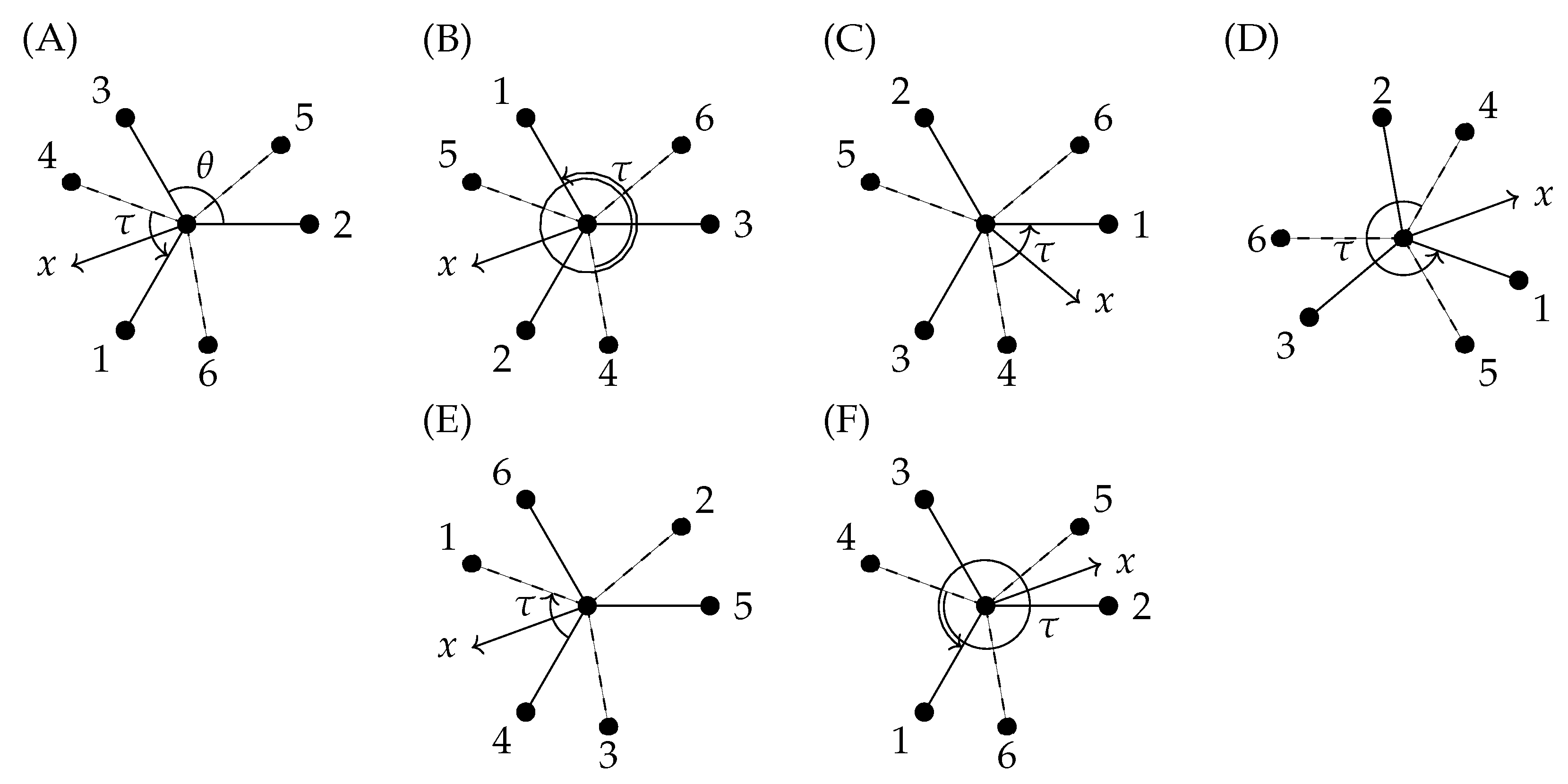
6.3. The Extended Molecular Symmetry Group G36(EM) and the Transformation of the Torsional Coordinate
6.4. Rigid-Symmetric-Rotor Function Representations
6.5. Symmetrisation of the Basis Set
7. Potential Energy Function of Ethane in a Symmetry Adapted Representation
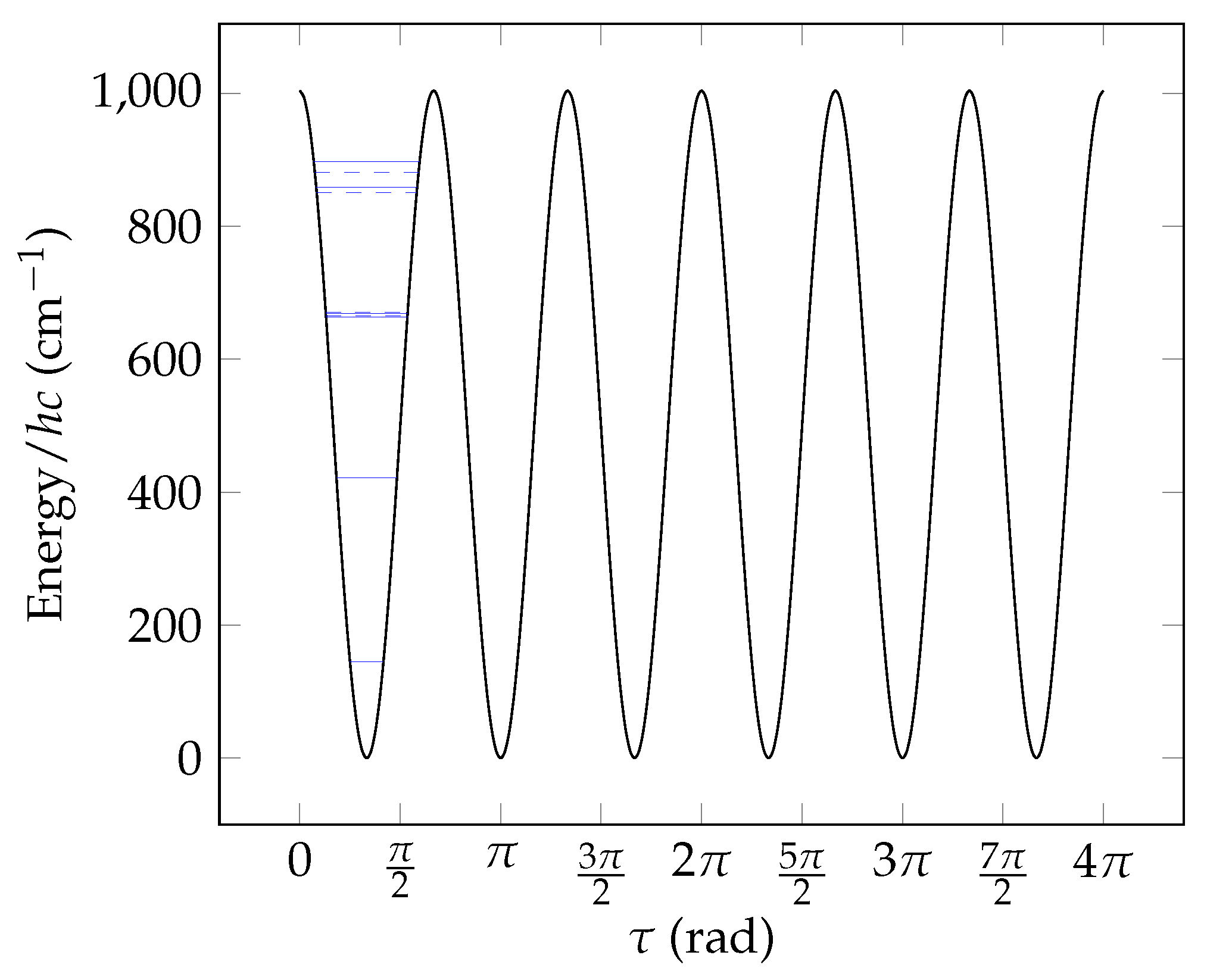
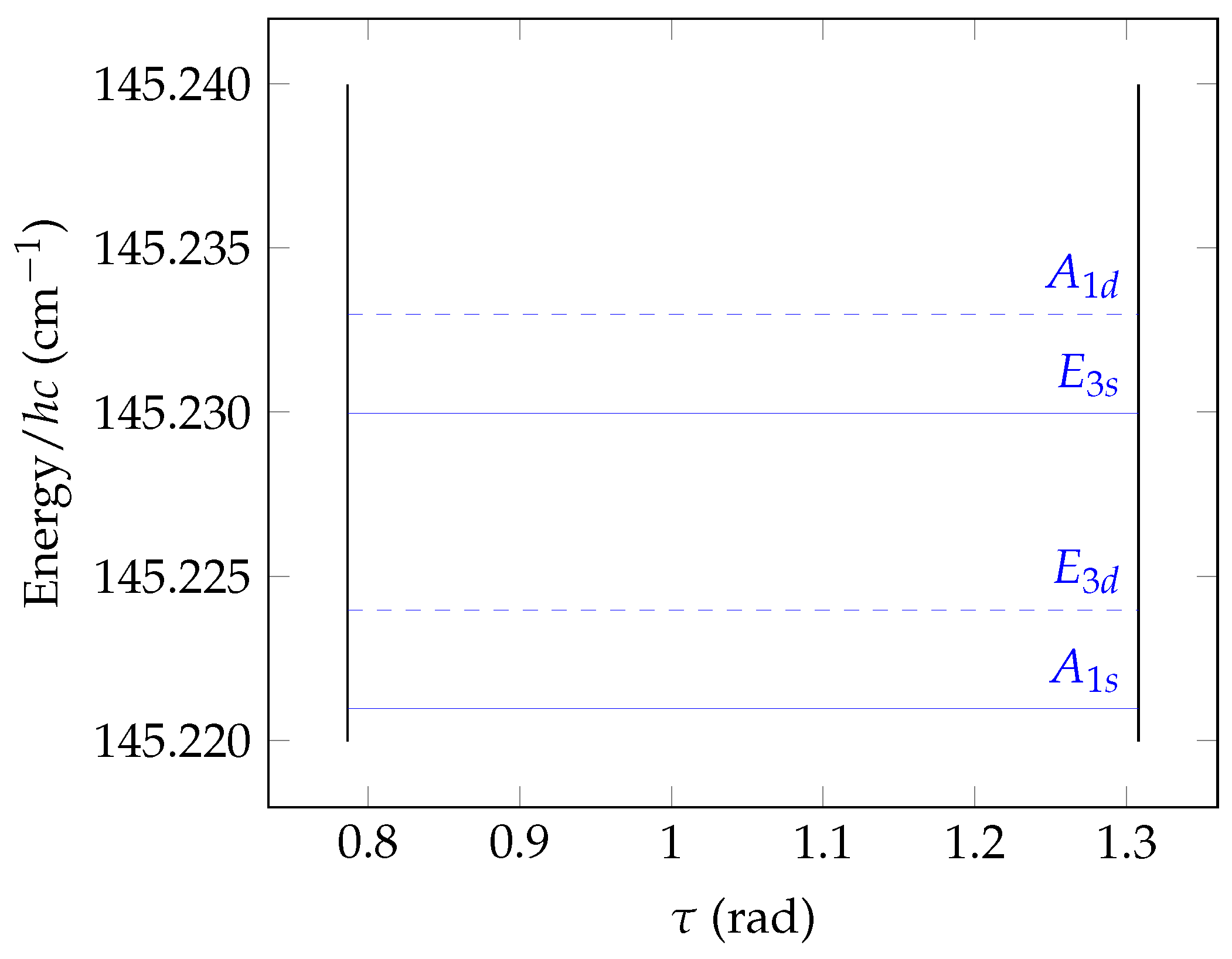
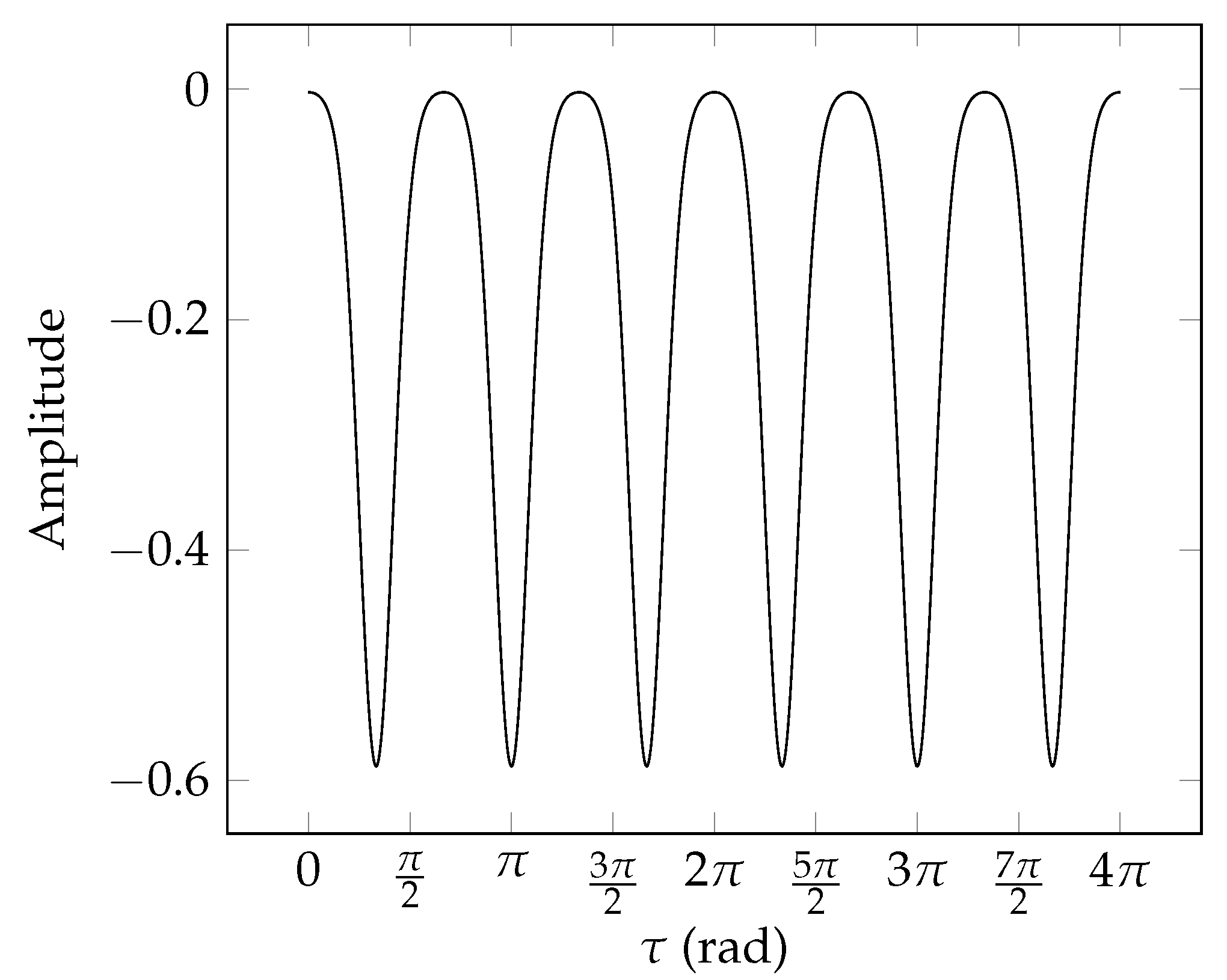
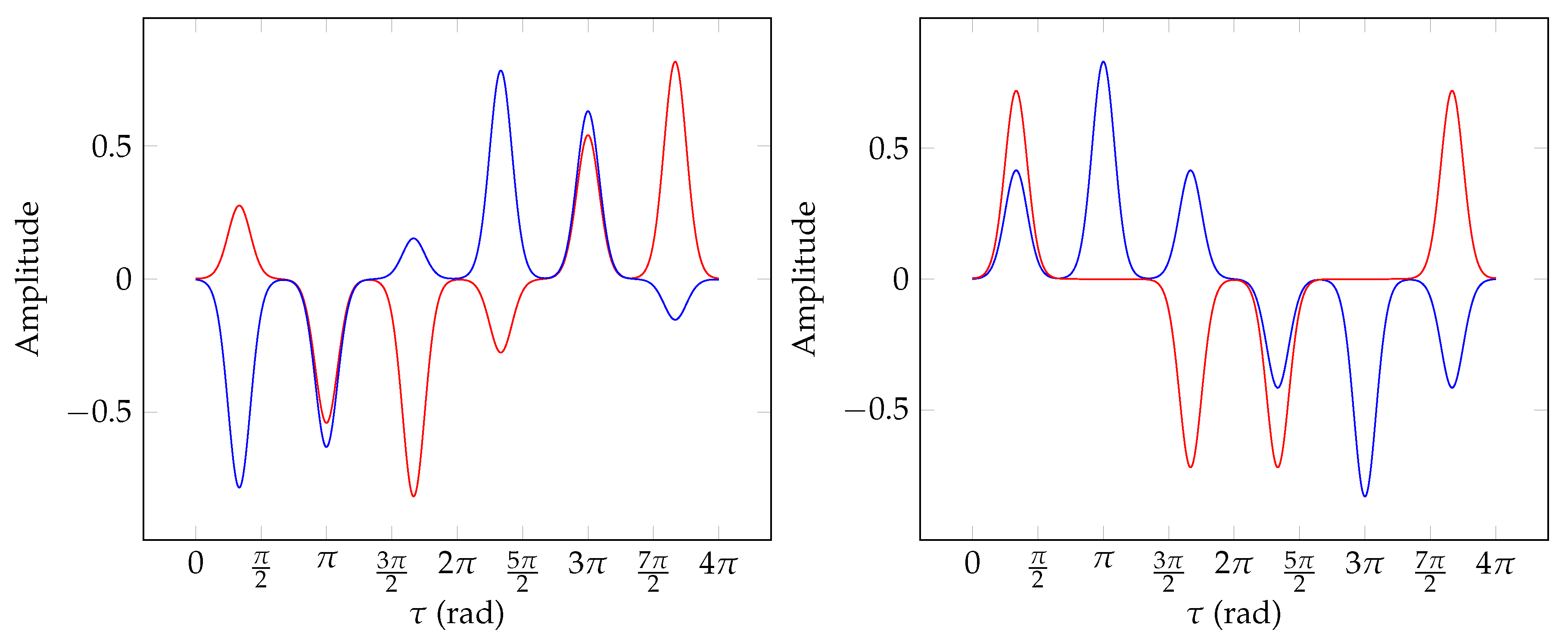
8. Numerical Example
8.1. Subset 2 Symmetrisation
8.2. Subset 4 Symmetrisation
8.3. Subset 5 Symmetrisation
8.4. Torsional Basis Function Symmetries
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Character Table of the Isomorphic Groups C and C
| 1 | 2 | 3 | |
|---|---|---|---|
| 1 | 1 | 1 | |
| 1 | 1 | −1 | |
| E | 2 | −1 | 0 |
Appendix B. The G36 Transformation Matrices
Appendix B.1. Ei Transformation Matrices in G36
Appendix B.1.1. One-Member Class Containing E
Appendix B.1.2. Two-Member Class Containing (123)(456) and (132)(465)
Appendix B.1.3. Three-Member Class Containing (14)(26)(35)(ab)*
Appendix B.1.4. Two-Member Class Containing (123)(456) and (132)(456)
Appendix B.1.5. Four-Member Class Containing (123) and (456)
Appendix B.1.6. Six-Member Class Containing (142635)(ab)*
Appendix B.1.7. Three-Member Class Containing (14)(25)(36)(ab)
Appendix B.1.8. Six-Member Class Containing (142536)(ab)
Appendix B.1.9. Nine-Member Class Containing (12)(45)*
Appendix B.2. G Transformation Matrices in G36
Appendix B.2.1. One-Member Class Containing E
Appendix B.2.2. Two-Member Class Containing (123)(456) and (132)(465)
Appendix B.2.3. Three-Member Class Containing (14)(26)(35)(ab)*
Appendix B.2.4. Two-Member Class Containing (123)(456) and (132)(456)
Appendix B.2.5. Four-Member Class Containing (123) and (456)
Appendix B.2.6. Six-Member Class Containing (142635)(ab)*
Appendix B.2.7. Three-Member Class Containing (14)(25)(36)(ab)
Appendix B.2.8. Six-Member Class Containing (142536)(ab)
Appendix B.2.9. Nine-Member Class Containing (12)(45)*
Appendix C. Derivation of the Transformation of Internal Coordinates
Appendix C.1. Bond Lengths
Appendix C.2. Bond Angles
Appendix C.3. Dihedral Angles
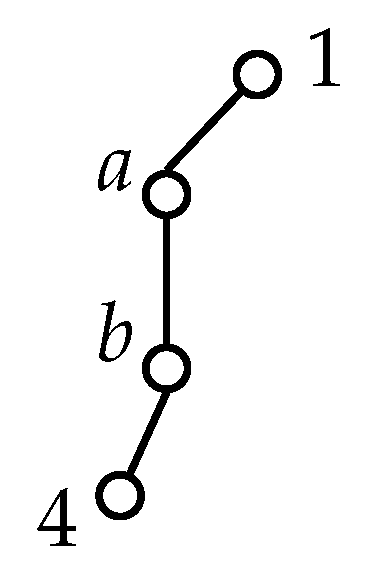
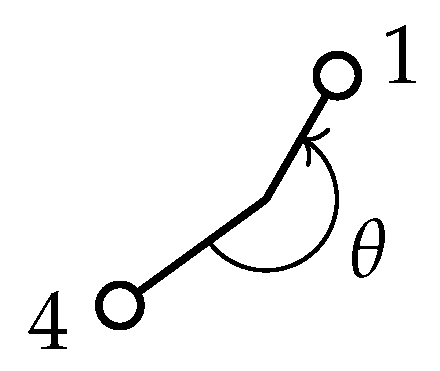
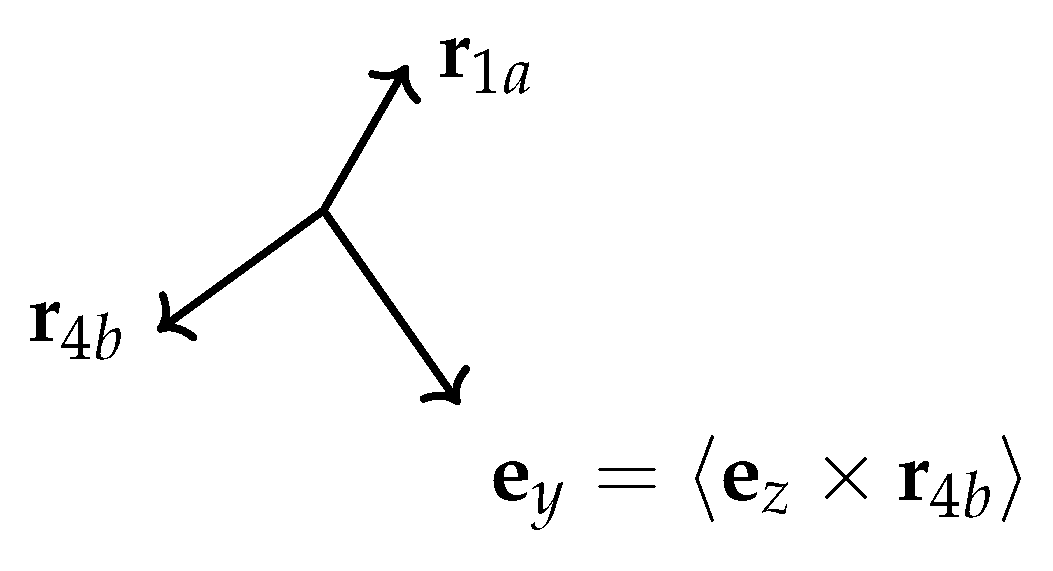
Appendix D. Transformation of τ under the Generating Operations of G36
References
- Bunker, P.R.; Jensen, P. Molecular Symmetry and Spectroscopy, 2nd ed.; NRC Research Press: Ottawa, ON, Canada, 1998. [Google Scholar]
- Chubb, K.L.; Jensen, P.; Yurchenko, S.N. Symmetry Adaptation of the Rotation-Vibration Theory for Linear Molecules. Symmetry 2018, 10, 137. [Google Scholar] [CrossRef]
- Yurchenko, S.N.; Thiel, W.; Jensen, P. Theoretical ROVibrational Energies (TROVE): A robust numerical approach to the calculation of rovibrational energies for polyatomic molecules. J. Mol. Spectrosc. 2007, 245, 126–140. [Google Scholar] [CrossRef]
- Smeyers, Y.G.; Bellido, M.N. Internal dynamics of nonrigid molecules. I. Application to acetone. Intern. J. Quantum Chem. 1981, 19, 553–565. [Google Scholar] [CrossRef]
- Carvajal, M.; Álvarez-Bajo, O.; Senent, M.L.; Domínguez-Gómez, R.; Villa, M. Raman and infrared spectra of dimethyl ether 13C-isotopologue (CH3O13CH3) from a CCSD (T) potential energy surface. J. Mol. Spectrosc. 2012, 279, 3–11. [Google Scholar] [CrossRef]
- Lattanzi, F.; Di Lauro, C. On the Physical Reasons for the Extension of Symmetry Groups in Molecular Spectroscopy. Symmetry 2010, 2, 213–229. [Google Scholar] [CrossRef]
- Lattanzi, F.; Di Lauro, C. Vibrational symmetry classification and torsional tunneling splitting patterns in G6(EM), G12, and G36(EM) molecules. Mol. Phys. 2005, 103, 697–708. [Google Scholar] [CrossRef]
- Hougen, J.T. Perturbations in the vibration-rotation-torsion energy levels of an ethane molecule exhibiting internal rotation splittings. J. Mol. Spectrosc. 1980, 82, 92–116. [Google Scholar] [CrossRef]
- Lattanzi, F.; di Lauro, C. Rotation–Torsion Analysis of the High-Resolution ν6 and ν8 Fundamentals of 70Ge2H6. J. Mol. Spectrosc. 1999, 198, 315–328. [Google Scholar] [CrossRef] [PubMed]
- Lauro, C.D.; Lattanzi, F.; Valentin, A. Rotational analysis of the ν6, ν8, ν3 + ν4 interacting infrared system of C2D6 between 960 cm−1 and 1180 cm−1. Mol. Phys. 1996, 89, 663–676. [Google Scholar] [CrossRef]
- Lattanzi, F.; Lauro, C.D.; Horneman, V.M. The high-resolution infrared spectrum of Si2H6: Rotation-torsion analysis of the ν5 and ν7 fundamentals, and torsional splittings in the degenerate vibrational states. Mol. Phys. 2004, 102, 757–764. [Google Scholar] [CrossRef]
- Lattanzi, F.; Lauro, C.D.; Horneman, V.M. Torsional splittings in the v12 = 1 vibrational state of Si2H6: Analysis of the ν6 + ν12 and ν9 + ν12(E) combination bands in the high resolution infrared spectrum. Mol. Phys. 2006, 104, 1795–1817. [Google Scholar] [CrossRef]
- Yachmenev, A.; Yurchenko, S.N. Automatic differentiation method for numerical construction of the rotational-vibrational Hamiltonian as a power series in the curvilinear internal coordinates using the Eckart frame. J. Chem. Phys. 2015, 143, 014105. [Google Scholar] [CrossRef] [PubMed]
- Yurchenko, S.N.; Barber, R.J.; Yachmenev, A.; Thiel, W.; Jensen, P.; Tennyson, J. A Variationally Computed T=300 K Line List for NH3. J. Phys. Chem. A 2009, 113, 11845–11855. [Google Scholar] [CrossRef] [PubMed]
- Yachmenev, A.; Yurchenko, S.N.; Jensen, P.; Thiel, W. A new “spectroscopic” potential energy surface for formaldehyde in its ground electronic state. J. Chem. Phys. 2011, 134, 244307. [Google Scholar] [CrossRef] [PubMed]
- Sousa-Silva, C.; Hesketh, N.; Yurchenko, S.N.; Hill, C.; Tennyson, J. High temperature partition functions and thermodynamic data for ammonia and phosphine. J. Quant. Spectrosc. Radiat. Transf. 2014, 142, 66–74. [Google Scholar] [CrossRef]
- Sousa-Silva, C.; Al-Refaie, A.F.; Tennyson, J.; Yurchenko, S.N. ExoMol line lists - VII. The rotation-vibration spectrum of phosphine up to 1500 K. Mon. Not. R. Astron. Soc. 2015, 446, 2337–2347. [Google Scholar] [CrossRef]
- Underwood, D.S.; Yurchenko, S.N.; Tennyson, J.; Jensen, P. Rotational spectrum of SO3 and theoretical evidence for the formation of sixfold rotational energy-level clusters in its vibrational ground state. J. Chem. Phys. 2014, 140. [Google Scholar] [CrossRef]
- Al-Refaie, A.F.; Yurchenko, S.N.; Yachmenev, A.; Tennyson, J. ExoMol line lists IX: A variationally computed line-list for hot formaldehyde. Mon. Not. R. Astron. Soc. 2015, 448, 1704–1714. [Google Scholar] [CrossRef]
- Yurchenko, S.N.; Tennyson, J. ExoMol line lists—IV. The rotation-vibration spectrum of methane up to 1500 K. Mon. Not. R. Astron. Soc. 2014, 440, 1649–1661. [Google Scholar] [CrossRef]
- Al-Refaie, A.F.; Ovsyannikov, R.I.; Polyansky, O.L.; Yurchenko, S.N.; Tennyson, J. A variationally calculated room temperature line-list for H2O2. J. Mol. Spectrosc. 2015, 318, 84–90. [Google Scholar] [CrossRef]
- Owens, A.; Yurchenko, S.N.; Yachmenev, A.; Tennyson, J.; Thiel, W. Accurate ab initio vibrational energies of methyl chloride. J. Chem. Phys. 2015, 142. [Google Scholar] [CrossRef] [PubMed]
- Owens, A.; Yurchenko, S.N.; Yachmenev, A.; Thiel, W. A global potential energy surface and dipole moment surface for silane. J. Chem. Phys. 2015, 143. [Google Scholar] [CrossRef] [PubMed]
- Adam, A.Y.; Yachmenev, A.; Yurchenko, S.N.; Jensen, P. Ro-vibrational averaging of the isotropic hyperfine coupling constant for the methyl radical. J. Chem. Phys. 2015, 143, 244306. [Google Scholar] [CrossRef] [PubMed]
- Owens, A.; Yurchenko, S.N.; Thiel, W.; Spirko, V. Accurate prediction of the ammonia probes of a variable proton-to-electron mass ratio. Mon. Not. R. Astron. Soc. 2015, 450, 3191–3200. [Google Scholar] [CrossRef]
- Al-Refaie, A.F.; Polyansky, O.L.; Ovsyannikov, R.I.; Tennyson, J.; Yurchenko, S.N. ExoMol line lists—XV. A new hot line list for hydrogen peroxide. Mon. Not. R. Astron. Soc. 2016, 461, 1012–1022. [Google Scholar] [CrossRef]
- Underwood, D.S.; Tennyson, J.; Yurchenko, S.N.; Huang, X.; Schwenke, D.W.; Lee, T.J.; Clausen, S.; Fateev, A. ExoMol molecular line lists—XIV. The rotation-vibration spectrum of hot SO2. Mon. Not. R. Astron. Soc. 2016, 459, 3890–3899. [Google Scholar] [CrossRef]
- Owens, A.; Yurchenko, S.N.; Yachmenev, A.; Tennyson, J.; Thiel, W. A global ab initio dipole moment surface for methyl chloride. J. Quant. Spectrosc. Radiat. Transf. 2016, 184, 100–110. [Google Scholar] [CrossRef]
- Owens, A.; Yurchenko, S.N.; Yachmenev, A.; Tennyson, J.; Thiel, W. A highly accurate ab initio potential energy surface for methane. J. Chem. Phys. 2016, 145. [Google Scholar] [CrossRef]
- Owens, A.; Yachmenev, A.; Thiel, W.; Fateev, A.; Tennyson, J.; Yurchenko, S.N. ExoMol line lists - XXIX. The rotation-vibration spectrum of methyl chloride up to 1200 K. Mon. Not. R. Astron. Soc. 2018, 479, 3002–3010. [Google Scholar] [CrossRef]
- Mant, B.P.; Yachmenev, A.; Tennyson, J.; Yurchenko, S.N. ExoMol molecular line lists—XXVII. Spectra of C2H4. Mon. Not. R. Astron. Soc. 2018, 478, 3220–3232. [Google Scholar] [CrossRef]
- Coles, P.A.; Yurchenko, S.N.; Kovacich, R.P.; Hobby, J.; Tennyson, J. A variationally computed room temperature line list for AsH3. Phys. Chem. Chem. Phys. 2019, 21, 3264–3277. [Google Scholar] [CrossRef] [PubMed]
- Mant, B.P.; Chubb, K.L.; Yachmenev, A.; Tennyson, J.; Yurchenko, S.N. The infrared spectrum of PF3 and analysis of rotational energy clustering effect. Mol. Phys. 2019, 1–14. [Google Scholar] [CrossRef]
- Tennyson, J.; Yurchenko, S.N. ExoMol: Molecular line lists for exoplanet and other atmospheres. Mon. Not. R. Astron. Soc. 2012, 425, 21–33. [Google Scholar] [CrossRef]
- Tennyson, J.; Yurchenko, S.N. The ExoMol project: Software for computing large molecular line lists. Intern. J. Quantum Chem. 2017, 117, 92–103. [Google Scholar] [CrossRef]
- Al-Refaie, A.F.; Yurchenko, S.N.; Tennyson, J. GPU Accelerated INtensities MPI (GAIN-MPI): A new method of computing Einstein-A coefficients. Comput. Phys. Commun. 2017, 214, 216–224. [Google Scholar] [CrossRef]
- Longuet-Higgins, H. The symmetry groups of non-rigid molecules. Molecular Physics 1963, 6, 445–460. [Google Scholar] [CrossRef]
- Available online: http://maxima.sourceforge.net/documentation.html (accessed on 20 September 2018).
- Yurchenko, S.N.; Yachmenev, A.; Ovsyannikov, R.I. Symmetry adapted ro-vibrational basis functions for variational nuclear motion: TROVE approach. J. Chem. Theory Comput. 2017, 13, 4368–4381. [Google Scholar] [CrossRef]
- Chubb, K.L.; Yachmenev, A.; Tennyson, J.; Yurchenko, S.N. Treating linear molecule HCCH in calculations of rotation-vibration spectra. J. Chem. Phys. 2018, 149, 014101. [Google Scholar] [CrossRef]
- Noumerov, B.V. A method of extrapolation of perturbations. Mon. Not. R. Astron. Soc. 1924, 84, 592–602. [Google Scholar] [CrossRef]
- Cooley, J.W. An Improved eigenvalue corrector formula for solving the Schrödinger equation for central fields. Math. Comp. 1961, 15, 363–374. [Google Scholar] [CrossRef]
- Hougen, J.T. A Group-Theoretical Treatment of Electronic, Vibrational, Torsional, and Rotational Motions in the Dimethylacetylene Molecule. Can. J. Phys. 1964, 42, 1920–1937. [Google Scholar] [CrossRef]
- Yamada, K.M.; Winnewisser, G.; Jensen, P. Internal rotation tunnelling in HSOH. J. Mol. Struct. 2004, 695–696, 323–337. [Google Scholar] [CrossRef]
- Yamada, K.M.; Jensen, P.; Ross, S.C.; Baum, O.; Giesen, T.F.; Schlemmer, S. The torsional and asymmetry splittings in HSOH. J. Mol. Struct. 2009, 927, 96–100. [Google Scholar] [CrossRef]
- Szalay, V.; Viglaska, D.; Rey, M. Internal- and rho-axis systems of molecules with one large amplitude internal motion: The geometry of rho. J. Chem. Phys. 2018, 149, 244118. [Google Scholar] [CrossRef] [PubMed]
| = = E | = (132)(456) | = (123)(465) | = (14)(25)(36)() | = (16)(24)(35)() | = (15)(26)(34)() |
|---|---|---|---|---|---|
| = | |||||
| = (132)(465) | (123) | (456) | (162435) | (152634) | (142536) |
| = (14)(26)(35) | (152436) | (163425) | (23)(56) | (12)(46) | (13)(45) |
| = (16)(25)(34) | (13)(46) | (23)(45) | (12)(56) | ||
| = (15)(24)(36) | (162534) | (143526) | (12)(45) | (13)(56) | (23)(46) |
| E | (123)(456) | (14)(26)(35)() | (123)(465) | (123) | (142635)() | (14)(25)(36)() | (142536)() | (12)(45) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 2 | 4 | 6 | 3 | 6 | 9 | ||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| 1 | 1 | 1 | 1 | 1 | 1 | −1 | −1 | −1 | ||
| 1 | 1 | −1 | 1 | 1 | −1 | 1 | 1 | −1 | ||
| 1 | 1 | −1 | 1 | 1 | −1 | −1 | −1 | 1 | ||
| 2 | 2 | 2 | −1 | −1 | −1 | 0 | 0 | 0 | ||
| 2 | 2 | −2 | −1 | −1 | 1 | 0 | 0 | 0 | ||
| 2 | −1 | 0 | 2 | −1 | 0 | 2 | −1 | 0 | ||
| 2 | −1 | 0 | 2 | −1 | 0 | −2 | 1 | 0 | ||
| G | 4 | −2 | 0 | −2 | 1 | 0 | 0 | 0 | 0 | |
| E | ||||||
| (16)(24)(34) | ||||||
| (15)(26)(34) | ||||||
| (153426) | ||||||
| (162435) | ||||||
| (143624) | ||||||
| (152634) | ||||||
| (163524) | ||||||
| (142536) | ||||||
| (123) | (23)(56) | |||||
| (13)(46) | ||||||
| (12)(45) | ||||||
| (152436) | (12)(46) | |||||
| (142635) | (23)(45) | |||||
| (162534) | (13)(56) | |||||
| (163425) | (13)(45) | |||||
| (153624) | (12)(56) | |||||
| (143526) | (23)(46) |
| Transformed | Transformed | G(EM) Generator | G Generator |
|---|---|---|---|
| (123)(456) | |||
| (132)(456) | |||
| c | (14)(26)(35)() | ||
| (14)(25)(36)() | |||
| K | |
|---|---|
| 0 (J even) | |
| 0 (J odd) | |
| (K even) | |
| (K odd) | |
| (K even) | |
| (K odd) | |
| (K even) | |
| (K odd) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mellor, T.M.; Yurchenko, S.N.; Mant, B.P.; Jensen, P. Transformation Properties under the Operations of the Molecular Symmetry Groups G36 and G36(EM) of Ethane H3CCH3. Symmetry 2019, 11, 862. https://doi.org/10.3390/sym11070862
Mellor TM, Yurchenko SN, Mant BP, Jensen P. Transformation Properties under the Operations of the Molecular Symmetry Groups G36 and G36(EM) of Ethane H3CCH3. Symmetry. 2019; 11(7):862. https://doi.org/10.3390/sym11070862
Chicago/Turabian StyleMellor, Thomas M., Sergei N. Yurchenko, Barry P. Mant, and Per Jensen. 2019. "Transformation Properties under the Operations of the Molecular Symmetry Groups G36 and G36(EM) of Ethane H3CCH3" Symmetry 11, no. 7: 862. https://doi.org/10.3390/sym11070862
APA StyleMellor, T. M., Yurchenko, S. N., Mant, B. P., & Jensen, P. (2019). Transformation Properties under the Operations of the Molecular Symmetry Groups G36 and G36(EM) of Ethane H3CCH3. Symmetry, 11(7), 862. https://doi.org/10.3390/sym11070862






