Abstract
This paper is concerned with the design of an improved El-Gamal cryptosystem based on chaos synchronization. The El-Gamal cryptosystem is an asymmetric encryption algorithm that must use the public and private keys, respectively, in the encryption and decryption processes. However, in our design, the public key does not have to appear in the public channel. Therefore, this proposed improved El-Gamal cryptosystem becomes a symmetric-like encryption algorithm. First, a discrete sliding mode controller is proposed to ensure the synchronization of master and slave chaotic systems; next, a novel improved El-Gamal cryptosystem is presented. In the traditional El-Gamal cryptosystem, the public key is static and needs to be open which provides an opportunity to attack. However, in this improved design, due to the chaos synchronization, the public key becomes dynamic and does not appear in public channels. As a result, drawbacks of long cipher text and time-consuming calculation in the traditional El-Gamal cryptosystem are all removed. Finally, several performance tests and comparisons have shown the efficiency and security of the proposed algorithm.
1. Introduction
With the rapid progress being made in science and internet technologies, the security requirement for information confidentiality is continually increasing. Against this backdrop, many theories, including chaos theory [1], have been used to address such information security issues. Chaos properties, such as broadband noise-like waveform, which depend sensitively on the system’s precise initial conditions (Butterfly effect) have been generally studied and these properties offer some advantages for solving and enhancing information security issues [2,3,4,5]. Another method is symmetric key encryption and public key encryption in modern cryptography. The common algorithms include RSA [6], El-Gamal [7], and ECC [8] among others [9,10]. In addition, the existant cryptographic systems are growing in number and diversity, and many reports have proposed improved encryption algorithms. However, operation speed is a neglected issue in proposed encryption topics. Therefore, in this paper, we will discuss the problems encountered in existing cryptosystems, and then design an improved El-Gamal cryptosystem based on chaotic synchronization in order to solve these problems.
So far, the El-Gamal encryption algorithm is still a popular public-key encryption algorithm. Its security depends upon the discrete logarithm difficult problem. However, in 2014, Wu [11] pointed out that the El-Gamal encryption algorithm has some shortcomings including its long cipher text and the time-consuming calculation. Many studies have proposed to propose the improved versions of the El-Gamal algorithm. The ElGamal-like [12,13] encryption methods enhance the complexity by adding exclusive operations; the MCEA [14] method defines the new element and uses the dual modulus to increase its complexity. Although the above methods can enhance the overall security, the speed is much slower than the traditional El-Gamal encryption system. Thus, it cannot solve the heavy operation problems.
Motivated by the aforementioned observations, we will discuss the synchronization controller design in master-slave chaotic systems, then use the random dynamic and unpredictable characteristics of synchronized chaotic signals to propose an improved El-Gamal cryptosystem. In this design, the random positive integers generated by the random synchronized chaotic signals do not appear in the public channel. Since we can obtain these random and dynamic keys at the transmitter and receiver by chaos synchronization, the long key is no longer necessary to resist attack in this improved algorithm. Thus, this proposed improved El-Gamal cryptosystem can balance speed and security.
The rest of this paper is organized as follows: In Section 2, we first formulate the problem of chaos synchronization. The discrete sliding mode controller (DSMC) design for synchronization of chaotic systems and the experimental simulations are proposed. In Section 3, we introduce traditional El-Gamal cryptosystem and our proposed cryptosystem and perform preliminary validation. In Section 4, we analyze the performance of the proposed cryptosystem and compare it with other methods. Finally, conclusions are presented in Section 5.
2. Problem Formulation of Chaos Synchronization
In this paper, we consider the design of an improved El-Gamal cryptosystem based on the chaos synchronization. Before constructing the improved El-Gamal algorithm, the first problem undertaken here is to solve the synchronization problem of master-slave chaotic systems. Now we first aim to propose a DSMC to solve the chaos synchronization problem. The discrete Lorenz system considered in this paper is directly introduced from the discrete-time dynamics of UCS (unified chaotic systems) with and sample time [15]. In fact, the DSMC approach developed in this paper can also be applied to other discrete chaotic systems, including lower/higher order ones, as long as the controller can be modified to achieve synchronization. To simplify our discussion, we consider the following master and slave discrete Lorenz systems.
Master discrete Lorenz system:
Slave discrete Lorenz system:
where and are the state variables of the master and slave systems, respectively. is the control input to ensure the synchronization between the master and slave systems.
To achieve the synchronization control, we define the error state as:
According to (1)–(3), we can obtain the dynamic equation of the error system as follows:
Form the error dynamics (4), it is clear that the problem of chaos synchronization is to discuss the stabilization problem of the system (4). As mentioned above, the aim of this work is firstly to propose a discrete controller u(k) such that the state error response of the given master (1) and slave (2) chaotic systems is stable. Accordingly, to achieve the control goal based on the DSMC technique, we need to construct an appropriate switching surface for the error dynamics (4) to result in a stable sliding motion. That is,
Then, we need to design a DSMC law which can guarantee the attraction of the sliding manifold. Now, we begin to discuss the design of the switching surface and the sliding mode synchronization controller. First, we select the switching surface as follows:
where and is the chosen parameter to satisfy . Therefore, when the system enters the sliding mode, , we have
Since is selected to satisfy , so will converge to zero, and because during the sliding motion , then will also converge to zero, and from (4c), we can find when converges to zero, the system will degenerate to ; therefore, will converge to zero, that is, the system can reach chaos synchronization.
In order to make the error system (4) successfully enter the sliding mode, , the sliding mode controller design is as follows:
where
Theorem 1:
In order to guarantee the occurrence of the sliding manifold, we consider the chaotic system as shown in (1) and (2), and the control input designed as shown in (8) and (9). The state trajectory will converge to and remain in the sliding mode. However, the state response of the master and slave systems will be synchronized.
Proof:
Using (4), (6) and (8), we have
From (10), we can obtain , and because is selected satisfying , we can ensure that the system will enter the sliding mode, . Also the state response of the master and slave systems will be synchronized as discussed above. ☐
In the following, we give an example to demonstrate the effectiveness of the proposed control method. The simulation tool of MATLAB is used. In the simulation test, first, the initial conditions are selected as . Then, is chosen such that . Therefore, the switching surface, , can be designed as follows:
At the same time, the controller can be designed as follows:
The simulation results are shown in Figure 1, Figure 2, Figure 3 and Figure 4. Figure 1 shows the state responses of master and slave systems corresponding to the proposed control inputs in (12). It shows that the master and slave systems can reach synchronization. Furthermore, Figure 2 and Figure 3, respectively, show the response of the error state and switching surface simulated by the system with the controller (12). In addition, the control input response is shown in Figure 4. From the simulation results, it can be observed that the master–slave system state is quickly controlled and enters sliding mode, , while the master–slave chaotic system error, as expected, converges to zero, and reaches synchronization.
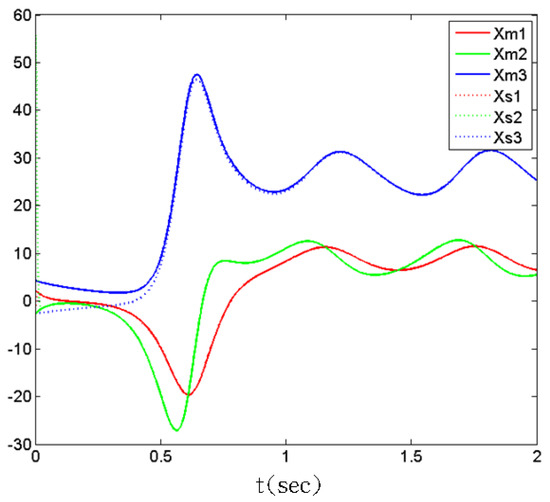
Figure 1.
State responses of master and slave chaotic systems, .
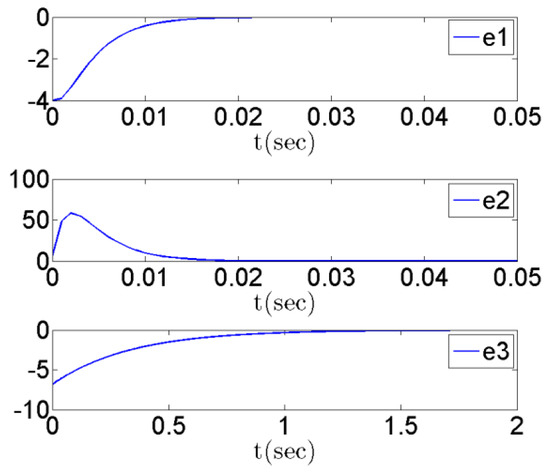
Figure 2.
State responses of error systems e(k), .
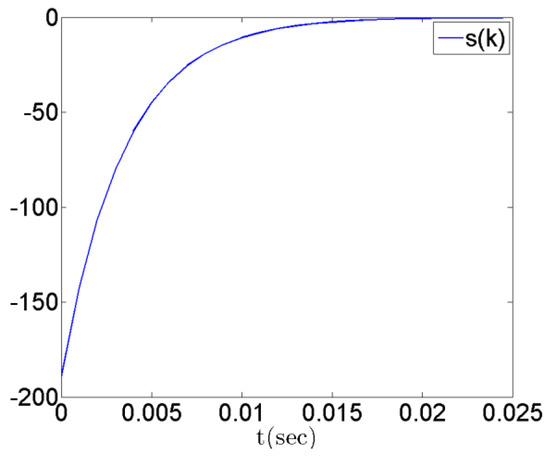
Figure 3.
Time response of switching surface s(k), .
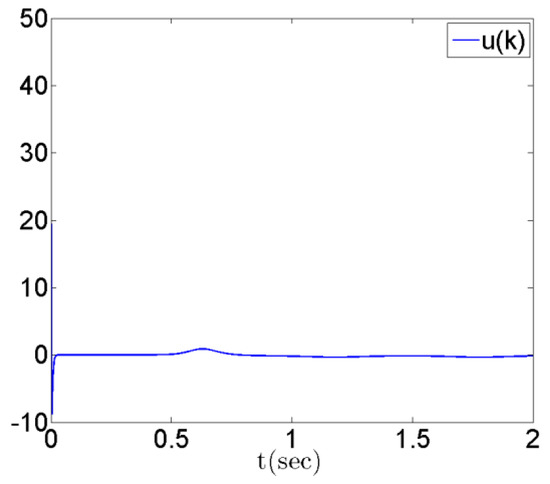
Figure 4.
Time response of discrete sliding mode controller u(k), .
After solving the synchronization problem of chaos systems, in the following, we will introduce the improved El-Gamal cryptosystem based on chaos synchronization.
3. The Design of Improved El-Gamal Cryptosystem
As is well known, El-Gamal encryption is one of the most famous public key cryptosystems. Its security depends on the discrete logarithm problem in Diffie-Hellman key exchange [16]; however, in [11], Wu points out that El-Gamal encryption algorithm has some shortcomings, including its long cipher text and the time-consuming calculation. Many studies in [12,13,14] show the problems of security and speed cannot be improved together. However, in this improved design, we firstly synchronize the master and slave chaotic systems in the transmitter (master system) and the receiver (slave system). Then, according to these synchronized random dynamic signals, the transmitter and the receiver simultaneously generate the same random dynamic positive integer and hidden public key. In addition, the hidden public key is dynamic and not necessary to be public in the public channel. Furthermore, the receiver can advance-calculate the dynamic private key, that improves the long cipher text and time-consuming calculation and increases its security. Before formulating the improved cryptosystem in detail, we briefly introduce the traditional and proposed El-Gamal encryption algorithms.
3.1. Traditional El-Gamal Encryption Algorithm
The main property of the El-Gamal asymmetric encryption algorithm, as shown in Figure 5, is in the operation process; it uses the different public key and private key for data encryption and decryption. Where the public key is used for encryption processing, the private key is used for decryption processing. The public key is open and private key is kept by individuals. In this paper, we will turn the public key further into dynamic private key or invisible public key based on the chaos dynamic synchronization. The encryption method of the traditional El-Gamal encryption algorithm [4] is as follows:
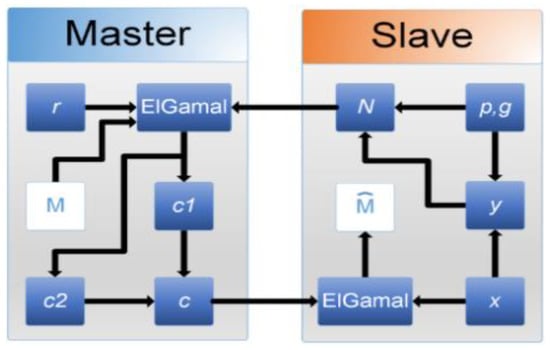
Figure 5.
Traditional El-Gamal architecture.
First, the public key and the private key are defined by steps 1–5:
Step 1: Get a random prime number , (Let be a cyclic multiplicative group)
Step 2: Calculate in finite domain and get generator (The results of must be different from each other)
Step 3: Select private key
Step 4: Calculate public key
Step 5: Let be the public key of the receiver, then adopt as the private key of the receiver.
After completing the definition of the public and the private key, the encryption and decryption algorithms are defined as steps 6–8:
Step 6: Select plaintext , and select random positive integer
Step 7: Encryption function: ciphertext , we could get ciphertext by calculating and
Step 8: Decryption function: plaintext , we could get plaintext by calculating
As shown in Figure 5, the traditional El-Gamal algorithm needs to generate the prime number , the primitive roots , and the private key , and the public key , by the slave system and then form the public key , and transmit to the master system. However, the ciphertext can be obtained by computing the plaintext , the public key , and the random positive integer at the master system. Then, the ciphertext will be sent to the slave system by the master system and use private key and the public key , and finally, we obtain the recovered plaintext through the decryption computation. In addition, it can be seen that the encryption signal of the El-Gamal algorithm includes a random positive integer , so that it has a random characteristic. That is, the same plaintext can be encrypted to generate many kinds of cipher text.
3.2. The Improved El-Gamal Encryption Algorithm
As mentioned, Wu [11] demonstrated that the method of attack resistance is to require the key of a sufficient length; at the same time, to operate encryption and decryption easily, we must choose the key of shorter length. In practice, the key of longer length can actually resist attack but will slow the encryption speed, as well as the long ciphertext and the time-consuming calculation and other issues in the traditional El-Gamal algorithm. Thus, in this paper, we will improve the El-Gamal algorithm. We remove the public key in the public channel to avoid the factorization concerning the public key Consequently, it is along with reducing the length of the ciphertext to improve the integral operation speed and ensure the security of El-Gamal. The random positive integers in this proposed improved El-Gamal algorithm is generated by the synchronization of master and slave chaotic systems. Its encryption and decryption process is shown in Figure 6.
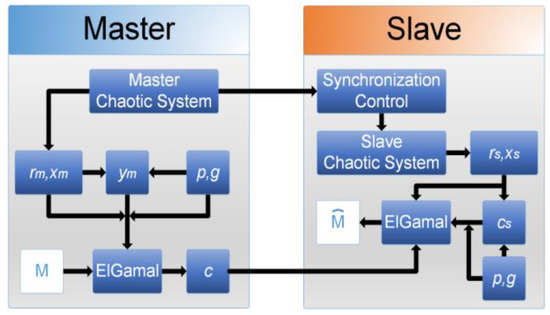
Figure 6.
Improved El-Gamal architecture.
The master-slave chaotic systems are synchronized by the synchronization controller presented in Section 2. Hence, the transmitter and receiver can simultaneously obtain the same random signal by the master-slave chaotic system. However, the El-Gamal algorithm requires two positive integers as encryption and decryption parameters, but the random signal generated by the chaotic system belongs to the floating-point number and cannot immediately obtain a positive integer. Therefore, in the master-slave system, we will use the numerical correction mechanism-that is, first amplify its signal and then take the absolute value so that we can achieve the purpose of eliminating the floating-point number of the random signal. Obviously, the master-slave chaos system can get the same random signals after synchronization, which are defined as and , respectively. In addition, other related parameters left can be obtained based on the traditional El-Gamal way, so the public key does not have to appear on the public channel and prevent the probability of being attacked, but also to achieve high-security features. Thus, the encryption and decryption function of the improved El-Gamal algorithm are given as follows:
- Encryption function: ,
- Decryption function: ,
where , , , , are random positive integers obtained by the numerical correction mechanism for the master-slave chaotic random signal, is the dynamic private key, and is the invisible public key. Since the synchronization controller is designed, we can ensure synchronization of the master-slave chaotic systems-that is, and . Therefore, the master and slave systems can dynamically generate the same key and make sure that in encryption and decryption processes.
Here, we use an example to test the above preliminary results. In the simulation test, the parameters are defined as , where are random positive integers obtained by the numerical correction mechanism for the master-slave chaotic random signal, are calculated by the above formula, and then the original signal , into the encryption function to obtain the encrypted signal , and finally, we will operate the decryption function to obtain the recovered signal , as shown in Figure 7, Figure 8 and Figure 9.
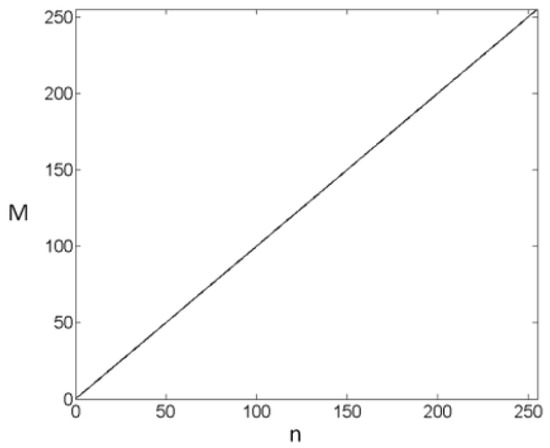
Figure 7.
Original signal M.
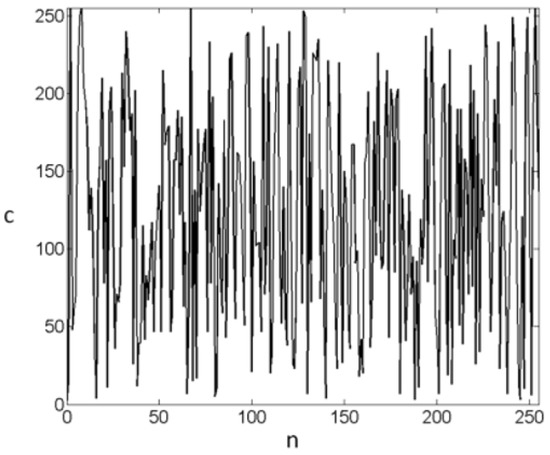
Figure 8.
Encrypted signal c.
Figure 9.
Recovered signal
From the above results in the simulation of the MATLAB platform, it proves that the inference method and the result of improved El-Gamal cryptosystem are feasible.
4. Performance Analysis
Experimental results are given to demonstrate the performance of the proposed cryptosystem. In the following performance analysis, the algorithm is performed on grayscale images. The different security tests are used to assess the performance such as visual effect, statistical analysis (NIST test), histogram, and encryption speed. Furthermore, two asymmetric cryptosystems, the traditional RSA [6] and El-Gamal [7] encryptions, are also tested for comparison.
4.1. Visual Effect of Encrypted Images
For a good algorithm, the visual effect analysis is indispensable; here we will encrypt the grayscale image of the size . Results are shown in Figure 10 and compared with the traditional RSA [6] and El-Gamal [7] encryptions. Where Figure 10a is the original Lena image, Figure 10b is the traditional RSA encrypted image, Figure 10c is the traditional El-Gamal encrypted image, and Figure 10d is the improved El-Gamal encrypted image. Figure 10 reveals that the encrypted image of the improved El-Gamal algorithm by our proposed method is the same as that of the traditional El-Gamal and RSA encryption, and all the encrypted images can achieve the visual effect of random noise images.

Figure 10.
(a) Original image and encrypted image; (b) RSA (c) El-Gamal (d) Improved El-Gamal.
4.2. Statistical Analysis
Although the previous section initially completed the visual assessment, in order to more accurately assess the randomness of encrypted images, we encrypt the grayscale image of the size , and then use the National Institute of Standards and Technology (NIST) [17] test suite to test the randomness of the encrypted image. In the NIST test, first, we set the test parameters including the sequences length bit, the number of subsequences, . Then, we use the encryption images of the improved El-Gamal and traditional El-Gamal and RSA to test the randomness. Finally, all the test results are shown in Table 1. In Table 1, the outcome of the test value is called the p value. When the then it passes the test. We say the randomness test pass if the . From Table 1, we can find that RSA only passes 10 tests because its public and private key are fixed, and then because of El-Gamal and improved El-Gamal have dynamic characteristics so pass all tests. However, we find that the p values in our approach are almost greater than the traditional El-Gamal. This means that our proposed algorithm has good randomness and can effectively resist the statistical attack. Therefore, we can conclude that the improved El-Gamal approach has better randomness than traditional El-Gamal and RSA.

Table 1.
Randomness test.
4.3. Histogram Analysis
The histogram with uniform distribution is the ideal target for image encryption, so we will analyze the histogram of image encryption in this section. Figure 11 shows the histograms of the original image and images encrypted by using algorithms of traditional RSA, traditional El-Gamal, and improved El-Gamal. It can be seen that the pixel values of Figure 11b–d are distributed between 0-255, close to the ideal uniform distribution. Furthermore, we use the chi-square test [18] to analyze the uniformity of the pixel value distribution. Then, the chi-square statistics value , of the image distribution with 256 degrees of freedom is defined as follows:
where is the cumulative number of gray values, , and is the expected cumulative number of each gray value. Table 2 shows the chi-square statistics values of the original image and encrypted image. However, we can know that the chi-square value is when in an assuming significance level of . For our proposed image encryption algorithm, the chi-square statistics is less than . Therefore, its distribution is uniform and its result better than those of other encryption methods.
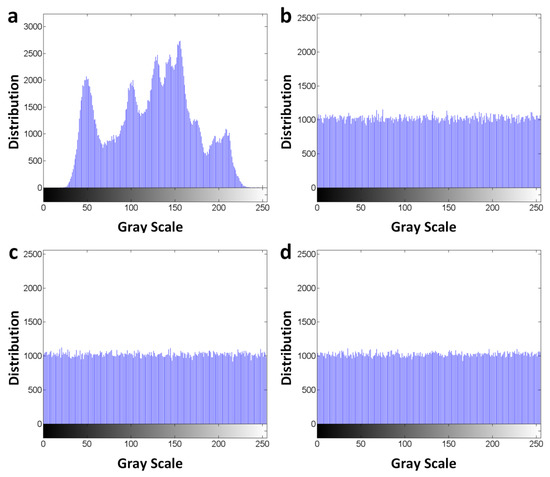
Figure 11.
(a) Histograms of the original image and the encrypted images, (b) RSA (c) El-Gamal (d) Improved El-Gamal.

Table 2.
Values of the original and encrypted images.
4.4. Speed Analysis
In this section, the speed analysis of image encryption is tested by using the Microsoft Visual Studio 2012 (C++) software-programming on a computer with 2.70 GHz Intel(R) Core(TM) i5-6400 CPU and 8G memory and uses some gray-scale images of different sizes to test computing time. Two algorithms are tested in this analysis and use the same method to encrypt the image, following the steps below. First, each pixel of the image is mapped to a sequence, and then encrypts its pixel and stores it in the new sequence. The test results are given in Table 3. It shows that our proposed algorithm is faster than the traditional algorithm because the length of the ciphertext of the improved algorithm is equal to that of the plaintext, which effectively solves the issue of long ciphertext of the traditional algorithm and then improves the integral operation speed.

Table 3.
Encrypted time of El-Gamal and Improved El-Gamal algorithms (in sec).
5. Conclusions
This paper proposes an improved El-Gamal cryptosystem based on chaotic synchronization. In this design, the traditional El-Gamal public key is hidden and does not appear in public channels in order to ensure that the possibility of attack can be reduced to zero. Therefore, not only can El-Gamal’s security features be retained, but the security of the traditional El-Gamal cryptosystem is significant;y promoted. Several tests, including visual effect, statistical analysis, histogram analysis and speed analysis have shown the efficiency and security of the proposed algorithm. From the performance analysis and comparison of results, we can conclude that the improved El-Gamal algorithm has better performance than other algorithms.
Author Contributions
All authors contributed to the paper. P.-Y.W. wrote the manuscript with the supervision from T.-L.L., J.-J.Y. and H.-H.T. are responsible for the design of the improved El-Gamal cryptosystem.
Funding
This work was financially supported by the Ministry of Science and Technology, Taiwan, under MOST-107-2221-E-366-002-MY2.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y.; Pun, C.M.; Chen, C.P. 2D Sine Logistic modulation map for image encryption. Inf. Sci. 2015, 297, 80–94. [Google Scholar] [CrossRef]
- Lin, J.S.; Huang, C.F.; Liao, T.L.; Yan, J.J. Design and implementation of digital secure communication based on synchronized chaotic systems. Digit. Signal Process. 2010, 20, 229–237. [Google Scholar] [CrossRef]
- Ye, G.; Huang, X. A feedback chaotic image encryption scheme based on both bit-level and pixel-level. J. Vib. Control. 2015, 22, 1171–1180. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y. An image encryption algorithm based on balanced pixel and chaotic map. Math. Probl. Eng. 2014, 216048, 7. [Google Scholar] [CrossRef]
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM. 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Elgamal, T. A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Trans. Inf. Theory. 1985, 31, 469–472. [Google Scholar] [CrossRef]
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Cheng, C.Y.; Lin, I.C.; Huang, S.Y. An RSA-Like Scheme for Multiuser Broadcast Authentication in Wireless Sensor Networks. Int. J. Distrib. Sens. Netw. 2015, 11, 743623. [Google Scholar] [CrossRef]
- Zhang, C.; Luo, Y.; Xue, G. A new construction of threshold cryptosystems based on RSA. Inf. Sci. 2016, 363, 140–153. [Google Scholar] [CrossRef]
- Wu, Z.; Su, D.; Ding, G. ElGamal algorithm for encryption of data transmission. In Proceedings of the IEEE 2014 International Conference on Mechatronics and Control (ICMC), Jinzhou, China, 3–5 July 2014. [Google Scholar]
- Chang, T.Y.; Hwang, M.S.; Yang, W.P. Cryptanalysis on an improved version of ElGamal-like public key encryption scheme for encrypting large message. Informatica 2012, 23, 537–562. [Google Scholar]
- Lee, W.B.; Wu, C.C.; Tsaur, W.J. A novel deniable authentication protocol using generalized ElGamal signature scheme. Inf. Sci. 2007, 177, 1376–1381. [Google Scholar] [CrossRef]
- Sharma, P.; Sharma, S.; Dhakar, R.S. Modified Elgamal Cryptosystem Algorithm (MECA). In Proceedings of the IEEE 2011 2nd International Conference on Computer and Communication Technology (ICCCT), Allahabad, India, 15–17 September 2011. [Google Scholar]
- Yan, J.J.; Chen, C.Y.; Tsai, J.S.H. Hybrid chaos control of continuous unified chaotic systems using discrete rippling sliding mode control. Nonlinear Anal. Hybrid Syst. 2016, 22, 276–283. [Google Scholar] [CrossRef]
- Diffie, W.; Hellman, M.E. New directions in cryptography. IEEE Trans. Inf. Theory. 1976, 22, 644–654. [Google Scholar] [CrossRef]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; Booz-Allen and Hamilton Inc.: Mclean, VA, USA, 2001. [Google Scholar]
- Lancaster, H.O.; Seneta, E. Chi-Square Distribution; Wiley & Sons: New York, NY, USA, 1969. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).