The Quantum Yang-Baxter Conditions: The Fundamental Relations behind the Nambu-Goldstone Theorem
Abstract
1. Introduction
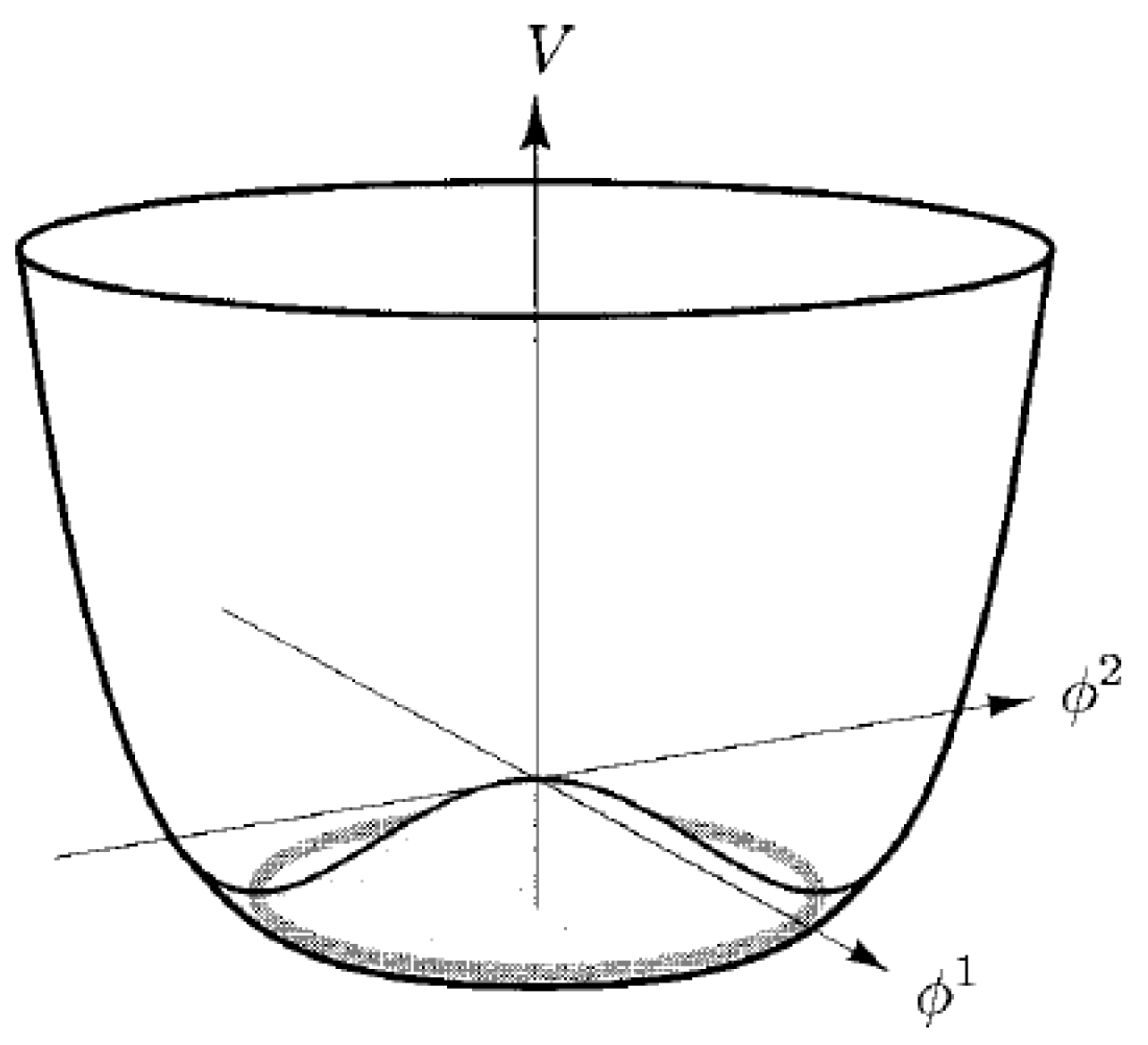
2. Spontaneous Symmetry Breaking: The Linear Model
2.1. The Nambu-Goldstone Theorem: Standard Counting Rule
2.2. Charge Conservation
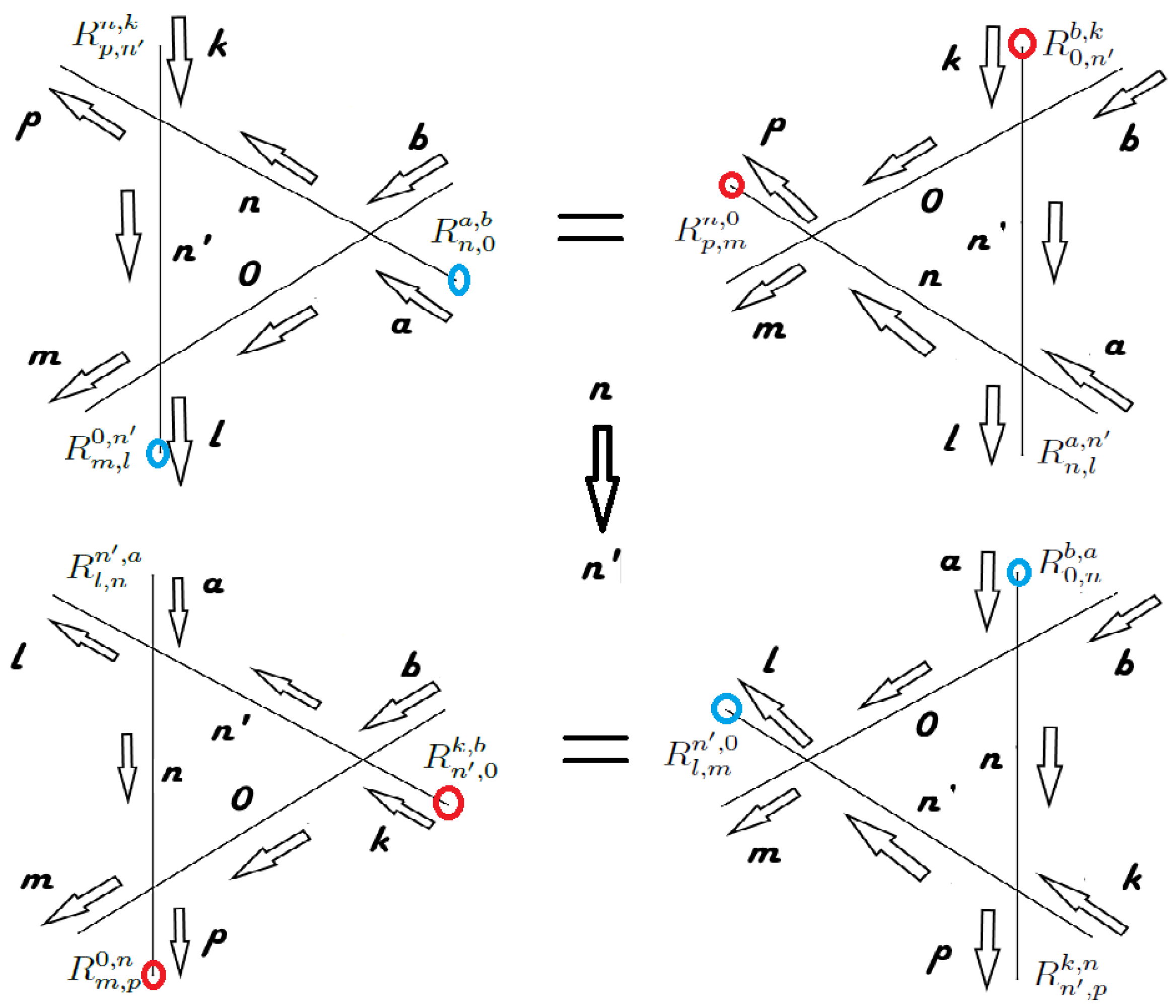
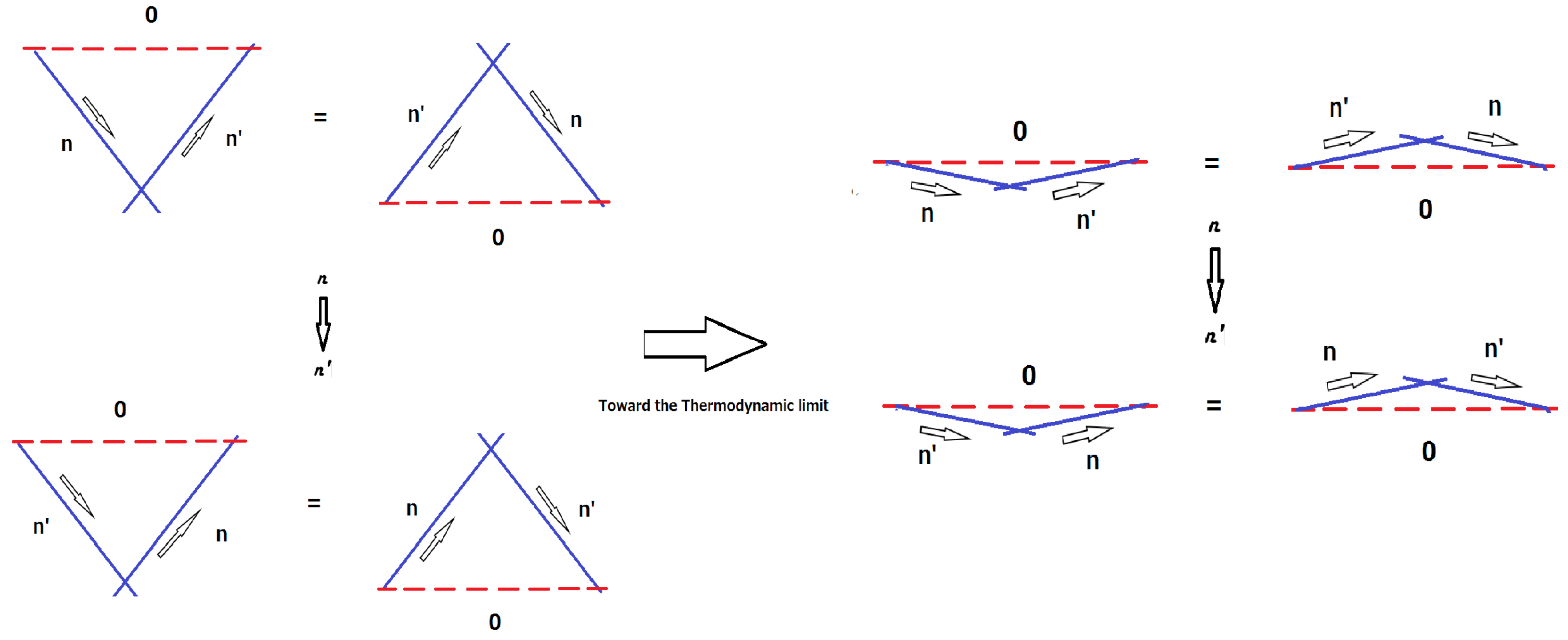
3. The Quantum Yang-Baxter Conditions
3.1. The Relations between the Order Parameter and the Conserved Charges
Exchange of the Intermediate Particles
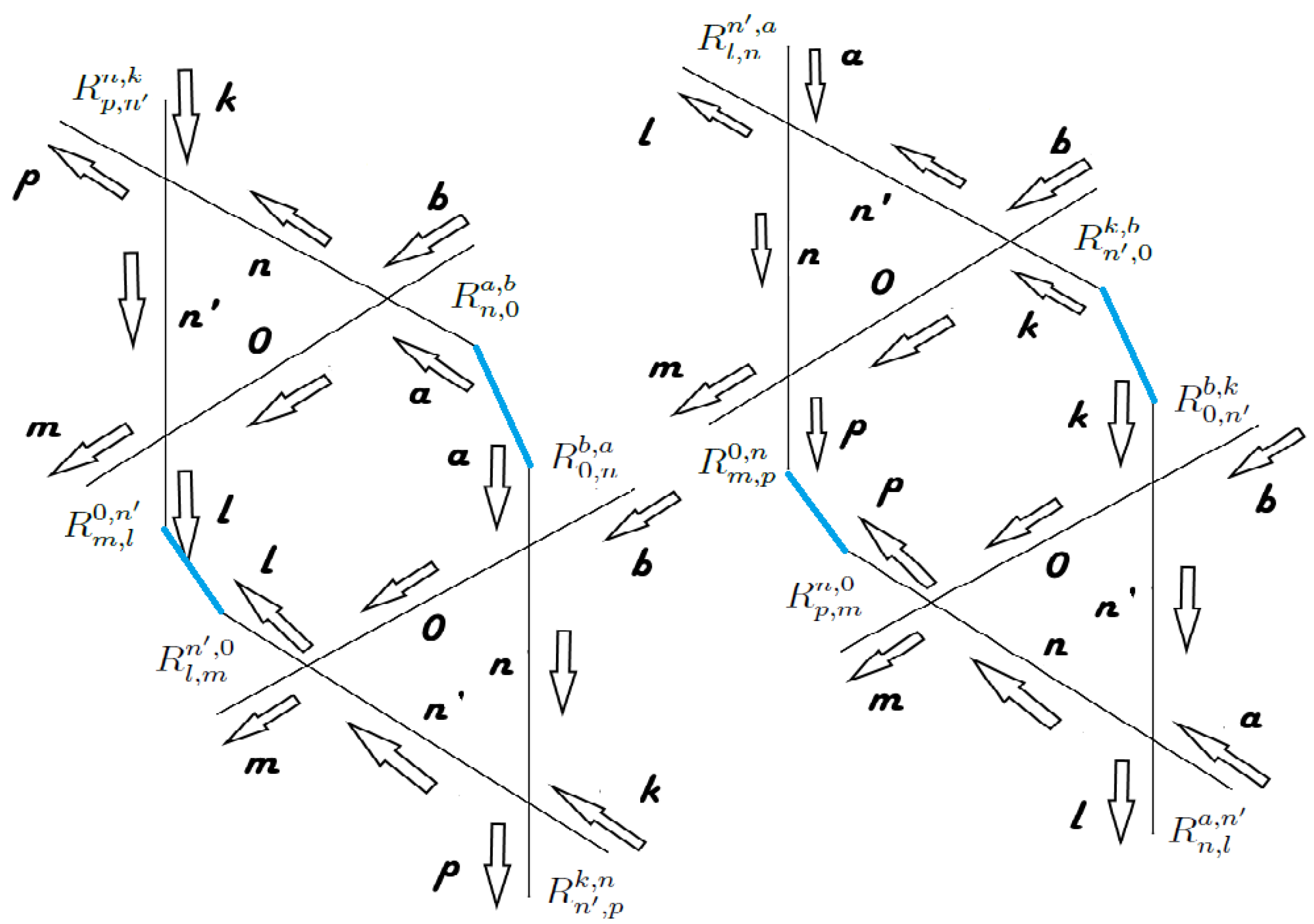
4. The Spontaneous Symmetry Breaking Condition and the Yang-Baxter Relations
4.1. Pairs of Nambu-Goldstone Bosons Representing the Same Degree of Freedom
4.2. Pairs of Nambu-Goldstone Bosons Independent
5. The Counting of Nambu-Goldstone Bosons Based on the Yang-Baxter Relations
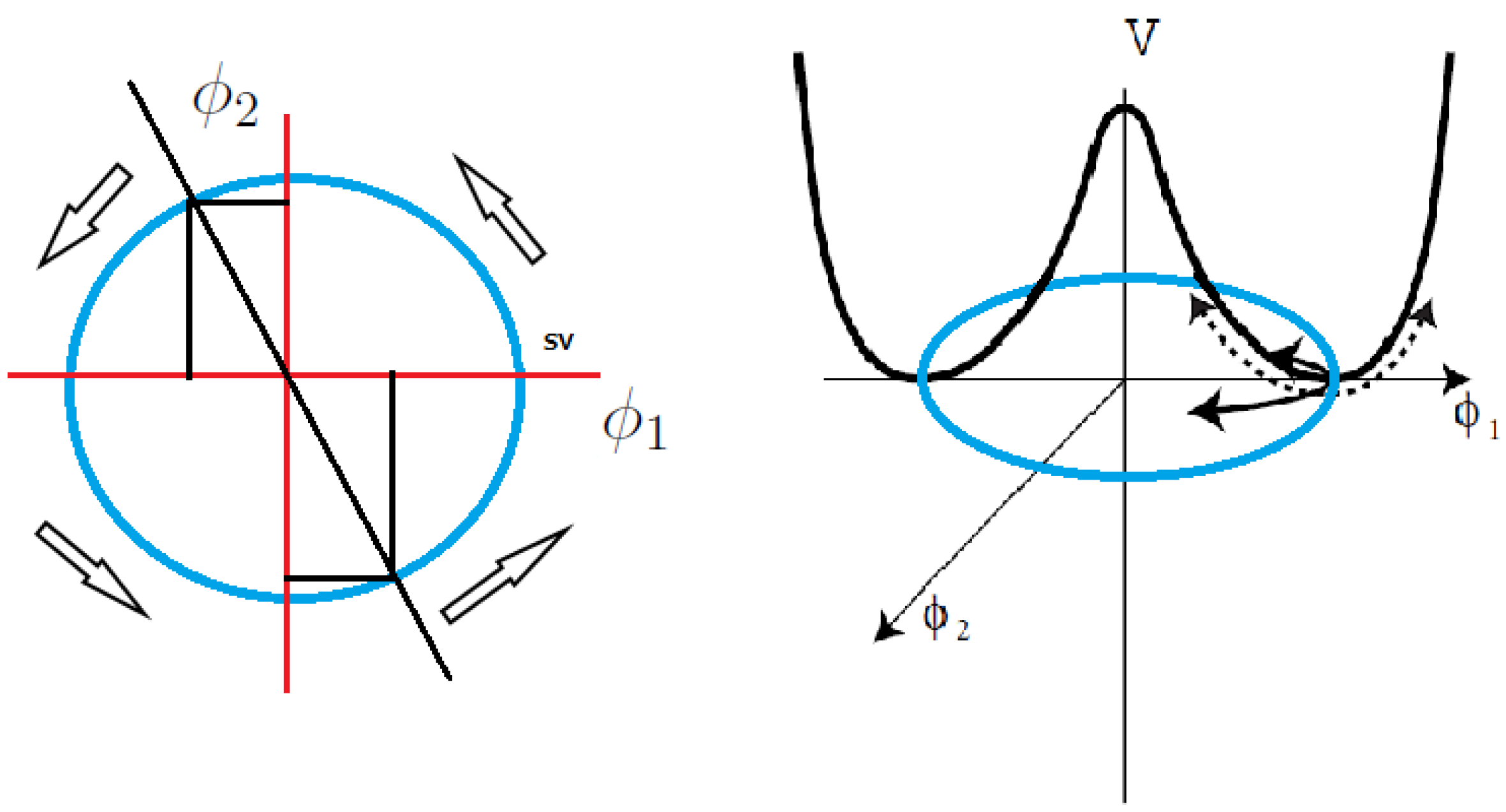
6. Sum of Vacuums and Theorems Connected with the Spontaneous Symmetry Breaking Phenomena
6.1. The Justification behind the Sum over the Vacuums
Further Justifications of the Sum over the Degenerate Vacuum
6.2. The Theorems Contained inside the Yang-Baxter Relations
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. I. Phys. Rev. 1961, 122, 345. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical model of elementary particles based on an analogy with superconductivity. II. Phys. Rev. 1961, 124, 246. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of superconductivity. Phys. Rev. 1957, 108, 1175. [Google Scholar] [CrossRef]
- Valatin, G. Comments on the theory of superconductivity. Il Nuovo Cimento 1958, 7, 843–857. [Google Scholar] [CrossRef]
- Bogoliubov, N.N. A New method in the theory of superconductivity. I. J. Exp. Theor. Phys. 1958, 34, 58. [Google Scholar] [CrossRef]
- Nambu, Y. Nobel Lecture: Spontaneous symmetry breaking in particle physics: A case of cross fertilization. Rev. Mod. Phys. 2009, 81, 1015. [Google Scholar] [CrossRef]
- Nambu, Y. Axial Vector Current Conservation in Weak Interactions. Phys. Rev. Lett. 1960, 4, 380. [Google Scholar] [CrossRef]
- Nambu, Y. Quasi-Particles and Gauge Invariance in the Theory of Superconductivity. Phys. Rev. 1960, 117, 648. [Google Scholar] [CrossRef]
- Nambu, Y.J. From Yukawa’s Pion to spontaneous symmetry breaking. J. Phys. Soc. Jpn. 2007, 76, 111002. [Google Scholar] [CrossRef]
- Anderson, P.W. Coherent excited states in the theory of superconductivity: Gauge invariance and the Meissner effect. Phys. Rev. 1958, 110, 827. [Google Scholar] [CrossRef]
- Englert, F.; Brout, R. Broken symmetry and the mass of gauge vector mesons. Phys. Rev. Lett. 1964, 13, 321. [Google Scholar] [CrossRef]
- Higgs, P.W. Broken symmetries and the masses of gauge bosons. Phys. Rev. Lett. 1964, 13, 508. [Google Scholar] [CrossRef]
- Higgs, P.W. Spontaneous symmetry breakdown without massless bosons. Phys. Rev. 1966, 145, 1156. [Google Scholar] [CrossRef]
- Weinberg, S. A model of leptons. Phys. Rev. Lett. 1967, 19, 1264. [Google Scholar] [CrossRef]
- Salam, A. Elementary Particles; Svartholm, W., Ed.; Almquist and Wiksell: Stockholm, Sweden, 1968; p. 367. [Google Scholar]
- Nielsen, H.B.; Chadha, S. On how to count Goldstone bosons. Nucl. Phys. B 1976, 105, 445–453. [Google Scholar] [CrossRef]
- Nambu, Y. Spontaneous Breaking of Lie and Current Algebras. J. Stat. Phys. 2004, 115, 7–17. [Google Scholar] [CrossRef]
- Watanabe, H.; Brauner, T. Number of Nambu-Goldstone bosons and its relation to charge densities. Phys. Rev. D 2011, 84, 125013. [Google Scholar] [CrossRef]
- Watanabe, H.; Brauner, T. Spontaneous breaking of continuous translational invariance. Phys. Rev. D 2012, 85, 085010. [Google Scholar] [CrossRef]
- Watanabe, H.; Murayama, H. Redundancies in Nambu-Goldstone Bosons. Phys. Rev. Lett. 2013, 110, 181601. [Google Scholar] [CrossRef]
- Watanabe, H.; Murayama, H. Effective Lagrangian for nonrelativistic systems. Phys. Rev. X 2014, 4, 031057. [Google Scholar] [CrossRef]
- Gongyo, S.; Karasawa, S. Nambu-Goldstone bosons and the Higgs mechanism without Lorentz invariance: Analysis based on constrained-system theory. Phys. Rev. D 2014, 90, 085014. [Google Scholar] [CrossRef]
- Hama, Y.; Hatsuda, T.; Uchino, S. Higgs mechanism with type-II Nambu-Goldstone bosons at finite chemical potential. Phys. Rev. D 2011, 83, 125009. [Google Scholar] [CrossRef]
- Yanagisawa, T. Nambu-Goldstone Bosons Characterized by the Order Parameter in Spontaneous Symmetry Breaking. J. Phys. Soc. Jpn. 2017, 86, 104711. [Google Scholar] [CrossRef]
- Bethe, H. On the theory of metals. 1. Eigenvalues and eigenfunctions for the linear atomic chain. Z. Phys. 1931, 71, 205. [Google Scholar] [CrossRef]
- Faddeev, L.D. How algebraic Bethe ansatz works for integrable model. arXiv 1996, arXiv:hep-th/9605187. [Google Scholar]
- Minahan, J.A. Review of AdS/CFT Integrability, Chapter I.1: Spin Chains in N=4 Super Yang-Mills. Lett. Math. Phys. 2012, 99, 33–58. [Google Scholar] [CrossRef]
- Jimbo, M. Introduction to the Yang-Baxter equation. Int. J. Mod. Phys. A 1989, 4, 3759–3777. [Google Scholar] [CrossRef]
- Witten, E. Integrable lattice models from gauge theory. arXiv 2016, arXiv:1611.00592. [Google Scholar] [CrossRef]
- Costello, K. Supersymmetric gauge theory and the Yangian. arXiv 2013, arXiv:1303.2632. [Google Scholar]
- Blaschke, D.; Ebert, D.; Klimenko, K.G.; Volkov, M.K.; Yudichev, V.L. Abnormal number of Nambu-Goldstone bosons in the color-asymmetric dense color superconducting phase of a Nambu-Jona-Lasinio-type model. Phys. Rev. D 2004, 70, 014006. [Google Scholar] [CrossRef]
- Lenz, F.; Griesshammer, H.W.; Stoll, D. Lectures on QCD: Applications; Springer Nature Switzerland AG: Basel, Switzerland, 1997. [Google Scholar]
- Peskin, M.; Schroeder, D. An Introduction to Quantum Field Theory; CRC Press: Boca Raton, FL, USA, 2018; p. 669. [Google Scholar]
- Ryder, L.H. Quantum Field Theory; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Lambe, L.A.; Radford, D.E. Introduction to the Quantum Yang-Baxter Equation and Quantum Groups: An Algebraic Approach; Originally Published by Kluwer Academic Publishers in 1997; Springer Science+Business Media: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Brauner, T. Spontaneous symmetry breaking and Nambu-Goldstone bosons in Quantum Many-Body systems. Symmetry 2010, 2, 609–657. [Google Scholar] [CrossRef]
- Miransky, V.A. Dynamical Symmetry Breaking in Quantum Field Theories; World Scientific: Singapore, 1993. [Google Scholar]
- Englert, F. A brief course in Spontaneous Symmetry Breaking II. Modern Times: The BEH Mechanism. arXiv 2002, arXiv:hep-th/0203097. [Google Scholar]
- Arraut, I. The origin of the mass of the Nambu-Goldstone bosons. Int. J. Mod. Phys. 2018, A33, 1850041. [Google Scholar] [CrossRef]
- Arraut, I. The Nambu-Goldstone theorem in non-relativistic systems. Int. J. Mod. Phys. 2017, A32, 1750127. [Google Scholar] [CrossRef]


© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arraut, I. The Quantum Yang-Baxter Conditions: The Fundamental Relations behind the Nambu-Goldstone Theorem. Symmetry 2019, 11, 803. https://doi.org/10.3390/sym11060803
Arraut I. The Quantum Yang-Baxter Conditions: The Fundamental Relations behind the Nambu-Goldstone Theorem. Symmetry. 2019; 11(6):803. https://doi.org/10.3390/sym11060803
Chicago/Turabian StyleArraut, Ivan. 2019. "The Quantum Yang-Baxter Conditions: The Fundamental Relations behind the Nambu-Goldstone Theorem" Symmetry 11, no. 6: 803. https://doi.org/10.3390/sym11060803
APA StyleArraut, I. (2019). The Quantum Yang-Baxter Conditions: The Fundamental Relations behind the Nambu-Goldstone Theorem. Symmetry, 11(6), 803. https://doi.org/10.3390/sym11060803



