Abstract
Sustainable and efficient development is one of the most critical challenges facing modern society if it wants to save the world for future generations. Airports are an integral part of human activity. They need to be adapted to meet current and future sustainable needs and provide useful services to the public, taking into account prospects and requirements. Many performance criteria need to be assessed to address issues that often conflict with each other and have different units of measurement. The importance of the criteria to evaluate the effectiveness of alternatives varies. Besides, the implementation of such decisions has different—not precisely described in advance—effects on the interests of different groups in society. Some criteria are defined using different scales. Stakeholders could only evaluate the implemented project alternatives for efficiency throughout the project life cycle. It is essential to find alternative assessment models and adapt them to the challenges. The use of hybrid group multi-criteria decision-making models is one of the most appropriate ways to model such problems. This article presents a real application of the original model to choose the best second runway alternative of the airport.
Keywords:
multiple criteria decision making; MCDM; transport; sustainable; airport; runway; hybrid; MULTIMOORA. 1. Introduction
In recent decades, scientists have devoted much attention to researching transport and logistics issues. Research reflects the growing awareness of sustainability among stakeholders and helps develop appropriate administrative ideas and guidelines for sustainable development [1,2]. Quality infrastructure and industrial base are two of the essential factors in the efficient operation of transport systems. A fuzzy set is a methodological concept of knowledge that people use worldwide to explore possible medium-sized samples of discrete alternatives with a tool that works well for decision makers [3,4]. This method allows researchers to work with many examples of discrete options. Private investors rarely take into account several objective criteria and usually make decisions based on subjective factors. Such projects are local and meet the priorities of a particular country’s transport policy. Developing cities face enormous pressure to transport infrastructure, which has a significant impact on economic activity in these cities [5,6]. Ližbetin [5] focuses on the research of the terminal network.
Standard cost–benefit analysis does not indicate significant economic consequences. It does not answer the question of who will benefit and who will lose [7]. Wang et al. [8] presented the reasons and the complex model of land use for transport purposes to assess the broader economic impacts of transport infrastructure projects. Semanjski and Gautama [9] stressed that cities are firmly based on efficient urban logistics to make them attractive for quality living and economic development. They proposed an extended multi-criteria decision-making method with the ability to integrate the views of different stakeholders and assess the costs associated with sustainability and the spatial context of the route. Moretti et al. [10] stated that transport infrastructure is a way of survival. There are three significant impacts of climate change on transport systems: infrastructure, transport operations and transport demand. The strategy developed or implemented to prevent the adverse effects of climate change on transport infrastructure has such important objectives: avoiding losses, protecting structures, controlling and reporting to consumers. It is useful for intelligent transport systems such as Automated Traffic Management, Passenger Information Systems, Early Warning Systems and Security Alerts.
The transport sector is a significant source of environmental noise and continues to make a considerable contribution (almost a quarter) to Europe’s greenhouse gas emissions. The development of sustainable vehicles and infrastructure systems can help to move towards sustainable mobility, reduce oil consumption and reduce greenhouse gas emissions from transport. Bigerna et al. [11] defined several variable conditions using the fuzzy, qualitative contrast analysis of data. The integration of economic, ecological and social factors at the same time in one business success assessment model is very rare [12,13]. Bajec and Tuljak-Suban [14] have proposed a unified Analytic Hierarchy Process (AHP) and Data Envelopment Analysis model (DEA) based on the assumption of unwanted performance criteria assessed on the scale of logistics service providers. Balbaa et al. [15] argued that increasing environmental pollution encourages researchers to find other clean, renewable energy [16] sources or to manage available sources optimally. Carlan et al. [17] have shown that using different vehicle types allow the combination of transport tasks with worldwide travel and reduces operating costs by 25–35% and carbon emissions by 34–38%. Innovation contributes to the development of sustainable transport. It is essential for stakeholders to undertake modernization and innovation processes [18] since they will enable them to incorporate additional value to its market offer and will increase their international competitiveness [19].
Nosal Hui et al. [20] demonstrated the possibility of using a Simple Additive Weighting approach (SAW) [21] to assess European and national policies in the field of transport, taking into account their impact on the use of innovation in the market. Lopez et al. [22] focused on exploring how technological innovations adopted by public transport companies can increase urban sustainability. They used a hierarchical analysis of importance (IPA), a AHP, to report the impact on ecology and social sustainability.
Cargo and passenger transport are an essential criterion in economic development, which encourages the mobility of persons. Paddeu et al. [23] highlighted that traffic flows in urban areas do not only have benefits but also have negative externalities such as environmental, social and transport activities. Moreover, passenger and freight transport safety are one of the critical criteria [24]. This criterion is more important than travel time or cost.
Airports are one of the critical elements of regional development. They have a substantial impact on regional development [25]. The effects of local development include features such as human capital and the use of high-tech industrial products. The higher the number of airport terminals, the faster the economic and prosperity growth in the region, contributing to population growth and welfare [25]. Airports are one of the essential elements of the international transport system, which has become an integral part of many people’s journeys throughout the world and becomes one of the main ones [26].
Vilnius Airport has reached the maximum design capacity of passenger flows, which affects not only traffic safety but also the further economic and social development of the country. Airport capacity depends on many criteria, including the location of runways, space availability, the ability to manage traffic flows at peak traffic volumes, and access to meteorological stations [27]. The best alternatives to airport development must be identified and ensure the safest movement of all traffic participants within the airport’s internal (person) area when developing the airport in harmony with the region needs.
The main parameters of the runway are the wind direction and speed but also include other criteria: meteorological conditions, traffic demand, adjacent airport flows, and adverse weather conditions, instruments of the flight rules, departure restrictions, environmental standards, overhead runways, distance between tracks, airspace constraints, procedural constraints (noise reduction), route layout, traffic in terminal access, and other criteria [27].
Scientific literature shows that the assessment and implementation of airport development and traffic safety measures are multi-criteria, discrete optimization tasks, all of which are very inaccurate. Many modern economic phenomena are uncertain. Meanwhile, decision makers usually treat them as precisely defined. Fuzzy logic is the right tool for modelling inaccurate, ambiguous and vague events [28,29].
2. Materials and Methods
Zadeh [30] offered a fuzzy set theory to define such problem-solving models. Many researchers use different Multi-Criteria Decision-Making (MCDM) methods and differently control target alternatives [31,32,33]. This fact justifies the use of several ways to determine the values of options and integrate them for the alternative’s multi-attribute utility function. Besides, the weights of the criteria are usually defined using different methods selected from the set of methods available to assess the importance of rules. Hybrid approaches are best suited to solve similar problems [34,35].
Decision making in groups is finding the best choice among many possible alternatives. The main problem is how to combine multiple input data into the separate representative product [36,37].
If the fuzzy data are available for the input and output variables system, then several rule blocks are useful to create several methods of creating method blocks [38]. Fuzzy relation summarizes the concept of classical relationships, which makes it possible to partially associate elements of the universe of discourse [39]. Triangular fuzzy sets are the essential models of membership classes as only three parameters fully define them. The semantics are apparent because the fuzzy sets are expressed based on knowledge of the concept spreads and their typical values. A linear change in membership level is the simplest membership model. The derivative of the triangular membership function could be used as a measure of sensitivity. When a derivative of a membership triangle function is a measure of sensitivity, its sensitivity is constant for each linear segment of the fuzzy set [40]. Changing fuzzy sets and adjusting their membership functions could change the semantics of fuzzy sets. Therefore, by allowing the various intensities of the association, we get a much more relevant mathematical model of the problem. Since Zadeh [30] established fuzzy sets, they developed rapidly. However, the inadequacy of fuzzy sets is because a fuzzy set only has a membership degree, and it cannot cope with some complex fuzzy information. Atanassov [41] later introduced the intuitionistic fuzzy set.
Nonetheless, in practical problems, the intuitionistic fuzzy set also has limitations; it cannot handle information that is between truth and falsity. Atanassov and Gargov extended the membership degree and non-membership degree to interval numbers and offered the interval-valued intuitionistic fuzzy set to explain information that is within the limits of truth and falsity [42]. Turksen [43] provided interval-valued fuzzy sets, which also used the membership degree and the non-membership degree to describe determinacy and indeterminacy. However, in certain circumstances, the membership degree and non-membership degree cannot express fuzzy information clearly. Therefore, Smarandache [44] introduced neutrosophic sets by increasing a hesitation degree to describe the difference between the membership degree and non-membership degree [45].
The objectives of sustainable development models are the involvement of innovative research tools, the analysis of urban development, the dynamics, ecology, and optimization of urban systems, carrying capacity and social needs [46,47,48]. Urban sustainability MCDM models could be a useful forecasting tool for evaluating trends in a developing city and for assisting decision makers to focus on finding, assessing and selecting best environmental development strategies [49,50].
Concerning problems, decision making aims at:
- The development of a flexible MCDM model that helps decision makers to choose the best alternative based on a set of parameters for specific problem-solving goals;
- The hybrid group MCDM model to select the most effective choice of the second runway of the airport approach for the planning of strategy.
The use of land for urban development is a specific MCDM problem with fuzzy and changing conditions, factors, and objectives of sustainability [51,52,53,54]. The solution model reflects a set of criteria that are important for local-specific state policy priorities, situations and values, for measuring and guiding future development trends.
Irving Fischer (1867–1947) and other early economists developed a concept of the Highest or Best Use. Property land use developers should use the three-step analysis to determine maximum land use potential, including asset analysis, property rights and limitations analysis, as well as market analysis (including future developments). The exact definition of the highest and best use is different, but, usually, the request should be:
- The law permits it (only alternatives that are allowed or may be allowed by law may be potentially applied);
- Physically feasible (depending on plot size, shape, topography, and other features);
- Financially sound (the efficient and best use of assets must be economically viable, use of the building must ensure an adequate income to justify construction costs and investor returns, the remaining economic life is evident; in the case of growth, the issue of commercial viability becomes the most problematic issue of local use);
- The logic of rational use: content and procedure, macro and micro, long-term and short-term effects.
The primary purpose of all multi-criteria methods is to formalize, find, and capture trade-offs between interest criteria. Multi-criteria optimization aims in determining the best feasible solution according to the requirements representing different effects. Multi-criteria decision processes are distinguished along with several aspects.
Franklin [55], de Condorcet [56], Edgeworth [57], and Pareto [58,59] were pioneers in multi-criteria decision making. Pareto (1848–1923)—Italian engineer, economist, and philosopher—presented the concept of Pareto efficiency and helped develop microeconomic science. Pareto Efficiency or Pareto Optimization is a state of non-redistributable selected resources to facilitate a particular person or preference criterion, while not compromising on at least one person or preference criterion. Pareto efficiency is a minimal concept of optimality that does not necessarily lead to a socially desirable distribution of resources. He says nothing about equality or the welfare of the whole society. It is a statement that it is not possible to change the value of a single variable without altering the other variables in the multi-objective optimization (Pareto Optimization) task. Because there is no essential information about permissible compromises among decision makers, these methods only provide a compromise curve (also known as Pareto optimal solutions). Then, the decision maker can choose the desired point, reflecting his approach to the compromise curve.
The first decision-making axioms were formed by Ramsey in 1931 [60]. Later, von Neumann and Morgenstern introduced the Theory of Games and Economic Behavior [61]. Keeney, Raiffa [62], Dyer, and Sarin [63] developed the multi-attribute preference function theory. Algorithmic thinking and model building in MCDM provides a contemporary, and one of the most attractive cross-disciplinary research approaches in science and Operations Research for explaining certain kinds of human behavior and decision making [64,65,66]. Zionts [67] focused on the applications of MCDM and started popularizing the acronym "MCDM". MCDM methods include two classes of methods, namely, continuous and discrete ways, based on the nature of the possible choices. Continuous Multi-Objective (Multi-Targeted) Decision-Making (MODM) approaches are methods to determine the best (optimal) value of a Multi-Objective Utility function that can acquire infinitely multiple values in a decision space of the concerned problem. Discrete MCDM methods or Multi-Attribute Decision-Making methods (MADM) are decision-aiding (decision-support)-based processes that determine the best choice between the finite number of predetermined alternatives, preferences, and tradeoffs among attributes (goals) or to estimate possible options and sort them by preference (Figure 1). A constructed multi-attribute preference function [68] is based on the elicited information. Discrete approaches are subdivided into weighting methods and ranking ways. Empirical MCDM techniques continue to be used, and their application to different problems expanded in recent decades.
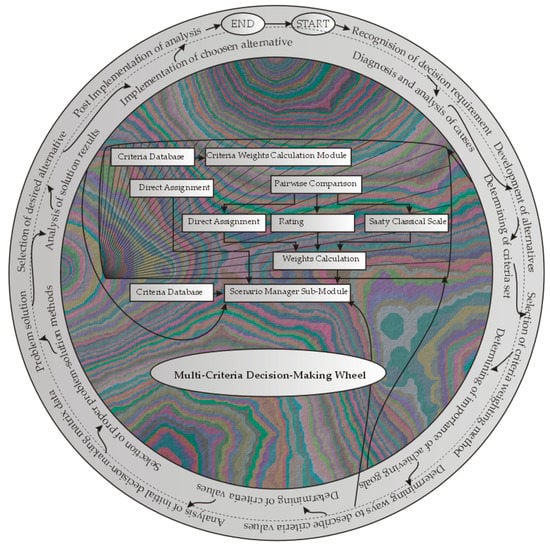
Figure 1.
Multi-criteria decision-making wheel.
The AHP (Analytic Hierarchy Process) encourages the adoption of sustainability concepts in urban development plans, which are very different and, therefore, jeopardize the idea of local balance. The AHP facilitates stakeholder groups to determine the relevance of the factors to be assessed and to integrate their decisions. To this end, it uses a well-grounded geometric mean and relative weighting ratio 9-point scale (one means equal importance and nine means extreme importance) procedures. Other types of scale related to the relative importance of the criteria, called nominal, ordinal or interval scale, may also be used. The results are similar to those obtained with Saaty’s 9-point scale. The systematic measurement and comparison of the importance of pairs of criteria is the basis for methods such as AHP [69] or SWARA (Step-wise Weight Assessment Ratio Analysis) [70] to determine the relative importance of criteria. There are many different subjective approaches for this reason: AHP [69], ANP [71], expert judgement method [72], SWARA [70,73], FARE (FActor RElationship) [74], etc. In 1965, Eckenrode [75] compared the efficiency of six methods (Ranking [76,77], Rating [75], Partial Paired Comparisons I [78], Partial Paired Comparisons II, Complete Paired Comparisons [79], and Successive Comparisons [80]) in collecting the judgment data and found no significant differences among the techniques. The values calculated by all of the methods correlates.
Decision makers developed hybrid procedures that combine the strategies of the three classes of methods described. The following information could be the basis for different classification schemes:
- The results of problem solutions—known or unknown;
- The consequences occurrence period—one or more;
- The number of alternatives—finite or infinite;
- The alone decision maker or group of decision makers;
- The indirectly assessed and modelled competitive response.
Strategic Decisions and Strategic Decision Making
Decision makers need to assess many uncertain factors when making strategic decisions. Implemented strategic projects have long-term consequences. They require a lot of money and natural resources to implement. Strategic solutions need alignment with the facts that stakeholders will face in a future reality.
Technical Complexity
The two most significant and most demanding challenges in solving strategic decisions are the specific levels of high uncertainty and complexity of solutions. It is difficult to decide whether real life needs a new project. It may be difficult to assess whether a project is successful or not because the project has not been implemented before. This uncertainty means that there is a lack of detailed knowledge of the impact of the project’s external environment on the functioning of potential strategies. Another source of risk arises when doubts arise as to what strategic goals or policy values should lead to a decision or choice of action.
The strategic implementation of the decisions will require many resources in various fields, such as marketing, finance, operations, research and development. The study of the interrelationship between these choices is a necessary part of such possessions.
Social Complexity
Strategic decision making is a social discourse and a complicated process through which leaders understand their strategic concerns and can act on them. A group of stakeholders discuss solutions in various written reports, speeches, letters to shareholders or informal conversations. Strategic seminars usually involve a group of executives representing critical organizational stakeholder groups that form the structure for the solution problem. Different interpretations of questions are the basis for understanding the problem and cognitive conflicts. Negotiations help to resolve disputes and create a collective mental foundation of the decision.
3. Problem-Solving Model
Many of the multi-criteria methods of decision aiding can be used to solve the problem. The choice of decision makers among these models depends on the objectives of the task, the type of initial data describing these goals, the type of decision makers, the groups of people interested in the decision, the timeliness of collecting data, time-honored decision makers, skills, and qualifications. As competition augments and technological differentiation becomes a design that is more difficult, precisely what is referred to as industrial design offers an efficient way to solve free market problems [81]. Usually, many interrelated economic, technological, ecological and social factors influence the various areas of project selection.
Some of the MADM techniques suffer from significant shortcomings [82]. It is the motivation of investigators to invent and adopt the new algorithms [83,84]. Zavadskas et al. [85] merged two different MCDM methods and introduced an original Weighted Aggregated Sum-Product assessment method (WASPAS), while the innovative combination of three different MCDM methods was introduced as a new Multiple Objective Optimization on the basis of Ratio Analysis Plus Full Multiplicative Form (MULTIMOORA) method [86,87]. Construction is slow to innovate. Choosing effective technological systems in a building is a complex, multi-criteria task. Zavadskas et al. [87] integrated six MCDM methods to assess the feasible options of construction technologies by using six MCDM methods: the ELECTRE III, ELECTRE IV, TOPSIS, VIKOR, SWARA, and MULTIMOORA. Later, Turskis and Juodagalvienė [88] presented a novel approach to solve complicated construction engineering problems based on ten MCDM methods: Game Theory, AHP, SAW, MEW (Multiplicative Exponential Weighting), TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution), EDAS (Evaluation based on Distance from Average Solution), ARAS (Additive Ratio Assessment), Full Multiplicative form, Laplace Rule, and Bayes Rule. Hashemi et al. [33] presented the group decision model based on grey-intuitionistic fuzzy-ELECTRE (ELimination Et Choix Traduisant la REalité (ELimination and Choice Expressing REality)) and VIKOR (Vlsekriterijumska Optimizacija I KOmpromisno Resenje).
In this study, the authors chose the fuzzy extension of the MULTIMOORA method (Figure 2). Brauers and Zavadskas [89] introduced a Multi-Objective Optimization by Ratio Analysis (MOORA) technique. Its anatomy is not complicated and so permits one to arrive at a final solution faster. The utilization of the MOORA is broad and covers various disciplines and industries [90,91]. In 2010, Brauers and Zavadskas extended the MOORA method with the purely multiplicative utility function [85]. It became a robust MULTIMOORA method (MOORA plus the full multiplicative form). In 2011, Brauers et al. [92] extended the MULTIMOORA method with fuzzy numbers.
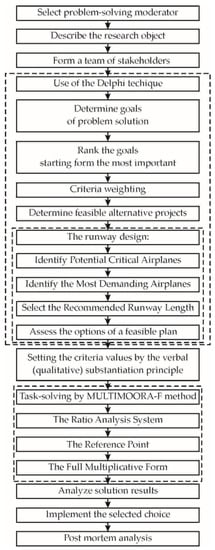
Figure 2.
Graphical structure of approach to solve the challenge.
3.1. Research object
Vilnius Airport (IATA: VNO, ICAO: EYVI) is the international airport of Vilnius, the capital of Lithuania. It is 7 km to south of the City Centre. It is the largest airport in Lithuania by passenger traffic (Table 1). The airport began operations in 1932 as Wilno–Porubanek, Porubanek. Today, Vilnius Airport has one runway and approximately 3.8 million passengers a year (Table 2). A state-owned enterprise, Lithuanian Airports manage the airport under the Ministry of Transport and Communications.

Table 1.
Passengers.

Table 2.
Runways.
The characteristics of the aircraft that regularly uses the airport or the future benefits and the type of runway end are the basis for selecting the appropriate standards for airport infrastructure development.
The main stages of the runway design are as follows:
- Identify potential critical airplanes;
- Identify the most demanding airplanes;
- Determine method;
- Select the recommended runway length;
- Describe available alternatives;
- Assess the feasible options and rank them;
- Analyze solution results;
- Implement the selected choice.
The alternative is an intersection of a runway with a planned land plot in the general plan of Vilnius (Figure 3). The other runway position is within the existing territory of the airport. The third alternative represents the location of a new runway, which requires the additional minimal area that is already provided by the general plan of the Vilnius city. The choice offers the possibility of constructing a parallel runway, the implementation of which requires the most significant land plot.
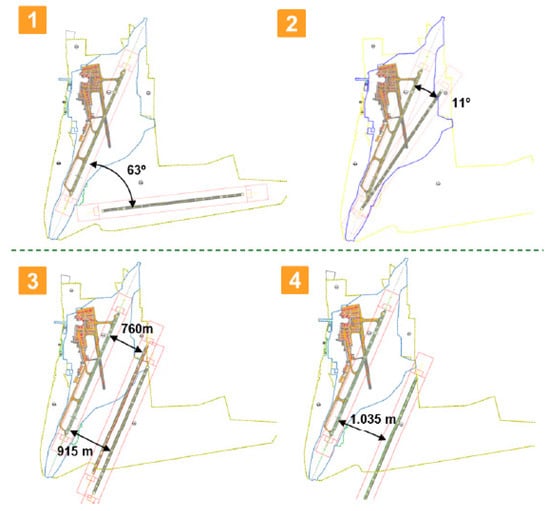
Figure 3.
Investigated four alternatives (1-4) to the second take-off run.
3.2. Setting the Criteria Values
The weighting of the criteria is determined by the verbal substantiation principle, which replaces the verbal (qualitative) estimates with fuzzy numbers according to Table 3 values. The basis of assessment is the following oral assessments: "bad", "satisfactory" and "good". The triangular dependency function is used to describe the work criteria. When each element consists of three numeric values (f1, f2, f3), the graphic (Figure 4) represents it.

Table 3.
Interpreting fuzzy numbers.
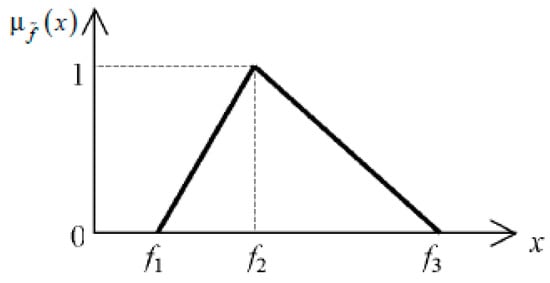
Figure 4.
Fuzzy element , which has a dependency function .
Its function of dependence is as follows:
Table 1 gives an oral rating (expressed in numbers).
The experts selected and evaluated the survey criteria according to the guidelines of the International Vilnius Airport Long-term Development Plan [93]. (Table 4).

Table 4.
Assessment of alternatives to the second runway.
3.3. Determination of Criteria Weights By Ranking Method
Criteria weights indicate how many times the usefulness (significance) of one criterion is more significant or lower than the next criterion. In this work, estimates of the rankings of experts assigned to the requirements (expert survey method) are the basis to criteria weighting. The experts participating in the expert survey (according to Kendall [94], they must be at least r ≥ 7), according to the importance: one means least importance and nine means extreme importance (Table 5). The higher the rating scale, the more valuable the criteria are, and this reduces the coherence of expert opinions. The precision of the multi-criteria task depends on the applied range of the selected points [95].

Table 5.
Expert judgement and weighting.
An expert survey yields only estimate. The formula determines the average rank rating :
where is an estimate of the expert attributed to the criterion; r—number of experts.
The following formula expresses the significance of the criteria qi:
The coherence of expert judgment is determined using Kendall’s concordance coefficient [94]. Calculated according to the formulas:
where S is the sum of the deviation of the criteria values from the mean squares; Tk – k is the number of related ranks; number of equal grades k; hl—the number of ranks in a group of related ranks, in terms of k expert; the grade assigned to a criterion of an expert; r—the number of experts; n—the number of evaluated criteria.
The study states that there are no related grades so that the following formula determines the concordance coefficient:
A set of values of the coefficient W is [0; 1], 0 ≤ W ≥ 1. The lower the compatibility of expert opinions, the more the coefficient of the concordance coefficient W approaches 0, the more harmonious W approaches 1.
The formula determines the significance of the concordance factor:
If the value of calculated by the last formula is greater than (from the table), the compatibility of expert opinions is acceptable. If these expert opinions are not harmonized.
3.4. Task-Solving by the MULTIMOORA-F Method
Brauers et al. [92] suggested the extension of MULTIMOORA with fuzzy criteria values. This method consists of three parts: a) The Ratio Analysis System of MOORA defines data normalization by comparing alternatives of an objective to all values of the objective; b) The ratio system is the basis for the Reference Point of MOORA; c) Purely multiplicative utility function is the basis for the Full Multiplicative Form. The third part of the MULTIMOORA method helps to avoid subjectivity, as it is not necessary to determine the coefficients of significance (weights) of the criteria here. It is the most sensible alternative to the values of the descriptive measures when compared with other multi-purpose methods.
The first step in the MULTIMOORA-F method is to construct a computable matrix: with element, where is the index of criterion, and is the alternative’s index is the number of considered alternatives, and is number of judgement criteria.
3.4.1. Calculation of Relative Sizes, the Fuzzy Ratio System of the MOORA Method
Output data, having different uncertain units of measure are normalized to non-dimensional sizes. Comparing the values of fuzzy numbers is the basis of normalization.
After normalization, calculate the sum of coefficients yi for each i-th alternative. Normalized values express aggregation or subtraction of fuzzy numbers.
where . —the number of maximized criteria (these criteria values are added). Values of the remaining (minimized) criteria are subtracted. Then every fuzzy number is converted to the best non-fuzzy performance value
3.4.2. The Fuzzy Reference Point Part of the MOORA Method
A ratio system is a basis to report the point of uncertainty. The shortest distance to the reference point is found using the coefficients calculated for Equation (9). Practically, it is very similar to the TOPSIS method in Manhattan City space [53,82] or has week similarity to the EDAS method [4]. The j-th coordinate represents the minimum or maximum of the reference point for the j criterion , where
Then each coefficient of the normalized matrix is recalculated, and the deviation gives the final rank from the reference point, and the alternative rank is determined based on the Tchebycheff metric and the Min–Max method:
3.4.3. Part of the Multiplicative Form of the MOORA Method
Each i - th alternative may include minimization and maximization of the utility function and is expressed by the formula:
where () and () – respectively, the maximized and minimized criterion of the product.
where i = 1, 2, …, g is an index of the maximizing criteria, while i = g+1, g+2, …, n is an index of the minimizing criteria, g is a number of maximizing criteria, and n is a number of criteria.
4. Practical Problem Solving Using the MULTIMOORA-F Method
In particular, a team of experts was formed to solve the problem. Experts have chosen individuals with experience in solving similar problems and a master’s degree in construction engineering.
In the first step of the task, a standard five-step Delphi methodology was applied to identify the most critical evaluation criteria. The efficiency criteria presented in Table 4 were selected. In the second stage of the task, the same experts ranked the requirements according to their importance. It attributes the ranking of criteria and those criteria weights. The experts identified the values of the efficiency criteria describing the alternatives presented in Table 5 (in the initial task solution matrix) using the Delphi methodology. Then, decision makers broadened work on the task according to the methodology given above (3.3.1–3.3.3). The initial model (Table 6) was normalized (Table 7), and then the alternatives were sorted according to the full part of the product (Table 8), the relationship between the Min–Max method (Table 9), and the deviation from the reference point (Table 10). The theory of dominance determines the final ranking of the alternatives (Table 11).

Table 6.
Initial decision matrix.

Table 7.
Normalized decision-making matrix.

Table 8.
Results of the task solution using the complete form of the product.

Table 9.
Weighted and normalized decision-making matrix and results of the task solution using the Min–Max method.

Table 10.
The distance from the point of reference and the result of the decision of the task using the reference point (RP).

Table 11.
The MULTIMOORA method of ranking alternatives: full part of the product form, part of the relationship system, part of the base point, and justification of dominance by theoretical methods of obtaining grades.
Decision makers consider all criteria of the MADM task as independent from each other, and the people making the decisions (experts) are essential in the determination of a set of criteria, values of qualitative measures and the definition of the importance of specific goals of the stakeholders. The development of composite indicators for integrated performance in societies typically relies on a priori assumptions rather than model-free, data-driven evidence [96]. Traditional variable selection processes tend not to consider relatedness and redundancy among variables, instead thinking only of individual correlations. The analysis of sensitivity and uncertainty is one of the complex problems in the application of the MADM models [97]. The majority of discrete optimization (MADM) parameters of a cumulative distribution function are unknown and, in most cases, the decision maker cannot define them. With the advent of advanced estimation techniques, mutual information has become a viable means of characterizing input–output interactions in complex problems. Lüdtke et al. [98] recommend entropy-based sensitivity analysis. The sensitivity analysis in this paper lays the theoretical foundations for an information-theoretic sensitivity analysis that assigns credit or influence to input variables in terms of their overall contribution to a system’s output entropy. It is based on the review of the difference between a change of input data and the results of the multi-attribute utility function [99].
The fuzzy entropy-based sensitivity analysis shows that criterion x2 has the most significant impact on the final solution in this particular matrix (approximately 14%). Criterion x4 and x7 are considered to be in the second and third places to influence the final decision (approximately 12.5% or approximately the same influential as the second criterion). The difference between the most important criterion x2 and the least essential criterion x5 is approximately 4%. Besides, the relative impact of the most important criterion is approximately thirty-five per cent higher than the least influential criterion.
5. Conclusions
The sustainability of urban development is the decision-making process of planning and implementing decisions under a variety of influencing factors in uncertain and dynamically changing conditions. Multi-criteria methods define sustainable development goals. They infringe on the interests of various groups of society in a different way. Knowledge-based agents represent specific urban development situations and determine the relative importance of sustainability issues to the community. Exact numbers cannot describe these purposes. Such tasks have to be fuzzy or intermediate/grey problem-solving models. Relevance or priorities during the negotiation process cover many sustainability criteria and help define sources of conflict and build a mutually acceptable compromise. Many city sustainability models include qualified judgment. The involvement of a community or stakeholder group is a crucial procedural function of the decision-making process, which is considered desirable in models of smart growth or New Urbanism. Interested parties define critical criteria and possible alternatives based on the integrated estimates of density, accessibility, availability and natural resources of the place, and land-use mix. Public attitudes towards regularly defined public policy priorities and the weights of sustainability criteria reflect the importance of stakeholders’ goals achievement in a specific situation reflect the full basis of decision making.
Scientists concluded that the ranks of the alternatives change when using various MCDM methods to determine them.
Airports are an integral part of human activity, and their sustainable development is a critical feature for the modern world. The criteria system has been developed to solve the problem by selecting the following efficiency criteria: —Use with dominant winds, significance ; —Airspace compatibility, ; —Increase in flight field capacity, —Investment need and new infrastructure, ; —Effects on the environment, ; —Noise reduction, ; —Earth demand, ; —Interruptions to construction works, , and —Cost-effectiveness, .
The MULTIMOORA method is one of the most versatile and most applied multi-criteria decision-making methods. Its application has proven to be successful in many decision-making tasks. The MULTIMORA method integrates three different ways to identify alternative rankings. Therefore, it is more reliable than many other approaches.
The results of the calculation indicate the non-uniform priorities distribution of alternatives. According to the theory of calculating the ratio, the other options distribute as follows , while based on the reference point theory: , and according to the complete form of the product: . The method of domination summarizes the results of the task and presents the final line of the alternatives priority, which is as follows (from the most effective to the least efficient): .
Stakeholders selected and successfully implemented the fourth alternative.
The given methodology can be used by selected and competent experts to perform various individual MCDM optimization tasks to find essential objectives, critical criteria, and best-predicted alternatives.
Author Contributions
Z.T. analyzed the literature, developed the research hypothesis, designed the research framework, calculated and wrote the paper. J.A. and V.K. reviewed and edited the paper. G.G. collected the data, analyzed the literature and the data.
Funding
This research received no external funding.
Acknowledgments
We appreciate the valuable comments of reviewers and editors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lee, P.-W.; Kwon, O.K.; Ruan, X. Sustainability Challenges in Maritime Transport and Logistics Industry and Its Way Ahead. Sustainability 2019, 11, 1331. [Google Scholar] [CrossRef]
- Kalibatas, D.; Turskis, Z. Multicriteria evaluation of inner climate by using MOORA method. Inf. Technol. Control 2008, 37, 79–83. [Google Scholar]
- Ziemiańczyk, U.; Krakowiak-Bal, A.; Peszek, A. Sharing of knowledge as a condition of rural area development–fuzzy-set qualitative comparative analysis approach. Contemp. Econ. 2017, 11, 471–478. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.K.; Zavadskas, E.K.; Amiri, M.; Turskis, Z. Extended EDAS method for fuzzy multi-criteria decision-making: An application to supplier selection. Int. J. Comput. Commun. Control 2016, 11, 358–371. [Google Scholar] [CrossRef]
- Ližbetin, J. Methodology for Determining the Location of Intermodal Transport Terminals for the Development of Sustainable Transport Systems: A Case Study from Slovakia. Sustainability 2019, 11, 1230. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Turskis, Z.; Antuchevičienė, J. A new combinative distance-based assessment (CODAS) method for multi-criteria decision-making. Econ. Comput. Econ. Cyber. Stud. Res. 2016, 50, 25–44. [Google Scholar]
- Medineckiene, M.; Zavadskas, E.K.; Björk, F.; Turskis, Z. Multi-criteria decision-making system for sustainable building assessment/certification. Arch. Civ. Mech. Eng. 2015, 15, 11–18. [Google Scholar] [CrossRef]
- Wang, W.; Zhong, M.; Hunt, J.D. Analysis of the Wider Economic Impact of a Transport Infrastructure Project Using an Integrated Land Use Transport Model. Sustainability 2019, 11, 364. [Google Scholar] [CrossRef]
- Semanjski, I.; Gautama, S. A Collaborative Stakeholder Decision-Making Approach for Sustainable Urban Logistics. Sustainability 2019, 11, 234. [Google Scholar] [CrossRef]
- Moretti, L.; Loprencipe, G. Climate Change and Transport Infrastructures: State of the Art. Sustainability 2018, 10, 4098. [Google Scholar] [CrossRef]
- Bigerna, S.; Micheli, S. Attitudes Toward Electric Vehicles: The Case of Perugia Using a Fuzzy Set Analysis. Sustainability 2018, 10, 3999. [Google Scholar] [CrossRef]
- Šaparauskas, J.; Zavadskas, E.K.; Turskis, Z. Selection of facade’s alternatives of commercial and public buildings based on multiple criteria. Int. J. Strateg. Prop. Manag. 2011, 15, 189–203. [Google Scholar] [CrossRef]
- Jankalová, M.; Jankal, R. Sustainability Assessment According to the Selected Business Excellence Models. Sustainability 2018, 10, 3784. [Google Scholar] [CrossRef]
- Bajec, P.; Tuljak-Suban, D. An Integrated Analytic Hierarchy Process—Slack Based Measure-Data Envelopment Analysis Model for Evaluating the Efficiency of Logistics Service Providers Considering Undesirable Performance Criteria. Sustainability 2019, 11, 2330. [Google Scholar] [CrossRef]
- Balbaa, A.; Swief, R.A.; El-Amary, N.H. Smart Integration Based on Hybrid Particle Swarm Optimization Technique for Carbon Dioxide Emission Reduction in Eco-Ports. Sustainability 2019, 11, 2218. [Google Scholar] [CrossRef]
- Štreimikienė, D.; Šliogerienė, J.; Turskis, Z. Multi-criteria analysis of electricity generation technologies in Lithuania. Renew. Energy 2016, 85, 148–156. [Google Scholar] [CrossRef]
- Carlan, V.; Sys, C.; Vanelslander, T. Innovation in Road Freight Transport: Quantifying the Environmental Performance of Operational Cost-Reducing Practices. Sustainability 2019, 11, 2212. [Google Scholar] [CrossRef]
- Sivilevičius, H.; Zavadskas, E.K.; Turskis, Z. Quality attributes and complex assessment methodology of the asphalt mixing plant. Balt. J. Road Bridge Eng. 2008, 3, 161–166. [Google Scholar] [CrossRef]
- Geldres-Weiss, V.V.; Monreal-Pérez, J.; Tornavoi-Carvalho, D.; Tello-Gamarra, J. A new measure of international product innovation. Contem. Econ. 2018, 12, 367–380. [Google Scholar] [CrossRef]
- Nosal Hoy, K.; Solecka, K.; Szarata, A. The Application of the Multiple Criteria Decision Aid to Assess Transport Policy Measures Focusing on Innovation. Sustainability 2019, 11, 1472. [Google Scholar] [CrossRef]
- MacCrimmon, K.R. Decisionmaking Among Multiple-Attribute Alternatives: A Survey and Consolidated Approach; No. RM-4823-ARPA; Rand Corporation: Santa Monica, CA, USA, 1968. [Google Scholar]
- López, C.; Ruíz-Benítez, R.; Vargas-Machuca, C. On the Environmental and Social Sustainability of Technological Innovations in Urban Bus Transport: The EU Case. Sustainability 2019, 11, 1413. [Google Scholar] [CrossRef]
- Paddeu, D.; Fancello, G.; Fadda, P. An experimental customer satisfaction index to evaluate the performance of city logistics services. Transport 2017, 32, 262–271. [Google Scholar] [CrossRef]
- Bureika, G.; Gaidamauskas, E.; Kupinas, J.; Bogdevičius, M.; Steišūnas, S. Modelling the assessment of traffic risk at level crossings of Lithuanian railways. Transport 2017, 32, 282–290. [Google Scholar] [CrossRef]
- Florida, R.; Mellander, C.; Holgersson, T. Up in the air: The role of airports for regional economic development. Ann. Reg. Sci. 2015, 54, 197–214. [Google Scholar] [CrossRef]
- O’Connor, K. Global air travel: Toward concentration or dispersal? J. Trans. Geogr. 2003, 11, 83–92. [Google Scholar] [CrossRef]
- Jones, D.G.; Lenox, M.; Onal, E.; Latorella, K.A.; Lohr, G.W.; Le Vie, L. Graphical User Interface Development and Design to Support Airport Runway Configuration Management; Technical Report; NASA/TM-2015-218806; NASA Langley Research Center: Hampton, VA, USA, 2015.
- Korol, T. The Implementation of Fuzzy Logic in Forecasting Financial Ratios. Contem. Econ. 2018, 12, 165–187. [Google Scholar] [CrossRef]
- Turskis, Z.; Dzitac, S.; Stankiuvienė, A.; Šukys, R. A Fuzzy Group Decision-making Model for Determining the Most Influential Persons in the Sustainable Prevention of Accidents in the Construction SMEs. Int. Comput. Commun. Control 2019, 14, 90–106. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Triantaphyllou, E. Multi-Criteria Decision Making Methods: A Comparative Study; Kluwer: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Turskis, Z.; Lazauskas, M.; Zavadskas, E.K. Fuzzy multiple criteria assessment of construction site alternatives for non-hazardous waste incineration plant in Vilnius city, applying ARAS-F and AHP methods. J. Environ. Eng. Landsc. Manag. 2012, 20, 110–120. [Google Scholar] [CrossRef]
- Hashemi, H.; Mousavi, S.M.; Zavadskas, E.K.; Chalekaee, A.; Turskis, Z. A new group decision model based on grey-intuitionistic fuzzy-ELECTRE and VIKOR for contractor assessment problem. Sustainability 2018, 10, 1635. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Antuchevičienė, J.; Šaparauskas, J.; Turskis, Z. MCDM methods WASPAS and MULTIMOORA: Verification of robustness of methods when assessing alternative solutions. Econ. Comput. Econ. Cyber. Stud. Res. 2013, 47, 5–20. [Google Scholar]
- Zavadskas, E.K.; Antuchevičienė, J.; Turskis, Z.; Adeli, H. Hybrid multiple-criteria decision-making methods: A review of applications in engineering. Sci. Iran. Trans. A Civ. Eng. 2016, 23, 1–20. [Google Scholar]
- Beg, I.; Rashid, T. Group decision making using intuitionistic hesitant fuzzy sets. Int. J. Fuzzy Logic Intell. Syst. 2014, 14, 181–187. [Google Scholar] [CrossRef]
- Tettamanzi, A.; Tomassini, M. Soft Computing: Integrating Evolutionary, Neural, and Fuzzy Systems; Springer: Berlin, Germany, 2001. [Google Scholar]
- Fuzzy Hybrid Computing in Construction Engineering and Management—Theory and Applications; Fayek, A.R., Ed.; Emerald Group Publishing: Bingley, UK, 2018. [Google Scholar]
- Grzegorzewski, P. On Separability of Fuzzy Relations. Int. J. Fuzzy Logic Intell. Syst. 2017, 17, 137–144. [Google Scholar] [CrossRef]
- Pedrycz, W.; Gomide, F. Fuzzy Systems Engineering: Toward Human-Centric Computing; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.; Gargov, G. Interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Turksen, I.B. Interval valued fuzzy sets based on normal forms. Fuzzy Sets Syst. 1986, 20, 191–210. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophy: Neutrosophic Probability, Set, and Logic: Analytic Synthesis & Synthetic Analysis. Available online: https://www.google.com.tw/url?sa=t&rct=j&q=&esrc=s&source=web&cd=3&cad=rja&uact=8&ved=2ahUKEwjF8vj495HgAhUJIIgKHTsxBFEQFjACegQIDxAB&url=https%3A%2F%2Fwww.researchgate.net%2Fpublication%2F266366834_Neutrosophy_Neutrosophic_probability_set_and_logic_Analytic_synthesis_and_synthetic_analysis&usg=AOvVaw38P0cCji8UDaORB1bDykIZ (accessed on 2 January 2019).
- Zhang, H.; Wang, F.; Geng, Y. Multi-Criteria Decision-Making Method Based on Single-Valued Neutrosophic Schweizer–Sklar Muirhead Mean Aggregation Operators. Symmetry 2019, 11, 152. [Google Scholar] [CrossRef]
- Cellura, M.; Beccali, G.; Mistretta, M. A decision support system software based on multi-criteria analysis for the selection of urban sustainability scenarios. In Proceedings of the RIO 02 - World Climate & Energy Event, Rio de Janeiro, Brazil, 6–11 January 2002; pp. 301–308. [Google Scholar]
- Zavadskas, E.K.; Kaklauskas, A.; Turskis, Z.; Kalibatas, D. An approach to multi-attribute assessment of indoor environment before and after refurbishment of dwellings. J. Environ. Eng. Landsc. Manag. 2009, 17, 5–11. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Vilutienė, T.; Turskis, Z.; Šaparauskas, J. Multi-criteria analysis of Projects’ performance in construction. Arch. Civ. Mech. Eng. 2014, 14, 114–121. [Google Scholar] [CrossRef]
- Zagorskas, J.; Zavadskas, E.K.; Turskis, Z.; Burinskienė, M.; Blumberga, A.; Blumberga, D. Thermal insulation alternatives of historic brick buildings in Baltic Sea Region. Energy Build. 2014, 78, 35–42. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Bagočius, V. Multi-criteria selection of a deep-water port in the Eastern Baltic Sea. Appl. Soft Comput. 2015, 26, 180–192. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Govindan, K.; Antuchevičienė, J.; Turskis, Z. Hybrid multiple criteria decision-making methods: A review of applications for sustainability issues. Ekonomska Istraživanja 2016, 29, 857–887. [Google Scholar] [CrossRef]
- Turskis, Z.; Zavadskas, E.K.; Antuchevičienė, J.; Kosareva, N. A hybrid model based on fuzzy AHP and fuzzy WASPAS for construction site selection. Int. J. Comput. Commun. Control 2015, 10, 113–128. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Mardani, A.; Turskis, Z.; Jusoh, A.; Nor, K.M. Development of TOPSIS method to solve complicated decision-making problems—An overview on developments from 2000 to 2015. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 645–682. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Antuchevičienė, J. Selecting a contractor by using a novel method for multiple attribute analysis: Weighted Aggregated Sum Product Assessment with grey values (WASPAS-G). Stud. Inf. Control 2015, 24, 141–150. [Google Scholar] [CrossRef]
- Franklin, B. Letter to Joseph Priestley; Fawcett: New York, NY, USA, 1772; Reprinted in the Benjamin Franklin Sampler, 1956. [Google Scholar]
- De Condorcet, M. Essay on the Application of Analysis to the Probability of Majority Decisions; Bibliotheque National de France: Paris, France, 1785. [Google Scholar]
- Edgeworth, F.Y. Mathematical Psychics: An Essay on the Application of Mathematics to the Moral Sciences; Kegan Paul & Co.: London, UK, 1881. [Google Scholar]
- Pareto, V. Cours d’Économie Politique; Université de Lausanne: Lausanne, Switzerland, 1896; Volume I. [Google Scholar]
- Pareto, V. Manuale di Economia Politica; Società a Editrice Libraria: Milan, Italy, 1906. [Google Scholar]
- Ramsey, F.P. Truth and Probability: The Foundations of Mathematics and Other Logical Essays; Routledge: Abingdon, UK, 2000. [Google Scholar]
- Von Neumann, J.; Morgenstern, O. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1944. [Google Scholar]
- Keeney, R.L.; Raiffa, H. Decisions with Multiple Objectives: Preferences and Value Tradeoffs; John Wiley: New York, NY, USA, 1976. [Google Scholar]
- Dyer, J.S.; Sarin, R.K. Measurable multiattribute value functions. Oper. Res. 1979, 27, 810–822. [Google Scholar] [CrossRef]
- Kochen, M.; MacKay, D.M.; Moran, M.E.; Scriven, M.; Uhr, L. Computers and Comprehension. RAND Memorandum. RM–4065–PR. In The Growth of Knowledge; Kochen, M., Ed.; Wiley: New York, NY, USA, 1967. [Google Scholar]
- Sitorus, F.; Cilliers, J.J.; Brito-Parada, P.R. Multi-criteria decision making for the choice problem in mining and mineral processing: Applications and trends. Expert Syst. Appl. 2018, 121, 393–417. [Google Scholar] [CrossRef]
- Simon, H.A. Theories of decision-making in economics and behavioral science. Am. Econ. Rev. 1959, 49, 253–283. [Google Scholar]
- Zionts, S. MCDM—If not a Roman numeral, then what? Interfaces 1979, 9, 94–101. [Google Scholar] [CrossRef]
- Fishbum, P.C. Utility Theory for Decision Making; John Wiley: New York, NY, USA, 1970. [Google Scholar]
- Saaty, T.L. A scaling method for priorities in hierarchical structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Keršulienė, V.; Zavadskas, E.K.; Turskis, Z. Selection of rational dispute resolution method by applying new step-wise weight assessment ratio analysis (SWARA). J. Bus. Econ. Manag. 2010, 11, 243–258. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision Making with Dependence and Feedback: The Analytic Network Process; RWS Publications: Pittsburgh, PA, USA, 1996. [Google Scholar]
- Zavadskas, E.K.; Vilutienė, T. A multiple criteria evaluation of multi-family apartment block’s maintenance contractors: I—Model for maintenance contractor evaluation and the determination of its selection criteria. Build. Environ. 2006, 41, 621–632. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antuchevičienė, J. An Extended Step-Wise Weight Assessment Ratio Analysis with Symmetric Interval Type-2 Fuzzy Sets for Determining the Subjective Weights of Criteria in Multi-Criteria Decision-Making Problems. Symmetry 2018, 10, 91. [Google Scholar] [CrossRef]
- Ginevicius, R. A new determining method for the criteria weights in multicriteria evaluation. Int. J. Inf. Technol. Decis. Mak. 2011, 10, 1067–1095. [Google Scholar] [CrossRef]
- Eckenrode, R.T. Weighting multiple criteria. Manag. Sci. 1965, 12, 180–192. [Google Scholar] [CrossRef]
- Barrett, M. A comparison of the Order of Merit method and the method of Paired Comparisons. Psychol. Rev. 1914, 21, 278–294. [Google Scholar] [CrossRef]
- Bartlett, C.J.; Heermann, E.; Rettig, S. A comparison of six different scaling techniques. J. Soc. Psychol. 1960, 51, 343–348. [Google Scholar] [CrossRef]
- Buel, W.D. A simplification of Hay’s method of recording paired comparisons. J. Appl. Psychol. 1960, 44, 347–348. [Google Scholar] [CrossRef]
- Bock, R.D.; Jones, L.V. The Measurement and Prediction of Judgemental Response: Statistical Methods; U.S. Army Test and Evaluation Command Project 7-S-0901-OIE; Psychometric Laboratory, University of North Carolina: Chapel Hill, NC, USA, 1963. [Google Scholar]
- Churchman, C.W.; Ackoff, R.L.; Arnoff, E.L. Introduction to Operations Research; Wiley: New York, NY, USA, 1957. [Google Scholar]
- Hashemkhani Zolfani, S.; Zavadskas, E.K.; Turskis, Z. Design of products with both International and Local perspectives based on Yin-Yang balance theory and SWARA method. Ekonomska Istraživanja 2013, 26, 153–166. [Google Scholar] [CrossRef]
- Aouadni, S.; Rebai, A.; Turskis, Z. The Meaningful Mixed Data TOPSIS (TOPSIS-MMD) Method and its Application in Supplier Selection. Stud. Inf. Control 2017, 26, 353–363. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Tamošaitienė, J. Selection of construction enterprises management strategy based on the SWOT and multi-criteria analysis. Arch. Civ. Mech. Eng. 2011, 11, 1063–1082. [Google Scholar] [CrossRef]
- Peldschus, F.; Zavadskas, E.K.; Turskis, Z.; Tamošaitienė, J. Sustainable assessment of construction site by applying game theory. Inzinerine Ekonomika 2010, 21, 223–237. [Google Scholar]
- Zavadskas, E.K.; Turskis, Z.; Antuchevičienė, J.; Zakarevičius, A. Optimization of weighted aggregated sum product assessment. Elektronika ir Elektrotechnika 2012, 122, 3–6. [Google Scholar] [CrossRef]
- Brauers, W.K.M.; Zavadskas, E.K. Project management by MULTIMOORA as an instrument for transition economies. Technol. Econ. Dev. Econ. 2010, 16, 5–24. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Volvačiovas, R.; Kildienė, S. Multi-criteria assessment model of technologies. Stud. Inf. Control 2013, 22, 249–258. [Google Scholar] [CrossRef]
- Turskis, Z.; Juodagalvienė, B. A novel hybrid multi-criteria decision-making model to assess a stairs shape for dwelling houses. J. Civ. Eng. Manag. 2016, 22, 1078–1087. [Google Scholar] [CrossRef]
- Brauers, W.K.M.; Zavadskas, E.K. The MOORA method and its application to privatization in a transition economy. Control Cyber. 2006, 35, 445. [Google Scholar]
- Gou, X.; Liao, H.; Xu, Z.; Herrera, F. Double hierarchy hesitant fuzzy linguistic term set and MULTIMOORA method: A case of study to evaluate the implementation status of haze controlling measures. Inf. Fusion 2017, 38, 22–34. [Google Scholar] [CrossRef]
- Brauers, W.K. Location Theory and Multi-Criteria Decision Making: An application of the MOORA method. Contem. Econ. 2018, 12, 241–252. [Google Scholar] [CrossRef]
- Brauers, W.K.; Baležentis, A.; Baležentis, T. MULTIMOORA for the EU Member States updated with fuzzy number theory. Technol. Econ. Dev. Econ. 2011, 17, 259–290. [Google Scholar] [CrossRef]
- ALG Europraxis. Vilnius International Airport Master Plan. Final Report: English Version. 2012; Available online: https://www.eib.org/attachments/registers/67622564.pdf (accessed on 1 May 2019).
- Kendall, M. Rank Correlation Methods; Hafner Publishing House: New York, NY, USA, 1955. [Google Scholar]
- Turskis, Z.; Zavadskas, E.K.; Zagorskas, J. Sustainable city compactness evaluation on the basis of GIS and Bayes rule. Int. J. Strat. Prop. Manag. 2006, 10, 185–207. [Google Scholar] [CrossRef]
- Servadio, J.L.; Convertino, M. Optimal information networks: Application for data-driven integrated health in populations. Sci. Adv. 2018, 4, e1701088. [Google Scholar] [CrossRef] [PubMed]
- Convertino, M.; Muñoz-Carpena, R.; Chu-Agor, M.L.; Kiker, G.A.; Linkov, I. Untangling drivers of species distributions: Global sensitivity and uncertainty analyses of MaxEnt. Environ. Modell. Softw. 2014, 51, 296–309. [Google Scholar] [CrossRef]
- Lüdtke, N.; Panzeri, S.; Brown, M.; Broomhead, D.S.; Knowles, J.; Montemurro, M.A.; Kell, D.B. Information-theoretic sensitivity analysis: A general method for credit assignment in complex networks. J. R. Soc. Interf. 2007, 5, 223–235. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: Hoboken, NJ, USA, 2008; ISBN 9780470725177. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).