Integral Transform Method to Solve the Problem of Porous Slider without Velocity Slip
Abstract
1. Introduction
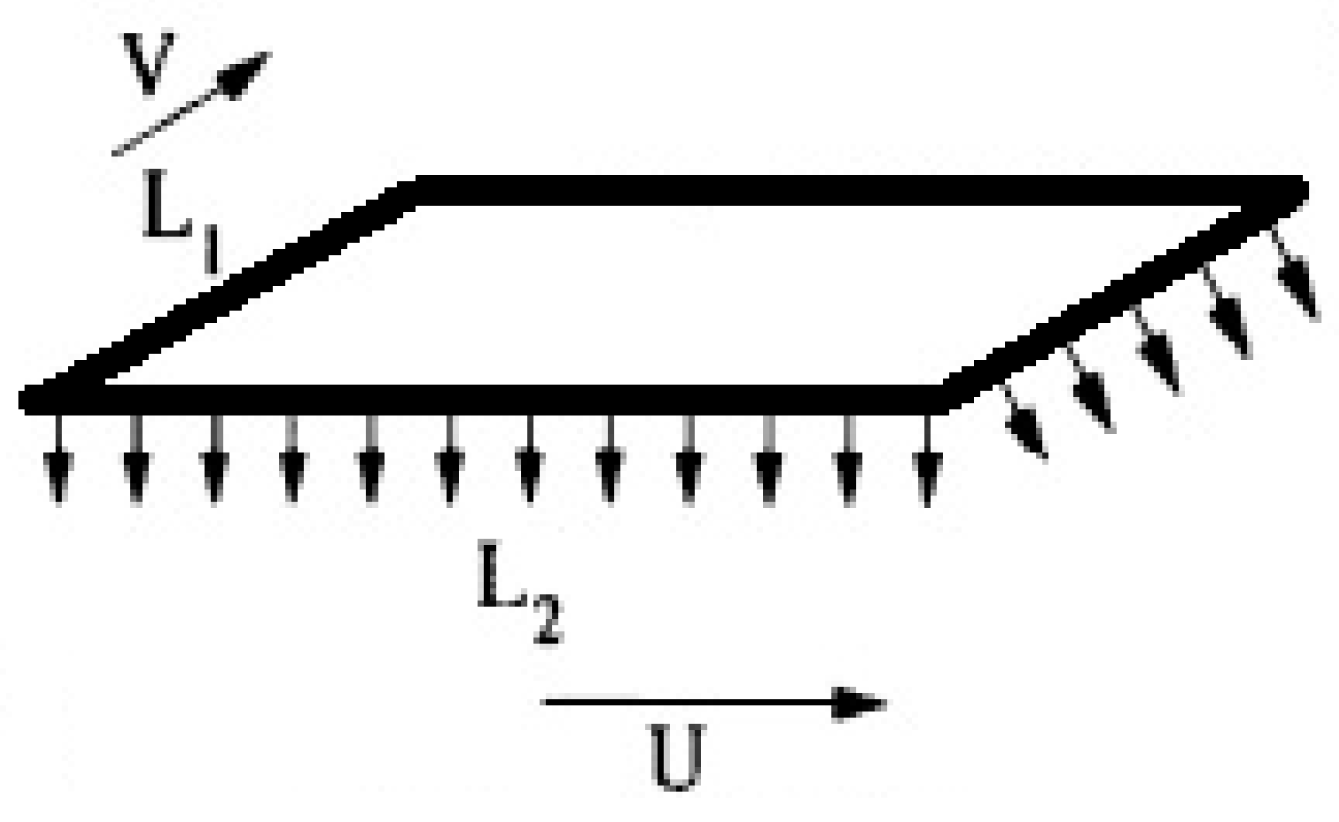
2. Problem Formulation
3. Integral Transform Method
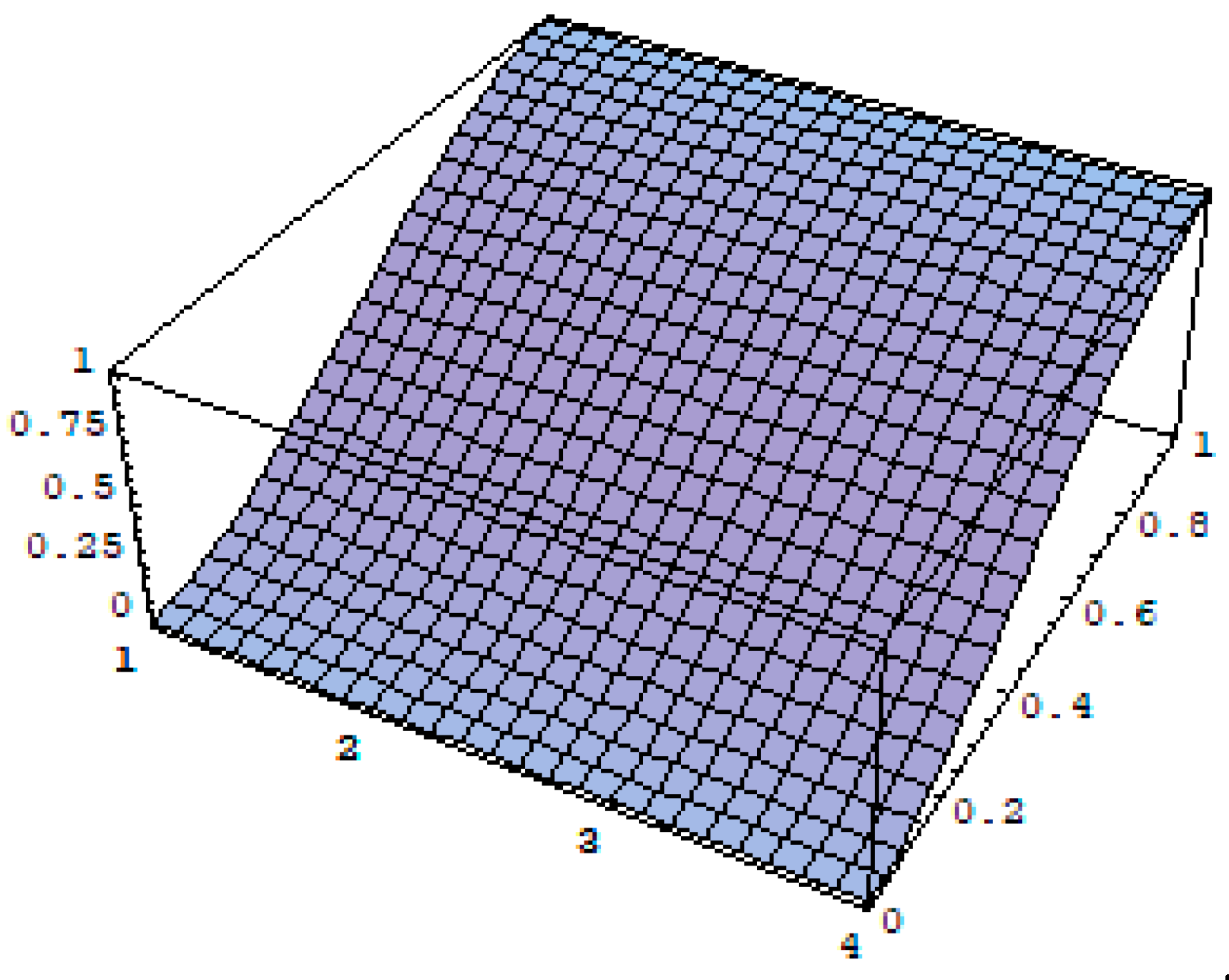
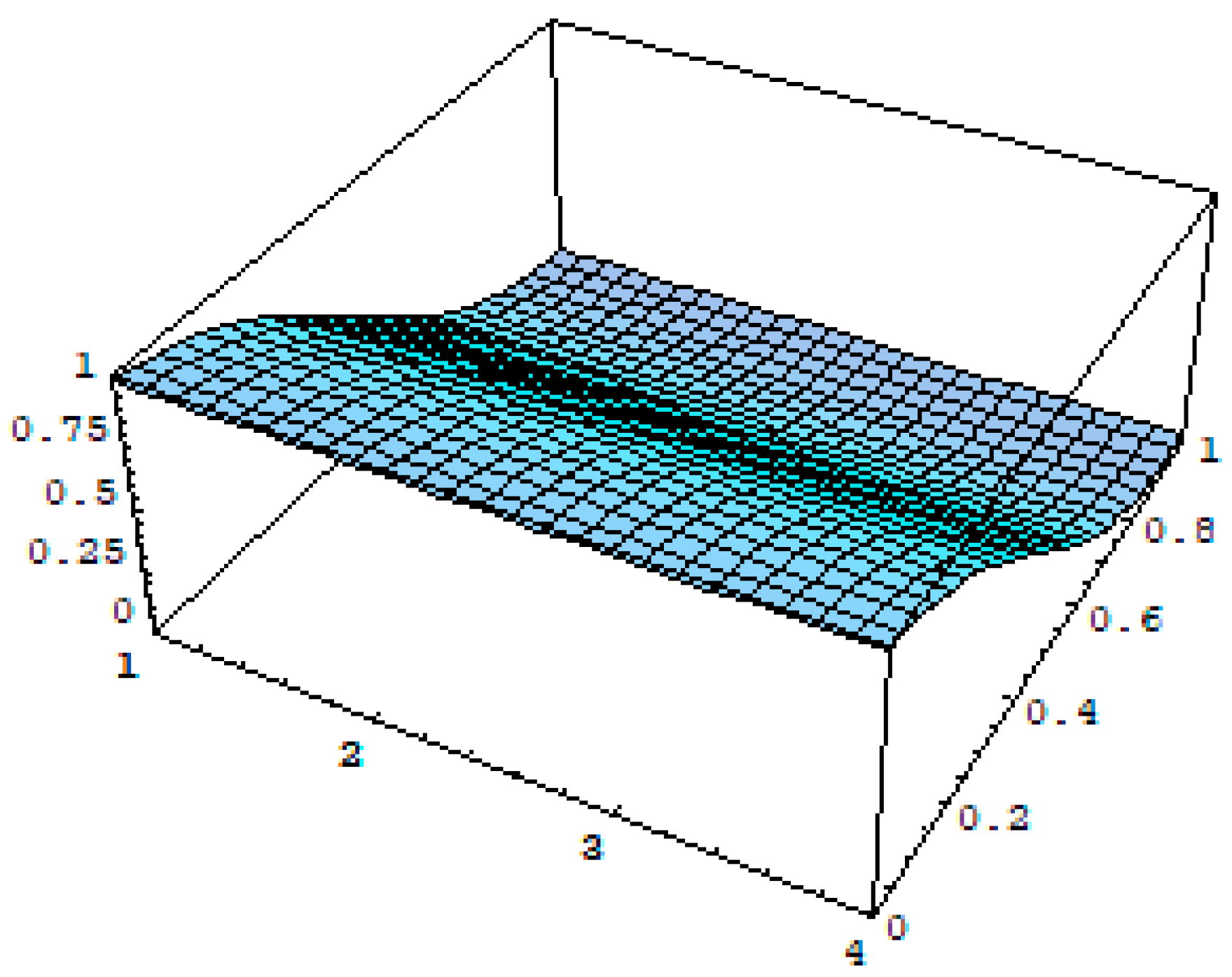
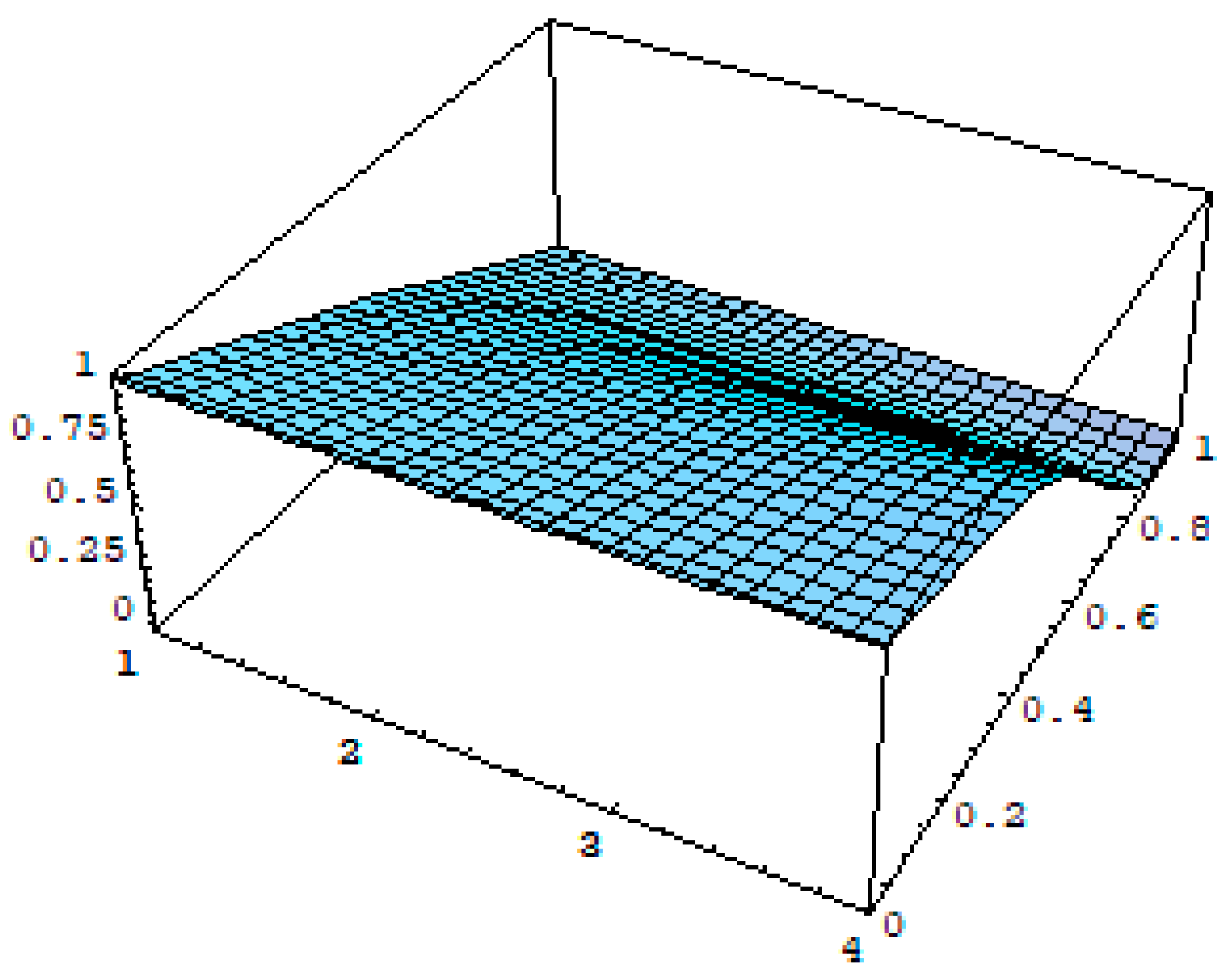
4. Graphs and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Nadeem, S.; Haq, R.U.; Akbar, N.S.; Khan, Z.H. MHD three-dimensional Casson fluid flow past a porous linearly stretching sheet. Alex. Eng. J. 2013, 52, 577–582. [Google Scholar] [CrossRef]
- Khan, Y.; Faraz, N.; Yildirim, A.; Wu, Q. A series solution of the long porous slider. Tribol. Trans. 2011, 54, 187–191. [Google Scholar] [CrossRef]
- Faraz, N. Study of the effects of the Reynolds number on circular porous slider via variational iteration algorithm-II. Comput. Math. Appl. 2011, 61, 1991–1994. [Google Scholar] [CrossRef]
- Rao, P.S.; Agarwal, S. Effect of permeability and different slip velocities at both the porous interface using couple stress fluids on the slider bearing load carrying mechanism. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 196–201. [Google Scholar] [CrossRef]
- Kumar, S.; Pai, N. Analysis of Porous Eliptical Slider through Semi-Analytical Technique. J. Adv. Res. Fluid Mech. Therm. Sci. 2018, 48, 80–90. [Google Scholar]
- Zhu, Z.; Nathan, R.; Wu, Q. Multi-scale soft porous lubrication. Tribol. Int. 2019, 137, 246–253. [Google Scholar] [CrossRef]
- Lang, J.; Nathan, R.; Wu, Q. Theoretical and experimental study of transient squeezing flow in a highly porous film. Tribol. Int. 2019, 135, 259–268. [Google Scholar] [CrossRef]
- Bujurke, N.M.; Patil, H.P.; Bhavi, S.G. Porous slider bearing with couple stress fluid. Acta Mech. 1990, 85, 99–113. [Google Scholar] [CrossRef]
- Wang, C.Y. A porous slider with velocity slip. Fluid Dyn. Res. 2012, 44, 065505. [Google Scholar] [CrossRef]
- Honchi, M.; Kohira, H.; Matsumoto, M. Numerical simulation of slider dynamics during slider-disk contact. Tribol. Int. 2003, 36, 235–240. [Google Scholar] [CrossRef]
- Shah, R.C.; Bhat, M.V. Ferrofluid lubrication in porous inclined slider bearing with velocity slip. Int. J. Mech. Sci. 2002, 44, 2495–2502. [Google Scholar] [CrossRef]
- Awati, V.B.; Jyoti, M. Homotopy analysis method for the solution of lubrication of a long porous slider. Appl. Math. Nonlinear Sci. 2016, 1, 507–516. [Google Scholar] [CrossRef]
- Khan, Y.; Wu, Q.; Faraz, N.; Yildirim, A.; Mohyud-Din, S.T. Three-dimensional flow arising in the long porous slider: An analytic solution. Z. Naturforsch. 2011, 66, 507–511. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Some issues on HPM and HAM methods: A convergence scheme. Math. Comput. Model. 2011, 53, 1929–1936. [Google Scholar] [CrossRef]
- Safari, M.; Ganji, D.D.; Moslemi, M. Application of He’s variational iteration method and Adomian’s decomposition method to the fractional KdV-Burgers-Kuramoto equation. Comput. Math. Appl. 2009, 58, 2091–2097. [Google Scholar] [CrossRef]
- Faraz, N.; Khan, Y. Study of the dynamics of rotor-spun composite yarn spinning process in forced vibration. Text. Res. J. 2012, 82, 255–258. [Google Scholar] [CrossRef]
| HAM [12] | Present | Error | |
|---|---|---|---|
| R | |||
| 0.2 | 12.4653341665 | 12.465334166 | −5E-10 |
| 1 | 14.365346654 | 14.365346654 | −0E+0 |
| 2 | 16.8235673555 | 16.8235673555 | −0E+0 |
| 3 | 19.3565458558 | 19.3565458558 | −0E+0 |
| 4 | 21.9473510772 | 21.9473510772 | −0E+0 |
| 5 | 24.5830707891 | 24.55234070789 | −5E-10 |
| 6 | 27.2533109825 | 27.2533109818 | −7E-10 |
| 7 | 29.9476951163 | 29.9476951136 | −2.7E-9 |
| 8 | 32.6611632416 | 32.6611632329 | −8.7E-9 |
| 9 | 35.3924710097 | 35.3924709848 | −2.49E-8 |
| 10 | 38.1449125507 | 38.1449125256 | −2.51E-8 |
| 51.6 | 149.6714726105 | 149.6714725836 | −2.69E-8 |
| 70 | 197.9636925814 | 197.9636925523 | −2.91E-8 |
| 100 | 275.9321654987 | 275.9321651777 | −3.21E-7 |
| 300 | 788.4398765432 | 788.4398762142 | −3.29E-7 |
| 500 | 1291.1159263487 | 1289.1236547891 | −1.99 |
| 1000 | 2526.4 | 2398.1243 | −128.27 |
| HAM [12] | Present | Error | |
|---|---|---|---|
| R | |||
| 0.2 | 1.0880258369 | 1.0880258369 | -0E-0 |
| 1 | 1.4053692581 | 1.4053692581 | -0E+0 |
| 2 | 1.7445321654 | 1.7445321654 | -0E+0 |
| 3 | 2.0361159263 | 2.0361159263 | -0E+0 |
| 4 | 2.2866753421 | 2.2866753421 | -0E+0 |
| 5 | 2.5287418529 | 2.5287418529 | -0E-0 |
| 6 | 2.9136985214 | 2.9136985214 | -0E-0 |
| 7 | 3.172839654 | 3.172839654 | -0E-0 |
| 8 | 3.6543219871 | 3.6543219866 | -5E-10 |
| 9 | 3.8293711234 | 3.8293711226 | -8E-10 |
| 10 | 4.1125836917 | 4.1125836759 | -1.58E-8 |
| 51.6 | 7.5531472583 | 7.5531472314 | -2.69E-8 |
| 70 | 8.7573572419 | 8.7573572108 | -3.11E-8 |
| 100 | 10.40147311 | 10.401472583 | -5.27E-7 |
| 300 | 17.81537007 | 17.815369258 | -8.12E-7 |
| 500 | 22.670 | 22.661 | -0.009 |
| 1000 | 30.432 | 30.429 | -3.00 |
| HAM [12] | Present | Error | |
|---|---|---|---|
| R | |||
| 0.2 | 1.0301258369 | 1.0301258369 | -0E-0 |
| 1 | 1.1531951623 | 1.1531951623 | -0E+0 |
| 2 | 1.3096314785 | 1.3096314785 | -0E+0 |
| 3 | 1.4658951623 | 1.4658951623 | -0E+0 |
| 4 | 1.6187258369 | 1.6187258369 | -0E+0 |
| 5 | 1.766159741 | 1.766159741 | -0E-0 |
| 6 | 1.9086456321 | 1.9086456321 | -0E-0 |
| 7 | 2.0464158231 | 2.0464158231 | -0E-0 |
| 8 | 2.1850474125 | 2.1850474125 | -0E-0 |
| 9 | 2.3368115987 | 2.3368115987 | -0E-0 |
| 10 | 2.5264314755 | 2.5264314755 | -0E-0 |
| 51.6 | 5.3011463295 | 5.30114632825 | -1.25E-9 |
| 70 | 6.1449236681 | 6.14492366789 | 2.1E-8 |
| 100 | 7.2881583541 | 7.2881580341 | -3.27E-7 |
| 300 | 12.5161258 | 12.5160446 | -8.12E-5 |
| 500 | 15.368124 | 15.258154 | -010997 |
| 1000 | 20.062 | 19.1583 | -0.9037 |
| HAM [12] | Num. [9] | Present | HPM [12] | Num. [9] | Present | HPM [12] | Num. [9] | Present | |
|---|---|---|---|---|---|---|---|---|---|
| R | |||||||||
| 0.2 | 12.465 | 12.465 | 12.465 | 1.0880 | 1.088 | 1.088 | 1.0301 | 1.0301 | 1.030 |
| 1 | 14.365 | 14.365 | 14.365 | 1.405 | 1.405 | 1.405 | 1.1531 | 1.153 | 1.153 |
| 2 | - | - | 16.8235 | - | - | 1.7445 | - | - | 1.30963 |
| 3 | - | - | 19.356 | - | - | 2.0361 | - | - | 1.4658 |
| 4 | - | - | 21.9473 | - | - | 2.2866 | - | - | 1.6187 |
| 5 | 24.586 | 24.584 | 24.584 | 2.4417 | 2.528 | 2.528 | - | - | 1.766 |
| 6 | - | - | 27.253 | - | - | - | - | - | 1.9086 |
| 7 | - | - | 29.9476 | - | - | - | - | - | 2.04641 |
| 8 | - | - | 32.6611 | - | - | - | - | - | 2.18504 |
| 9 | - | - | 35.3924 | - | - | - | - | - | 2.33681 |
| 10 | - | - | 38.1449 | - | - | - | - | - | 2.52643 |
| 11 | - | - | 40.9267 | - | - | - | - | - | 2.79796 |
| 12 | - | - | 43.7471 | - | - | - | - | - | 3.2218 |
| 13.8 | 48.9043 | 48.484 | 48.484 | 4.0229 | 4.022 | 4.022 | - | - | 4.70844 |
| 15 | - | - | 52.2461 | - | - | - | - | - | 6.53822 |
| 16 | - | - | 54.6612 | - | - | - | - | - | 8.72019 |
| 51.6 | 149.67 | 149.67 | 149.67 | 7.553 | 7.553 | 7.553 | 5.301 | 5.301 | 5.301 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faraz, N.; Khan, Y.; Lu, D.C.; Goodarzi, M. Integral Transform Method to Solve the Problem of Porous Slider without Velocity Slip. Symmetry 2019, 11, 791. https://doi.org/10.3390/sym11060791
Faraz N, Khan Y, Lu DC, Goodarzi M. Integral Transform Method to Solve the Problem of Porous Slider without Velocity Slip. Symmetry. 2019; 11(6):791. https://doi.org/10.3390/sym11060791
Chicago/Turabian StyleFaraz, Naeem, Yasir Khan, Dian Chen Lu, and Marjan Goodarzi. 2019. "Integral Transform Method to Solve the Problem of Porous Slider without Velocity Slip" Symmetry 11, no. 6: 791. https://doi.org/10.3390/sym11060791
APA StyleFaraz, N., Khan, Y., Lu, D. C., & Goodarzi, M. (2019). Integral Transform Method to Solve the Problem of Porous Slider without Velocity Slip. Symmetry, 11(6), 791. https://doi.org/10.3390/sym11060791







