1. Introduction
The brain is an important organ that serves as the center of the nervous system of human [
1]. The cerebral cortex plays a key role on brain cognitive functions [
2]. A healthy person has corresponding cognitive activities while being stimulated by the external environment. Multiple brain regions in the cerebral cortex cooperate to complete these activities through different brain functional connection pathways [
3]. The brain functional connection pathways have an important contribution to understand the brain functional network models [
4,
5]. Revealing brain functional connection pathways will provide a scientific basis and reference for diagnosis and treatment [
6,
7].
Analyzing brain functional connection pathways is one of the basic problems in the study of brain function. The component analysis algorithms were common methods in the early stage. Friston et al. proposed a PCA-based brain functional connection pathway analysis method in 1993 [
8], and then they studied the function connection between different brain regions when people processed color and emotion tasks in 1999 [
9]. Londei et al. used ICA to detect the activated brain areas and analyzed the functional correlation between the relevant areas by the Granger causality test [
10]. Although these methods can obtain functional connection model of the whole brain, they wast a lot of time and space. Clustering algorithms are another kind of common methods to divide brain networks and study brain functional pathways, such as center-based algorithms [
11] and heuristic algorithms [
12]. However, the results of these algorithms depend heavily on the number of clustering centers and other parameters that do not describe the nature of the brain functional pathways itself. In recent years, ROI-based algorithms have become new hotspots to analyze brain functional connection pathways, as the brain data can be effectively simplified [
13,
14]. The ROIs, namely regions of interests, have to be selected as the prior knowledge empirically [
15] while performing brain functional analysis by these methods. The division of brain structure or the coordinates published in the latest research are usually used as the basis for selecting ROIs [
16]. Liu et al. obtained a brain functional connection pathway by an attribute reduction algorithm of rough set successfully and interpreted these knowledge from ROIs [
17].
The brain functional connection pathways analysis has been widely used to study the neural mechanism associated with different types of mental disorders. They provide a great help in diagnosis, monitoring and treatment of mental disorders. Desseilles et al. found the functional connection pathway is abnormal between frontal parietal lobe network and visual cortex in patients with severe depression [
18]. Salomon et al. compared the difference of whole brain function between schizophrenia patients and normal control group in both resting state and working state. The results show that the whole brain functional connection pathways of schizophrenia patients are lower than the normal in both resting state and working state, and the abnormality was more prominent in resting state [
19]. Admon et al. compared brain functional connectivity patterns of 33 servicemen in Iraq before and after their service. They found that the subjects with decreased hippocampus gray matter density exhibit more post-traumatic stress disorder (PTSD) symptoms than those with increased hippocampus gray matter density. Meanwhile, the former’s function connection between hippocampus and prefrontal cortex is significantly reduced [
20].
However, only a single brain functional connection pathway is obtained by using the previous methods. In fact, there are multi-pathways in the brain, and these multi-pathways are very important for us to understand the relationship between structure and function of different brain regions. The research on multi-pathways will certainly provide more ideas for the study of brain function. Thus, it is necessary to study a multi-reduction method and use it to the analysis of multiple brain functional connection pathways.
A set of multi-reduction contains different attribute combinations, which have the same decision capabilities [
21]. Multi-reductions provide more insights from different perspectives than a single reduction and can form a multi-knowledge system [
22]. Unfortunately, it is a major challenge to obtain multi-reduction [
23]. Wu et al. [
24] proposed a method to obtain multi-reduction based on positive region by replacing the non-core attributes. Firstly, the core attributes are collected to get a reduction. Then, the multi-reduction set is obtained through the replacement of non-core attributes one by one. However, their algorithm cost much more time in computing equivalence classes more than once. Thus, it is worth exploring some new reduction approaches to the multi-pathways from functional magnetic resonance imaging analysis.
In this paper, we propose a novel multi-reduction algorithm for analyzing the brain functional connection pathways from functional Magnetic Resonance Imaging (fMRI) data. After proposing and proving a reduction equivalence theorem, a binary discernibility matrix is introduced for obtaining a single reduction dynamically. Since the size of the binary discernibility matrix is dynamically decreased during attribute reduction, the computational time is significantly reduced. Then, the multi-reduction can be obtained by a strategy of non-core attributes replacement. After testing on benchmark data, we employ the proposed algorithm to obtain multiple pathways from brain cognitive functional imaging successfully. The multi-reduction obtained by our algorithm provides a novel comprehensive view for brain functional connection pathways.
2. Multi-Reduction and Binary Discernibility Matrix Methodology
In this section, the relevant concepts of multi-reduction and binary discernibility matrix are defined and the reduction theorems are proved theoretically.
2.1. Multi-Reduction
In rough set theory, an information system [
25] is defined as a 4-tuple
, where
U is the universe of discourse, a non-empty finite set of
N objects
.
A is also a non-empty finite set that contains all attributes. For every
,
and
is the value set of the attribute
a.
If
,
, the information system is denoted as a decision table by
.
C and
D are, respectively, called the condition attribute and the decision attribute sets. For two subsets of attributes in decision table, the input features form the set
C while the class indices are
D. Let
I be a subset of
A, the equivalence relation [
26]
is denoted as follows.
All equivalence classes of the relation
are denoted by
. For simplicity of notation,
replaces
. The condition and decision classes are, respectively, noted
and
. For an attributes subset
,
denotes a partition of the universe, where
is an equivalence class of
B. The positive region on equivalence classes
for
D is defined as follows:
where
represents the cardinality of the set
.
According to the positive region on the equivalence relation of decision attribute D, the reduction can be defined as shown in Definition 1.
Definition 1. [Reduction] For a given decision table , the attributes subset B is called a reduction of C, if and .
According to Definition 1, a reduction is an attributes subset of the condition attributes, which retains the capacity of the same classification to partition the universe as the whole condition attributes. In fact, the reduction is usually unique.
Definition 2. [Multi-reduction] Let represent the multi-reduction set, it is a set including multiple reductions of C defined by Equation (
3)
. 2.2. Binary Discernibility Matrix
To obtain reduction from an information system, positive region based reduction algorithms [
27] have been widely used in the past. However, many symbolic logic operations have to be conducted by using these algorithms. A binary discernibility matrix [
28] can transform the equivalence relation between different attributes into a matrix containing only 0 and 1. Thus, the binary discernibility matrix based reduction algorithms are simpler, more intuitive and easier to understand.
Definition 3. [Binary discernibility matrix] The binary discernibility matrix of the reduced decision table is denoted by where , . is an unordered object pair and can be defined as follows: According to Definition 3, the two objects in positive regions but with different decision values and the two objects in positive and non-positive regions, respectively, are distinguished by “1” in the matrix. Otherwise, the two objects are equivalent, and the corresponding value in the discernibility matrix is “0”.
A reduction equivalence theorem between positive region based reduction algorithms and binary discernibility matrix based algorithms are proposed and proved as follows.
Theorem 1 (Reduction Equivalence Theorem)
. For a given decision table , if a reduction is obtained through the binary discernibility matrix, it must be equivalent to a reduction through its positive region.
Proof of Theorem 1. Let
B be a reduction through the binary discernibility matrix
M. Let
be the objects set of positive region in
T. For
,
according to Equation (
4). The objects set of positive region in
M is denoted as
. Thus,
. Therefore,
.
B is a reduction which satisfies Definition 1, the theorem follows. □
As Theorem 1 illustrated, the binary discernibility matrix provides an efficient approach to obtain the reduction. We just need to partition the objects in different object pairs through the binary discernibility matrix. According to the generated objects pairs by Equation (
4), an unordered object pair
can be discerned only by considering the attributes
with
instead of the whole attributes. All attributes would be added into a candidate reduction set according to the attribute importance that is defined as follows.
The larger the
is, the more important the
is, and the stronger the ability of
to partition the object pair
is. Especially,
means
is a redundant attribute and cannot help us to discern any object pair. An attribute is called a core attribute when it can only be used to partition one object pair. The set of core attributes can be collected as follows.
If , any attribute in condition attributes is not a core attribute.
3. Dynamic Multi-Reduction Algorithm
In this section, the dynamic single reduction and multi-reduction algorithm based on a binary discernibility matrix are proposed successively. We analyze these two algorithms in detail.
To obtain multi-reduction, the decision table is transformed into a binary discernibility matrix by using Equation (
4). A core attribute set can be obtained by using Equation (
6), and then a reduction called a seed reduction is obtained from the core attribute set, as shown in Algorithm 1. In Algorithm 1, two acceleration mechanisms are used in Steps 3 and 4 to dynamically improve the algorithmic efficiency, respectively. Rows and columns that do not affect the next calculation are deleted in Step 3 to reduce the binary discernibility matrix. Then, the attributes with a value of “1” for the first objects pair in the current matrix are chosen in Step 4. Since only these attribute importance have to be calculated by Equation (
5), the computational times of the algorithm are greatly reduced. In Steps 5 and 6, attributes are added to the seed reduction one by one according to their importance until the matrix becomes empty.
| Algorithm 1 Dynamic Single Reduction Algorithm (DSRA). |
Input:
M and the attributes set R,
Output:
seed-reduction - 1:
; - 2:
whiledo - 3:
For , the column of attribute and the rows about object pairs which satisfy can be deleted to obtain a new reduced matrix ; - 4:
Choose the object pair in the first row of new and calculate the importance of attributes in the set by Equation ( 5); - 5:
, ; - 6:
according the attribute importance one by one; - 7:
end while - 8:
ifthen - 9:
Output the reduction ; - 10:
else - 11:
There is no reduction. - 12:
end if
|
In Algorithm 1, the loop of Steps 2–7 is performed times at most. The time complexities of Steps 3–6 are , , and , respectively. Thus, the time complexity of the loop is . The time complexity of Algorithm 1 is no more than . , which is obtained based on R, is a seed-reduction for acquiring more reductions used in Algorithm 2.
The different reduction can be obtained by replacing the non-core attributes. According to outputted by Algorithm 1, any non-core attribute in can be replaced by attributes in . Through recalling Algorithm 1, new reduction can be obtained by the replacement of different . The dynamic multi-reduction algorithm (DMRA) is summarized in Algorithm 2.
In Algorithm 2, after initializing the attributes and multi-reduction set in Step 1, a binary discernibility matrix can be given using Equation (
6) in Step 2. Then, the core attribute
can be obtained using Equation (
6) in Step 3. Algorithm 1 is called to find a seed reduction in Step 5, then more reductions are obtained by a non-core attributes replacement strategy from Step 7 to Step 14. Finally, in Steps 15 and 16, we remove the redundancy in the final reduction set
and output it.
In Algorithm 2, the matrix M according to T is generated in Step 2 and its time complexity is . The time complexity of Step 3 for getting the core attributes set is . The time complexities of calling Algorithm 1 in Steps 5 and 9 is . The loop from Step 7 to Step 14 will run times. The procedure from Step 10 to Step 12 will cost time. Thus, the time complexity of Steps 7–14 is . The time complexity in Step 15 to remove the redundancy reduction is . Thus, the total time complexity of Algorithm 2 is not more than . It can be found that the amount of the attributes has a greater influence on the time complexity of Algorithm 2.
| Algorithm 2 Dynamic Multi-Reduction Algorithm (DMRA). |
Input:
Decision table T
Output:
Multi-reduction- 1:
Initialize the attributes set and multi-reduction set ; - 2:
Obtain the binary discernibility matrix by Equation ( 4); - 3:
Collect the set of core attribute by Equation ( 6); - 4:
; - 5:
Obtain a seed reduction by Algorithm 1; - 6:
; - 7:
for to do - 8:
; - 9:
Recall Algorithm 1 to get a new reduction ; - 10:
if then - 11:
; - 12:
end if - 13:
; - 14:
end for - 15:
Remove the redundancy in . - 16:
Output .
|
4. Experimental Results
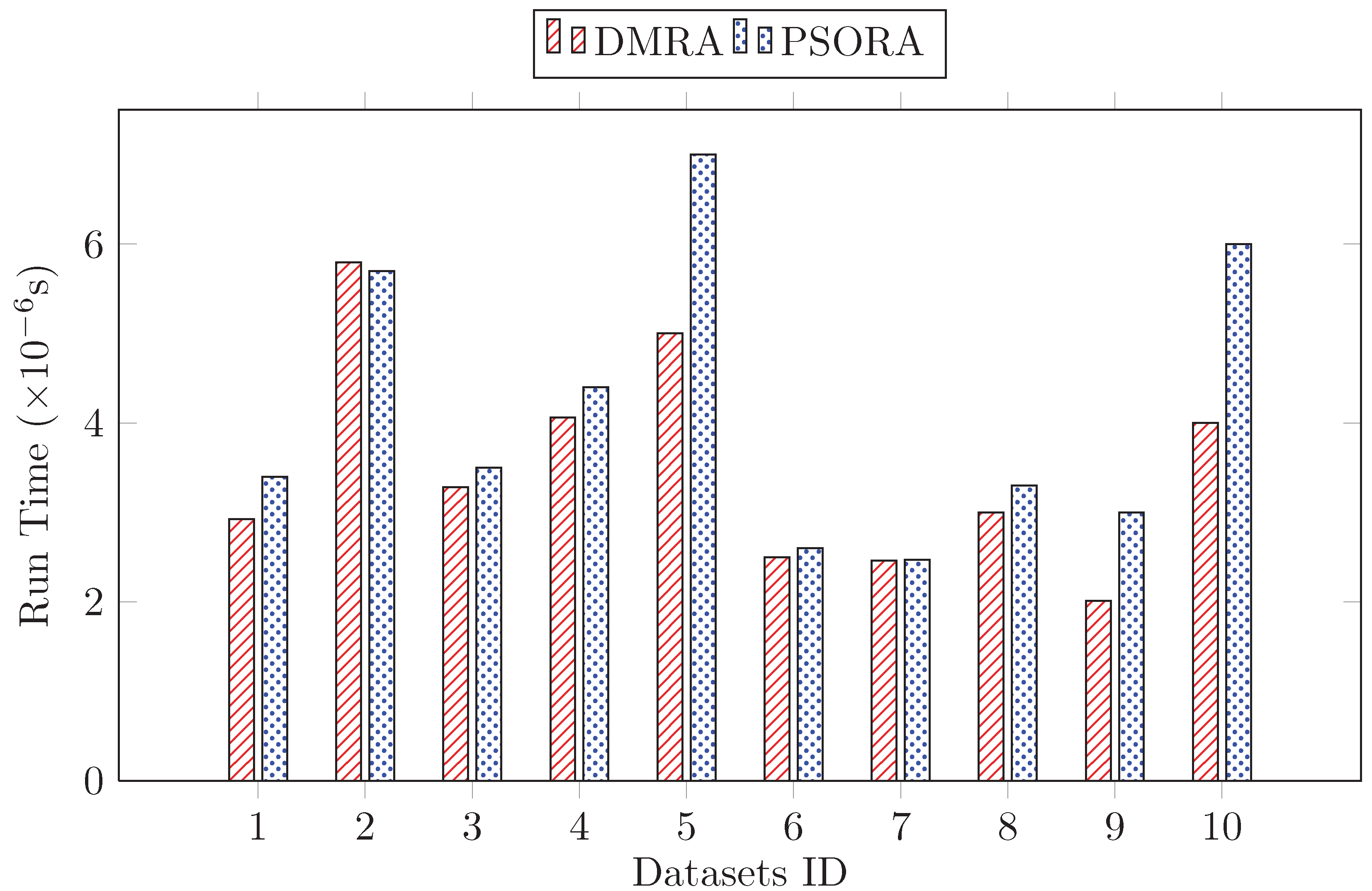
We carried out multi-reduction experiments on 10 datasets from the UCI Machine Learning Repository to show the superiority of DMRA over PSORA in execution time and classification accuracy. Then, DMRA was used to obtain multiple brain functional connection pathways from brain functional magnetic resonance imaging.
4.1. Test and Comparative Experiments
To illustrate the effectiveness of the proposed algorithm, we carried out multi-reduction experiments on 10 well-knowledge benchmark datasets from the UCI Machine Learning Repository, which are listed in
Table 1. These datasets such as Glass, Heart and Iris are frequently used to test rough set methods. Some new datasets (e.g., Breast Tissue and SPECT Heart) were also considered in our experiments. The results in the number of core attributes and reductions are also listed in
Table 1. Then, we compared the run time of getting the first reduction of DMRA with particle swam optimization based reduction algorithm (PSORA) [
17]. The results are shown in
Figure 1. We also compared the classification accuracy of DMRA and PSORA (
Table 2).
As shown in
Figure 1, the run time of getting the first reduction by DMRA was always faster than PSORA. The more attributes the dataset contained, the more obvious the speed advantage of the DMRA was. For datasets with fewer attributes, namely Datasets 2, 6 and 7, there was little difference in the running time by using the two algorithms. However, for datasets with more attributes, namely Datasets 5, 9 and 10, DMRA had obvious time advantage. The brain data usually contain many attributes. Thus, the proposed DMRA could obtain reduction results more quickly than PSORA on brain data.
In
Table 2, we list the highest, lowest and the average accuracy rate of the different multi-reductions obtained by DMRA, and compare these accuracy rates with raw data and PSORA. No matter using the DMRA or PSORA, the classification accuracy rate was improved, and the best classification accuracy could always be obtained by a reduction obtained by DMRA. The average accuracy rate of multi-reductions obtained by DMRA was higher on all datasets than PSORA. Thus, the proposed DMRA was superior to PSORA in execution time and classification accuracy rate.
Next, we applied the DMRA algorithm to the analysis of multiple brain functional connection pathways.
4.2. Experimental Design
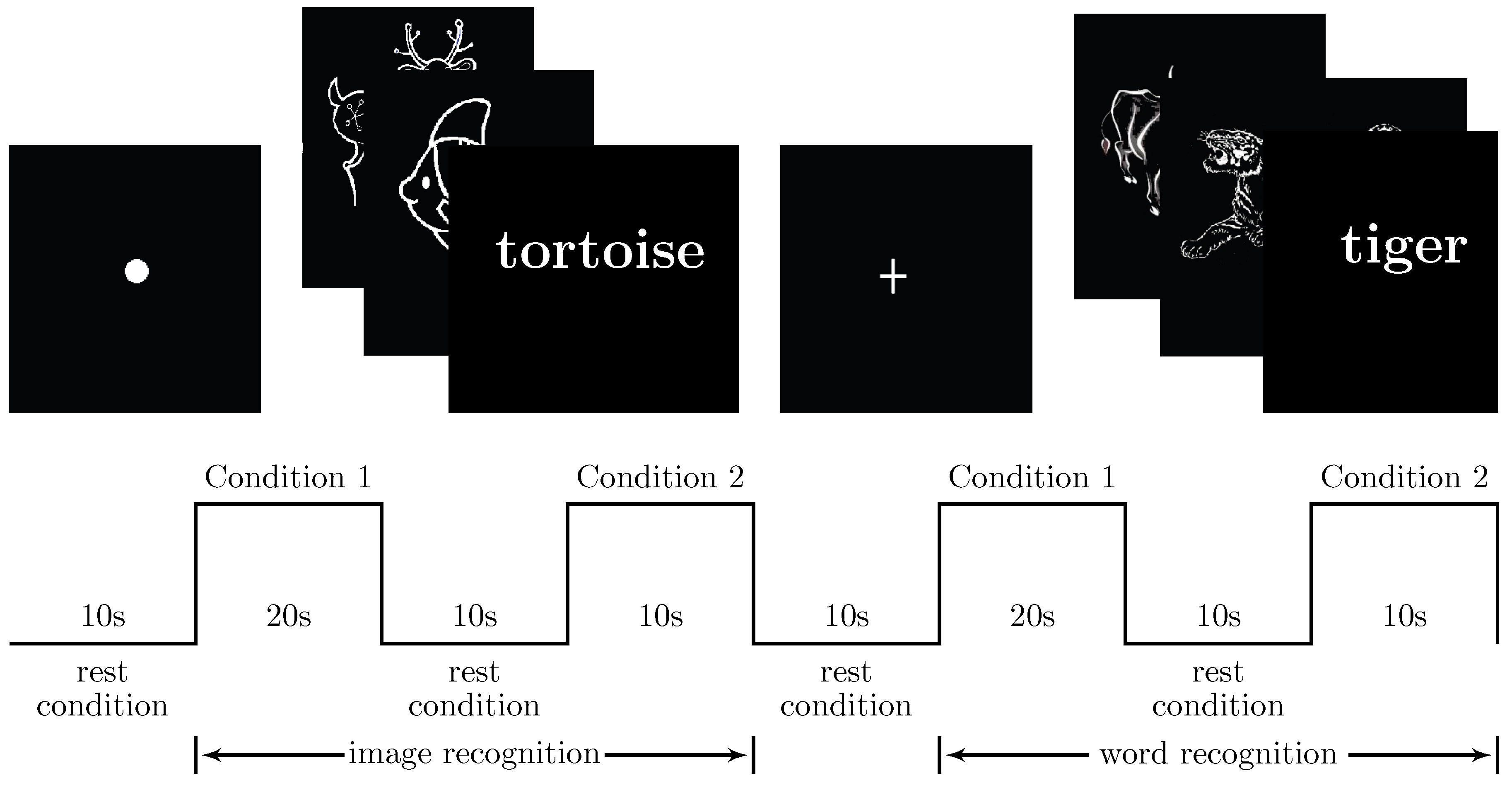
Our brain functional magnetic resonance imaging was acquired using a 3.0T Siemens Magnetron Vision Scanner on 21 young subjects (12 men and 9 women, aged from 17 to 20 years). All subjects were recruited from undergraduate students. Informed consent was obtained before their participation. The cognitive task was a kind of memory experiment, and the cognitive tasks were input in block design [
29].
There were two kinds of stimuli in the experiment: images and words. The subjects were demanded to remember the stimuli shown in Condition 1 and to determine whether the stimulus shown in Condition 2 appeared in Condition 1 or not. The block design is shown in
Figure 2. Conditions 1 and 2 lasted 12 s and 10 s, respectively, and the rest condition was 10 s so that the subjects could relax.
Brodmann Areas (BA) [
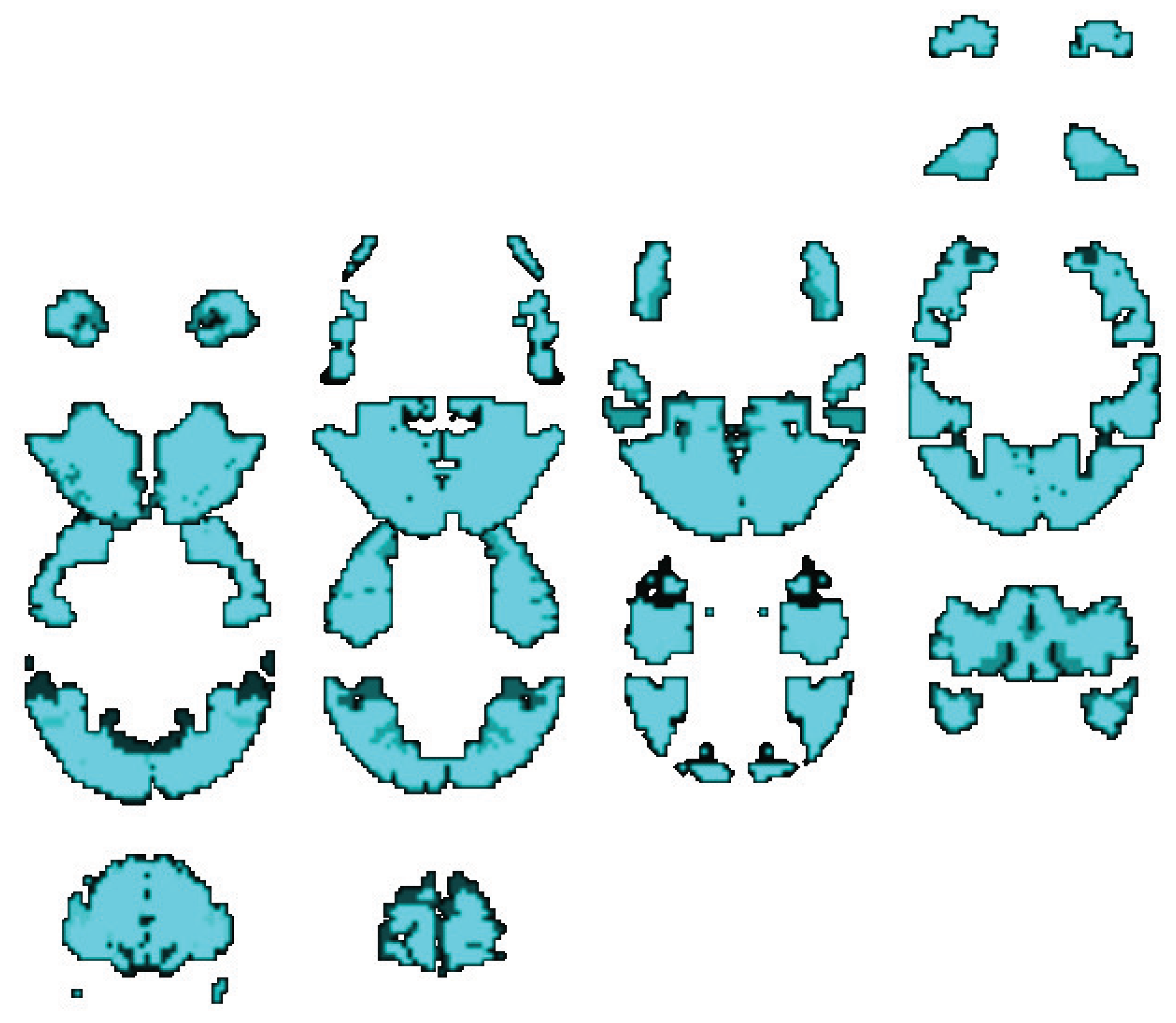
30] system was used in this study, which was originally defined and numbered by the German anatomist Korbinian Brodmann based on the cytoarchitectural organization of neurons. Each hemisphere of brain is divided into 52 areas in BA. According to our cognitive tasks, we selected 16 areas (BA4, BA6, BA17, BA18, BA19, BA22, BA27, BA37, BA38, BA39, BA40, BA41, BA42, BA44, BA45, and BA46) as the ROIs in the frontal lobe, as shown in
Figure 3. For the sake of simplicity in rough set, the brain areas are described with corresponding attribute labels in
Table 3.
We used the statistical parameter mapping (SPM) [
31] to obtain the activated brain area from the fMRI images and counted the number of activated voxels in every BA. In SPM, the data preprocessing covered the following steps: time correction, head correction, standardization and Gaussian smooth. Then, the generalized linear model (GLM) was employed to extract the activated voxels. After ascertaining the positions of the activated voxels through Student’s T-test, the number of the activated voxels could be determined within every BA area. Then, the cognitive decision table
T could be built, in which the condition attributes were the 16 BAs and the value of each objects in different attributes was the number of activated voxels.
We used the cognitive decision table
T as the input of Algorithm 2. The attributes set
and multi-reduction set
was initialized at first, and the binary discernibility matrix
M could be obtained by Equation (
4). Then, we obtained the set of core attribute
by Equation (
6). Algorithm 1 was used to obtain the first reduction
. Let the set of multi-reductions be
. Then, the non-core attributes
in
were replaced according to Steps 7–14 in Algorithm 2. At the end of the algorithm cycle,
, which contained three reduction results, could be outputted. The
provided the attribute (namely BA) combinations and their correlations to describe the multiple brain cognitive functional connection pathways.
4.3. Discussion of Experimental Results
Three reductions in
were obtained by DMRA algorithm from the cognitive decision table, as shown in
Table 4. The value of the table represents the order of attributes in an attribute reduction and “-” denotes the reduced attributes. The connection pattern of the brain functional pathway was dependent on the order of attributes in a reduction.
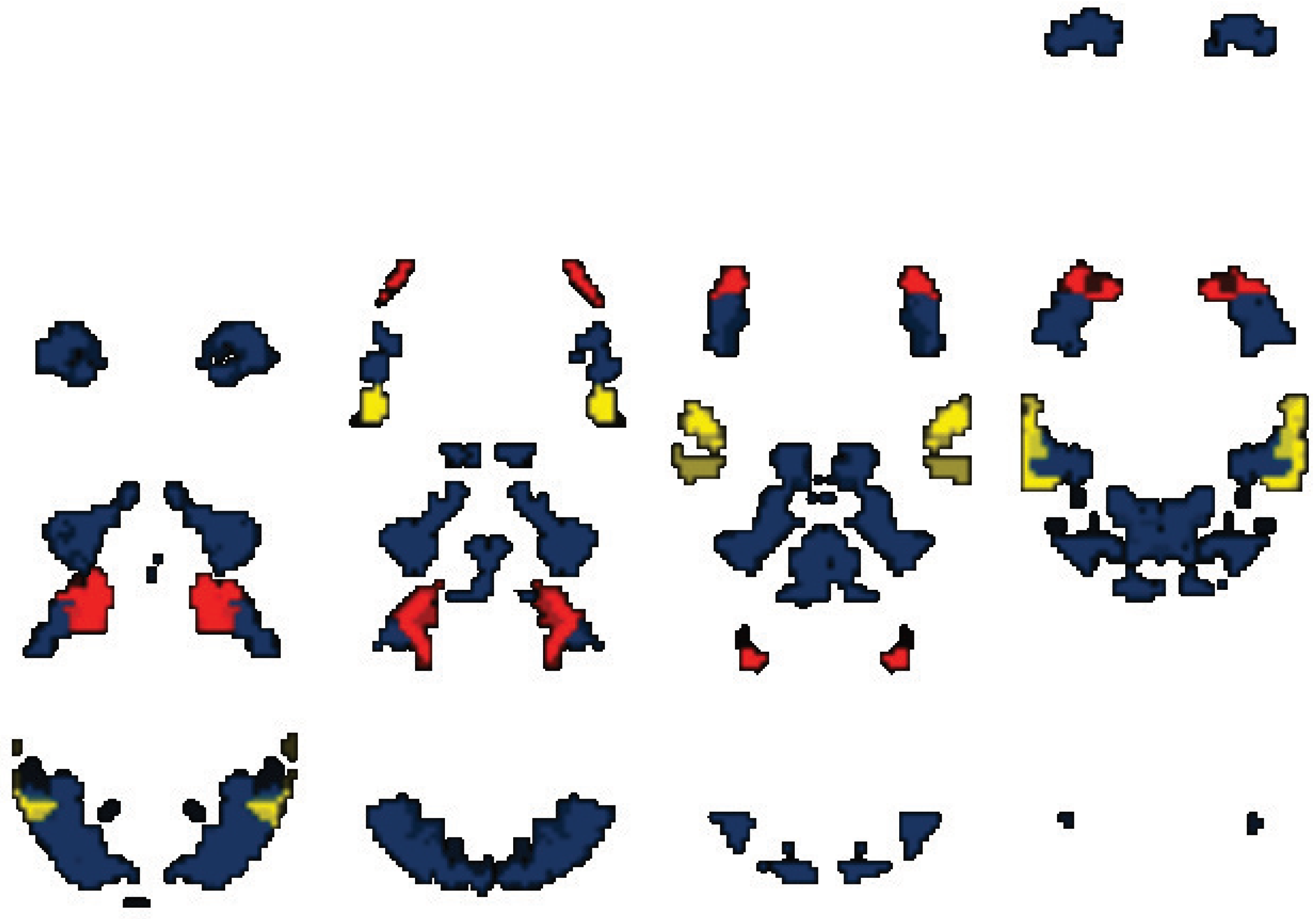
Considering the three reductions obtained through our algorithm (
Table 4), BA17, BA19, BA27, BA38, BA39, BA41, BA42 and BA45 were common in these reductions. We regard these eight brain areas as the core attributes, which are closely related to the memory behavior of brain. BA27, BA38, BA41 and BA42 are in the temporal lobe related to memory. BA17 and BA19 are in the occipital lobe related to visual. There are also some areas related to language, including BA39 and BA45. Reductions 1 and 2 have BA40, but BA46 in the frontal cortex replaces BA40 of the same order in Reduction 3. That means BA40 and BA46 may have similar effects in the brain, and they can be replaced by each other sometimes. The coronal position figures of the three reductions for brain functional connection pathways are, respectively, shown in
Figure 4,
Figure 5 and
Figure 6. The common brain areas are the blue highlight in these figures. BA40 or BA46 is the red highlight. The last area in each reduction is the yellow highlight.
According to the three multi-reductions, three brain functional connection pathways about memory can be formed by the order of attributes in
Table 4 as follows.
;
;
.
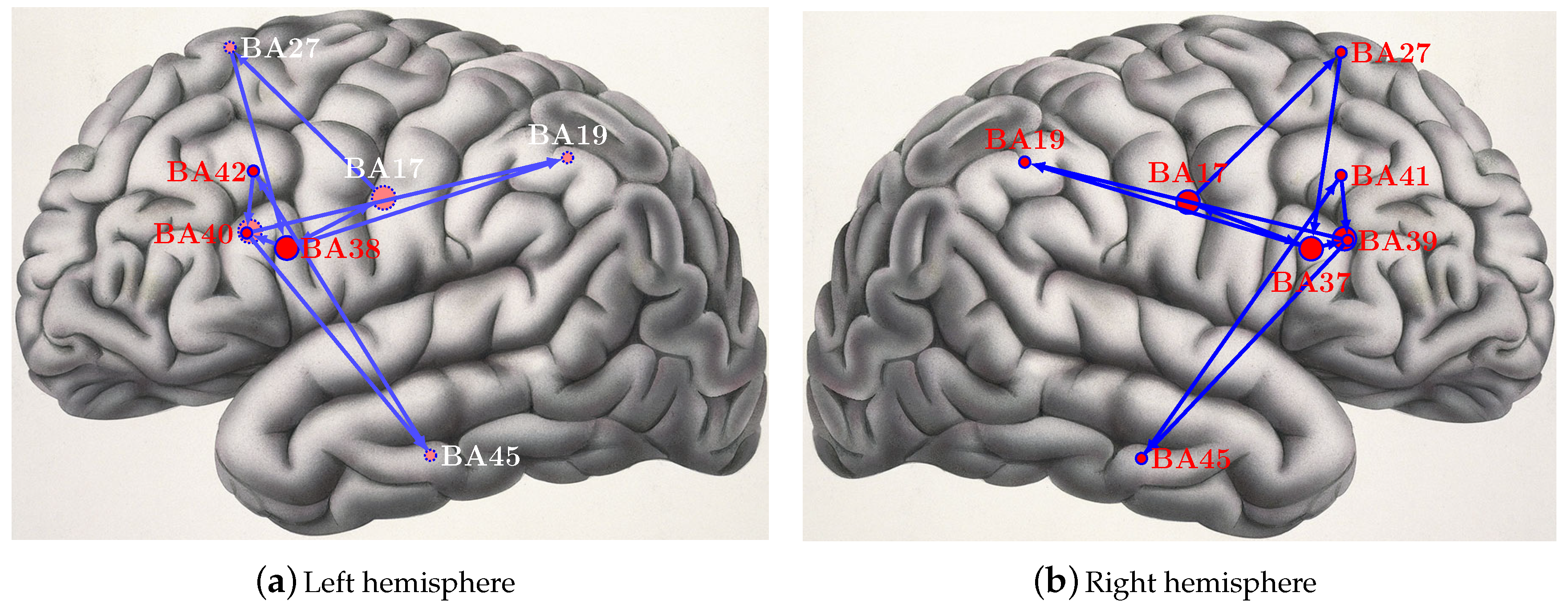
The functional connection pathway derived from the first reduction in
Table 4 are shown as an example in
Figure 7. The different size of circles represents the activation intensity of brain areas.
5. Conclusions
In this paper, we propose a dynamic multi-reduction approach, in which a binary discernibility matrix is formulated from the decision table in rough set theory. Only the attributes which can discern object pairs are considered, and the attributes importance is measured according to the discernibility matrix. The superiority of DMRA in execution time and classification accuracy are shown by testing on benchmark datasets and comparing with PSORA. Experiments show that the proposed DMRA can effectively deal with attribute reduction of numerical data. It not only helps us to obtain accurate multi-reductions, but also reduces the computational time complexity. The more are attributes contained in the dataset, the more obvious is the advantage of our algorithm over the traditional algorithm. Our DMRA was then applied to analyze brain functional imaging. The areas of interest and its activating features with cognitive tasks was transformed into a decision table. Finally, eight BAs closely related to the memory behavior of brain and three brain functional connection pathways about memory were obtained, while only one brain functional connection pathway can be obtained by the previous approaches. The multi-reduction theory provides a comprehensive analysis approach to complete the knowledge discovery in brain functional imaging. It would make a significant influence on brain functional connection analysis.