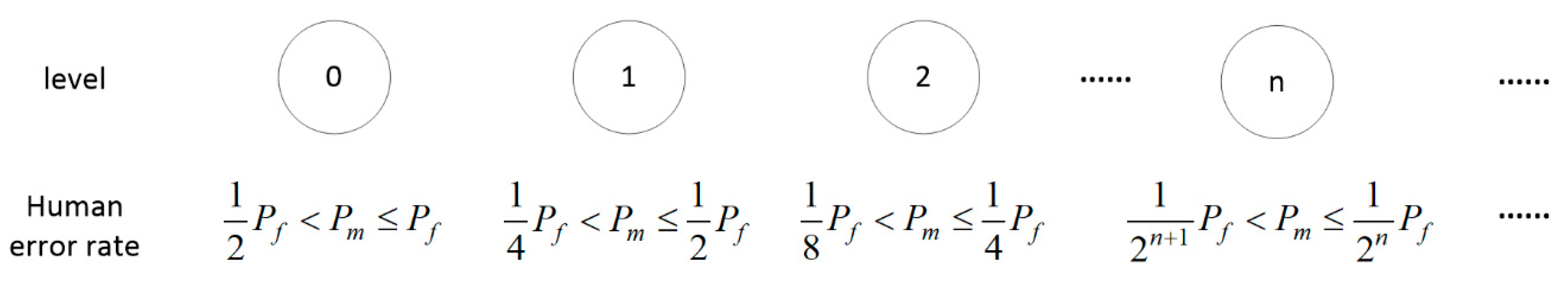1. Introduction
For some systems that require the continuous execution of multiple missions, all the maintenance activities need to be performed during maintenance breaks. However, due to maintenance resource constraints, it is not always feasible to repair all the components. In order to solve such problems, Rice et al. [
1] first proposed a maintenance policy called selective maintenance in 1998. In such a strategy, in view of actual resource requirements such as maintenance time, only some components can be repaired during maintenance breaks in order to enable the next mission to perform successfully. Therefore, a selective maintenance policy greatly saves maintenance resources. Based on this theory, Cassady et al. [
2] defined a more complex system, whose components have two states, functioning or failed, and then presented an optimization model with the goal of maximizing system reliability. Cassady et al. [
3] also assumed that the life of all components follow a Weibull distribution, and the maintenance activities can be divided into three types, namely minimal repair of failed components, replacement of failed components, or replacement of functioning components. To improve the selective maintenance optimization, a selective maintenance model considering multiple missions was studied by Maillart et al. [
4]. Additionally, Schneider et al. [
5] included a situation in which one or more future missions may be canceled. Yang et al. [
6] considered a frequency-based maintenance optimization, and gave a heuristic game framework to find a feasible solution. Diallo et al. [
7] applied selective maintenance for large, serial,
k-out-of-n systems and considered both preventive maintenance actions and corrective maintenance actions. Duan et al. [
8] solved the selective maintenance problem for a multi-component system with stochastic maintenance quality by using a simulated annealing algorithm. Khatab et al. [
9] focused on a system that needs to perform consecutive missions separated by scheduled breaks. Ali et al. [
10] considered that the repairing and replacement costs of all components are random.
However, in addition to binary systems (see [
2]), many systems exhibit multiple discrete functioning states in their degradation process. Such a system is defined as a multi-state system (MSS). The degradation of MSS can be regarded as a discrete process. For example, the output capacities of a power production plant will degrade continuously during the mission (such as 100 MW, 80 MW, 50 MW). Since an MSS has many states, it is more complicated for maintenance managers to make optimal plans. Chen et al. [
11] first applied selective maintenance to a multi-state series-parallel system and gave an optimization model. Liu et al. [
12] focused on an MSS that consisted of multiple binary components considering imperfect repair. Lisnianski et al. [
13] proposed that the states of components can be represented by the performance rate, which simplifies the calculation process and establishes the relationship between the overall system and the components.
Some researchers have found that the components that make up the MSS can also have multiple states. Pandey et al. [
14] applied selective maintenance in an MSS that consisted of multiple multi-state components. In such a case, imperfect maintenance (see [
15,
16,
17]) of a multi-state component is considered to be a maintenance option, along with the “replacement” and the “do nothing” options. Dao et al. [
18,
19] considered the economic dependence and structural dependence between multi-state components, and gave the calculation model of maintenance time and costs. Due to the inefficiency of the enumeration method (see [
1]) in solving complicated optimization problems, Lust et al. [
20] proposed a tabu search-based metaheuristic that allows the quality of the solution obtained by the construction heuristic to be improved. Xu et al. [
21] applied five differential evolution (DE) algorithms to solve the selective maintenance optimization problem and determined the optimal one.
It has been observed that the majority of the papers on selective maintenance ignore the effect of human reliability on the maintenance tasks. However, the reduction of human error is one of the major interests for the enhancement of system safety and availability (Moieni et al. [
22]). For the selective maintenance problem, an optimal plan can save maintenance time and costs during the maintenance breaks and maximize the reliability of an MSS to perform the next mission. However, some components may not be repaired to the best state, or may not even receive maintenance at all. Such a maintenance policy will increase the risk of mission failure. Human error will further increase this risk, and cannot be neglected in selective maintenance modeling. It is reasonable for maintenance managers to set a standard to choose suitable maintenance workers. Zaitseva et al. [
23] considered a mathematical model for human reliability analysis, and used Dynamic Reliability Indices to estimate the reliability of an MSS. Zhao et al. [
24] assumed that the state after the maintenance of multi-state components when human error has occurred followed uniform distribution, but did not consider the influence of the different levels of workers on the state determination process.
One of the weaknesses of the existing models for the selective maintenance of MSSs considering human reliability is that there is no relationship between workers and maintenance tasks. Generally, human error usually means that the components are completely failed after maintenance. However, for multi-state components, human error does not necessarily lead to failure. For example, the output power of a laser system can be in many states. Human error will lead to the reduction of output power, but the overall system can still operate. A human reliability model considering the characteristics of multi-state components is needed for MSS reliability analysis and maintenance decision making.
In this paper, we will study the selective maintenance problem for a multi-state series-parallel system considering human reliability. For a multi-state component, if the state after maintenance does not meet the target state required by the maintenance plan (it may totally fail or occupy an intermediate state between the failed and target state), we consider that human error has occurred in this component during the maintenance break. Therefore, human error does not mean that the component has totally failed after maintenance, but rather it may merely be at a lower working level.
In order to estimate the different level of workers in the maintenance of multi-state components, we use performance influencing factors (PIFs) to calculate the human error probability (HEP). Hollnagel et al. [
25] and Kontogiannis [
26] applied PIFs in the quantification of the HEP, respectively. According to the different HEPs, we can evaluate the working levels of different maintenance workers. Additionally, we developed a discrete distribution instead of 0–1 or uniform distribution to determine the state of components after a worker has made a human error during the maintenance break. We also proposed a method to determine the distribution by dividing human reliability into several discrete levels; then, a more accurate degradation model for the MSS is obtained. The universal generating function (UGF) is employed to evaluate the reliability of the MSS for the next mission. A selective maintenance optimization model is established to maximize the system reliability in the next mission under the constraints of maintenance time and costs. Sometimes, the maintenance manager has flexibility regarding time, but is constrained by budget or vice versa. Therefore, the effect of the variation of resources on selective maintenance planning considering human reliability is also investigated. Additionally, this paper also compares the influence of human reliability under different performance requirements. The optimization model is solved by a genetic algorithm (GA). For the problems discussed above, the following assumptions are made in this paper:
The MSS in this paper consists of multi-state components that are all repairable;
All the maintenance activities are performed by one maintenance worker, and there is no maintenance activity during a mission; and
The states of each component at the end of each mission are known.
In this paper, we focus on the selective maintenance modeling of an MSS considering human reliability. The structure of this paper is arranged as follows. After the introduction in
Section 1,
Section 2 describes the MSS structure and the human error probability calculation model. The state distribution after maintenance and the selective maintenance optimization model considering human reliability are given in
Section 3. An illustrative example and some comparative studies are presented in
Section 4.
Section 5 contains the summary and conclusions.
3. Selective Maintenance Modeling Considering Human Reliability
From what we discussed above, the state distribution after maintenance changes with the
of the maintenance worker. By dividing human reliability into different levels, we can determine the state distribution with different
values. For binary systems and components, the failure rate of a maintenance task is equal to
, so it is unnecessary to analyze different levels of human reliability. However, for MSSs and multi-state components, the failure of maintenance tasks does not mean that the system and its components have totally failed. Therefore, in order to establish the degradation model during the next mission, it is indispensable to determine the state distribution after maintenance if human error occurs. In this paper, we determine the human reliability level of maintenance workers by comparing
and
. Given the
, whenever the
(worker in lowest level when
) drops by half, the level is considered to have changed.
Figure 1 shows the human reliability level set.
In order to establish the selective maintenance optimization model, it is crucial to estimate the system reliability to perform the next mission. Let denotes the state of component after human error has occurred (the true state). First, determine the distribution of according to the human reliability level of the maintenance worker. Second, analyze the degradation process of each component during the next mission. Then, with the constraints of maintenance resources, an optimization model can be established to obtain the optimal maintenance plan and select the suitable worker.
3.1. State Determination after Human Error
If the maintenance worker did not make a human error, the state of component
after the maintenance break is
(
). However, once a worker has made an error,
satisfies
. Then, we use the conclusion of the BCG Experience Curve to estimate
. BCG Experience Curve refers to that there is a consistent correlation between the costs and total cumulative output. In short, if a production mission is executed repeatedly, its production cost will decrease. Each time the production is doubled, the cost (including management, marketing, distribution and manufacturing, etc.) will fall at a constant and measurable rate (approximately 10% to 30% per year). The proficiency of the workers is one of the most fundamental factors affecting the curve change. Yelle [
29] made a detailed summary of the development history of the Experience Curve. According to the basic principle of the curve, an increase in production leads to an increase in the operational proficiency of workers, which in turn reduces production costs. High worker proficiency means lower HEP, which reduces operational losses due to human error. In this paper, human errors affect the state of components after maintenance, and thus affect the estimation of system reliability. Therefore, whether in a profit-oriented enterprise or a reliability-oriented industrial environment, a general conclusion is that the reduction of HEP will reduce unnecessary operational losses. Based on this theory, we apply the BCG Experience Curve in the distribution determination process after maintenance. The following assumptions are considered in this paper.
If human error occurs in a multi-state component , the true state after maintenance is lower than the target state (). The probability distribution of is related to the human reliability level of the worker who performs the task during this maintenance break;
Experienced maintenance workers not only have lower HEP, but also have lower operational losses after human error occurs, i.e., the component has a higher probability of being in a better state when a human error occurs;
When satisfies , the state of component after human error satisfies ;
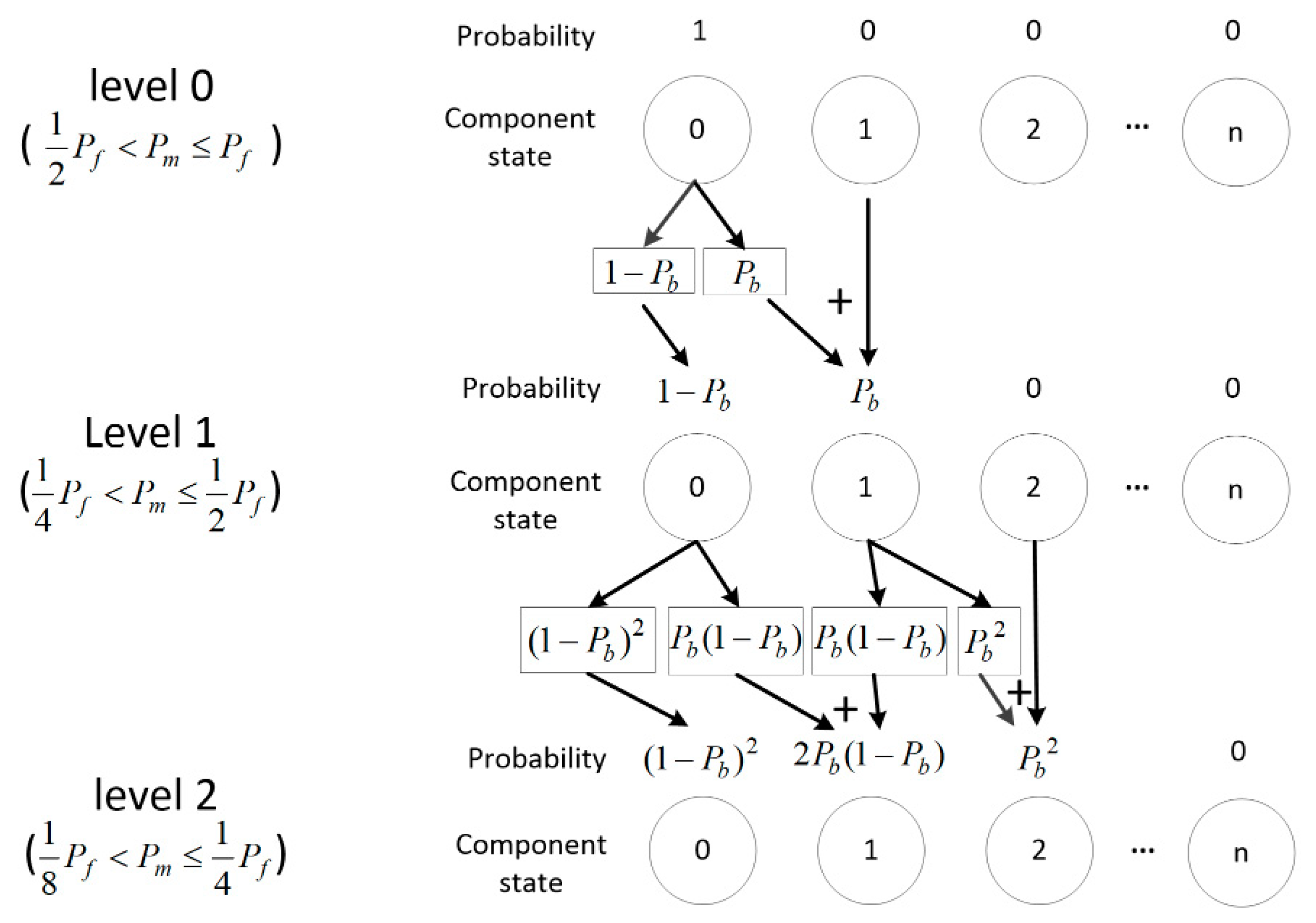
Let denotes the transition rate between adjacent human reliability levels. The probability distribution of is determined by and .
Let
denote the probability of
when the human reliability level is
. Clearly,
. If the human reliability level changes, the probability distribution of
will change accordingly, and
in the new distribution is calculated by
, i.e., the probability of each state is transferred according to
. Given the human reliability level set and
,
Figure 2 shows an example of the distribution determination process when the human reliability level changes from 0 to 2. The distribution of
in each level is given by Equations (14) to (17).
If , repeat Equation (17). According to the above equations (14) to (17), we can obtain the probability distribution of the state after a human error is made by maintenance worker . Additionally, we can see that if is infinitely close to 0, we obtain . This conclusion is similar to that of the BCG Experience Curve. It means that the worker is more skilled and the HEP is lower, so the operational losses due to human error are also lower.
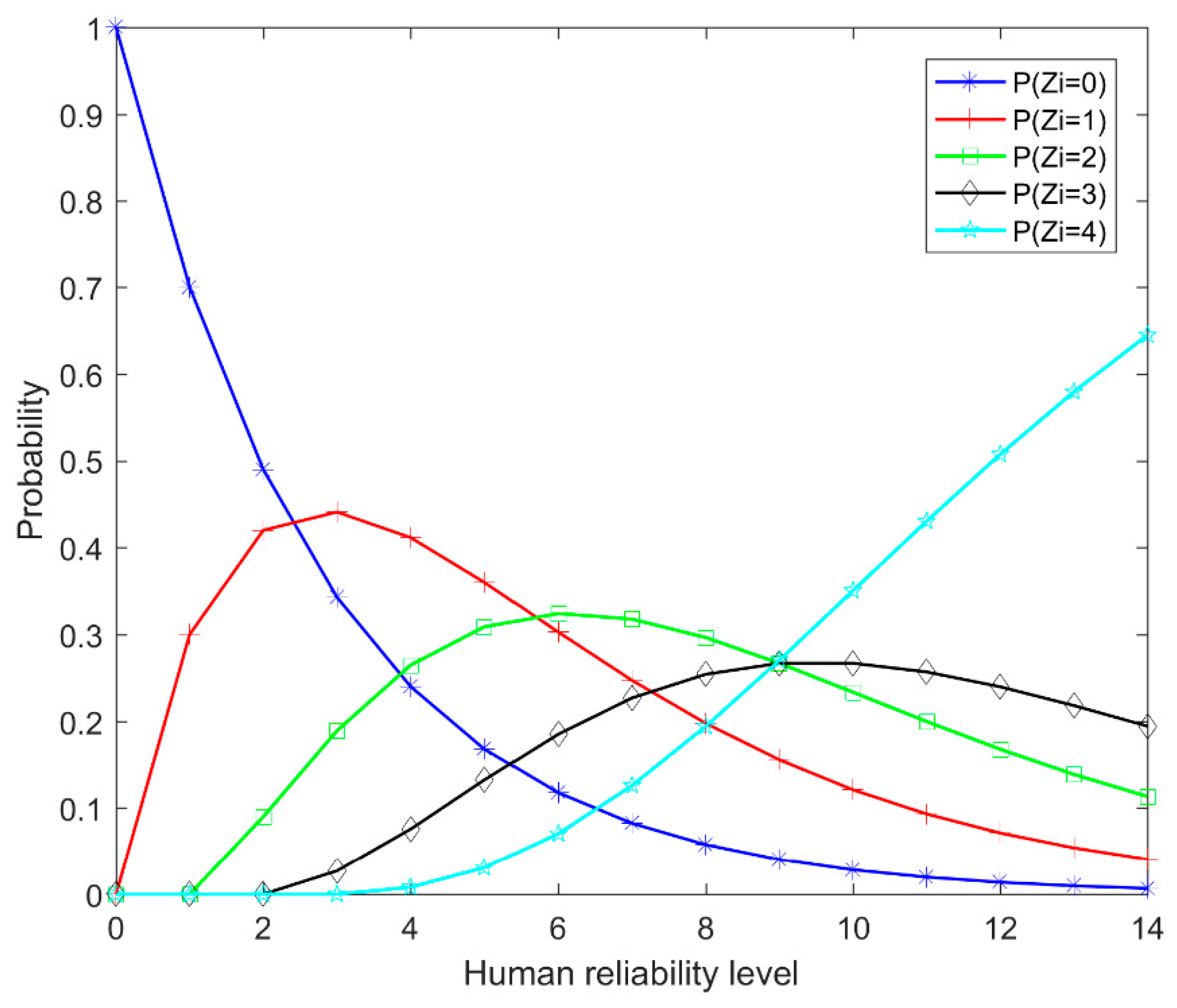
The following example is given to illustrate the working principle of this model. Consider a component that has six states,
, and the initial HEP is
, the transition rate is
, the initial state is 0, and the target state is 5. The probability that this component has different human reliability is shown in
Figure 3. It can be seen that as the HEP decreases, there is a higher probability that the component will be in a higher state. If we use the selective maintenance model proposed in [
24], the probability of components in different states after maintenance is equal for all workers, i.e.,
, which is unable to reflect the different levels of workers.
Table 1 shows the probability ranking of component
in each level.
3.2. Estimation of Component State Degradation and Multi-State System Reliability
The multi-state component degrades during the next mission. The degradation process of a multi-state component can be found in [
14,
30]. Assume that the components will not age during the maintenance break, and the degradation processes of all the components in the next mission are independent. As the mission progresses, the state of each component will progressively degrade, and the performance rate will also decrease. Let
denote the time required to perform the next mission. In this paper, the probability that component
with state
after maintenance by worker
degrading to state
at the end of the next mission,
, is given. Since
and
, the probabilities
form a transition probability matrix in the next mission, which is given by:
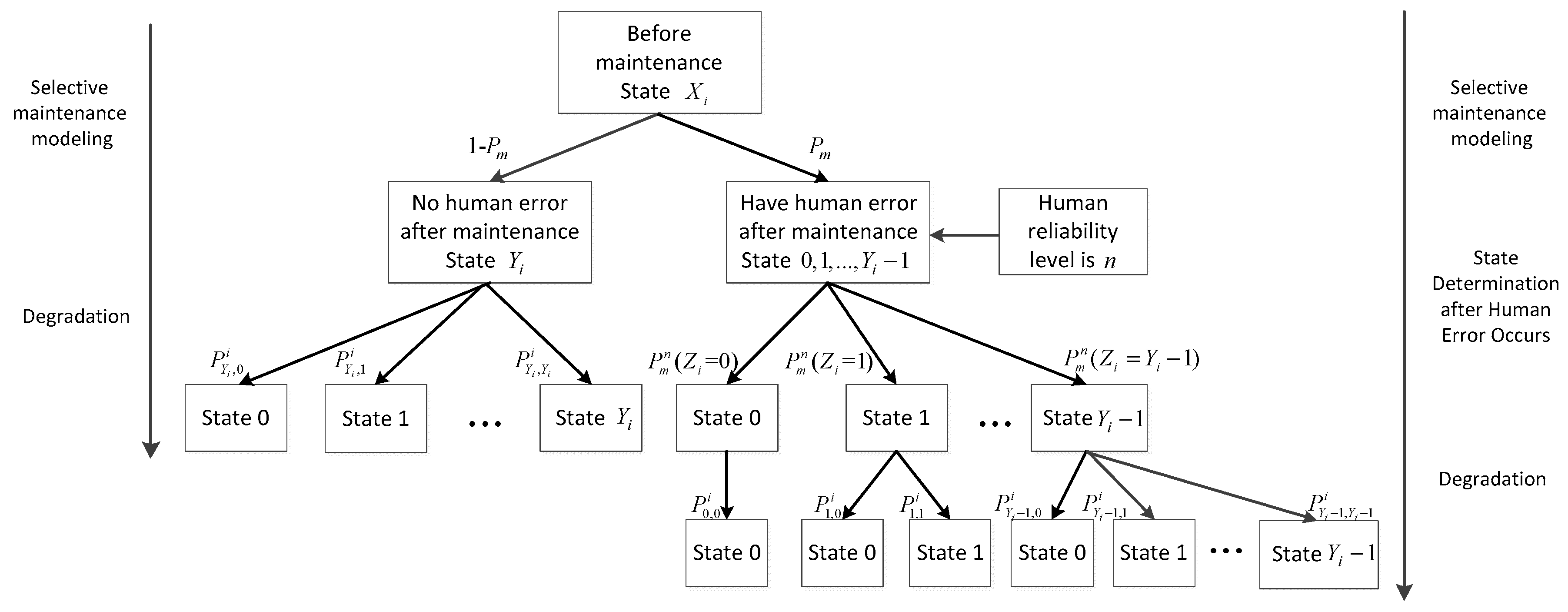
The state change process of component
between entering the maintenance break and the end of the next mission considering human reliability is shown in
Figure 4. The probability of the next event occurring is marked next to the connecting lines.
The state distribution of components after the next mission is given by the universal generating function (UGF) (see [
12,
14,
31]). The UGF is defined by Liu et al. [
12] as a polynomial function to represent the probability mass function of a discrete random variable. For component
, the performance rate distribution at time
can be represented as:
According to equations (1) to (3) discussed in
Section 2, the UGF of the overall system can be expressed by:
Equation (20) extends the UGF in [
14] by considering human reliability. Clearly, if
, the state after maintenance is
and the UGF is similar to that proposed in [
14]. However, if
, the state after maintenance follow a discrete distribution, which is proposed in
Section 3.1. Therefore, the reliability of the system will decrease, since the performance is reduced.
As the performance rate decreases, the functioning level of the MSS gets worse. Whether the mission can be successfully completed depends on the performance rate of the MSS at the end of the next mission. Let
denote the performance rate requirement of the MSS at the end of the next mission. If
is not less than
, the mission is considered successful. Therefore, the reliability of the MSS to perform the next mission is given by:
where
is the states vector set of all the components after maintenance, and
is the states vector set of all the components after degradation. Therefore,
represents the probability that the state of the overall system is
at the end of the next mission. If the performance rate of state
is greater than
, the mission is considered successful, and vice versa.
Through Equation (21), we can obtain the system reliability under a selective maintenance plan considering human reliability.
For example, consider a simple MSS that consists of two components in parallel. Each component has three states, the performance rates of which are 0, 10, and 20, and the HEP of the maintenance worker is 0.1. According to equations (14) to (17), the probability that a component is in each state after human error occurs is
,
. The state of each component entering the maintenance break is
and the target state is
. The probabilities of degradation are
,
,
,
,
,
,
,
,
,
,
, and
. Therefore, the performance rate distribution of each component at time
can be represented as:
Therefore, the composition function is given by:
If the performance rate requirement of the MSS at the end of the next mission is 10, the reliability of the MSS to perform the next mission is 0.6434.
3.3. Optimization Model
Selective maintenance is a risky policy, since some components of the system cannot be perfectly functional in the next mission. Additionally, the risk of the selective maintenance is further increased by human error. In such a case, a suitable maintenance worker must be selected for this maintenance task. The optimization model in this paper is for finding the best selective maintenance subset for maximizing the probability of successfully completing the next mission. The associated integer decision variable is
. Let
and
denote the maintenance time and costs limitation. The resulting nonlinear optimization problem is given by:
In the above formulations, the objective of function (25) is to maximize the reliability of the overall system under the maintenance by worker
, which has been formulated in
Section 3.2. Constraints (26) and (27) exhibit the limited available maintenance resources to perform maintenance. The calculation method of
and
is given in
Section 2.2. Constraints (28) and (29) show that the state after maintenance must be an integer value between
and the maximum state
for all
, since the maintenance does not worsen the state of the components. For a given MSS’s configuration, this nonlinear optimization problem can be solved. The following section presents an example and discusses how the human reliability may have an important impact on the selective maintenance model. In this experiment, the duration and costs are given in time and monetary units, respectively.
Different maintenance workers have different HEPs, and not all workers are qualified for the maintenance task. After the model gives the optimal maintenance plan, let
denotes the reliability of the system without considering human reliability, and let
be the minimum acceptable reliability for the MSS to perform the next mission considering human reliability. Then,
can be calculated by:
where
represents the risk factor for human error, with a higher value of
indicating a higher requirement for human reliability.
For a maintenance worker
, if the optimal reliability satisfies
given by the optimization model, the worker can be selected to perform maintenance tasks. Since this is a typical constrained nonlinear optimization problem involving integer variables only, a genetic algorithm (GA) is employed to solve the discrete mathematics problem in this paper. More details about GA can be found in [
32].
4. Case Analysis
Consider a multi-state series-parallel system (
Figure 5) consisting of 10 components that are numbered 1 to 10. Components 1, 4, and 10 have five states, while Components 2, 3, 5, 6, 7, 8, and 9 have four states. The overall system consists of six subsystems, which are numbered 1 to 6. Subsystems 1, 3, and 6 consist of only one component; Subsystems 2 and 4 consist of two components, and Subsystem 5 consists of three components. The basic information of the maintenance task in this break is shown in
Table 2. The maintenance time and costs for each component are shown in
Table 3. The degradation information of all the components after the next mission is shown in
Table 4. The information of three maintenance workers (
) is shown in
Table 5. The parameters of the genetic algorithms are shown in
Table 6. For this maintenance break, the state set before maintenance is
.
According the calculation method given in
Section 2.3, the HEPs of three maintenance workers in this paper are 0.0166, 0.0544, and 0.1174, respectively, and the genetic algorithm program was run multiple times using the MATLAB software (MathWorks, Natick, MA, USA). The results are shown in
Table 7 and
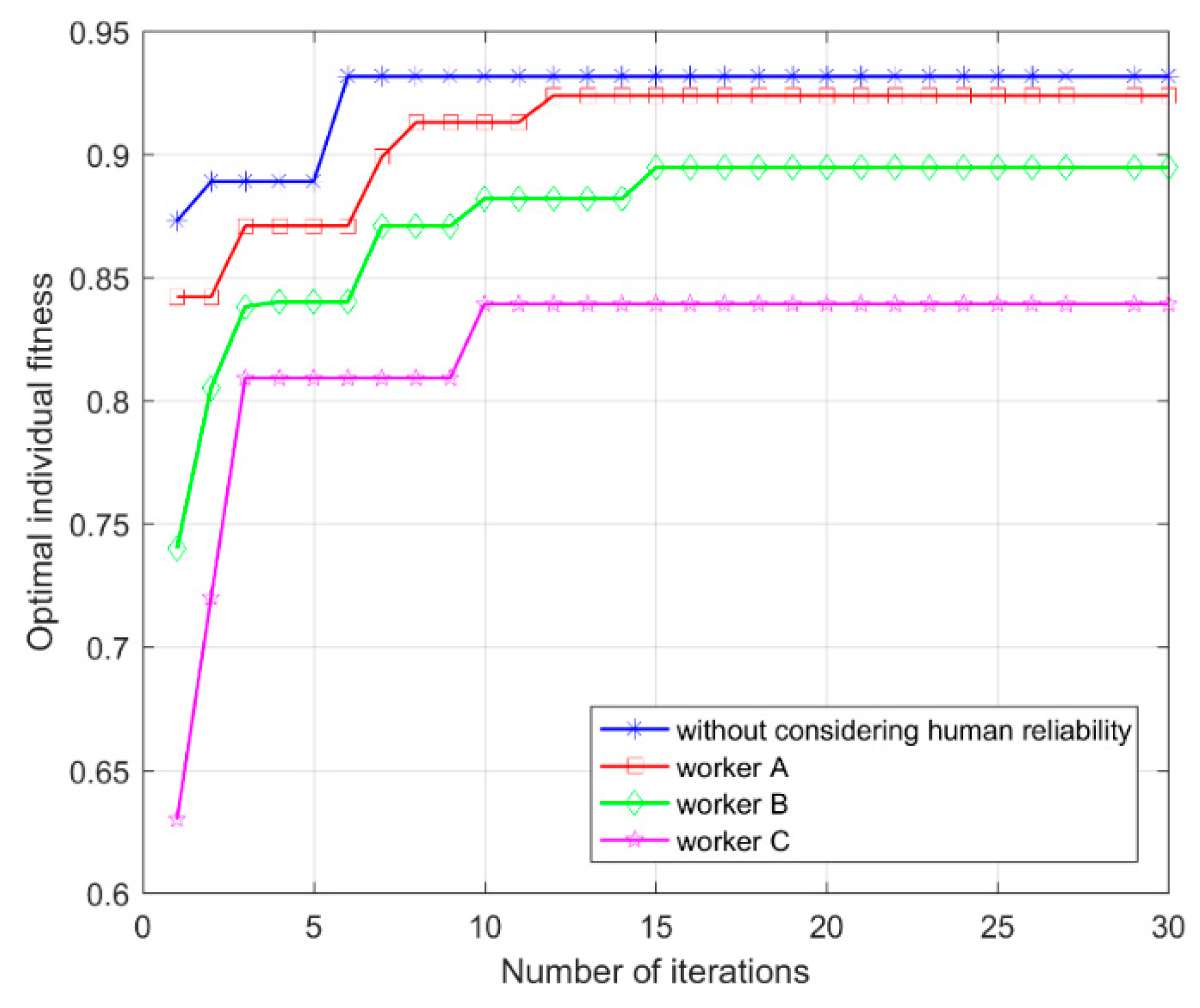
Figure 6. The optimal maintenance plan is found to be
, and the optimal maintenance options were found to be “Repair” for Components 1, 4, 5, 6, 8, and 10, “Imperfect Maintenance” for Components 2, 7, and 9, and “Do Nothing” for Component 3. The time and costs required for the optimal selective maintenance plan are 533 units and 182 units, respectively. The reliability of the optimal selective maintenance plan for the system to perform the next mission without considering human reliability is 0.9316. According to
Table 7, the reliability of the MSS after maintenance by workers A, B, and C is 0.9239, 0.8948, and 0.8391, respectively. Clearly, the system reliability will be reduced when human reliability is taken into account in the selective maintenance optimization model, i.e., ignoring human error will lead to overestimation of the system performance rate at the end of the next mission. According to the maintenance information given in
Table 2, the minimum reliability requirement for the MSS considering human reliability is 0.9037. If the system reliability after considering human reliability is greater than 0.9037, the maintenance worker can perform the maintenance task; otherwise, the worker needs to be replaced with a more qualified worker. Clearly, worker A meets the minimum reliability requirements, and can perform this maintenance task. However, workers B and C do not meet the minimum reliability requirements. If maintenance worker B or C is responsible for the maintenance task without considering the human reliability, the optimal reliability will be 0.9316 after solving the optimization model. This value is seriously overestimated compared to the true reliability, and does not meet the minimum reliability requirements (
). If the maintenance task is still carried out by maintenance worker B or C, the performance rate of the MSS at the end of the next mission may not meet the requirements, resulting in unnecessary operational losses.
In this case, the maintenance resources and performance rate requirement () are factors that affect the reliability of the MSS to perform the next mission, and also affect the selection of the maintenance worker. Loose resource limitations reduce the risk of selective maintenance and reduce the requirements of HEP for maintenance workers. However, tighter resource limitations lead to a lower system reliability.
In this case, the maintenance time and costs of all the components are 688 and 221, respectively.
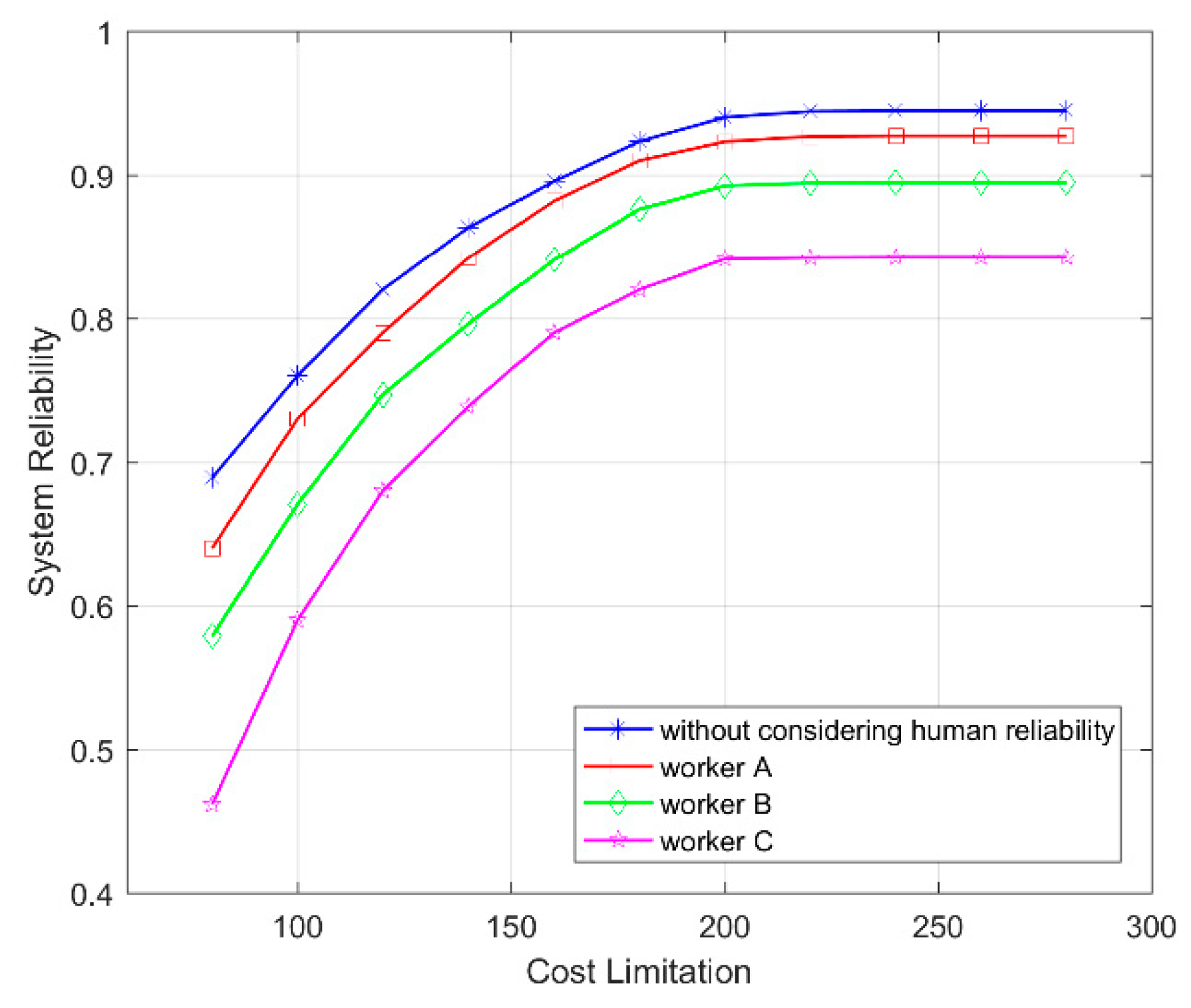
Figure 7 and
Figure 8 show the effect of human reliability under different constraints of maintenance time and costs. When comparing different time limitations, it is considered that there is no limit on the costs. Similarly, time limitations are not considered when comparing different cost limitations. As the limitations become tighter, the reliability of the system becomes lower, and the higher the HEP is, the faster the reliability decreases. This indicates that the error is magnified when the limitation of resources is tighter.
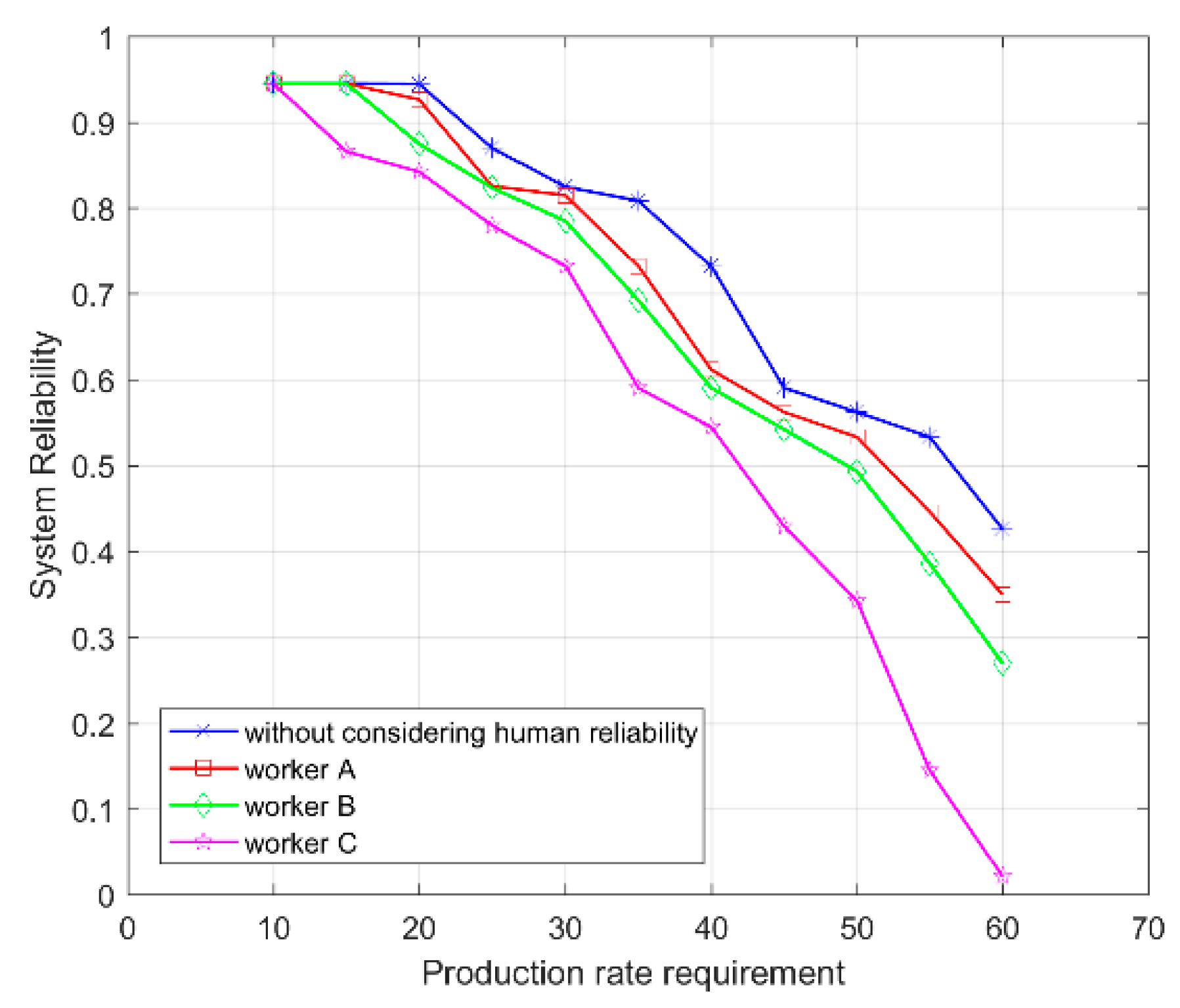
Figure 9 shows the system reliability under different performance rate requirements. It can be seen that the tighter the requirements, the lower the reliability of the system, the higher the HEP of the maintenance workers, and the faster the reliability decreases.
By comparing the system reliability with different limitations of time, costs, and performance rate, the importance of considering human reliability is fully proven. When the limitations are tighter, the impact of human reliability on the system reliability is more obvious.