Task-Level Re-Execution Framework for Improving Fault Tolerance on Symmetry Multiprocessors

Abstract

Hard real-time systems are employed in military, aeronautics, and astronautics fields where deployed systems are susceptible to software faults that can result in functional errors. Thus, there is a need to use fault-tolerant (FT) real-time scheduling. Among the various fault-tolerant real-time scheduling techniques, re-execution has been applied widely to existing real-time systems owing to its simplicity and applicability. However, re-execution requires multiple executions of every task, and some tasks miss their deadlines owing to the prolonged execution time; therefore, it has been found to be suitable for only soft real-time systems. In this paper, we propose an FT policy that can be incorporated into most (if not all) existing real-time scheduling algorithms on multiprocessor systems, which improves the reliability of the target system without a tradeoff against schedulability. As a case study, we apply the FT policy to existing fixed-priority scheduling and earliest deadline zero-laxity scheduling, and we demonstrate that it enhances reliability without schedulability loss.

1. Introduction

A computer system is referred to as a real-time system if the correctness of the system depends on not only its logical output, but also the time when the output is produced. Such times referring to the correctness of real-time are called deadlines, and the requirement to meet these deadlines is referred to as the timing constraint. There are two fundamental problems with designing a real-time system: the design of a real-time scheduling algorithm for assigning task priorities to meet deadlines and schedulability analysis for satisfying timing constraints [1].

A hard real-time system requires strict satisfaction of timing constraints; otherwise, such breaches may result in catastrophic consequences such as significant economic loss and threats to human lives. Hard real-time systems have been employed in many fields such as the military, aeronautics, and astronautics in which systems are susceptible to faults that produce a functional error. For example, a satellite system is deployed in a harsh operational environment where the state of the software can be affected by cosmic radiation [2]. In addition, such systems tend to be situated in remote and inaccessible locations, which necessitates the use of fault-tolerant real-time scheduling.

In hard real-time systems, there are several popular fault-tolerant real-time scheduling techniques such as check pointing with rollback, dual/triple modular redundancy, and re-execution [3,4,5]. The check pointing with rollback technique saves the state of the system on a stable storage at each checkpoint, and the systems rolls back to the latest checkpoint if a transient fault is detected. The dual/triple modular redundancy technique executes identical copies for each task simultaneously on multicore platforms, and their results are voted on to produce a single output. The re-execution technique executes the task multiple times and selects a correct output (without a transient fault) from the multiple executions. Thus, it re-executes the task when the correct output is not obtained at the given times of execution to improve reliability. The faults can mainly be categorized as permanent and transient [3,6]. Permanent faults normally indicate malfunction of any part that requires replacement with a spare part to restore system functionality. Transient faults are short-term faults where the system functionality is restored using a software–based approach such as re-execution.

Although re-execution with respect to a transient fault is an effective fault-tolerant technique for real-time scheduling, it is known to be suitable for only soft real-time systems [3]. This is because the technique’s main aim is to improve reliability, which can be measured based on the metric of the probability of successful executions (in terms of functionality) without any transient faults, and strict conformance to meeting a deadline is not the main requirement. The re-execution technique requires multiple executions of every task, so some deadlines may be missed owing to the prolonged execution time. Thus, studies [3,5] have focused on improving the reliability of mixed-criticality systems or energy-sensitive real-time systems while inevitably sacrificing the schedulability of the systems.

In this paper, we propose a fault-tolerant (FT) policy that can be incorporated into most existing (if not all) real-time scheduling algorithms, which improves the reliability of the target system without sacrificing schedulability. We target identical multiprocessor systems where each processor’s architecture is exactly the same. The FT policy employs the re-execution technique in conjunction with a new deadline-based schedulability analysis proposed in this paper for the re-execution technique while ensuring that the delayed finishing time of each task’s execution due to re-execution is never later than its corresponding deadline. The delayed finishing time of each task is dependent on how many times each task is executed. Here, the ${\lambda }_k$ of a task is the execution count, and the ${\lambda }_k$-assignment problem is addressed to improve reliability while conserving schedulability. As a case study, we apply the FT policy to existing fixed-priority (FP) scheduling and earliest deadline zero-laxity (EDZL) scheduling, and we demonstrate that it enhances reliability without schedulability loss.

In summary, the contributions of this paper are as follows.

• It proposes the FT policy to improves reliability of the target system scheduled by a given real-time scheduling algorithm without sacrificing schedulability.
• A new deadline-based schedulability analysis designed for the re-execution technique is proposed, which can be incorporated into the FT policy.
• FT policy incorporated into FP and EDZL scheduling are proposed as a case study.
• The conducted experiments demonstrate that the FT policy dramatically improves the performance compared to the existing techniques (utilizing the predetermined ${\lambda }_k$) when we consider the schedulability and reliability simultaneously.

The remainder of this paper is organized as follows. Section 2 presents the system model, including the task and fault models, and the safety metric. Section 3 introduces the proposed FT scheduling framework, called the FT policy. As a case study, the FT policy is applied to FP scheduling and EDZL scheduling, and its performance is evaluated in Section 4. Section 5 discusses related work. Section 6 concludes the paper.

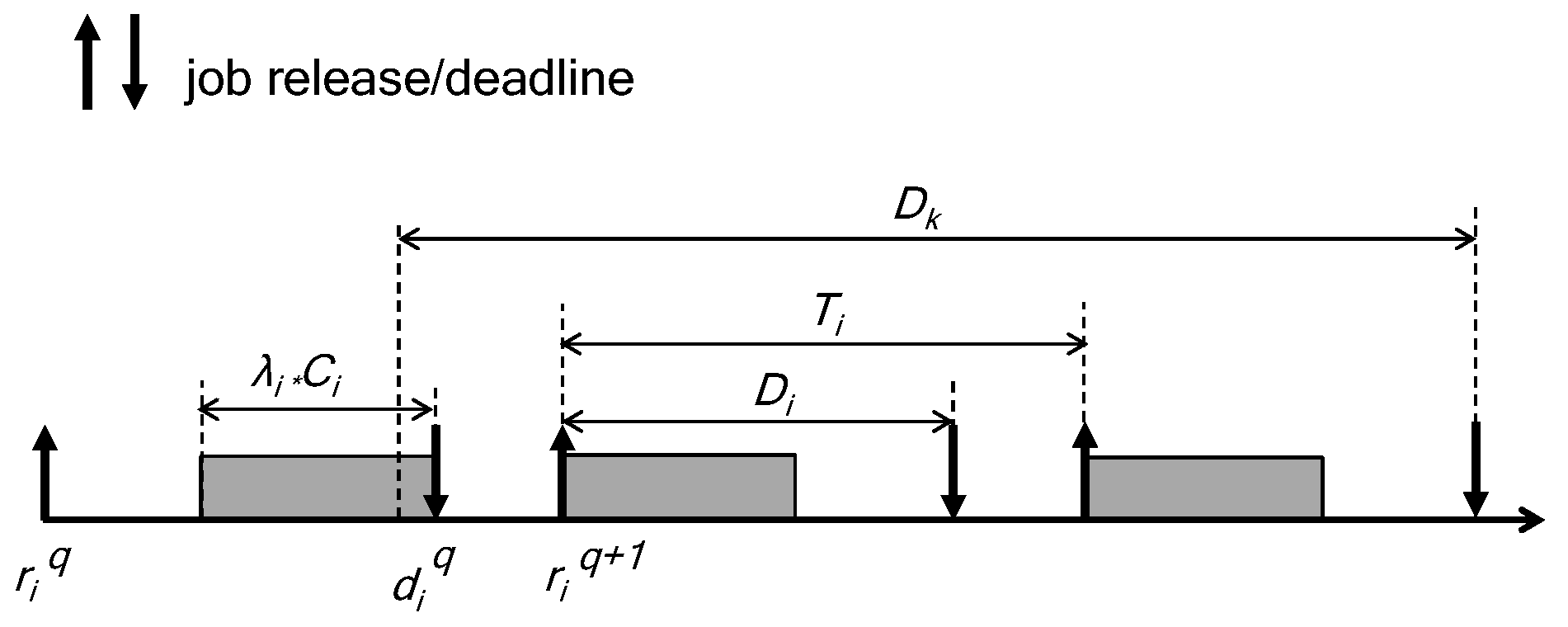
2. The System Model

In this section, we describe our system and fault models including the task and system reliability, and the system safety for a performance metric.

2.1. The Task Model

We consider a task set $\tau$ following the Liu and Layland model [1], scheduled on m processors in a hard real-time system. A task ${\tau }_k=(T_k,C_k,D_k)$ in a task set $\tau$ is supposed to invoke a series of jobs, of which the length between two consecutive job’s release times is at least $T_k$ time units. Each job should complete its worst-case execution $C_k$ within the relative deadline $D_k$. The q-th job $J_k^q$ of a task ${\tau }_k$ is released at $r_k^q$, and its has its absolute deadline $d_k^q$, meaning that $J_k^q$ should finish its execution before or at $d_k^q$ to be schedulable. The finishing time of a job $J_k^q$ is denoted by $f_k^q$. A job $J_k^q$ is said to be schedulable if $f_k^q$ is smaller than or equal to $d_k^q$. Thus, a task ${\tau }_k$ is schedulable if every job of ${\tau }_k$ is schedulable, and a task set $\tau$ is schedulable when every task ${\tau }_k$ is schedulable. We target a constrained-deadline task system in which $C_k\le D_k\le T_k$ holds for every task ${\tau }_k\in \tau$.

We consider a global preemptive work-conserving scheduling algorithm. An algorithm is referred to as global, preemptive, and work-conserving if a job can migrate from one processor to the other one, a lower-priority job’s execution can be hindered by a higher-priority job, and the scheduler always tries to keep the processors busy when there are released jobs with remaining execution. Moreover, a single job cannot execute in parallel. We assume quantum-based time where a time unit describes a quantum length of 1, meaning that all task parameters are specified by multiples of the quantum length.

2.2. The Fault Model

Among two types of faults (i.e., permanent and transient), we consider the transient fault that appears for a short time without damaging the device. Transient faults determine the reliability of a task ${\tau }_k$ (called the task reliability of ${\tau }_k$), which is defined as the probability of its successful execution (in terms of functionality) without any transient fault. An average arrival rate $\gamma$ is the expected number of failures occurring per second. Using a given fault arrival rate $\gamma$ and an exponential distribution, the task reliability (as a performance metric for fault tolerance) $R_k$ of task ${\tau }_k$ is expressed as [5]

$$\begin{array}{c}\hfill R_k=e^{-\gamma C_k}.\end{array}$$

(1)

For example, the task reliability $R_k$ of ${\tau }_k$ for given $\gamma =0.001$ and $C_k=300$ is $e^{-0.001·300}\approx 0.7408$. Thus, the system reliability $R\left(\tau \right)$ is defined as the average of the task reliability of tasks in $\tau$ calculated as

$$\begin{array}{c}\hfill R\left(\tau \right)=\frac{{\sum }_{{\tau }_k\in \tau }{R}_k}{\left|\tau \right|}.\end{array}$$

(2)

We assume that a transient fault can affect the reliability but not change the worst-case execution time $C_k$ of a task ${\tau }_k$.

When it comes to an FT technique, we adopt re-execution to improve the reliability of the target system suffering from transient faults. In the re-execution technique, the fault (if any) is supposed to be detected at the end of a job execution, and the job is re-executed when the correct output is not obtained. Specifically, each job instance of a task ${\tau }_k$ is executed $N_k$ times, and the job is re-executed if the correct output (with no transient fault) is not obtained after $N_k$ executions, thereby resulting in $N_k$ + 1 executions. ${\lambda }_k$ is the number of times that every job of a task ${\tau }_k$ is executed under the re-execution technique. For a given $N_k$, ${\lambda }_k$ is calculated by

$$\begin{array}{c}\hfill {\lambda }_k=N_k+1.\end{array}$$

(3)

We suppose that at most one transient fault can occur for a single job instance by following a common assumption [7]. Moreover, each execution over the ${\lambda }_k$ executions shares the same absolute deadline $d_k^q$.

By the definition of reliability, $1-R_k$ implies the possibility that a job of a task ${\tau }_k$ does not successfully execute without any transient fault. Since a job is executed ${\lambda }_k$ times when the correct output is not obtained over $N_k$ executions in the re-execution technique, the reliability of a task ${\tau }_k$ is expressed as follows:

$$\begin{array}{c}\hfill R_k=1-{(1-e^{-\gamma C_k})}^{{\lambda }_k}.\end{array}$$

(4)

For example, the task reliability $R_k$ of ${\tau }_k$ for given $\gamma =0.001$, $C_k=300$, and ${\lambda }_k=3$ is $1-{(1-e^{-0.001·300})}^3\approx 0.9826$.

The reliability of a hard real-time system should be maintained at a high level, and every single execution of a task should be finished before its corresponding absolute deadline. To support this requirement, we propose a new metric, i.e., system safety, to quantify the system’s reliability and schedulability simultaneously. The system safety $S\left(\tau \right)$ is given by $R\left(\tau \right)$ (i.e., $R\left(\tau \right)·1$) if $\tau$ is schedulable and 0 (i.e., $R\left(\tau \right)·0$) otherwise. Thus, the system safety indicates the system reliability of a schedulable task set.

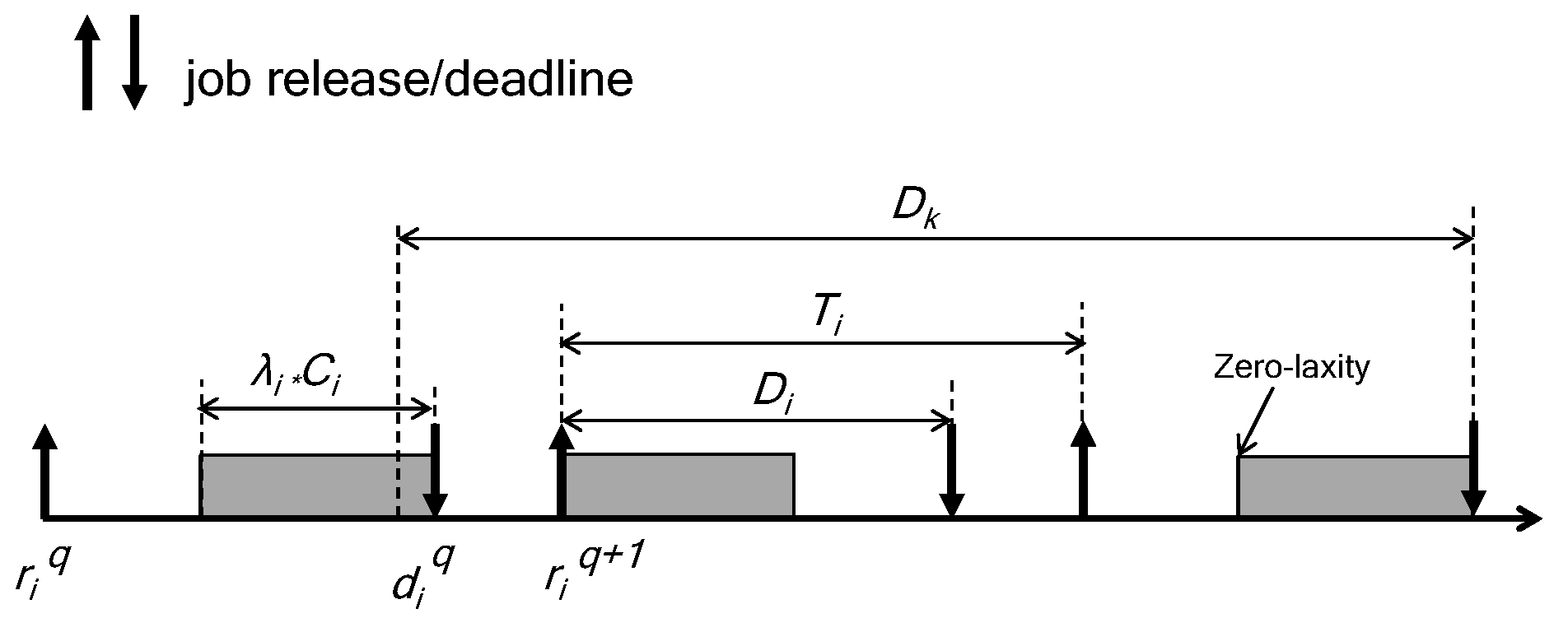
3. The Fault-Tolerant Scheduling Framework

In this section, we present the FT policy that can be incorporated into most (if not all) existing real-time scheduling algorithms, which can improve reliability by exploiting the re-execution technique without sacrificing the schedulability of task sets under the scheduling algorithm. Thus, we perform a schedulability analysis to support the use of the policy.

3.1. The Scheduling Algorithm Incorporating FT Policy

As mentioned in Section 1, we aim at improving the reliability of the target systems without degrading the schedulability. Basically, the re-execution technique increases the number of times that every job of a task ${\tau }_k$ is executed. Thus, it inevitably prolongs the finishing time of every job of ${\tau }_k$, and conditionally (depending on the scheduling policy) increases interference in the other tasks. Based on this reasoning, we need to address the following questions:

Q1

How can ${\lambda }_k$ of ${\tau }_k$ be determined without compromising the schedulability of ${\tau }_k$?

Q2

How can ${\lambda }_k$ of ${\tau }_k$ be determined without compromising the schedulability of the other tasks ${\tau }_i$?

To address both questions (Q1–2), we should guarantee that the increased finishing time (due to ${\lambda }_k$ of ${\tau }_k$) of every job $J_k^q$ (likewise, $J_i^q$) of a task ${\tau }_k$ (likewise, ${\tau }_i\in \tau \backslash {\tau }_k$) should be less than or equal to the corresponding absolute deadline $d_k^q$ (likewise, $d_i^q$). One may argue that the finishing time $f_k^q$ of a job $J_k^q$ will be prolonged exactly by ${\lambda }_k·C_k$ (e.g., in the case of the detection of a transient fault) for a given ${\lambda }_k$. However, such a phenomenon only occurs when ${\tau }_k$ is highest priority so that every job $f_k^q$ of ${\tau }_k$ does not suffer from any interference from the other tasks. Depending on the considered scheduling algorithm (e.g., whether a task-level or job-level priority assignment policy), the increased finishing time $f_k^q$ can be greater than ${\lambda }_k·C_k$ due to the interference of other tasks while executing for ${\lambda }_k·C_k$ for a given ${\lambda }_k$. Therefore, we should ensure an upper bound on the interference from other tasks while executing for ${\lambda }_k·C_k$, and carefully consider this for determining ${\lambda }_k$ of ${\tau }_k$ to conserve schedulability.

The FT policy effectively assigns the value of ${\lambda }_k$ using the ${\lambda }_k$-assignment algorithm so that the prolonged finishing time $f_k^q$ never exceeds $d_k^q$. With ${\lambda }_k$ of every task ${\tau }_k$, a task set τ is scheduled according to the base scheduling algorithm. Every job $J_k^q$ is executed at least ${\lambda }_k-1$ times, and once again when the correct output is not obtained.

Algorithm 1 illustrates how the FT-policy-incorporated scheduling algorithm operates. Before the system starts, ${\lambda }_k$ for every task ${\tau }_k$ is assigned by a given ${\lambda }_k$-assignment algorithm (Line 1); we will describe how ${\lambda }_k$-assignment algorithm operates in Section 3.3. For every time instant t, a job $J_k^q$ of a task ${\tau }_k$ is inserted in a ready queue $Q_{ready}$ whenever $J_k^q$ is released (Lines 3–5). Released jobs in $Q_{ready}$ are scheduled according to a given base scheduling algorithm (Line 6). Each job in $Q_{ready}$ is executed at least ${\lambda }_k-1$ times and once again if a fault is detected (Lines 7–9). Finally, $J_k^q$ is removed from $Q_{ready}$ when the execution of $J_k^q$ is completed.

Algorithm 1 The FT-policy-incorporated scheduling algorithm.

1: ${\lambda }_k$ for every ${\tau }_k$ is assigned by a given ${\lambda }_k$ assignment algorithm (Algorithm 2)  2: for Every time instance t do  3: if $J_k^q$ is released by ${\tau }_k$ then  4:  Insert $J_k^q$ into $Q_{ready}$  5: end if  6: Schedule jobs in $Q_{ready}$ according to a given base scheduling algorithm  7: if ${\lambda }_k-1$ times of executions are completed for $J_k^q$, and a fault is detected then  8:  Execute $J_k^q$ again.  9: end if 10: if $J_k^q$ finishes its execution then 11:  Delete $J_k^q$ from $Q_{ready}$ 12: end if 13: end for

3.2. Schedulability Analysis

Since our goal is to ensure schedulability while improving reliability, we must be able to judge whether the task set $\tau$ is schedulable with the given values of ${\lambda }_k$ for every task ${\tau }_k$. To do so, we utilize a deadline-based analysis technique that has been widely used in real-time multiprocessor scheduling [8,9,10] and modify it to support the FT policy.

Deadline-based analysis for multiprocessor systems employs the concept of interference [11]. The interference in ${\tau }_k$ in an interval $[a,b)$, which is denoted by $I({\tau }_k,a,b)$, is the cumulative length of all sub-intervals in $[a,b)$ such that a job of ${\tau }_k$ cannot be executed due to the execution of other higher-priority jobs even though it is ready to be executed. In addition, the interference of ${\tau }_i$ with ${\tau }_k$ in $[a,b)$, which is denoted by $I({\tau }_k\leftarrow {\tau }_i,a,b)$, is the cumulative length of all sub-intervals in $[a,b)$ such that a job of ${\tau }_i$ is executed even though a job of ${\tau }_k$ is ready to be executed. Since the execution of a job (in a ready queue) of ${\tau }_k$ is hindered when m other jobs are executed at the same time instance, $I({\tau }_k,a,b)$ under any global work-conserving can be upper-bounded by [11]

$$\begin{array}{c}\hfill I({\tau }_k,a,b)=\frac{{\sum }_{{\tau }_i\in \tau \backslash \left\{{\tau }_k\right\}}I({\tau }_k\leftarrow {\tau }_i,a,b)}{m}.\end{array}$$

(5)

As derived in [11], the relationship between $I({\tau }_k,a,b)$ and $I({\tau }_k\leftarrow {\tau }_i,a,b)$ for any arbitrary positive x is as follows.

$$\begin{array}{c}\hfill I({\tau }_k,a,b)<x\iff \sum _{{\tau }_i\in \tau \backslash \left\{{\tau }_k\right\}}min\left(I({\tau }_k\leftarrow {\tau }_i,a,b),x\right)<m·x.\end{array}$$

(6)

We also let $\mathbf{I}({\tau }_k\leftarrow {\tau }_i)$ be the maximum interference of ${\tau }_i$ $\in \tau \backslash \left\{{\tau }_k\right\}$ with ${\tau }_k$ in an interval of length $D_k$ between $r_k^q$ and $f_k^q$ of any job $J_k^q$ of ${\tau }_k$, which is expressed as

$$\begin{array}{c}\hfill \mathbf{I}({\tau }_k\leftarrow {\tau }_i)\triangleq \underset{t|\mathrm{the}\mathrm{release}\mathrm{time}\mathrm{of}\mathrm{any}\mathrm{job}\mathrm{of}{\tau }_k}{max}I({\tau }_k\leftarrow {\tau }_i,t,t+D_k).\end{array}$$

(7)

Any job of ${\tau }_k$ is successfully executed before its deadline if the maximum interference in ${\tau }_k$ in an interval of length $D_k$ starting from the release time of any job of ${\tau }_k$ is strictly less than $D_k-C_k+1$. The deadline-based schedulability analysis is expressed as follows using Equations (6) and (7).

Lemma 1

(Theorem 5 in [8]). Suppose that a task set τ is scheduled by a global, preemptive, and work-conserving algorithm. Thus, τ is schedulable if the following inequality holds for all ${\tau }_k\in \tau$.

$$\begin{array}{c}\hfill \sum _{{\tau }_i\in \tau \backslash \left\{{\tau }_k\right\}}min\left(\mathbf{I}({\tau }_k\leftarrow {\tau }_i),D_k-C_k+1\right)<m·(D_k-C_k+1).\end{array}$$

(8)

Proof. 

We briefly summarize the proof of Theorem 5 in [8]. To miss a deadline for a job of ${\tau }_k$ scheduled on m processors, the job executes in at most $C_k-1$ time instances. At each time instance, at least m other jobs are required to hinder the execution of a job of ${\tau }_k$. Hence, at least $m·(D_k-(C_k-1))$ amount of interference of other tasks with ${\tau }_k$ is required to miss the job’s deadline. □

We now develop $\mathbf{I}({\tau }_k\leftarrow {\tau }_i)$ for any work-conserving scheduling algorithm incorporating the FT policy. To upper-bound $\mathbf{I}({\tau }_k\leftarrow {\tau }_i)$, we exploit the notion of the workload of a task ${\tau }_i$ in an interval of length ℓ, which is defined as the amount of computation time required for ${\tau }_k$ in the interval of length ℓ [12]. Figure 1 describes the scenario where the workload of a task ${\tau }_k$ is maximized under any preemptive scheduling incorporating the FT policy with a given value of ${\lambda }_i$. As seen in Figure 1, the left-most job of ${\tau }_i$ starts its execution at the beginning of the interval and finishes at $d_i^q$, which executes for ${\lambda }_i·C_i$ without any interference or delay. Thus, the following jobs are released and scheduled as soon as possible. Thus, the workload $W_i(\ell )$ of a task ${\tau }_i$ under any preemptive scheduling incorporating the FT policy with a given value of ${\lambda }_i$ in an interval of length ℓ is upper-bounded as

$$\begin{array}{c}\hfill W_i(\ell )=F_i(\ell )·{\lambda }_i·C_i+min\left({\lambda }_i·C_i,\ell +D_i-{\lambda }_i·C_i-F_i(\ell )·T_i\right)\end{array}$$

(9)

where $F_i(\ell )$ is the number of jobs executed for $\lambda ·C_i$ calculated by

$$\begin{array}{c}\hfill F_i(\ell )=⌊\frac{\ell +D_i-{\lambda }_i·C_i}{T_i}⌋.\end{array}$$

(10)

Thus, the following theorem is derived.

Theorem 1.

Suppose that a task set τ (which holds that ${\lambda }_k·C_k\le D_k$ for every ${\tau }_k\in \tau$) is scheduled by the FT policy with a given base algorithm. Thus, τ is schedulable if the following inequality holds for all ${\tau }_k\in \tau$

$$\begin{array}{c}\hfill \sum _{{\tau }_i\in \tau \backslash \left\{{\tau }_k\right\}}min\left(W_i\left(D_k\right),D_k-{\lambda }_k·C_k+1\right)<m·(D_k-{\lambda }_k·C_k+1).\end{array}$$

(11)

Proof. 

To miss a deadline for a job of ${\tau }_k$ under the FT policy with a given base algorithm on m processors, the job executes in at most ${\lambda }_k·C_k-1$ time instances. At each time instance, at least m other jobs are required to hinder the execution of a job of ${\tau }_k$. Hence, at least $m·(D_k-({\lambda }_k·C_k-1))$ amount of interference of other tasks with ${\tau }_k$ is required to miss the job’s deadline. □

3.3. The ${\lambda }_k$-Assignment Algorithm

Under the base scheduling algorithm employing the FT policy, it is guaranteed that increased the finishing time of any job $J_k^q$ due to a given ${\lambda }_k$ of ${\tau }_k$ is never later than its absolute deadline $d_k^q$. The FT policy assigns such ${\lambda }_k$ by exploiting the ${\lambda }_k$-assignment algorithm, which is described in this subsection.

The ${\lambda }_k$-assignment algorithm selects a task ${\tau }_j$ of a task set $\tau$ according to a given selection algorithm, and increases the value of ${\lambda }_j$ one by one while checking that the increased value of ${\lambda }_j$ does not make the schedulable task set unschedulable with a given schedulability analysis. (Note that we use another task index j to indicate a selected task ${\tau }_j$ for avoiding confusion since k indicates the index of an arbitrary task as we presented in Section 2.) It repeats this for every task ${\tau }_j$ in $\tau$. A number of selection algorithms can be applied for this such as highest-priority first (i.e., selected in an order of scheduling priority).

Algorithm 2 presents how the ${\lambda }_k$-assignment algorithm operates. It first sets ${\lambda }_k$ to zero for every task ${\tau }_k$ (Line 1). For every task ${\tau }_j$ selected by a given selection algorithm (Line 2), it increases the value of ${\lambda }_j$ of a task ${\tau }_j\in \tau$ one by one until $\tau$ is deemed unschedulable (Lines 3–5). Note that a task ${\tau }_j$ that holds ${\lambda }_j·C_j>D_j$ naturally misses its deadline without any interference, so we assume that $\tau$ containing such ${\tau }_j$ is unschedulable. Thus, it decreases ${\lambda }_j$ by one to make $\tau$ schedulable (Line 6). Lines 3–6 are repeated for each task ${\tau }_j$ selected by a given selection algorithm. The time complexity of Algorithm 2 is obtained as follows. It first initiates ${\lambda }_k$ for every task ${\tau }_k$ in Line 1, which needs $O\left(n\right)$ where n is the number of tasks in a task set $\tau$. Thus, it considers a task ${\tau }_j\in \tau$ one by one in Line 2, which requires $O\left(n\right)$. In Line 3, it repeatably conducts the schedulability analysis proposed in Theorem 1 while the condition in Line 3 holds. Since the calculation of the left-hand side and right-hand side in Equation (11) are done with $O\left(n\right)$ and $O\left(1\right)$ (i.e., constant time), the analysis requires $O\left(n\right)$ in terms of time complexity. Because ${\lambda }_j$ increases by one at each iteration, Line 3 in Algorithm 2 can be conducted at most $\frac{C_j}{D_j}$ times. Lines 4 and 6 are performed in a constant time. As a result, the time complexity of Algorithm 2 is $O(n)+O(n)·(O(n)·\frac{C_j}{D_j})$ = $O(n^2)·\frac{C_j}{D_j}$.

Algorithm 2${\lambda }_k$-Assignment Algorithm

1: ${\lambda }_k\leftarrow 0$ for all tasks ${\tau }_k\in \tau$  2: for ${\tau }_j$ from the first task to the last one selected by a given selection algorithm do  3: while $\tau$ is deemed schedulable by Theorem 1, and ${\lambda }_j·C_j\le D_j$ holds do  4:  ${\lambda }_j\leftarrow {\lambda }_j+1$  5: end while  6: ${\lambda }_j\leftarrow {\lambda }_j-1$  7: end for

4. Case Study

In this section, we apply the FT policy to FP scheduling and EDZL scheduling (we denote it by FT-FP-A and FT-EDZL-A, respectively) as a case study.

4.1. Schedulability Analysis for FT-FP-A

In FP scheduling, a priority is assigned to a task rather than each job. Thus, only a higher-priority task ${\tau }_i$ can interfere with a job $J_k^q$ of a lower-priority task ${\tau }_k$. Well-known FP scheduling algorithms include rate monotonic (RM) [13] and earliest quasi-deadline first (EQDF) [14]; a task whose $T_k$ (likewise $D_k-C_k$) is smaller than that of other tasks has a higher priority under the RM (likewise EQDF) scheduling algorithm. We denote FP scheduling incorporating the FT policy with ${\lambda }_k$-assignment algorithm A employing any sorting algorithm by FT-FP-A. Let $HP\left({\tau }_k\right)$ be a set of tasks whose priorities are higher than ${\tau }_k$. Thus, Theorem 1 is re-formulated for FP scheduling as follows.

Theorem 2.

Suppose that a task set τ (which holds that ${\lambda }_k·C_k\le D_k$ for every ${\tau }_k\in \tau$) is scheduled by FT-FP-A. Thus, τ is schedulable if the following inequality holds for all ${\tau }_k\in \tau$

$$\begin{array}{c}\hfill \sum _{{\tau }_i\in HP\left({\tau }_k\right)}min\left(W_i\left(D_k\right),D_k-{\lambda }_k·C_k+1\right)<m·(D_k-{\lambda }_k·C_k+1).\end{array}$$

(12)

Proof. 

To miss a deadline for a job of ${\tau }_k$ under FT-FP-A scheduling on m processors, the job executes in at most ${\lambda }_k·C_k-1$ time instances due to the existence of higher-priority tasks. At each time instance, at least m other jobs are required to hinder the execution of a job of ${\tau }_k$. Hence, at least $m·(D_k-({\lambda }_k·C_k-1))$ amount of interference of tasks in $HP\left({\tau }_k\right)$ with ${\tau }_k$ is required to miss the job’s deadline. □

Thus, we schedule a given task set $\tau$ by FT-FP-A (Algorithm 1) exploiting ${\lambda }_k$-assignment algorithm A (Algorithm 2 with Theorem 2 instead of Theorem 1 in Line 3).

4.2. Schedulability Analysis for FT-EDZL-A

The EDZL scheduling algorithm assigns a higher priority to a job $J_k^q$ whose absolute deadline $d_k^q$ is earlier than that of other jobs such as earliest deadline first (EDF) scheduling. Thus, it promotes the job’s priority (to the highest) at time instance t at which the job’s laxity (The laxity of a job $J_k^q$ is defined as the difference between $d_k^q-t$ (i.e., the remaining time instances up to $d_k^q$) and the remaining executions of $J_k^q$ to finish.) is zero (i.e., $d_k^q-t$ is equal to the remaining execution time of the job) because the job would miss its deadline otherwise.

For deadline-based schedulability analysis for FT-EDZL-A, we first upper-bound $\mathbf{I}({\tau }_k\leftarrow {\tau }_i)$ under work-conserving EDF scheduling. Figure 2 illustrates the worst-case release pattern of higher-priority jobs of ${\tau }_i$ in an interval $D_k$. As shown in Figure 2, the interference from higher-priority jobs to $J_k^q$ is maximized when their absolute deadlines are aligned because $J_i^q$ whose $d_i^q$ is later than $d_k^q$ cannot interfere with $J_k^q$. Thus, the upper bound of the amount of interference from the jobs of ${\tau }_i$ to a job of ${\tau }_k$ is calculated by $E\left(D_k\right)$ as follows:

$$\begin{array}{c}\hfill E\left(D_k\right)=⌊\frac{D_k}{T_i}⌋·{\lambda }_i·C_i+min\left({\lambda }_i·C_i,D_k-⌊\frac{D_k}{T_i}⌋·T_i\right).\end{array}$$

(13)

Thus, we schedule a given task set $\tau$ by FT-EDZL-A (Algorithm 1) exploiting ${\lambda }_k$-assignment algorithm A (Algorithm 2 with Theorem 3 instead of Theorem 1 in Line 3).

Under EDZL scheduling, a job $J_i^q$ can interfere with $J_k^q$ even if $J_i^q$’s deadline is later than $J_k^q$’s deadline. This happens only when $J_i^q$ is in the zero-laxity state and its priority is promoted. Figure 3 illustrates a job (the right-most one in the figure) of ${\tau }_i$ is in the zero-laxity state. The key characteristic of such a job is that it finishes its execution at its absolute deadline. Thus, Figure 3 also derives the same upper bound of the amount of interference from the jobs of ${\tau }_i$ to a job of ${\tau }_k$ with Equation (13).

In order for a job to miss its absolute deadline under EDZL scheduling on an m-processor platform, there should be at least $m+1$ zero-laxity jobs at the same time instance. Based on this reasoning, we derive the following schedulability conditions for FT-EDZL-A.

Theorem 3.

Suppose that a task set τ (which holds that ${\lambda }_k·C_k\le D_k$ for every ${\tau }_k\in \tau$) is scheduled by FT-EDZL-A. Thus, τ is schedulable if the following inequality holds for at least $\tau -m$ tasks ${\tau }_k\in \tau$

$$\begin{array}{c}\hfill \sum _{{\tau }_i\in \tau \backslash \left\{{\tau }_k\right\}}min\left(E_i\left(D_k\right),D_k-{\lambda }_k·C_k\right)<m·(D_k-{\lambda }_k·C_k).\end{array}$$

(14)

Proof. 

To be in the zero-laxity state for a job of ${\tau }_k$ under FT-EDZL-A scheduling on m processors, the job is interfered in $D_k-{\lambda }_k·C_k$ time instances. At each time instance, at least m other jobs are required to hinder the execution of a job of ${\tau }_k$. Thus, at least $m·(D_k-{\lambda }_k·C_k)$ amount of interference of higher-priority jobs with ${\tau }_k$ is required to be in the zero-laxity state for a job of ${\tau }_k$. Moreover, there should be at least $m+1$ zero-laxity jobs at the same time instance in order for a job to miss its absolute deadline on an m-processor platform. Thus, the theorem holds. □

4.3. Evaluation Environment

In this subsection, we evaluate the performance of the considered scheduling algorithms incorporating the proposed FT policy.

For our evaluation, we randomly generate task sets based on a well-known task set generation framework [8,15,16]. For the input parameters, we consider the number of processors $m\in \{2,4,8,16\}$ and the individual task utilization ($C_i/T_i$) distribution (bimodal or exponential with its input parameter chosen in $\{0.1,0.3,0.5,0.7,0.9\}$ [17]). For a given bimodal input parameter p, the $C_i/T_i$ value is uniformly selected in [0, 0.5) and [0.5, 1) with probability p and $1-p$, respectively. For a given exponential input parameter $1/\beta$, the value is selected according to the exponential distribution whose probability density function is $\beta ·exp(-\beta ·x)$. For each task, $T_i$ is uniformly chosen in $[1,1000]$, $C_i$ is determined by the bimodal or exponential parameter, and $D_i$ is uniformly chosen in $[C_i,T_i]$. We generate 10,000 task sets for each value of m. We then measure the number of tasks sets deemed schedulable by the proposed schedulability analysis, as well as the average system safety of task sets (defined as the average of the considered task sets’ system safety), as performance metrics.

We consider the following schedulability tests (as well as the corresponding scheduling algorithms for measuring the system safety):

• $\mathsf{EDZL}$: for the EDZL scheduling algorithm (Equation (14) with every ${\lambda }_k=1$);
• $\mathsf{RM}$ (also denoted by $\mathsf{RM}$-$\mathsf{1}$): for the RM scheduling algorithm (Equation (12) with every ${\lambda }_k=1$),
• $\mathsf{EQDF}$: for the EQDF scheduling algorithm (Equation (12) with every ${\lambda }_k=1$);
• $\mathsf{FT}$-$\mathsf{EDZL}$-$\mathsf{Any}$: for the EDZL scheduling algorithm incorporating the FT policy in which the ${\lambda }_k$-assignment algorithm increases ${\lambda }_k$ in an order of index k (Equation (14) with ${\lambda }_k$ determined by a given ${\lambda }_k$-assignment algorithm);
• $\mathsf{FT}$-$\mathsf{RM}$-$\mathsf{Inverse}$: for the RM scheduling algorithm incorporating the FT policy in which the ${\lambda }_k$-assignment algorithm increases ${\lambda }_k$ in an order of task priority (Equation (12) with ${\lambda }_k$ determined by a given ${\lambda }_k$-assignment algorithm);
• $\mathsf{FT}$-$\mathsf{EQDF}$-$\mathsf{Inverse}$: for the EQDF scheduling algorithm incorporating the FT policy in which the ${\lambda }_k$-assignment algorithm increases ${\lambda }_k$ in an order of task priority (Equation (12) with ${\lambda }_k$ determined by a given ${\lambda }_k$-assignment algorithm);
• $\mathsf{RM}$-$\mathsf{2}$: for the RM scheduling algorithm (Equation (12) with every ${\lambda }_k=2$);
• $\mathsf{RM}$-$\mathsf{3}$: for the RM scheduling algorithm (Equation (12) with every ${\lambda }_k=3$).

4.4. Example of a Task Set: ACSW in Satellite Systems

In this subsection, we illustrate an actual real-time system whose operational characteristic can be specified by task parameters described in the previous subsection. A reconnaissance satellite system is a compelling example of a real-time system, which is equipped with a reconnaissance antenna to obtain a signal image of the target terrain by transmitting and receiving radio frequency signals. In a reconnaissance satellite system, antenna controller software (ACSW) [18] controls a reconnaissance antenna, of which tasks are scheduled by RM on RTEMS (real-time executive for multi-processor systems) [19] as a space-specific RTOS (real-time operating system). ACSW typically consists of five main tasks named tHigh, tMilbus, tOne, tTwo, and tSync, respectively, whose high-level description of main operation is described as follows.

• tHigh retrieves a single macro command (MCMD) from an MCMD queue in every period and invokes a job corresponding to the MCMD.
• tMilbus is responsible for receiving MCMDs from the ground station by utilizing the MIL-STD-1553B protocol [20] and verifies the integrity of each MCMD before the MCMD is inserted into an MCMD queue.
• tOne performs internal mode transitions such as turning on/off relevant equipment and transmits internal telemetries via the SpaceWire protocol [21].
• tTwo conducts various executions such as fault detection, formatting network packets that will be transferred to the ground station.
• tSync executes a job for the operation preparation whenever there are surplus computing resources.

Table 1. Task parameters (millisecond base) of antenna controller software (ACSW).

	${\mathit{T}}_{\mathit{i}}$	${\mathit{D}}_{\mathit{i}}$	WCET	BCET	ACET
tHigh	62.5	50	2.98	0.08	0.14
tMilbus	125	100	0.54	0.11	0.21
tOne	250	200	30.08	0.05	0.29
tTwo	500	400	231.72	37.7	147.5

describes task parameters of the five tasks. $T_i$ and $D_i$ are determined by the system designer by considering the operating concept of the ACSW. That is, tHigh takes an MCMD from an MCMD queue every 62.5 ms, tMilbus receives an MCMD from the ground station every 125 ms, an internal mode transition occurs by tOne every 250 ms, and tTwo transmits the system status to the ground station every 500 ms. tSync does not have specified task parameters because it executes without deadlines when the other tasks are inactive. Thus, WCET, best case execution time (BCET), and average case execution time (ACET) are measured on a multiprocessor platform equipped with 256 Mbps SDRAM and FT-Leon3 CPU architecture (80 Mhz clock rate). Since the task set generation method described in the previous subsection considers a number of task sets whose parameters are randomly selected, it can cover various real-time embedded systems in which tasks conduct different roles in various operation scenarios.

4.5. Evaluation Results

Figure 4a,b plot the number of tasks deemed schedulable under the considered schedulability tests according to varying task set utilization $\left({\sum }_{{\tau }_k\in \tau }{C}_k/T_k\right)$ for $m=4$ and $m=16$, respectively. Note that the FT policy does not compromise the schedulability of the base scheduling algorithm B, so algorithm B in Figure 4a,b also represents B incorporating the FT policy. For example, the number of task sets deemed schedulable by $\mathsf{EDZL}$ and $\mathsf{FT}$-$\mathsf{EDZL}$-$\mathsf{Any}$ is the same. As shown in Figure 4a,b, $\mathsf{EQDF}$ (largely) outperforms $\mathsf{EDZL}$, which performs better than $\mathsf{RM}$.

Figure 4c,d show the average system safety (i.e., the average system reliability of schedulable task sets) of task sets under the considered techniques for $\gamma =0.001$. As shown, the average system safety of the considered techniques decreases with increasing task set utilization because the system safety is zero when the task set $\tau$ is unschedulable. Similar to Figure 4a,b, $\mathsf{EQDF}$ (largely) is shown to outperform $\mathsf{EDZL}$, which also outperforms $\mathsf{RM}$. This is because a better-performing schedulability analysis finds a higher number of schedulable task sets whose system safety is not zero. Moreover, the $\mathsf{FT}$-series improves the average system safety for every task set utilization since the FT policy increases (or at least does not decrease) ${\lambda }_k$ of all tasks, thereby increasing the system reliability.

A comparison of Figure 4e,f to Figure 4c,d, respectively, shows that the average system safety of considered techniques decreases due to a higher error rate $\gamma$ (i.e., 0.01 compared to 0.001). However, the performance gap between the schedulability tests of the base algorithms (i.e., $\mathsf{EQDF}$, $\mathsf{EDZL}$, and $\mathsf{RM}$) and those incorporating the FT policy becomes larger as $\gamma$ increases. This phenomenon happens because the system reliability is dramatically degraded with an increasing value of $\gamma$ (as Equation (2) implies), but ${\lambda }_k$ assigned by the FT policy makes up such system-safety degradation. Figure 4 excludes the evaluation results regarding the FT policy in which the ${\lambda }_k$-assignment algorithm increases ${\lambda }_k$ in an order of lower task priority (e.g., denoted by $\mathsf{FT}$-$\mathsf{RM}$-$\mathsf{Reverse}$) because the trends demonstrated are similar to those shown in Figure 4c–f.

Figure 5 presents the average system safety of task sets under RM with different ${\lambda }_k$ assignments for $\gamma =0.01$. As shown in Figure 5, the higher number of re-executions (i.e., a greater value of ${\lambda }_k$) dramatically decreases the average system safety. It indicates that the schedulability is more important than the system reliability to obtain a high level of the average system safety. That is, a greater value of $N_k$ improves the system reliability according to Equation (4), while schedulability is not guaranteed when such an increase of $N_k$ is conducted not in conjunction with schedulability analysis. Thus, the higher number of re-executions compromises the average system safety due to the degraded schedulability even though it may improve reliability. Note that the system safety is 0 for an unschedulale task set according to the definitions of the system safety, as presented in Section 2.

5. Related Work

While a number of FT techniques have been previously implemented using hardware, hybrid software-based techniques such as checkpointing with rollback and re-execution have been proposed recently [3,4,5]. The former manages checkpoints at which the state of the system is saved on stable storage and recovered at the latest checkpoint in case of a transient fault. The latter executes tasks multiple times (e.g., ${\lambda }_k-1$ times) and chooses a correct output (if any) obtained over multiple executions. If all outputs during the ${\lambda }_k-1$ executions are not correct, the tasks are re-executed to improve reliability. Some tasks are executed multiple times under this technique, so they may miss their deadlines. Thus, existing studies [4,5] have focused on improving the reliability of mixed-criticality systems or energy-sensitive real-time systems while inevitably sacrificing the schedulability of the systems.

In multiprocessor domains, we can utilize the power of multiprocessors to tolerate faults. One popular approach for this is primary-backup approaches [22,23,24]. In this approach, the backup of a task does not need to be executed if its primary executes successfully. Backup overloading allows backup copies of primary tasks to be scheduled in a time-overlapping manner for task efficiency [22]. Backup overloading was improved by Manimaran and Murthy [23]. Another efficient overloading algorithm on multiprocessors was proposed with dynamic logical grouping among copies of tasks [24].

There are other ways to support fault tolerance in multiprocessors [25,26]. Cirinei et al. proposed a dynamic reconfiguration of multiprocessor hardware platforms considering the tradeoff between performance and fault tolerance (through simultaneous replication) [25]. Liberato et al. proposed FT global multiprocessor scheduling by re-executing an instance of a faulty job [26].

6. Conclusions

We proposed an FT policy that can be incorporated into most (if not all) existing real-time scheduling algorithms on multiprocessor systems, which improves the reliability of a target system without sacrificing schedulability. Our study was inspired by the fact that existing re-execution techniques enforce multiple executions of some tasks to improve system reliability, which can result in a loss of schedulability of schedulable tasks. Our proposed FT policy employs the re-execution technique in conjunction with deadline-based schedulability analysis while ensuring that schedulable task sets under the FT policy never become unschedulable. As a case study, we applied the FT policy to existing FP scheduling and EDZL scheduling and evaluate its performance regarding schedulability and reliability. In future, we plan to extend our work to mixed-criticality systems and try to apply better schedulability analysis techniques such as response-time analysis to improve the analytical capability of the FT policy.