1. Introduction
Chaotic time series exist in a wide range of areas, such as nature, the economy, society, and industry. They contain many important and valuable information, useful for complex system modeling and prediction. Time series data mining is an important means of the control and decision-making of practical problems in various fields [
1,
2]. In recent years, scholars have carried out a great amount of research work on chaotic time series analysis and prediction. Han et al. [
3] proposed an improved extreme learning machine combined with a hybrid variable selection algorithm for the prediction of multivariate chaotic time series, which can achieve high predictive accuracy and reliable performance. Chandra [
4] put forward a competitive cooperative coevolution algorithm to train recurrent neural networks (RNNs) for chaotic time series prediction. Yaslan et al. [
5] presented a hybrid model based on empirical mode decomposition (EMD) and support vector regression (SVR) for electricity load forecasting. Chen [
6] proposed a prediction model of a radial basis function (RBF) neural network optimized by an artificial bee colony algorithm for prediction of traffic flow time series. A multilayered echo state machine with the addition of multiple layers of reservoirs was introduced in [
7], and it could be more robust than the echo state network with a conventional reservoir in dealing with chaotic time series prediction.
The time series prediction models proposed in recent years are usually divided into three types: statistical models, artificial intelligence models, and hybrid models. The statistical models mainly include autoregressive (AR) models [
8], the autoregressive moving average (ARMA), the autoregressive integrated moving average (ARIMA) [
9], multivariate linear regression, the Gaussian process [
10], and so on. Since statistical models require time series to be subject to certain a priori assumptions, such as stationarity, they are not ideal for practical systems with many uncertainties. With the development of computational intelligence, artificial intelligence models have obtained widespread attention. They are data-driven methods that do not require any a priori assumptions and thus have a wide range of applications. Commonly used artificial intelligence models include support vector regression [
11], RBF neural networks [
12], Elman neural networks [
4], echo state networks [
7], deep neural networks [
13], extended Kalman filters [
14], adaptive neuro-fuzzy inference systems (ANFISs) [
15,
16,
17], etc. So as to improve the performance of single-model-based prediction models, a novel framework based on decomposition algorithm has been introduced for time series prediction [
18]. Multiple decomposition methods have been put forward to analyze time series, thus forming the hybrid prediction models [
19]. The subsequences obtained by the decomposition algorithms are much easier to predict than the original time series, which brings forward a new means of predicting nonlinear and non-stationary time series [
20]. Ren et al. [
21] introduced a hybrid model, EMD combined with kNN, for wind speed prediction. The model generated a set of feature vectors from the components obtained by EMD, and kNN was then employed for prediction. The suggested hybrid model performed well for long-term wind speed forecasting. An ensemble EMD (EEMD)–ARIMA model has been proposed to predict annual runoff time series [
22]. According to the experimental results, it was concluded that the introduction of EEMD could observably improve prediction performance, and the EEMD–ARIMA model was superior to the ARIMA. It is confirmed that hybrid models perform better than their corresponding single models in chaotic time series prediction.
Though these existing hybrid prediction models have indeed increased the performance of chaotic time series prediction, they still cannot handle the chaotic time series with strong non-stationary and nonlinear very well. Hence, the hybrid models can be further improved to obtain more accurate predictions. For the sake of enhancing the accuracy of actual chaotic time series prediction, we put forward a novel hybrid model based on a two-layer decomposition technique and an optimized back propagation neural network (BPNN). The main contents and contributions of this paper are summarized as follows.
A hybrid model based on a two-layer decomposition technique is proposed in this paper. For the sake of solving the problem that the prediction model based on single decomposition technique cannot completely deal with the nonlinear and non-stationary of chaotic time series, this paper puts forward a two-layer decomposition technique based on CEEMDAN and VMD, which is able to fully extract the complex characteristics of time series and improve prediction accuracy.
A firefly algorithm (FA) is applied to optimize the weights between input and hidden layer, the weights between the hidden and output layer and the thresholds of neuron nodes, which can reduce the human interference of parameter settings and improve the function approximation ability of the neural network. A BPNN optimized by the FA is applied to predict the subsequences obtained by two-layer decomposition.
The real world chaotic time series, daily maximum temperature time series in Melbourne, is used to assess the validity of the proposed hybrid model. The experimental results indicate that our hybrid model has a significant improvement in prediction accuracy compared to the existing single-model-based approaches and hybrid models based on the single layer decomposition technique.
The remainder of the paper is organized as follows. Preliminaries and related works are introduced in
Section 2. In
Section 3, we introduce the principles and the implementation steps of the proposed method.
Section 4 presents the experiments illustrating the availability of the proposed model. Finally, conclusions and future directions are demonstrated in
Section 5. For the convenience of reading, the notations used in this paper are shown in
Table 1.
4. Experimental Results
In this section, the daily maximum temperature time series in Melbourne is applied to analyze and verify the availability of the presented method. The experimental data is collected from the real world. The evaluation criteria are selected as root-mean-squared error (RMSE), normalized root-mean-square error (NRMSE), mean absolute percentage error (MAPE), and symmetric mean absolute percentage error (SMAPE). All prediction errors shown next are the mean values of 50 experimental results. The expressions are as follows:
where
denotes the real value,
denotes the predicted value, and
denotes the number of samples.
The daily maximum temperature time series in Melbourne is used in the experiment. The dataset contains the daily maximum temperature from 3 January 1981 to 31 December 31 1990, a total of 3650 samples, which is shown in
Figure 2. The training set is made up of the first 3000 samples, and the testing set is composed of the remaining 650. In order to compare the effectiveness of the model, six other methods were used in the comparative experiments: an RBF neural network, [
36], an ANFIS [
37], the original BP model, FABP, FABP with CEEMDAN decomposition (CEEMDAN–FABP), and FABP with VMD decomposition (VMD–FABP). The experimental environment involved the Windows 7 operating system, and all experiments were carried out using MATLAB R2016a on a 3.50 GHz, Intel(R) Core i3-4150M CPU with 6 GB RAM.
Figure 3 shows the decomposition results of the original time series based on CEEMDAN, which adaptively obtains 13 IMFs. CEEMDAN has good anti-noise performance, so this paper leaves out the de-noising process of the original time series.
In this paper, sample entropy is an indicator for judging the way IMF predicts.
Figure 4 shows the sample entropies of the IMFs. The entropy of the original time series is 0.81, which is indicated by the dotted line. In this research, the IMF components, whose entropy is greater than the entropy of the original time series, are predicted separately, because these IMFs are highly complex. The IMFs whose entropies are smaller than the original time series are combined and superimposed. After the combined operation, the model complexity and computational time are significantly reduced, while ensuring accuracy of prediction. Based on the results in
Figure 4, the first four IMF components should be predicted separately, while the IMF components from 5 to 13 should be combined for prediction.
We obtained the prediction results of five IMF components, as shown in
Figure 5. It can be observed that the prediction curve of each IMF is able to track the actual values, and the prediction trend is basically consistent. Due to the high frequency characteristics of IMF1, accurate prediction and tracking is more difficult, resulting in larger prediction errors for IMF1.
Figure 6 shows the final prediction results of the hybrid model of CEEMDAN and FABP. It can be seen that the prediction curve can track the real curve well and that the prediction error is small. The prediction result can be obtained in the case of the original time series without denoising.
The prediction errors presented in
Figure 5 and
Figure 6 are shown in
Table 2. As can be seen from
Table 2, the overall prediction error of the time series is 0.7763, while the prediction error of IMF1 is 0.6361. Therefore, if the prediction accuracy of IMF1 can be improved, the overall prediction accuracy will be greatly improved. Based on the above analysis, we propose the application of a two-layer decomposition strategy to further decompose the IMF1 component.
The IMF1 component is decomposed into six subsequences based on the VMD algorithm. The decomposition results of the IMF1 component are shown in
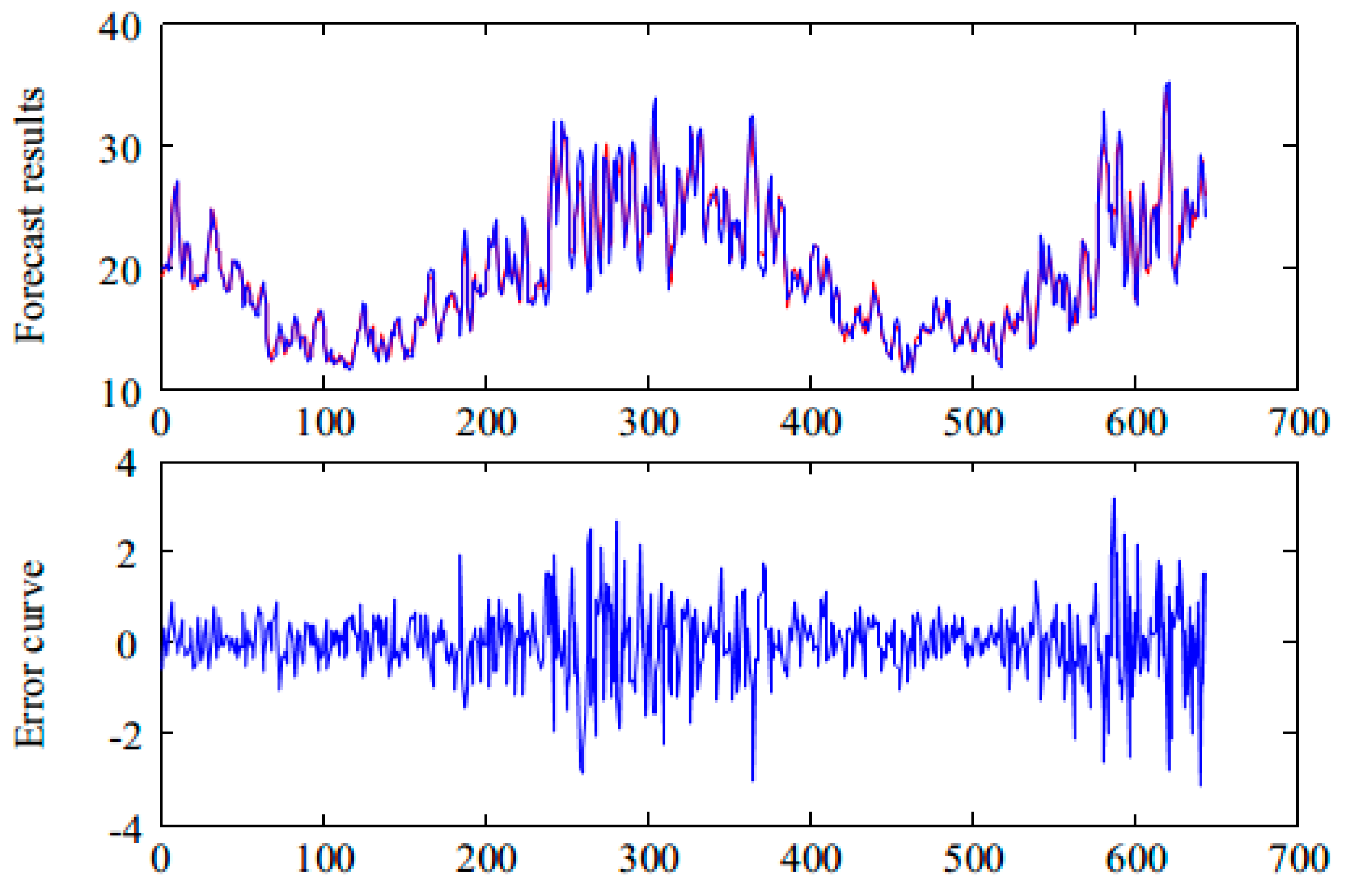
Figure 7. We use FABP to predict VMF1, …, VMF6, and we combine the prediction results to obtain the prediction results of the IMF1 component. Next, we combine the prediction results of IMF1 with IMF2, …, IMF5’ components, thereby obtaining the prediction results of daily maximum temperature time series in Melbourne, which are shown in
Figure 8. The error indexes of different prediction models are shown in
Table 3. It can be seen that the proposed two-layer decomposition algorithm can significantly reduce the prediction error and improve prediction accuracy compared with the direct prediction. This is mainly because the decomposition algorithm converts complex original signals into several simple and easy-to-analyze sub-signals, which is conducive to analysis and prediction. Based on the two-layer decomposition model, the prediction error is smaller than the single-layer approach, and the prediction performance is improved.
We conducted one-step-, two-step-, three-step-, and five-step-ahead prediction experiments on the time series. The corresponding prediction errors, including RMSE, NRMSE, MAPE, and SMAPE, are shown in
Table 3,
Table 4,
Table 5 and
Table 6. According to the results presented in the tables, the proposed model has a minimum prediction error in multiple prediction experiments, which indicates that the hybrid model of CEEMDAN–VMD–FABP has the best prediction performance. We can also say that the hybrid model based on the two-layer decomposition approach is better than the hybrid models based on a single decomposition approach. Surprisingly, although the ANFIS performed poorly in one-step prediction, its one-step prediction and multi-step prediction have similar effects, especially in the five-step ahead prediction experiment, and its performance is better than the RBF in multi-step prediction. The ANFIS method shows stability ability in terms of prediction, although the overall effect was not satisfactory. The prediction results of other models except for the ANFIS basically conform to the actual law. The more advanced the steps are, the more difficult it is to predict the chaotic time series.
To show the above experimental results more intuitively, we transform the error values, i.e. the RMSE, NRMSE, MAPE, and SMAPE shown in
Table 3,
Table 4,
Table 5 and
Table 6, into a column chart, presented in
Figure 9. It can be seen that the proposed hybrid model of CEEMDAN–VMD–FABP has the best performance. The proposed two-layer decomposition model has minimum prediction error in one-step-, two-step-, three-step-, and five-step-ahead prediction.
Moreover, we compared the training time and testing time in one-step-ahead prediction. Under different prediction steps, the running time is not much different, so we only list the running time of one-step prediction in
Table 3. As can be seen in the table, the testing time of each method is not much different. Although the method proposed in this paper has the longest training time, the experimental results prove that the proposed two-layer decomposition model can obtain the best prediction accuracy, which shows the effectiveness of the proposed method. Moreover, even if the training time is long, the overall running time is only a few minutes (not long), completely within the acceptable range.
5. Conclusions
In this paper, we propose a two-layer decomposition technique consisting of CEEMEAN and VMD. We obtained a group of subsequences by a two-layer decomposition method. These subsequences were separately predicted, and the prediction results were combined to obtain the final result. For the prediction, we used a BPNN optimized by a firefly algorithm. From this work, the following can be concluded:
The actual time series is usually non-stationary and noisy. It is generally difficult to analyze the original time series. CEEMDAN is an anti-noise decomposition method, and VMD can handle non-stationary signals very well. Therefore, subsequences decomposed by CEEMDAN and VMD are easy to analyze and predict.
After decomposition of the original signal, the BPNN was used for prediction. At this stage, the parameters in the BPNN greatly influenced prediction accuracy. Therefore, in order to reasonably select the model parameters, the FA algorithm was introduced to optimize the parameters of BP.
In general, in order to improve prediction accuracy, the following can be considered for further study: Firstly, original input variables were analyzed to eliminate factors that are not conducive to analysis and prediction. Secondly, we optimized the prediction model at the prediction stage. We studied the two aspects simultaneously, and the experimental results demonstrate the effectiveness of the proposed method.