Eigenvalue Based Approach for Assessment of Global Robustness of Nonlinear Dynamical Systems
Abstract
:1. Notations, Motivation and Introduction
1.1. Notations
1.2. Motivation and Introduction
2. Results
2.1. Auxiliary Lemma
2.2. Main Result
- (A1)
- in some left neighborhood of where is the largest pointwise eigenvalue of
- (A2)
- for all is where function is continuous on and satisfies
- (A3)
- (i)
- When A is negative definite, then Assumption A1 of Theorem 1 is automatically satisfied because is also negative definite ([34] Corollary 14.2.7), and
- (ii)
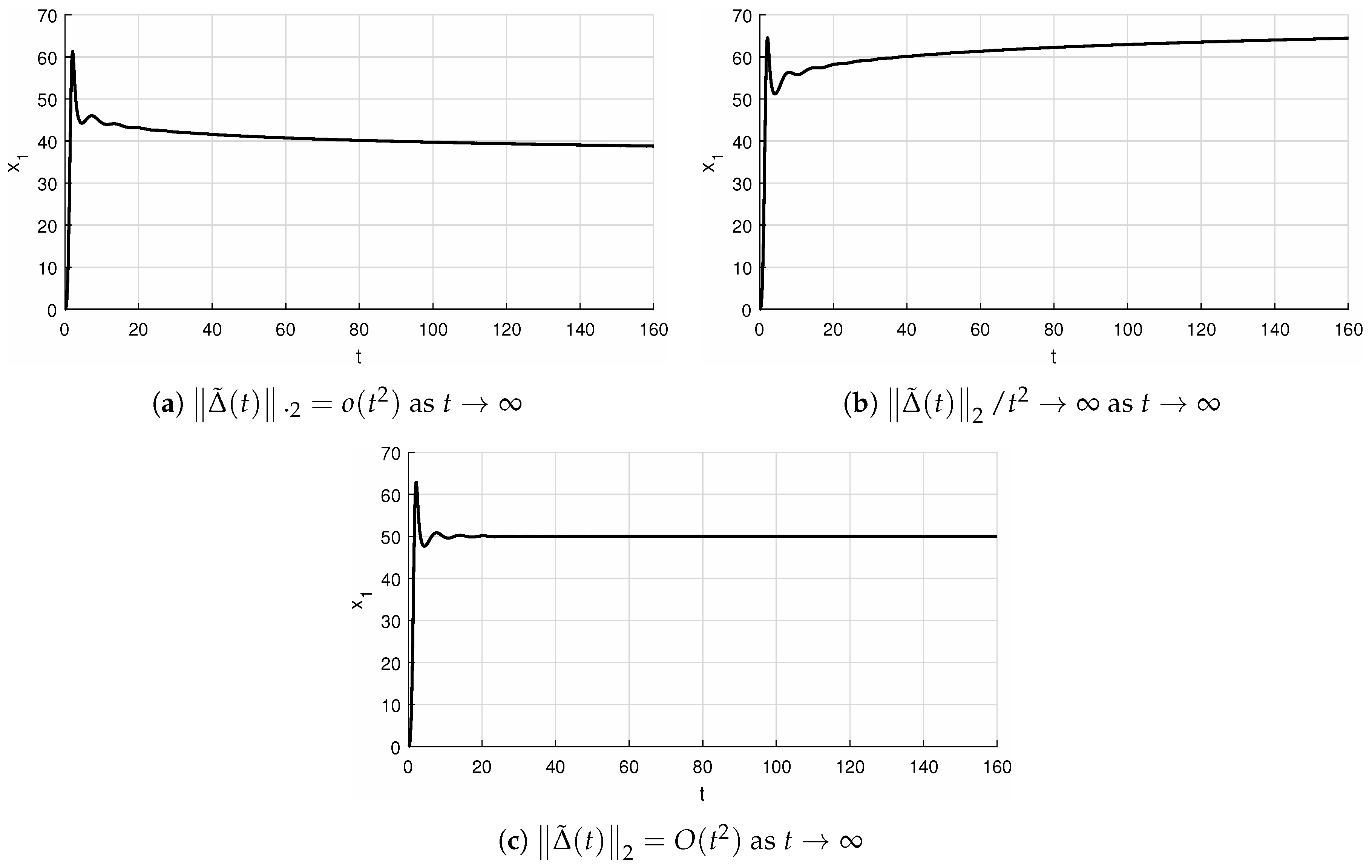
- in connection with Assumption A3, it is worth noting that Assumption A3 reduces to as ensuring the vanishing at infinity of all solutions of perturbed system cf. Example 2 below, where non-constant allows convergence to zero of all solutions of perturbed system for a wider class of perturbations, where even unbounded perturbations are admissible.
3. Simulation Experiments in MATLAB®
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Buscarino, A.; Fortuna, L.; Frasca, M. Experimental robust synchronization of hyperchaotic circuits. Phys. D Nonlinear Phenom. 2009, 238, 1917–1922. [Google Scholar] [CrossRef]
- Fortuna, L.; Frasca, M. Optimal and Robust Control: Advanced Topics with MATLAB®; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Buscarino, A.; Gambuzza, L.V.; Porfiri, M.; Fortuna, L.; Frasca, M. Robustness to Noise in Synchronization of Complex Networks; Scientific Reports 3; Nature Publishing Group: New York, NY, USA, 2013. [Google Scholar]
- Buscarino, A.; Fortuna, L.; Frasca, M.; Iachello, M.; Pham, V.T. Robustness to noise in synchronization of network motifs: Experimental results. Chaos Interdiscip. J. Nonlinear Sci. 2012, 22, 043106. [Google Scholar] [CrossRef]
- Gambuzza, L.V.; Buscarino, A.; Fortuna, L.; Porfiri, M.; Frasca, M. Analysis of dynamical robustness to noise in power grids. IEEE J. Emerg. Sel. Top. Circuits Syst. 2017, 7, 413–421. [Google Scholar] [CrossRef]
- Ge, H.; Chen, G.; Yu, H.; Chen, H.; An, F. Theoretical Analysis of Empirical Mode Decomposition. Symmetry 2018, 10, 623. [Google Scholar] [CrossRef]
- Yang, S.; Li, P.; Wen, H.; Xie, Y.; He, Z. K-Hyperline Clustering-Based Color Image Segmentation Robust to Illumination Changes. Symmetry 2018, 10, 610. [Google Scholar] [CrossRef]
- Du, B.; Zhou, H. A Robust Optimization Approach to the Multiple Allocation p-Center Facility Location Problem. Symmetry 2018, 10, 588. [Google Scholar] [CrossRef]
- Cao, Q.; Cao, C.; Wang, F.; Liu, D.; Sun, H. Robust Adaptive Full-Order TSM Control Based on Neural Network. Symmetry 2018, 10, 726. [Google Scholar] [CrossRef]
- Yang, X.-B.; He, Y.-G.; Li, C.-L. Dynamics Feature and Synchronization of a Robust Fractional-Order Chaotic System. Complexity 2018, 2018, 8797314. [Google Scholar] [CrossRef]
- Xu, X.; Xue, H.; Peng, Y.; Xu, Q.; Yang, J. Robust Exponential Stability of Switched Complex-Valued Neural Networks with Interval Parameter Uncertainties and Impulses. Complexity 2018, 2018, 4981812. [Google Scholar] [CrossRef]
- Pérez-Cruz, J.H. Stabilization and Synchronization of Uncertain Zhang System by Means of Robust Adaptive Control. Complexity 2018, 2018, 4989520. [Google Scholar] [CrossRef]
- Fang, S. Robust Impulsive Stabilization of Uncertain Nonlinear Singular Systems with Application to Transportation Systems. Math. Probl. Eng. 2018, 2018, 1893262. [Google Scholar] [CrossRef]
- Rodríguez-Mata, A.E.; Flores, G.; Martínez-Vásquez, A.H.; Mora-Felix, Z.D.; Castro-Linares, R.; Amabilis-Sosa, L.E. Discontinuous High-Gain Observer in a Robust Control UAV Quadrotor: Real-Time Application for Watershed Monitoring. Math. Probl. Eng. 2018, 2018, 4940360. [Google Scholar] [CrossRef]
- Zhang, J.-X.; Yang, G.-H. Adaptive asymptotic stabilization of a class of unknown nonlinear systems with specified convergence rate. Int. J. Robust Nonlinear Control 2019, 29, 238–251. [Google Scholar] [CrossRef]
- Vrabel, R. Stabilisation and state trajectory tracking problem for nonlinear control systems in the presence of disturbances. Int. J. Control 2017. [Google Scholar] [CrossRef]
- Petersen, I.R.; Tempo, R. Robust control of uncertain systems: Classical results and recent developments. Automatica 2014, 50, 1315–1335. [Google Scholar] [CrossRef]
- Liu, K.-Z.; Yao, Y. Robust Control: Theory and Applications; John Wiley & Sons: Singapore, 2016. [Google Scholar]
- Coddington, E.A.; Levinson, N. Theory of Ordinary Differential Equations; McGraw-Hill: New York, NY, USA, 1955. [Google Scholar]
- Hartman, P. Ordinary Differential Equations, 2nd ed.; Classics in Applied Mathematics Series 38; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. [Google Scholar]
- Chicone, C. Ordinary Differential Equations with Applications; Springer-Verlag New York, Inc.: New York, NY, USA, 1999. [Google Scholar]
- Vrabel, R. On local asymptotic stabilization of the nonlinear systems with time-varying perturbations by state-feedback control. Int. J. Gen. Syst. 2019, 1, 80–89. [Google Scholar] [CrossRef]
- Vrabel, R. Local null controllability of the control-affine nonlinear systems with time-varying disturbances. Eur. J. Control 2018, 40, 80–86. [Google Scholar] [CrossRef]
- Pavlov, A.; Pogromsky, A.; van de Wouw, N.; Nijmeijer, H. Convergent dynamics, a tribute to Boris Pavlovich Demidovich. Syst. Control Lett. 2002, 52, 257–261. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 2002. [Google Scholar]
- Sontag, E.D. Smooth stabilization implies coprime factorization. IEEE Trans. Automat. Control 1989, 34, 435–443. [Google Scholar] [CrossRef]
- Sontag, E.D.; Wang, Y. On characterizations of the input-to-state stability property. Syst. Control Lett. 1995, 24, 1283–1294. [Google Scholar] [CrossRef]
- Perko, L. Differential Equations and Dynamical Systems, 3rd ed.; Texts in Applied Mathematics 7; Springer-Verlag New York, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Slotine, J.-J.E.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Vidyasagar, M. Nonlinear System Analysis, 2nd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Rugh, W.J. Linear System Theory, 2nd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Coppel, W.A. Stability and Asymptotic Behavior of Differential Equations; D. C. Heath and Company: Boston, MA, USA, 1965. [Google Scholar]
- Harville, D.A. Matrix Algebra From a Statistician’s Perspective; Springer: New York, NY, USA, 2008. [Google Scholar]
- Ioannou, A.; Sun, J. Robust Adaptive Control; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Shamma, J.S.; Athans, M. Guaranteed properties of gain scheduled control for linear parameter-varying plants. Automatica 1991, 27, 559–564. [Google Scholar] [CrossRef]
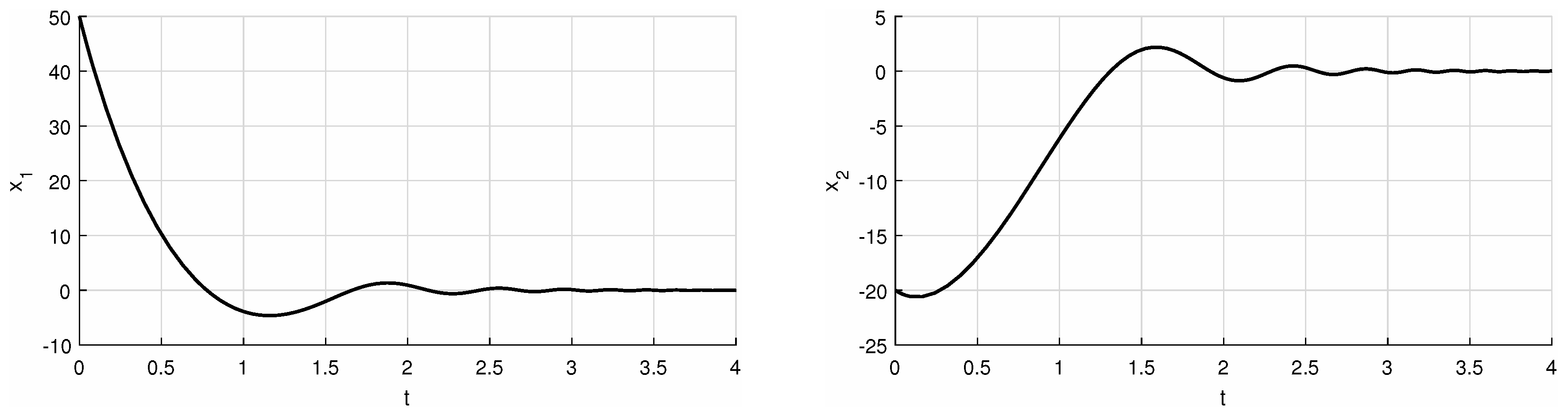
| f = @(t,x) [(-2)*x(1)+(exp(t))*x(2)+(atan(x(1)+x(2))/(t+1)); (-exp(t))*x(1)+(-2)*x(2)+(exp(-t)/(x(1)^2+1))] [t,xa] = ode45(f,[0 4],[50 -20]); hold~on pbaspect([2 1 1]) plot(t,xa(:,1), ’k’, ’LineWidth’,1.5) % 1 or 2 grid on xlabel(’t’) ylabel(’x_1’) % 1 or 2 print(’example_first_x_1’,’-deps’) % 1 or 2 |
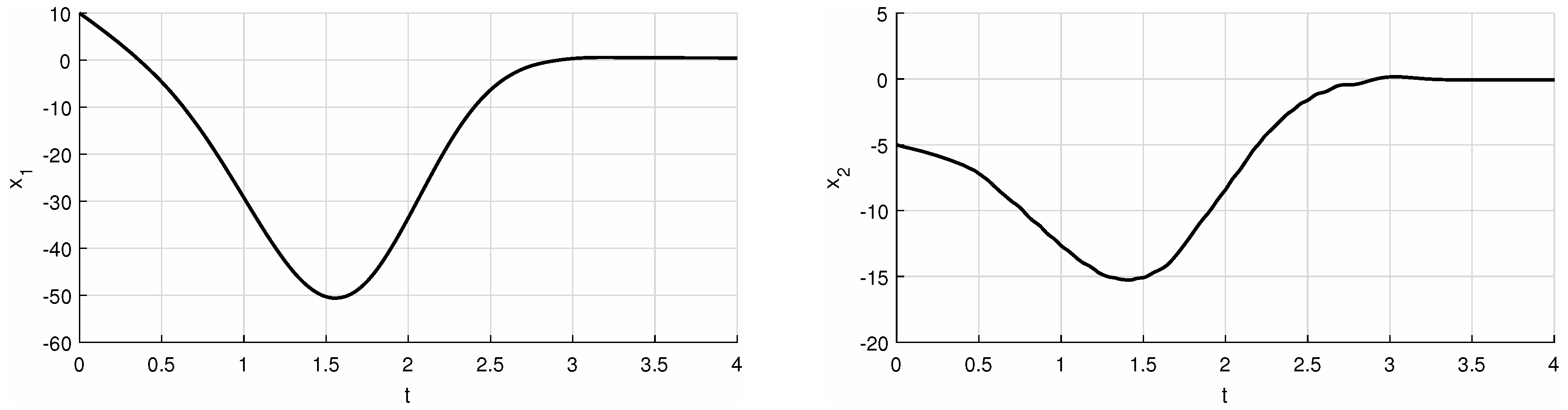
| syms b b=5; f = @(t,x) [(-t^2+sin(t))*x(1)+(b)*x(2)+t^(1.5); (0)*x(1)+(1-t^2+sin(t))*x(2)+3*cos(t*x(1)-x(2))] [t,xa] = ode45(f,[0 4],[10 -5]); hold~on pbaspect([2 1 1]) plot(t,xa(:,1), ’k’, ’LineWidth’,1.5) % 1 or 2 grid on xlabel(’t’) ylabel(’x_1’) % 1 or 2 print(’example_second_x_1’,’-deps’) % 1 or 2 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vrabel, R. Eigenvalue Based Approach for Assessment of Global Robustness of Nonlinear Dynamical Systems. Symmetry 2019, 11, 569. https://doi.org/10.3390/sym11040569
Vrabel R. Eigenvalue Based Approach for Assessment of Global Robustness of Nonlinear Dynamical Systems. Symmetry. 2019; 11(4):569. https://doi.org/10.3390/sym11040569
Chicago/Turabian StyleVrabel, Robert. 2019. "Eigenvalue Based Approach for Assessment of Global Robustness of Nonlinear Dynamical Systems" Symmetry 11, no. 4: 569. https://doi.org/10.3390/sym11040569
APA StyleVrabel, R. (2019). Eigenvalue Based Approach for Assessment of Global Robustness of Nonlinear Dynamical Systems. Symmetry, 11(4), 569. https://doi.org/10.3390/sym11040569





