Edge Detection Algorithm of a Symmetric Difference Kernel SAR Image Based on the GAN Network Model
Abstract
:1. Introduction
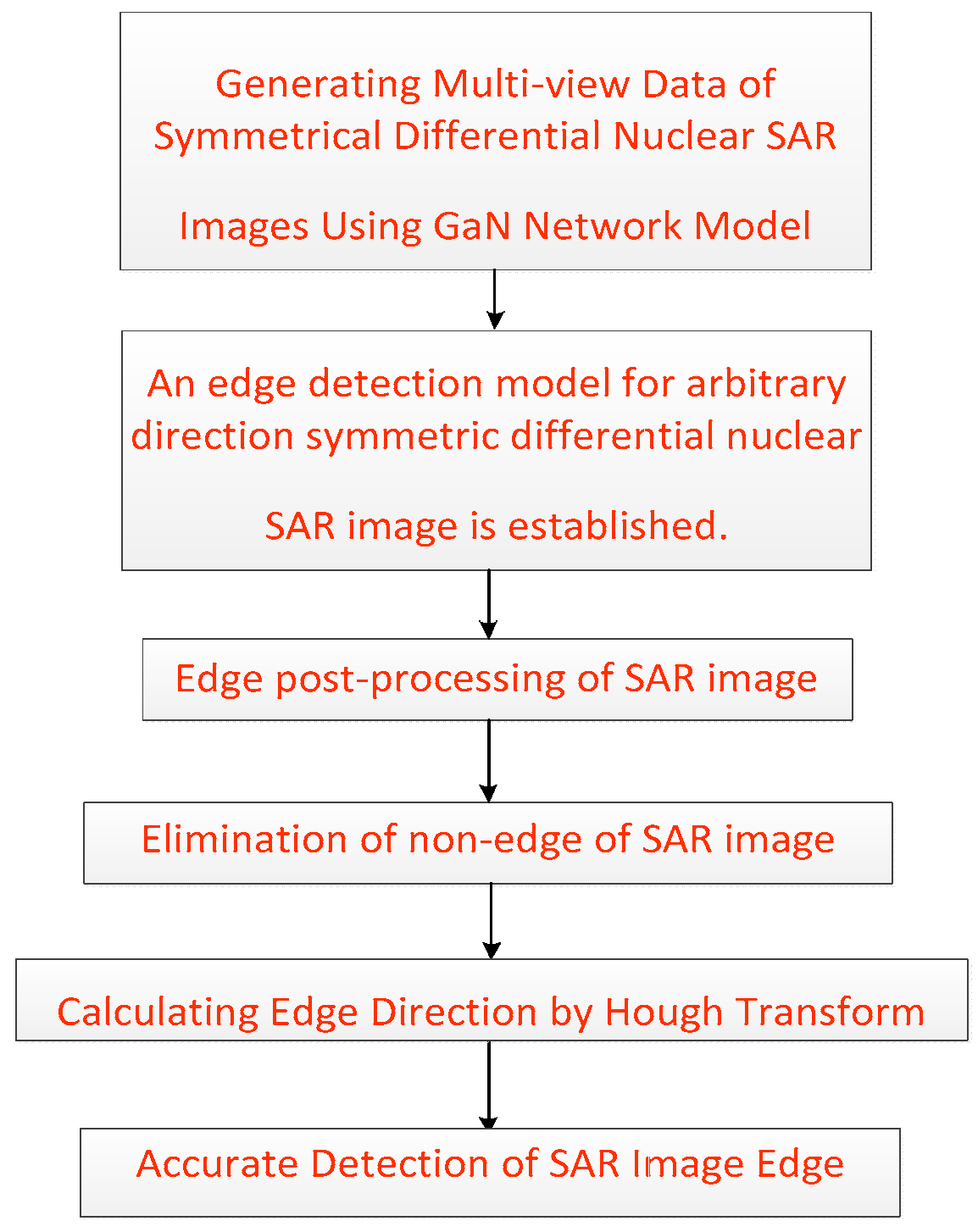
2. Edge Detection Algorithm of a Symmetric Difference Kernel Sar Image Based on the Gan Network Model
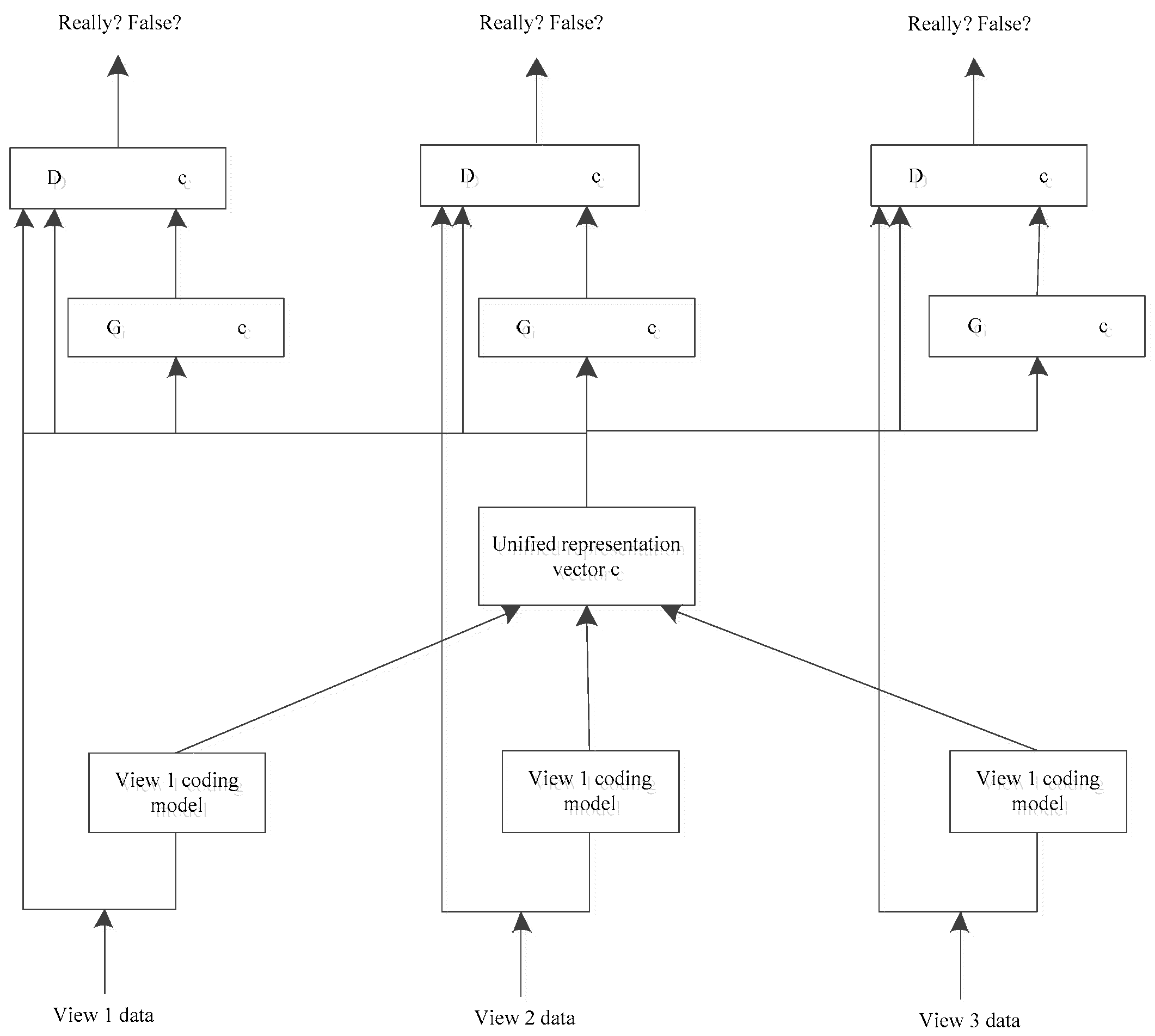
2.1. GAN Network Model
2.2. Multi View Data Generation of Symmetric Difference Kernel SAR Images Based on the GAN Network Model
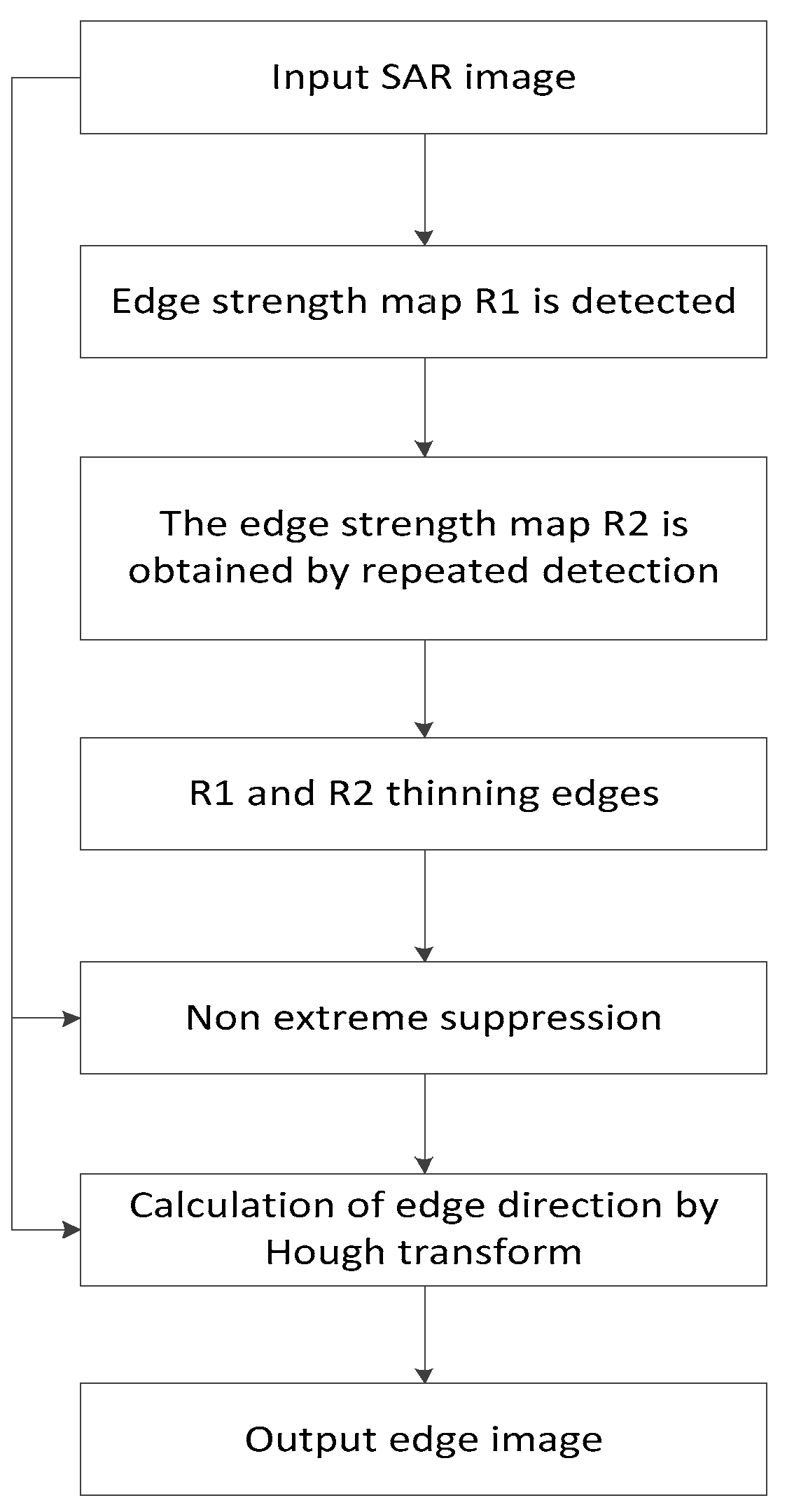
2.3. Edge Detection of Symmetric Difference Kernel SAR Images
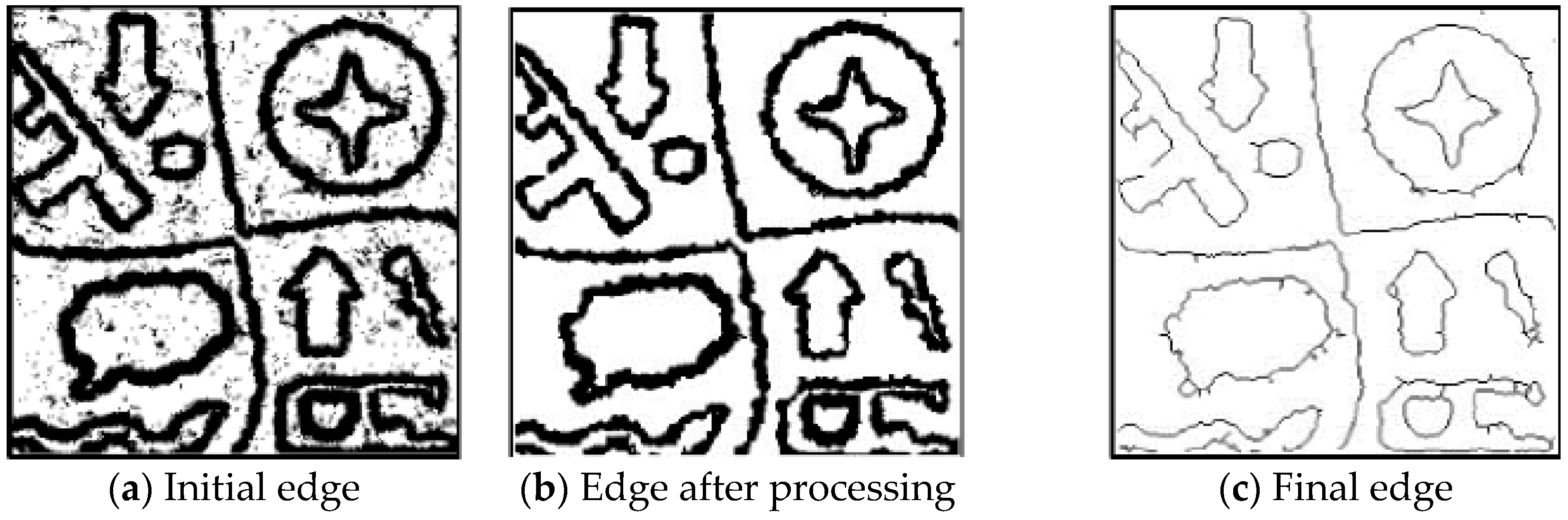
2.3.1. Initial Edge
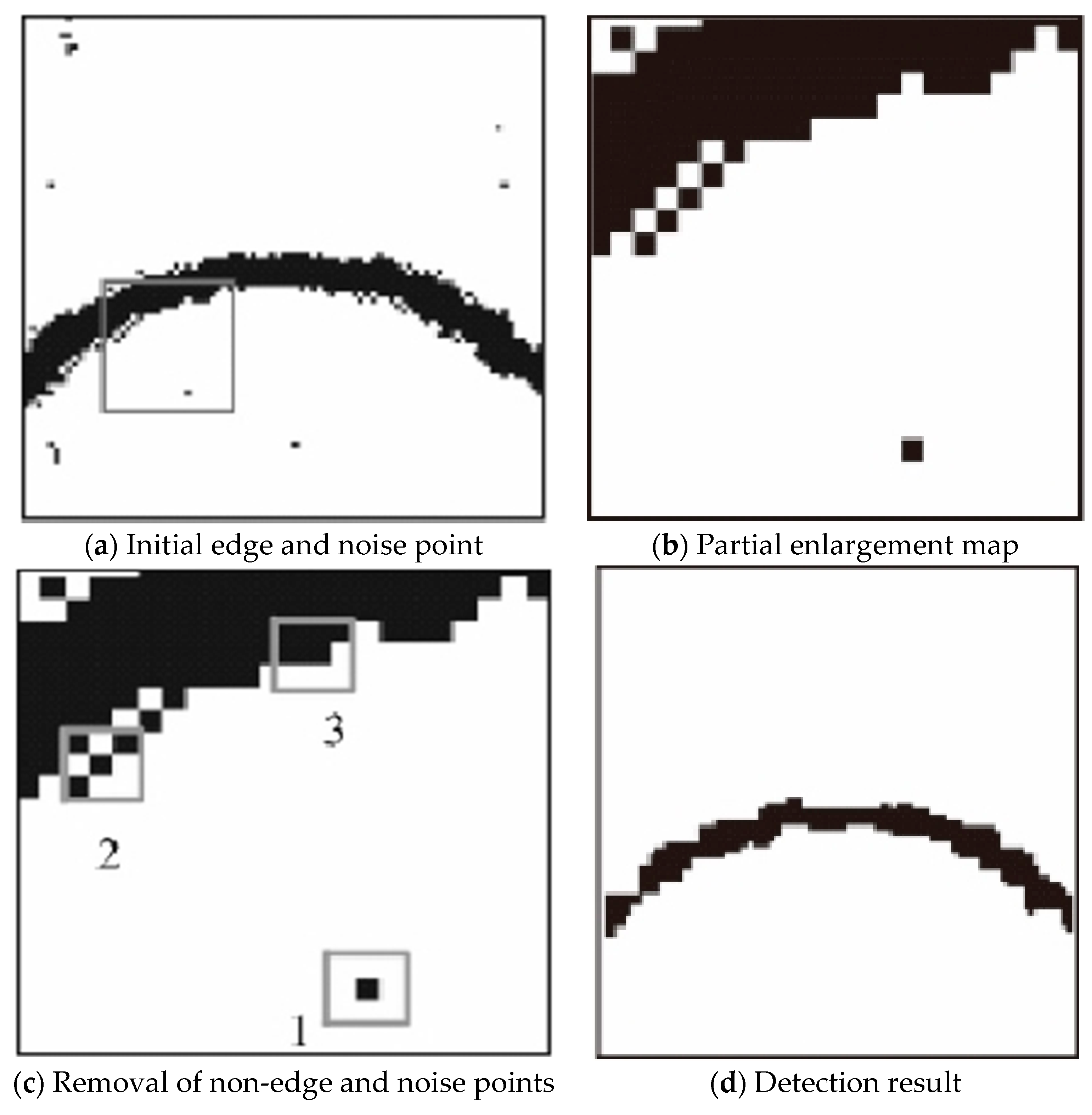
2.3.2. Edge Post Processing
2.3.3. Calculation of Edge Direction by Hough Transform
3. Experimental Analysis
3.1. Classification Effect Analysis of Multi View Data for Symmetric Difference Kernel SAR Images
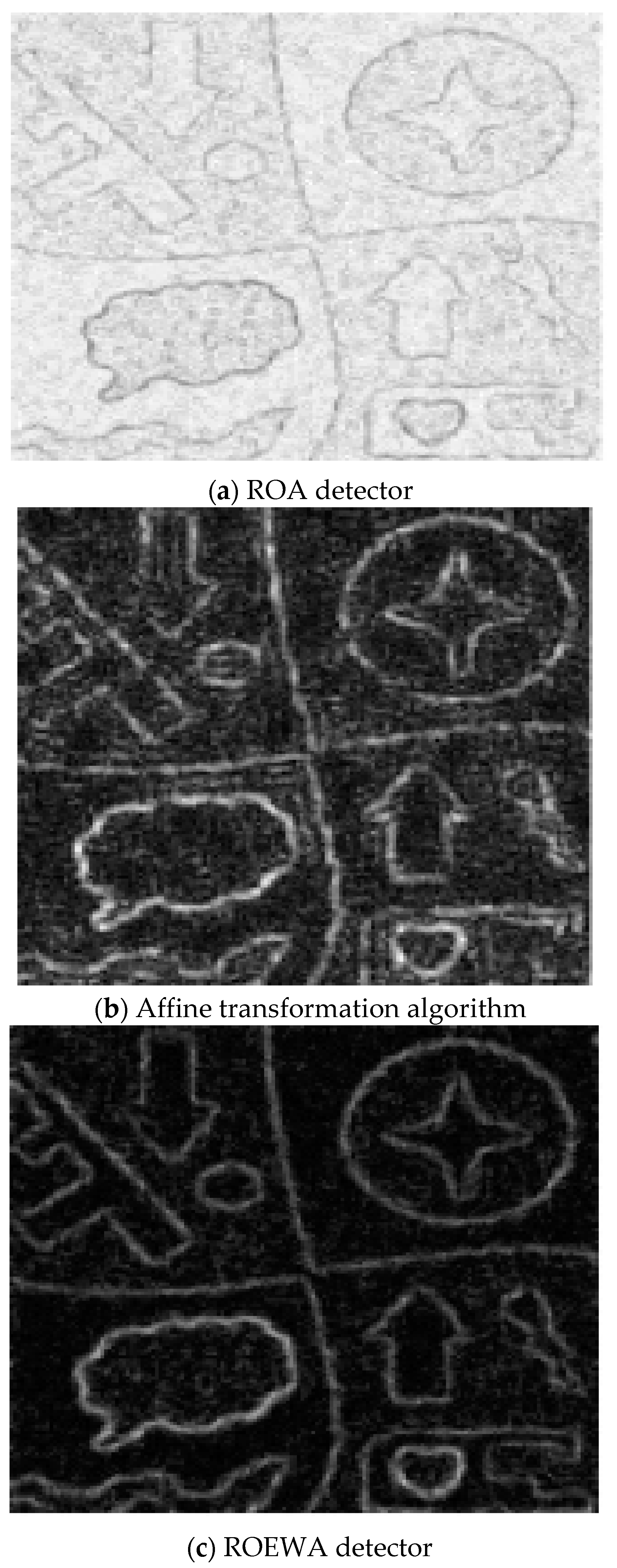
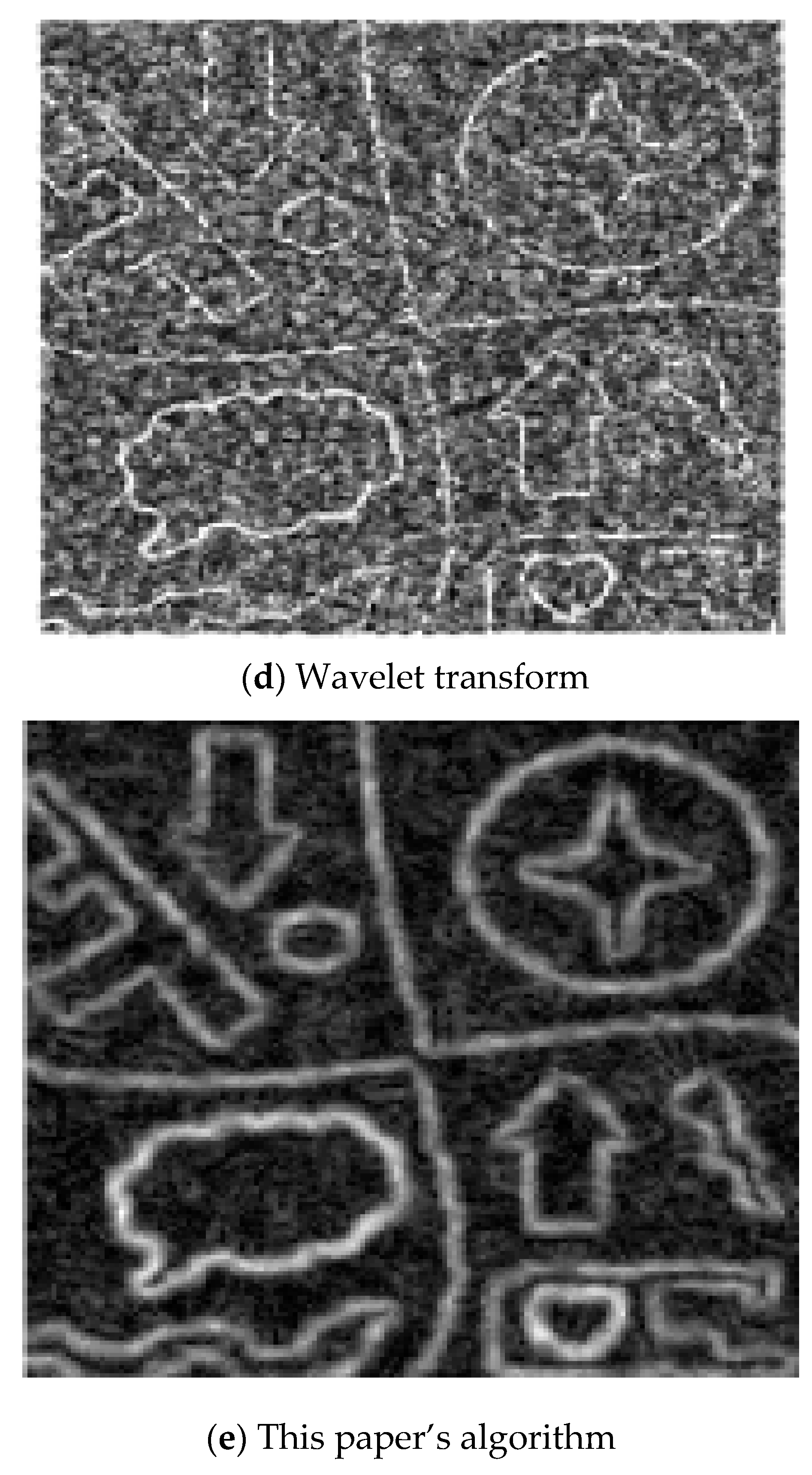
3.2. Edge Detection Based on Symmetric Difference Kernel SAR Simulation
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Li, F.; Fang, F.; Zhang, G. Unsupervised change detection in SAR images using curvelet and L1-norm based soft segmentation. Int. J. Remote Sens. 2016, 37, 3232–3254. [Google Scholar] [CrossRef]
- Yan, W.; Shi, S.; Pan, L. Unsupervised change detection in SAR images based on frequency difference and a modified fuzzy c-means clustering. Int. J. Remote Sens. 2018, 39, 3055–3075. [Google Scholar] [CrossRef]
- Wang, X.; Jia, Z.; Yang, J. Change detection in SAR images based on the logarithmic transformation and total variation denoising method. Remote Sens. Lett. 2017, 8, 214–223. [Google Scholar] [CrossRef]
- Quan, S.; Xiong, B.; Yang, L. Evaluation of different SAR change detectors based on vehicle recognition with MSTAR data set. Remote Sens. Lett. 2015, 6, 539–547. [Google Scholar] [CrossRef]
- Furse, C.M.; Chen, J.Y.; Gandhi, O.P. The use of the frequency-dependent finite-difference time-domain method for induced current and SAR calculations for a heterogeneous model of the human body. IEEE Trans. Electromagn. Compat. 2015, 36, 128–133. [Google Scholar] [CrossRef]
- Zhuang, H.; Deng, K.; Fan, H. A novel approach based on structural information for change detection in SAR images. Int. J. Remote Sens. 2018, 39, 2341–2365. [Google Scholar] [CrossRef]
- Hoekman, D.H.; Reiche, J. Multi-model radiometric slope correction of SAR images of complex terrain using a two-stage semi-empirical approach. Remote Sens. Environ. 2015, 156, 1–10. [Google Scholar] [CrossRef]
- Jia, M.; Wang, L. Novel class-relativity non-local means with principal component analysis for multitemporal SAR image change detection. Int. J. Remote Sens. 2018, 39, 1068–1091. [Google Scholar] [CrossRef]
- Verma, O.P.; Parihar, A.S. An optimal fuzzy system for edge detection in color images using bacterial foraging algorithm. IEEE Trans. Fuzzy Syst. 2017, 25, 114–127. [Google Scholar] [CrossRef]
- Saheba, S.M.; Upadhyaya, T.K.; Sharma R, K. Lunar surface crater topology generation using adaptive edge detection algorithm. IET Image Process. 2016, 10, 657–661. [Google Scholar] [CrossRef]
- Leng, X.; Ji, K.; Xing, X.; Zou, H.; Zhou, S. Hybrid bilateral filtering algorithm based on edge detection. IET Image Process. 2017, 10, 809–816. [Google Scholar] [CrossRef]
- González-Hidalgo, M.; Massanet, S.; Mir, A. On the choice of the pair conjunction–implication into the fuzzy morphological edge detector. IEEE Trans. Fuzzy Syst. 2015, 23, 872–884. [Google Scholar] [CrossRef]
- Alshayeji, M.; Alroomi, S.A.; Abed, S. Optic disc detection in retinal fundus images using gravitational law-based edge detection. Med. Boil. Eng. Comput. 2016, 55, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Cai, J.; Huang, P.; Chen, L. An efficient circle detector not relying on edge detection. Adv. Space Res. 2016, 57, 2359–2375. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhou, Y.; Zhou, H. Ultrasound image edge detection based on a novel multiplicative gradient and Canny operator. Ultrason. Imaging 2015, 37, 238–250. [Google Scholar] [CrossRef] [PubMed]
- Salehi, M.; Namdari, F. Fault classification and faulted phase selection for transmission line using morphological edge detection filter. IET Gener. Transm. Distrib. 2018, 12, 1595–1605. [Google Scholar] [CrossRef]
- Veni, S.H.K.; Suresh, L.P. An analysis of various edge detection techniques on illuminant variant images. Anaesthesia 2015, 61, 617. [Google Scholar]
- Sun, Q.; Liang, F.; Wang, F. Investigation on the geometrical characteristics of secondary arc by image edge detection. IEEE Trans. Plasma Sci. 2018, 46, 2016–2025. [Google Scholar] [CrossRef]
- Gao, W.; Wang, W.F. The fifth geometric-arithmetic index of bridge graph and carbon nanocones. J. Differ. Equ. Appl. 2017, 23, 100–109. [Google Scholar] [CrossRef]
- Dayal, A. Improving adaptive frameless rendering. Int. J. Comput. Appl. 2018, 40, 110–120. [Google Scholar] [CrossRef]
- Huang, A.D.; Zhong, Z.; Wu, W. An artificial neural network-based electrothermal model for gan hemts with dynamic trapping effects consideration. IEEE Trans. Microw. Theory Tech. 2016, 64, 2519–2528. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Tang, J.L. Clustering sorting algorithm based on digital channelized receiver. J. China Acad. Electron. Inf. Technol. 2017, 12, 143–148. [Google Scholar]
- Hirano, M.; Tsuzuki, N.; Ikeda, S.; Kobayashi, R. Logdrive: A proactive data collection and analysis framework for time-traveling forensic investigation in IaaS cloud environments. J. Cloud Comput. 2018, 7, 18. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, C.H.; Wang, R. Harmonic detection algorithm based on third-order generalized-integrator. J. Power Supply 2018, 16, 131–136. [Google Scholar]
- Zhang, J.; Gao, A.T.; Han, Y.S. A health prognostic algorithm for Li-ion battery based on particle filter. Chin. J. Power Sources 2015, 39, 1377–1380. [Google Scholar]
- Liu, E.; Jing, X.J. PD algorithm based on two self-balancing vehicle upright control. Autom. Instrum. 2015, 1, 203–206. [Google Scholar]
- Han, Y.; Byun, Y. Automatic and accurate registration of VHR optical and SAR images using a quadtree structure. Int. J. Remote Sens. 2015, 36, 2277–2295. [Google Scholar] [CrossRef]
- Yang, A.; Li, Y.; Kong, F.; Wang, G.; Chen, E. Security control redundancy allocation technology and security keys based on Internet of Things. IEEE Access 2018, 6, 50187–50196. [Google Scholar] [CrossRef]
- Mnak, G.; Altun, I.; Olgun, M. Fixed points of f-contractive type fuzzy mappings. J. Intell. Fuzzy Syst. 2017, 33, 1435–1439. [Google Scholar] [CrossRef]
- Esteban, M.; Núñez, E.P.; Torres, F. Bifurcation analysis of hysteretic systems with saddle dynamics. Appl. Math. Nonlinear Sci. 2017, 2, 449–464. [Google Scholar] [CrossRef]
- Simone, A.; Navara, M.; Pták, P. States on systems of sets that are closed under symmetric difference. Math. Nachr. 2016, 288, 1995–2000. [Google Scholar] [CrossRef]


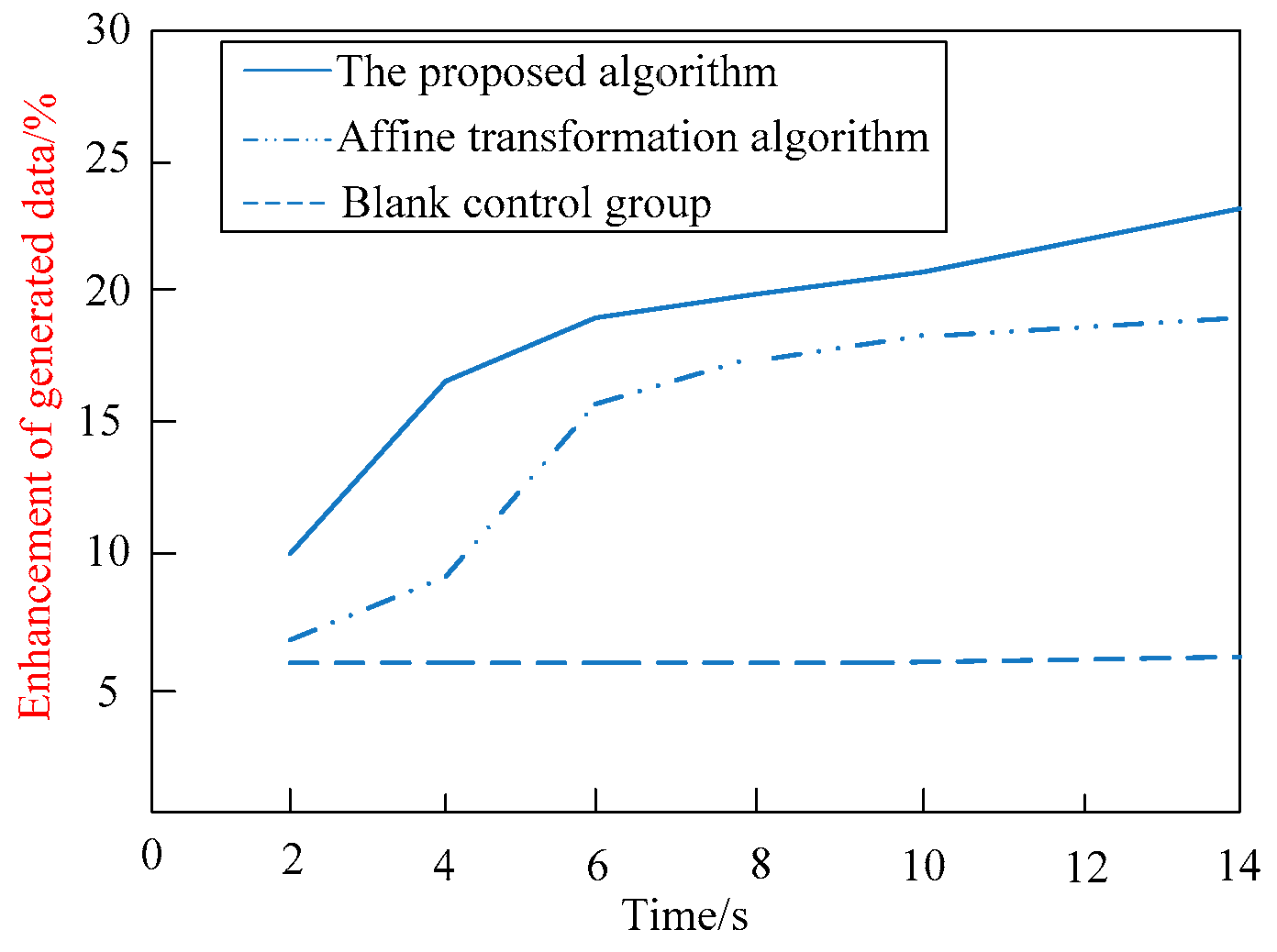
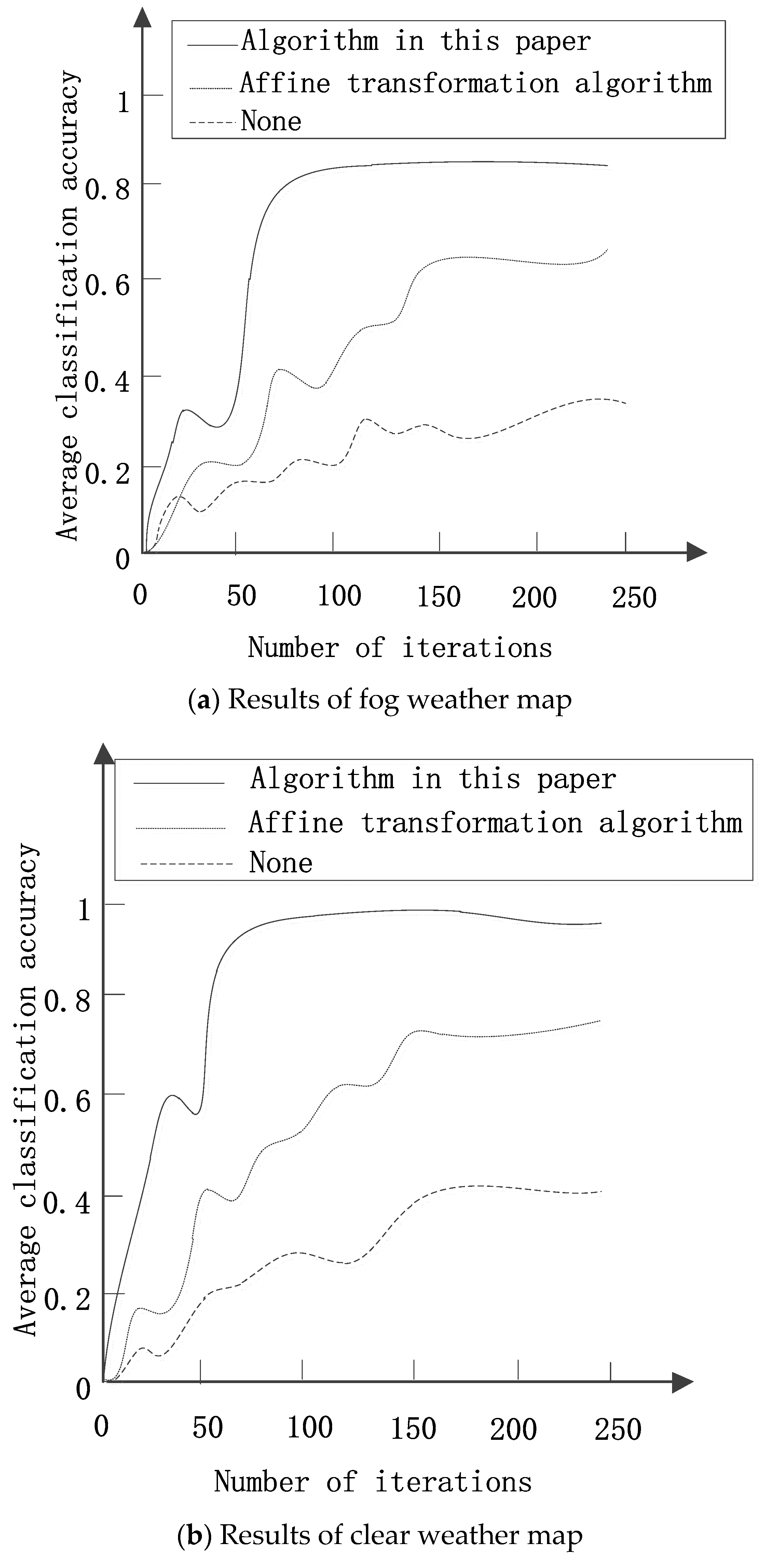



| Number | Data Set | Data Generation Algorithm | Average Classification Accuracy/% | Overfitting Ratio |
|---|---|---|---|---|
| 1 | Heavy fog weather situation map | None | 22.3 | 4.48 |
| 2 | Heavy fog weather situation map | Affine transformation algorithm | 75.4 | 1.33 |
| 3 | Heavy fog weather situation map | Algorithm in this paper | 89.1 | 1.08 |
| 4 | Clear weather situation map | None | 35.6 | 2.17 |
| 5 | Clear weather situation map | Affine transformation algorithm | 77.2 | 1.21 |
| 6 | Clear weather situation map | Algorithm in this paper | 93.8 | 0.94 |
| 7 | Thunderstorm weather situation map | None | 12.1 | 3.47 |
| 8 | Thunderstorm weather situation map | Affine transformation algorithm | 65.2 | 1.31 |
| 9 | Thunderstorm weather situation map | Algorithm in this paper | 79.5 | 1.25 |
| This Paper’s Algorithm | Canny Operator | ROA Detector | |
|---|---|---|---|
| B0 | 96.85 | 40.00 | 38.79 |
| S0 | 54.97 | 40.00 | 38.79 |
| B1 | 44.29 | 24.91 | 42.10 |
| S1 | 84.29 | 79.88 | 80.89 |
| B2 | 10.06 | 5.83 | 7.14 |
| S2 | 94.35 | 85.71 | 88.03 |
| B3 | 2.73 | 4.69 | 5.03 |
| S3 | 97.08 | 90.40 | 93.06 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Liu, Y.; Liu, T.; Li, Y.; Ye, W. Edge Detection Algorithm of a Symmetric Difference Kernel SAR Image Based on the GAN Network Model. Symmetry 2019, 11, 557. https://doi.org/10.3390/sym11040557
Zhang Z, Liu Y, Liu T, Li Y, Ye W. Edge Detection Algorithm of a Symmetric Difference Kernel SAR Image Based on the GAN Network Model. Symmetry. 2019; 11(4):557. https://doi.org/10.3390/sym11040557
Chicago/Turabian StyleZhang, Ziwen, Yijun Liu, Tie Liu, Yang Li, and Wujian Ye. 2019. "Edge Detection Algorithm of a Symmetric Difference Kernel SAR Image Based on the GAN Network Model" Symmetry 11, no. 4: 557. https://doi.org/10.3390/sym11040557
APA StyleZhang, Z., Liu, Y., Liu, T., Li, Y., & Ye, W. (2019). Edge Detection Algorithm of a Symmetric Difference Kernel SAR Image Based on the GAN Network Model. Symmetry, 11(4), 557. https://doi.org/10.3390/sym11040557





