NHPP Software Reliability Model with Inflection Factor of the Fault Detection Rate Considering the Uncertainty of Software Operating Environments and Predictive Analysis

Abstract

The non-homogeneous Poisson process (NHPP) software has a crucial role in computer systems. Furthermore, the software is used in various environments. It was developed and tested in a controlled environment, while real-world operating environments may be different. Accordingly, the uncertainty of the operating environment must be considered. Moreover, predicting software failures is commonly an important part of study, not only for software developers, but also for companies and research institutes. Software reliability model can measure and predict the number of software failures, software failure intervals, software reliability, and failure rates. In this paper, we propose a new model with an inflection factor of the fault detection rate function, considering the uncertainty of operating environments and analyzing how the predicted value of the proposed new model is different than the other models. We compare the proposed model with several existing NHPP software reliability models using real software failure datasets based on ten criteria. The results show that the proposed new model has significantly better goodness-of-fit and predictability than the other models.

1. Introduction

The core technologies of the fourth industrial revolution, such as artificial intelligence (AI), big data, the Internet of Things (IoT), are implemented in software, and software is essential as a mediator to create new values by fusing these technologies in all industries. As the importance and role of software in a computer system keep growing, a fatal software error can cause significant damage. For the effective operation of software, it is imperative to reduce the possibilities of software failures and maintain high levels of reliability. Software reliability is defined as the probability that the software will run without a fault for a certain period. It is vital for developing skills and theories to improve the software reliability. However, the development of a software system is a difficult and complex process. Therefore, the main focus of software development is on improving the reliability and stability of a software system. The number of software failures and the time interval of each failure have a significant influence on the reliability of software. Therefore, the prediction of software failures is a research field that is important not only for software developers, but also for companies and research institutes. Software reliability models can be classified according to the applied software development cycle. Before the testing phase, a reliability prediction model is used that predicts reliability using information such as past data or language used, development domain, complexity, and architecture. After the test phase, a software reliability model is used, which is a mathematical model of software failures such as the frequency of failures and failure interval times. A model makes it easier to evaluate the software reliability using the fault data collected in the test or operating environment. In addition, the model can measure the number of software failures, software failure interval, and software reliability; and failure rate can be estimated and variously predicted.

Although various types of software reliability models have been studied, software defects and failures generally do not occur at the same time intervals. Based on this, a non-homogeneous Poisson process (NHPP) software reliability model was developed. The NHPP models determine mathematically handled software reliability; they are used extensively because of their potential for various applications. Most of the previous NHPP software reliability models were developed based on the assumptions that faults detected in the testing phase are removed immediately with no debugging time delay, new faults are not introduced, and software systems used in the field environments are the same as or close to those used in the development-testing environment. Based on this, Goel and Okumoto [1] presented a stochastic model for the software failure phenomenon using an NHPP; this model describes the failure observation phenomenon by an exponential curve. Also, there have been some other software reliability models that describe either S-shaped curves or a mixture of exponential and S-shaped curves [2,3,4]. As the Internet became popular in the mid-1990s, due to rapid changes in industrial structure and environment, a software reliability model with a variety of operating environments begun to be studied. In early 2000, considering the uncertainty of the operating environment, researchers began to try new approaches such as the application of calibration factors [5,6,7]. Based on this, Teng and Pham [8] generalized the software reliability model considering the uncertainty of the environment and its effects upon software failure rates. Recently, Inoue et al. [9] proposed the software reliability model with the uncertainty of testing environments. Li and Pham [10,11] proposed NHPP software reliability models considering fault removal efficiency and error generation, and the uncertainty of operating environments with imperfect debugging and testing coverage. Song et al. [12,13,14,15] studied NHPP software reliability models with various fault detection rates considering the uncertainty of operating environments. Zhu and Pham [16] proposed an NHPP software reliability model with a pioneering idea by considering software fault dependency and imperfect fault removal. However, previous NHPP software reliability models [1,2,3,4,17,18,19,20,21,22,23,24,25] did not take into account the uncertainty of the software operating environment, and did not consider the learn-curve in the fault detection rate function [8,9,10,11,13,14,26,27].

In this paper, we discuss a new model with inflection factor of the fault detection rate function considering the uncertainty of operating environments, and the predictive analysis. We examine the goodness-of-fit and the predictability of a new software reliability model and other existing NHPP models based on several datasets. The explicit solution of the mean value function for the new software reliability model is derived in Section 2. Criteria for model comparisons, prediction, and selection of the best model are discussed in Section 3. Model analysis and results through numerical examples are discussed in Section 4. Section 5 presents conclusions and remarks.

2. NHPP Software Reliability Modeling

2.1. A General NHPP Software Reliability Model

$N\left(t\right) (t\ge 0$) represents the cumulative number of failures up to the point of execution time $t$ when the software failure/defect follows the NHPP.

$$Pr\left\{N\left(t\right)=n\right\}=\frac{{\left\{m\left(t\right)\right\}}^n}{n!}exp\left\{-m\left(t\right)\right\}, n=0,1,2,3\dots .$$

Assuming that $m\left(t\right)$ is a mean value function, the relationship between the mean value function $m\left(t\right)$ and the intensity function $\lambda \left(t\right)$ is

$$m\left(t\right)={{\displaystyle \int }}_0^t\lambda (s)ds.$$

A general mean value function $m\left(t\right)$ of NHPP software reliability models using the differential equation is as follows [19]:

$$\frac{d m\left(t\right)}{dt}=b\left(t\right)\left[a\left(t\right)-m\left(t\right)\right].$$

(1)

Solving Equation (1) by using different functions $a\left(t\right)$ and $b\left(t\right)$, the following mean value function m(t) is observed [19],

$$m\left(t\right)=e^{-B\left(t\right)}\left[m_0+{{\displaystyle \int }}_{t_0}^{t}a\left(s\right)b\left(s\right)e^{B\left(s\right)}bs\right]$$

(2)

where $B\left(t\right)={{\displaystyle \int }}_{t_0}^{t}b(s)ds$, and $m\left(t_0\right)=m_0$ is the marginal condition of Equation (2), with $t_0$ representing the start time of the testing process.

2.2. A New NHPP Software Reliability Model

A general mean value function $m\left(t\right)$ of NHPP software reliability models using the differential equation considering the uncertainty of operating environments is as follows [26]:

$$\frac{d m\left(t\right)}{dt}=\eta \left[b\left(t\right)\right]\left[N-m\left(t\right)\right]$$

(3)

where $m\left(t\right)$ is the mean value function, $b\left(t\right)$ is the fault detection rate function, $N$ is the expected number of faults that exist in the software before testing, and $\eta$ is a random variable that represents the uncertainty of the system fault detection rate in the operating environments with a probability density function [26],

$$m\left(t\right)={{\displaystyle \int }}_{\eta }^{}N\left(1-e^{-\eta {{\displaystyle \int }}_0^{t}b\left(x\right)dx}\right)dg\left(\eta \right).$$

(4)

We find the following mean value function $m\left(t\right)$ using the differential equation by applying the random variable $\eta$; it has a generalized probability density function with two parameters $\alpha \ge 0$ and $\beta \ge 0$, where the initial condition m(0) = 0:

$$m\left(t\right)=N{\left(1-\frac{\beta }{\beta +{{\displaystyle \int }}_0^{t}b\left(s\right)ds}\right)}^{\alpha }.$$

(5)

In this paper, we consider a fault detection rate function $b\left(t\right)$ to be as follows:

$$b\left(t\right)=\frac{b}{1+a{e}^{-bt}}, a, b>0$$

(6)

where $b$ is the failure detection rate and $a$ represents the inflection factor.

We obtain a new mean value function $m\left(t\right)$ of NHPP software reliability model subject to the uncertainty of operating environments that can be used to determine the expected number of software failures detected by time $t$ by substituting the function $b\left(t\right)$ in Equation (5):

$$m\left(t\right)=N{\left(1-\frac{\beta }{\beta +ln\left(\frac{a+e^{bt}}{1+a}\right)}\right)}^{\alpha }$$

In this paper, the advantages of the proposed new model take into account the learn-curve in the fault detection rate function and the uncertainty of the operating environments.

3. Parameter Estimation and Criteria for Model Comparisons

3.1. Parameter Estimation and Models for Comparison

Many NHPP software reliability models use the least square estimation (LSE) and the maximum likelihood estimation (MLE) methods to estimate the parameters. However, if the expression of the mean value function $m\left(t\right)$ of the software reliability model is too complicated, an accurate estimate may not be obtained from the MLE method. Here, we derived the parameters of the mean value function $m\left(t\right)$ using the Matlab and R programs based on the LSE method. Table 1 summarizes the mean value functions of existing NHPP software reliability models and the proposed new model; among them, NHPP software reliability models 18, 19, and 20 consider the uncertainty of the environment.

Table 1. Software reliability models.

No.	Model	$\mathit{m}\left(\mathit{t}\right)$
1	Goel–Okumoto (GO) [1]	$m\left(t\right)=a\left(1-e^{-bt}\right)$
2	Yamada et al. (Y-DS) [2]	$m\left(t\right)=a\left(1-\left(1+bt\right)e^{-bt}\right)$
3	Ohba (O-IS) [3]	$m\left(t\right)=\frac{a\left(1-e^{-bt}\right)}{1+\beta e^{-bt}}$
4	Yamada et al.(Y-Exp) [4]	$m\left(t\right)=a(1-e^{-\gamma \alpha \left(1-e^{-\beta t}\right)})$
5	Yamata et al. (Y-Ray) [4]	$m\left(t\right)=a(1-e^{-\gamma \alpha \left(1-e^{-\beta t^2/2}\right)})$
6	Yamada et al. (Y-ID 1) [17]	$m\left(t\right)=\frac{ab}{\alpha +b}\left(e^{\alpha t}-e^{-bt}\right)$
7	Yamada et al. (Y-ID 2) [17]	$m\left(t\right)=a\left[1-e^{-bt}\right]\left[1-\frac{\alpha }{b}\right]+\alpha at$
8	Hossain-Dahiya (HD-GO) [18]	$m\left(t\right)=log[(e^a-c)/(e^{a{e}^{-bt}}-c)]$
9	Pham et al. (P-GID 1) [19]	$m\left(t\right)=\frac{a\left[1-e^{-bt}\right]\left[1-\frac{\alpha }{b}\right]+\alpha at}{1+\beta e^{-bt}}$
10	Pham–Zhang (P-GID) [20]	$m\left(t\right)=\frac{1}{1+\beta e^{-bt}}\left(\left(c+a\right)\left[1-e^{-bt}\right]-\left[\frac{ab}{b-\alpha }\left(e^{-\alpha t}-e^{-bt}\right)\right]\right)$
11	Zhang et al. (Z-FR) [21]	$m\left(t\right)=\frac{a}{p-\beta }\lfloor 1-{\left(\frac{\left(1+\alpha \right)e^{-bt}}{1+\alpha e^{-bt}}\right)}^{\frac{c}{b}\left(p-\beta \right)}\rfloor$
12	Teng-Pham (TP) [8]	$m\left(t\right)=\frac{a}{p-q}\lfloor 1-{\left(\frac{\beta }{\beta +\left(p-q\right)ln\left(\frac{c+e^{bt}}{c+1}\right)}\right)}^{\alpha }\rfloor$
13	Pham Zhang IFD (PZ-IFD) [22]	$m\left(t\right)=a\left(1-e^{-bt}\right)\left(1+\left(b+d\right)t+bd{t}^2\right)$
14	Pham (DP 1) [23]	$m\left(t\right)=\alpha \left(\gamma t+1\right)(\gamma t-1+e^{-\gamma t})$
15	Pham (DP 2) [23]	$m\left(t\right)=m_0\left(\frac{\gamma t+1}{\gamma t_0+1}\right)$$e^{-\gamma \left(t-t_0\right)}$ $+\alpha \left(\gamma t+1\right)(\gamma t-1+\left(1-\gamma t_0\right)e^{-\gamma \left(t-t_0\right)}$
16	Kapur et al. (SRGM-3) [24]	$m\left(t\right)=\frac{A}{1-\alpha }\lfloor 1-{\left(\left(1+bt+\frac{b^2{t}^2}{2}\right)e^{-bt}\right)}^{p\left(1-\alpha \right)}\rfloor$
17	Roy et al. (R-M-D) [25]	$m\left(t\right)=a\alpha \left[1-e^{-bt}\right]-\left[\frac{ab}{b-\beta }\left(e^{-\beta t}-e^{-bt}\right)\right]$
18	Chang et al. (C-TC) [27]	$m\left(t\right)=N\left[1-{\left(\frac{\beta }{\beta +{\left(at\right)}^b}\right)}^{\alpha }\right]$
19	Pham (P-Vtub) [26]	$m\left(t\right)=N\left[1-{\left(\frac{\beta }{\beta +a^t{}^b-1}\right)}^{\alpha }\right]$
20	Song et al. (S-3PFD) [12]	$m\left(t\right)=N\left[1-\left(\frac{\beta }{\beta -\frac{a}{b}ln\left(\frac{\left(1+c\right)e^{-bt}}{1+c{e}^{-bt}}\right)}\right)\right]$
21	Proposed New Model	$m\left(t\right)=N{\left(1-\frac{\beta }{\beta +ln\left(\frac{a+e^{bt}}{1+a}\right)}\right)}^{\alpha }$

3.2. Criteria for Model Comparison

We use ten criteria to estimate the goodness-of-fit of the proposed model, and use one criterion to compare the predicted values.

(1)  Mean squared error (MSE)

$$MSE=\frac{{{\displaystyle \sum }}_{i=1}^n{\left(\widehat{m}\left(t_i\right)-y_i\right)}^2}{n-m}$$

The MSE measures the average of the squares of the errors that is the average squared difference between the estimated values and the actual data.

(2)  Root mean square error (RMSE)

$$RMSE=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^n{\left(\widehat{m}\left(t_i\right)-y_i\right)}^2}{n-m}}$$

The RMSE is a frequently used measure of the differences between values predicted by a model or an estimator and the values observed.

(3)  Predictive ratio risk (PRR) [22]

$$PRR={{\displaystyle \sum }}_{i=1}^n{\left(\frac{\widehat{m}\left(t_i\right)-y_i}{\widehat{m}\left(t_i\right)}\right)}^2$$

The PRR measures the distance of the model estimates from the actual data against the model estimate.

(4)  Predictive power (PP) [22]

$$PP={{\displaystyle \sum }}_{i=1}^n{\left(\frac{\widehat{m}\left(t_i\right)-y_i}{y_i}\right)}^2$$

The PP measures the distance of the model estimates from the actual data.

(5)  Akaike’s information criterion (AIC) [28]

$$AIC=-2logL+2m$$

AIC is measured to compare the capability of each model in terms of maximizing the likelihood function (L), while considering the degrees of freedom. $L$ and $log L$ are given as follows:

$$L={{\displaystyle \prod }}_{i=1}^n\frac{\left(m(t_i\right)-m\left(t_{i-1}\right){)}^{y_i-y_{i-1}}}{\left(y_i-y_{i-1}\right)!}{e}^{-\left(m\left(t_i\right)-m\left(t_{i-1}\right)\right)},$$

$$log L={{\displaystyle \sum }}_{i=1}^n\left\{\left(y_i-y_{i-1}\right)ln\left((m\left(t_i\right)-m\left(t_{i-1}\right)\right)-\left(m\left(t_i\right)-m\left(t_{i-1}\right)\right)-ln\left(\left(y_i-y_{i-1}\right)!\right)\right\}.$$

(6)  R-square (R²) [10]

$$R^2=1-\frac{{{\displaystyle \sum }}_{i=1}^n{\left(\widehat{m}\left(t_i\right)-y_i\right)}^2}{{{\displaystyle \sum }}_{i=1}^n{\left(y_i-\overline{y_i}\right)}^2}$$

The R² measures how successful fit is in explaining the variation of the data.

(7)  Adjusted R-square (Adj R²) [10]

$$Adj R^2=1-\frac{\left(1-R^2\right)\left(n-1\right)}{n-m-1}$$

The Adjusted R² is a modification to R² that adjusts for the number of explanatory terms in a model relative to the number of data points.

(8)  Sum of absolute errors (SAE) [13]

$$SAE={{\displaystyle \sum }}_{i=1}^n\left|\widehat{m}\left(t_i\right)-y_i\right|$$

The SAE measures the absolute distance of the model.

(9)  Mean absolute errors (MAE) [29]

$$MAE=\frac{{{\displaystyle \sum }}_{i=1}^n\left|\widehat{m}\left(t_i\right)-y_i\right|}{n-m}$$

The MAE measures the deviation by the use of absolute distance of the model.

(10)  Variance [16]

$$Variance=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^n{\left(y_i-\widehat{m}\left(t_i\right)-Bias\right)}^2}{n-1}}$$

The variance measures the standard deviation of the prediction bias, where Bias is given as:

$$Bias =\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n\left(\widehat{m}\left(t_i\right)-y_i\right).$$

(11)  Sum of squared errors for predicted value (Pre SSE) [11]

$$Pre SSE={{\displaystyle \sum }}_{i=k+1}^n{\left(\widehat{m}\left(t_i\right)-y_i\right)}^2$$

We use the data points up to time $t_k$ to estimate the parameters of the mean value function $m\left(t\right)$, then measure the square of the error between the estimated value and the actual data after the time $t_k$, obtained by substituting the estimated parameter into the mean value function.

Here, $\widehat{m}\left(t_i\right)$ is the estimated cumulative number of failures at $t_i$ for $i=1, 2,\cdots ,n$; $y_i$ is the total number of failures observed at time $t_i$; $n$ is the total number of observations; $m$ is the number of unknown parameters in the model.

The smaller the value of these nine criteria, i.e., MSE, RMSE, PRR, PP, AIC, SAE, MAE, Variance, and Pre SSE, the better is the fit of the model (closer to 0). On the other hand, the higher the value of the two criteria, i.e., ${\mathrm{R}}^2$ and ${\mathrm{Adj}\mathrm{R}}^2$, the better is the fit of the model (closer to 1).

3.3. Confidence Interval

It is possible to check whether the value of the mean value function is included in the confidence interval at each point, $t_i$, or not and how much the confidence interval actually contains the value. We use the following Equation (7) to obtain the confidence interval [22] of the proposed new model and existing NHPP software reliability models;

$$\widehat{m}\left(t\right)\pm Z_{\alpha /2}\sqrt{\widehat{m}\left(t\right)},$$

(7)

where $Z_{\alpha /2}$ is $100\left(1-\alpha \right)$, the percentile of the standard normal distribution.

4. Numerical Examples

4.1. Data Information

Datasets #1 and #2 were reported by [22] based on system test data for a telecommunication system. Both, the automated and human-involved tests are executed on multiple test beds. The system records the cumulative of faults by each week. In Datasets #1 and #2, the week index is from week 1 to 21, and there are 26 and 43 cumulative failures in 21 weeks, respectively. Detailed information can be seen in [22]. Datasets #3, #4, and #5 were reported by [22] based on the on-line communication system. Here as well, the system records the cumulative of faults by each week. In Datasets #3, #4, and #5, the week index is from week 1 to 12, and there are 26, 55, and 55 cumulative failures in 12 weeks, respectively. Detailed information can be seen in [22].

4.2. Results of the Estimated Parameters

Table 2, Table 3, Table 4, Table 5 and Table 6 summarize the results of the estimated parameters using the LSE technique and the values of the ten criteria (MSE, RMSE, PRR, PP, AIC, ${\mathrm{R}}^2$, ${\mathrm{Adj}\mathrm{R}}^2$, SAE, MAE, and Variance) of all 21 models in Table 1. First, for comparison of the goodness-of-fit, we obtained the parameter estimates and the criteria of all models using all data sets; when $t=1, 2,\cdots ,21$ from Dataset #1 and #2, and when $t=1, 2,\cdots ,12$ from Dataset #3, #4 and #5. As shown in Table 2, Table 3, Table 4, Table 5 and Table 6, we can see that the proposed new model has the best results when comparing the ten criteria to the other models.

Table 2. Results of Model Parameter Estimation and Criteria for Comparison from Dataset #1.

No.	Model	Parameter Estimation	MSE	RMSE	PRR	PP	AIC	R2	Adj R2	SAE	MAE	Variation
1	GO	$\widehat{a}$= 3,923,854.7292 $\widehat{b}$= 3.2 × 10−7	3.8672	1.9665	1.3107	4.7001	65.3539	0.9582	0.9535	33.7895	1.7784	2.0637
2	Y-DS	$\widehat{a}$= 39.82198 $\widehat{b}$= 0.1104	1.4938	1.2222	12.0730	0.9675	63.9400	0.9838	0.9820	19.9951	1.0524	1.1926
3	O-IS	$\widehat{a}$= 26.6845,$\widehat{b}$= 0.2918 $\widehat{\beta }$= 21.6851	0.6745	0.8213	2.8475	0.6556	64.1770	0.9931	0.9919	12.9369	0.7187	0.7996
4	Y-Exp	$\widehat{a}$= 92,075.4308,$\widehat{\alpha }$= 0.3562 $\widehat{\beta }$= 0.0005147,$\widehat{\gamma }$= 0.07514	4.3392	2.0831	1.3380	4.8827	69.3634	0.9580	0.9475	33.9888	1.9993	2.1300
5	Y-Ray	$\widehat{a}$= 29.0366,$\widehat{\alpha }$= 5.9677 $\widehat{\beta }$= 0.000374,$\widehat{\gamma }$= 4.8158	1.1421	1.0687	30.3583	1.2435	67.6217	0.9889	0.9862	16.6930	0.9819	0.9920
6	Y-ID 1	$\widehat{a}$= 1091.828,$\widehat{b}$= 0.00098 $\widehat{\alpha }$= 0.0209	3.4470	1.8566	0.9414	2.7339	67.6756	0.9647	0.9584	30.9144	1.7175	1.8285
7	Y-ID 2	$\widehat{a}$= 2.3351,$\widehat{b}$= 0.2451 $\widehat{\alpha }$= 0.6469	2.5766	1.6052	0.6847	0.9081	66.5843	0.9736	0.9689	25.0483	1.3916	1.5265
8	HD-GO	$\widehat{a}$= 709.7827,$\widehat{b}$= 0.00181 $\widehat{c}$= 0.0998	4.1786	2.0442	1.3722	5.0982	67.3785	0.9572	0.9496	34.3708	1.9095	2.1867
9	P-GID 1	$\widehat{a}$= 10.6281,$\widehat{b}$= 0.37304 $\widehat{\alpha }$= 0.0817,$\widehat{\beta }$= 17.0709	1.2140	1.1018	8.5407	1.1317	66.6636	0.9883	0.9853	17.7928	1.0466	1.0894
10	P-GID 2	$\widehat{a}$= 7.1732,$\widehat{b}$= 0.2784 $\widehat{\alpha }$= 0.2249,$\widehat{\beta }$= 16.7796 $\widehat{c}$= 19.9096	0.8041	0.8967	3.4790	0.7162	68.1690	0.9927	0.9902	13.3027	0.8314	0.8203
11	Z-FR	$\widehat{a}$= 0.5193,$\widehat{b}$= 0.4377 $\widehat{\alpha }$= 5.5458,$\widehat{\beta }$= 6.9059 $\widehat{c}$= 4.6241,$\widehat{p}$= 6.9172	1.7715	1.3310	1.8532	0.6332	70.9195	0.9849	0.9784	19.2629	1.2842	1.1597
12	TP	$\widehat{a}$= 6.7122,$\widehat{b}$= 0.1818 $\widehat{\alpha }$= 0.0687,$\widehat{\beta }$= 0.053 $\widehat{c}$= 0.7196,$\widehat{p}$= 0.1544 $\widehat{q}$= 0.1534	3.6887	1.9206	0.7722	1.9488	74.7613	0.9706	0.9548	27.8156	1.9868	1.6781
13	PZ-IFD	$\widehat{a}$= 6.3355,$\widehat{b}$= 0.1287 $\widehat{d}$= 0.0129	2.8339	1.6834	0.7156	1.6161	66.8070	0.9710	0.9658	27.3902	1.5217	1.6445
14	P-DP 1	$\widehat{\alpha }$= 2.7 × 10−6 $\widehat{\gamma }$= 165.8689	14.5826	3.8187	172.8372	3.7900	75.9409	0.8423	0.8248	65.7605	3.4611	4.7568
15	P-DP 2	$\widehat{\alpha }$= 6879.0649,$\widehat{\gamma }$= 0.00408 ${\widehat{t}}_0$= 0.3483,${\widehat{m}}_0$= 3.9986	9.1284	3.0213	2.1272	22.1461	78.5680	0.9117	0.8896	48.5622	2.8566	2.7857
16	K-SRGM 3	$\widehat{A}$= 24.989,$\widehat{b}$= 0.1385 $\widehat{\alpha }$= 0.1012,$\widehat{p}$= 3.5204	1.2295	1.1088	768.1366	2.3759	70.3312	0.9881	0.9851	17.7006	1.0412	1.1036
17	R-M-D	$\widehat{a}$= 40.2018,$\widehat{b}$= 0.1152 $\widehat{\alpha }$= 0.9319,$\widehat{\beta }$= 0.1402	2.0059	1.4163	6379037.0905	1.7234	80.0129	0.9806	0.9757	22.3624	1.3154	1.5591
18	C-TC	$\widehat{a}$= 0.00432,$\widehat{b}$= 2.234 $\widehat{\alpha }$= 9959.1698,$\widehat{\beta }$= 15.2504 $\widehat{N}$= 26.8334	1.0939	1.0459	102.3904	1.7481	70.5589	0.9900	0.9867	16.0422	1.0026	0.9842
19	P-Vtub	$\widehat{a}$= 1.0985,$\widehat{b}$= 1.2978 $\widehat{\alpha }$= 1.5176,$\widehat{\beta }$= 11.3848 $\widehat{N}$= 25.7412	0.7178	0.8472	4.3863	0.7200	69.0114	0.9935	0.9913	12.7522	0.7970	0.7803
20	S-3PFD	$\widehat{a}$= 0.038, = 0.292 $\widehat{\beta }$= 0.002,$\widehat{N}$= 26.889 $\widehat{c}$= 1488.598	0.7590	0.8712	2.8538	0.6565	68.1694	0.9931	0.9908	12.9491	0.8093	0.7980
21	New Model	$\widehat{a}$= 108,232.8195 $\widehat{b}$= 1.0047,$\widehat{\alpha }$= 0.2176 $\widehat{\beta }$= 155.5011,$\widehat{N}$= 47.7965	0.5864	0.7658	0.5024	1.2025	66.7301	0.9947	0.9929	11.3783	0.7111	0.6906

Table 3. Results of Model Parameter Estimation and Criteria for Comparison from Dataset #2.

No.	Model	Parameter Estimation	MSE	RMSE	PRR	PP	AIC	R2	Adj R2	SAE	MAE	Variation
1	GO	$\widehat{a}$= 5899.3694 $\widehat{b}$= 0.0036	6.6537	2.5795	0.6859	1.0870	78.3163	0.9718	0.9687	43.1731	2.2723	2.6349
2	Y-DS	$\widehat{a}$= 62.3045 $\widehat{b}$= 0.1185	3.2732	1.8092	44.3612	1.4298	81.0873	0.9862	0.9846	32.5216	1.7117	1.8123
3	O-IS	$\widehat{a}$= 46.5437,$\widehat{b}$= 0.2409 $\widehat{\beta }$= 12.2242	1.8704	1.3676	5.9546	0.8965	76.9477	0.9925	0.9912	21.9605	1.2200	1.3693
4	Y-Exp	$\widehat{a}$= 616.2702,$\widehat{\alpha }$= 0.1998 $\widehat{\beta }$= 0.00048,$\widehat{\gamma }$= 36.8345	7.9598	2.8213	0.7015	1.1835	82.2610	0.9699	0.9623	44.2608	2.6036	2.7046
5	Y-Ray	$\widehat{a}$= 47.0086,$\widehat{\alpha }$= 6.2232 $\widehat{\beta }$= 0.00029,$\widehat{\gamma }$= 6.3708	3.2147	1.7929	111.4178	1.8451	85.7632	0.9878	0.9848	27.7602	1.6330	1.8734
6	Y-ID 1	$\widehat{a}$= 647.4658,$\widehat{b}$= 0.00295 $\widehat{\alpha }$= 0.0158	6.2463	2.4993	0.6833	0.7512	80.9818	0.9750	0.9705	40.9177	2.2732	2.4195
7	Y-ID 2	$\widehat{a}$= 68.4424,$\widehat{b}$= 0.0265 $\widehat{\alpha }$= 0.0511	5.9996	2.4494	0.7308	0.6707	80.8924	0.9760	0.9717	39.9577	2.2199	2.3415
8	HD-GO	$\widehat{a}$= 709.7826,$\widehat{b}$= 0.00307 $\widehat{c}$= 0.7659	7.3398	2.7092	0.7035	1.2045	80.2859	0.9706	0.9654	44.4142	2.4675	2.7776
9	P-GID 1	$\widehat{a}$= 46.4854,$\widehat{b}$= 0.2410 $\widehat{\alpha }$= 0.000067,$\widehat{\beta }$= 12.2127	1.9814	1.4076	5.9524	0.8964	78.9480	0.9925	0.9906	21.9749	1.2926	1.3673
10	P-GID 2	$\widehat{a}$= 0.000032,$\widehat{b}$= 0.2409 $\widehat{\alpha }$= 1.6139,$\widehat{\beta }$= 12.2219 $\widehat{c}$= 46.5445	2.1042	1.4506	5.9510	0.8963	80.9477	0.9925	0.9900	21.9644	1.3728	1.3683
11	Z-FR	$\widehat{a}$= 283.299,$\widehat{b}$= 0.173997 $\widehat{\alpha }$= 520.118,$\widehat{\beta }$= 0.27156 $\widehat{c}$= 1.8366,$\widehat{p}$= 6.9716	1.8601	1.3639	3.9072	0.7296	84.2304	0.9938	0.9911	20.1020	1.3401	1.2316
12	TP	$\widehat{a}$= 192.3412,$\widehat{b}$= 0.3131 $\widehat{\alpha }$= 0.029,$\widehat{\beta }$= 0.1954 $\widehat{c}$= 1 0.0202,$\widehat{p}$= 0.5938 $\widehat{q}$= 0.3842	3.5100	1.8735	6.2127	0.9182	86.2875	0.9891	0.9832	28.6293	2.0450	1.6235
13	PZ-IFD	$\widehat{a}$= 13.1083,$\widehat{b}$= 0.1154 $\widehat{d}$= 0.0057	5.1126	2.2611	1.0650	0.6546	80.1375	0.9795	0.9759	36.4678	2.0260	2.1645
14	P-DP 1	$\widehat{\alpha }$= 7.6 × 10−7 $\widehat{\gamma }$= 403.0753	43.7600	6.6151	613.6285	4.5758	104.7474	0.8149	0.7943	122.0195	6.4221	8.8176
15	P-DP 2	$\widehat{\alpha }$= 3343.5848,$\widehat{\gamma }$= 0.00728 ${\widehat{t}}_0$= 0.3771,${\widehat{m}}_0$= 7.7754	21.3006	4.6153	1.4148	5.4631	96.7740	0.9194	0.8992	76.4876	4.4993	4.2597
16	K-SRGM 3	$\widehat{A}$= 21.2662,$\widehat{b}$= 0.3874 $\widehat{\alpha }$= 0.6255,$\widehat{p}$= 0.8962	3.9525	1.9881	439.7196	2.0575	90.5520	0.9850	0.9813	32.8146	1.9303	1.9720
17	R-M-D	$\widehat{a}$= 157.3012,$\widehat{b}$= 0.0144 $\widehat{\alpha }$= 1.2327,$\widehat{\beta }$= 0.3454	4.6378	2.1536	6.7102	0.9139	83.3777	0.9824	0.9781	34.4805	2.0283	2.0045
18	C-TC	$\widehat{a}$= 0.00607,$\widehat{b}$= 1.864 $\widehat{\alpha }$= 9445.7865,$\widehat{\beta }$= 93.4027 $\widehat{N}$= 48.9629	3.3003	1.8167	57.3169	1.5788	86.4442	0.9882	0.9843	28.8335	1.8021	1.7301
19	P-Vtub	$\widehat{a}$= 1.2575,$\widehat{b}$= 0.98699 $\widehat{\alpha }$= 1.4559,$\widehat{\beta }$= 16.4583 $\widehat{N}$= 45.2916	1.9851	1.4089	4.7454	0.8092	80.7744	0.9929	0.9906	21.7860	1.3616	1.3047
20	S-3PFD	$\widehat{a}$= 3.078,$\widehat{b}$= 0.2410 $\widehat{\beta }$= 0.170,$\widehat{N}$= 46.8430 $\widehat{c}$= 999.493	2.1046	1.4507	5.9567	0.8967	80.9477	0.9925	0.9900	21.9661	1.3729	1.3680
21	New Model	$\widehat{a}$= 9198.8054 $\widehat{b}$= 0.7274,$\widehat{\alpha }$= 0.2584 $\widehat{\beta }$= 5.9777,$\widehat{N}$= 50.2841	0.8470	0.9203	0.1159	0.1355	77.0423	0.9970	0.9960	14.0367	0.8773	0.8232

Table 4. Results of Model Parameter Estimation and Criteria for Comparison from Dataset #3.

No.	Model	Parameter Estimation	MSE	RMSE	PRR	PP	AIC	R2	Adj R2	SAE	MAE	Variation
1	GO	$\widehat{a}$= 464.5247 $\widehat{b}$= 0.00536	9.0920	3.0153	0.9284	1.4443	62.4128	0.9069	0.8862	28.2200	2.8220	2.8899
2	Y-DS	$\widehat{a}$= 35.8316 $\widehat{b}$= 0.2396	7.0034	2.6464	13.4415	1.6025	63.3503	0.9283	0.9124	24.4671	2.4467	2.5391
3	O-IS	$\widehat{a}$= 26.9254,$\widehat{b}$= 0.6204 $\widehat{\beta }$= 30.0163	5.1138	2.2614	22.9009	1.4436	57.8013	0.9529	0.9352	18.2801	2.0311	2.1767
4	Y-Exp	$\widehat{a}$= 6456.5057,$\widehat{\alpha }$= 0.1461 $\widehat{\beta }$= 0.00495,$\widehat{\gamma }$= 0.5332	11.3652	3.3712	0.9284	1.4442	66.4149	0.9069	0.8537	28.2211	3.5276	2.8900
5	Y-Ray	$\widehat{a}$= 28.4774,$\widehat{\alpha }$= 23.884 $\widehat{\beta }$= 2.3 × 10−6,$\widehat{\gamma }$= 746.3198	7.4818	2.7353	36.8584	1.5855	66.0682	0.9387	0.9037	21.3831	2.6729	2.5201
6	Y-ID 1	$\widehat{a}$= 316.6384,$\widehat{b}$= 0.00789 $\widehat{\alpha }$= 0.0016	10.1040	3.1787	0.9243	1.4515	64.3742	0.9069	0.8720	28.1806	3.1312	2.8893
7	Y-ID 2	$\widehat{a}$= 4.4246,$\widehat{b}$= 0.4623 $\widehat{\alpha }$= 0.5756	9.9746	3.1583	1.2645	1.2271	64.9967	0.9081	0.8736	29.0765	3.2307	2.8578
8	HD-GO	$\widehat{a}$= 446.4583,$\widehat{b}$= 0.00558 $\widehat{c}$= 1 × 10−9	10.1022	3.1784	0.9279	1.4447	64.4008	0.9069	0.8720	28.2149	3.1350	2.8889
9	P-GID 1	$\widehat{a}$= 27.1316,$\widehat{b}$= 0.5709 $\widehat{\alpha }$= 2.1 × 10−11,$\widehat{\beta }$= 22.163	5.8233	2.4132	14.4703	1.3672	59.5427	0.9523	0.9250	18.2613	2.2827	2.1505
10	P-GID 2	$\widehat{a}$= 1 × 10−10,$\widehat{b}$= 0.6204 $\widehat{\alpha }$= 0.0387,$\widehat{\beta }$= 30.0163 $\widehat{c}$= 26.9254	6.5749	2.5642	22.9009	1.4436	61.8013	0.9529	0.9136	18.2801	2.6114	2.1767
11	Z-FR	$\widehat{a}$= 46.9742,$\widehat{b}$= 0.1457 $\widehat{\alpha }$= 0.1382,$\widehat{\beta }$= 0.1987 $\widehat{c}$= 0.0596,$\widehat{p}$= 0.4732	14.9849	3.8710	0.9416	1.4419	70.2105	0.9079	0.7975	28.0342	4.6724	2.8709
12	TP	$\widehat{a}$= 107.787,$\widehat{b}$= 2.6× 10−8 $\widehat{\alpha }$= 0.2044,$\widehat{\beta }$= 1.1 × 10−7 $\widehat{c}$= 1.1232,$\widehat{p}$= 0.00142 $\widehat{q}$= 0.000061	18.2859	4.2762	0.9453	1.4258	72.7010	0.9064	0.7426	28.3832	5.6766	2.9222
13	PZ-IFD	$\widehat{a}$= 281.2703,$\widehat{b}$= 0.0083 $\widehat{d}$= 0.000031	10.2029	3.1942	1.0336	1.2844	64.9647	0.9060	0.8707	29.1055	3.2339	2.8893
14	P-DP 1	$\widehat{\alpha }$= 2.0 × 10−6 $\widehat{\gamma }$= 1115.343	34.4416	5.8687	246.9020	2.6126	86.7862	0.6474	0.5690	54.1442	5.4144	6.8563
15	P-DP 2	$\widehat{\alpha }$= 2070.3183,$\widehat{\gamma }$= 0.0125 ${\widehat{t}}_0$= 8.7785,${\widehat{m}}_0$= 19.516	21.2667	4.6116	1.0306	1.5407	72.4094	0.8258	0.7263	41.3919	5.1740	3.9346
16	K-SRGM 3	$\widehat{A}$= 27.2536,$\widehat{b}$= 0.1691 $\widehat{\alpha }$= 0.00,$\widehat{p}$= 9.476	7.2970	2.7013	444.6336	1.9569	71.8813	0.9402	0.9061	20.6929	2.5866	2.5289
17	R-M-D	$\widehat{a}$= 35.969,$\widehat{b}$= 0.24269 $\widehat{\alpha }$= 0.9901,$\widehat{\beta }$= 0.2427	8.7525	2.9585	15.6161	1.6246	67.6920	0.9283	0.8873	24.4048	3.0506	2.5408
18	C-TC	$\widehat{a}$= 0.2739,$\widehat{b}$= 2.604 $\widehat{\alpha }$= 12.2099,$\widehat{\beta }$= 50.5848 $\widehat{N}$= 26.7229	7.9859	2.8259	302.4876	1.9056	71.5591	0.9428	0.8951	19.7573	2.8225	2.4696
19	P-Vtub	$\widehat{a}$= 1.9764,$\widehat{b}$= 0.8427 $\widehat{\alpha }$= 33.7789,$\widehat{\beta }$= 804.4101 $\widehat{N}$= 25.8336	6.1408	2.4781	9.4191	1.1932	59.4576	0.9560	0.9193	18.0194	2.5742	2.0513
20	S-3PFD	$\widehat{a}$= 10.6227,$\widehat{b}$= 0.6211 $\widehat{\beta }$= 1.3819,$\widehat{N}$= 27.808 $\widehat{c}$= 397.0025	6.6075	2.5705	23.0454	1.4412	61.9886	0.9526	0.9132	18.3461	2.6209	2.1986
21	New Model	$\widehat{a}$= 9643.4774 $\widehat{b}$= 1.3046,$\widehat{\alpha }$= 0.3131 $\widehat{\beta }$= 1.4073,$\widehat{N}$= 27.70003	4.4412	2.1074	1.7190	0.7376	54.3482	0.9682	0.9416	15.4691	2.2099	1.7189

Table 5. Results of Model Parameter Estimation and Criteria for Comparison from Dataset #4.

No.	Model	Parameter Estimation	MSE	RMSE	PRR	PP	AIC	R2	Adj R2	SAE	MAE	Variation
1	GO	$\widehat{a}$= 270.1056 $\widehat{b}$= 0.02075	18.3634	4.2853	0.3249	0.4503	80.3676	0.9519	0.9412	41.4895	4.1490	4.1060
2	Y-DS	$\widehat{a}$= 69.8210 $\widehat{b}$= 0.2627	14.0418	3.7472	6.7145	0.8711	82.3170	0.9632	0.9550	35.4185	3.5418	3.6596
3	O-IS	$\widehat{a}$= 59.0235,$\widehat{b}$= 0.4417 $\widehat{\beta }$= 9.7336	10.8677	3.2966	2.6138	0.6298	75.1254	0.9744	0.9647	28.1022	3.1225	3.0973
4	Y-Exp	$\widehat{a}$= 5981.4323,$\widehat{\alpha }$= 0.0778 $\widehat{\beta }$= 0.0199,$\widehat{\gamma }$= 0.6051	22.9599	4.7916	0.3250	0.4498	84.3686	0.9518	0.9243	41.5089	5.1886	4.1045
5	Y-Ray	$\widehat{a}$= 57.701,$\widehat{\alpha }$= 58.8436 $\widehat{\beta }$= 2.6 × 10−8,$\widehat{\gamma }$= 30,017.6386	16.6108	4.0756	20.8256	1.0967	86.7089	0.9652	0.9453	31.4668	3.9334	3.9710
6	Y-ID 1	$\widehat{a}$= 270.1054,$\widehat{b}$= 0.02075 $\widehat{\alpha }$= 1.4 × 10−8	20.4038	4.5171	0.3249	0.4503	82.3676	0.9519	0.9338	41.4896	4.6100	4.1060
7	Y-ID 2	$\widehat{a}$= 270.1041,$\widehat{b}$= 0.0208 $\widehat{\alpha }$= 9.9 × 10−8	20.4110	4.5179	0.3238	0.4546	82.3842	0.9518	0.9338	41.3885	4.5987	4.1220
8	HD-GO	$\widehat{a}$= 270.1056,$\widehat{b}$= 0.0208 $\widehat{c}$= 1 × 10−9	20.4111	4.5179	0.3238	0.4546	82.3843	0.9518	0.9338	41.3882	4.5987	4.1221
9	P-GID 1	$\widehat{a}$= 59.0239,$\widehat{b}$= 0.4417 $\widehat{\alpha }$= 1.4 × 10−10,$\widehat{\beta }$= 9.7338	12.2261	3.4966	2.6139	0.6298	77.1255	0.9744	0.9597	28.1025	3.5128	3.0972
10	P-GID 2	$\widehat{a}$= 1 × 10−10,$\widehat{b}$= 0.4418 $\widehat{\alpha }$= 0.1819,$\widehat{\beta }$= 9.7336 $\widehat{c}$= 59.0235	13.9727	3.7380	2.6113	0.6298	79.1245	0.9744	0.9530	28.0991	4.0142	3.0944
11	Z-FR	$\widehat{a}$= 88.285,$\widehat{b}$= 0.2295 $\widehat{\alpha }$= 1.1342,$\widehat{\beta }$= 0.1063 $\widehat{c}$= 0.1169,$\widehat{p}$= 1.0616	25.7905	5.0784	0.4037	0.4399	85.8969	0.9594	0.9107	38.1771	6.3629	3.7579
12	TP	$\widehat{a}$= 5.5526,$\widehat{b}$= 0.1157 $\widehat{\alpha }$= 2.7637,$\widehat{\beta }$= 0.2783 $\widehat{c}$= 0.1523,$\widehat{p}$= 0.0844 $\widehat{q}$= 0.0632	36.2811	6.0234	0.3289	0.4475	90.2214	0.9524	0.8692	41.3061	8.2612	4.0814
13	PZ-IFD	$\widehat{a}$= 13.351,$\widehat{b}$= 0.3015 $\widehat{d}$= 1 × 10−10	18.9582	4.3541	0.5563	0.4514	82.7552	0.9553	0.9385	41.5660	4.6184	3.9404
14	P-DP 1	$\widehat{\alpha }$= 5.5 × 10−8 $\widehat{\gamma }$= 3036.6077	146.2340	12.0927	193.5342	2.9279	132.5762	0.6166	0.5314	120.1415	12.0141	15.5642
15	P-DP 2	$\widehat{\alpha }$= 71,469.8104,$\widehat{\gamma }$= 0.00313 ${\widehat{t}}_0$= 8.7 × 10−6,${\widehat{m}}_0$= 13.8578	64.8252	8.0514	0.7452	1.5864	108.7149	0.8640	0.7863	71.5589	8.9449	6.8673
16	K-SRGM3	$\widehat{A}$= 47.998,$\widehat{b}$= 0.9041 $\widehat{\alpha }$= 0.2937,$\widehat{p}$= 0.394	18.9589	4.3542	23.2982	1.1112	91.8189	0.9602	0.9375	34.9075	4.3634	3.8929
17	R-M-D	$\widehat{a}$= 66.7919,$\widehat{b}$= 0.2313 $\widehat{\alpha }$= 1.10797,$\widehat{\beta }$= 0.23129	16.9597	4.1182	2.1336	0.6528	83.0580	0.9644	0.9441	35.9526	4.4941	3.5372
18	C-TC	$\widehat{a}$= 0.3805,$\widehat{b}$= 1.7675 $\widehat{\alpha }$= 6021.5496 $\widehat{\beta }$= 33,686.7619,$\widehat{N}$= 61.0142	18.1240	4.2572	7.6284	0.8839	86.1250	0.9667	0.9390	32.2656	4.6094	3.5264
19	P-Vtub	$\widehat{a}$= 2.3187,$\widehat{b}$= 0.6928 $\widehat{\alpha }$= 13.81799,$\widehat{\beta }$= 269.3212 $\widehat{N}$= 55.7854	12.2331	3.4976	1.2508	0.4708	76.2949	0.9775	0.9588	26.5196	3.7885	2.8320
20	S-3PFD	$\widehat{a}$= 223.3416,$\widehat{b}$= 0.4424 $\widehat{\beta }$= 4.4956,$\widehat{N}$= 59.245 $\widehat{c}$= 1213.0757	13.9742	3.7382	2.6264	0.6308	79.1281	0.9744	0.9530	28.0662	4.0095	3.0997
21	New Model	$\widehat{a}$= 42763.1241 $\widehat{b}$= 1.6385,$\widehat{\alpha }$= 0.2005 $\widehat{\beta }$= 12.6879,$\widehat{N}$= 65.868	6.7120	2.5908	0.1812	0.1363	70.5195	0.9877	0.9774	18.2230	2.6033	2.0735

Table 6. Results of Model Parameter Estimation and Criteria for Comparison from Dataset #5.

No.	Model	Parameter Estimation	MSE	RMSE	PRR	PP	AIC	R2	Adj R2	SAE	MAE	Variation
1	GO	$\widehat{a}$= 94.3479 $\widehat{b}$= 0.0733	4.0245	2.0061	0.2932	0.1627	57.7077	0.9855	0.9822	19.4198	1.9420	1.9150
2	Y-DS	$\widehat{a}$= 57.5047 $\widehat{b}$= 0.3437	8.2095	2.8652	7.3903	0.6184	69.6185	0.9704	0.9638	20.9577	2.0958	3.0188
3	O-IS	$\widehat{a}$= 65.8343,$\widehat{b}$= 0.2055 $\widehat{\beta }$= 1.2874	4.0555	2.0138	0.4802	0.1903	60.1404	0.9868	0.9819	17.0533	1.8948	1.8479
4	Y-Exp	$\widehat{a}$= 3344.357,$\widehat{\alpha }$= 0.1819 $\widehat{\beta }$= 0.0718,$\widehat{\gamma }$= 0.1584	5.0365	2.2442	0.2929	0.1625	61.7078	0.9855	0.9771	19.4216	2.4277	1.9171
5	Y-Ray	$\widehat{a}$= 62.3356,$\widehat{\alpha }$= 0.038 $\widehat{\beta }$= 0.0315,$\widehat{\gamma }$= 51.9474	15.0669	3.8816	18.8397	0.8508	81.3798	0.9565	0.9316	26.5145	3.3143	3.7589
6	Y-ID 1	$\widehat{a}$= 94.3479,$\widehat{b}$= 0.0733 $\widehat{\alpha }$= 1.1 × 10−9	4.4716	2.1146	0.2932	0.1627	59.7077	0.9855	0.9800	19.4198	2.1578	1.9150
7	Y-ID 2	$\widehat{a}$= 94.3479,$\widehat{b}$= 0.0733 $\widehat{\alpha }$= 1 × 10−10	4.4716	2.1146	0.2932	0.1627	59.7077	0.9855	0.9800	19.4198	2.1578	1.9150
8	HD-GO	$\widehat{a}$= 94.3479,$\widehat{b}$= 0.0733 $\widehat{c}$= 0.000109	4.4716	2.1146	0.2932	0.1627	59.7077	0.9855	0.9800	19.4198	2.1578	1.9150
9	P-GID 1	$\widehat{a}$= 65.8343,$\widehat{b}$= 0.2055 $\widehat{\alpha }$= 3.8 × 10−8,$\widehat{\beta }$= 1.2874	4.5624	2.1360	0.4802	0.1903	62.1404	0.9868	0.9793	17.0533	2.1317	1.8479
10	P-GID 2	$\widehat{a}$= 0.0023,$\widehat{b}$= 0.2055 $\widehat{\alpha }$= 0.2328,$\widehat{\beta }$= 1.2874 $\widehat{c}$= 65.832	5.2142	2.2835	0.4803	0.1903	64.1404	0.9868	0.9759	17.0539	2.4363	1.8480
11	Z-FR	$\widehat{a}$= 27.83996,$\widehat{b}$= 0.1217 $\widehat{\alpha }$= 5.0642,$\widehat{\beta }$= 0.2853 $\widehat{c}$= 1.3182,$\widehat{p}$= 0.7382	6.0591	2.4615	0.4518	0.1844	66.1861	0.9869	0.9711	17.0776	2.8463	1.8421
12	TP	$\widehat{a}$= 14.3726,$\widehat{b}$= 0.1574 $\widehat{\alpha }$= 10.3379,$\widehat{\beta }$= 2.9351 $\widehat{c}$= 0.1765,$\widehat{p}$= 0.2112 $\widehat{q}$= 0.05296	7.8879	2.8085	0.3120	0.1652	67.7199	0.9858	0.9609	18.9981	3.7996	1.8967
13	PZ-IFD	$\widehat{a}$= 6.4775,$\widehat{b}$= 0.6673 $\widehat{d}$= 1 × 10−10	9.0608	3.0101	0.8594	0.2657	62.8008	0.9706	0.9595	25.3217	2.8135	2.9951
14	P-DP 1	$\widehat{\alpha }$= 0.0115 $\widehat{\gamma }$= 6.5411	183.4378	13.5439	432.0333	3.4669	124.8012	0.3380	0.1909	136.0472	13.6047	18.4397
15	P-DP 2	$\widehat{\alpha }$= 36,611.3949,$\widehat{\gamma }$= 0.004045 ${\widehat{t}}_0$= 15.3658,${\widehat{m}}_0$= 90.9356	43.7504	6.6144	0.5473	1.0956	81.2894	0.8737	0.8015	57.2136	7.1517	5.6431
16	K-SRGM3	$\widehat{A}$= 55.9248,$\widehat{b}$= 5.8366 $\widehat{\alpha }$= 0.2215,$\widehat{p}$= 0.029	6.6314	2.5751	1.9490	0.3686	66.8324	0.9809	0.9699	19.5164	2.4396	2.3443
17	R-M-D	$\widehat{a}$= 39.8594,$\widehat{b}$= 0.18996 $\widehat{\alpha }$= 1.7852,$\widehat{\beta }$= 0.1900	4.6755	2.1623	0.4548	0.1884	62.0841	0.9865	0.9788	17.5748	2.1969	1.8633
18	C-TC	$\widehat{a}$= 0.1375,$\widehat{b}$= 1.0738 $\widehat{\alpha }$= 16,035.1043 $\widehat{\beta }$= 24,002.2196,$\widehat{N}$= 80.5179	5.6419	2.3753	0.4285	0.1883	64.2419	0.9857	0.9739	18.3880	2.6269	1.9083
19	P-Vtub	$\widehat{a}$= 2.3789,$\widehat{b}$= 0.6047 $\widehat{\alpha }$= 1.2364,$\widehat{\beta }$= 14.6987 $\widehat{N}$= 64.9314	4.4144	2.1010	0.2444	0.1304	62.5181	0.9888	0.9796	16.5855	2.3694	1.6903
20	S-3PFD	$\widehat{a}$= 0.05496,$\widehat{b}$= 0.2072 $\widehat{\beta }$= 0.0245,$\widehat{N}$= 68.5181 $\widehat{c}$= 25.0097	5.2143	2.2835	0.4812	0.1905	64.1366	0.9868	0.9759	17.0484	2.4355	1.8470
21	New Model	$\widehat{a}$= 276.2278 $\widehat{b}$= 1.1084,$\widehat{\alpha }$= 0.2693 $\widehat{\beta }$= 54.0622,$\widehat{N}$= 93.8052	2.3671	1.5385	0.0412	0.0333	58.7819	0.9940	0.9890	11.4867	1.6410	1.2284

As can be seen from Table 2, the MSE, RMSE, PRR, SAE, MAE, and Variance values for the proposed new model are the lowest values compared to all models in Table 1. The MSE value of the proposed new model is 0.5864, which is smaller than the value of MSE of other models. The RMSE value is 0.7658, PRR value is 0.5024, SAE value is 11.3783, MAE value is 0.7111, and Variance value is 0.6903, which are smaller than the corresponding values of other models. The ${\mathrm{R}}^2$ and ${\mathrm{Adj}\mathrm{R}}^2$ values for the proposed new model are the largest values as compared to all models. The ${\mathrm{R}}^2$ value of the proposed model is 0.9947, and the ${\mathrm{Adj}\mathrm{R}}^2$ value is 0.9929, which are larger than the corresponding values of other models.

From Table 3, we can see that the MSE, RMSE, PRR, PP, SAE, MAE, and Variance values for the proposed new model are the lowest values in comparison with every model in Table 1. The MSE value of the proposed new model is 0.8470, which is smaller than that of other models. The RMSE value is 0.9203, PRR value is 0.1159, PP value is 0.1355, SAE value is 14.0367, MAE value is 0.8773, and Variance value is 0.8232, which are smaller than the corresponding values of other models. The AIC value is 77.0423, which is the second lowest value. The ${\mathrm{R}}^2$ and ${\mathrm{Adj}\mathrm{R}}^2$ values for the proposed new model are the largest values compared to all models. The value of ${\mathrm{R}}^2$ for the proposed model is 0.9970 and the ${\mathrm{Adj}\mathrm{R}}^2$ is 0.9960, which are larger than the respective values of other models.

As can be seen from Table 4, the MSE, RMSE, PP, AIC, SAE, and Variance values for the proposed new model are the lowest values compared to all other models in Table 1. The MSE value of the proposed new model is 4.4412, which is smaller than that of the other models. The RMSE value is 2.1074, PP value is 0.7376, AIC value is 54.3482, SAE value is 15.4691, and Variance value is 1.7189, which are smaller than the value of other models. The MAE value is 2.2099, which is the second lowest value. The ${\mathrm{R}}^2$ and ${\mathrm{Adj}\mathrm{R}}^2$ values for the proposed new model are the largest values compared to all models. The ${\mathrm{R}}^2$ value of the proposed model is 0.9682 and the ${\mathrm{Adj}\mathrm{R}}^2$ value is 0.9416, which are larger than the value of other models.

As seen from Table 5, the MSE, RMSE, PRR, PP, AIC, SAE, MAE, and Variance values for the proposed new model are the lowest values in comparison with every model in Table 1. The MSE value of the proposed new model is 6.7120, RMSE value is 2.5908, PRR value is 0.1812, PP value is 0.1363, AIC value is 70.5195, SAE value is 18.2230, MAE value is 2.6033, and Variance value is 2.0735, which are smaller than the value of other models. The values of ${\mathrm{R}}^2$ and ${\mathrm{Adj}\mathrm{R}}^2$ for the proposed new model are the largest values compared to all models. The value of ${\mathrm{R}}^2$ for the proposed model is 0.9877 and that of ${\mathrm{Adj}\mathrm{R}}^2$ is 0.9774, which are larger than the respective values of other models.

As depicted in Table 6, the MSE, RMSE, PRR, PP, SAE, MAE, and Variance values for the proposed new model are the lowest values as compared to all other models in Table 1. The MSE value of the proposed new model is 2.3671, RMSE value is 1.5385, PRR value is 0.04121, PP value is 0.0333, SAE value is 11.4867, MAE value is 1.6410, and Variance value is 1.2284, which are smaller than the corresponding values of other models. The AIC value is 58.7819, which is the second lowest value. The ${\mathrm{R}}^2$ and ${\mathrm{Adj}\mathrm{R}}^2$ values for the proposed new model are the largest values compared to all models. The value of ${\mathrm{R}}^2$ for the proposed model is 0.9940 and that of ${\mathrm{Adj}\mathrm{R}}^2$ is 0.9890, which are larger than the corresponding values of other models.

Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 show graphs of the mean value functions for all models based on Datasets #1–#5, respectively. Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 show graphs of the 95% confidence interval of the proposed new model, which serve to confirm whether the value of the mean value function is included in the confidence interval of each time point. Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 show graphs of the relative error value of all models, which serve to confirm its ability to provide better accuracy.

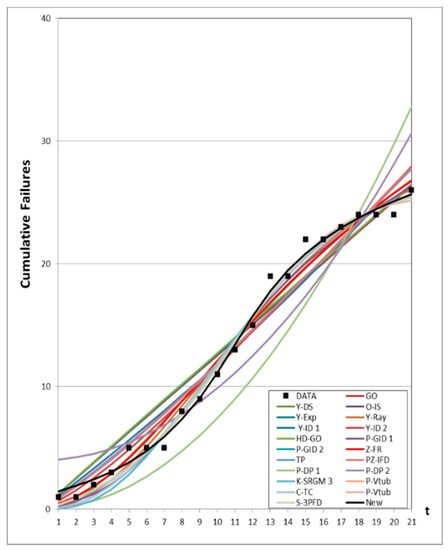
Figure 1. Mean value functions of all models for Dataset #1.

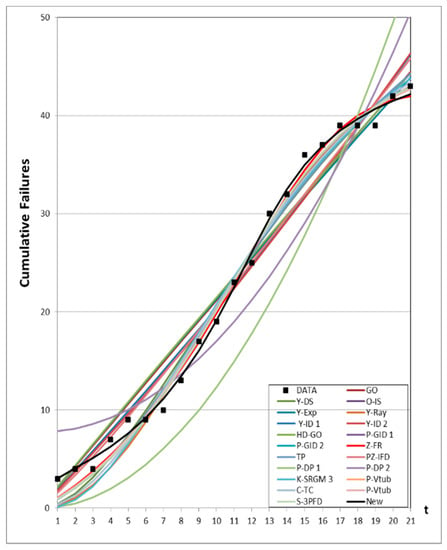
Figure 2. Mean value functions of all models for Dataset #2.

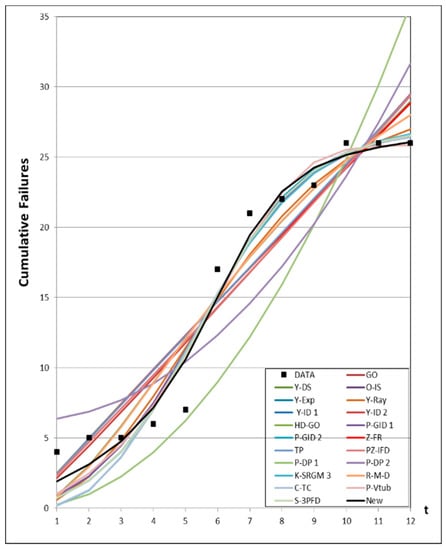
Figure 3. Mean value functions of all models for Dataset #3.

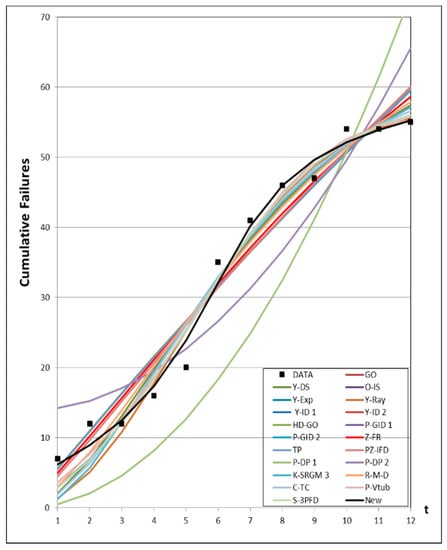
Figure 4. Mean value functions of all models for Dataset #4.

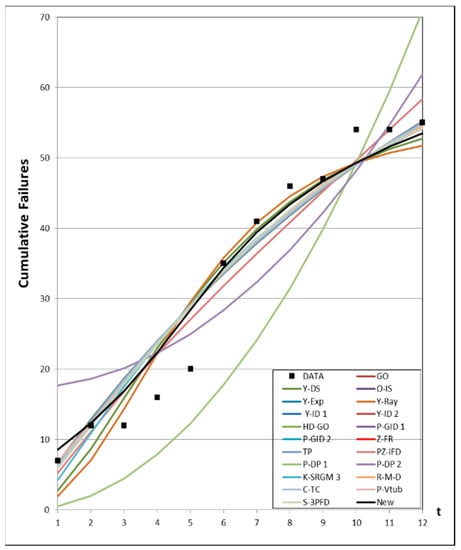
Figure 5. Mean value functions of all models for Dataset #5.

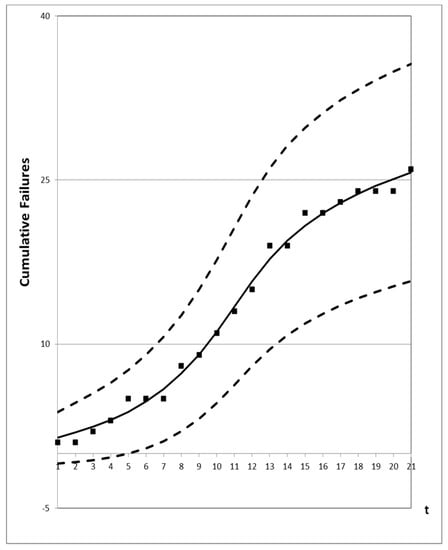
Figure 6. 95% confidence interval of the proposed new model for Dataset #1.

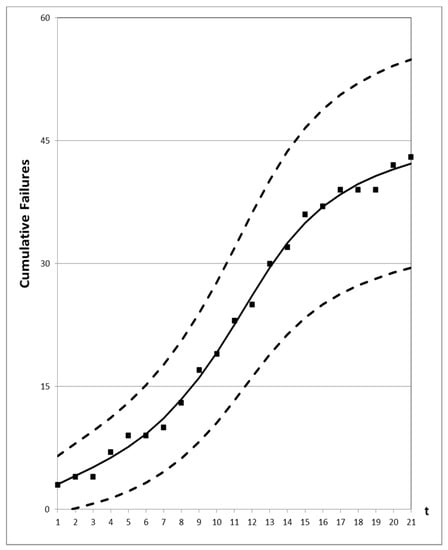
Figure 7. 95% confidence interval of the proposed new model for Dataset #2.

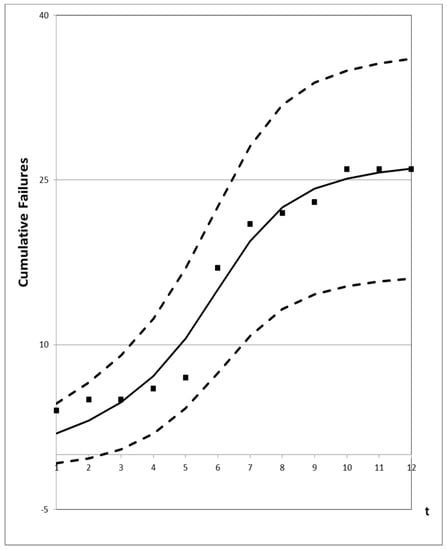
Figure 8. 95% confidence interval of the proposed new model for Dataset #3.

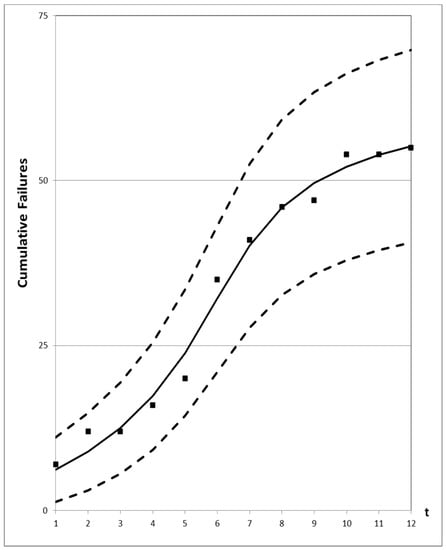
Figure 9. 95% confidence interval of the proposed new model for Dataset #4.

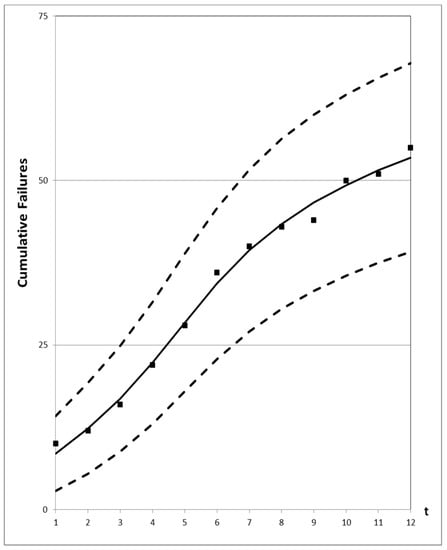
Figure 10. 95% confidence interval of the proposed new model for Dataset #5.

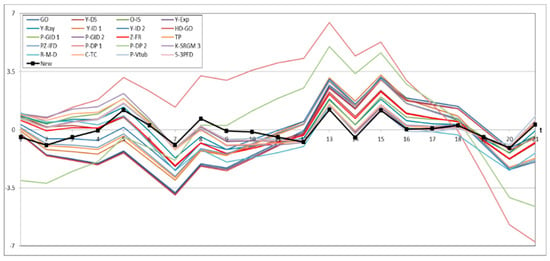
Figure 11. Relative error value of all models for Dataset #1.

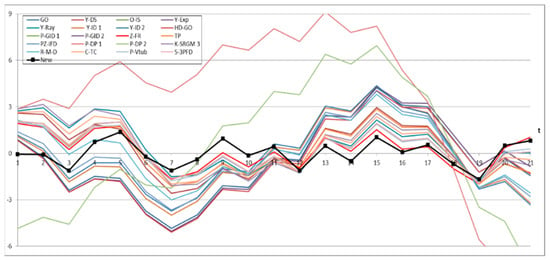
Figure 12. Relative error value of all models for Dataset #2.

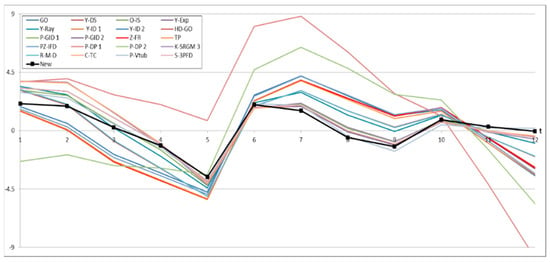
Figure 13. Relative error value of all models for Dataset #3.

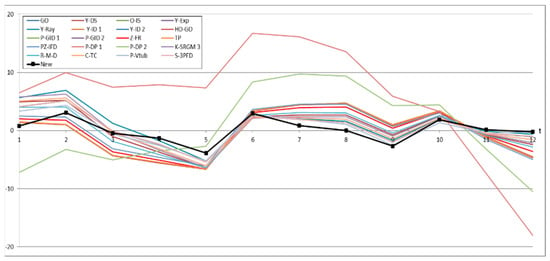
Figure 14. Relative error value of all models for Dataset #4.

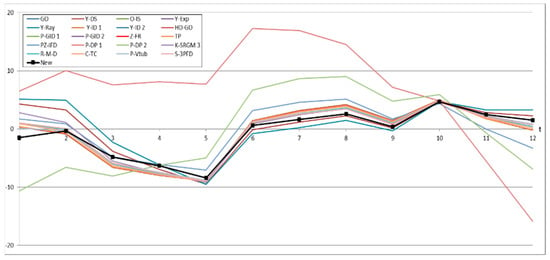
Figure 15. Relative error value of all models for Dataset #5.

4.3. Prediction Analysis

In this paper, we use Dataset #1 and #2 to compare how the predicted values of each model are different to fulfill the objective of this paper. We compare the goodness-of-fit of all models by using up to 75% of the dataset and compare the predicted value of all models using the remaining 25% of dataset. For comparison of the goodness-of-fit, we obtained the parameter estimates and the criteria (MSE, RMSE, PRR, PP, AIC, ${\mathrm{R}}^2$, ${\mathrm{Adj}\mathrm{R}}^2$, SAE, MAE, and Variance) for all models when $t=1, 2,\cdots ,16$, and, for comparison of the predicted value, we obtained the PreSSE value of all models when $t=17, 18,\cdots ,21$ from Dataset #1 and #2.

First of all, as seen in Table 7 and Table 8 for comparison of the goodness-of-fit, it is evident that the proposed new model has the best results when comparing the ten criteria with the other models. As seen from Table 7, the MSE, RMSE, PRR, SAE, and Variance values for the proposed new model are the lowest values compared to all models in Table 1. The MSE value of the proposed new model is 0.5915, which is smaller than the corresponding value of other models. The RMSE value is 0.7691, the PRR value is 0.3380, the SAE value is 8.2769, and the Variance value is 0.6591, which are smaller than the value of other models. The ${\mathrm{R}}^2$ and ${\mathrm{Adj}\mathrm{R}}^2$ values for the proposed new model are the largest values compared to all models. The value of ${\mathrm{R}}^2$ for the proposed model is 0.9923 and that of ${\mathrm{Adj}\mathrm{R}}^2$ is 0.9885, which are larger than the respective values of other models. As seen from Table 8, the MSE, RMSE, PRR, PP, SAE, MAE, and Variance values for the proposed new model are the lowest values in comparison with all models in Table 1. The MSE value of the proposed new model is 0.7827, RMSE value is 0.8847, PRR value is 0.1103, PP value is 0.1306, SAE value is 9.9671, MAE value is 0.7576, and Variance value is 0.7576, which are smaller than the corresponding values of other models. The ${\mathrm{R}}^2$ and ${\mathrm{Adj}\mathrm{R}}^2$ values for the proposed new model are the largest values compared to all models. The value of ${\mathrm{R}}^2$ for the proposed model is 0.9959 and that of ${\mathrm{Adj}\mathrm{R}}^2$ is 0.9939, both of which are larger than the respective values of other models. Finally, as shown in Table 7 and Table 8 for the comparison of the predicted value, it is evident that the proposed new model has the best results when comparing the criterion of PreSSE with the other models. As it can be seen from Table 7, the PreSSE value for the proposed new model is the lowest value as compared to all models in Table 1. The PreSSE value of the proposed new model is 2.6780, which is smaller than that of the other models. The PreSSE value of the proposed new model is 8.6532, which is smaller than the value of PreSSE of other models in Table 8. Figure 16 and Figure 17 show graphs of the goodness-of-fit and prediction of mean value functions for all models from Datasets #1 and #2, respectively.

Table 7. Results of Model parameter estimation, criteria, and prediction for comparison-Dataset #1.

No.	Model	Parameter Estimation	MSE	RMSE	PRR	PP	AIC	R2	Adj R2	SAE	MAE	Variation	PreSSE
1	GO	$\widehat{a}$= 2439.1963 $\widehat{b}$= 0.00052	4.8579	2.2041	1.3269	4.8721	53.2386	0.9199	0.9076	29.4319	2.1023	2.5172	5.7456
2	Y-DS	$\widehat{a}$= 81.5159 $\widehat{b}$= 0.0657	0.8455	0.9195	25.1885	1.1392	52.1261	0.9861	0.9839	11.1007	0.7929	0.9257	128.7087
3	O-IS	$\widehat{a}$= 32.2358,$\widehat{b}$= 0.2378 $\widehat{\beta }$= 16.9353	0.6685	0.8176	1.4552	0.4588	52.1602	0.9898	0.9872	9.4132	0.7241	0.7726	36.1311
4	Y-Exp	$\widehat{a}$= 8326.9505,$\widehat{\alpha }$= 0.5383 $\widehat{\beta }$= 0.00029,$\widehat{\gamma }$= 0.9697	5.6573	2.3785	1.3088	4.7500	57.2550	0.9201	0.8910	29.2644	2.4387	2.4581	6.0419
5	Y-Ray	$\widehat{a}$= 54.2003,$\widehat{\alpha }$= 0.0486 $\widehat{\beta }$= 0.00296,$\widehat{\gamma }$= 35.7066	1.0206	1.0102	39.9442	1.3655	56.1363	0.9856	0.9803	11.9100	0.9925	0.9885	70.2926
6	Y-ID 1	$\widehat{a}$= 174.82114,$\widehat{b}$= 0.00407 $\widehat{\alpha }$= 0.08606	1.0997	1.0487	0.4140	0.6004	53.9407	0.9832	0.9790	10.7461	0.8266	0.9927	518.5369
7	Y-ID 2	$\widehat{a}$= 26.9978,$\widehat{b}$= 0.0173 $\widehat{\alpha }$= 0.3124	0.8788	0.9374	0.9227	0.4135	53.3683	0.9865	0.9832	8.7974	0.6767	0.8735	299.6604
8	HD-GO	$\widehat{a}$= 709.7826,$\widehat{b}$= 0.00179 $\widehat{c}$= 27.17296	5.3433	2.3116	1.3283	4.8597	55.3403	0.9182	0.8978	29.6288	2.2791	2.4842	6.2455
9	P-GID 1	$\widehat{a}$= 12.7655,$\widehat{b}$= 0.2324 $\widehat{\alpha }$= 0.095,$\widehat{\beta }$= 6.7409	0.7999	0.8944	1.9120	0.5175	54.5868	0.9887	0.9846	9.6560	0.8047	0.8168	89.6441
10	P-GID 2	$\widehat{a}$= 0.00079,$\widehat{b}$= 0.2378 $\widehat{\alpha }$= 6.79798,$\widehat{\beta }$= 16.9353 $\widehat{c}$= 32.235	0.7900	0.8888	1.4552	0.4588	56.1602	0.9898	0.9847	9.4132	0.8557	0.7726	36.1309
11	Z-FR	$\widehat{a}$= 339.2109,$\widehat{b}$= 0.2114 $\widehat{\alpha }$= 208.6339,$\widehat{\beta }$= 0.1286 $\widehat{c}$= 0.2734,$\widehat{p}$= 13.3842	0.7917	0.8897	1.3398	0.4410	57.6773	0.9907	0.9845	9.2198	0.9220	0.7383	4.4041
12	TP	$\widehat{a}$= 1.9773,$\widehat{b}$= 0.2819 $\widehat{\alpha }$= 0.6614,$\widehat{\beta }$= 0.2226 $\widehat{c}$= 2.2607,$\widehat{p}$= 0.0576 $\widehat{q}$= 0.0702	1.2346	1.1111	0.7866	0.4119	61.1905	0.9869	0.9755	8.9309	0.9923	0.8616	258.9145
13	PZ-IFD	$\widehat{a}$= 3.0369,$\widehat{b}$= 0.1407 $\widehat{d}$= 0.1038	0.8589	0.9268	1.1519	0.4317	53.2961	0.9869	0.9836	8.8436	0.6803	0.8636	268.2888
14	P-DP 1	$\widehat{\alpha }$= 0.00053 $\widehat{\gamma }$= 13.6882	2.5693	1.6029	89.2144	2.1491	55.2758	0.9577	0.9511	19.9041	1.4217	2.0091	803.4099
15	P-DP 2	$\widehat{\alpha }$= 16,554.0442,$\widehat{\gamma }$= 0.00323 ${\widehat{t}}_0$= 1.1159,${\widehat{m}}_0$= 1.8408	1.4601	1.2083	0.6654	2.0357	56.3830	0.9794	0.9719	12.3365	1.0280	1.0812	598.1091
16	K-SRGM 3	$\widehat{A}$= 43.9312,$\widehat{b}$= 1.3062 $\widehat{\alpha }$= 2.2423,$\widehat{p}$= 0.0265	1.0199	1.0099	20.5291	0.9348	56.6049	0.9856	0.9804	10.1636	0.8470	0.9148	264.3312
17	R-M-D	$\widehat{a}$= 153.5748,$\widehat{b}$= 0.0327 $\widehat{\alpha }$= 1.0556,$\widehat{\beta }$= 0.0463	0.9091	0.9535	2.6861	0.5630	55.2528	0.9872	0.9825	9.2852	0.7738	0.8606	188.6321
18	C-TC	$\widehat{a}$= 0.0288,$\widehat{b}$= 1.6825 $\widehat{\alpha }$= 193.5851,$\widehat{\beta }$= 167.6135 $\widehat{N}$= 86.0872	1.0215	1.0107	8.9612	0.8232	57.6870	0.9868	0.9802	10.0127	0.9102	0.8859	160.1096
19	P-Vtub	$\widehat{a}$= 1.2816,$\widehat{b}$= 0.9844 $\widehat{\alpha }$= 1.1473,$\widehat{\beta }$= 20.7523 $\widehat{N}$= 31.4297	0.7830	0.8849	1.3879	0.4508	56.1136	0.9899	0.9848	9.3983	0.8544	0.7681	32.5458
20	S-3PFD	$\widehat{a}$= 0.1496,$\widehat{b}$= 0.2372 $\widehat{\beta }$= 0.1982,$\widehat{N}$= 36.9478 $\widehat{c}$= 62.4407	0.8172	0.9040	1.3089	0.4455	56.1928	0.9894	0.9841	9.7423	0.8857	0.7774	45.9267
21	New Model	$\widehat{a}$= 10453.17249 $\widehat{b}$= 0.53348,$\widehat{\alpha }$= 0.4174 $\widehat{\beta }$= 0.1175,$\widehat{N}$= 24.9924	0.5915	0.7691	0.3380	0.6053	54.8572	0.9923	0.9885	8.2769	0.7524	0.6591	2.6780

Table 8. Results of Model parameter estimation, criteria, and prediction for comparison-Dataset #2.

No.	Model	Parameter Estimation	MSE	RMSE	PRR	PP	AIC	R2	Adj R2	SAE	MAE	Variation	PreSSE
1	GO	$\widehat{a}$= 3631.5077 $\widehat{b}$= 0.00058856	8.0914	2.8445	0.6812	1.1134	61.1966	0.9463	0.9380	36.5962	2.6140	3.0456	13.3815
2	Y-DS	$\widehat{a}$= 92.9084 $\widehat{b}$= 0.08688	2.7180	1.6486	70.6100	1.6218	65.0441	0.9820	0.9792	19.8586	1.4185	1.8435	157.7642
3	O-IS	$\widehat{a}$= 76.8382,$\widehat{b}$= 0.1513 $\widehat{\beta }$= 9.348	1.5104	1.2290	2.7478	0.6084	61.0251	0.9907	0.9884	15.2338	1.1718	1.1949	276.1112
4	Y-Exp	$\widehat{a}$= 16,029.2962,$\widehat{\alpha }$= 0.2561 $\widehat{\beta }$= 0.000375,$\widehat{\gamma }$= 1.3887	9.4224	3.0696	0.6816	1.1158	65.1857	0.9464	0.9269	36.5870	3.0489	3.0523	13.4557
5	Y-Ray	$\widehat{a}$= 83.3575,$\widehat{\alpha }$= 0.06002 $\widehat{\beta }$= 0.005,$\widehat{\gamma }$= 20.2075	3.7509	1.9367	122.7334	1.9015	70.1373	0.9787	0.9709	20.9782	1.7482	2.1406	64.8807
6	Y-ID 1	$\widehat{a}$= 1829.4685,$\widehat{b}$= 0.00074 $\widehat{\alpha }$= 0.0672	1.7208	1.3118	1.5540	0.4759	61.5783	0.9894	0.9867	16.5054	1.2696	1.2638	826.9275
7	Y-ID 2	$\widehat{a}$= 2404.9698,$\widehat{b}$= 0.00049 $\widehat{\alpha }$= 0.1324	1.6375	1.2796	2.2863	0.5616	61.5103	0.9899	0.9874	15.9021	1.2232	1.2062	605.1401
8	HD-GO	$\widehat{a}$= 709.7827,$\widehat{b}$= 0.00306 $\widehat{c}$= 1× 10−9	9.1979	3.0328	0.6912	1.1752	63.4061	0.9433	0.9292	37.7317	2.9024	3.1490	12.6426
9	P-GID 1	$\widehat{a}$= 45.3264,$\widehat{b}$= 0.1489 $\widehat{\alpha }$= 0.0343,$\widehat{\beta }$= 5.1894	1.6792	1.2958	2.9736	0.6315	63.1427	0.9904	0.9870	15.3907	1.2826	1.2188	306.8552
10	P-GID 2	$\widehat{a}$= 0.00085,$\widehat{b}$= 0.1513 $\widehat{\alpha }$= 0.8954,$\widehat{\beta }$= 9.34796 $\widehat{c}$= 76.8381	1.7850	1.3360	2.7477	0.6084	65.0251	0.9907	0.9860	15.2335	1.3849	1.1948	276.1485
11	Z-FR	$\widehat{a}$= 110.9274,$\widehat{b}$= 0.1443 $\widehat{\alpha }$= 243.7368,$\widehat{\beta }$= 0.04498 $\widehat{c}$= 2.4367,$\widehat{p}$= 2.1721	1.8974	1.3774	2.9162	0.6253	66.7569	0.9910	0.9850	14.8415	1.4841	1.1887	129.7523
12	TP	$\widehat{a}$= 3.1572,$\widehat{b}$= 0.1481 $\widehat{\alpha }$= 5.3435,$\widehat{\beta }$= 0.1162 $\widehat{c}$= 18.143,$\widehat{p}$= 0.0997 $\widehat{q}$= 0.0547	2.1636	1.4709	2.7535	0.6092	68.9644	0.9908	0.9827	15.1312	1.6812	1.1850	244.6593
13	PZ-IFD	$\widehat{a}$= 31.2103,$\widehat{b}$= 0.038 $\widehat{d}$= 0.0429	1.6279	1.2759	2.2668	0.5577	61.4700	0.9900	0.9875	15.9819	1.2294	1.2277	583.1510
14	P-DP 1	$\widehat{\alpha }$= 0.00055 $\widehat{\gamma }$= 17.3503	10.7490	3.2786	328.0224	2.9526	72.2485	0.9287	0.9177	44.4948	3.1782	4.6393	2211.9360
15	P-DP 2	$\widehat{\alpha }$= 59,270.7316,$\widehat{\gamma }$= 0.00215 ${\widehat{t}}_0$= 6.7491,${\widehat{m}}_0$= 10.6115	2.4626	1.5693	0.2884	0.4953	63.5555	0.9860	0.9809	17.6701	1.4725	1.4047	1310.6154
16	K-SRGM 3	$\widehat{A}$= 7.5932,$\widehat{b}$= 0.799 $\widehat{\alpha }$= 0.9886,$\widehat{p}$= 0.6217	3.2377	1.7994	153.8475	1.7084	71.3605	0.9816	0.9749	20.3997	1.7000	1.9248	253.8031
17	R-M-D	$\widehat{a}$= 3618.8593,$\widehat{b}$= 0.00207 $\widehat{\alpha }$= 1.1458,$\widehat{\beta }$= 0.0255	1.7907	1.3382	2.7803	0.6101	63.5428	0.9898	0.9861	16.0428	1.3369	1.2495	500.8745
18	C-TC	$\widehat{a}$= 0.0624,$\widehat{b}$= 1.3996 $\widehat{\alpha }$= 58.5612,$\widehat{\beta }$= 3755.7385 $\widehat{N}$= 2468.2417	2.3527	1.5338	8.7659	0.9162	67.1476	0.9877	0.9816	17.5609	1.5964	1.3852	383.3217
19	P-Vtub	$\widehat{a}$= 1.8042,$\widehat{b}$= 0.6499 $\widehat{\alpha }$= 2.9707,$\widehat{\beta }$= 103.1556 $\widehat{N}$= 66.0397	1.5601	1.2490	1.2753	0.4419	64.0424	0.9919	0.9878	14.5886	1.3262	1.0982	233.1903
20	S-3PFD	$\widehat{a}$= 0.0649,$\widehat{b}$= 0.1509 $\widehat{\beta }$= 0.07298,$\widehat{N}$= 83.3809 $\widehat{c}$= 64.9276	1.7861	1.3365	2.7395	0.6073	65.0284	0.9907	0.9860	15.2673	1.3879	1.2011	278.3163
21	New Model	$\widehat{a}$= 14,718.555 $\widehat{b}$= 0.5631,$\widehat{\alpha }$= 0.3272 $\widehat{\beta }$= 0.1884 $\widehat{N}$= 41.8677	0.7827	0.8847	0.1103	0.1306	61.2342	0.9959	0.9939	9.9671	0.9061	0.7576	8.6532

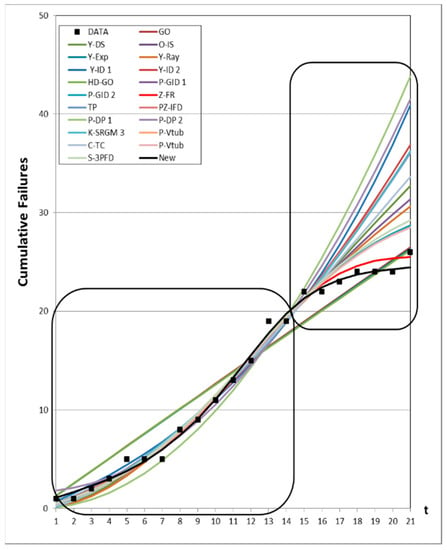
Figure 16. Goodness-of-fit and prediction of mean value functions of all models for Dataset #1.

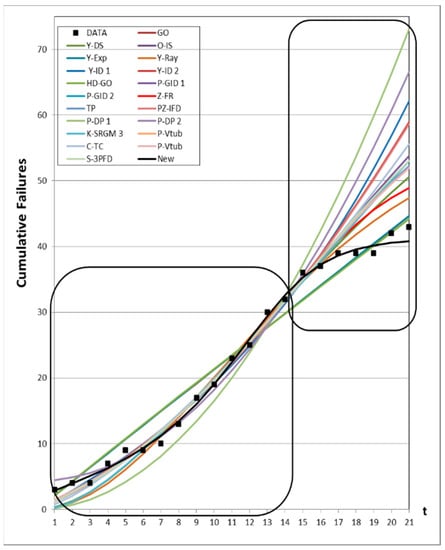
Figure 17. Goodness-of-fit and prediction of mean value functions of all models for Dataset #2.

5. Conclusions

The software is used in a variety of environments; however, it is typically developed and tested in a controlled environment. The uncertainty of the operating environment is considered because the environment in which the software is operated varies. Therefore, we consider the uncertainty of the operating environment and the learn-curve in the fault detection rate function. In this paper, we discussed a new model with inflection factor of the fault detection rate function considering the uncertainty of operating environments and analyzed how the predicted values of the proposed new model are different than the other models. We provided numerical proof by goodness-of-fit and also predicted the values for all models, and compared the proposed new model with several existing NHPP software reliability models based on eleven criteria (MSE, RMSE, PRR, PP, AIC,${\mathrm{R}}^2$, ${\mathrm{Adj}\mathrm{R}}^2$, SAE, MAE, Variance, and Pre SSE). As shown with the numerical examples, the results prove that the proposed new model has significantly better goodness-of-fit and predicts the value better than the other existing models. Future work will involve broader validation of this conclusion based on recent data sets. In addition, we need to apply Bayesian and big-data estimation method to estimate parameters, and also need to consider the multi-release point.