An m-Polar Fuzzy Hypergraph Model of Granular Computing
Abstract
:1. Introduction
2. Fundamental Features of -Polar Fuzzy Hypergraphs
- , , ⋯, ,
- , for all and for all .
2.1. Uncertainty Measures of m-Polar Fuzzy Hierarchical Quotient Space Structure
- 1.
- , ,…, , for all ,
- 2.
- , ,…, , ,…, , for all
- 1.
- , ,…, , for all ,
- 2.
- , ,…, , ,…, , for all
- 3.
- for all , , i.e.,
2.2. Information Entropy of m-PFHQSS
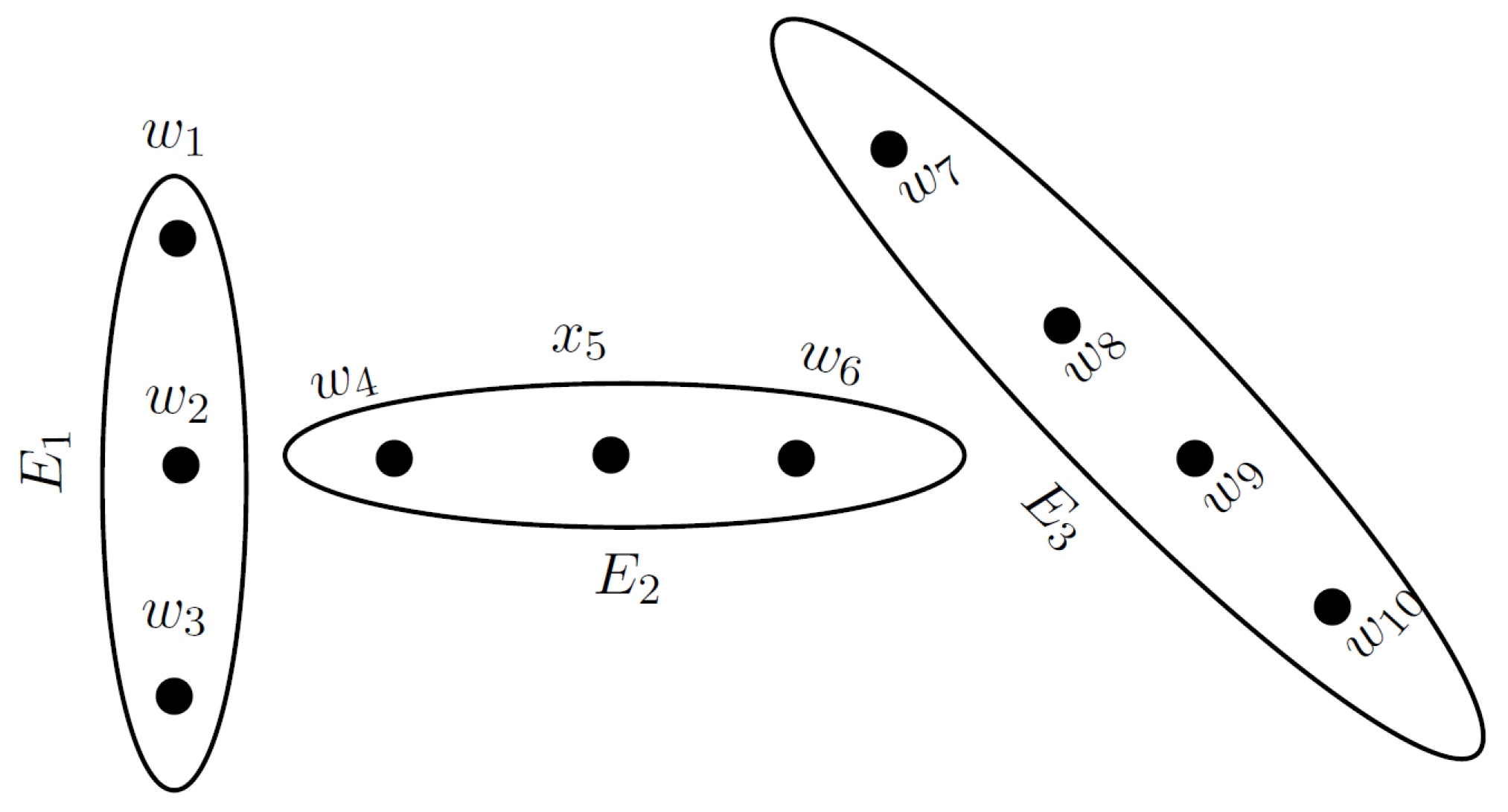
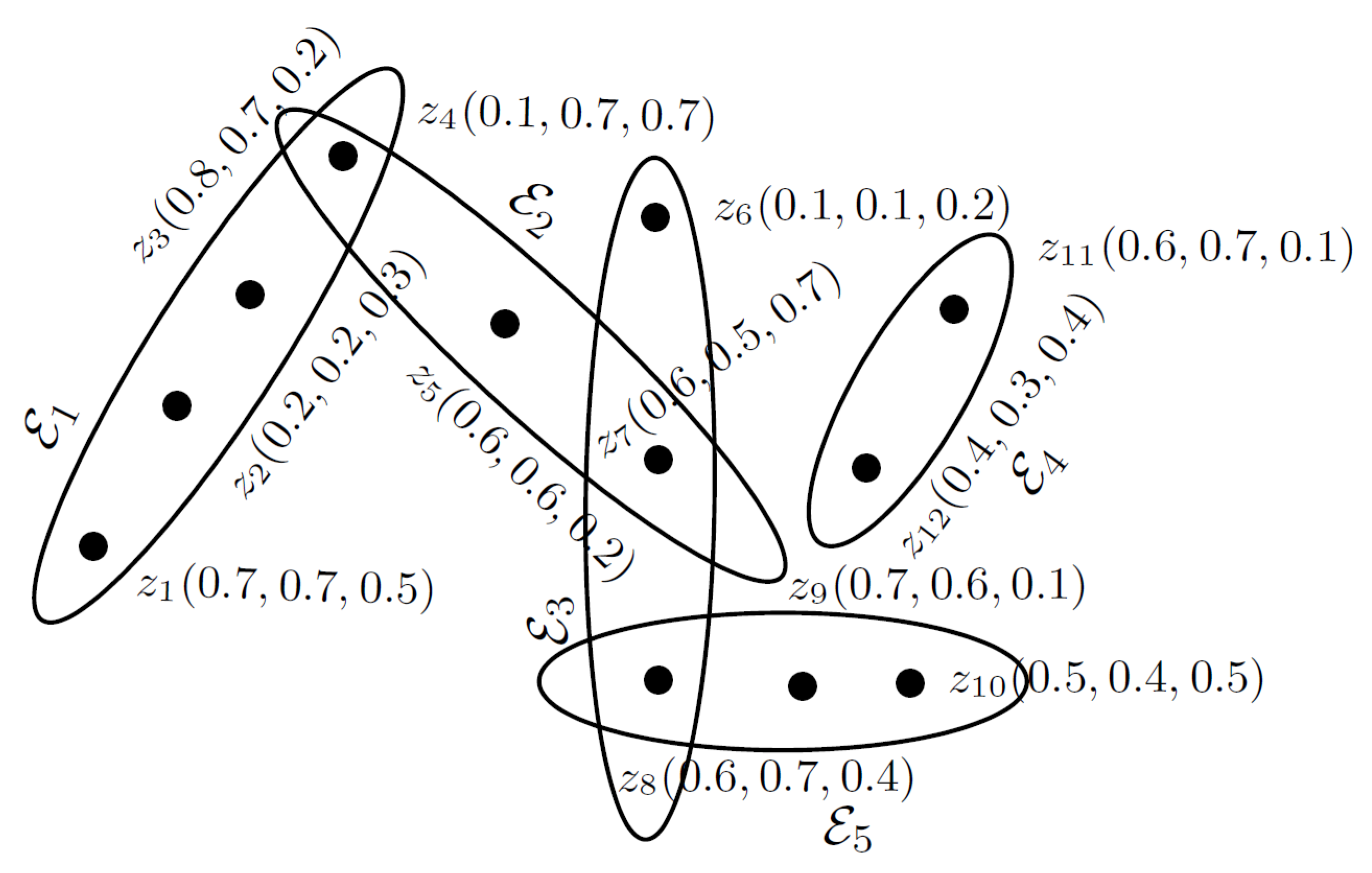
3. An -Polar Fuzzy Hypergraph Model of Granular Computing
- each is non-empty,
- for , ,
- .
- each is non-empty,
- .
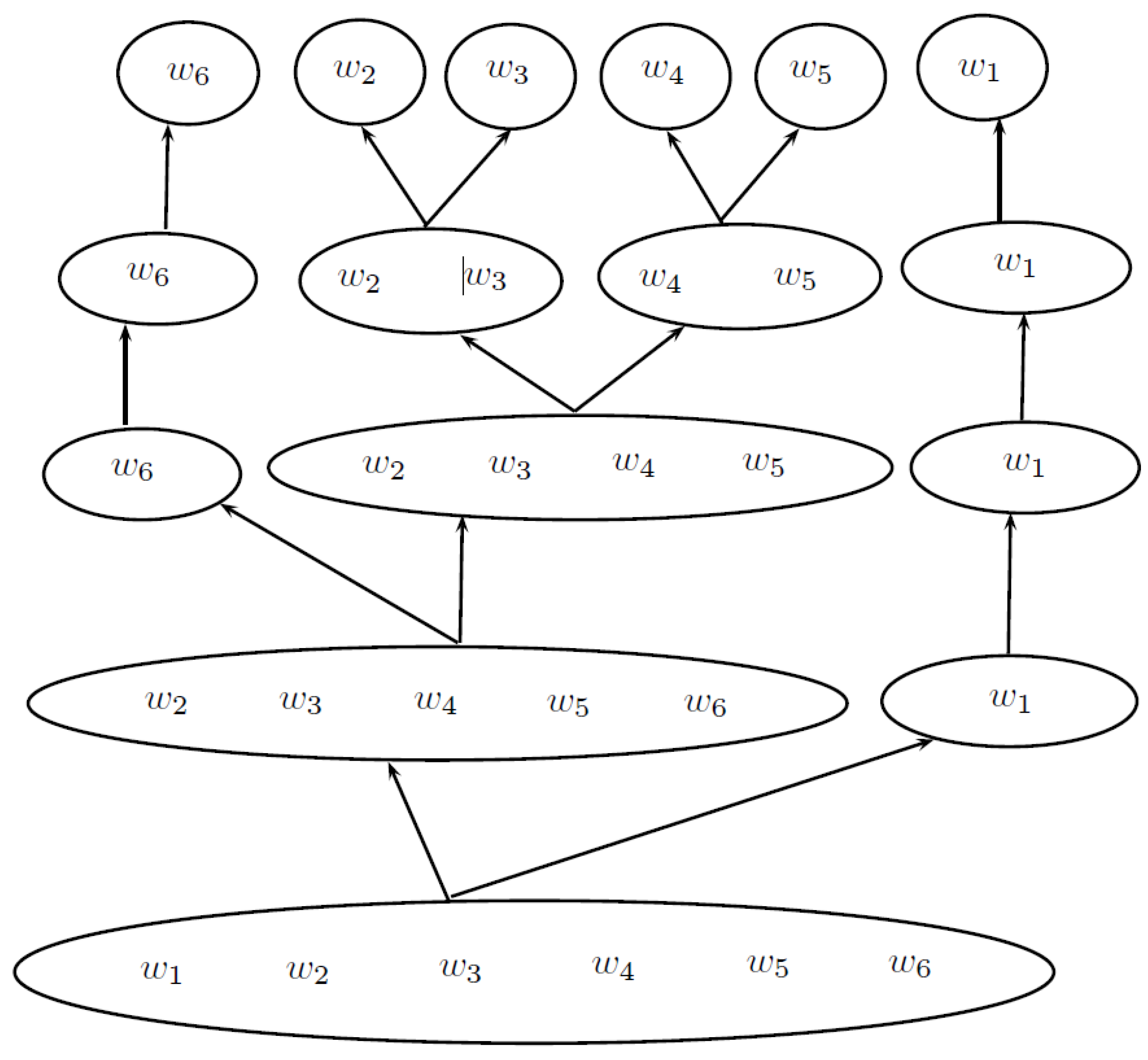
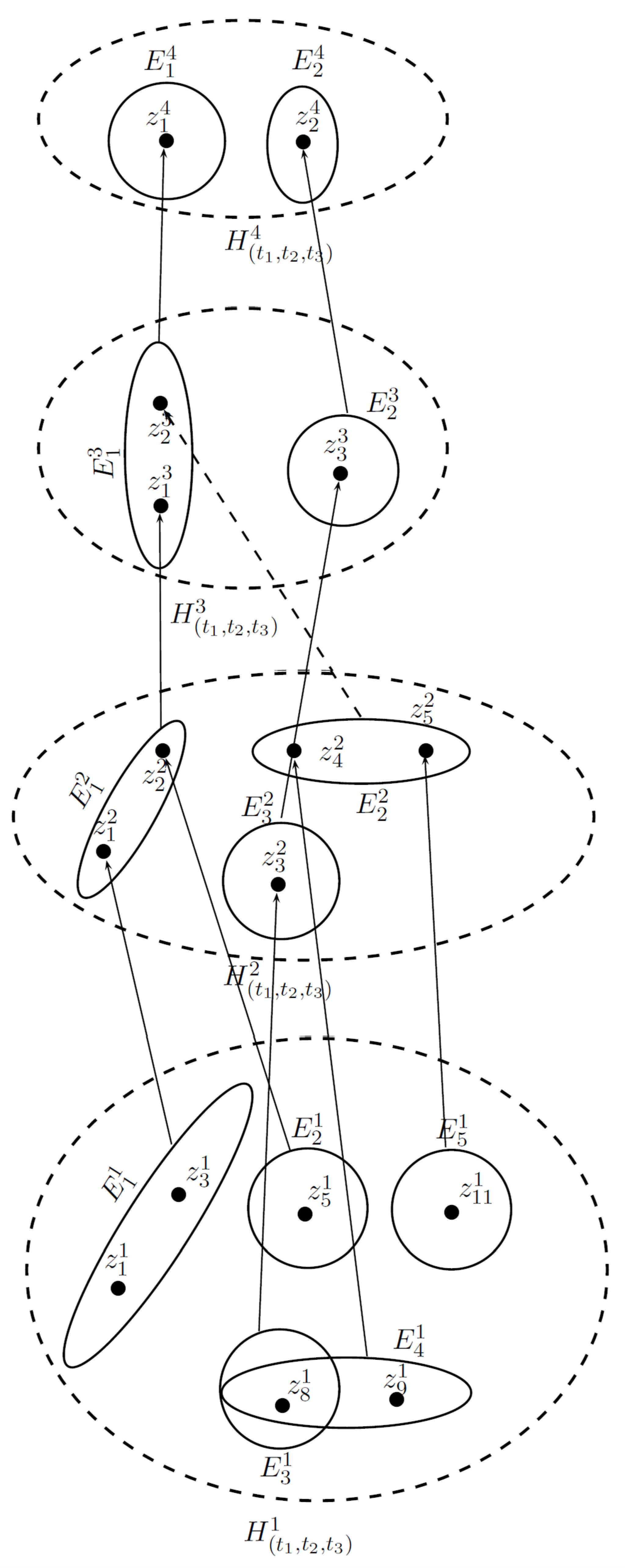
Formation of Hierarchical Structures
| Algorithm 1: The procedure of bottom-up construction for the level hypergraph model. |
|
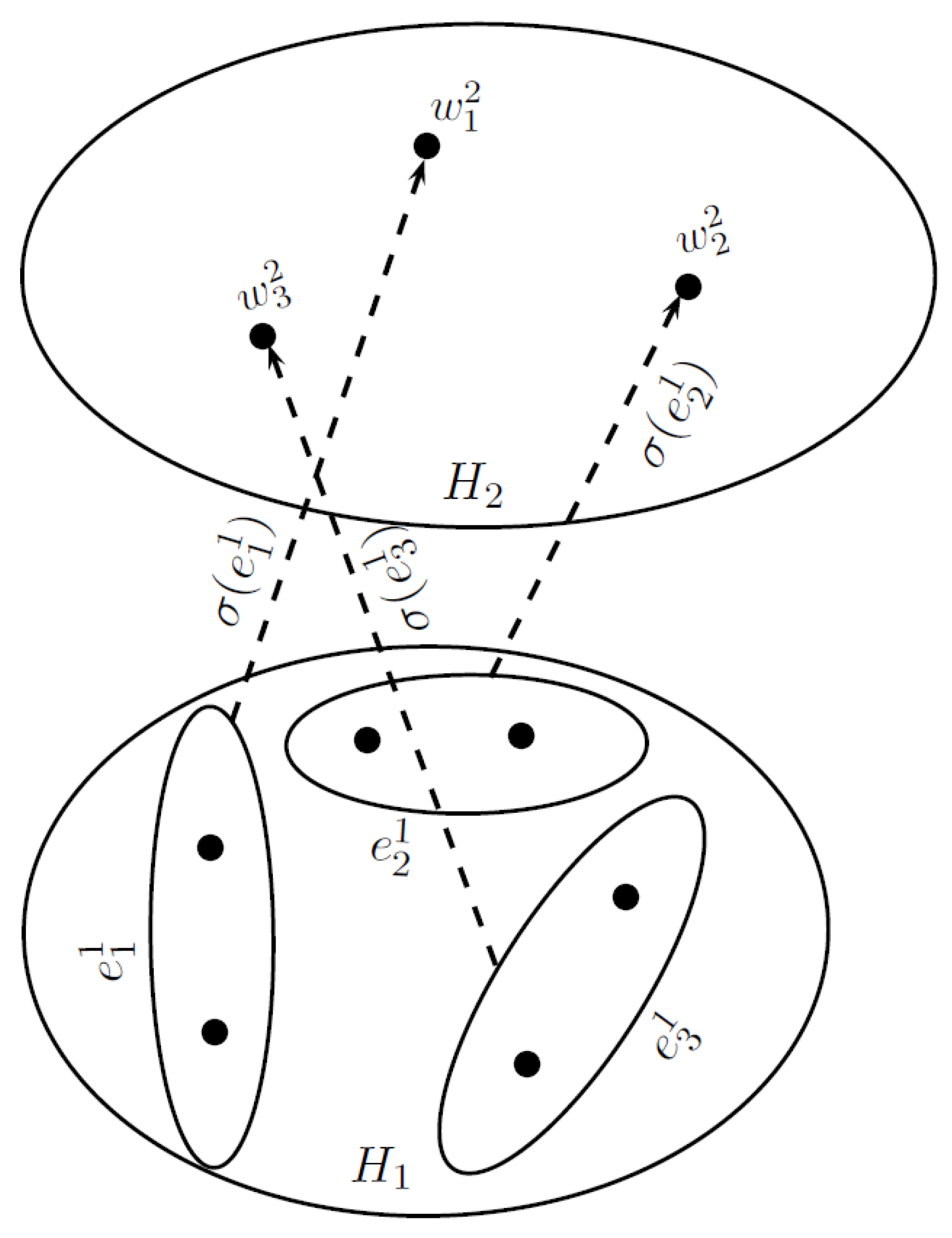
- (i)
- ω maps the empty set to an empty set, i.e., ,
- (ii)
- ,
- (iii)
- ,
- (iv)
- = ,
- (v)
- = ,
- (vi)
- if and only if .
- (ii)
- As we know that for all , we have , since , we have .
- (iii)
- Let and , then it is obvious that and . It follows from (ii) that , and we denote by that edge set of on which the vertex set of is mapped under , i.e., . Then, and . Since the relationship between hyperedges at the new level is the same as that of relations among vertices at the original level, we have . Hence, we conclude that .
- (iv)
- Assume that , then for all implies that and . Further, we have = .. Since the relationship between hyperedges at the new level is the same as that of relations among vertices at the original level, we have . Hence, we conclude that = .
- (v)
- Assume that . Then, we have = .. Since, the relationship between hyperedges at the new level is the same as that of the relations among the vertices at the original level, we have . Hence, we conclude that = .
- (vi)
- First we show that implies that . Since , which implies that and . Furthermore, . Since the relationship between hyperedges at the new level is the same as that of relations among vertices at the original level, we have , i.e., . Hence, implies that .We now prove that implies that . Suppose on the contrary that whenever , then there is at least one vertex , but , i.e., . Since and the relationship between hyperedges at the new level is the same as that of relations among vertices at the original level, we have , but , i.e., , which is a contradiction to the supposition. Thus, we have that implies that . Hence, if and only if .
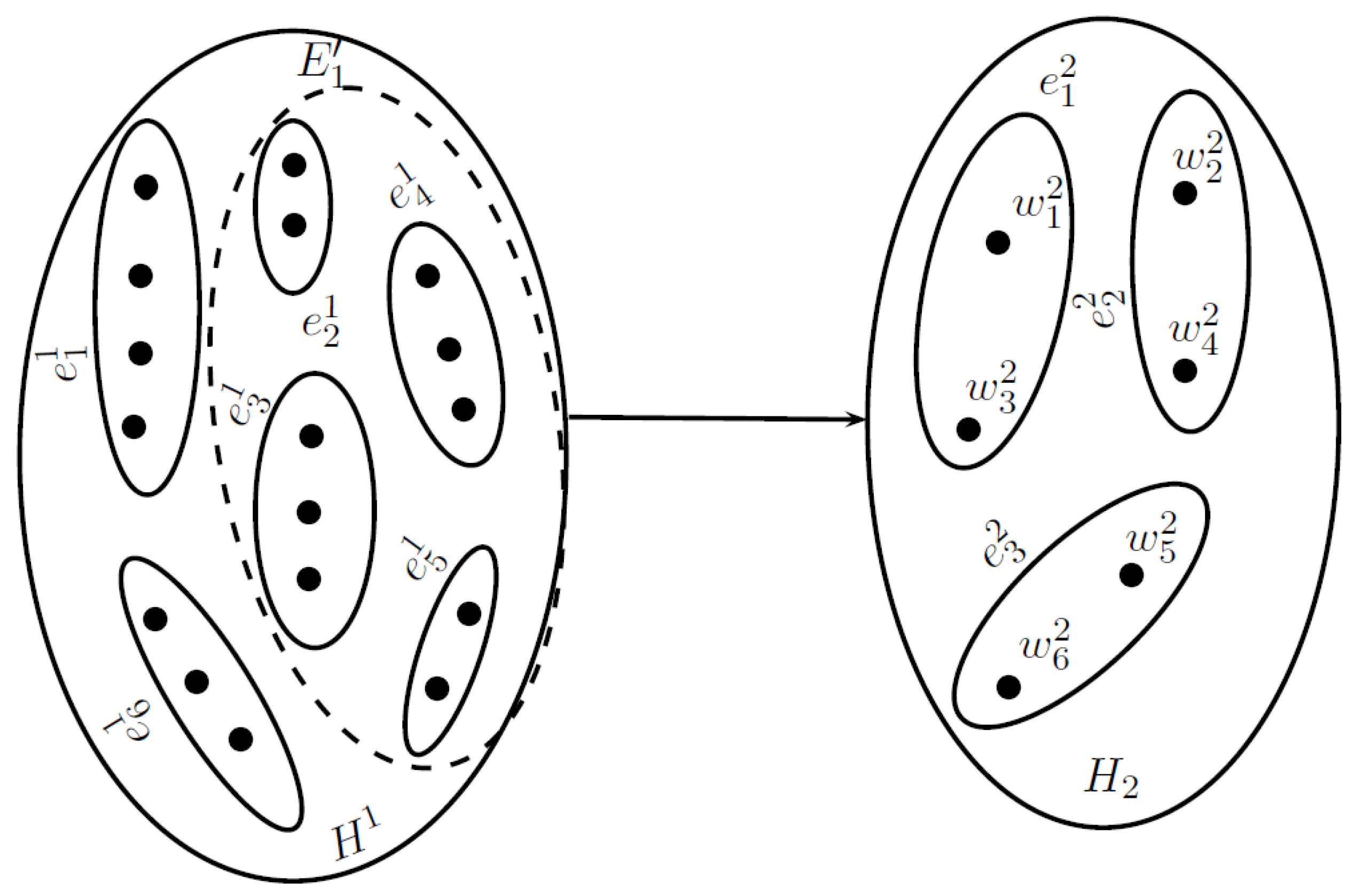
- (i)
- ,
- (ii)
- σ maps the set of hyperedges of onto the set of vertices of , i.e., ,
- (iii)
- .
- (ii)
- According to the definition of , we have . Since, the hyperedges define a partition of hypergraph, so we have , , , ⋯, . Then,.
- (iii)
- Assume that , then it is obvious that and . Suppose on the contrary, there exists at least one vertex , but . implies that . Since , which is a contradiction to our assumption. Hence, .
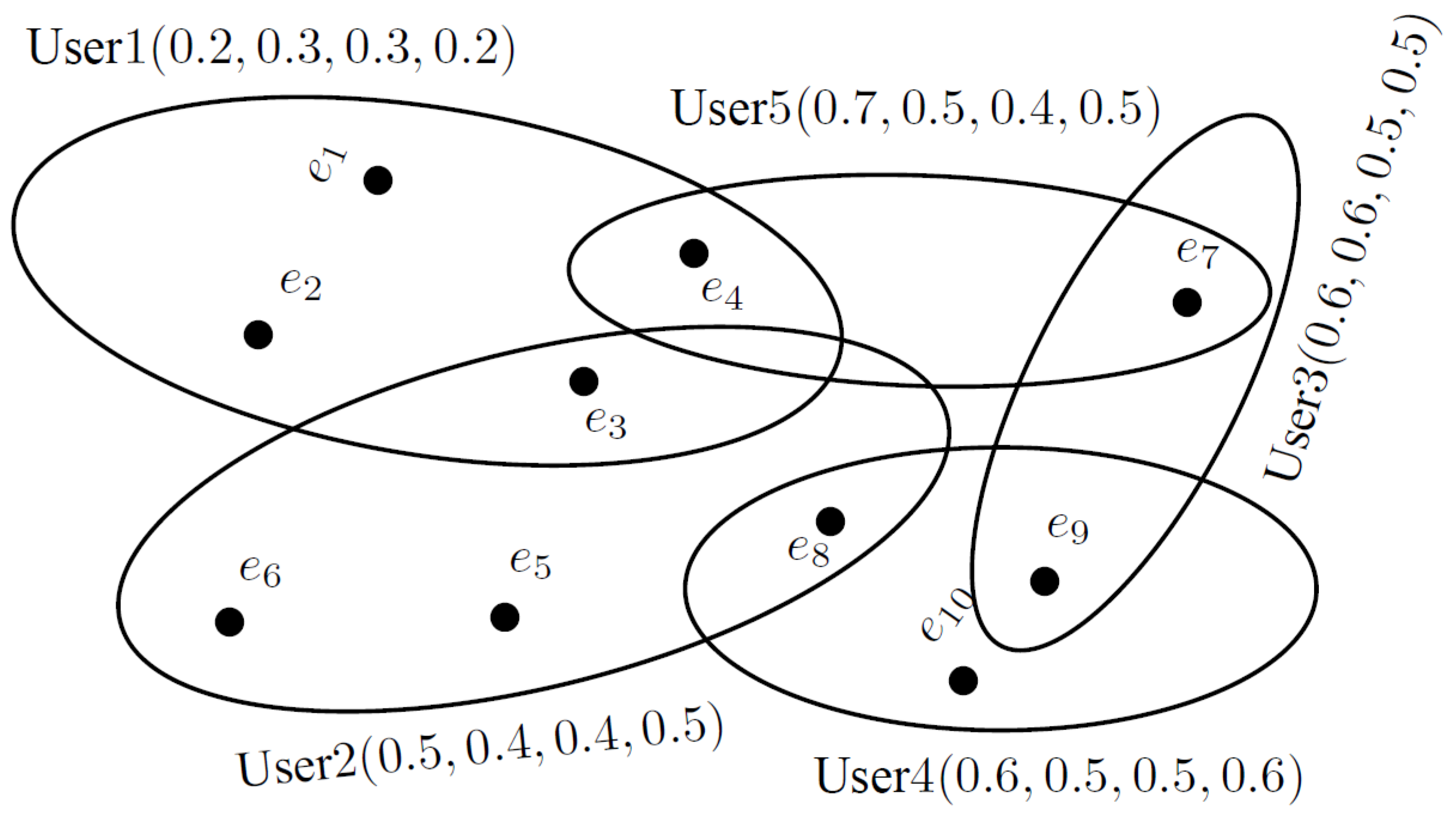
4. A Granular Computing Model of Web Searching Engines
| Algorithm 2: Algorithm for the method of the bottom-up construction. |
| clc |
| =input(‘=’); T=input(‘=’); q=1; |
| while q==1 |
| [r, m]=size();N=zeros(r, r);N=input(‘N=’); [, r]=size(N); D=ones, m)+1; |
| for l=1: |
| if N(l,:)==zeros(1, r) |
| D(l,:)=zeros(1, m); |
| else |
| for k=1:r |
| if N(l, k)==1 |
| for j=1:m |
| D(l, j)=min(D(l, j),(k, j)); |
| end |
| else |
| s=0; |
| end |
| end |
| end |
| end |
| D |
| =input(‘=’); |
| if size()==, m] |
| if =D |
| if size(T)==[1, m] |
| S=zeros(, r);s=zeros(, 1); |
| for l=1: |
| for k=1:r |
| if N(l, k)==1 |
| if (k,:)>=T(1,:) |
| S(l, k)=1; |
| s(l, 1)=s(l, 1)+1; |
| else |
| S(l, k)=0; |
| end |
| end |
| end |
| end |
| S |
| if s==ones(, 1) |
| q=2; |
| else |
| ; |
| end |
| else |
| fprintf(‘error’) |
| end |
| else |
| fprintf(‘error’) |
| end |
| else |
| fprintf(‘error’) |
| end |
| end |
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Lin, T.Y. Granular computing: From rough sets and neighborhood systems to information granulation and computing with words. In Proceedings of the European Congress on Intelligent Techniques and Soft Computing, Aachen, Germany, 8–12 September 1997. [Google Scholar]
- Zhang, L.; Zhang, B. Hierarchy and Multi-Granular Computing, Quotient Space Based Problem Solving; Tsinghua University Press: Beijing, China, 2014; pp. 45–103. [Google Scholar]
- Berge, C. Graphs and Hypergraphs; North-Holland Publishing Company: Amsterdam, The Netherlands, 1973. [Google Scholar]
- Liu, Q.; Jin, W.B.; Wu, S.Y.; Zhou, Y.H. Clustering research using dynamic modeling based on granular computing. In Proceedings of the IEEE International Conference on Granular Computing, Beijing, China, 25–27 July 2005; pp. 539–543. [Google Scholar]
- Wong, S.K.M.; Wu, D. Automated mining of granular database scheme. In Proceedings of the IEEE International Conference on Fuzzy Systems, St. Louis, MO, USA, 25–28 May 2002; pp. 690–694. [Google Scholar]
- Chen, G.; Zhong, N.; Yao, Y. A hypergraph model of granular computing. In Proceedings of the IEEE International Conference on Granular Computing, Hangzhou, China, 26–28 August 2008; pp. 130–135. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zhang, W.-R. Bipolar fuzzy sets and relations: A computational framework forcognitive modeling and multiagent decision analysis. In Proceedings of the First International Joint Conference of the North American Fuzzy Information Processing Society Biannual Conference, the Industrial Fuzzy Control and Intellige, San Antonio, TX, USA, 18–21 December 1994; pp. 305–309. [Google Scholar]
- Chen, J.; Li, S.; Ma, S.; Wang, Z. m-Polar fuzzy sets: An extension of bipolar fuzzy sets. Sci. World J. 2014, 2014, 416530. [Google Scholar] [CrossRef] [PubMed]
- Rosenfeld, A. Fuzzy graphs. In Fuzzy Sets and Their Applications to Cognitive and Decision Processes; Academic Press: New York, NY, USA, 1975; pp. 77–95. [Google Scholar]
- Akram, M. m-Polar fuzzy graphs. In Studies in Fuzziness and Soft Computing; Springer: Berlin, Germany, 2019; Volume 371, pp. 1–284. [Google Scholar]
- Kaufmann, A. Introduction a la Thiorie des Sous-Ensemble Flous; Masson: Paris, France, 1977. [Google Scholar]
- Gong, Z.; Wang, Q. On the connection of fuzzy hypergraph with fuzzy information system. J. Intell. Fuzzy Syst. 2017, 44, 1665–1676. [Google Scholar] [CrossRef]
- Wang, Q.; Gong, Z. An application of fuzzy hypergraphs and hypergraphs in granular computing. Inf. Sci. 2018, 429, 296–314. [Google Scholar] [CrossRef]
- Akram, M.; Sarwar, M. Novel applications of m-polar fuzzy hypergraphs. J. Intell. Fuzzy Syst. 2017, 32, 2747–2762. [Google Scholar] [CrossRef]
- Akram, M.; Sarwar, M. Transversals of m-polar fuzzy hypergraphs with applications. J. Intell. Fuzzy Syst. 2017, 33, 351–364. [Google Scholar] [CrossRef]
- Akram, M.; Shahzadi, G. Hypergraphs in m-polar fuzzy environment. Mathematics 2018, 6, 28. [Google Scholar] [CrossRef]
- Akram, M.; Luqman, A. Intuitionistic single-valued neutrosophic hypergraphs. Opsearch 2017, 54, 799–815. [Google Scholar] [CrossRef]
- Akram, M.; Luqman, A. Bipolar neutrosophic hypergraphs with applications. J. Intell. Fuzzy Syst. 2017, 33, 1699–1713. [Google Scholar] [CrossRef]
- Mordeson, J.N.; Nair, P.S. Fuzzy Graphs and Fuzzy Hypergraphs, 2nd ed.; Physica Verlag: Heidelberg, Germany, 2001. [Google Scholar]
- Parvathi, R.; Akram, M.; Thilagavathi, S. Intuitionistic fuzzy shortest hyperpath in a network. Inf. Process. Lett. 2013, 113, 599–603. [Google Scholar]
- Yang, J.; Wang, G.; Zhang, Q. Knowledge distance measure in multigranulation spaces of fuzzy equivalence relation. Inf. Sci. 2018, 448, 18–35. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, R.; Huang, H.; Wang, J. Some picture fuzzy Dombi Heronian mean operators with their application to multi-attribute decision-making. Symmetry 2018, 10, 593. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, B. The Theory and Applications of Problem Solving-Quotient Space Based Granular Computing; Tsinghua University Press: Beijing, China, 2007. [Google Scholar]
- Zhang, L.; Zhang, B. The structural analysis of fuzzy sets. J. Approx. Reason. 2005, 40, 92–108. [Google Scholar] [CrossRef]
- Yao, Y.Y. A partition model of granular computing. In Transactions on Rough Sets I. Lecture Notes in Computer Science; Peters, J.F., Skowron, A., Grzymala-Busse, J.W., Kostek, B., Swiniarski, R.W., Szczuka, M.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]






| A | |||||
|---|---|---|---|---|---|
| A | Core Technology | Scalability | Content Processing | Query Functionality |
|---|---|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luqman, A.; Akram, M.; Koam, A.N.A. An m-Polar Fuzzy Hypergraph Model of Granular Computing. Symmetry 2019, 11, 483. https://doi.org/10.3390/sym11040483
Luqman A, Akram M, Koam ANA. An m-Polar Fuzzy Hypergraph Model of Granular Computing. Symmetry. 2019; 11(4):483. https://doi.org/10.3390/sym11040483
Chicago/Turabian StyleLuqman, Anam, Muhammad Akram, and Ali N.A. Koam. 2019. "An m-Polar Fuzzy Hypergraph Model of Granular Computing" Symmetry 11, no. 4: 483. https://doi.org/10.3390/sym11040483
APA StyleLuqman, A., Akram, M., & Koam, A. N. A. (2019). An m-Polar Fuzzy Hypergraph Model of Granular Computing. Symmetry, 11(4), 483. https://doi.org/10.3390/sym11040483





