Abstract
This paper assesses the bootstrap confidence intervals of a newly proposed process capability index (PCI) for Weibull distribution, using the logarithm of the analyzed data. These methods can be applied when the quality of interest has non-symmetrical distribution. Bootstrap confidence intervals, which consist of standard bootstrap (SB), percentile bootstrap (PB), and bias-corrected percentile bootstrap (BCPB) confidence interval are constructed for the proposed method. A Monte Carlo simulation study is used to determine the efficiency of newly proposed index over the existing method by addressing the coverage probabilities and average widths. The outcome shows that the BCPB confidence interval is recommended. The methodology of the proposed index has been explained by using the real data of breaking stress of carbon fibers.
1. Introduction
Process capability indices are used to assess the given production process, or whether not to produce items according to the given specifications. The efficiency of these indices required that the process follows a normal distribution [1,2,3]. However, the involvement of different noise factors, sometime may result in the non-normal behaviors of the production process [4]. In case of non-normal processes, the normality based classical process capability index (PCI) may give unreliable and misleading results [5]. Several methods have been proposed [1,3,4,5,6,7] to estimate PCIs and deal with non-normality issue. However, until now, we could not rely ona single method that creates efficiently under all situations [4]. Moreover, it is also argued that all methods showed a variable performance under different non-normal distributions [3]. Therefore, the evaluation of different non-normal PCIs, under different distributions, is an important research area for practitioners and statisticians.
In this regard [4], the proposed non-normal PCI for Weibull and Log-normal distribution, using the relationships among the parameters of the Weibull, Gumbel, and Log-normal distribution. Using different examples, they discussed the point estimation of proposed PCIs and concluded that the proposed PCIs could be used as standard indices. However, the applicability of these indices required more research. Furthermore, the point estimation of all indices was compared with there commended minimum value, in order to assess the capability of a particular process. Since PCIs are viewed as a random variable, so the comparison of the point estimation of indices with any fixed minimum value is criticized by many researchers [8,9]. Therefore, it is more practical to provide confidence intervals for PCIs or at least lower limits to ensure that the process will not be worse than the lower interval value [10].
Confidence intervals depict useful information about the parameter of a population, based on a random sample. The classical CIs are mostly used for obtaining exact limits, but there are some situations in which the exact CIs are unavailable. These situations attributed to the use of another conventional approach for constructing CIs. Likewise, point estimation, most of the work for construction of the CIs for PCIs are based on normality assumption. The construction of CIs for non-normal PCIs, non-parametric technique called bootstrap is commonly used by [11]. The bootstrap technique is a computer-orientation statistical tool to estimate biases, standard errors, confidence intervals, and so forth, where estimates are more complicated [12]. The idea of the bootstrapping method was introduced by Efron [13], and later on, Efron and Tibshirani [14], have proposed three types of bootstrap confidence intervals. In this paper, a bootstrap confidence interval for non-normal PCIs for Weibull distribution is proposed.
Recently [4] there is research that shows the process capability indices for non-normal distributions like Weibull and log-normal, whereas bootstrap confidence intervals have not been studied. Therefore, in the present research work we focused on bootstrap confidence intervals, which have been extensively employed to obtain confidence intervals for various PCIs. Various bootstrap estimation methods, for constructing confidence intervals, have been developed, namely, standard bootstrap (SB), percentile bootstrap (PB), and bias-corrected percentile bootstrap (BCPB).
In Section 2, we presented the process capability index , using Weibull distribution and three methods of bootstrap confidence interval estimations. The simulation study, using the selected sample size, different shape, and scale parameters are presented in Section 3. In Section 4, a numerical example is provided to illustrate the use of process capability indices and some conclusions are given in Section 5.
2. Materials and Methods
Process capability index measures the performance of product, in such a way that the capability of the process relates to the specified tolerance requirements. The manufacture process is assumed to be normally distributed with mean and standard deviation ; lower specification limit (LSL), and upper specification limit (USL), then the process capability index is defined as:
Suppose, the process mean and standard deviation are unknown, then they are estimated from the sample data , which is drawn from the normal distribution. If , and are the true estimate of the unknown parameter and fora normal distribution. Then the sample process capability index can be defined as
If , and are the estimators of mean and standard deviation, when samples are drawn from normal distribution, these estimates happen to be extremely unstable. Clements [15] has proposed an alternative method to handling the process capability for non-normal data. Based on Clements idea, the non-normal process capability index is defined as:
where is the -th quantile of the process, i.e., , and , and of the analyzed distribution, respectively. Recently, the authors in [15], proposed non-normal capability index for the Weibull distribution, using , and as mean and standard deviation of the logarithm of the analyzed process, and although in the logarithm matrix, they are analogous to those of the normal distribution. Based on this fact, they proposed the Weibull process capability index is given by
where , is the Euler–Mascheroni constant .
2.1. Bootstrap Confidence Intervals
Among various bootstrap methods to obtain the confidence intervals, a mainly used methods are the SB, PB, and the BCPB method [14]. The bootstrap methods has been suggested by [16] in the following manner. Let be a random sample of size n drawn from any distribution of interest say . i.e., . Let represents the estimator of PCI say defined in Equation (4). The bootstrap procedure required the following steps [1].
- Obtained a bootstrap sample of size i.e., from original sample by putting as mass at each point.
- Let where be the mth bootstrap sample, then mth bootstrap estimator of is computed as
- We get re-samples, for each sample a values of are obtained. Each of these would be estimate of . From the set all these estimates would constitute an empirical bootstrap distribution of , see [1].
In this study, we assumed bootstrap resamples. The construction of confidence intervals of the PCI using bootstrap techniques are described as follows.
2.1.1. Standard Bootstrap (SB) Confidence Interval
The mean and standard deviation for bootstrap estimates of are obtained as follows:
Thus the SB confidence interval (CI) is:
where is obtained by using quantiles of the standard normal distribution.
2.1.2. Percentile Bootstrap (PB) Confidence Interval
If ; I = 1, 2, …, B be the ordered collection of bootstrap estimates of then confidence interval of is calculated as:
For a 95% confidence intervalwith , this would be:
2.1.3. Bias-Corrected Percentile Bootstrap (BCPB) Confidence Interval
A third method of bootstrap confidence interval, BCPB is based on correct the probable bias. The step by step procedure to obtain BCPB method as follows:
- The probability is calculated using the (ordered) distribution of as:
- Let and represents the cumulative and inverse cumulative distribution functions ofa standard normal variable , then:
- The percentiles of the ordered distribution of is obtained as:
Finally, the BCPB confidence interval is given as:
The performance of three bootstrap methods of confidence intervals are studied by using average width and coverage probabilities are defined as:
where and are confidence interval based on B = 1000 replicates.
3. Simulation Study
In this section, a simulation study is conducted to compare the performance of three methods of bootstrap confidence intervals when the process follows Weibull distribution. In this simulation we examine performance for sample sizes n = {10, 15, 20, 25, 30, 35, 40}; the scale parametric values η = (5.0, 5.5, 6.0); shape parametric combination values β = {2.5, 3.0, 3.5} and are displayed in Table 1, Table 2 and Table 3. The lower and upper specification limits are set as 1, and 29, respectively. We have used the Monte Carlo simulation approach in this article to evaluate the performance of the proposed SB, PB, and BCPB confidence intervals of . A detailed study of the average length and coverage probabilities of the proposed SB, PB, and BCPB confidence intervals for is provided in Table 1, Table 2 and Table 3 for some selective choices of n, η and β. From Table 1, Table 2 and Table 3, we observed that the average widths decrease with the increase in sample size, in all the parametric combinations, as anticipated. The average widths increases for SB, PB, and BCPB as β increases for a fixed η, moreover as η value increases average widths also increases for SB, PB, and BCPB for fixed combinations of β. Furthermore, noticed that the average coverage probabilities, in three methods confidence intervals in all the parametric combinations, achieved the nominal level. However, it was marginally less than 95% confidence level. Among three methods of bootstrap confidence intervals regarding the average widths, we noticed that BCPB < PB < SB, thus BCPB performed well with respect to average width. Furthermore, in case of the average coverage probability, SB shows better performance and BCPB closer competitor to the SB method. Therefore, we conclude that BCPB shows an overall better performance of the bootstrap confidence intervals for Weibull distribution.

Table 1.
The average widths 95% bootstrap confidence intervals and coverage probabilities of for Weibull distribution when η = 5.0.

Table 2.
The average widths 95% bootstrap confidence intervals and coverage probabilities of for Weibull distribution when η = 5.5.

Table 3.
The average widths 95% bootstrap confidence intervals and coverage probabilities of for Weibull distribution when η = 6.0.
4. Illustrative Examples
In this section, the following real data set corresponds to an uncensored data set from [17] on breaking the stress of carbon fibers (in Gba) is considered and describe the proposed methods of confidence intervals:
0.39, 0.81, 0.85, 0.98, 1.08, 1.12, 1.17, 1.18, 1.22, 1.25, 1.36, 1.41, 1.47, 1.57, 1.57, 1.59, 1.59, 1.61, 1.61, 1.69, 1.69, 1.71, 1.73, 1.80, 1.84, 1.84, 1.87, 1.89, 1.92, 2.00, 2.03, 2.03, 2.05, 2.12, 2.17, 2.17, 2.17, 2.35, 2.38, 2.41, 2.43, 2.48, 2.48, 2.50, 2.53, 2.55, 2.55, 2.56, 2.59, 2.67, 2.73, 2.74, 2.76, 2.77, 2.79, 2.81, 2.81, 2.82, 2.83, 2.85, 2.87, 2.88, 2.93, 2.95, 2.96, 2.97, 2.97, 3.09, 3.11, 3.11, 3.15, 3.15, 3.19, 3.19, 3.22, 3.22, 3.27, 3.28, 3.31, 3.31, 3.33, 3.39, 3.39, 3.51, 3.56, 3.60, 3.65, 3.68, 3.68, 3.68, 3.70, 3.75, 4.20, 4.38, 4.42, 4.70, 4.90, 4.91, 5.08, 5.56.
The goodness of fit for our model by plotting the superimposed for the data shows that the Weibull distribution is a good fit. This is shown in Figure 1andthe goodness of fit is emphasized with Q-Q plot, displayed in the following Figure 1. The maximum likelihood estimates of the two-parameters of Weibull distribution for the breaking stress of carbon fibres are = 2.7928 and = 2.9435, and by using the Kolmogorov-Smirnov test, we found that the maximum distance between the data and the fitted of the Weibull distribution is 0.06 with p-value is 0.8586. Therefore, the Weibull distribution provides a reasonable fit for the breaking stress of carbon fibres. The process capability of Weibull distribution, using breaking stress of carbon fibresis, displayed in Figure 2. If LSL = 0.5 and USL = 9.5 then using Equation (4) is 1.0005 whereas using Equation (3) is 0.90297. Hence our proposed method of process capability index performs better than the traditional process capability index.
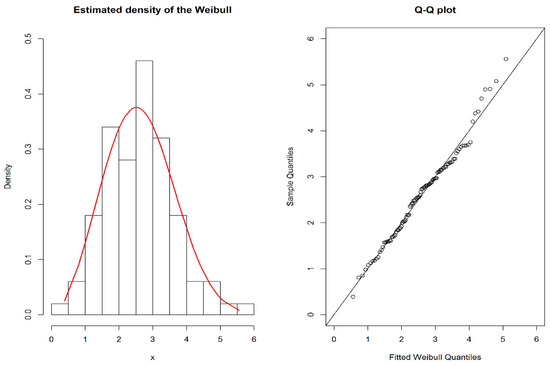
Figure 1.
Density plot and Q-Q plot of the fitted Weibull distribution for the breaking stress of carbon fibres.
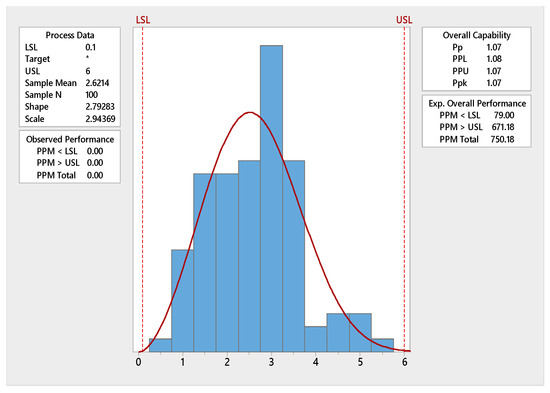
Figure 2.
Capability of Weibull distribution for proposed method using breaking stress of carbon fibers.
5. Comparison of Proposed Cpkw Index with the Existing Cpk
The performance of the proposed process capability index has been made with the existing process capability index proposed by Clements [15], using the coverage probabilities and average widths. The values of coverage probabilities and average widths are compared using breaking stress of carbon fibres data, which was fitted for Weibull distribution with parameters are = 2.792827 and = 2.943466. The Bootstrap confidence intervals and widths of the, and are given in Table 4 for the given example. A numerical example shows that the width of class intervals are considered large in traditional method as compared to the bootstrap approach for . Moreover, between three Bootstrap methods, BCPB sows better performance than other two methods of Bootstrapping, the simulation results also show the same. Therefore, the proposed process capability index comparatively better than traditional process capability index in case Weibull distribution.

Table 4.
Bootstrap confidence intervals and widths of the new and Clements traditional .
Furthermore, the proposed new process capability index and traditional process capability index are also compared with exponential Weibull distribution, which was first introduced by Mudholkar and Srivastava [18] as an extension of the Weibull family. The probability density function of exponential Weibull distribution with scale parameter σ and shape parameters λ and θ is given as follows:
The proposed process capability index is given below:
The breaking stress of carbon fibres data is fitted to exponential Weibull distribution with parameters are = 2.6879, = 2.4161 and = 1.3097. The Bootstrap confidence intervals and widths of the, and are given in Table 4 for the exponential Weibull distribution for this data set. The results shows that the proposed process capability index for Weibull distribution show lower confidence width than the exponential Weibull distribution.
6. Conclusions
In this article, we developed an interval estimation of newly proposed non-normal process capability index for Weibull distribution using the logarithm of the analyzed data. A comparison is made between SB, PB, and BCPB confidence intervals and their coverage probabilities using simulation studies. A confidence interval is better performed if the average width is low and with higher coverage probability. Compared to Clements [15], the non-normal process capability index, the proposed method gives the smaller widths of confidence intervals. Therefore, we conclude thatthe proposed procedure has been very powerful and enriching the process capability index. Using a Monte Carlo simulation technique, we evaluated the performance of the proposed bootstrap confidence intervals with respect to the coverage probabilities and average widths of each confidence interval. The results indicated that the basic-corrected percentile bootstrap (BCPB) confidence interval showed better coverage probability and smaller widths, as compared to other two confidence intervals, for the proposed and traditional method. Hence it is concluded that the BCPB interval is more suitable than the other two methods. The methodology was illustrated using areal data set of breaking stress of carbon fibres and depicted a similar pattern, as observed using simulation studies. Our future research work may include the study of process capability indices for more non-normal distributions using the transformation of variables. The proposed method can be extended for abroad family of distributions as future research.
Author Contributions
Conceived and designed the experiments, G.S.R., M.A. (Mohammed Albassam), M.A. (Muhammad Aslam); performed the experiments, M.A. (Muhammad Aslam); analyzed the data, M.A. (Muhammad Aslam); contributed reagents/materials/analysis tools, M.A. (Muhammad Aslam); wrote the paper, M.A. (Mohammed Albassam), M.A. (Muhammad Aslam).
Funding
This article was funded by the Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah. The authors, therefore, acknowledge with thanks DSR technical and financial support.
Acknowledgments
The authors are deeply thankful to the editor and reviewers for their valuable suggestions to improve the quality of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kashif, M.; Aslam, M.; Al-Marshadi, A.H.; Jun, C.-H. Capability Indices for Non-Normal Distribution Using Gini’s Mean Difference as Measure of Variability. IEEE Access 2016, 4, 7322–7330. [Google Scholar] [CrossRef]
- Panichkitkosolkul, W. Confidence Intervals for the Process Capability Index Cp Based on Confidence Intervals for Variance under Non-Normality. Malays. J. Math. Sci. 2016, 10, 101–115. [Google Scholar]
- Senvar, O.; Sennaroglu, B. Comparing performances of clements, box-cox, Johnson methods with weibull distributions for assessing process capability. J. Ind. Eng. Manag. 2016, 9, 634. [Google Scholar] [CrossRef]
- Piña-Monarrez, M.R.; Ortiz-Yañez, J.F.; Rodríguez-Borbón, M.I. Non-normal Capability Indices for the Weibull and Lognormal Distributions. Qual. Reliab. Eng. Int. 2016, 32, 1321–1329. [Google Scholar] [CrossRef]
- Senvar, O.; Kahraman, C. Type-2 fuzzy process capability indices for non-normal processes. J. Intell. Fuzzy Syst. 2014, 27, 769–781. [Google Scholar]
- Besseris, G. Robust process capability performance: An interpretation of key indices from a nonparametric viewpoint. TQM J. 2014, 26, 445–462. [Google Scholar] [CrossRef]
- Sennaroglu, B.; Senvar, O. Performance comparison of box-cox transformation and weighted variance methods with weibull distribution. J. Aeronaut. Space Technol. 2015, 8, 49–55. [Google Scholar] [CrossRef]
- Chou, Y.M.; Own, D.B.; Salvador, A.; Borrego, A.A. Lower Confidence Limits on Process Capability Indices. J. Qual. Technol. 1990, 22, 223–229. [Google Scholar] [CrossRef]
- Porter, L.J.; Oakland, J.S. Process capability indices—An overview of theory and practice. Qual. Reliab. Eng. Int. 1991, 7, 437–448. [Google Scholar] [CrossRef]
- Wu, H. Development of a Weighted Variance Approach to Modify Cerrent Process Capability Indices; The University of Alabama Huntsville: Huntsville, AL, USA, 1998. [Google Scholar]
- Balamurali, S. Bootstrap confidence limits for the process capability index Cpmk. Int. J.Qual. Eng. Technol. 2012, 3, 79–90. [Google Scholar] [CrossRef]
- Panichkitkosolkul, W.; Saothayanun, L. Bootstrap confidence intervals for the process capability index under half-logistic distribution. Maejo Int. J. Sci. Technol. 2012, 6, 272–281. [Google Scholar]
- Efron, B. Bootstrap methods: Another look for the Jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Stat. Sci. 1986, 1, 54–77. [Google Scholar] [CrossRef]
- Clements, J.A. Process capability calculations for non-normal distributions. Qual. Prog. 1989, 22, 95–97. [Google Scholar]
- Tosasukul, J.; Budsaba, K.; Volodin, A. Dependent bootstrap confidence intervals for a population mean. Thail. Stat. 2009, 7, 43–51. [Google Scholar]
- Nichols, M.D.; Padgett, W.J. A bootstrap control chart for Weibull percentiles. Qual. Reliab. Eng. Int. 2006, 22, 141–151. [Google Scholar] [CrossRef]
- Mudholkar, G.S.; Srivastava, D.K. Exponentiated Weibull family for analyzing bathtub failure-rate data. IEEE Trans. Reliab. 1993, 42, 299–302. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).