1. Introduction
Ordering decision alternatives is an important part of a decision-making analysis and is performed before making the actual decision. Any ranking of decision alternatives is determined by a scoring function. The decision alternatives are ordered with the use of a chosen scoring function which takes into account the decision-maker’s preferences with respect to all given issues as well as their relative importance. Because decision alternatives are often characterized by several contradictory criteria, multi-criteria techniques are useful for these alternatives [
1]. The most popular techniques used for supporting a decision-making process are:
The Simple Additive Weighting method (SAW)/The Simple Multi Attribute Rating Technique (SMART) [
2,
3];
The Analytic Hierarchy Process [
4];
Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) [
5].
Each of these methods has its advantages and disadvantages, thus selecting the ‘best’ method for a particular problem is a really difficult task. The choice between mentioned techniques depends on the decision-making problem, types of criteria, available information, the decision-maker’s cognitive abilities, and properties of the multi-criteria technique. The SAW method is the most popular approach for classical multiple attribute decision-making. In this paper, we focus on applications of the SAW method for ordering decision alternatives.
In real decision-making problems, the options cannot be assessed in a quantitative form, but still may be in a qualitative one. This implies the usability of the linguistic approach for evaluating decisions. The approximate technique may represent qualitative/quantitative options verbally by means of a linguistic variable whose values are words or sentences in a natural or artificial language. One possibility of modelling linguistic values is the application of fuzzy sets [
6,
7,
8].
In a general case of fuzzy numbers, the fuzzy SAW (F-SAW) method was introduced by Chou and Chang [
9]. The ordered fuzzy numbers (OFN) were intuitively introduced by Kosiński and his co-writers [
10] as an extension of the concept of fuzzy numbers (FN) introduced by Dubois and Prade [
11]. Roszkowska and Kacprzak [
12] tentatively introduced the oriented fuzzy Simple Additive Weighting (OF-SAW) method based on trapezoidal ordered fuzzy numbers (TrOFN) in scoring negotiation offers. A significant drawback of Kosiński’s theory is that there exist such OFNs which, in fact, are not FNs [
13]. For this reason, Kosiński’s theory of OFN was revised in [
14]. Therefore, in [
15], the OF-SAW method is modified in a way that is compatible with revised theory of OFN [
14].
In [
12,
15] we meet OF-SAW methods applying a defuzzification procedure which distorts fuzzy numbers. In this way, we lose a lot of information about linguistically evaluated decision alternatives. This undermines the credibility of requests received.
On the other hand, any decision made is not fuzzy. For this reason, defuzzification is inevitable. In our opinion, defuzzification should always be the last step of the procedure. This leads to the following principle of decision support based on imprecise data: First, calculation; then defuzzification.
The main goal of this paper therefore, is to avoid the defuzzification stage in any scoring method based of TrOFN in the decision evaluation of decision alternatives. To our best knowledge, TrOFNs are so far only used in scoring functions describing the SAW method [
2,
3] or TOPSIS [
5]. In TOPSIS, we always use a scoring function valued with crisp real numbers. Thanks to this, in the case of using TOPSIS, the values of its scoring function do not require the use of defuzzification methods. On the other hand, the SAW method is a scoring method based on the concept of a weighted average of ratings performance. Therefore, if any SAW method uses TrOFN to score the decision alternatives, then it is determined by its scoring function of the values of TrOFNs. Since the main purpose of this article is to avoid the defuzzification stage of the scoring function valued in TrOFN, our focus will be restricted to the SAW method based on TrOFN. We propose using a fuzzy relation which compares OFNs pairwise. In this way, we can compare linguistically evaluated decision alternatives without losing information about the imprecision and orientation of linguistic evaluation. This approach is more realistic.
The paper is organized as follows.
Section 2 outlines the elements of mathematical fuzzy sets theory. The trapezoidal OFN (TrOFN), their defuzzification and fuzzy ordering of TrOFN are discussed there. The OF-SAW method equipped with fuzzy scoring order is presented in
Section 3. In
Section 4, we discuss some results from examples of the OF-SAW empirical application for ranking negotiation offers. Here we focus on the effects of replacing the defuzzified scoring function with a fuzzy one. Conclusions obtained are generalized for the case of decision alternatives and fuzzy scoring function in
Section 5.
Section 6 concludes the article, summarizes the main findings of this research, and proposes some future research directions. For the convenience of readers, all acronyms used are interpreted in Nomenclature.
2. Elements of Fuzzy Sets Theory
Let
be an arbitrary space of all considered states. The family of all crisp subsets in the space
is indicated by the symbol
. Then, any information is given as a classification of considered states. The basic tool for imprecise information is the concept of fuzzy subset
which may be described as the set of ordered pairs
where
is its membership function. In multi-valued logic terms, the value
is interpreted as the ‘truth value’ of the sentence
. Basic set theory operations and relations are defined in the usual way, suggested by Zadeh [
16]. The family of all fuzzy subsets in the space
is indicated by the symbol
. For any fuzzy subset
we can distinguish its support
determined as follows:
2.1. Fuzzy Numbers
An imprecise number is a family of values in which each considered value belongs to it in a varying degree. A commonly accepted model of imprecise number is the fuzzy number (FN), defined as a fuzzy subset of the real line
. The most general definition of FN was given by Dubois and Prade [
11]. In this paper, we restrict our considerations to the case of trapezoidal FN (TrFN) defined as fuzzy subsets in the space
of all real numbers in the following way.
Definition 1. For any nondecreasing sequence , the trapezoidal fuzzy number (TrFN) is the fuzzy subset determined explicitly by its membership functions as follows: The space of all TrFNs is denoted by the symbol . The TrFN represents the crisp number . Therefore, we can write . For any the TrFN is interpreted as an imprecise number “about ”. Understanding the phrase “about ” depends on the applied pragmatics of the natural language.
Let us consider the pair
of TrFNs represented respectively by their membership functions
. On the set
of all TrFNs, we introduce the relation
, which reads:
In agreement with the Zadeh’s Extension Principle, this relation is a fuzzy order
determined by its membership function
given as follows [
17]:
From the point of view of multivalued logic, the value may be interpreted as a truth-value of the sentence (4).
2.2. Ordered Fuzzy Numbers
In this paper, we restrict our considerations to the case of trapezoidal OFN (TrOFN), defined as fuzzy subsets in the space of all real numbers in the following way.
Definition 2. For any monotonic sequence , the trapezoidal ordered fuzzy number (TrOFN) is the pair of the orientation and fuzzy subset determined explicitly by its membership functions as follows [
14]:
The space of all TrOFNs is denoted by the symbol
. Any TrOFN is interpreted as imprecise number with additional information about the location of the approximated number. This information is given as the orientation of TrOFN. The fulfilment of the condition
determines the positive orientation of any TrOFN
. For any
the positively oriented TrOFN
is interpreted as an imprecise number “about or slightly above
”. The space of all positively oriented TrOFNs is denoted by the symbol
. The fulfilment of the condition
determines the negative orientation of TrOFN
. For any
the negatively oriented TrOFN
is interpreted as an imprecise number “about or slightly below
”. The space of all negatively oriented OFN is denoted by the symbol
. For the case
, TrOFN
represents a crisp number
, which is not oriented. Understanding the phrases ”about or slightly above
” and “about or slightly below
“ depend on the applied pragmatics of the natural language. Summing up, we can write:
For the case
the membership function of TrFN
is equal to the membership function of TrOFN
. This fact implies the existence of isomorphism
given for any nondecreasing sequence
by the identity
Kosiński has introduced the arithmetic operators of dot product
for TrOFNs in the following way:
Therefore, the unary minus operator
on
is extended to minus operator
on
by the identity
In [
18], the sum
for TrOFNs is determined as follows:
The subtraction operation
on
is extended to subtraction operation
on
by the identity
Kosiński (13) has shown that for any OFN
we have
2.3. Defuzzification of Ordered Fuzzy Numbers
Ranking of OFNs plays a very important role in fuzzy decision-making. Despite many ranking methods proposed in literature, there is no universal technique. In [
15], the rankings of decision alternatives are determined with the use of the concept of the defuzzification functional, extended for TrOFN.
Definition 3. Defuzzification functional is the map which, for any monotonic sequence , satisfies the following conditions: In [
15] the following defuzzification methods are used:
The weighted maximum (WM) functional
The first maximum (FM) functional
The last maximum (LM) functional
The middle maximum (MM) functional
The gravity center (GC) functional
The geometrical mean (GM) functional
The use of the defuzzification functional causes the loss of detailed information about the membership function.
2.4. Relation of “Greater than or Equal to” for Trapezoidal Ordered Fuzzy Numbers
Two TrOFNs may be immediately compared [
18]. Let us consider the pair
represented by the pair
, respectively, of their membership functions. On the set
of all OFNs, we introduce the relation
, which reads:
This relation is a fuzzy order defined by means of its membership function fulfilling the conditions:
For any pair
, the extension law
For any pair
, the sign exchange law
For any pair
, the law of parties’ subtraction of inequality
From the point of view of multivalued logic, the value
may be interpreted as truth-value of the earlier sentence (23). The fuzzy order
is transitive, i.e., we meet
The variability of membership function is explicitly described in detail as follows:
Theorem 1. For any pair fulfilling the condition [18]we have: if then
For any finite set
we can distinguish the set of its maximal elements given as a fuzzy subset [
18]
The fuzzy subset
is determined by its membership function
given by the identity [
17]
For any , the support is always nonempty. Due to that we can formulate the following theorem.
Theorem 2. For a given finite subset we havethen if Proof. Let a finite fixed subset
be given. Conditions (32) and (33) imply
Therefore, for fixed
, we can always say
If
, then condition (22) implies
From conditions (36) and (38), condition (34) follows directly. This means that condition (24) is necessary for .
Let condition (24) be fulfilled. Then we meet condition (28). In this case, let us take into account the case when
. According to conditions (22) and (25), we then have
Along with transitivity (17) it causes
Contradiction! This means that condition (24) is sufficient for . □
3. The Oriented Fuzzy SAW with Fuzzy Order
In decision-making, we meet situations dealing with imprecision, in which the use of a linguistic assessment instead of numerical values may be more useful. In information science, natural language words are values of related linguistic variables. Then, each decision alternative is evaluated with the use of a linguistic order scale determined by a fixed linguistic variable. From a decision-making point of view, the linguistic variable evaluation methodologies are reviewed in [
1,
19,
20,
21]. The semantic meaning of linguistic values may be imprecise. Thus, any linguistic variable may be described with the use of fuzzy set theory [
6,
7,
8]. In agreement with suggestions given in [
9], any linguistic value is represented by a kind of fuzzy number. Then, each decision alternative is evaluated with the use of the Numerical Order Scale (NOS) given as a sequence of some kind of FNs.
In this paper, we will consider any NOS given as a sequence of TrOFN. Such NOS is denoted by the symbol NOS-TrOFN. An example of NOS-TrOFN is constructed and justified in [
15].
If we consider the multi-criterial decision-making problem, it may be simplified by the use of a scoring function with arguments given by means of any kind of NOS. To our best knowledge, NOS determined by TrOFNs is so far only used in the scoring functions describing the Simple Additive Weighting (SAW) method [
2,
3] or Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) [
5]. In TOPSIS, we always use a scoring function valued with crisp real numbers. Thanks to this, in the case of using TOPSIS, the values of its scoring function do not require the use of defuzzification methods. On the other hand, the SAW method is a scoring method based on the concept of a weighted average of performance ratings. Therefore, if NOS is given as a sequence of some kind of FNs then any SAW method is determined by its scoring function valued with FNs. Since the main purpose of this article is to avoid the defuzzification stage of the scoring function values defined for NOS-TrOFN, our focus will be on the SAW method based on TrOFN. The SAW method is also known as the Simple Multi Attribute Rating Technique (SMART) [
2,
3].
We consider here a multi-criteria decision-making problem with
evaluation criteria
and
decision alternatives
, where
is an assumed evaluation template. For
criteria, we have the weight vector
where
and
is the weight of the criterion
denoting the importance of this criterion in the evaluation of the alternatives. Any alternative is evaluated with the use of the evaluation function
determined for fixed NOS
The main goal of the application of a SAW method is to determine an order
, which reads:
For fixed NOS, the individual SAW methods differ from each other with the applied order .
Originally, the SAW method uses a NOS given as a finite subset of positive real numbers. For the case of NOS-TrOFN, the SAW method was first generalized in [
12]. Then in [
15], the SAW method has been adapted to the requirements of the revised OFNs’ theory. The SAW algorithm generalized in this way will be called Oriented Fuzzy SAW (OF-SAW). The OF-SAW can be described by the following procedure:
Procedure 1:
Step 1: Define the set of evaluation criteria;
Step 2: For each evaluation , determine its scope ;
Step 3: Determine the evaluation template
Step 4: Define a NOS-TrOFN ;
Step 5: Determine the scoring function
given for any
as an aggregated evaluation index
where the coefficients
are criterion weights satisfying condition (42);
Step 6: Define the evaluation function
fulfilling for each
the condition
Step 7: Determine the set of evaluated decision alternatives;
Step 8: Evaluate each alternative
by the value
where
Step 9: Determine a scoring order by means of obtained values .
In [
15], we consider SAW methods equipped with scoring orders
given for each pair
as follows:
where
is one of the defuzzification functionals given by formulas (17)–(22). In this way, ordering of alternatives is given as a partially ordered set
, which loses all information about imprecision and orientation of linguistic evaluation.
In this paper, we will study the SAW method pre-equipped with the initial order given for each pair
by the formula:
where
is a fuzzy order described by (24)–(26). It implies that the order (37) is a fuzzy relation
. This order includes all the gathered information on the imprecision and orientation of linguistic evaluation. Thanks to that, it is the most faithful order of linguistic evaluation alternatives.
For any subset
, we set the best alternative
given as follows:
where
For any , the support is always nonempty.
Identity (38) defines the best alternative as an alternative characterized by the maximal value of scoring function. According to (32), for any subset
, the best alternative
is determined by its membership function
, given by the identity
The fuzzy subset may be used as an imprecise recommendation of the best alternative. An analogous fuzzy set cannot be defined by means of ordering methods determined with use of the defuzzification functional. If the support contains an insufficient number of decision alternatives, then the induced partial order is the additional and always accessible support of decision-making evaluation alternatives. This order is determined based on the fuzzy order with the following procedure:
Procedure 2:
Step 1: Perform the substitutions , ;
Step 2: Perform the substitutions ;
Step 3: Perform the substitutions
Step 4: If the condition
is satisfied then go back to Step 2. Otherwise, go to Step 5 in which the induced order of decision-making alternatives will be determined;
Step 5: Each recommendation
belongs only to one set
. For any given number
and any recommendation
, the value
dominates the values
. Thanks to that, any pair
is ordered as follows:
In this way, the partially ordered set is uniquely determined.
Above, we propose an ordering of alternatives given as a partially ordered set , which takes into account all information about the imprecision and orientation of linguistic evaluation. On the other hand, applying the defuzzification procedure distorts OFNs. In this way, we lose a lot of information about linguistically evaluated decision alternatives. Thus, in our opinion, the above proposed new method of alternatives’ ordering is more reliable than ordering methods determined with use of the defuzzification functional. Therefore, the order will be called the faithful order.
In this article, we will compare the SAW method equipped with faithful order with individual SAW methods equipped with orders described by the equivalency (49).
Let us notice that for any pair
we have
which is denoted as
We see that any subset is an equivalence class determined by a faithful order . Summing up all the above considerations, the sequence of equivalence classes uniquely determines the partially ordered set .
In a general case, any partially ordered set
is a form of information on the preferences of individual decision alternatives. On the other hand, each partially ordered set
is unequally characterized by such a sequence
of its disjoint equivalence classes so that for any pair
we have
This approach is especially useful in negotiating problems when each negotiating party uses an opposite order.
In this paper, an amount of information is expressed in bits. A more numerous sequence of equivalence classes sets a more detailed order on the set of decision alternatives. This means that along with the increase in the number of elements of the sequence , the amount of information described by the partially ordered set grows. Therefore, the number will be used in comparing the individual SAW methods equipped with different orders .
4. Illustrative Example
In [
21], an example describes in detail the evaluation of decision alternatives
given as the negotiation packages [
22]. In [
15], this example was used for a discussion on the usefulness of NOS-TrOFN and OF-SAW methods for the evaluation of negotiation packages. There, we considered the SAW methods equipped with partial orders determined by the equivalency (49) for each defuzzification method (17)–(22). All of the scoring function values
received here are shown in
Table 1.
Table 1 also shows the results
of defuzzification of these values with the use of all applied defuzzification methods.
In [
15], rankings of decisions alternatives are determined by each order (49). We observe that these orders are partial or strict ones. Thus, observed rankings are described by tired ranks [
23], presented in
Table 2. Each row of this table lists different ranks of the chosen negotiation package.
Let us consider now the proposed ordering method determined without any defuzzification functional. In the first step, we determine all values
of membership function of the initial order. These values are presented in
Table 3.
In the next step, we determine the set of the best decision alternatives
In the face of a low number of the set
, we proceed to the determination of a ranking of decision alternatives. To do so, we use Procedure 2 to determine the following equivalence classes:
Obtained in this way, ranking of negotiation packages is described by means of tired ranks [
23] in
Table 2. Each of the partial orders determines a sequence of equivalence classes. For any considered order, the numbers of those equivalence classes are presented in
Table 2.
On the other hand, an increase of equivalence classes means an increase in the amount of information on the order. The real growth of information on the order can be caused only by the increase in information on ordered objects. In case of the use of the defuzzification functional we only have to do with the total loss of information on imprecision and orientation of evaluation. It means that using the defuzzification functional can enlarge the available source of information only of deceptive information, i.e., the information which can change the true picture. The mechanism of creating deceptive information will be discussed basing on Example 1.
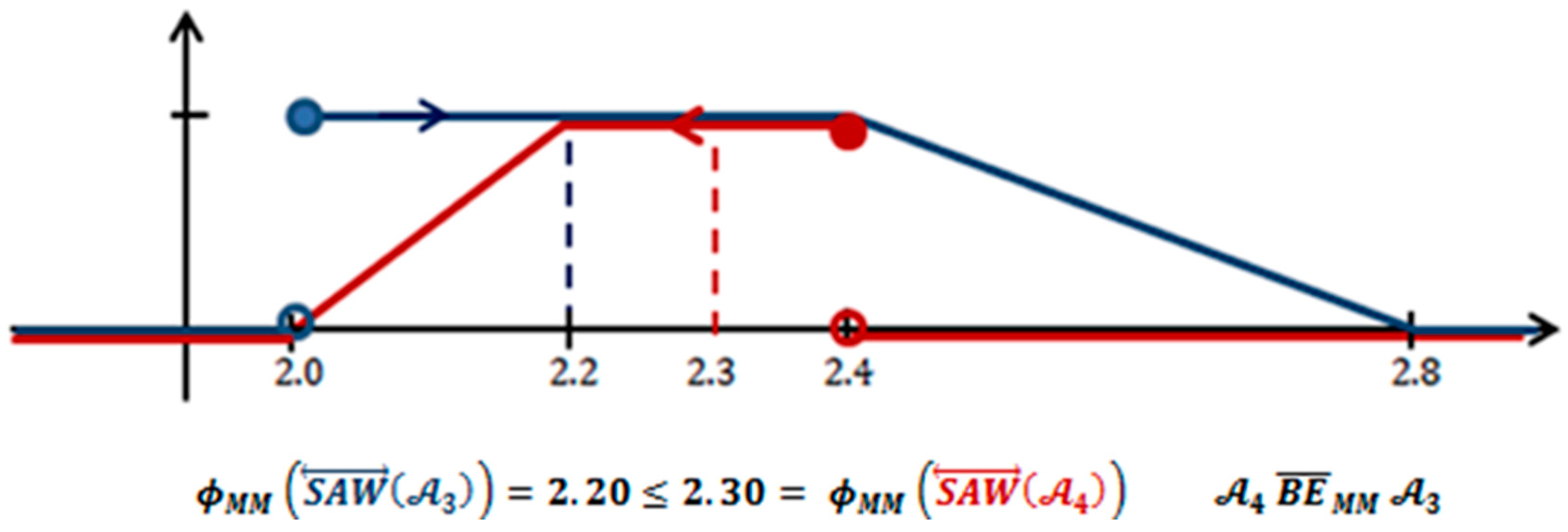
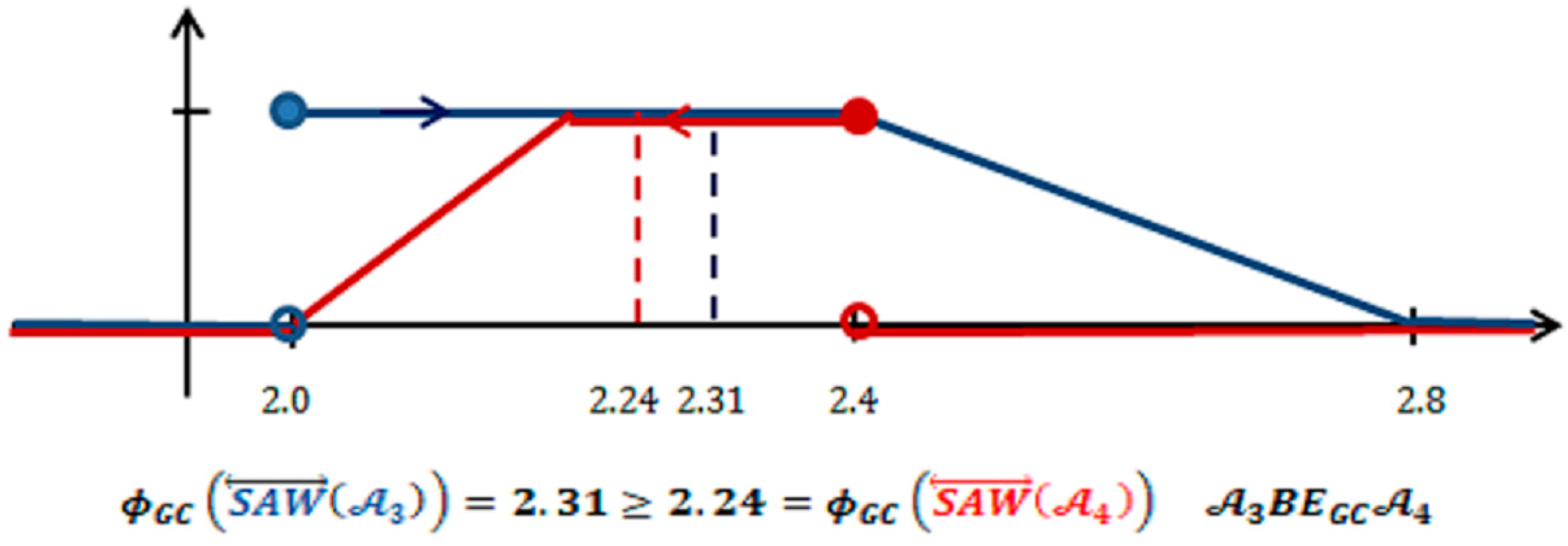
Example 1. Figure 1 and Figure 2 present the diagram of the membership function of in blue and in red. The comparison of those values clearly proves that we get . From the point of view of the faithful order, both negotiation packages are equivalent. This evaluation seems to be right. In Figure 1 the dashed line represents and . We can observe that here we get . It is an example of deceptive information because it was created as the result of decreasing the number of information on the compared objects. In Figure 2, the dashed line represents the values of and . Here, we can observe that . It is also an example of deceptive information because it was created due to the decrease of information on the objects being compared. Using deceptive information can lead to results deviating from the real ranking of decision alternatives, which will increase the hazard of making a wrong decision.
Summing up, in the analyzed case we can say that the OF-SAW method equipped with faithful order is more reliable than an OF-SAW method equipped with an order determined by the use of defuzzified values of a scoring function.
5. Generalization of Conclusions
Let us remind you that by the symbol, we denote order determined by (49) with the use of defuzzified values of a scoring function. In the previous chapter, it was proved that there exists such an empirical case that the application of OF-SAW method equipped with faithful order is more reliable than the application of an OF-SAW method equipped with the order . Therefore, in the analyzed case of the evaluation of decision alternatives, the recommended order is . This conclusion can be easily generalized as a case of the assessment of any set of decision alternatives ordered with use by OF-SAW method. The following features of partial orders determined on the set of decision alternatives can be helpful.
Theorem 3. If and are the sequences of equivalence classes determined respectively by the orders , then we have Proof. Let us consider any equivalence class
. If
then the condition (63) is obvious. Therefore, let us assume that
Then for any pair of various decision alternatives
we have
The conditions (27) and (67) imply that
The inequalities (27) and (70) imply that
Without losing the generality of considerations we can assume that
According to (54) and (55), we get
which—along with (51), and (52)—gives
Then, Theorem 2 along with condition (71) prove
From (65) we get
which eventually proves
. This way we proved that for any pair
we get
This conclusion implies condition (63). Inequality (64) is a direct consequence of satisfying condition (63). □
Condition (63) allows us to determine that the use of defuzzification procedures can cause a revelation of deceptive information. This conclusion applies to any OF-SAW method. The previous section shows that there exists a case of using the OF-SAW method in which the deceptive information is revealed. Using the deceptive information can, in turn, lead to a determination of a decision alternatives ranking which is far from reality—which increases the chance of making a wrong decision. In such case, in any decision problem we should quit the orders determined on any defuzzification procedure. If we determine the ranking of decision alternatives assessed by the OF-SAW method, then the recommended order is the faithful order
established in
Section 3.
In an extreme case, the use of defuzzification procedures can totally blur the true picture of a real order of decision alternatives. The emphatic example of such a possibility is the result of the numerical experiment presented in Example 2.
Example 2. The order of the following set of evaluated decision alternatives is the main topic of our considerations Each decision alternative is attributed a value of any given scoring function expressed as a TrOFN. Let us assume that these are the values presented in Table 4. From a practical point of view, all those values are approximately equal. Table 4 also shows the results of defuzzification of these values with the use of all applied defuzzification methods. Observed rankings are described by tired ranks [23] which are presented in Table 5. The ranking of decision alternatives determined by faithful order is given as one class of equivalence. It means that all decision alternatives are equivalent. The faithful order is here the equivalence relation. This result is consistent with the common understanding of the obtained values of scoring function as almost equal. This order is compared with the rankings established by the use of defuzzified values . All the rankings obtained here are described by tired ranks [23] in Table 5. In Table 5, also the number of equivalence classes established by all orders was presented. We observe that these orders are partial or strict ones. Each row of this table lists different ranks of a given decision alternative. We see that the obtained orders differ significantly. The above example shows that using the defuzzification functional can significantly change the true picture of the ranking of decisions alternatives.
6. Recapitulation
In this paper we evaluate decision alternatives by Ordered Fuzzy Simple Additive Weighting (OF-SAW) method. Attention was paid to the linguistic approach based on ordered fuzzy numbers (OFN), which can be implemented to evaluate decision alternatives. In our approach, the decision maker’s preferences over the criterion are represented by trapezoidal OFN (TrOFN).
First, by using the fuzzy relation “greater than or equal to” for TrOFNs , we define imprecise recommendation determined as the fuzzy set of recommended decision alternatives. This approach is applicable only for the case when the imprecise recommendation support contains an insufficient number of decision alternatives. An imprecise recommendation cannot be defined by means of ordering methods determined with the use of the defuzzification functional.
If imprecise recommendation is not applicable, then we propose using the crisp faithful order, which is determined to use all information on imprecision and orientation of evaluation. For this reason, we say that faithful order is the real order of evaluated decision alternatives. The faithful order is compared with orders outlined with the use of any defuzzification method. In case of the use of the defuzzification functional, we only have to do with the total loss of information on imprecision and orientation of evaluation. It means that using the defuzzification functional can enlarge the available source of deceptive information, i.e., the information which can change the true picture. In
Section 5, it is proved that the use of defuzzification procedures can always cause the reveal of deceptive information. In the case study and numerical experiment, we show that the use of defuzzification methods has a significant impact on the ordering of decision alternatives. In an extreme case, the use of defuzzification procedures can totally blur the true picture of a real order of decision alternatives.
Using deceptive information can lead to results deviating from real ranking of decision alternatives, which will increase the hazard of making a wrong decision.
For above reasons, we can say that the OF-SAW method equipped with the fuzzy relation is significantly better than OF-SAW methods equipped with an order outlined with the use of any defuzzification method.
The Theorem 3 is satisfied by any ranking determined by any scoring function that is evaluated by TrOFNs. Therefore, we can say that using the multi-criterial scoring method equipped with the fuzzy relation is significantly better than the method equipped with order outlined with use of the defuzzification method. In general, decision alternatives evaluated by OFNs should be ranked by the fuzzy relation.
In [
14] it was shown that the set of all fuzzy numbers (FN) is formally identical to a set of all positively-oriented OFN enlarged by a set of all real numbers. Therefore. the achieved results can easily be used in case of the linguistic approach based on FN.
On the other hand, further research on comparison of FN and OFN for linguistic evaluation of decision alternatives should be undertaken. This way the results of F-SAW use can be compared with the results of OF-SAW use.
By the term “oriented fuzzy ranking (OF-R) method”, we mean an application of scoring function evaluated with TrOFNs for ordering the set of decision alternatives. It is obvious that any OF-SAW method is a special kind of an OF-R method. In our research, the SAW method is treated as a kind of benchmark for evaluating the features of any scoring function. Nonetheless, all results reached for the OF-SAW method can be easily generalized to the case of any OF-R method. From a mathematical point of view, this generalization is a very simple task.
The results of this paper entitle us to formulate the following hypothesis:
Hypothesis: Decision alternatives evaluated by OFNs should be ranked with use of the faithful order determined in Section 3. The verification of that hypothesis should be the subject of further research.