Polynomial Least Squares Method for Fractional Lane–Emden Equations

Abstract

This paper applies the Polynomial Least Squares Method (PLSM) to the case of fractional Lane-Emden differential equations. PLSM offers an analytical approximate polynomial solution in a straightforward way. A comparison with previously obtained results proves how accurate the method is.

1. Introduction

The equation analyzed in this article was published at the end of the 19th century by Jonathan Homer Lane in [1] and at the beginning of the 20th century explored in detail by Robert Emden in [2]. In the decades that followed, the equation Lane-Emden raised the interest of many researchers who used different methods to determine numerical or analytical solution for the equation.

In this paper we start by considering the following Lane-Emden Fractional Differential Equation [3,4,5]:

$$D^{\alpha }y\left(x\right)+\frac{k}{x}·D^{\beta }y\left(x\right)+f(x,y\left(x\right))=g\left(x\right),x>0,1<\alpha \le 2,0<\beta \le 1$$

(1)

together with the conditions:

$$y\left(0\right)=A,y^{\prime }\left(0\right)=B$$

(2)

where $x\in [0,1]$, k, A and B are real constants, $f(x,y(x\left)\right)=h\left(x\right)·y\left(x\right)$, with $h\left(x\right)$ and $g\left(x\right)\in C[0,1]$.

$D^{\alpha }$ and $D^{\beta }$ denote the Caputo fractional derivatives:

$$D^{\alpha }y\left(x\right)=\frac{1}{\Gamma (2-\alpha )}·{\int }_0^x{(x-\zeta )}^{-\alpha +1}·y^{″}\left(\zeta \right)d\zeta ,1<\alpha \le 2.$$

$$D^{\beta }y\left(x\right)=\frac{1}{\Gamma (1-\beta )}·{\int }_0^x{(x-\zeta )}^{-\beta }·y^{\prime }\left(\zeta \right)d\zeta ,0<\beta \le 1.$$

The above fractional Lane-Emden equation can demonstrate various phenomena arising in mathematical physics and astrophysics. In recent years many researchers sought solutions for this type of equation. Among them we mention: Mechee et al. (2012) by using the Collocation Method [3], Akgul, Kazemi et al. (2018) by using a hybrid numerical method combining Chebyshev wavelets and a finite difference approach [5], Yuzbasi (2011) by using the Bessel Collocation Method [6], Podlubny (1999), Fazly and Wei (2015) and Davila, Dupaigne and Wei (2014) by using analytical methods [7,8,9], Saeed (2017) by using the Haar Adomian Method [10], Atabakzadeh, Akrami and Erjaee by using the Chebyshev operational matrix method [11].

We remark that finding accurate approximate solutions to the problem (1) and (2) is usually not a simple task due to the presence of a singularity in 0.

Depending on the values of the constants and functions involved in (1) and (2), there are several particular types of equations with important practical applications, e.g., thermionic currents, gravitational potential of the degenerate white-dwarf stars or isothermal gas spheres. Many studies have been devoted to finding solutions for it, such as [12,13,14,15,16].

This paper has the following structure: The first section will introduce the Polynomial Least Squares Method (PLSM) [17] which permits determination of analytical approximate polynomial solutions for problems of the type (1) and (2). In the second section we will compare approximate solutions obtained by using PLSM with corresponding approximate solutions obtained in previous studies by means of other methods.

2. The Polynomial Least Squares Method

Attached to the problem (1) and (2), we have in view the operator:

$$\mathcal{D}\left(y\left(x\right)\right)=D^{\alpha }y\left(x\right)+\frac{k}{x}·D^{\beta }y\left(x\right)+h\left(x\right)·y\left(x\right)-g\left(x\right).$$

(3)

We will compute approximate polynomial solutions $\tilde{y}\left(x\right)$ of (1) and (2) on the interval [0, 1], satisfying the conditions:

$$\left|\mathcal{D}\right(\tilde{y}\left(x\right)\left)\right|<ϵ,ϵ>0$$

(4)

$$\tilde{y}\left(0\right)=A,{\tilde{y}}^{\prime }\left(0\right)=B.$$

(5)

Definition 1.

An ϵ-approximate polynomial solution of the problem (1) and (2) is an approximate polynomial solution $\tilde{y}\left(x\right)$ satisfying the relations (4) and (5).

Definition 2.

A weak ϵ-approximate polynomial solution of the problem (1) and (2) is an approximate polynomial solution $\tilde{y}\left(x\right)$ satisfying the relation:

$${\int }_0^1{\left|\mathcal{D}\left(\tilde{y}\left(x\right)\right)\right|}^{2}dx\le ϵ$$

(6)

together with the initial conditions (5).

Definition 3.

We have in view the polynomials $P_n\left(x\right)=a_0+a_{1}x+a_2{x}^2+\cdots +a_n{x}^n$, $a_i\in \mathbb{R}$, $i=\overline{0,n}$ satisfying the conditions:

$$P_n\left(0\right)=A,P_n^{\prime }\left(0\right)=B.$$

One calls the sequence of polynomials $P_n\left(x\right)$ convergent to the solution of the problem (1) and (2) if $\underset{n\to \infty }{lim}\mathcal{D}\left(P_n\left(x\right)\right)=0.$

Theorem 1.

The problem (1) and (2) admits a sequence of weak approximate polynomial solutions.

Proof. 

We compute a weak $ϵ$-approximate polynomial solution, in the sense of the Definition 2, of the type:

$$\tilde{y}\left(x\right)=\sum _{k=0}^n{d}_k{x}^k$$

(7)

where $d_0,d_1,\cdots ,d_n$ are constants calculated as follows:

(1)

We substitute the approximate solution (7) in the Equation (1) and obtain the remainder:

$$\mathcal{D}\left(\tilde{y}\left(x\right)\right)=D^{\alpha }\tilde{y}\left(x\right)+\frac{k}{x}·D^{\beta }\tilde{y}\left(x\right)+h\left(x\right)·\tilde{y}\left(x\right)-g\left(x\right).$$

(8)

(2)

We attach to problem (1) and (2) the real functional:

$$\mathcal{J}(d_2,d_3\cdots ,d_n)=\underset{0}{\overset{1}{\int }}{\mathcal{D}}^2\left(\tilde{y}\left(x\right)\right)dx$$

(9)

where $d_0,d_1$ are computed as functions of $d_2,d_3\cdots ,d_n$ by using the initial conditions (5).

(3)

We compute $d_2^0,d_3^0,\cdots d_m^0$ as values which give the minimum of the functional (9) and the value of $d_0^0$, $d_1^0$ as functions of $d_2^0,d_3^0,\cdots ,d_m^0$ using the initial conditions.

(4)

Using the constants $d_0^0,d_1^0,\cdots ,d_m^0$ thus determined, we construct the polynomial:

$$T_n\left(x\right)=\sum _{k=0}^n{d}_k^0{x}^k.$$

(10)

□

Theorem 2.

The sequence of polynomials $T_n\left(x\right)$ from (10) satisfies the property:

$$\underset{n\to \infty }{lim}\underset{0}{\overset{1}{\int }}{\mathcal{D}}^2\left(T_n\left(x\right)\right)dx=0.$$

(11)

Moreover, $\forall ϵ>0,\exists n_o\in \mathbb{N},n>n_0$ such that $\forall n\in \mathbb{N},n>n_0$ it follows that $T_n\left(x\right)$ is a weak ϵ-approximate polynomial solution of the problem (1) and (2).

Proof. 

Taking into account the way the coefficients of polynomial $T_n\left(x\right)$ are computed and also the relations (8)–(10), the following inequalities are satisfied:

$$0\le \underset{0}{\overset{1}{\int }}{\mathcal{D}}^2\left(T_n\left(x\right)\right)dx\le \underset{0}{\overset{1}{\int }}{\mathcal{D}}^2\left(P_n\left(x\right)\right)dx,\forall n\in \mathbb{N}$$

(12)

It follows that:

$$0\le \underset{n\to \infty }{lim}\underset{0}{\overset{1}{\int }}{\mathcal{D}}^2\left(T_n\left(x\right)\right)dx\le \underset{n\to \infty }{lim}\underset{0}{\overset{1}{\int }}{\mathcal{D}}^2\left(P_n\left(x\right)\right)dx=0,(\forall )n\in \mathbb{N}.$$

(13)

We obtain:

$$\underset{x\to \infty }{lim}\underset{0}{\overset{1}{\int }}{\mathcal{D}}^2\left(T_n\left(x\right)\right)dx=0$$

(14)

From this we obtain that $(\forall )ϵ>0,\exists n_o\in \mathbb{N}$ such that $(\forall )n\in \mathbb{N},n>n_0$. It results that $T_n\left(x\right)$ is a weak ϵ-approximate polynomial solution of the problem (1) and (2). □

Remark 1.

As far as the above remark is concerned, in order to find ϵ-approximate polynomial solutions of the problem (1) and (2) by using the (PLSM), we will first determine weak approximate polynomial solutions, $\tilde{y}\left(x\right)$ following the previously described steps 1 to 4. If $\left|\mathcal{D}\right(\tilde{y}\left(x\right)\left)\right|<ϵ$, then $\tilde{y}\left(x\right)$ is also an ϵ-approximate polynomial solution.

Error Estimation

We denote with $\mathcal{L}$ the following operator:

$$\mathcal{L}\left(y\left(x\right)\right)=D^{\alpha }y\left(x\right)+\frac{k}{x}·D^{\beta }y\left(x\right)+h\left(x\right)·y\left(x\right)$$

(15)

thus, Equation (1) becomes:

$$\mathcal{L}\left(y\right(x\left)\right)=g\left(x\right)$$

(16)

where $x>0$, $y\left(x\right):[0,1]\to \mathbb{R}$, $1<\alpha \le 2$, $0<\beta \le 1$, together with the conditions:

$$y\left(0\right)=A,y^{\prime }\left(0\right)=B$$

(17)

With $\tilde{y}$ an approximate solution for the problem (15)–(17), using (for simplicity) the notation:

$$\mathcal{R}\left(x\right)=\mathcal{R}(x,\tilde{y}\left(x\right))=D^{\alpha }y\left(x\right)+{\displaystyle \frac{k}{x}}·D^{\beta }y\left(x\right)+h\left(x\right)·y\left(x\right)-g\left(x\right),$$

we obtain:

$$\mathcal{R}\left(x\right)=\mathcal{L}\left(\tilde{y}\left(x\right)\right)-g\left(x\right)$$

(18)

which means as $\tilde{y}$ satisfies:

$$\mathcal{L}\left(\tilde{y}\left(x\right)\right)=D^{\alpha }\tilde{y}\left(x\right)+\frac{k}{x}·D^{\beta }\tilde{y}\left(x\right)+h\left(x\right)·\tilde{y}\left(x\right)=g\left(x\right)+\mathcal{R}\left(x\right)$$

(19)

with initial conditions:

$$\tilde{y}\left(0\right)=A,{\tilde{y}}^{\prime }\left(0\right)=B$$

(20)

We define the error function in the following way: $\tilde{e}\left(x\right)=y\left(x\right)-\tilde{y}\left(x\right)$, where $y\left(x\right)$ is the exact solution for the problem (1) and (2) and we obtain the differential equation for error function:

$$\mathcal{L}\left(\tilde{e}\left(x\right)\right)=\mathcal{L}\left(y\left(x\right)\right)-\mathcal{L}\left(\tilde{y}\left(x\right)\right)=-\mathcal{R}\left(x\right)$$

(21)

with the conditions:

$$\tilde{e}\left(0\right)=0,{\tilde{e}}^{\prime }\left(0\right)=0$$

(22)

The problem for the error function becomes so : $\mathcal{L}\left(\tilde{e}\left(x\right)\right)=-\mathcal{R}\left(x\right)$ or:

$$D^{\alpha }\tilde{e}\left(x\right)+\frac{k}{x}·D^{\beta }\tilde{e}\left(x\right)+h\left(x\right)·\tilde{e}\left(x\right)=-\mathcal{R}\left(x\right)$$

(23)

with $\tilde{e}\left(0\right)=0,{\tilde{e}}^{\prime }\left(0\right)=0$.

Solving the (23) equation in the same manner as described above, we obtain the approximation $\tilde{e}\left(x\right)$, we will be able to determine the absolute maximum error:

$$\tilde{\mathcal{E}}=max\left\{|\tilde{e}\left(x\right)|,0\le x\le 1\right\}$$

(24)

In this manner we estimate the error without knowing the exact solution of the initial problem (1) and (2).

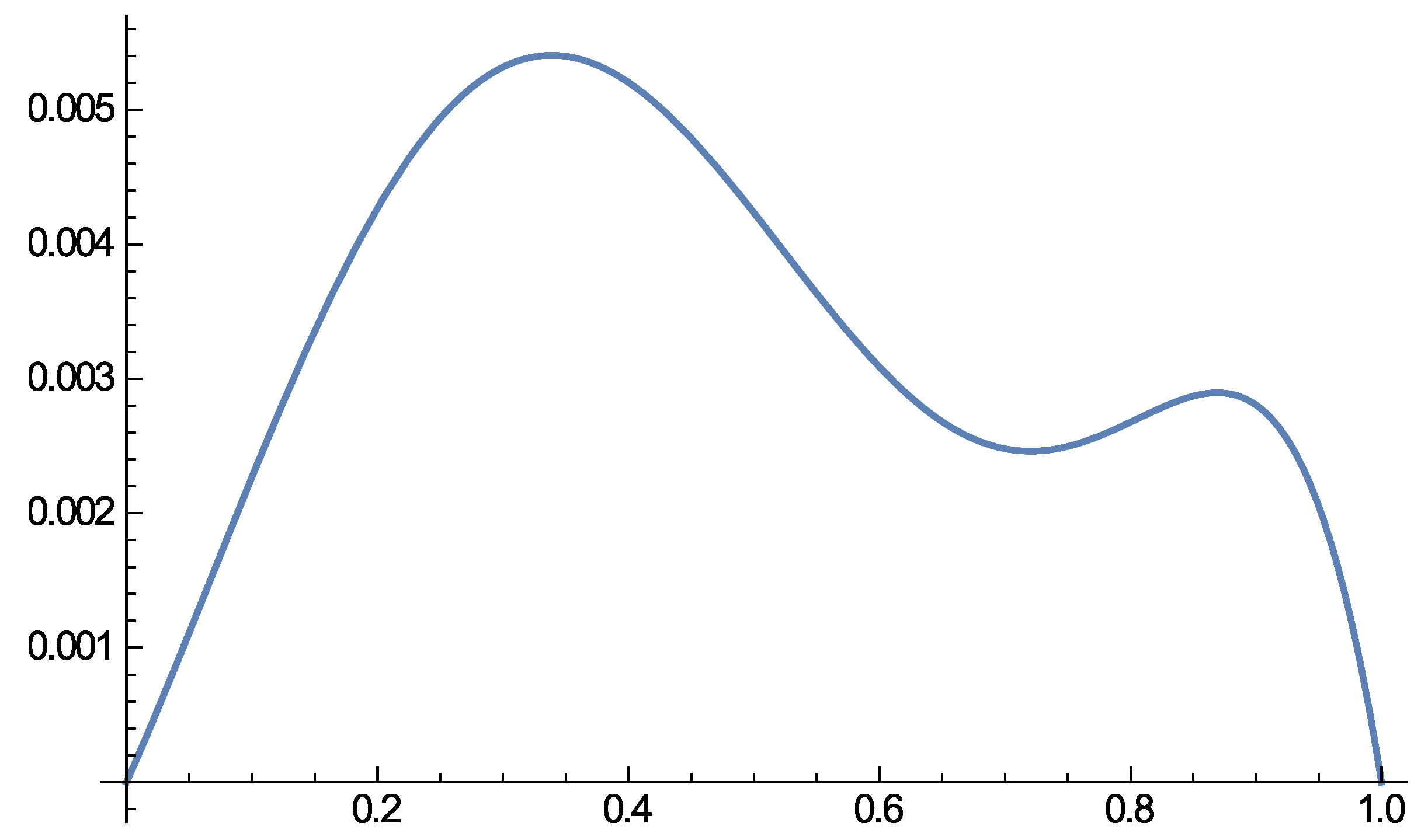
3. Applications

3.1. Application 1

Consider the fractional Lane-Emden equation [3]:

$$D^{\alpha }y\left(x\right)+{\displaystyle \frac{1}{x^{\alpha -\beta }}}·D^{\beta }y\left(x\right)+{\displaystyle \frac{1}{x^{\alpha -2}}}y\left(x\right)=g\left(x\right)$$

(25)

with $g\left(x\right)=x^{\{2-\alpha \}}\left(6x\left({\displaystyle \frac{\Gamma (4-\beta )+\Gamma (4-\alpha )}{\Gamma (4-\alpha )\Gamma (4-\beta )}}+{\displaystyle \frac{x^2}{6}}\right)-2\left({\displaystyle \frac{\Gamma (3-\beta )+\Gamma (3-\alpha )}{\Gamma (3-\alpha )\Gamma (3-\beta )}}+{\displaystyle \frac{x^2}{2}}\right)\right)$, $\alpha =\frac{3}{2},$ $\beta =\frac{1}{2}$ together with the initial conditions:

$$y\left(0\right)=1,y^{\prime }\left(0\right)=0.$$

(26)

The exact solution of the problem (25) and (26) is: $y\left(x\right)=x^3-x^2.$

An approximate solution of this problem using the collocation method was proposed in [3] and the solution presented absolute errors larger than ${10}^{-8}$.

Using the Polynomial Least Squares Method (PLSM) presented in the previous section, we choose an approximate solution $\tilde{y}\left(x\right)$ of the type:

$$\tilde{y}\left(x\right)=d_0+d_1·x+d_2·x^2+d_3·x^3.$$

By using the boundary conditions we compute ${\tilde{c}}_0=0$, ${\tilde{c}}_1=0$ and the approximate solution becomes: $\tilde{y}\left(x\right)=d_2·x^2+d_3·x^3$.

The corresponding functional (9) is:

$$\begin{array}{c}\hfill \mathcal{J}(d_2,d_3)=\frac{d_2^2}{6}+\frac{10d_2^2}{3\sqrt{\pi }}+\frac{200d_2^2}{9\pi }+\frac{2d_2{d}_3}{7}+\frac{536d_2{d}_3}{75\sqrt{\pi }}+\frac{448d_2{d}_3}{9\pi }+\frac{d_2}{21}-\frac{12d_2}{25\sqrt{\pi }}\\ \hfill -\frac{16d_2}{3\pi }+\frac{d_3^2}{8}+\frac{56d_3^2}{15\sqrt{\pi }}+\frac{784d_3^2}{25\pi }+\frac{d_3}{28}-\frac{8d_3}{25\sqrt{\pi }}-\frac{2912d_3}{225\pi }+\frac{1}{168}-\frac{2}{25\sqrt{\pi }}+\frac{856}{225\pi }.\end{array}$$

In order to find the minimum of this functional we can compute the stationary points by equating to zero its partial derivatives with respect to $d_2$ and $d_3$. We obtain as expected $d_2=-1,d_3=1$ and it is easy to show (by means of the second derivative) that this stationary point is indeed the minimum. It follows that by using PLSM we are able to find the exact solution of the problem, $\tilde{y}\left(x\right)=x^3-x^2$.

3.2. Application 2

We consider the fractional Lane-Emden Equation [3]:

$$D^{\alpha }y\left(x\right)+{\displaystyle \frac{1}{x^{\alpha -\beta }}}·D^{\beta }y\left(x\right)+{\displaystyle \frac{1}{x^{\alpha -2}}}y\left(x\right)=g\left(x\right)$$

(27)

with $g\left(x\right)=x^{\{2-\alpha \}}\left(-6x\left({\displaystyle \frac{\Gamma (4-\beta )+\Gamma (4-\alpha )}{\Gamma (4-\alpha )\Gamma (4-\beta )}}+{\displaystyle \frac{x^2}{6}}\right)+2\left({\displaystyle \frac{\Gamma (3-\beta )+\Gamma (3-\alpha )}{\Gamma (3-\alpha )\Gamma (3-\beta )}}+{\displaystyle \frac{x^2}{2}}\right)\right)$, $\alpha =\frac{3}{2},$ $\beta =1$ together with the initial conditions:

$$y\left(0\right)=1,y^{\prime }\left(0\right)=0.$$

(28)

The exact solution of the problem (27) and (28) is: $y\left(x\right)=-x^3+x^2.$

Again, an approximate solution of this problem using the collocation method was proposed in [3] and the solution presented absolute errors larger than ${10}^{-8}$ .

Applying PLSM and using the same steps as in the previous example, we are again able to find the exact solution of the problem: $\tilde{y}\left(x\right)=-x^3+x^2.$

3.3. Application 3

Consider the following Lane-Emden fractional differential Equation [5]:

$$D^{\alpha }y\left(x\right)+{\displaystyle \frac{k}{x^{\alpha -\beta }}}·D^{\beta }y\left(x\right)+\frac{1}{1-x}·y\left(x\right)=g\left(x\right),0<x<1$$

(29)

together with the conditions:

$$y\left(0\right)=0,y\left(1\right)=cos\left(1\right).$$

(30)

where $g\left(x\right)={\displaystyle \frac{x^3}{1-x}}cos\left(x\right)-5xsin\left(x\right)+4cos\left(x\right)$, $\alpha =1.9$ and $\beta =0.9$.

The exact solution of the problem is $y\left(x\right)=x^{2}cos\left(x\right)$ ([5]).

For this problem, by using PLSM we obtain the approximate analytical solution:

$$\begin{array}{c}\hfill \tilde{y}\left(x\right)=-0.215146·x^6+0.415059·x^5-0.549661·x^4-0.164992·x^3+1.03409·x^2+0.0209532·x.\end{array}$$

The absolute error of the approximation, computed as the absolute value of the difference between the exact solution and the approximate one, is presented in Figure 1.

4. Conclusions

The Polynomial Least Squares Method (PLSM) is considered as a simple, efficient, accurate method for calculating approximate polynomial solutions for Lane–Emden-type fractional differential equations.

The comparison with anterior results highlights the accuracy of the method. At the same time, the fact that the solutions are polynomials of relatively small degree leads to solutions that are not only precise but also that present a very simple expression.

Since the method does not actually depend on a particular equation, it can be easily applied to other types of equations, even strongly nonlinear ones.