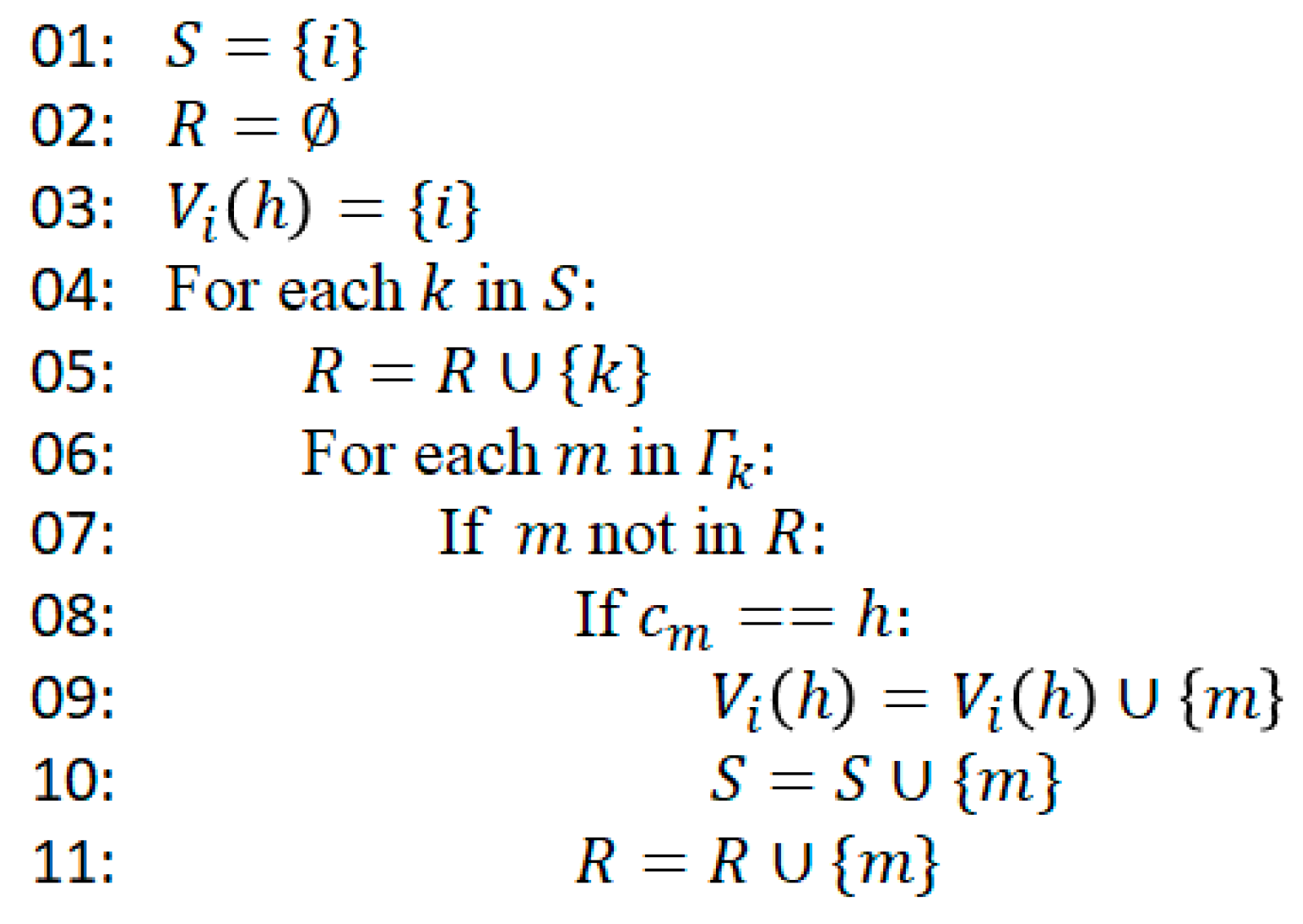1. Introduction
Identifying critical nodes accurately is of great importance in order to understand the structure and function of a network [
1,
2,
3,
4,
5]. This will allow us to better control many kinds of dynamical processes, such as the outbreak of epidemics [
6,
7,
8], conduct successful advertisements for e-commercial products [
9], and prevent catastrophic outages in power grids [
10]. The widely used metrics to measure the node importance are degree, closeness [
11], betweenness [
12], H-index [
13], coreness [
14] and so on. It is generally believed that nodes that have more neighbors are more important than those having less neighbors [
15,
16,
17]. Recently, Kitsak et al. [
18] argued that the location of a node is more significant than the number of its linked neighbors. Many research results show that coreness is a better indicator of a node’s influence on spreading dynamics than degree [
18,
19,
20,
21,
22].
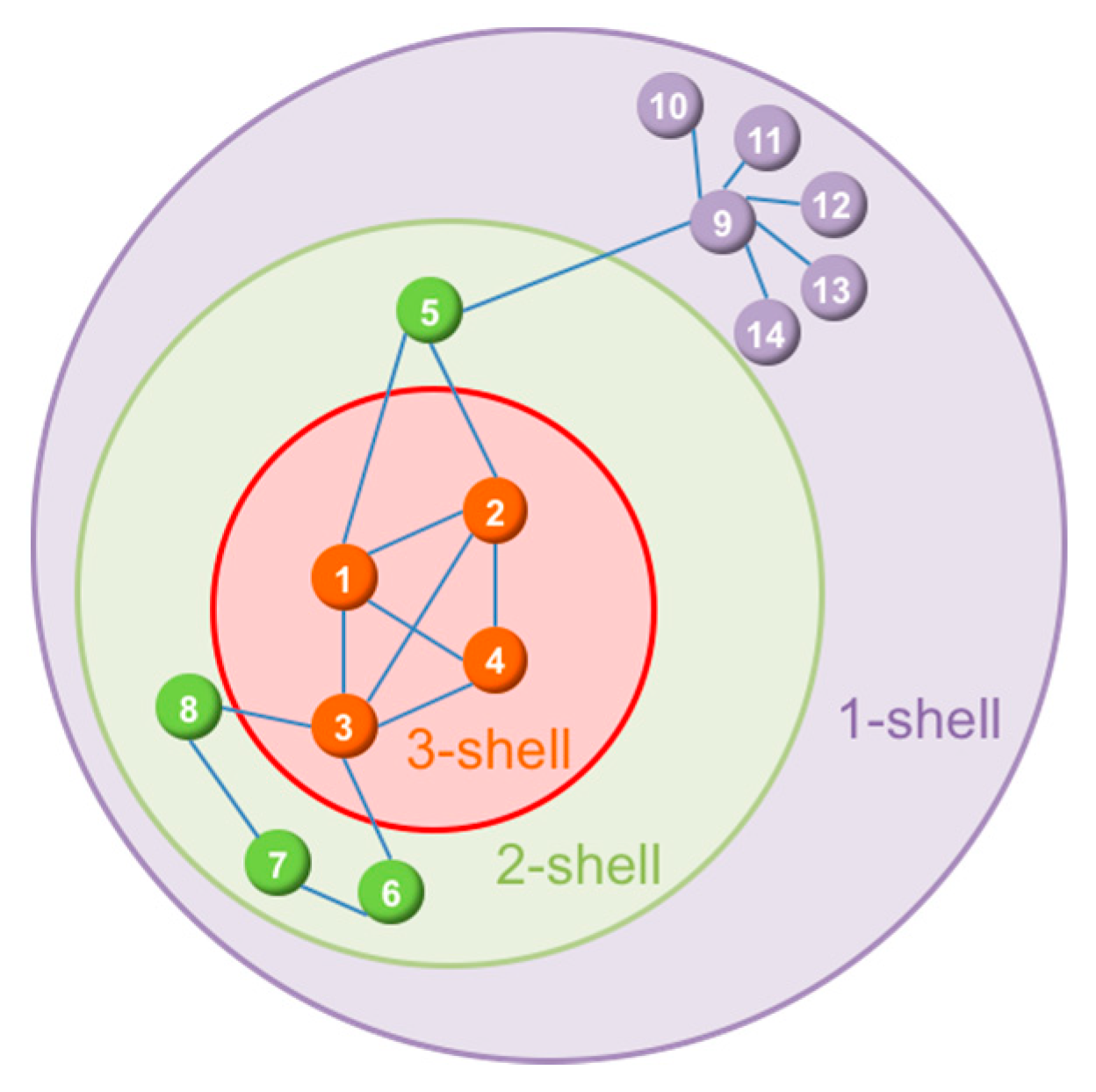
The traditional way of calculating the coreness of a node is the
k-core decomposition [
23,
24], as shown in
Figure 1. In a simple undirected network, all the isolated nodes form the 0-shell are removed from the network. Next, it removes all nodes with degree
. This causes new nodes with degree
to appear. These nodes are also removed, and the process is continued until the nodes remaining are those of degree
. The removed nodes and their associated links form the 1-shell. The pruning process is repeated to remove the nodes with degree
iteratively, and all the nodes and links removed in this round constitute the 2-shell. The process is continued until all higher-layer shells have been identified and all nodes have been removed. Then, each node
is assigned a shell layer
, called the coreness of node
. The
k-core decomposition is simple and intuitive process used to calculate the coreness of nodes. However, when considering a dynamic network whose topological structure is varying, the
k-core decomposition process has to be restarted in order to determine the coreness of nodes, which will be a time-consuming task, especially for a large-scale dynamic network. Therefore, it is of great necessity to establish a fast updating method to handle the coreness determination in a dynamic network [
24,
25,
26,
27].
Lv, et al. [
28] proposed an asynchronous updating algorithm to calculate the
k-shell indices. In this algorithm, they defined an operator
, which reveals the relationship between degree, H-index and coreness and obtains a new method for calculating the coreness of nodes. In each step, it randomly selects one node to update its intermediate value towards the
k-shell index by the operator
, the degree of each node is used as the initial input of the operator
. This operator
is iteratively calculated until the value for each node goes into its steady state. Ultimately the steady value of each node is its coreness. Compared with the traditional
k-core decomposition, this algorithm uses only local information of the networks and can implement a distributed computing, which significantly improves the computational efficiency. Subsequently, Lee et al. [
29] proposed two methods to optimize the asynchronous iterative order of nodes, which further improved the computational efficiency of the asynchronous updating algorithm.
From the
k-core decomposition method [
23,
24] to the asynchronous updating algorithm [
28], then to the algorithm that optimizes the asynchronous iteration order of nodes [
29], people have made great progress in the coreness calculation.
In this paper, we study how the coreness of nodes will vary in a dynamic network with local structural variation when the initial coreness of each node is known. Mastering the variation rules of the coreness will not only provide a theoretical basis to improve the computational efficiency of coreness calculation, but also provide a computing basis for the study related to the application of the coreness in the dynamic networks.
The rest of this paper is organized as follows. In
Section 2, we introduce
operator method in detail.
Section 3 is devoted to reveal the coreness variation rule by a symmetric pair of experiments on real networks. The CHDE and CHAE algorithms are proposed to fast update the coreness during the local structural variation as well. Results on five real networks are shown in
Section 4.
Section 5 provides our conclusions.
2. Operator Method for Coreness Calculation
Denote as a simple network, where is the set of nodes and is the set of links. The degree and coreness of an arbitrary node are denoted as and respectively. The number of nodes and links are represented by and , respectively.
According to the research of Lv et al. [
24], when the
operator reaches the steady state, the stable value of each node is the coreness. At this time, the coreness of node
and the coreness of its neighbors
still satisfy the relation of operator
, that is:
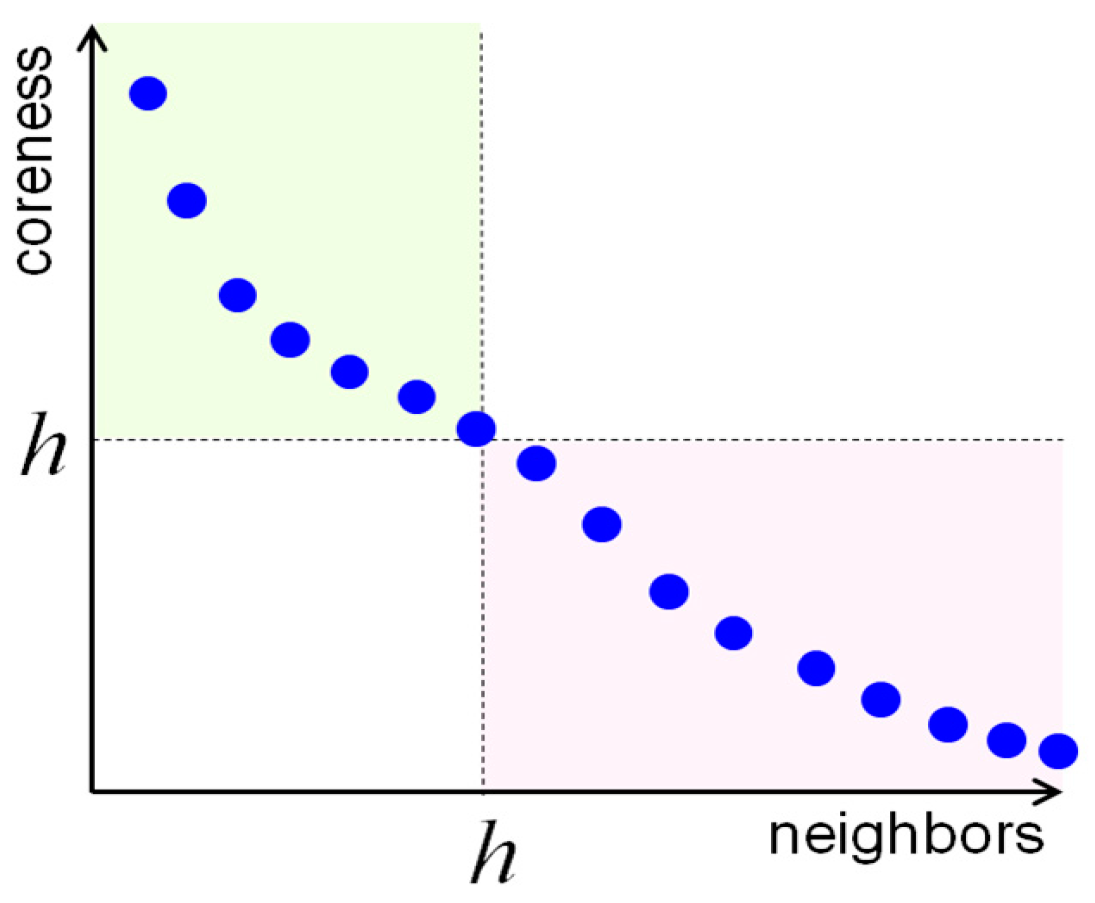
The operator
relationship is shown in
Figure 2. Assuming
, where
is the set of the neighbor nodes of node
. All the neighbors of node
are arranged along the horizonal axis by a decreasing order of their coreness,
. Then the coreness of node
is equal to the side length of the largest square with no points inside (
Figure 2), i.e.,
.
3. Coreness Variation in Dynamic Networks
In this section, we will discuss how the coreness of nodes will vary when there is a local variation in the network structure. It is necessary to clarify the time scale of variations before discussing the variations of the network structure. The structure of some networks varies very slowly. For example, infrastructure networks such as road networks, railway networks and so on. Their structural variations are counted by year. The structure of some networks varies rapidly. For example, WWW, instant messaging networks, social media networks, etc. Their structural variations are counted by second. When the time scale of the observation is approximately equivalent to the time scale of the structural variation, the observed variations in the network structure can be considered as local variations. This paper interprets the local variations in the network structure as: “deleting an edge” or “adding an edge” which are denoted as DE experiment and AE experiment, respectively.
We executed DE and AE experiments on five real networks. Their basic topological characteristics are shown in
Table 1. We tried to answer the following questions: (1) which nodes will get their coreness varied? (2) What conditions are met by the nodes that their coreness will vary?
3.1. DE Experiments
Denote as the deleted edge in the network, where and represent the nodes forming the edge. Results show that the nodes whose coreness has varied in DE experiment have the same coreness before the edge deleted, i.e., they all come from the same k-shell layer, and fall into the same (k−1)-shell layer.
3.1.1. Classification of Nodes with the Same Coreness
Assuming that the neighbor nodes of node are arranged in the descending order by their coreness as . Comparing and , all nodes with the coreness can be divided into and types as the following conditions.
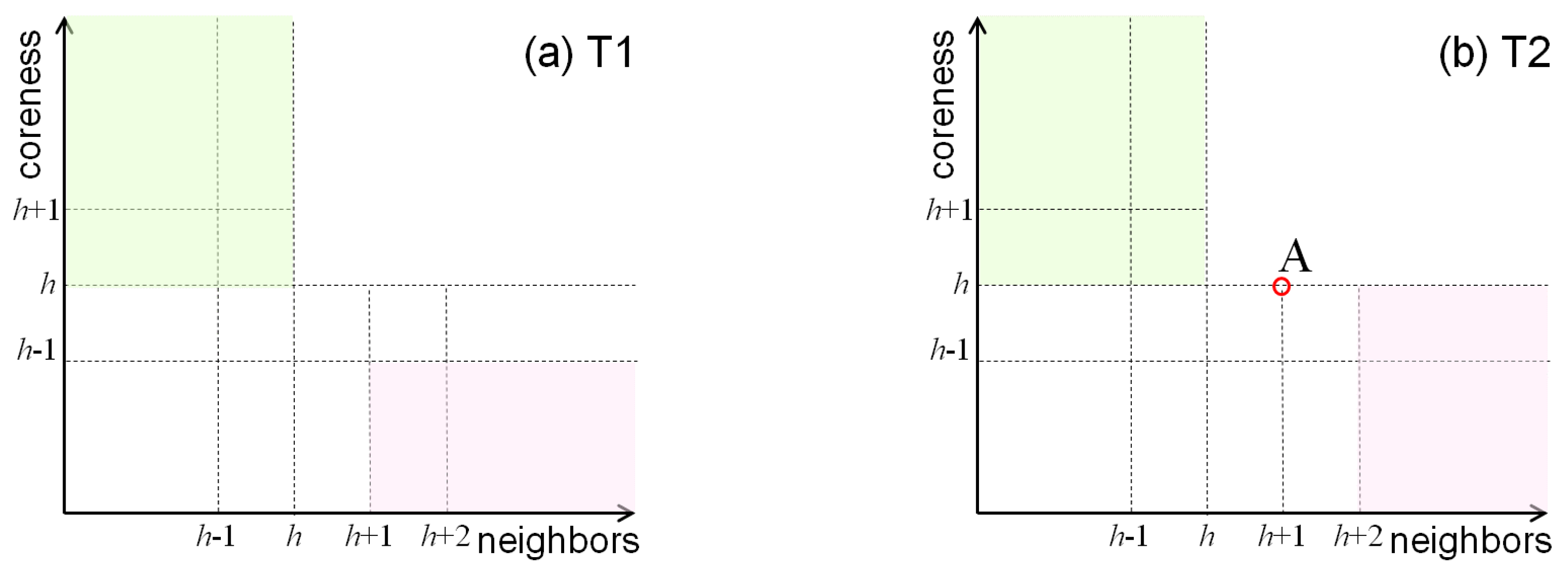
:
. Which means, the coreness of the first
neighbor nodes is greater than, or equal to
(green zone in
Figure 3a), and the coreness of rest neighbor nodes is less than
(red zone in
Figure 3a).
:
. Which means, the coreness of the first
neighbor nodes is greater than or equal to
(green zone in
Figure 3b), the coreness of the
th neighbor node is
(point A of
Figure 3b), and the coreness of rest neighbor nodes is less than or equal to
(red zone in
Figure 3b).
The classification above is a complete classification of the nodes having the same coreness , that is, will contain all the nodes with the same coreness .
3.1.2. Coreness Variation Rule and CHDE Algorithm
When
, we assume
. Node
just loses a neighbor in the red zone in
Figure 2, and its coreness does not vary. While, node
loses a neighbor in the green zone in
Figure 2, and whether its coreness varies will be determined by the following coreness variation rules.
(1) If , then . Here, represents the coreness of node after the edge deleted. If the coreness variation begins from node can spread out, then the coreness variation can only spread in the connected subgraph, , which includes node , and in which all nodes have the same initial coreness .
(2) If , then , and the coreness of other nodes will not vary.
According to the coreness variation rules mentioned above, combined with the
operator method [
29], we propose the CHDE algorithm to quickly update the coreness of related nodes. The process is as follows:
Step 1: Judge the type of node
. If
, then find out the connected subgraph
by the searching algorithm (
Figure 4). Otherwise if
, the coreness of any node will not vary, and the CHDE algorithm ends.
Step 2: Update the coreness of all nodes in the connected subgraph
by the
operator method [
29].
When , the coreness variations of node , node , and other related nodes can still be determined and updated by the CHDE algorithm. The modification in ’Step 1’ of CHDE algorithm is to judge the type of both node and node , and find out the connected subgraph and . The modification in ‘Step 2’ is updating the coreness in both and .
3.2. AE Experiments
Denote as the added edge in the network, where and represent the nodes forming the edge. Results show that the nodes whose coreness varies in the AE experiment have the same coreness before the edge added, i.e., they all come from the same k-shell layer, and go up into the same (k+1)-shell layer.
3.2.1. Classification of Nodes with the Same Coreness
Assuming that the neighbor nodes of node are arranged in the descending order by their coreness as . Comparing and , all nodes with the coreness can be divided into and types as the following conditions.
:
. Which means, the coreness of the first
neighbor nodes is greater than or equal to
(green zone in
Figure 5a), and the coreness of rest neighbor nodes is less than
(red zone in
Figure 5a).
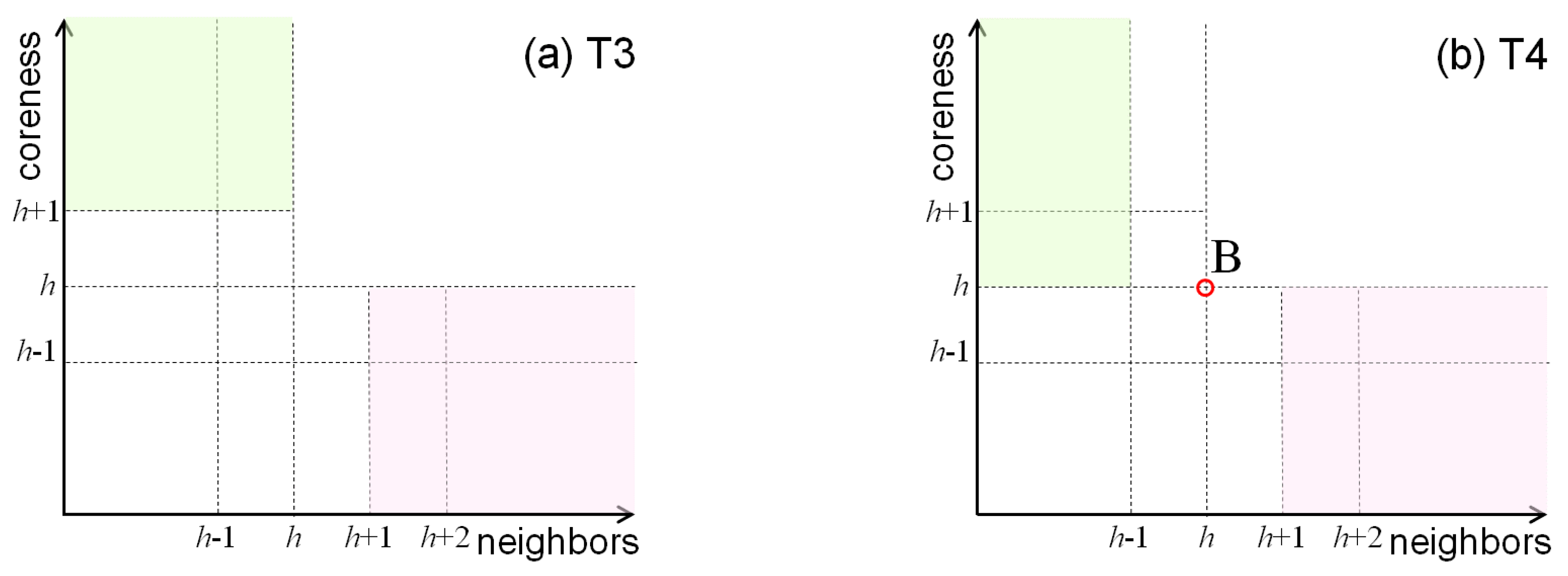
:
. Which means, the coreness of the first
neighbor nodes is greater than or equal to
(green zone in
Figure 5b), the coreness of the
-th neighbor node is
(point B in
Figure 5b), and the coreness of rest neighbor nodes is less than or equal to
(red zone in
Figure 5b).
The classification above is a complete classification of the nodes having the same coreness , that is, will contain all the nodes with the same coreness .
3.2.2. Coreness Variation Rule and CHAE Algorithm
When
, we assume
. Node
gets a new neighbor in the red zone in
Figure 2, and its coreness does not vary. While, node
gets a neighbor in the green zone in
Figure 2, and whether its coreness varies will be determined by the following coreness variation rules.
(1) If then . Here, represents the coreness of node after the edge added. Particularly, the coreness of other nodes in the network does not vary.
(2) If , whether the increase to cannot be determined directly. Then, a searching algorithm has to be employed find out the connected subgraph , which includes node , and in which all nodes have the same initial coreness .
According to the coreness variation rule mentioned above, combined with the
operator method [
29], we propose the CHAE algorithm to quickly update the coreness of related nodes. The specific process is as follows:
Step1: Judge the type of node
. If
, then find out the connected subgraph
by the searching algorithm (
Figure 4). Otherwise, if
,
, then the CHAE algorithm ends.
Step 2: Set the coreness of all nodes in the connected subgraph
as
, then update the coreness of all nodes in
by the
operator method [
29].
When , the coreness variations can be determined and updated by the CHAE algorithm. Since node and node are connected together, the CHAE algorithm can be applied directly without any modification.
4. Case Study
In this section, we define the relative computational efficiency to test the computational efficiency of CHDE and CHAE algorithms, with respect to the
k-core decomposition algorithm. The relative computational efficiency is tested on the five real networks (
Table 1). There are five combinations of the type of node
and node
in DE and AE experiments (
Table 2). It is worth noting that when
the node
and node
are completely equivalent in DE and AE experiments, so the two combinations (
and
in DE and
and
in AE) are not listed in
Table 2. We will not discuss the combinations (2) and (5) in DE and combinations (1) and (3) in AE in the rest part of this section either, since our method is obviously better than
k-core decomposition method. Because the time consumption of our method is almost zero in these combinations, while the
k-core decomposition method still has to decompose the network.
4.1. Computational Efficiency of CHDE Algorithm
For each combination, 100 edges are randomly selected to be deleted for each real network. Then, both CHDE and
k-core decomposition algorithms are applied to calculate the coreness of nodes, and the time consumption is recorded as
and
, respectively. Due to the randomness in the searching process of CHDE algorithm and the decomposing process of
k-core decomposition algorithm, therefore, when an edge is deleted, the coreness of nodes is calculated 100 times independently for both algorithms. To prove the improvement of the computational efficiency of the CHDE algorithm quantitatively comparing to the
k-core decomposition algorithm, we define the relative computational efficiency:
where
represents the
th calculation when
is deleted. In the definition, we let the shortest time consumed in 100 calculations (best) of the
-core decomposition algorithm compare to the longest time consumed in the 100 calculations (worst) of the CHDE algorithm when
deleted.
Results (
Table 3) show that the computational efficiency of CHDE algorithm is generally better than the
k-core decomposition algorithm. All results in
Table 3 are obviously larger than 1, which means CHDE algorithm is overall more efficient than
k-core decomposition algorithm. On average, the lowest computational efficiency of CHDE algorithm is still 20.30 times of
k-core decomposition algorithm, which appears on the US Power Grid network. Among the BEST group results, CHDE algorithm achieves more than 1000 times more efficient than
k-core decomposition algorithm in two combinations related to ca-AstroPh and loc-brightkite networks. Generally speaking, the larger the network is, the more remarkable the advantage of CHDE algorithm is.
4.2. Computational Efficiency of CHAE Algorithm
For each combination, 100 pairs of nodes are randomly selected to be added for each real network. Then, both CHAE and
k-core decomposition algorithms are applied to calculate the coreness of nodes, and the time consumption is recorded as
and
, respectively. Due to the randomness in the searching process of CHAE algorithm and the decomposing process of
k-core decomposition algorithm, in the instance of when an edge is added, the coreness of nodes is therefore calculated 100 times independently for both algorithms. To prove the improvement of the computational efficiency of the CHAE algorithm quantitatively comparing to the
k-core decomposition algorithm, we define the relative computational efficiency:
where
represents the
th calculation when the edge
is added. In the definition, we let the shortest time consumed in 100 calculations (best) of the
-core decomposition algorithm compare to the longest time consumed in the 100 calculations (worst) of the CHAE algorithm when
added.
Results (
Table 4) show that the computational efficiency of CHAE algorithm is generally better than the
k-core decomposition algorithm. Similar to CHDE, all results for CHAE algorithm in
Table 4 are obviously larger than 1 as well, which proves CHAE algorithm is totally more efficient than
k-core decomposition algorithm. On average, the lowest computational efficiency of CHAE algorithm is still 8.93 times of
k-core decomposition algorithm, which appears on the US Power Grid network, too. In the worst situation,
is smaller than
. The possible reason is that the connected subgraph
for AE (adding an edge) is more like to larger than that for DE (deleting an edge). Among the BEST group results, CHAE algorithm achieves more than 1000 times more efficient than
k-core decomposition algorithm in all three combinations on ca-AstroPh network. Similar to CHDE algorithm, the larger the network is, the more remarkable the advantage of CHAE algorithm is.
5. Discussion
When observing a dynamic network in a short enough time window, all the structural variations can be looked on as the local variation like deleting an edge or adding an edge. Based on this thinking, in this paper, we carried out DE and AE experiments to reveal the coreness variation rules, and presented CHDE and CHAE fast coreness updating algorithm.
In the DE and AE experiments, we found the following coreness variation rules: If a local structural variation can cause coreness variation of node(s), then all the nodes whose coreness varied will have the same initial coreness (), i.e., the coreness before the DE and AE action. This means that all the nodes whose coreness varied, belonged to the same shell layer (-shell). In DE experiments, these nodes’ coreness would decrease by 1, fall into the -shell layer, and form one or two connected subgraph(s). In AE experiments, those nodes’ coreness would increase by 1, go up into the -shell layer, and form one connected subgraph.
To reveal the mechanism of the coreness variation, all nodes with the same coreness (e.g.,
) were divided into
and
types in DE experiments (
Figure 3), and
and
types in AE experiments (
Figure 5). In DE experiment, the variation of coreness was caused by
node of the deleted edge. Beginning the searching process from the
node will find out one or two connected subgraph(s) with the initial coreness
, which is the outmost range of the nodes whose coreness will vary. Comparing to the DE experiment, the situation in AE experiment was a little bit more complex. The reliable strategy is to begin the searching process from the
node of the added edge, and find out a connected subgraph with the initial coreness
, which is the outmost range of the nodes whose coreness could vary.
According to the experimental results mentioned above, we established the CHDE and CHAE algorithms to fast updating the coreness for the local structural variation of deleting and adding an edge. Results showed that the proposed algorithms are overall superior to the k-core decomposition algorithm in terms of computational efficiency.
This paper is a start on the exploration of how the coreness of nodes varies, and how to fast update the coreness in a tolerable time when there is a local variation in the network structure. There are still many problems to be discussed in future. For instance, how the coreness of nodes will vary when more complex structural variations happen; how to go a further step to optimize the computational efficiency of the coreness updating algorithm; etc.