A Two-Dimensional Mathematical Model of Heat Propagation Equations and Their Significance for Soil Temperature
Abstract
:1. Introduction
2. Finite Element Methods
2.1. Finite Element Methods Description
2.1.1. Different Types of d.o.f
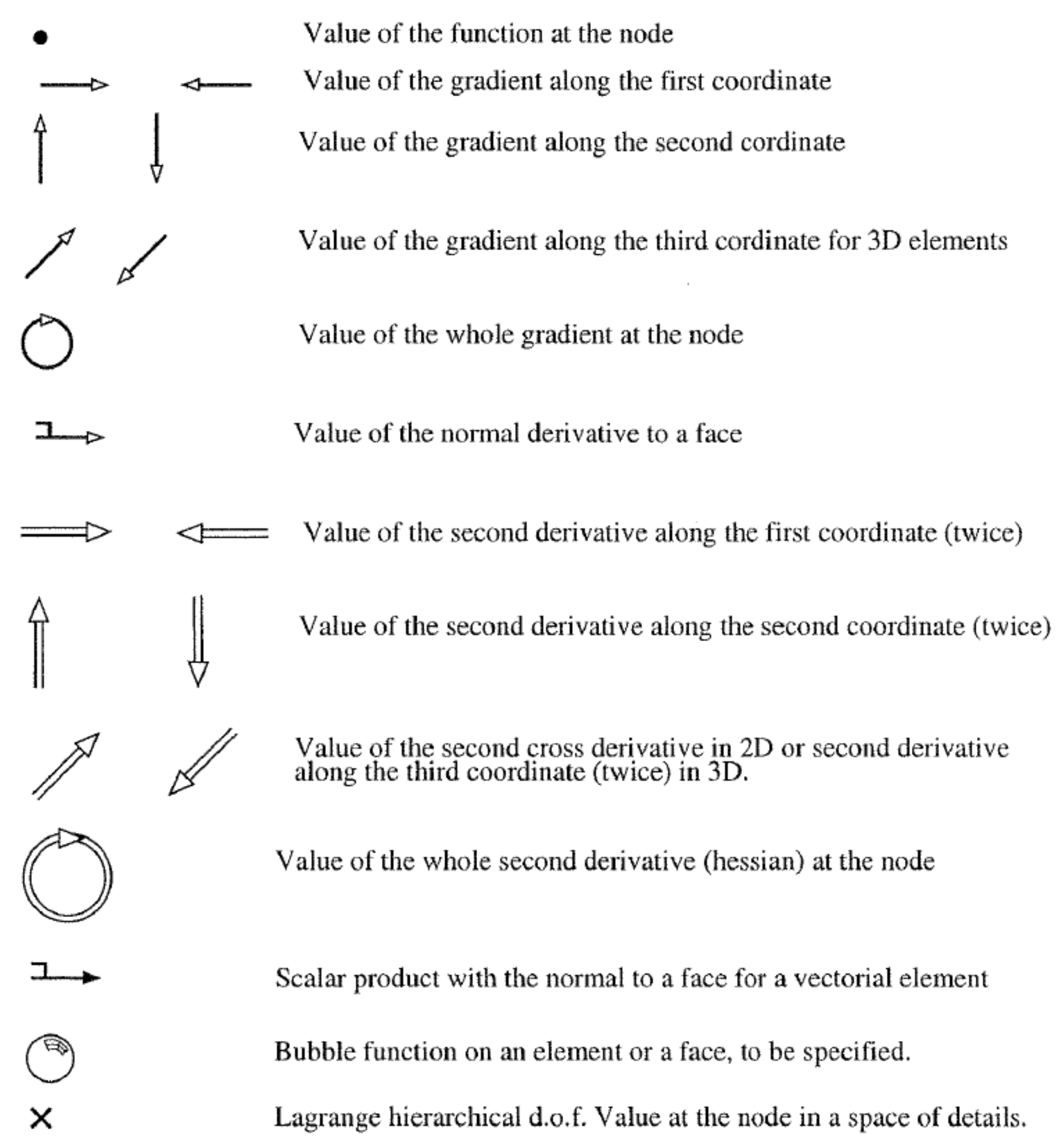
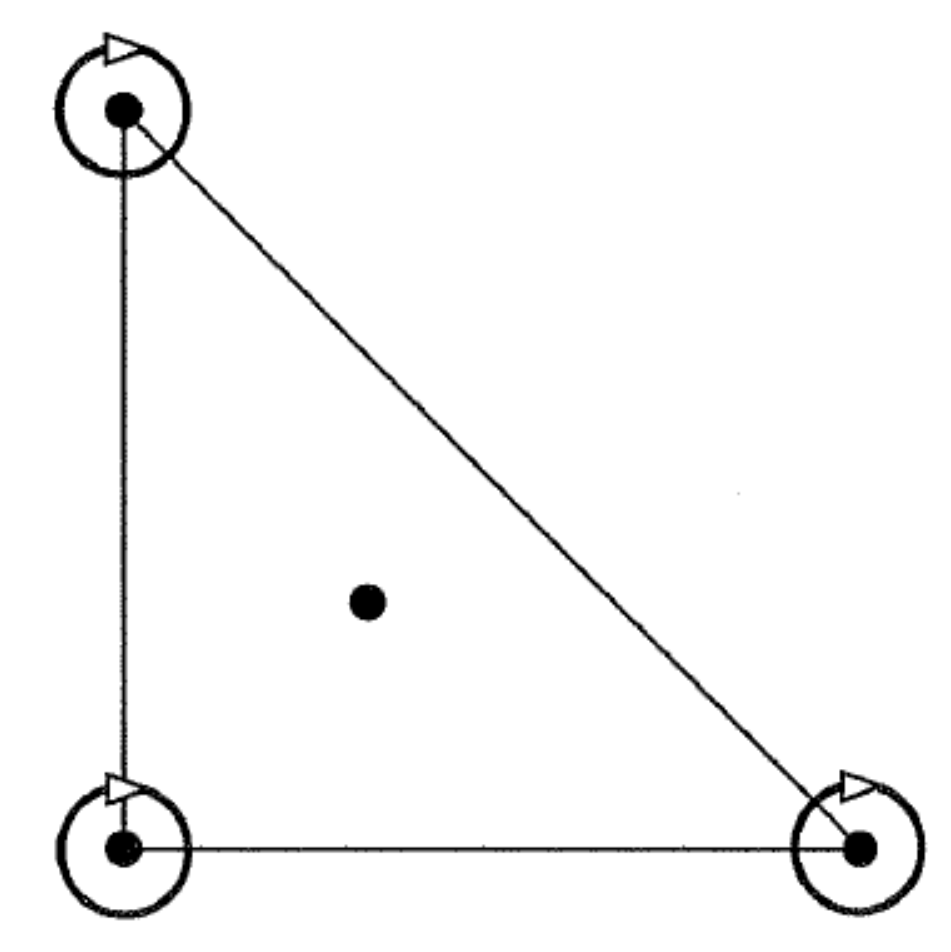
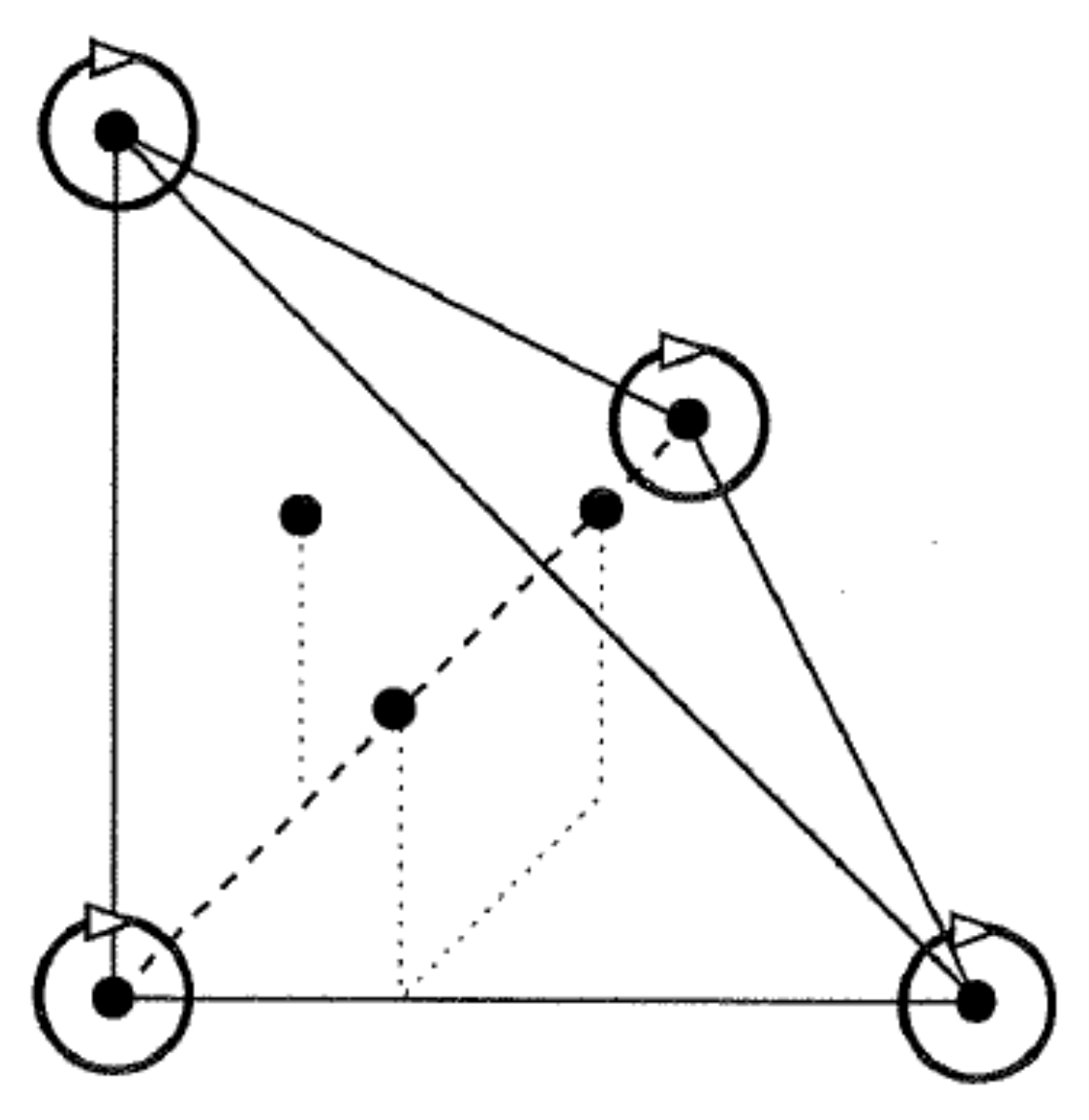
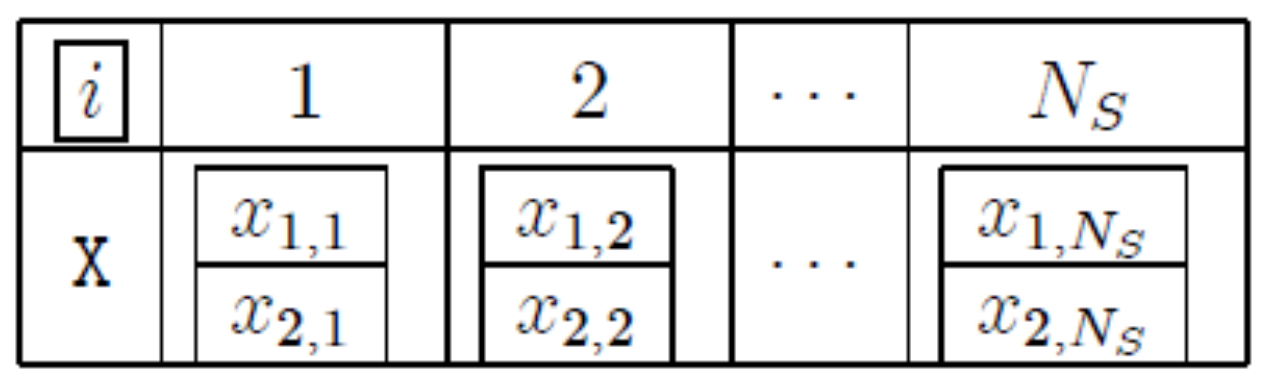
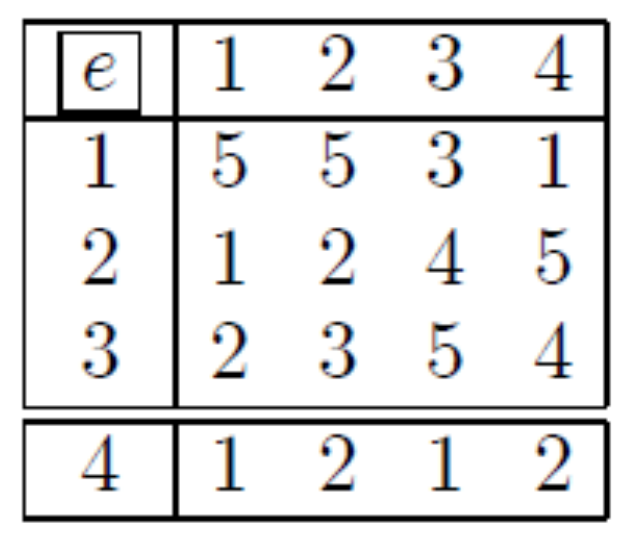
2.1.2. Graphical Codification of d.o.f
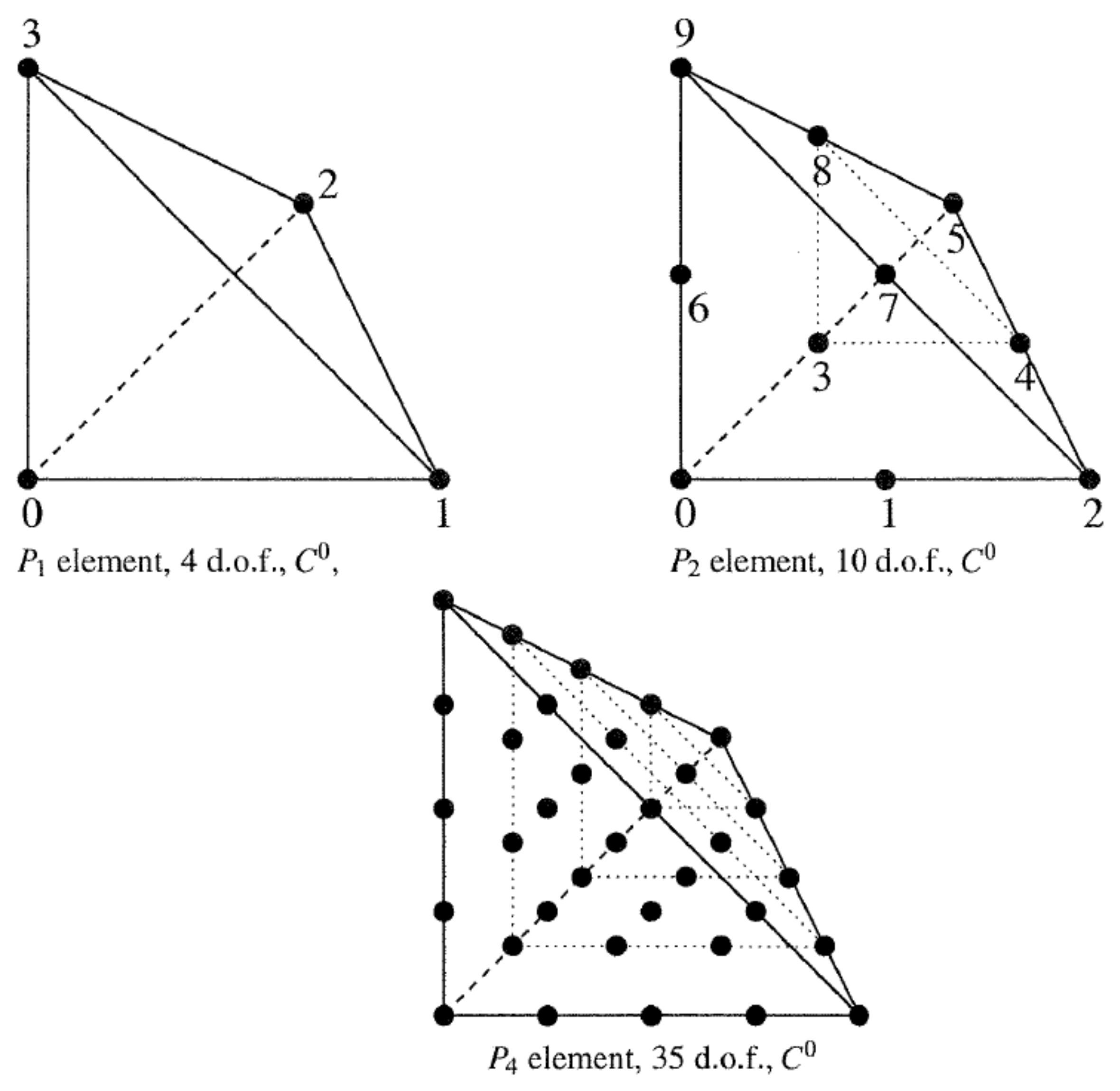
2.2. Classical Lagrange Elements on Simplifies
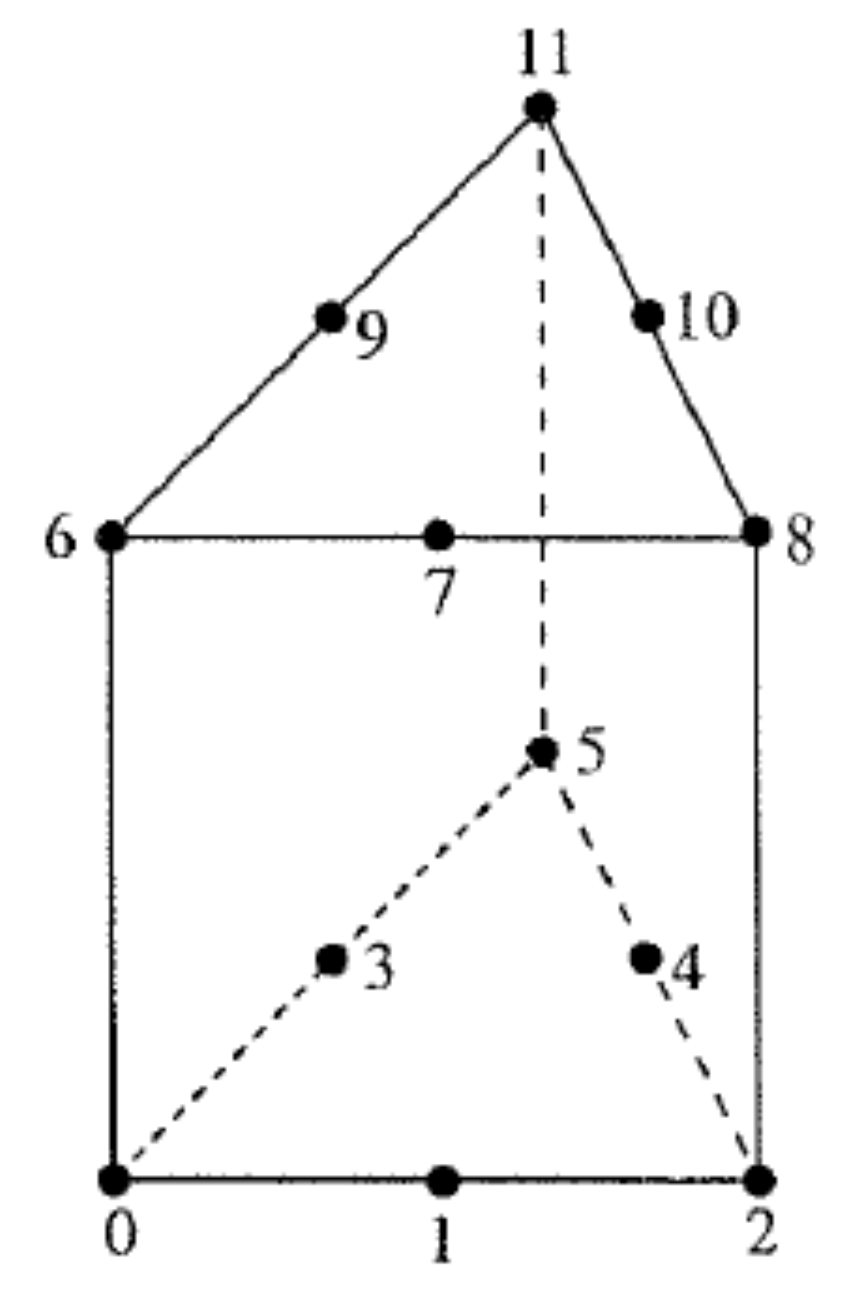
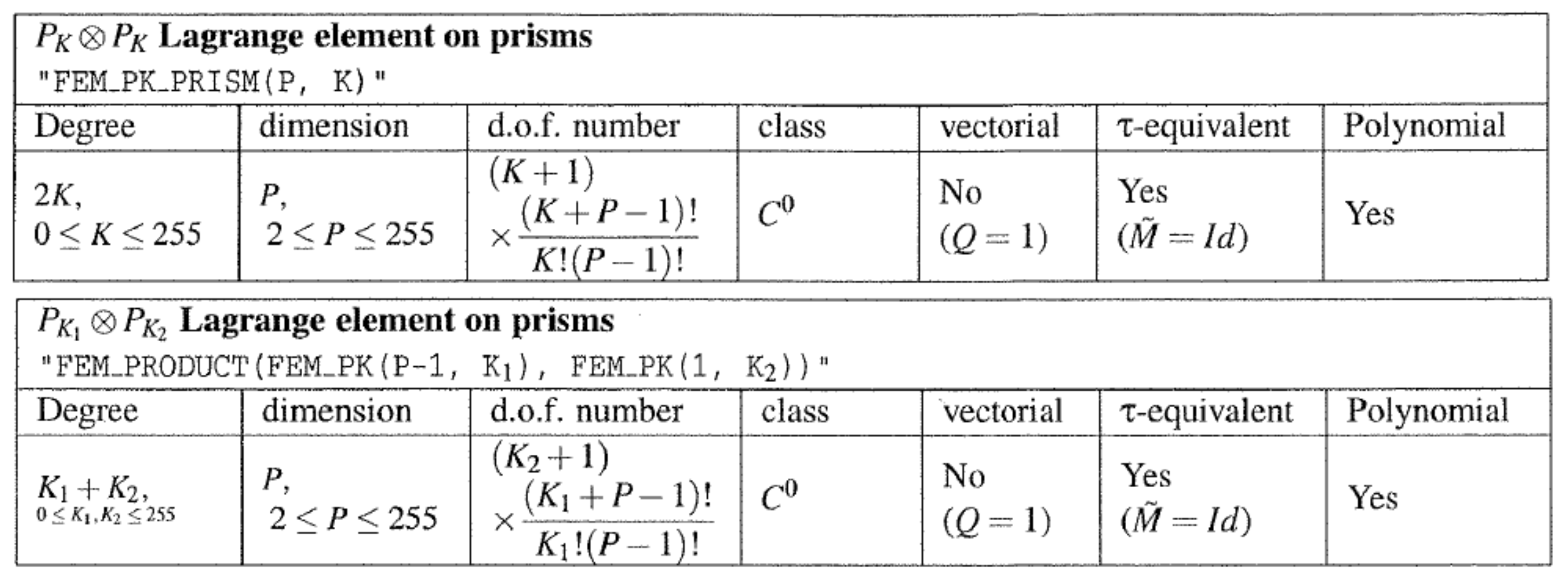
2.3. Other Geometries of Classical Lagrange
2.4. Elements with Hierarchical Basis
Hierarchical Elements with Respect to the Degree
2.5. Elements with Hierarchical Basis
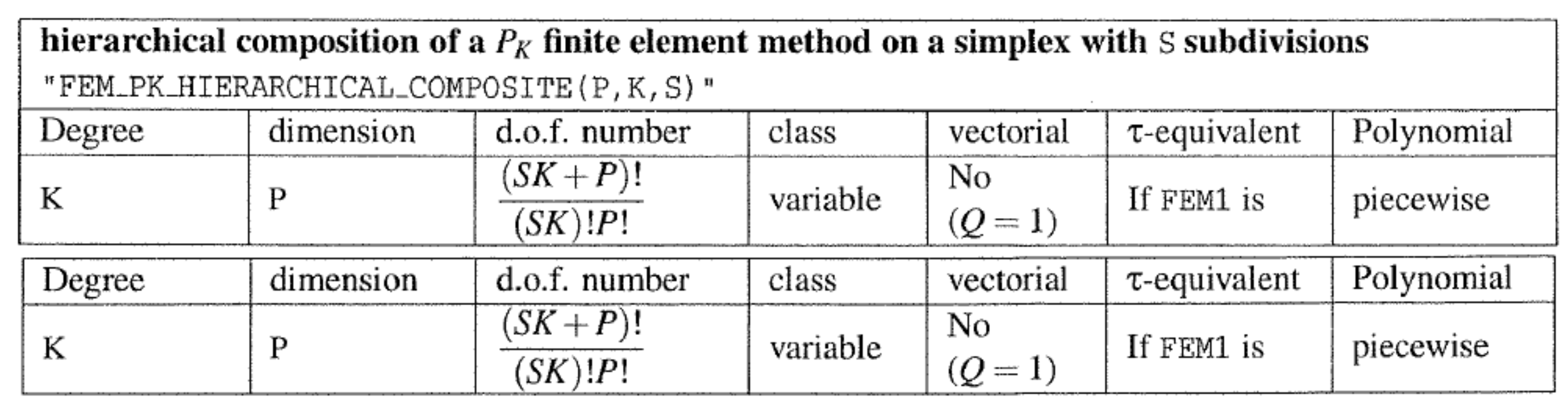
2.5.1. Composite Elements
2.5.2. Hierarchical Composite Elements
2.6. Specific Elements in Dimension 1
2.6.1. GaussLobatto Element
2.6.2. Hermite Element
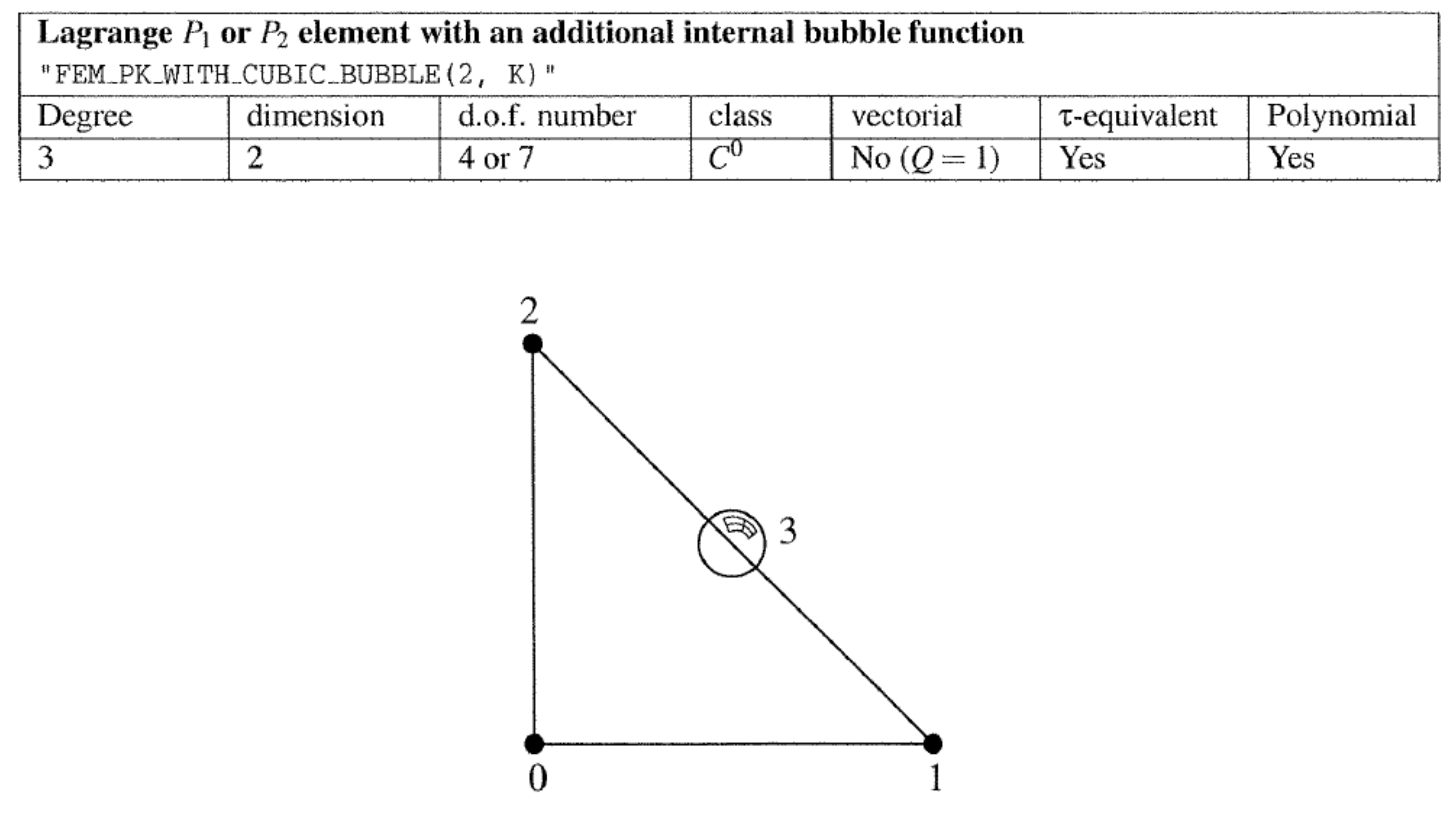
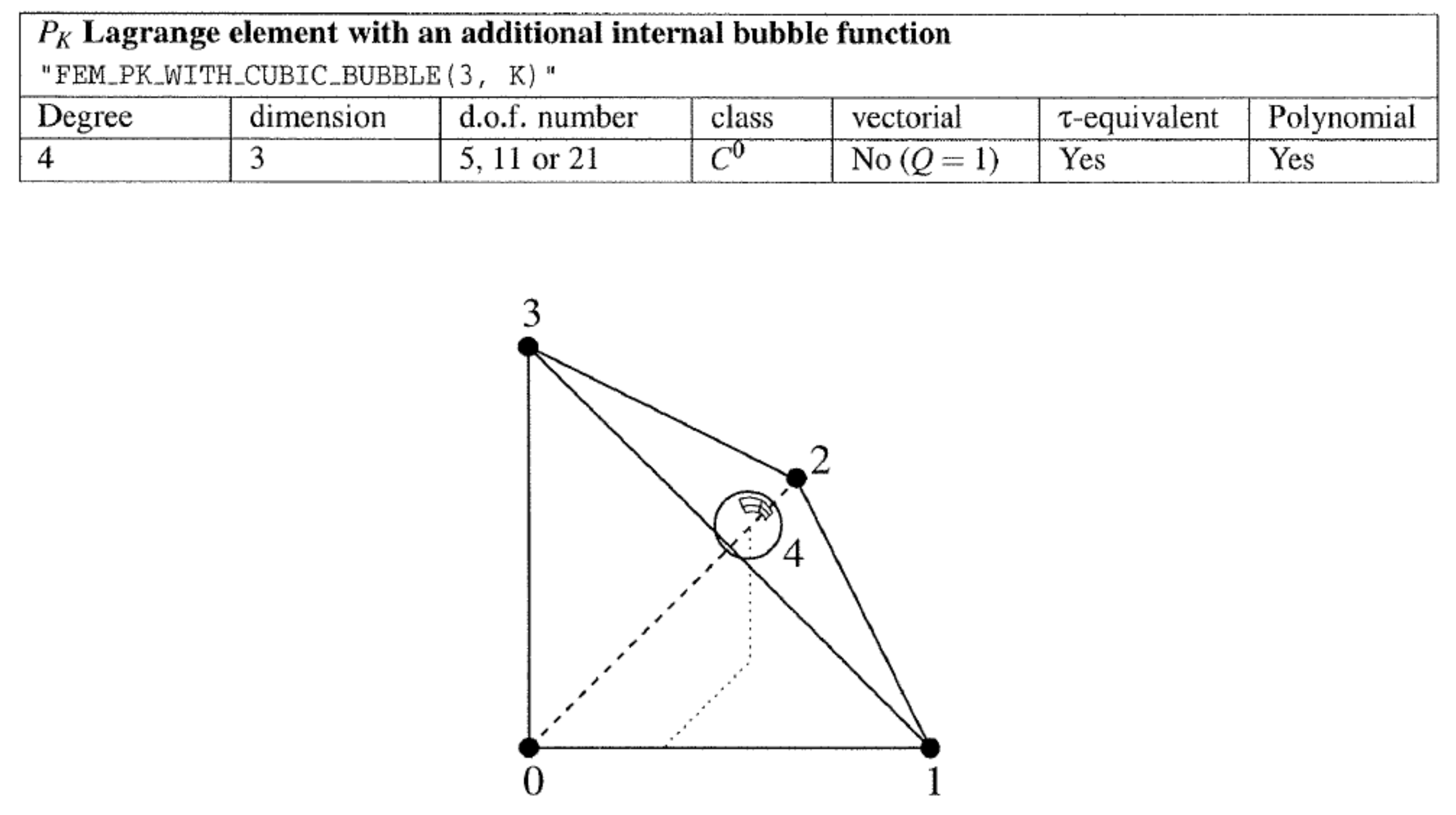
2.6.3. Lagrange Element with an Additional Bubble Function
2.7. Specific Elements in Dimension 2
2.7.1. Elements with Additional Bubble Functions
2.7.2. Non Conforming Element
2.7.3. Hermite Element
2.7.4. Argyric Element
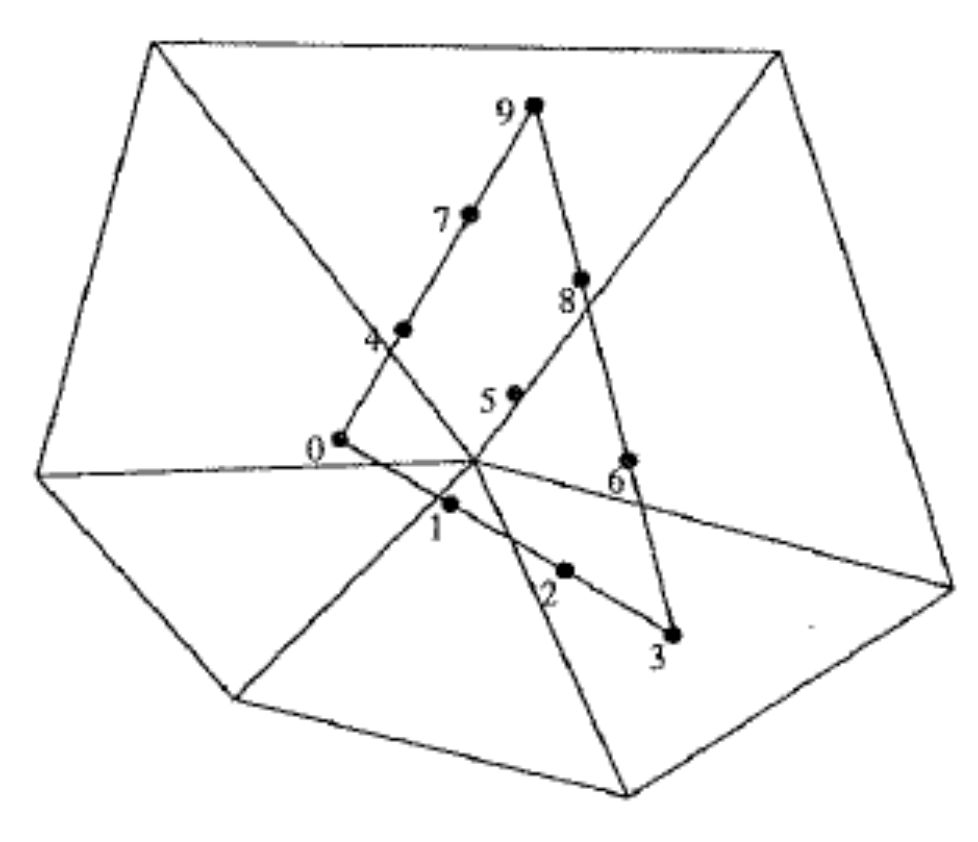
2.8. Specific Elements in Dimension 3
2.8.1. Elements with additional Bubble Functions
2.8.2. Hermite Element
2.9. Interpolation of Elements on Different Meshes
3. Integration Methods
3.1. Integration Methods Description
3.2. Exact Integration Methods
3.3. Newton Cotes Integration Methods
3.4. Gauss Integration Methods on Dimension 1
3.5. Gauss Integration Methods on Dimension 2
4. Implementation of the Finite Element Method
4.1. Data Structure of a Mesh
- The list of nodes
- The connectivity table
4.1.1. The List of Nodes
- number of nodes.
- The coordinates of each node .
4.1.2. Connectivity Table
- : number of elements.
- For each element is given: number of the node j of element e.
- Dimension 1For each elementFor the one-dimensional case, the connectivity table is implicit from the list of vertices. It is therefore useless to store.
- Dimension 2: For a mesh in triangles,: number of triangles.: ,
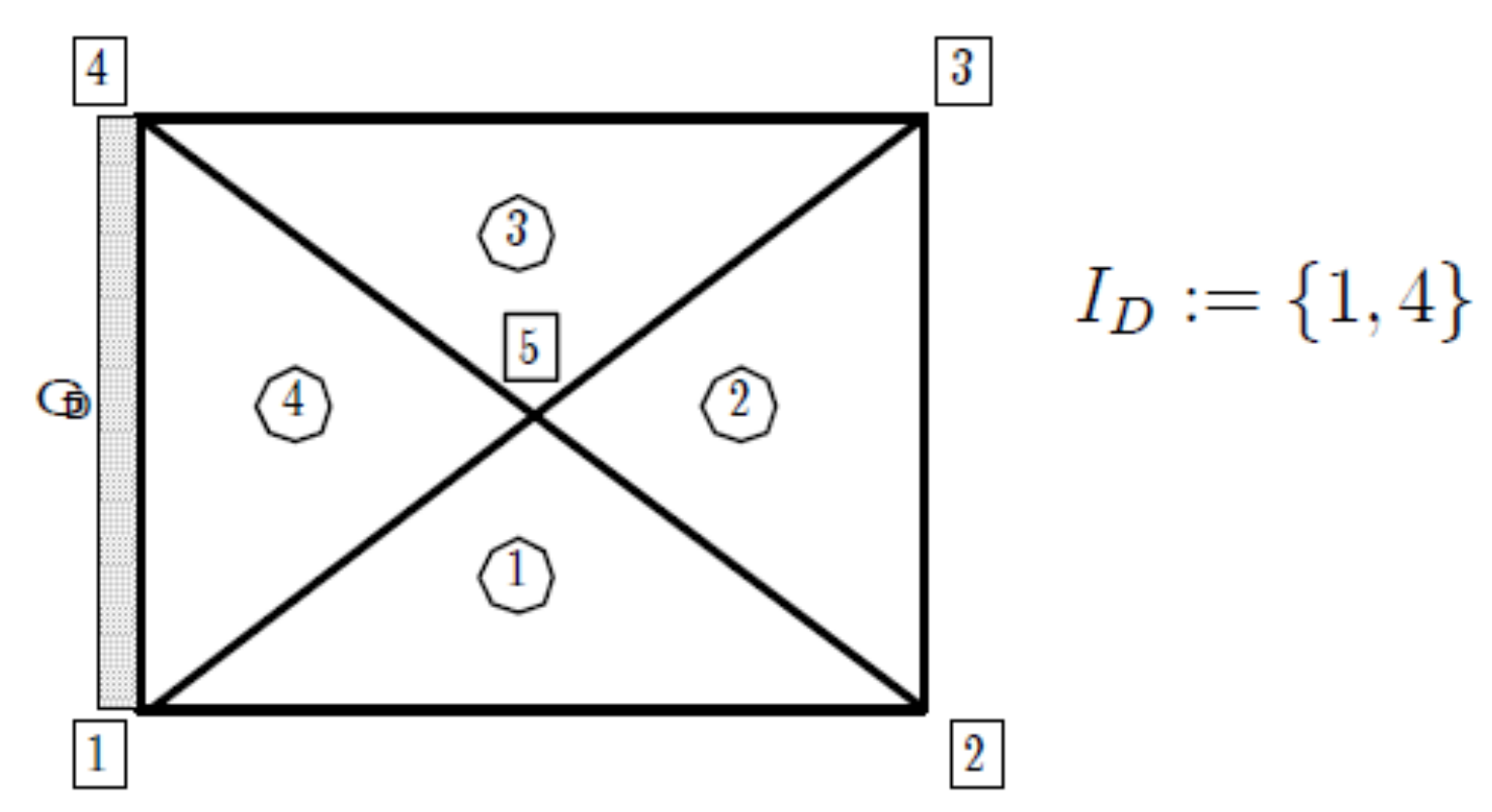
4.2. Meshing and Boundary Conditions
- Dimension 1 : , ,
- Dimension 2 :
- Without any restriction if
- Under the following angle condition if Ω is a polygonal domain of
4.3. Assembling
4.4. Elementary Matrices
- Elementary Stiffness Matrix
- Elementary Mass Matrix
- Elementary Volume Loading Matrix
- Elementary Stiffness Matrix Concentrated on the Edgewhere is a face (edge in two dimension) on and is the number of nodal values on , and are the respective restrictions of and on .
- Elementary Loading Matrix concentrated on the EdgeMatrices and forces concentrated in dimension are introduced at the initialization or the end of the assembling process.
4.5. Elementary Matrices in One Dimension
- Elementary stiffness matrixwhere is the element length. Then we havewhere is the mean value of the function on the elementthat we can approach by the trapezes formula or the middle point one
- Condensed mass matrixGenerally, it is sufficient to calculate the integral (4) in an approximate way by the method of trapezeswith , . This gives a diagonal matrix
- Elementary loading MatrixHere again we can use the trapeze formula to approximate the integral (5)with , . This gives the elementary matrix
- Matrices concentrated on the edgeIt is here matrices with a single non-zero coefficient which are given directly fromby
4.6. Elementary Matrices in Dimension Two
- Elementary stiffness matrixThe following method of determining the elementary matrix is in fact general. She can be used for the determination of any elementary matrix and in the framework of any finite element method. We have by definitionThen if we denote by the mean value of onWe now express and using their polynomial coefficients and a matrix writingWe can then calculateWe then use the relation which makes it possible to connect the polynomial coefficients with the nodal valueswhich can be written in matrix formwhereand likewiseTo express the polynomial coefficients using the nodal values, we calculate the inverse .This inversion is in fact the determination of the basic functions on the element of the finite element. As can be seen, this determination can be made (for this element and for any finite element) in a completely implicit way by programming.Using all previous relationships, we getHence we obtain the elementary stiffness matrix by a simple calculationThe mean value of can be obtained by an approximate integration formula as in dimension onewhere is the value pf at vertix , and value of at the center of gravity of .
- Stiffness Matrix concentrated on the edgeWe usually have the data provided by the mesh (otherwise we can build by programming) from the list of edges on the border, each with a reference number that allows you, among other things, to know if the edge is contained in or does not cover . We can therefore assume that we have the following data: number of edges on the borderAnd for each edge .: number of the first vertex: number of the second vertexthus, We can traverse the edges and calculate the elementary matrix giving the contribution to stiffness concentrated onwhere . If we approach this integral by the trapeze formula, we getwhere is the edge length and , .
- Condensed mass matrix.The condensed mass matrix without using the matrix and by using the integration formula approached from the verticeswhere , , are values of on the vertices of , we have then:The fact that the conditional mass matrix is ​​diagonal will be decisive in some solving problems in dynamics, that is to say, depending also on the time t.
- Elementary loading MatrixWe have the same as for the elementary loading Matrix of volume in dimension onewith , .The elementary loading matrix concentrated on the edge is given in the same way bywith , .
- Assembling. The total stiffness matrix is defined byUsing the decomposition of the integral onand the definition (3) of the elementary stiffness matrix, we obtain the following relation between the total stiffness matrix and the elementary stiffness matricesWe then identify the coefficient of in both members of this realation to getConsequences:This last formula summarizes the assembling process. it has several consequences.
- A coefficient is null if and are not the vertices of a same element. In other words, degrees of freedom and are not coupled (i.e., or the equation relating to depends on the unknown ) only if and belong to the same element.
- To form , simply browse the elements by adding successively the contribution of each elementary matrix to the total matrix with , .
5. Time Dependent Problems
5.1. Evolution Problems Models
5.1.1. Model Problems
- Parabolic problemwhere is the initial data of the problem.
- Hyperbolic problemwhere now the problem requires two initial data and .
5.1.2. Variational Formulation
5.2. Semi-Discretization in Space
5.2.1. Finite Element Method
- In segments if is a segment,
- In triangles if is a polygonal domain of the plane,
- in tetrahedrons if is a polyhedral domain of space.
5.2.2. Reduction to a Differential System
5.2.3. Matrix Properties of the Differential System
5.3. Time Diagrams
5.3.1. -Scheme for the Parabolic Equations
5.3.2. Neumark Scheme
- Order two approximation of the second derivative by a derivation in the sense of centered finite differences
- Order two approximation for the second member to improve stability propertiesThen we get the schemewithWe need two initial data: and , we havelet calculate using Taylor development of order 2we haveBy going back to (16), we can calculate
5.4. Modal Analysis
5.4.1. Resolution of a Differential System by Diagonalization
- System of order 1
- System of order 2withif
5.4.2. Problem with Generalized Eigenvalues
5.4.3. Modal Resolution
6. Application
6.1. Obtaining Initial Data
- The experimental setup are based on the the weather data on 7–10 March 2017. Temperature measurements are taken in in agricultural ground soil at and 50 cm levels, where the maximum and minimum values of the temperature are recorded.
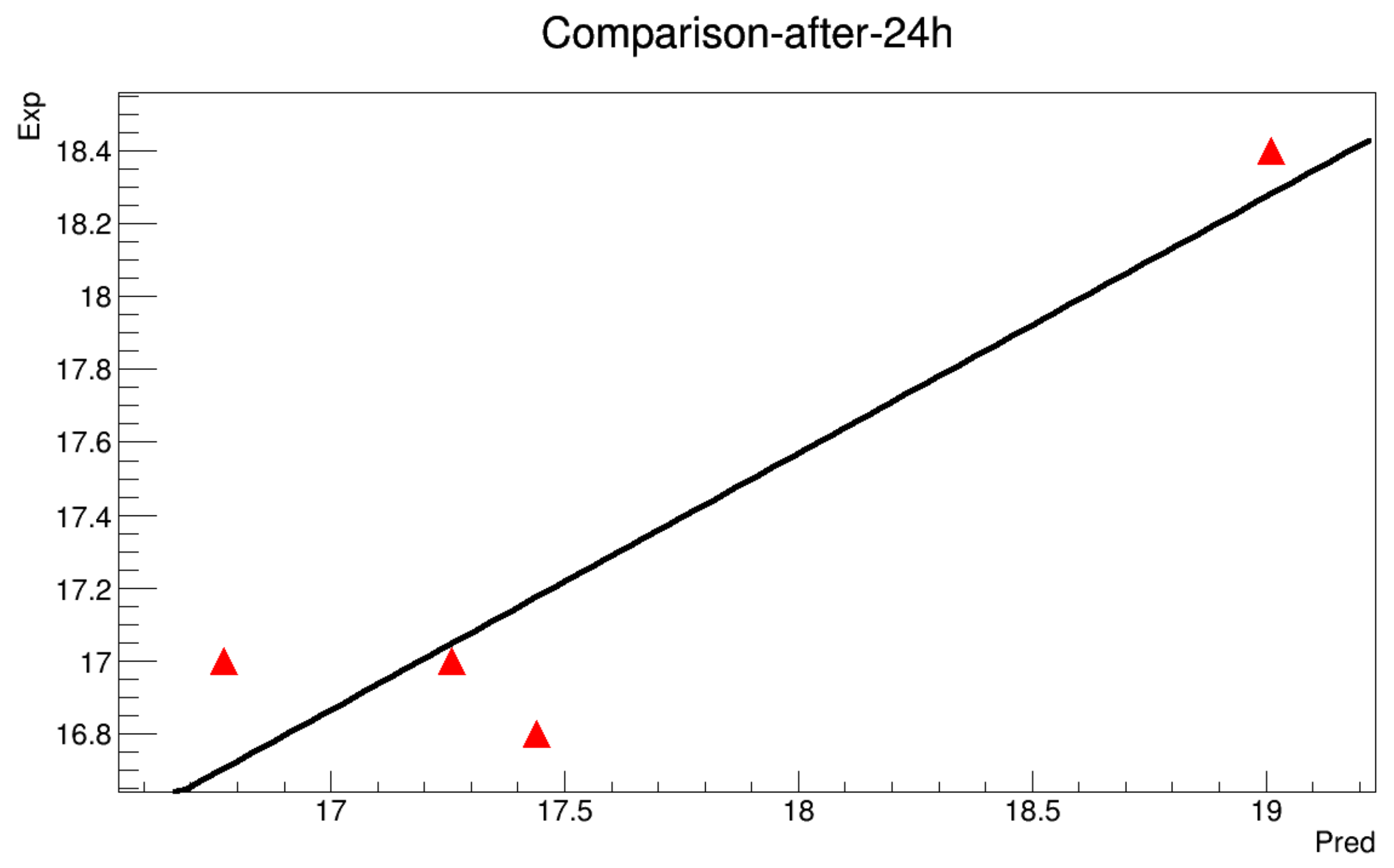
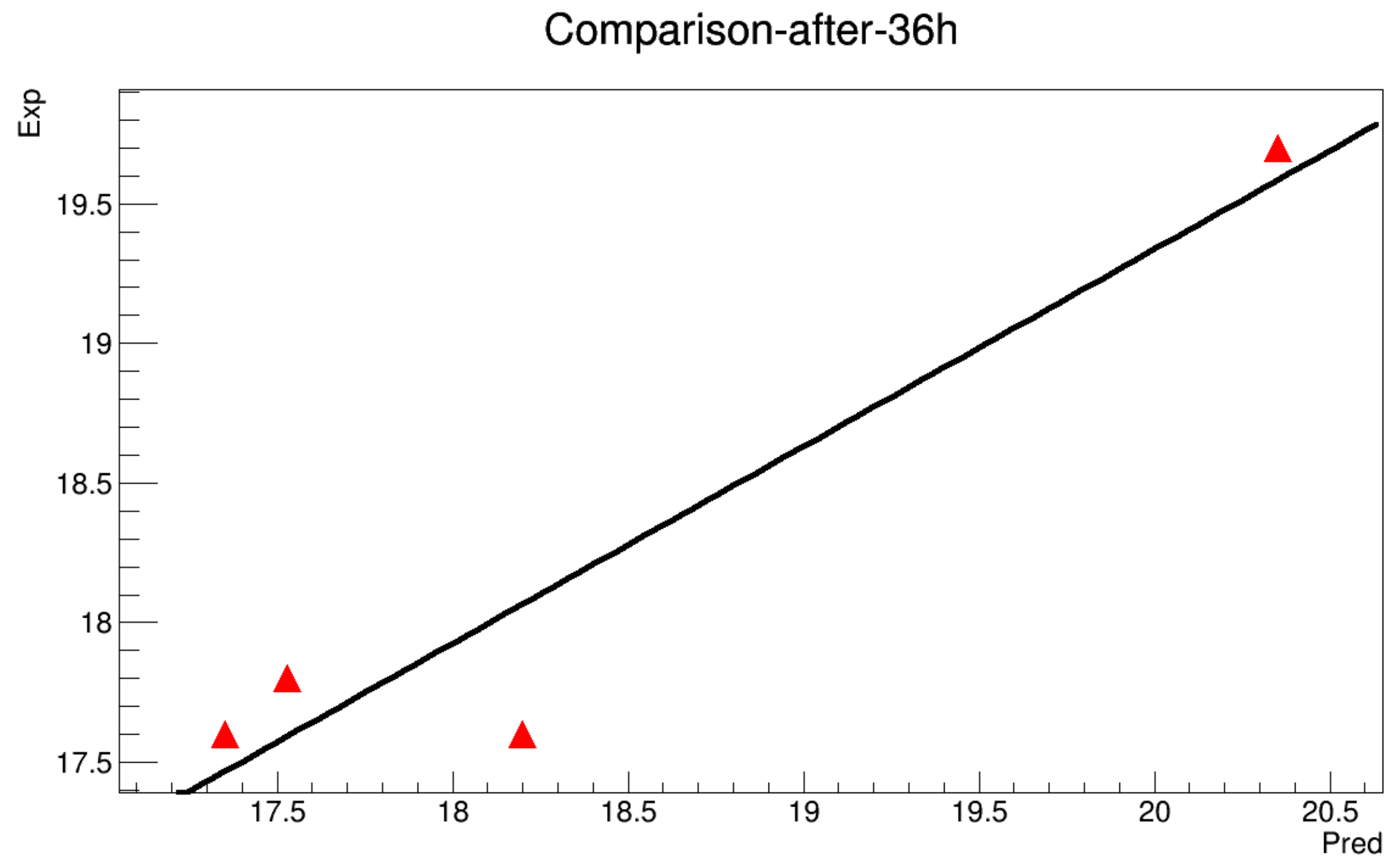
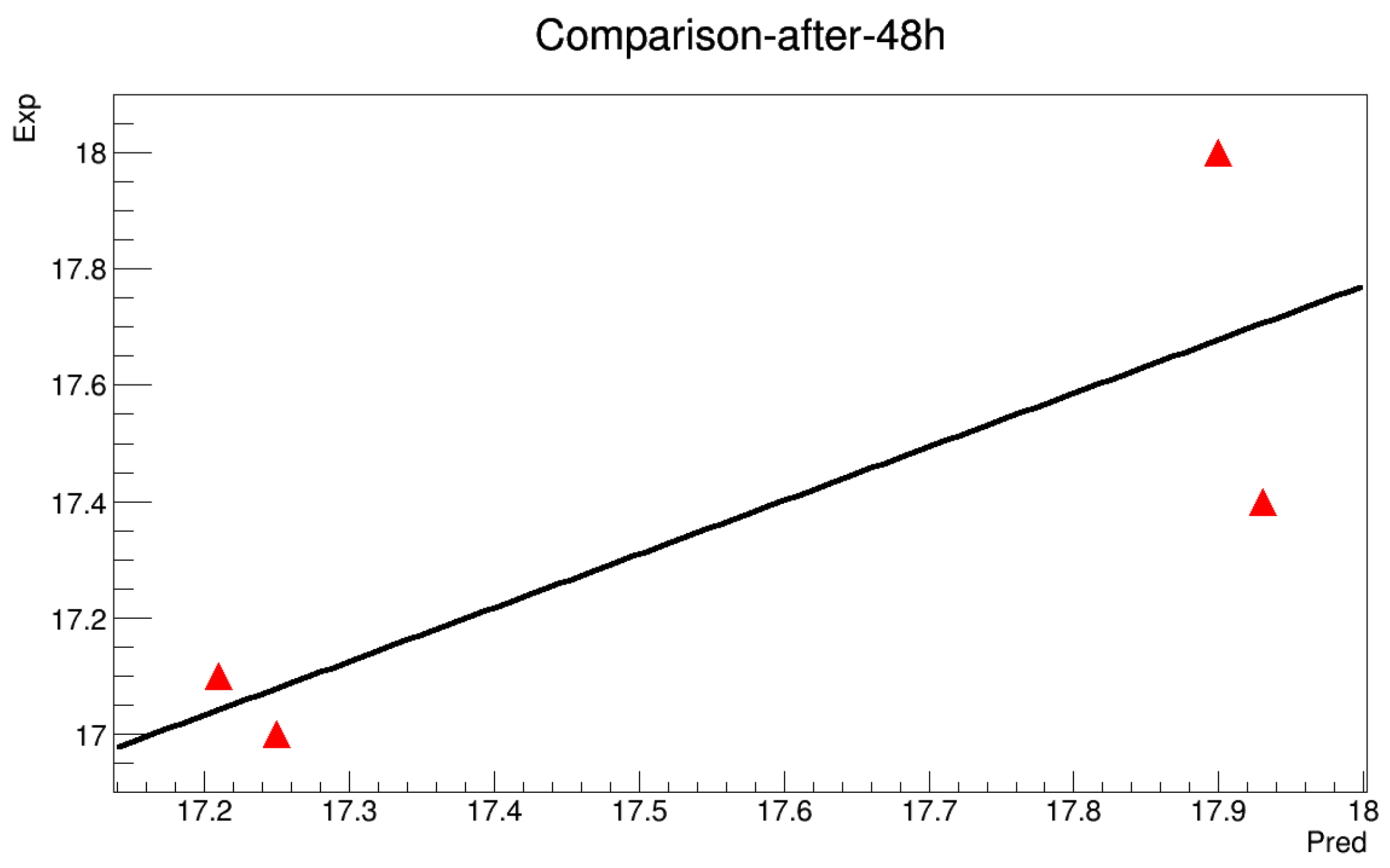
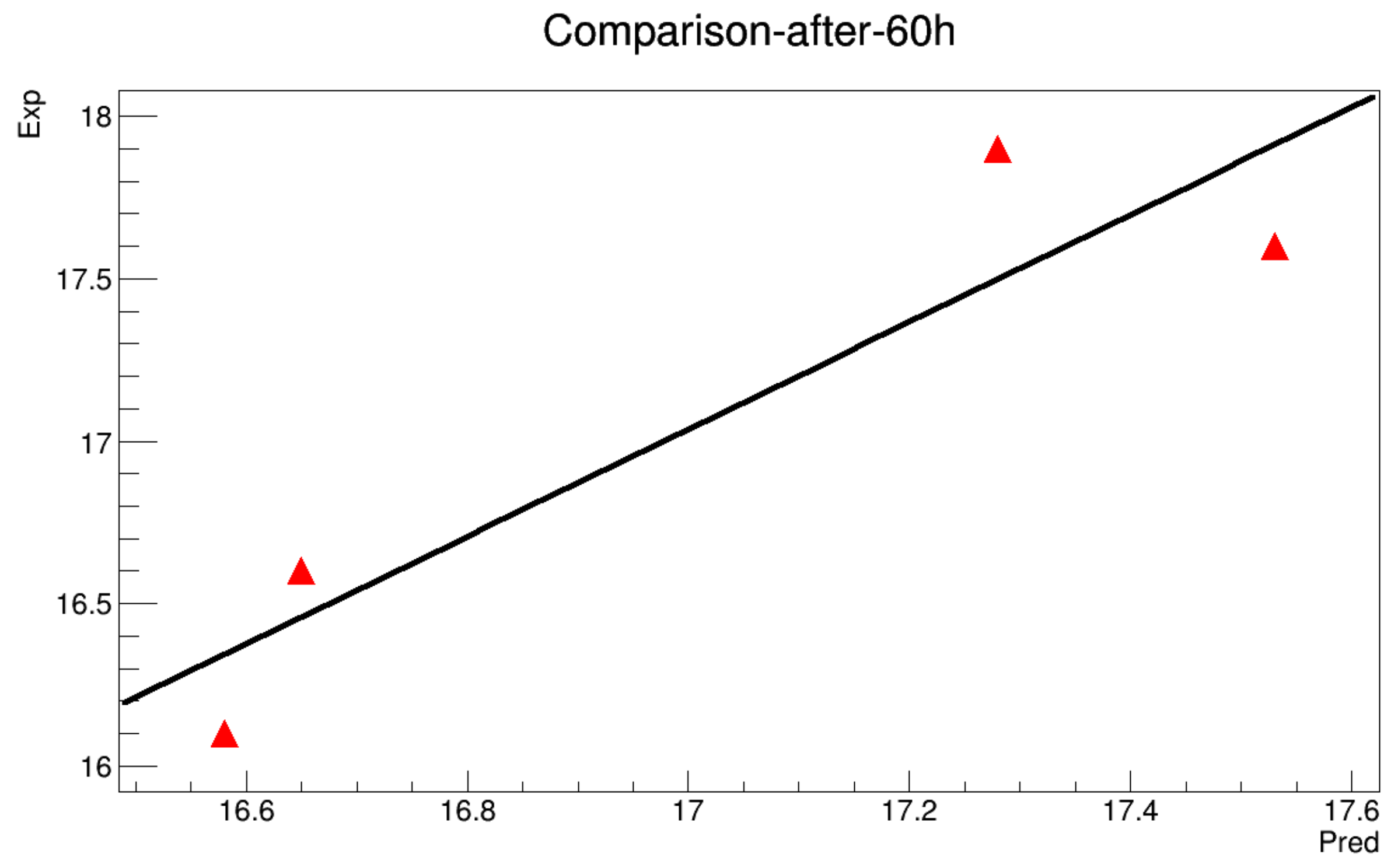
- It’s known that for any numerical prediction model, the data at the boundaries of the domain are indispensable. Hence, the boundary designating the ground temperature is determined for each 10 min through a linear interpolation along the minimum and the maximum values for a given day, while the boundary is determined by referring to a previous work presented in [21]. The heat storage along the soil depth almost deals with the upper 60 cm layer. However, the experimental data show a deeper dependence of the temperature, i.e., depths exceeding 60 cm seem to be sensitive to climatic variations.It ’s possible to estimate the temperature at 60 cm depth in the soil by studying the variation of the thermal gradient (the experimental data at 60 cm depth is not available) and considered to be a constant value for the whole experiment during 24 h (such an assumption is validated in a previous work), and the results are shown in Figure A1.
- Taking and cm .
- The model will be run to get a value each 10 min along 12 h. The obtained results are then compared with the real data in order to estimate the mean squared error.
- There are two modes of calculations: The first one so-called with initialization, means that the model can be turned while the data is initialized at 6 h, 12 h and 18 h. The second mode is called without initialization, where the model is executed for the whole deadline without any reset of the data.
6.2. Realistic Experience
6.2.1. Without Initialization
6.2.2. With Initialization
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Without Initialization
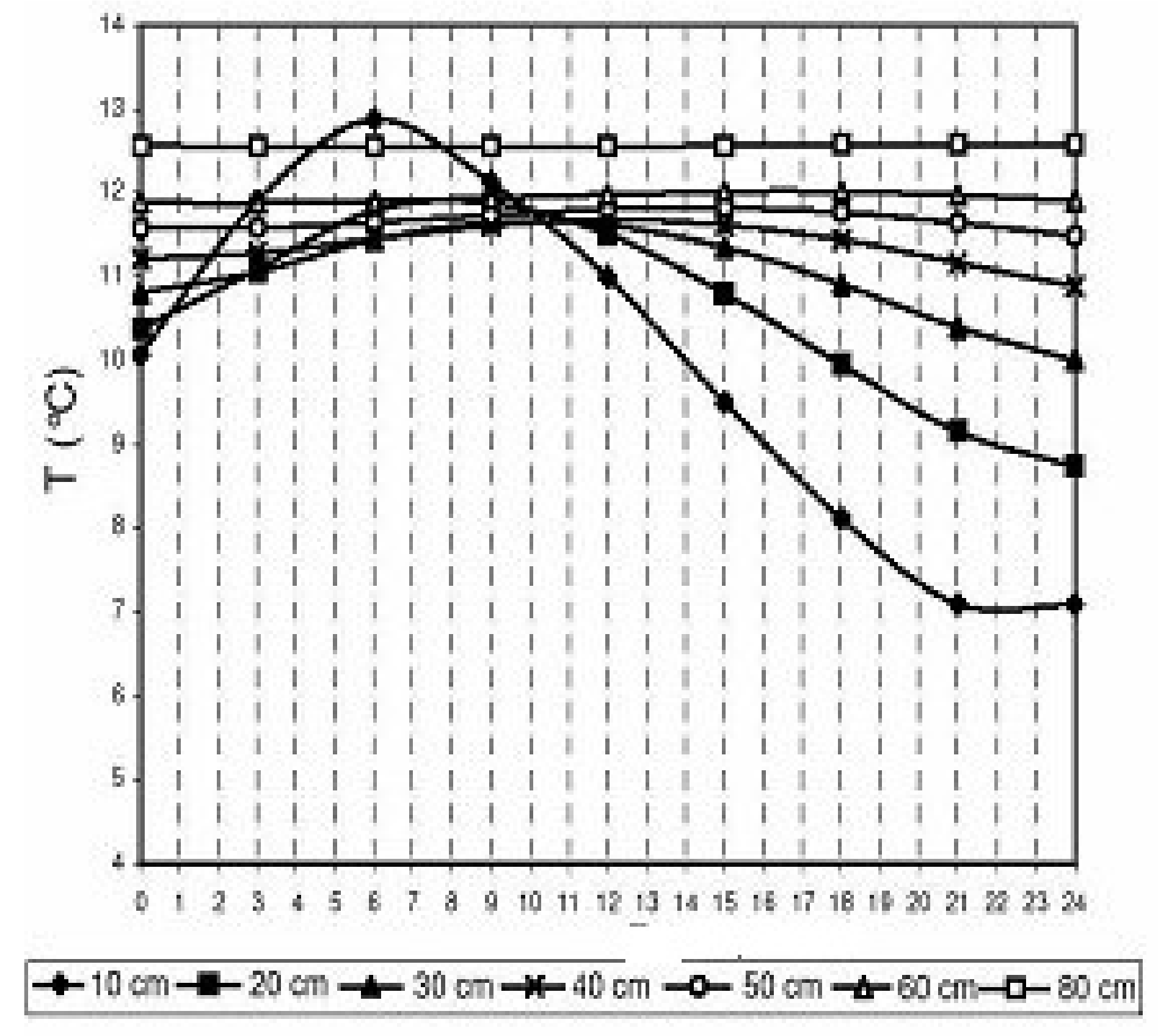
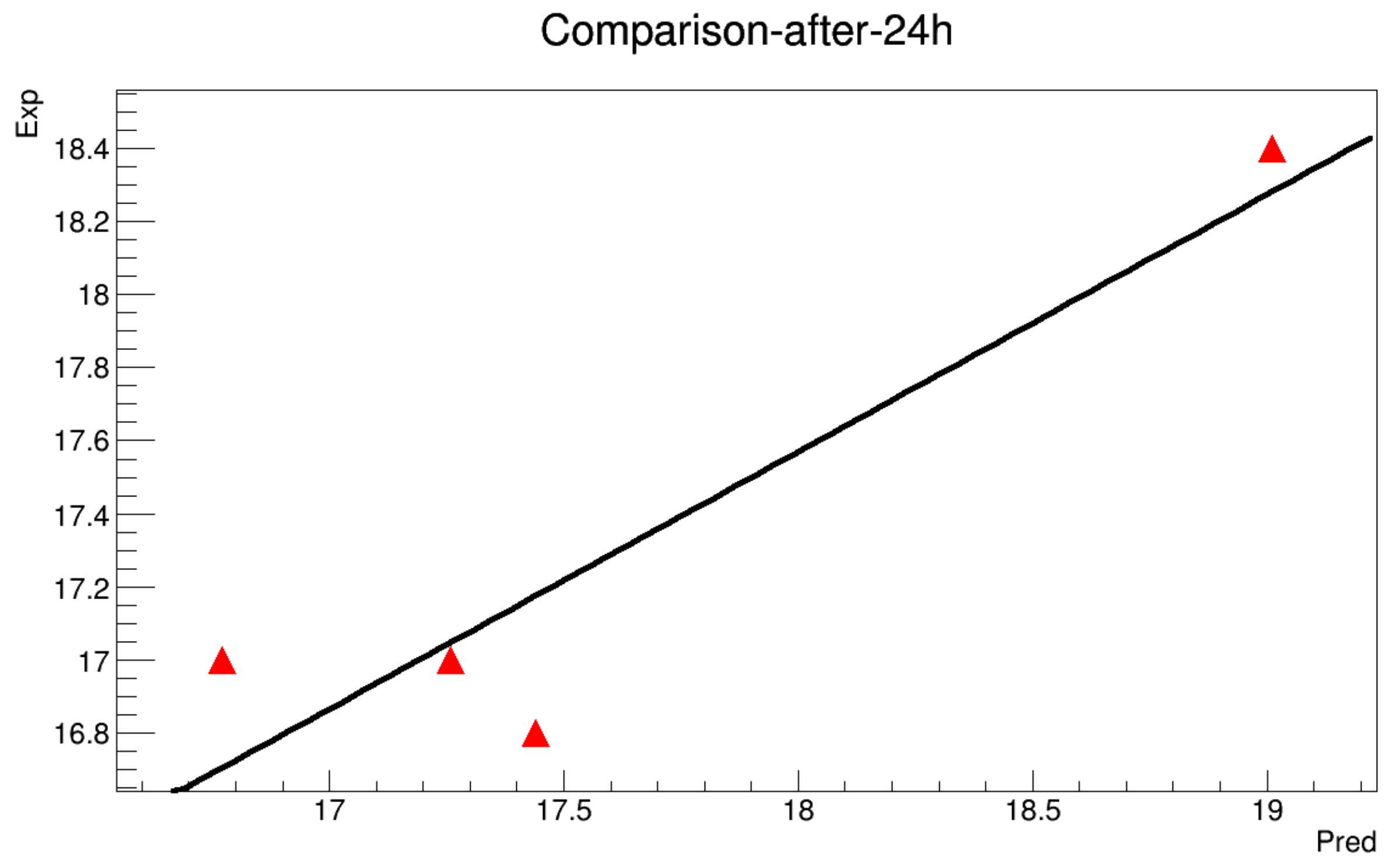

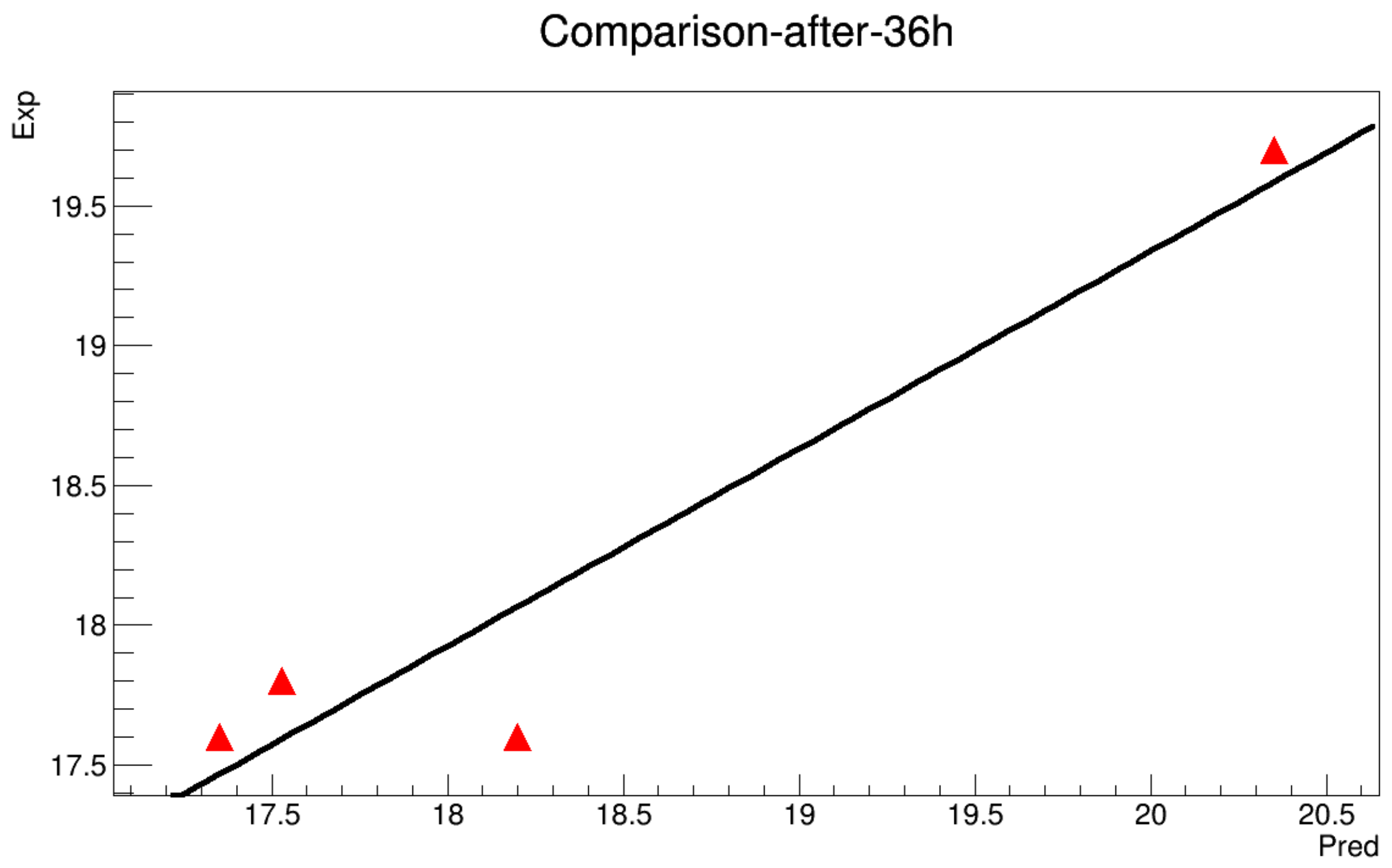
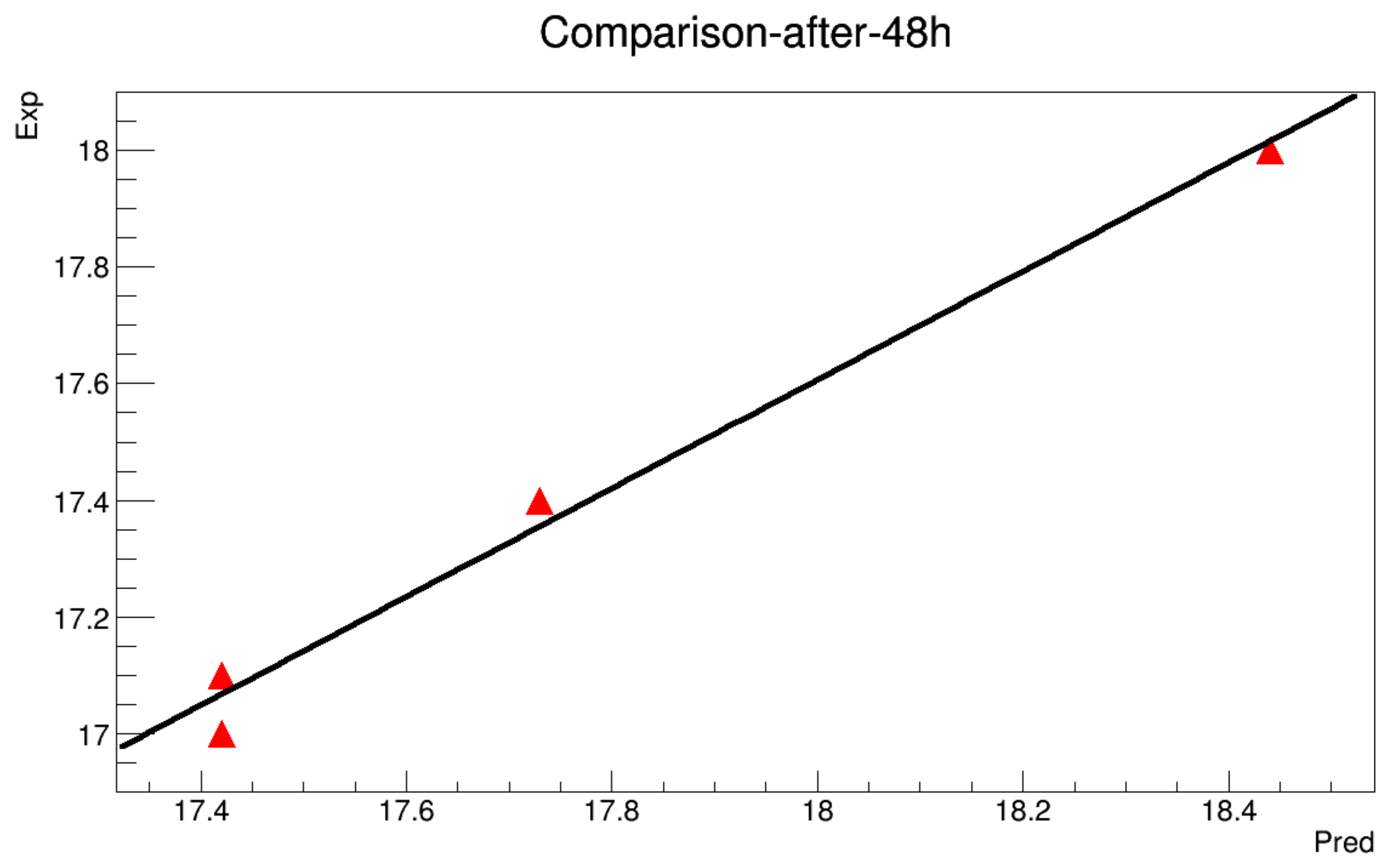
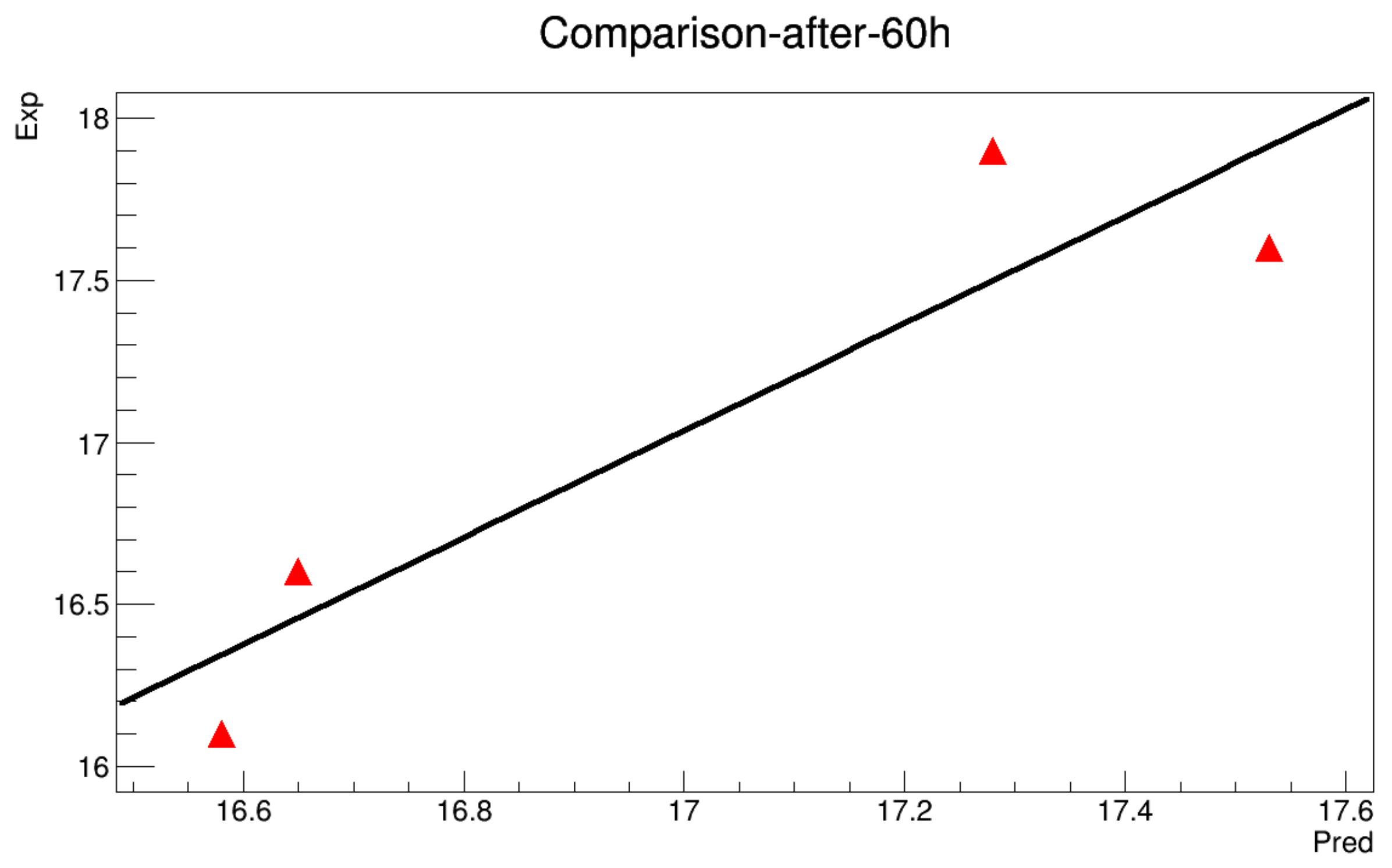
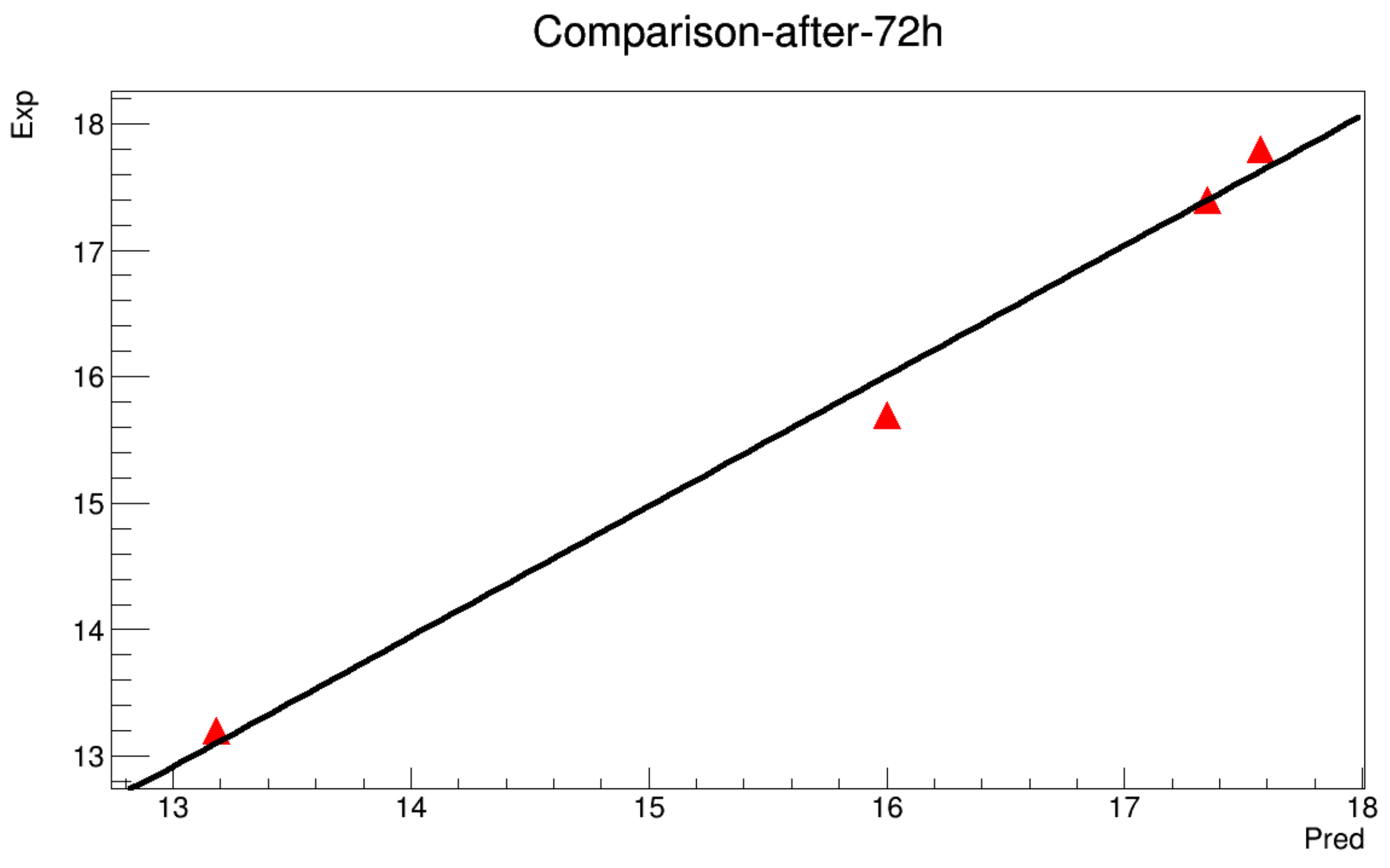

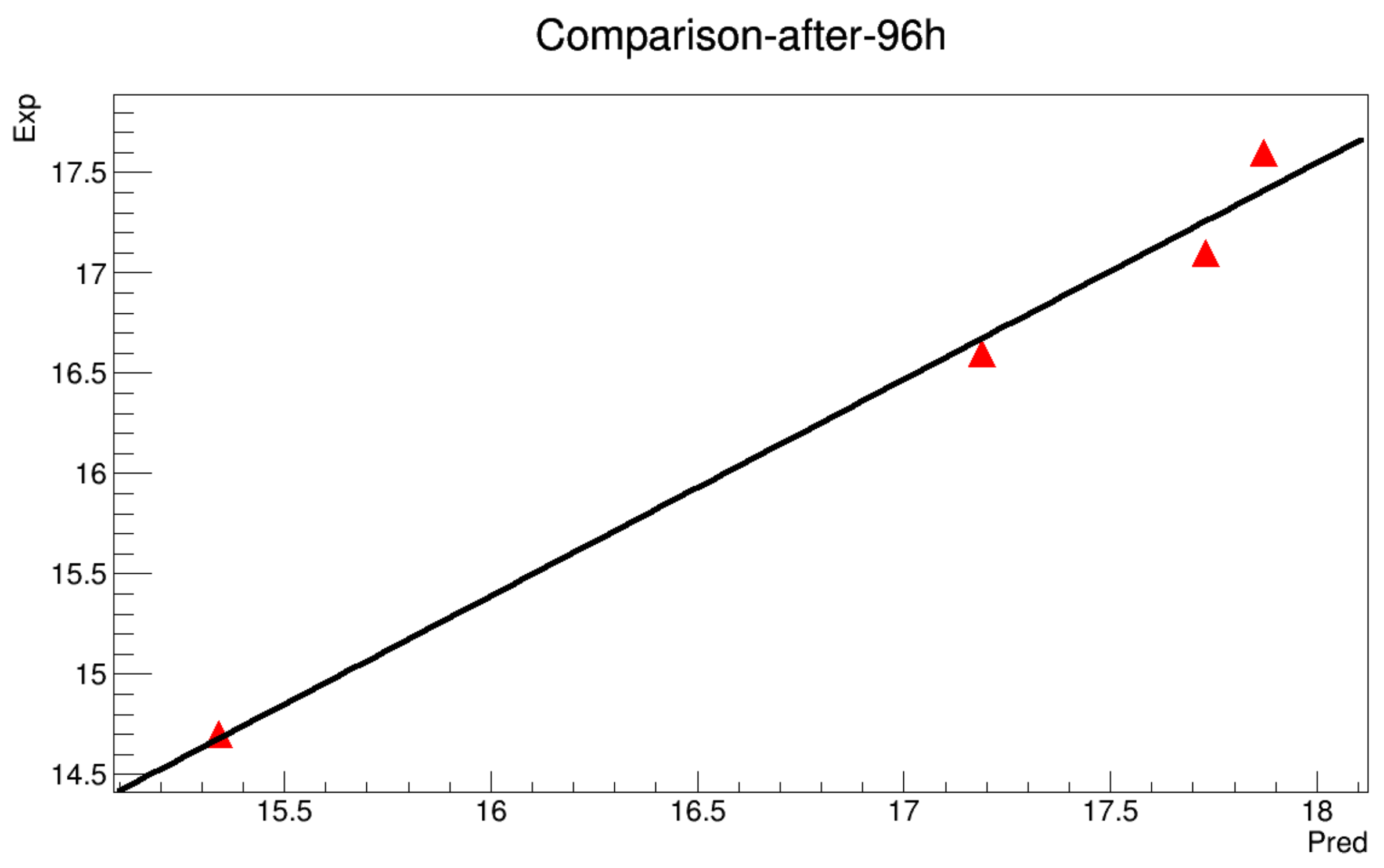

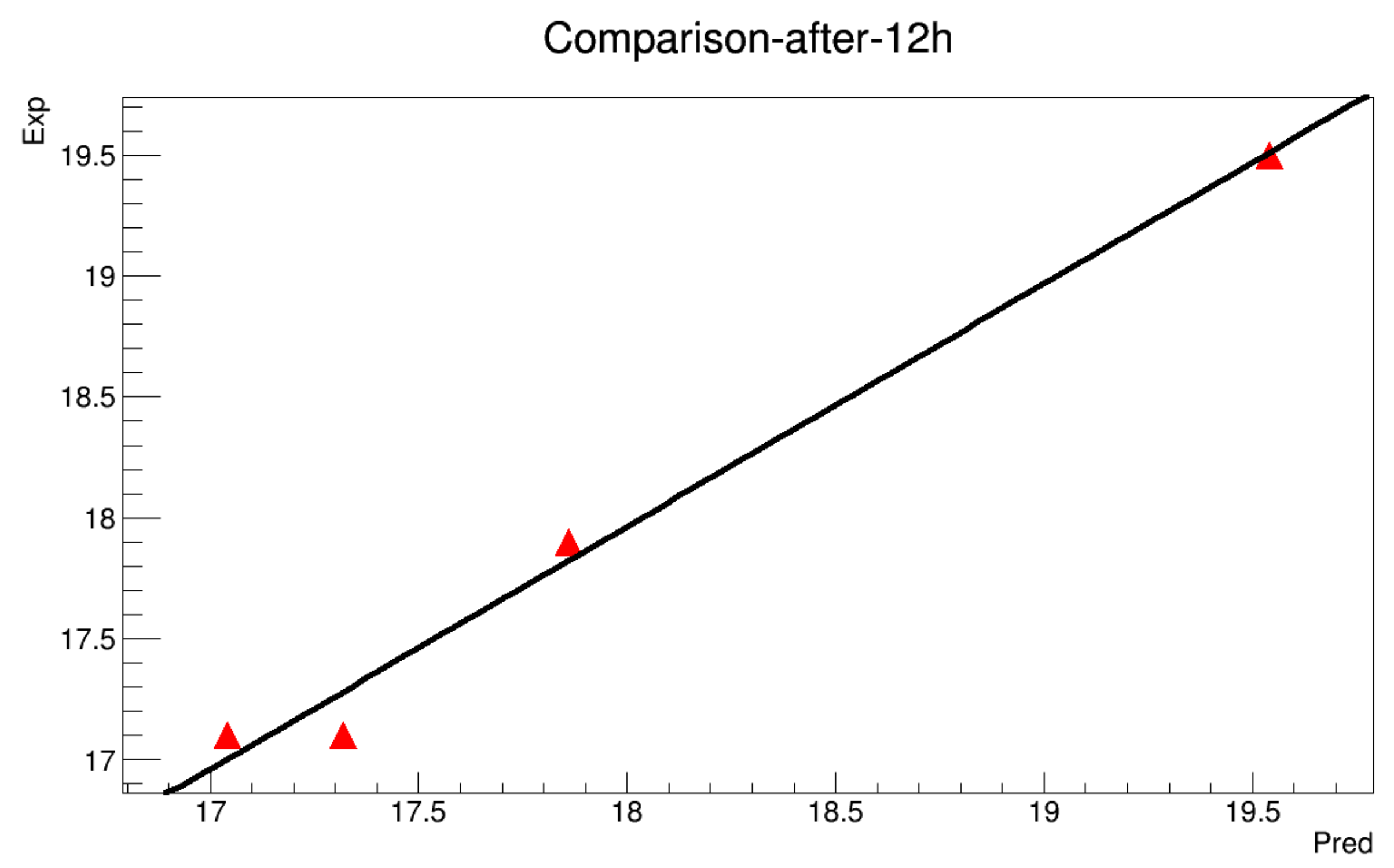
Appendix A.2. With Initialization
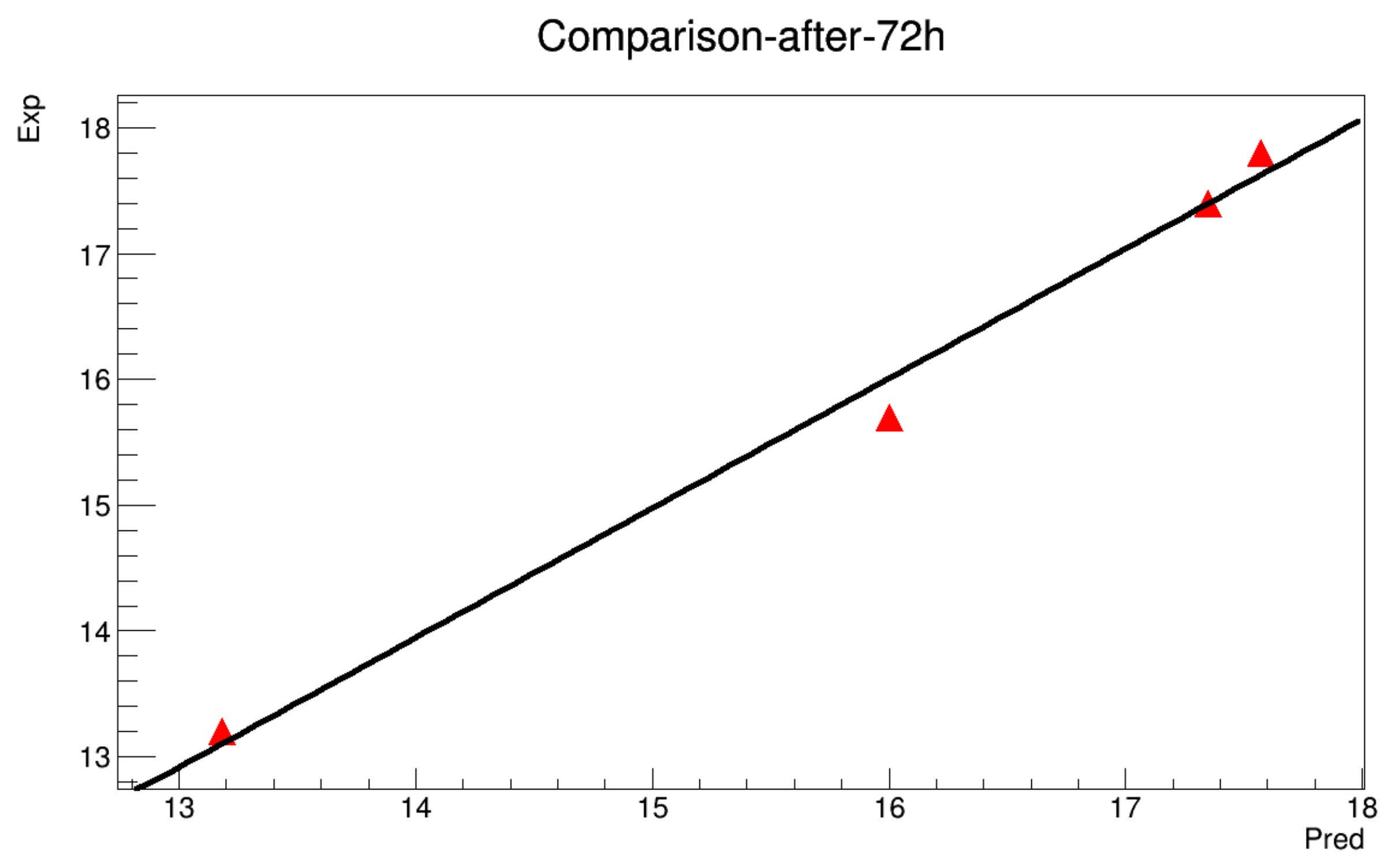
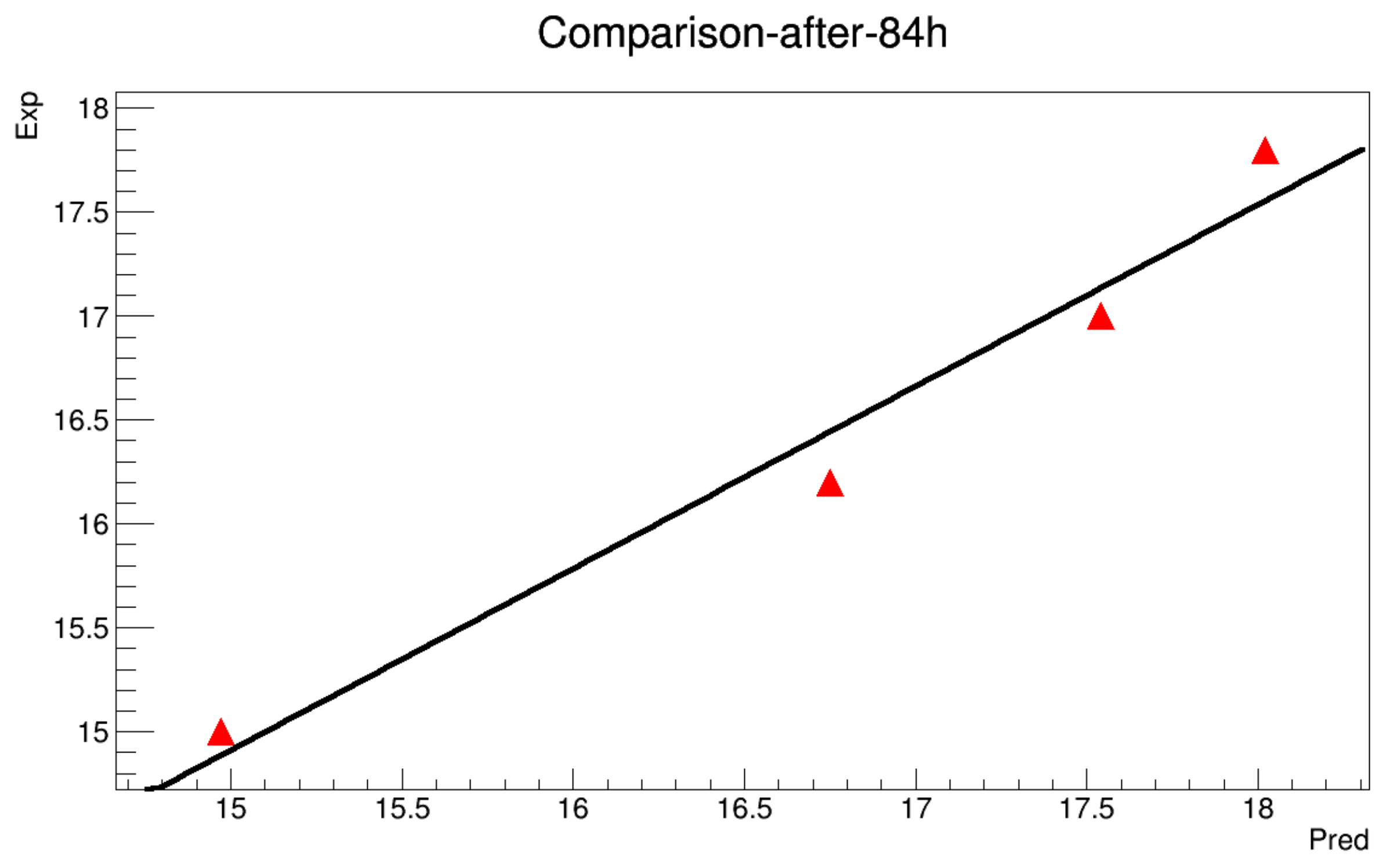
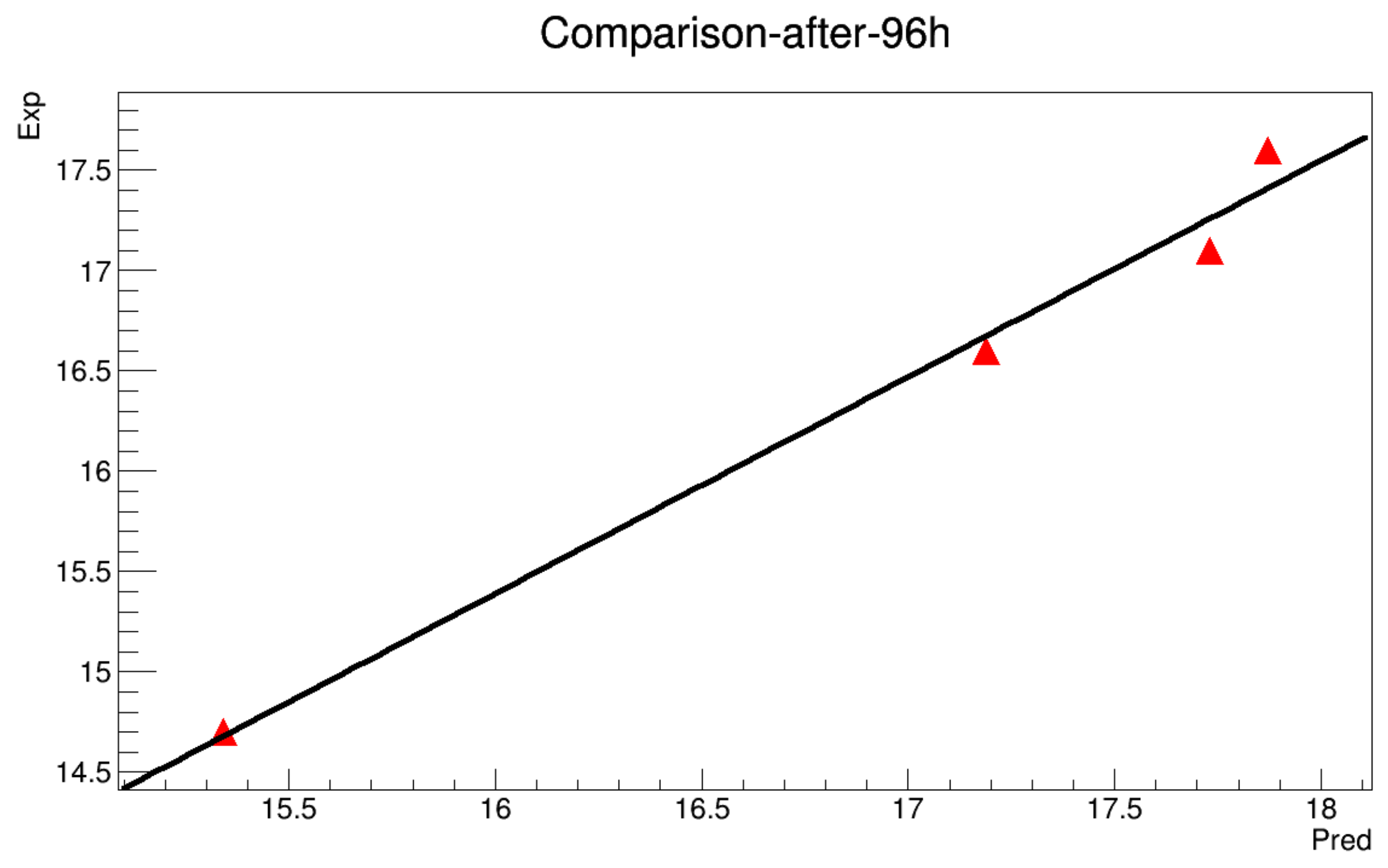
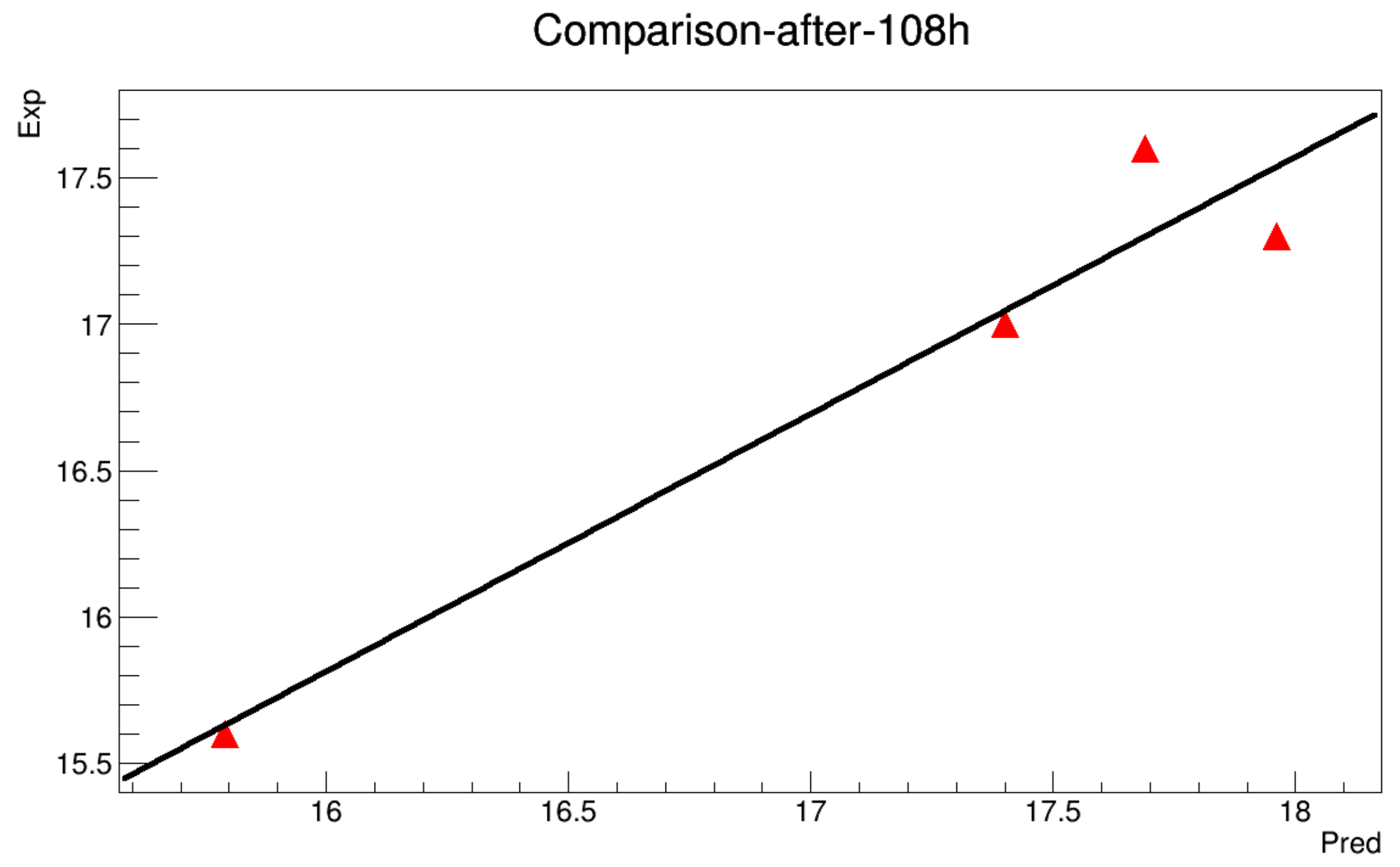
References
- Ainsworth, M. Dispersive and dissipative behavior of high order Discontinuous Galerkin finite element methods. J. Comput. Phys. 2004, 198, 106–130. [Google Scholar] [CrossRef]
- Boulaaras, S.; Guefaifia, R. Existence of positive weak solutions for a class of Kirrchoff elliptic systems with multiple parameters. Math. Meth. Appl. Sci. 2018, 41, 5203–5210. [Google Scholar] [CrossRef]
- Boulaaras, S.; Allahem, A. Existence of positive solutions of nonlocal p(x)-Kirchhoff evolutionary systems via Sub-Super Solutions Concept. Symmetry 2019, 11, 253. [Google Scholar] [CrossRef]
- Batteen, M.L.; Han, Y.-J. On the computational noise of finite-difference schemes used in ocean models. Tellus 1981, 33, 387–396. [Google Scholar] [CrossRef]
- Beckers, J.-M.; Deleersnijder, E. Stability of a fbtcs scheme applied to the propagation of shallow-water inertia-gravity waves on various space grids. J. Comput. Phys. 1993, 108, 95–104. [Google Scholar] [CrossRef]
- Glowinski, R. Numerecal Methods for Nolinear Variational Problems; Springer: Berlin, Germany, 1982. [Google Scholar]
- Guyot, G. Cours de Bioclimatologie, Chapitre II: Echanges de Chaleur et de Masse par Conduction et Convection’; INRA Bioclimatologie, BP: Montfavet, France, 1992. [Google Scholar]
- Boulaaras, B.; Haiour, M. L∞-asymptotic behavior for a finite element approximation in parabolic quasi-variational inequalities related to impulse control problem. Appl. Math. Comput. 2011, 217, 6443–6450. [Google Scholar] [CrossRef]
- Boulaaras, S.; Haiour, M. A General Case for the Maximum Norm Analysis of an Overlapping Schwarz Methods of Evolutionary HJB Equation with Nonlinear Source Terms with the Mixed Boundary Conditions. Appl. Math. Int. Sci. 2015, 9, 1247–1257. [Google Scholar]
- Haiour, M.; Boulaaras, S. Overlapping domain decomposition methods for elliptic quasi-variational inequalities related to impulse control problem. Proc. Math. Sci. 2011, 4, 481–493. [Google Scholar] [CrossRef]
- Boulaaras, S.; Haiour, M. The theta time scheme combined with a finite element spatial approximation of Hamilton-Jacobi-Bellman equation. Computat. Math. Model. 2014, 25, 423–438. [Google Scholar] [CrossRef]
- Ciarlet, P.G. Introductionà L’analyse Numérique Matricielle et à L’optimisation; Masson: Paris, France, 1990. [Google Scholar]
- Allahem, A.; Boulaaras, S.; Zennir, K.; Haiour, M. A new mathematical model of heat equations and its application on the agriculture soil. Eur. J. Pure Appl. Math. 2018, 11, 110–137. [Google Scholar] [CrossRef]
- Cushman-Roisin, B. Introduction to Geophysical Fluid Dynamics; Prentice-Hall: Upper Sadle River, NJ, USA, 1994. [Google Scholar]
- Boulaaras, S.; Haiour, M. The finite element approximation of evolutionary Hamilton–Jacobi–Bellman equations with nonlinear source terms. Indag. Math. 2013, 24, 161–173. [Google Scholar] [CrossRef]
- Haxaire, R. Characterization and Modelisation of Air Flows on a Greenhouse. Ph.D. Thesis, University of Nice, Nice, France, 1999. [Google Scholar]
- Majda, A. Introduction to PDE’s and Waves for the Atmosphere and Ocean; American Mathematical Society: Providence, RI, USA, 2003. [Google Scholar]
- Guefaifia, R.; Boulaaras, S. Existence of positive solution for a class of (p(x), q(x))-Laplacian systems. Rend. Circ. Mater. Palermo Ser. II 2018, 67, 93–103. [Google Scholar]
- Rostand, V.; Le Roux Raviart-Thomas, D.Y.; Douglas, B. Marini finite element approximations of the shallow water equations. Int. J. Numer. Methods Fluids 2007. [Google Scholar] [CrossRef]
- White, L.; Deleersnijder, E. Diagnoses of vertical transport in a three-dimensional finiteelement model of the tidal circulation around an island. Estuar. Coast. Shelf Sci. 2007, 74, 655–669. [Google Scholar] [CrossRef]
- Nebbali, S.R. Makhlouf, D.Ã. Termination de la Distribution du Champ de Temperatures Dans le Sol, par un Modele Semi-Analytique. In Conditions aux Limites Pour les Besoins de Simulation d. une Serre de Cculture; Universite Mouloud Mammeri: Tizi-Ouzou, Algerie, 2000. [Google Scholar]






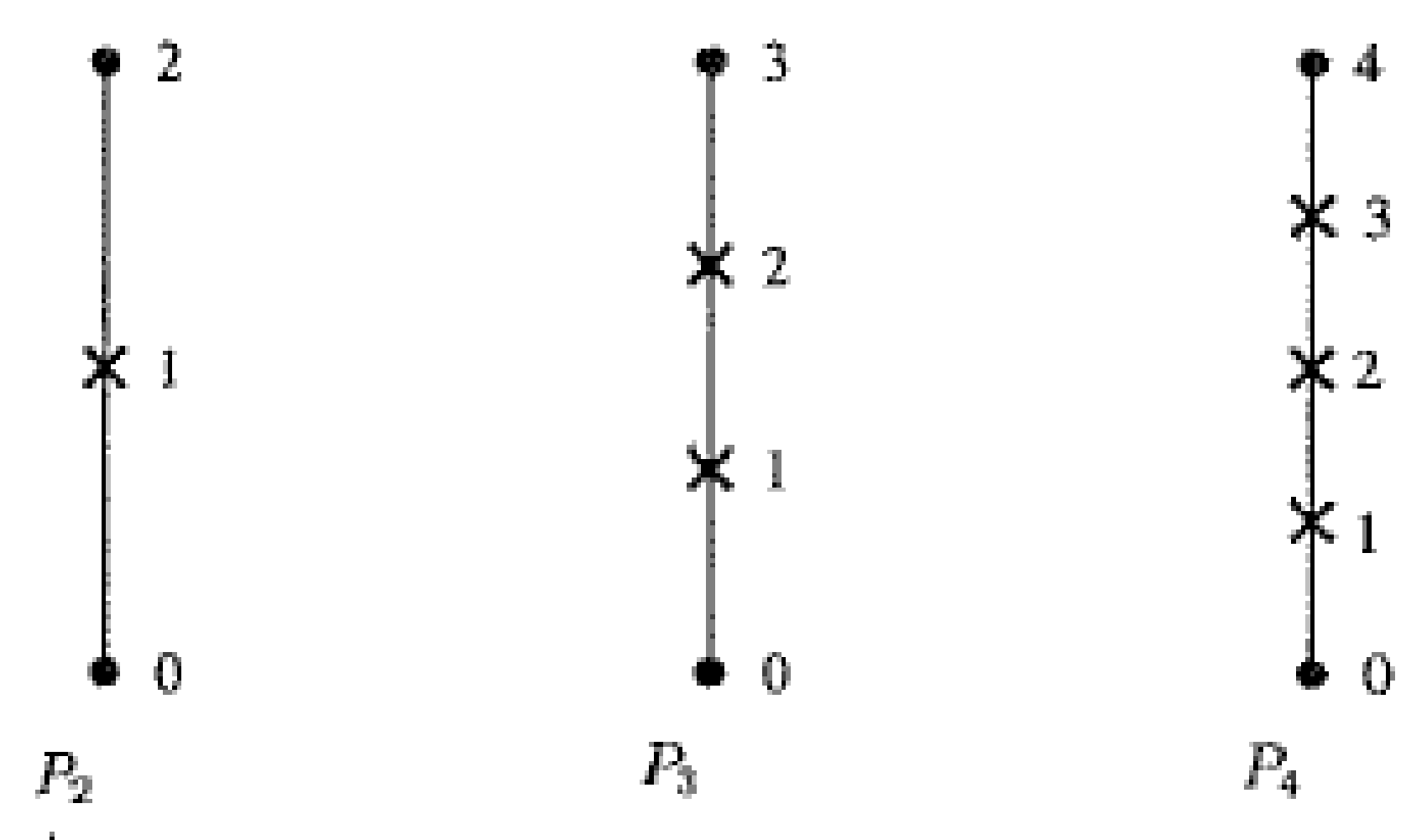

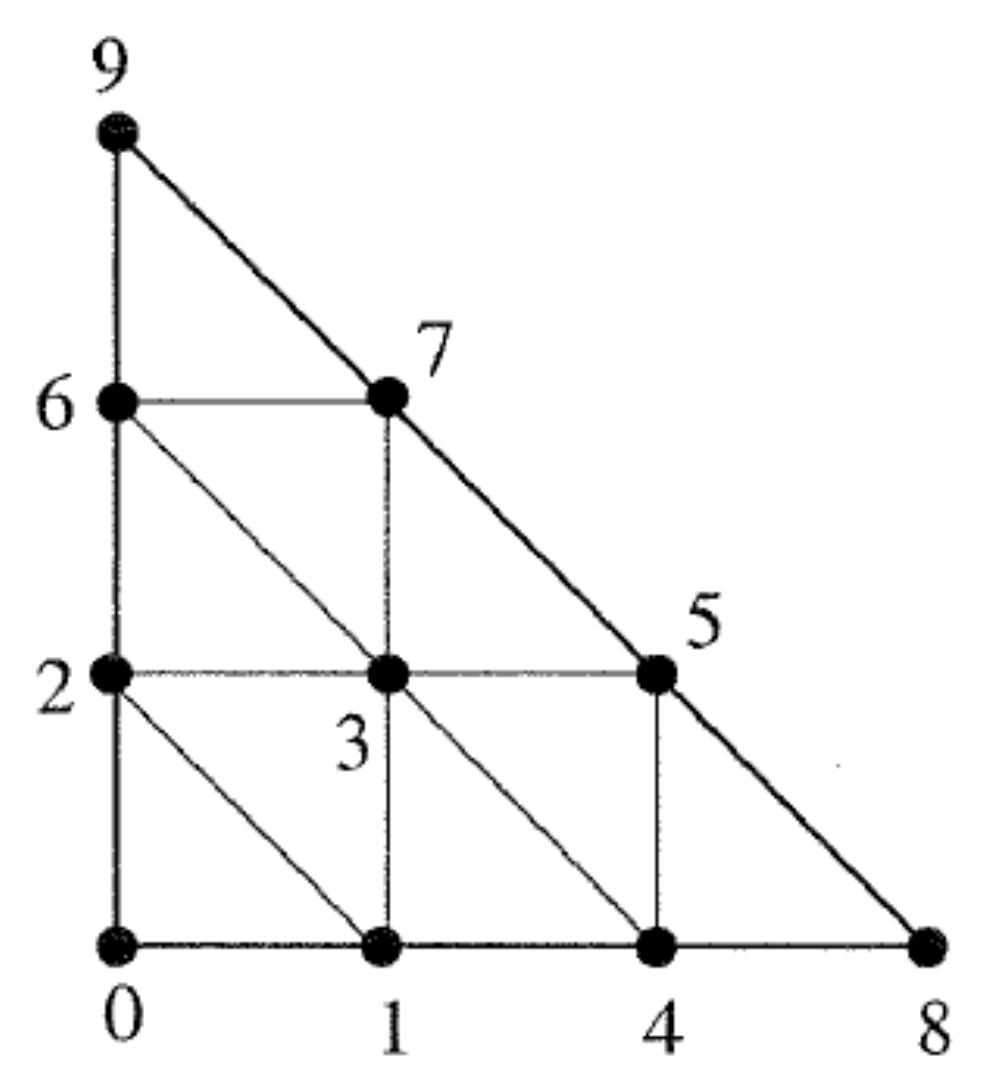

























| Type | Expression | Commentary |
|---|---|---|
| Lagrange type | Value of on the node . The most simple d.o.f. allows the Lagrange interpolation | |
| Hierarchical Lagrange Type | Difference between the value of on the node and the value of some other base functions. This is generally the bubble functions type of d.o.f. | |
| Mean type | Value of the mean value of on the element. Exists also for the restriction on a face | |
| Derivative type | or | Value of a derivative of on the node . This kind of d.o.f. makes the element no to be -equivalent. denotes the normal derivative with respect to a face |
| Second derivative | Value of a second derivative of on the node . This kind of d.o.f. makes also the element no to be -equivalent. |
| Classical “” Lagrange Element “FEM-PK ()” | ||||||
|---|---|---|---|---|---|---|
| Degree | Dimension | d.o.f. number | class | vectorial | -equivalent | Polynomial |
| K, | P, | , (Q = 1) | Yes | Yes | ||
| Discontinuous “” Lagrange Element “FEM-PK-DISCONTINUOUS ()” | ||||||
|---|---|---|---|---|---|---|
| Degree | Dimension | d.o.f. number | class | vectorial | -equivalent | Polynomial |
| K, | P, | , () | Yes | Yes | ||
| Lagrange Element on Parallelepipeds “FEM-QK ()” | ||||||
|---|---|---|---|---|---|---|
| Degree | Dimension | d.o.f. number | class | vectorial | -equivalent | Polynomial |
| , | P, | , () | Yes | Yes | ||
| Graphic | Coordinates | Weights | Function to Call/Order | |
|---|---|---|---|---|
| x | y | |||
 | 1/3 | 1/3 | 1/2 | ”IM-TRIANGLE(1)” 1 point, order 1 |
 | 1/6 2/3 1/6 | 1/6 1/6 2/3 | 1/6 1/6 1/6 | ”IM-TRIANGLE(2)” 3 points, order 2 |
 | 1/3 1/5 3/5 1/5 | 1/3 1/5 1/5 3/5 | 27/96 25/96 25/96 25/96 | ”IM-TRIANGLE(3)” 4 points, order 3 |
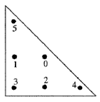 | a 1−2a a b 1−2b b | a a 1−2a b b 1−2b | c c c d d d | ”IM-TRIANGLE(4)” 6 points, order 4, a = 0.445948490915965, b = 0.091576213509771 c = 0.111690794839005 d = 0.054975871827661 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhahbi, A.B.; Boulaaras, S.; Radwan, T.; Mezouar, N.; Zennir, K.; Haiour, M.; Allahem, A.; Ghanem, S. A Two-Dimensional Mathematical Model of Heat Propagation Equations and Their Significance for Soil Temperature. Symmetry 2019, 11, 478. https://doi.org/10.3390/sym11040478
Dhahbi AB, Boulaaras S, Radwan T, Mezouar N, Zennir K, Haiour M, Allahem A, Ghanem S. A Two-Dimensional Mathematical Model of Heat Propagation Equations and Their Significance for Soil Temperature. Symmetry. 2019; 11(4):478. https://doi.org/10.3390/sym11040478
Chicago/Turabian StyleDhahbi, Anis Ben, Salah Boulaaras, Taha Radwan, Nadia Mezouar, Khaled Zennir, Mohamed Haiour, Ali Allahem, and Sewelem Ghanem. 2019. "A Two-Dimensional Mathematical Model of Heat Propagation Equations and Their Significance for Soil Temperature" Symmetry 11, no. 4: 478. https://doi.org/10.3390/sym11040478
APA StyleDhahbi, A. B., Boulaaras, S., Radwan, T., Mezouar, N., Zennir, K., Haiour, M., Allahem, A., & Ghanem, S. (2019). A Two-Dimensional Mathematical Model of Heat Propagation Equations and Their Significance for Soil Temperature. Symmetry, 11(4), 478. https://doi.org/10.3390/sym11040478







