Abstract
Slow-hash algorithms are proposed to defend against traditional offline password recovery by making the hash function very slow to compute. In this paper, we study the problem of slow-hash recovery on a large scale. We attack the problem by proposing a novel concurrent model that guesses the target password hash by leveraging known passwords from a largest-ever password corpus. Previously proposed password-reused learning models are specifically designed for targeted online guessing for a single hash and thus cannot be efficiently parallelized for massive-scale offline recovery, which is demanded by modern hash-cracking tasks. In particular, because the size of a probabilistic context-free grammar (PCFG for short) model is non-trivial and keeping track of the next most probable password to guess across all global accounts is difficult, we choose clever data structures and only expand transformations as needed to make the attack computationally tractable. Our adoption of max-min heap, which globally ranks weak accounts for both expanding and guessing according to unified PCFGs and allows for concurrent global ranking, significantly increases the hashes can be recovered within limited time. For example, 59.1% accounts in one of our target password list can be found in our source corpus, allowing our solution to recover 20.1% accounts within one week at an average speed of 7200 non-identical passwords cracked per hour, compared to previous solutions such as oclHashcat (using default configuration), which cracks at an average speed of 28 and needs months to recover the same number of accounts with equal computing resources (thus are infeasible for a real-world attacker who would maximize the gain against the cracking cost). This implies an underestimated threat to slow-hash protected password dumps. Our method provides organizations with a better model of offline attackers and helps them better decide the hashing costs of slow-hash algorithms and detect potential vulnerable credentials before hackers do.
1. Introduction
Slow-hash algorithms are regarded as safe protections of low-entropy passwords without secret keys. Even if there exists a large leak of slow-hash protected passwords, it is still not a big concern yet for the compromised service [1,2,3]. In this paper, we mainly focus on one of the most popular slow-hash algorithms for practical password storage, the bcrypt hash.
Traditional brute-force recovery [4,5] enumerates all combinations of characters. It causes time and space explosion and is not considered practical for cracking bcrypt hashes. Using a large number of already leaked accounts and passwords, there is chance to crack more accounts with fewer number of guesses. Previous password-reused based online guessing techniques have shown some potential for offline recovery. Das et al. [6] found that, by applying a few popular transform rules to passwords from other sites, one has a strong possibility to guess a password of the same user in another site. Wang et al. [7] proposed several learning models for cross-site online guessing when given the victim’s one sister password and some personally identifiable information. Despite their success for online guessing, it is still difficult to use them to recover bcrypt-hashed passwords. Firstly, the number of matched accounts is usually very small w.r.t. the size of a given database, as reported by [6,7,8]. The data used by researchers and security analysts only accounts for a small portion of the one circulating in the dark web, resulting in the asymmetry of information. Secondly, cross-site recovery techniques leave the unmatched accounts out of the guessing scope. A straightforward solution is to perform a cross-site recovery followed by a brute-force recovery. This order may not be optimal because some weak passwords of unmatched accounts can be easier to recover than strong passwords of matched accounts. Thirdly, the existing cross-site recovery models have to try a constant number of guesses for each target account (e.g., 1000) because, unlike trawling models which generate a fixed sequence of guesses (i.e., transformation rules) for all accounts, cross-site models have varied source passwords for different accounts which make the subsequent expansions less deterministic than those in trawling models. For bcrypt, this means a long time will be spent on a difficult account (e.g., 20s in total, assuming that the hashing process costs 0.02s for each of the 1000 guesses) before it has chance to recover the remaining accounts, among which many could be easier to crack.
In this paper, we propose to perform efficient recovery of leaked slow-hash (the bcrypt hash, particularly) password of a site, leveraging large corpora of passwords from multiple sources for both training and guessing. The compromised credential verification service provider VeriClouds Co. (Seattle, WA, USA) claimed in its whitepapers [9] that between 15% and 40% of a typical company’s credentials already exist in the proprietary database. This finding indicates a promising direction to base massive hash recovery mainly on password reuse.
We target the overall efficiency of slow-hash recovery, i.e., recovering the most accounts with the least cost. Our main focus is not about improving the success rate for each individual account, but rather how to optimize the entire system’s efficiency. No study has been conducted for this setting. The main insight is to consider the recovery of all accounts holistically, and to dynamically adjust the order of attempts so that more promising (account, candidate password) pairs are tried earlier. This reordering is critical for our setting because every attempt is expensive, and it is impossible to finish, say, 1000 attempts for all accounts in a reasonable time. We perform the reordering by globally ranking the (account, candidate password) pairs, while the candidate passwords for each account are generated using a learning model called probabilistic context-free grammar (PCFG for short), which is the mainstream method typically for online guessing. The probability learned by PCFG is utilized for ranking.
Though the idea of global ranking is intuitive, there are several challenges. First, we need to handle both accounts with and without leaked passwords, which is not done by previous PCFG models. Second, the global ranking can take a long time and consume a lot of memory, which delays the recovery and has scalability issues. These challenges are solved by integrating several ideas—unified PCFGs, symmetrical multithread collaboration, and incremental transformation with materialization—into a novel concurrent model. Unified PCFGs combine the trawling model with the targeted guessing model and prioritize guesses for both cross-site and none cross-site accounts. Symmetrical multithread collaboration separates the processes of password hashing and grammar expanding, making them cooperate efficiently. Incremental transformation reduces the time and memory needed for sorting by avoiding enumeration. Materialization can further transfer inactive candidates which occupy a lot of memory to the disk and sort them externally.
In summary, the contributions of this paper are:
- Recovering slow hashes by reusing passwords from a large source corpus. Our corpus is the largest ever studied in literature to our knowledge. Based on it, we find cross-site passwords account for a large proportion of the target sites, which can be exploited for hash recovery.
- Identifying a less-studied issue which degrades the efficiency of massive-scale slow-hash recovery: weak accounts are blocked by stronger accounts during expanding and guessing. We solve this by proposing concurrent global prioritization and overcome two key shortcomings of the usage of a huge global heap which the method brings in.
- Helping organizations to better protect their data. Our algorithm models the behavior of real-world attackers who would try the best to maximize the cracking profit before it is finally exceeded by the cost. Based on it, organizations can better balance the hashing costs with the sever load, and can proactively detect weak credentials before financial and reputational damages happen.
The rest of this paper is organized as follows. Section 2 introduces existing recovery methods and the challenges of slow-hash recovery. Section 3 presents the statistics of the VeriClouds dataset, an overview of our proposed framework, and the details of the design. The experimental results are given in Section 4. Section 5 concludes this paper and points out some future research directions.
2. Related Work
2.1. Offline Password Guessing
Human-chosen passwords are well-known to be predictable on average [10], which leave room for password guessing. An attacker can carry out online guessing by trying a series of possible password candidates against the publicly facing server. Another way to launch an attack is offline guessing, during which the attacker recovers hashed (e.g., SHA1, MD5) passwords from a breached database, without the need to query the publicly facing server. While an online attack is facing mitigations including rate-limiting password entry attempts, single sign-on and two-factor authentication, an offline guessing attack is easier to accomplish as it is free from the limit of number of guesses. We study the problem of offline password recovery in this paper.
Typical types of offline guessing include:
Brute-force and mask attacks. Brute-force method simply enumerates all possible strings by trying all combinations of characters from given charsets. This is inefficient and only used in practice when guessing short or randomly generated passwords. Mask attack reduces the password candidate keyspace by configuring the attack to explore a more specific and popular structure, such as trying upper-case letters only on the first position. Mask attack can be effective for short passwords as it requires less exhaustion.
Dictionary and mangled wordlist attacks. Dictionary attack, also known as wordlist attack, simply tries all words in a list. Many modern cracking tools like Hashcat [4] and John the Ripper [5] base their core attack modes on an improved version called mangled wordlist attack or rule-based attack. In this case, the attacker applies transformation rules to the words from wordlists. There are a few variations such as concatenating words from multiple wordlists (i.e., combinator attack) and combining wordlists with masks (i.e., hybrid attack). The number of available candidates increases with the exploration of keyspace being still restrained, which makes this category of attack very successful in practice.
Markov models. The Markov model was first introduced to the field of password cracking by Narayanan et al. [11] as a template-based model. In that work, Markov chain was only used for assigning probabilities to letter-based segments. Later, Castelluccia et al. [12] proposed to use whole-string Markov models (i.e., n-gram models) for evaluating password strength and they do not divide a password into segments. Ma et al. [13] studied many variations of Markov models under different configurations and found that Markov models tend to be more efficient than other existing methods for certain datasets.
Probabilistic context-free grammar. To generate guesses in decreasing probability order, Weir et al. [10] proposed to use a probabilistic context-free grammar (PCFG). They divided passwords into different templates according to character category. For example, ‘password123’ belongs to the 8-letter-and-3-digit template, symbolized as L8D3. The probabilities of the templates are trained from a large corpus. Additionally, Komanduri [14] proposed substantial improvements to Weir’s PCFG, such as intelligent skipping and pattern compaction, to make guessing more effective.
Neural Networks. Melicher et al. [15] proposed to use artificial neural networks to model text passwords’ resistance to guessing attacks. They showed that neural networks can often guess passwords more effectively than state-of-the-art approaches, when beyond 1010 guesses and on non-traditional password policies.
In addition to the above methods, there is research such as [16] which studied the impact of using multiple well-configured attack algorithms in parallel. This can approximate passwords’ vulnerability to a real-world expertized attacker. However, we would like to focus on PCFG. As Ref. [17] pointed out, PCFG shows better performance in the short term (i.e., given limited guessing attempts), which fits the situation of bcrypt recovery. Due to the slow nature of bcrypt, we can achieve much fewer attempts within a limited time than traditional hash algorithms. Thus, other algorithms such as Markov models and neural networks can barely handle the task.
2.2. Password Reuse
In this case, an attacker tries to guess the target account’s password using the passwords matched (usually by email address) from other breached sources. This kind of attack has become quite common in recent days and its power has been manifested and reinforced by recent studies. These studies proposed to make the full exploitation of the source passwords by mangling them with rules related to the victim’s personal information and personally identifiable information (PII).
Methods leveraging password history of the same website. Zhang et al. [18] provided an algorithmic framework for predicting future passwords from expired ones due to a password expiration policy. Their algorithm modeled users’ behaviors of password modification when they were forced to change them, and their experimental results well verified the conjecture that users tend to generate future passwords based on old passwords.
Methods leveraging leaked passwords in other websites. Das et al. [6] identified a few popular rules users often use to transform a basic password between sites, by analyzing several hundred thousand leaked passwords from eleven web sites. Using a fixed order of these rules, they are the first to propose a cross-site guessing algorithm, which is able to guess 30% of the transformed passwords within 100 attempts. Wang et al. [19] proposed to use the Bayesian model to generate a customized order of rules to improve the performance of [6]. Han et al. [20] examined the state-of-the-art Intra-Site Password Reuses (ISPR) and Cross-Site Password Reuses (CSPR) based on the leaked passwords of 668 million members in China. By utilizing the patterns used by the same user, they achieved a major improvement in guessing success rate compared to John the Ripper.
Methods leveraging leaked passwords and personal information. Li et al. [21] extracted some of the most popular password structures, which can be expressed by personal information (e.g., name, birthdates, phone number, national ID, email address and user name). Based on the findings, they proposed a semantics-rich algorithm, Personal-PCFG, to crack passwords by generating personalized guesses. Wang et al. [7] proposed TarGuess, a framework that can characterize seven typical targeted guessing scenarios with sound mathematical models. They used customized PCFG models to address the issue of cross-site online guessing, when given the victim’s one sister password and some PII.
2.3. Bcrypt Recovery
As with offline guessing, the target passwords are typically stored in the hashed (and possibly randomly salted) form of (s, h) = (salt,Hash(pwd, salt)). The salt is used to resist mitigations such as rainbow table [22]. Despite this, the hashed password still can easily be checked by re-computing the hash and comparing it to h, as traditional cryptographic hash functions are fast to compute.
A widely used method to defend against that is using modern hash functions which are slow to evaluate, for example, bcrypt [23], scrypt [24], PBKDF2 [25] and argon2 [26]. We focus on bcrypt in this paper.
The bcrypt password hash. Being used as the default password hash algorithm in many today’s services, bcrypt [23] was designed to be resistant to brute force attacks and to remain secure despite of hardware improvements. The usage of expensive key setup with user-defined cost setting makes this hash algorithm very slow. Rapid random 32-bit lookups using Blowfish’s variable S-boxes typically require 4 KB of local memory per instance and make bcrypt unfriendly to CPU- or GPU-based parallelization.
Famous bcrypt dumps and their difficulty. We mainly study the three famous public bcrypt dumps, Dropbox, Ashley Madison (AM for short) and Edmodo (passwords in it were hashed with MD5+bcrypt and then obfuscated). They are extensively studied by researchers, perhaps by attackers as well. The difficulty to recover these data is well illustrated in the report presented by Jens [27]. The report summarized the performance of hashcat (v1.32, with a single GPU and the default settings for configurable algorithms) for various hash algorithms. The hashing speed is 1–10 BH/s for MD5 and SHA1-512, while it sharply decreases to 10-100 KH/s for bcrypt, slowing down by five orders of magnitude. In addition, the hashing speed does not necessarily correspond to the cracked accounts per unit time, which could be much slower. Indeed, it is reported that a few passwords can be recovered from these bcrypt dumps unless exploiting implementation bugs of the algorithm itself, if they exist [1,2,3].
Special-purpose hardware based cracking. Despite the security enforcement of bcrypt against common-purpose hardware improvements, it is possible to achieve much better performance with bcrypt implementations on homogeneous and heterogeneous multiprocessing platforms. Malvoni et al. [28] proposed one such implementation that was integrated into the John the Ripper password cracker and resulted in improved energy efficiency by a factor of 35+ compared to heavily optimized implementations on modern CPUs. Our work, however, concentrates on common-purpose hardware, as it is cheap and readily available for a real-world attacker. Special-purpose hardware implementations are orthogonal and complementary to our approach.
Recently, Blocki et al. [20,29,30] proposed theoretical, economic models to evaluate the economics of offline password cracking for different slow-hash algorithms. However, they did not realize that password reuse could be a major contribution to boost slow-hash recovery. Furthermore, their work, which heavily relied on the idealized recovery metric, failed to answer the practical issues a real-world attacker would face with limited computational resources. As far as we are concerned, there is no previous study on developing a practical guessing algorithm specifically for slow hashes such as bcrypt, by optimizing the entire system’s efficiency rather than improving the success rate for each individual account.
2.4. Recovery Metric
Weir et al. [31] proposed a metric called guess-number graph to evaluate the performance of guessing algorithms, which has then been adopted by most research works. The guess number of a password is its rank in the sequence generated by a specific algorithm in the order of decreasing probability. The graph plots the fraction of cracked passwords w.r.t. various guess numbers.
However, traditional guess-number graph cannot reflect the temporal and spatial performance of slow-hash algorithms and the size of the target dataset, which are the major factors in our scenario of massive-scale slow hash recovery. In addition, it is non-trivial work to calculate the guessed number of passwords for all cross-site accounts, since the source passwords are so diversified that transformation-rule sequences, which are applied, are likely to be different.
The empirical metric we are to use should be different from their metric. Thus, we propose to plot the average number of cracked accounts versus elapsed time, named recovery-speed graph, which describes the wall-clock performance of offline cracking. The time of model training is not included, as the training can be done before the data leakage happens. Identical cross-site password pairs are also not considered.
3. Our Solution
Data and recovery model. Here, we will briefly describe the VeriClouds corpus, which is closely related to our study. The total amount of credentials in the VeriClouds corpus is 9,118,017,411 by 1 March 2018, collected from more than 90% [9] of the leaked databases on the deep/dark web and from paste sites such as PasteBin. This dump includes most of the recent famous breaches and therefore is of perfect quality. For example, the fraction of overlapped Dropbox’ accounts is up to 59% with the VeriClouds corpus. There are a large number of email addresses with upper-case letters in VeriClouds dump, which may be caused due to implementation errors, since no widely used mail systems are case-sensitive to email addresses. These email addresses are lowercased to increase chances of matching cross-site accounts. Table 1 gives some typical sources of the dump. As it is merely a combo list, it is hard to exactly count the overlapped credentials with the listed sources. This dataset is larger in magnitude than the ones ever studied in previous works [6,7,8]. VeriClouds has made the data private and reclaimed any personal or academic access since 2018, due to the policy change after the Facebook–Cambridge Analytica data scandal. The fourth author of this paper is a co-founder of VeriClouds, who exclusively maintains the dataset to guarantee data safety. Note that we do not directly exploit the data in this paper and the other authors have no access to it, in case of moral issues.

Table 1.
Typical sources of the VeriClouds dump.
System goal. Given fixed computational resources, we aim to maximize the speed of cracking. It implies we can maximize the number of recovered accounts in a fixed time—in other words, we can minimize the time to recover a fixed fraction of accounts.
We set out to build a system for efficient recovery of bcrypt-hashed passwords. We have determined four design criteria that we felt such a system should satisfy so as to be useful:
- Effective: Recover a substantial proportion of the target dataset.
- Efficient: Make the more promising (account, password) pairs to be attempted earlier.
- Parallelizable: Perform as many trials as possible per unit time.
- Scalable: Handle a large dataset with restricted memory resource.
Previous recovery methods do not satisfy 1, 2. A naive global ranking method that prioritizes candidates from all accounts, however, does not satisfy 3, 4.
Figure 1 depicts the system architecture. The work flow can be briefly described as follows.
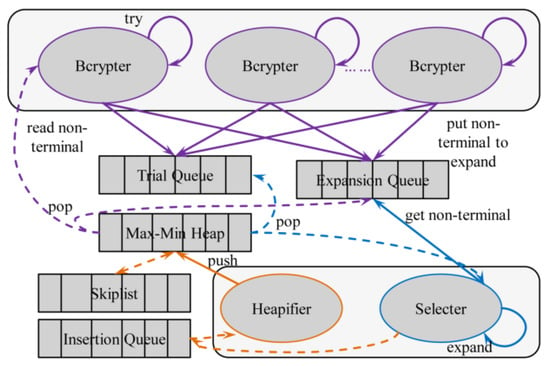
Figure 1.
System architecture.
PCFG Expansion: To meet the 1st criterion, we explore differentiated PCFG models for different accounts. Each heap elements, once popped from the heap, is expanded (by Selecter) according to the PCFG rules of the corresponding account. The derived results will be pushed back to the heap to maintain the global order of priority.
Global Ranking: Candidates of all accounts are dynamically inserted to or removed from a max-min heap [32], which ensures that a candidate with higher probability will always be popped before any other one with lower probability. This relates to our 2nd criterion. To settle the problem described in the 4th criterion, a skiplist [33] is used (by Heapifier) to migrate some of the candidates when the heap size becomes extremely large.
Bcrypt Trial: During the recovery, a candidate is hashed with bcrypt and compared with the target hash. If both hashes are the same, the account is claimed to be cracked. In our design, the bcrypt-trial procedures (Bcrypters) can be separated from PCFG expansion (Selecter), so that we can assign each Bcrypter to a single core. The system works asynchronously such that maximal parallelization can be achieved, and thus satisfies the 3rd criterion.
We will describe each component in detail in the following subsections.
3.1. PCFG Expansion
• Model formulation
We model the procedure of recovering multiple bcrypt-hashed accounts as a grammar bundle (also can be called a grammar forest), which is defined as
The forest is a combination of two different types of PCFG models. The trawling PCFG model [10,11,12,13,14] Gt is a tuple <Σ, V, E, λ, s>, where:
- Σ is the set of 95 printable ASCII codes.
- V = {s; Li, Di, Si} (i ∈ {1, 2, …, 16}), where Li, Di, Si each stands for an alphabetic/digital/symbolic string of length i (called segment).
- s ∈ V is the start symbol.
- E is a set of rules in the form of v → v’, where v ∈ V and v’ ∈ (V ∪ Σ)∗.
- λ:E → [0, 1] assigns each rule to a probability and it fulfills the constraint
The password-reuse based PCFG model [7] Gr is a tuple <Σr, Vr, Er, λr, sr>. Er, λr, sr are defined as the same with Gt, while:
Σr = Σ ∪ {src, C1, …, C4; R1, R2; L1, …, L5; Yes, No; No’}
Vr = V ∪ {C, LT, R, SM; ti, td, hi, hd; ti’, td’, hi’, hd’}
In the above definition, src is a sister password of the same account from the source corpus. We will explain the transforming rules shown up in Σr, Vr later.
We use the function Γ: (Gr, Gt’) → Gr’ = <Σr’, Vr’, Er’, λr’, sr’> and the factor α to integrate another trawling model Gt’ = <Σ’, V’, E’, λ’, s’> (using a similar definition with Gt) into Gr for cross-site accounts, where
Vr’= Vr’∪ {sr’},
Er’= Er ∪ {sr’ → s’, sr’ → sr},
λr’(sr’→ s’) = 1 − α, λr’(sr’ → sr) = α, λr’(e) = λr (e)(e ∈ Er).
The factor α corresponds to those users who tend to use passwords transformed from cross-site passwords.
This definition of grammar bundle makes our model differed from [7], since we manage to model the behaviors of both cross-site password reuse and password trawling. The following theorem can be proved.
Theorem 1.
(Correctness of the grammar bundle) Each tree in the forest is a PCFG grammar.
Proof.
Obviously, the sum of probabilities of all rules start with v (v ∈ Gt, Gt’ or Gr) equals 1. In addition, for all rules beginning with sr’, we have Σe start with sr’ Pr(e) = Pr(sr’ → s’) +Pr(sr’ → sr) = (1 − α) + α = 1. Thus, for any specific left-hand side variable in the rules of Gr’, the sum of the probabilities of all of its productions must sum to 1. □
• Training
We train λ, λ’ on 1 million passwords of a similar service (training site) with the target site. Each password is divided into segments. For each segment, we add up the count of its occurrences. For instance, 4abc$$ can be parsed as D1L3S2 and each of the occurrences of rules s → D1L3S2, D1 → 4, L3 → abc, S2 → $$ will be added by one. The probabilities of rules are calculated according to their counts.
To train λr, we first collect password pairs (src_pw, train_pw) by matching the training site with the source site w.r.t. email addresses. After filtering out the 10,000 most common passwords from the training site, for each of the remaining pairs, both the source and target passwords are split into segments. Then, we go through two phases of training, which is the same as the procedure described in [7]. We sequentially apply cross-site transformation rules (capitalization (C1, …, C4), leet (L1, …, L5), reversal (R1, R2), sub-word movement (SM), structural manipulation (ti, td, hi, hd), segmental manipulation (ti’, td’, hi’, hd’)) on src_pw, and count the occurrence of a rule if it makes the resulted password src_pw’ closer to train_pw in terms of Levenshtein distance [34]. We here describe each rule in detail. C1 capitalizes all letters; C2 capitalizes the 1st letter; C3 lowers all letters; C4 lowers all letters; L1, L2, L3, L4, L5 each performs the substitution of ‘a’ <-> ‘@’, ‘s’ <-> ‘$’, ‘o’ <-> ‘0’, ‘i’ <-> ‘1’, ‘e’ <-> ‘3’; R1 reverses all characters; R2 reverses each segment; SM moves sub-words within a password; ti inserts a segment at the tail; td deletes the last segment; hi inserts a segment at the head; hd deletes the first segment; ti’ inserts a character at the tail of a segment; td’ deletes the last character of a segment; hi’ inserts a character at the head of a segment; hd’ deletes the first character of a segment. Since most passwords are not longer than 16, only passwords within 16 characters are considered.
The α factor for Γ is trained in an approximate way. We simply count the fraction of accounts that are not filtered out during the training of λr.
• Expansion
Starting from s and sr’, we can repeatedly apply transform rules to derive lists of guesses. Candidates are generated in the descending order of probability according to their corresponding grammar tree. For example, the guessing list of Gt can be 123456 (Pr(s → D6) Pr(D6 → 123456) = 0.016), 4abc$$4 (Pr(s → D1L3S2D1)·Pr(D1 → 4)·Pr(L3 → abc) Pr(S2 → $$) Pr(D1 → 4) = 0.008), etc. The left-hand side of a rule in Gt is called a terminal if it only contains ASCII chars; otherwise, it is called as a non-terminal. The parameterized model Gr’, when given the password princess, generates princess1 (Pr(sr’ → sr)·Pr(sr → princess1)·Pr(sr → L8)·Pr(C → No)·Pr(LT → No) Pr(R → No) Pr(SM → No) Pr(L8 → ti) Pr(ti → D1) Pr(D1 → 1) Pr(L8 → No0) Pr(D1 → No0) = 0.018), Princess1 (Pr(sr’→ sr) Pr(sr → princess1) Pr(C → C3) Pr(LT → No) Pr(R → No) Pr(SM → No) Pr(L8D1 →No) Pr(L8 → No’) Pr(D1 → No’) = 0.012), etc.
3.2. Global Ranking
Weir et al. [10] and Komanduri [14] studied offline cracking without using leaked passwords for matching accounts. As a consequence, all accounts will have identical trials, and a single priority queue is the only choice. For the scenario we are studying, each matched account needs to have a different trial. None of the works we have found so far uses a single global queue to perform the trials, for this scenario [6,7].
According to criterion 2, we need to sort (acc, cand) pairs (where acc is the id of the account and cand is the candidate password). Under the definition of F, we find the probabilities of candidates generated by different grammar trees to be comparable with each other. Therefore, we can globally sort all of them by probability and try the highest first instead of guessing within the local trees. This prioritization is supposed to make fewer attempts to achieve the same number of successful guesses, which means that the model will be updated sooner. Algorithm 1 outlines the global sort algorithm. The kernel of the algorithm is to use the priority heap PQ to store generated candidates from all accounts and perform global sort when dequeuing (PQ.PopMax()) or enqueuing (PQ.Push()) an element. The efficient sorting procedure is internally guaranteed by the well-known heap data structure (binary tree) itself [35].
| Algorithm 1. GlobalSort. |
| Input:PQ:max-min heap, EQ:expansion queue, TQ:trial queue, IQ:insertion queue Output: 4 updated queues 1 while True do 2 if EQ!=0 then 3 cand<-EQ.Get() 4 else 5 with PQ.lock do 6 cand<-PQ.PopMax() 7 if isPseudTerminal(cand) or isTerminal(cand) then 8 TQ.Put(cand) 9 else 10 cands<-IncTranse(cand) 11 foreach e in cands do 12 IQ.Put(cands) |
We now dive deep into the optimization details in our global sort algorithm.
• Incremental transformation.
Due to the large number of accounts and potential guesses, we cannot perform ranking after all the candidate passwords are generated for all accounts in the leaked source. Thus, the priority queue only stores a subset of sorted (acc, cand) pairs which have been generated so far. When there is an idle thread for bcrypt trial, the head of the queue, i.e., the most promising guess (acc, cand) can be fed to that thread for trial.
In a naive design of the password-reuse based PCFG Gr, only after sequentially extending a given candidate using all six types of cross-site transformation rules in a round, we can then use the resulting new candidates (called pseudo-terminals as they are still non-terminals) for guessing. After trying the candidates by hashing them with bcrypt algorithm, they are enqueued again for next-round’s expansion. Expanding the six classes of rules all at once will cause thread blocking due to exponential blow-up of the size of resulted candidates.
To overcome that, we use a stepped expanding strategy for non-terminals of Gr. Once a non-terminal is dequeued for expansion, it only takes one of the six classes of transformation rules, i.e., the successor of the last rule used along the sequence: C, LT, R, SM, structural rules, segmental rules, C, LT, R, SM, structural rules, segmental rules. The resulting non-terminals will then be enqueued in one batch. The space of alphabetic segments can be huge, which, however, can be resolved by quantifization [14]. We can prove that the order of dequeuing the fully transformed passwords remains correct.
Theorem 2.
(Correctness of incremental transformation) The pseudo-terminal currently dequeued for guessing always has a probability not lower than any pseudo-terminal that will be dequeued later.
Proof.
Let P1 stands for the current pseudo-terminal dequeued from the priority queue. Assume that there will be some pseudo-terminal P2 dequeued later, with Pr(P2) >Pr(P1). At the time when P1 is dequeued, there must be some predecessor P2’ in the priority queue that will finally be extended into P2 after l(l ≥ 0) steps of extension. Therefore, Pr(P2’) ≥ Pr(P2). However, the property of priority queue ensures that all elements stored within are correctly sorted, and thus Pr(P1) ≥ Pr(P2’). Thus, we have Pr(P1) ≥ Pr(P2), which violates the assumption. □
• Lazy generation
When a candidate is being hashed and verified in a bcrypt trial thread, the ranking algorithm does not generate transformations for it until the bcrypt trial fails. This saves unnecessary enqueue and dequeue operations.
• Collapsing common candidates
Different accounts share the same model (Gt for cross-site users and Gt’ for the others) to generate common candidates. Each common candidate is stored only once for all accounts in the queue, which saves a large amount of space. In contrast, given distinct source passwords of different accounts, Gr has to generate different candidates accordingly.
• Materializing passwords of lower probability
By using the notion of materializing, we mean to transfer certain data in the memory to the disk. When the memory is full, system performance degrades. Previous optimizations such as intelligent skipping and quantifization [14] do not fit into our scenario, as the probabilities of generated candidates appear to be ‘flat’ (i.e., same or very close) due to the usage of global prioritization over very large numbers of accounts. Unlike Gt, there can be different instances of expansion trees for different cross-site accounts using Gr. To alleviate the situation, when the number of pseudo-terminals in the priority queue exceeds a certain threshold l, we remove the elements at the tail. These elements have lower probabilities and will not be tried earlier than the preceding l pseudo-terminals. In other words, if we can only run the recovery procedure for d = l/r (r is the average recovered accounts per day) days, they are unlikely to be used. Therefore, removing these unpromising pairs can make room for other candidates with higher probabilities.
In practice, we relax the restriction by simply cut off the queue’s ‘tail’ beyond a threshold. To make the removal operation efficient, we use a max-min heap [32] instead of traditional heaps, such that both popping the maximal or the minimal element can be done in O(log n) time, where n ≤ N is the length of the queue. A max-min heap is a complete binary tree that is defined all the same as the one defined in a traditional heap sort algorithm, except that each node at an even level in the tree is greater than all of its descendants, while each node at an odd level in the tree is less than all of its descendants.
These non-terminals removed from max-min heap are not dropped but stored on the disk. We use a customized skiplist [33] for incremental and efficient external sort, in which inserting an element requires an expected time of O(log n) and dequeuing the max element only needs constant time. A skiplist is built in layers, where the bottom layer is an ordinary ordered linked list and an element in each layer i appears in layer i + 1 with some fixed probability p (p = 1/2 in this case). We introduces duplicated keys for indexing elements, as the probabilities (i.e., keys) of some non-terminals can be the same. Elements in the skiplist will be loaded back into memory once needed, as described in detail in Algorithm 2. As for the concurrent race condition issue, we use a conservative and thus more efficient strategy. For each shared queue, we use a fine-grained lock to avoid race conditions caused by enqueue/dequeue operations. However, we do not strictly enforce the state consistence of different queues. For example, we do not use a big lock to enclose the sequence of a dequeue operation of the insertion queue followed by an enqueue operation of skiplist. Moreover, we do not use a lock when reading the maximal or minima element in the heap. These optimizations may introduce some inconsistence, but the performance gained will overwhelm the accuracy sacrificed since the probabilities of candidates co-existing in the heaps in a short period of time are fairly close.
Other queues which are used for caching parallel tasks, i.e., trial queue, expansion queue and insertion queue, also need to transfer overflowed data to the file system, to avoid too much memory consumption. Unlike the method used for heaps, the materialization for these queues is intuitive since they follow the first-in-first-out (i.e., FIFO) principle. Overflowed elements can be directly moved to the disk without the need of sorting.
We use a toy example depicted in Figure 2 to describe all proposed algorithms in the paper. In this case, there are 1,000,000 accounts in the target site to recover. Some are cross-site accounts (e.g., usr1, usr999999), and the other are not (e.g., usr0). The sister passwords for usr1 and usr999999 from the given source site are ‘princess’ and ‘monkeys’ respectively.
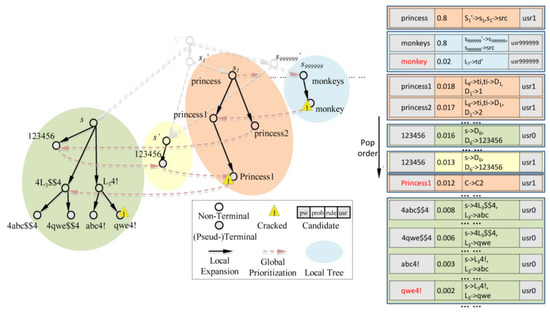
Figure 2.
Globally-prioritized expansion (partial; α = 0.8).
| Algorithm 2. Materialization. |
| Input:PQ:max-min heap, SL:skiplist, IQ:insertion queue Output: 3 updated queues 1 while True do 2 if IQ!=0 then 3 cand<-IQ.Get() /* candidate to insert */ 4 if cand.prob>=SL.ReadMax() then 5 with PQ.lock do 6 if Len(PQ)>=MAX_LEN then 7 if cand.prob<=PQ.ReadMin() then 8 SL.Push(cand) 9 else 10 pq_min<-PQ.PopMin() 11 SL.Push(pq_min) 12 PQ.Push(cand) 13 else 14 SL.Push(cand) 15 with PQ.lock do 16 if Len(PQ)<MAX_LEN then 17 sl_max<-SL.PopMax() 18 PQ.Push(sl_max) |
Example 1.
(Running of Algorithm 1 for the toy example) As with the toy example, the corresponding execution trace of GlobalSort (i.e., the Selecter thread) can be explained as follows. Let’s only consider two accounts usr0, usr999999 and use only two types of cross-site transform rules (capitalization and segmental transformation) for simplicity. Given a previous state (Iter i) of the heap, trail queue and expansion queue, Selecter decides where to fetch a new candidate and how to deal with it. Via this toy example, we can see how the global sort algorithm prioritizes promising passwords and saves unnecessary computational cost for lower-probability passwords. For example, vulnerable accounts like usr999999 can be tried much earlier in our algorithm than traditional methods.
Let’s analyze the time complexity and space complexity. Let n be number of accounts, and m be the maximal candidates we can generate for each account. The count of loops is O(n·m). The most expensive operation in each loop is the PQ.PopMax() which can be done within O(lg(n·m)). The costs of heap insertion and skiplist insertion are also O(lg(n·m)), but it can be reduced as the two types of insertions can be done asynchronously via the Heapifier thread. The upper-bound memory requirement is constant as we restrain the maximal heap size to MAX_LEN.
3.3. Bcrypt Trial
Unlike traditional PCFGs which can adopt embarrassing parallelization by simply dividing and distributing the data for different threads, our model cannot be parallelized easily because of the unified heap. The individual processes need coordination. We propose symmetrical multithread collaboration to decouple the password hashing and expanding processes.
In our design, the bcrypt trial component Bcrypter takes a triplet (acc, cand, hash) as input (where acc is the account id, cand is the candidate password and hash is the bcrypt hash to recover), hashes the password and compares it with the leaked bcrypt hash. If they are identical, it reports a cracked account. Otherwise, it pushes the candidate into the lazy generation task queue (i.e., expansion queue) for the Selecter thread to expand. Likewise, Selecter will push a task into the trial queue for Bcrypter to perform hashing when it gets a terminal or pseudo-terminal from the heap. In this way, Bcrypter is, to a large extent, decoupled with heavy operations such as heap sorting.
Since bcrypt hashing is the most time-consuming procedure, and one single bcrypt hashing procedure cannot be accelerated using multiple cores due to the special design of the bcrypt algorithm, we use multiple threads to allow running multiple bcrypt hashing instances. To maximize the utilization of a multi-core system, we set the number of bcrypt trial threads to be the total number of cores minus 2. The other two cores are reserved for the sort and expanding components, i.e., Heapifier and Selecter.
Algorithm 3 outlines the algorithm. The cost of time and space of BcryptTrial is similar to GlobalSort.
| Algorithm 3. Bcrypt Trial. |
| Input:PQ:max-min heap, EQ:expansion queue, TQ:trial queue, sets of recovered accounts Output: Updated queues and sets 1 while True do 2 if TQ!=0 then 3 cand<-TQ.Get() 4 else 5 with PQ.lock do 6 cand<-PQ.PopMax() 7 if not(isPseudTerminal(cand) or isTerminal(cand)) then 8 EQ.Put(cand) 9 break 10 isCracked<-try(cand) 11 if isCracked then 12 Output: <cand.usr:cand.password> 13 if isTerminal(cand) and not isAllUsrTried(cand) then 14 TQ.Put(cand) 15 if not isCracked or not isTerminal(cand) then 16 EQ.Put(cand) |
Example 2.
(Running of Algorithm 3 for the toy example) We use the same data as that in Example 1. Only one single Bcrypter thread is used for simplicity. The execution trace of Bcrypter can be longer than that of Selecter. Note that the bcrypt trial can be much slower than that depicted in our example. There is only one non cross-site account (i.e., usr0), so we can directly drop 123456 after trying it for usr0. We can observe that only terminals and pseudo-terminals can be inserted into Trial Queue.
Combining Examples 1 and 2, Figure 3 shows an illustrative running trace of the entire multi-thread system. After iter i + 1, Selecter’s decisions together with those of Bcrypter(s) will cooperatively result in a new state (Iter i + 1). From the example, we can see that expansion queue and trial queue, which act as candidate caches, are higher prioritized than the heap in every decision procedure of Selecter and Bcrypter. Selecter and Bcrypter can directly fetch cached candidates without accessing the heap, the cost of which is usually very expensive due to lock contentions and the inserting/popping operations followed by sorting. Still, when trial queue is empty, Bcrypter will never take breaks as it can continue to fetch candidates from the heap instead of the cache, which is similar to Selecter.
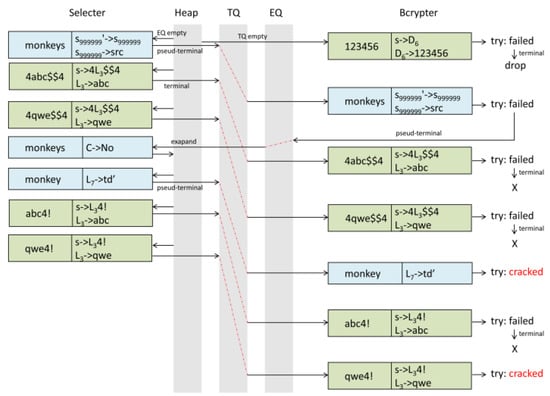
Figure 3.
The coordination of GlobalSort and BcryptTrial in the toy example.
4. Experimental Evaluation
This section presents an experimental evaluation of the techniques proposed in this paper. The goals of the evaluation are comparing the efficiency of the proposed solution with existing works, and studying the impact of the two main techniques: global ranking and parallelization.
4.1. Experimental Setting
We study the recovery performance of the system for given target datasets, for a period of seven days. As discussed in Section 2.4, we use the metric of recovery-speed graph instead of a guess-number graph, in order to better evaluate the performance of slow-hash recovering algorithms.
Methods compared:
- oclHashcat. We use the default configuration of oclHashcat and pipe the output of trawling PCFG [10] into it for guessing. In the default configuration, oclHashcat will not try the next account until all candidates are tried or a correct guess is made for the current account. The PCFG is trained on 1 million passwords randomly sampled from Linkedin.
- TarGuessII+Trawling PCFG. TarGuessII can be parallelized, naively but inefficiently, by segmenting the data and assigning each segment to a core. The password-reused model is trained on cross-site password pairs from the source site of Linkedin to the target site of 000webhost, though it would be better to train distinctly for different target sites. We vary the number of trials per account (k) by 100, 1000, and 10000. The trawling model is similarly trained as the one used for oclHashcat.
- BcryptRecover. This implements our method. The training configuration is the same with TarGuessII.
For the sake of privacy, we will not directly access the sensitive data for study. For each of the data sources, we generate a password list whose data size, account coverage, hashing strategy and password distribution are similar to the original source. We use a VeriClouds-styled list as the source dataset, whose statistical features have been described in Section 3. To compare the effectiveness of the three methods above, we test them on several bcrypt datasets as the targets, whose statistics are as shown in Table 2. The Dropbox-styled list is based on Dropbox, which is a famous service for providing cloud storage. The related breach happened in July 2012 and half of the data is hashed with bcrypt. The AM-styled list is based on Ashley Madison (AM), which is a massive dating site and suffered a breach in July 2015. The Edmodo-styled list is based on Edmodo, which is an education platform hacked in May 2017. Note that AM dump was found to contain a programming error of the hashing procedure, which makes a large fraction of accounts faster to crack [36]. We do not exploit the bug though, for the sake of fair comparison with other datasets. We also consider a CSDN-styled list, which is based on csdn.net (CSDN). CSDN is known as a plain-text password dump, which is well-suited to being used for comparing different hash algorithms by re-hashing the passwords. To evaluate the impact of global ranking and parallelization, we deliberately compare different configurations of our algorithm on the Dropbox-styled target list, still using the VeriClouds-styled list as the source dataset. Experiments are performed in AWS EC2 SMP [37], configured as Ubuntu Server 14.04 LTS 64bit (HVM), SSD Volume Type, with 16 cores/nodes (using the Amazon Compute hardware configuration [38]) and 64 GB RAM. The master node hosts the Selecter, one slave is used for Heapifier, and each of the remaining 14 slaves contains a Bcrypter. TarGuessII and BcryptRecover are written in Python. The number of threads always equals the number of cores, if not explicitly declared in the paper.

Table 2.
The statistics of bcrypt dumps and recovery results after one week.
4.2. Comparison of Various Approaches
This section presents the overall performance of the various approaches on several bcrypt dumps. Table 2 displays the target dataset, the fraction of overlapped accounts with the source corpus, and the cracked fraction after seven days.
The fractions of cross-site accounts in the target dumps are much larger than previous reports. Let’s pick the CSDN-styled list for an illustration, since it appeared in most datasets used for earlier works. For instance, Das et al. [6] only ended up with 6077 unique users of CSDN (which only accounts for 0.1% of the total CSDN dataset) by analyzing a data collection of 10 sites with 7,962,678 records. As with Wang et al. [7], the maximal overlapped CSDN accounts are just the 3.4% accounts from the Dodonew breach in their experimental corpus.
Figure 4 plots the recovery-speed graphs for the three methods to be compared on the three bcrypt datasets, the Dropbox-styled list, the AM-styled list and the Edmodo-styled list. For the Dropbox-styled list, the top speed of BcryptRecover is about 18,000 hashes recovered per hour. The speeds of oclHashcat and TarGuessII + Trawling PCFG remain steadily below 500 (28 and 498 for k = 100, respectively), while BcryptRecover stays at a much higher speed of 7200 than the other methods for the entire seven days. Our method slows down with time, since the most promising passwords can be recovered have been efficiently cracked in a short period of time. To reach the same cracked fraction of 20.1%, our approach takes one week, while the other approaches are unlikely to be feasible for real-world attackers since they would need several months of recovery. For the AM-styled list and the Edmodo-styled list, we see similar trends. The cracked fraction of the Edmodo-styled list is smaller than the Dropbox-styled list and the AM-styled list, since it is an education site used by young children who account for at least two thirds [3] of the total accounts and do not often use MySpace, LinkedIn and other online services that have been breached.
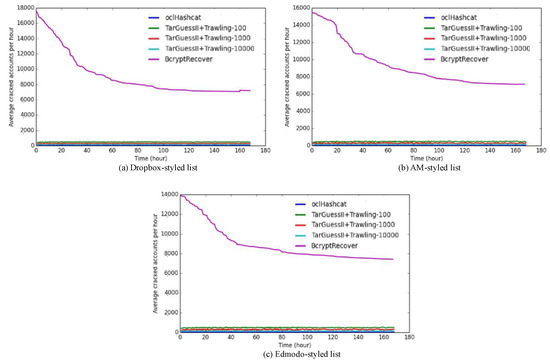
Figure 4.
Overall recovery performance for non-identical passwords (each of the subfigures (a), (b) and (c) corresponds to the recovery-speed graph of the Dropbox-styled list, the AM-styled list and the Edmodo-styled list).
In summary, our solution is faster with orders of magnitude, when the same number of accounts is recovered. The cracked rate of our approach is not worse than existing approaches, which means the quality of the attempts is not sacrificed for the purpose of efficiency.
4.3. Impact of Global Ranking
To evaluate the impact of global ranking, we compare BcryptRecover to two alternative methods using the Dropbox-styled list:
- LocalFullTrans. This is exactly TarGuessII + Trawling PCFG, in which we consider a typical value 1000 for k. All the candidate passwords of a single round are generated and sorted at once before the bcrypt recovery begins, instead of being generated step by step according to the types of transformation rules.
- GlobalFullTrans. It replaces the incremental transformation strategy of BcryptRecover (alias GlobalIncTrans) with the expanding strategy of LocalFullTrans.
The temporal performance is depicted as a recovery-speed graph, and the spatial performance is plotted as number of accounts of the target site vs. the space required by each method.
From Figure 5, we can see again that the usage of a global heap indeed makes promising accounts to be cracked earlier, which gives GlobalIncTrans and GlobalFullTrans a big advantage of cracking speed over LocalFullTrans. However, the full transformation strategy results in a significant delay of the recovery—the average number of accounts cracked per hour of GlobalFullTrans falls far below GlobalIncTrans.
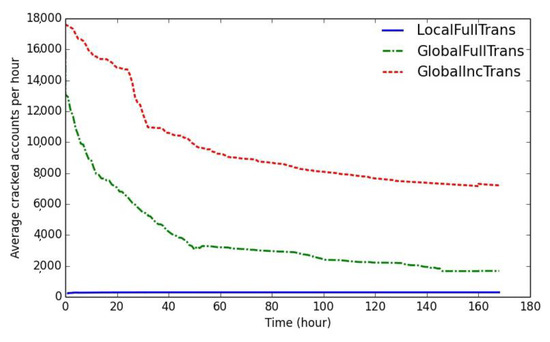
Figure 5.
Temporal impact of global ranking.
To compare the memory consumptions of these methods, we randomly sampled from the Dropbox-styled list a group of test data with varied number of accounts (from 100,000 to 2,600,000 with an incremental step of 500,000). Figure 6 shows that GlobalFullTrans requires 12 GB more space than GlobalIncTrans for the data size of 600,000 accounts and is infeasible for our VM when the number of accounts grows to more than 1,100,000. GlobalIncTrans also uses a huge global heap, but it saves the memory needed for enumerating candidates within a whole round. The memory footprint won’t ever grow after a certain threshold, as GlobalIncTrans manages to materialize extra elements beyond the heap length limit of MAX LEN. LocalFullTrans needs much less memory as compared with the other two methods, since it only uses a small local heap for each account.
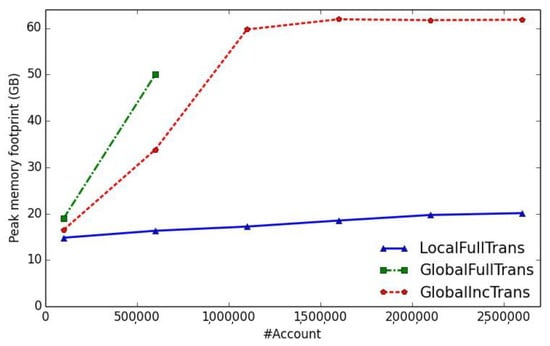
Figure 6.
Spatial impact of global ranking.
4.4. Impact of Parallelization
This section evaluates the impact of multi-thread technique in our solution. We compare the performance with varied number of threads on the Dropbox-styled list. Besides Bcrypter threads, two other threads should be reserved for Selecter and Heapifier.
From the results in Figure 7, it is clear that the performance becomes worse when we reduce the number of threads, but our solution always outperforms the baseline, as shown in Figure 4a. When the total #threads exceeds the #cores, little gain is achieved by increasing #threads. The reason lies in the fact that bcrypt hashing requires a lot of memory per instance thus making it hard for CPU-based parallelization. Moreover, the lock contention also becomes severe when the number of threads scales up.
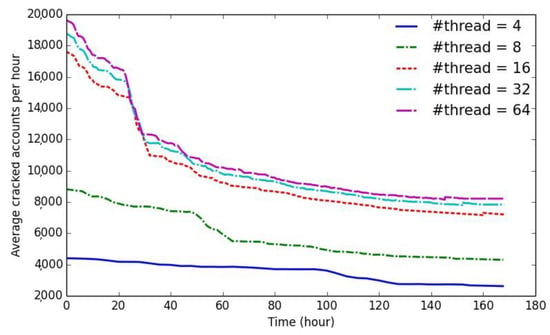
Figure 7.
Multi-thread performance.
5. Conclusions
In this work, we attack the problem of speed boost for massive-scale slow-hash recovery. We largely increase the number of accounts can be recovered within a limited period of time, by prioritizing weak accounts in a concurrent manner. Several optimization methods are proposed to make this global prioritization parallelizable and scalable. Our method can also serve as a better metric, among others, for evaluating the strength of the credential storage policy taken by web services.
The VeriClouds corpus mentioned in our study, however, is still a small part of the whole corpus that the hacker community can gather with the ever-growing number of breaching incidents. The potential fraction of a target dump that can be recovered, hence conjecturally, could be far beyond the results presented in this paper. Our result has a very practical implication of real-world threats. Generally, an attacker needs to make a trade-off between the recovery profit and the cost. For example, given t days to recover u accounts on an AWS VM rent by r dollars per day and the profit gained per account as p, the total profit versus total cost becomes u·p vs. t·r. The attacker has to crack as many accounts as possible within the same time for more gains. In the service providers’ view, on the other hand, by accurately modeling the attacker’s behavior, they can better manage the risk of the database. One policy he can conduct is to carefully determine the work factors by balancing the load of servers and the strength of dataset, which can be evaluated using metrics like our proposed recovery model. Another countermeasure is to proactively detect and supervise weak accounts before financial and reputational damage to the organization become reality.
Future works on this topic may include mining deeper into the source data. Firstly, we can match accounts using some kind of correlational analysis [39,40,41,42,43] instead of simply using email addresses. Secondly, other TarGuess models [7], which utilize PII info, can also be used to improve the result of the proposed guessing algorithm.
Author Contributions
T.W., implemented the proposed method and composed the paper; Y.Y., revised the paper; C.W., provided the idea and helped with the composition of the paper; R.W., contributes partially to the idea and maintains the dataset used in the paper.
Funding
This research was supported by the Mobile Research Funding of the Chinese Education Ministry (MCM) under Grant No. MCM20170404.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Why You Shouldn’t Panic about Dropbox Leaking 68 Million Passwords. Available online: https://www.forbes.com/sites/thomasbrewster/2016/08/31/dropbox-hacked-but-its-not-thatbad/#675839355576 (accessed on 8 May 2017).
- Lessons Learned from Cracking 4000 Ashley Madison Passwords. Available online: https://arstechnica.com/informationtechnology/2015/08/cracking-all-hacked-ashleymadison-passwords-could-take-a-lifetime/ (accessed on 15 December 2017).
- Deep Dive into the Edmodo Data Breach. Available online: https://medium.com/4iqdelvedeep/deep-dive-into-theedmodo-data-breach-f1207c415ffb (accessed on 22 November 2017).
- Hashcat. Available online: https://hashcat.net/oclhashcat/ (accessed on 1 September 2017).
- John the Ripper. Available online: http://www.openwall.com/john/ (accessed on 1 December 2017).
- Das, A.; Bonneau, J.; Caesar, M.; Borisov, N.; Wang, X. The tangled web of password reuse. In Proceedings of the NDSS 2014, San Diego, CA, USA, 23–26 February 2014. [Google Scholar]
- Wang, D.; Zhang, Z.; Wang, P.; Yan, J.; Huang, X. Targeted online password guessing: An underestimated threat. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security (CCS 2016), Vienna, Austria, 24–28 October 2016; pp. 1242–1254. [Google Scholar]
- Han, W.; Li, Z.; Ni, M.; Gu, G.; Xu, W. Shadow attacks based on password reuses: A quantitative empirical view. IEEE Trans. Depend. Secur. Comput. 2016. [Google Scholar] [CrossRef]
- VeriClouds Whitepapers & Resources. Available online: https://www.vericlouds.com/resources/ (accessed on 3 March 2018).
- Weir, M.; Aggarwal, S.; de Medeiros, B.; Glodek, B. Password cracking using probabilistic context-free grammars. In Proceedings of the 2009 30th IEEE Symposium on Security and Privacy, Berkeley, CA, USA, 17–20 May 2009; pp. 391–405. [Google Scholar]
- Narayanan, A.; Shmatikov, V. Fast dictionary attacks on passwords using time-space tradeoff. In Proceedings of the 12th ACM Conference on Computer and Communications Security (CCS 2005), Alexandria, VA, USA, 7–11 November 2005; pp. 364–372. [Google Scholar]
- Castelluccia, C.; Durmuth, M.; Perito, D. Adaptive password-strength meters from Markov models. In Proceedings of the 2012 Network and Distributed Systems Security Symposium, San Diego, CA, USA, 5–8 February 2012; pp. 23–26. [Google Scholar]
- Ma, J.; Yang, W.; Luo, M.; Li, N. A study of probabilistic password models. In Proceedings of the 2014 IEEE Symposium on Security and Privacy, San Jose, CA, USA, 18–21 May 2014; pp. 689–704. [Google Scholar]
- Komanduri, S. Modeling the Adversary to Evaluate Password Strengh with Limited Samples. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2016. [Google Scholar]
- Melicher, W.; Ur, B.; Segreti, S.; Komanduri, S.; Bauer, L.; Christin, N.; Cranor, L. Fast, lean and accurate: Modeling password guessability using neural networks. In Proceedings of the 25th USENIX Conference on Security Symposium, Austin, TX, USA, 10–12 August 2016; pp. 1–17. [Google Scholar]
- Ur, B.; Segreti, S.M.; Bauer, L.; Christin, N.; Cranor, L.F.; Komanduri, S.; Kurilova, D.; Mazurek, M.L.; Melicher, W.; Shay, R. Measuring real-world accuracies and biases in modeling password guessability. In Proceedings of the 24th USENIX Conference on Security Symposium (USENIX SEC 2015), Washington, DC, USA, 12–14 August 2015; pp. 463–481. [Google Scholar]
- Wang, D.; Wang, P. On the implications of Zipf’s law in passwords. In Proceedings of the European Symposium on Research in Computer Security, Heraklion, Greece, 26–30 September 2016; pp. 1–21. [Google Scholar]
- Zhang, Y.; Monrose, F.; Reiter, M. The security of modern password expiration: An algorithmic framework and empirical analysis. In Proceedings of the 17th ACM conference on Computer and Communications Security (CCS 2010), Chicago, IL, USA, 4–8 October 2010; pp. 176–186. [Google Scholar]
- Wang, C.; Jan, S.T.K.; Hu, H.; Wang, G. Empirical analysis of password reuse and modification across online service. arXiv, 2017; arXiv:1706.01939. [Google Scholar]
- Harsha, B.; Blocki, J. Just in Time Hashing. In Proceedings of the 2018 IEEE European Symposium on Security and Privacy (EuroS&P), London, UK, 24–26 April 2018; pp. 368–383. [Google Scholar]
- Li, Y.; Wang, H.; Sun, K. A study of personal information in human-chosen passwords and its security implications. In Proceedings of the 35th Annual IEEE International Conference on Computer Communications (INFOCOM 2016), San Francisco, CA, USA, 10–14 April 2016; pp. 1–9. [Google Scholar]
- Oechslin, P. Making a faster cryptanalytic time-memory trade-off. In Proceedings of the Annual International Cryptology Conference (CRYPTO 2003), Santa Barbara, CA, USA, 17–21 August 2003; pp. 617–630. [Google Scholar]
- Provos, N.; Mazières, D. A future-adaptable password scheme. In Proceedings of the USENIX Annual Technical Conference 1999 (FREENIX Track), Monterey, CA, USA, 6–11 June 1999; pp. 81–91. [Google Scholar]
- Percival, C. Stronger Key Derivation via Sequential Memory-Hard Functions. Presentation at BSDCan 2009. Available online: http://www.tarsnap.com/scrypt/scrypt.pdf (accessed on 10 May 2018).
- Kaliski, B. PKCS #5: Password-Based Cryptography Specification Version 2.0. RFC 2898. 2000. Available online: http://tools.ietf.org/html/rfc2898 (accessed on 6 April 2018).
- Biryukov, A.; Dinu, D.; Khovratovich, D. Argon2: New generation of memory-hard functions for password hashing and other applications. In Proceedings of the 2016 IEEE European Symposium on Security and Privacy (EuroS&P), Saarbrucken, Germany, 21–24 March 2016; pp. 292–302. [Google Scholar]
- Steube, J. PRINCE: Modern Password Guessing Algorithm. Presentation at Passwords 2014. Available online: https://hashcat.net/events/p14-trondheim/prince-attack.pdf (accessed on 16 December 2017).
- Malvoni, K.; Designer, S.; Knezovic, J. Are your passwords safe: Energy-efficient bcrypt cracking with low-Cost parallel hardware. In Proceedings of the 8th USENIX Workshop on Offensive Technologies (WOOT 2014), San Diego, CA, USA, 19 August 2014. [Google Scholar]
- Blocki, J.; Harsha, B.; Zhou, S. On the economics of offline password cracking. In Proceedings of the 2018 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 20–24 May 2018. [Google Scholar]
- Blocki, J.; Harsha, B.; Kang, S.; Lee, S.; Xing, L.; Zhou, S. Data-Independent Memory Hard Functions: New Attacks and Stronger Constructions. 2018. Available online: https://eprint.iacr.org/2018/944 (accessed on 10 May 2018).
- Weir, M.; Aggarwal, S.; Collins, M.; Stern, H. Testing metrics for password creation policies by attacking large sets of revealed passwords. In Proceedings of the 17th ACM Conference on Computer and Communications Security (CCS 2010), Chicago, IL, USA, 4–8 October 2010; pp. 162–175. [Google Scholar]
- Min-Max Heap. Available online: https://en.wikipedia.org/wiki/Min-max_heap (accessed on 10 May 2018).
- Skip List. Available online: https://en.wikipedia.org/wiki/Skip_list (accessed on 3 April 2018).
- Levenshtein Distance. Available online: https://en.wikipedia.org/wiki/Levenshtein_distance (accessed on 10 May 2018).
- Heapsort. Available online: https://en.wikipedia.org/wiki/Heapsort (accessed on 3 April 2018).
- Once Seen as Bulletproof, 11 Million+ Ashley Madison Passwords Already Cracked. Available online: https://arstechnica.com/informationtechnology/2015/09/once-seen-as-bulletproof-11-million-ashley-madison-passwords-already-cracked/ (accessed on 11 December 2017).
- AWS EC2. Available online: https://aws.amazon.com/ec2/?ft=n (accessed on 22 August 2017).
- Amazon EC2 Instance Types. Available online: https://aws.amazon.com/ec2/instance-types/?nc1=h_ls (accessed on 10 May 2018).
- Ding, Z.; Jia, Y.; Zhou, B.; Han, Y. Mining topical influencers based on the multi-relational network in micro-blogging sites. China Commun. 2013. [Google Scholar] [CrossRef]
- Wang, P.; Lu, K.; Li, G.; Zhou, X. DFTracker: Detecting double-fetch bugs by multi-taint parallel tracking. Front. Comput. Sci. 2018, 1–17. [Google Scholar] [CrossRef]
- Wu, Z.; Lu, K.; Wang, X.; Zhou, X. Collaborative technique for concurrency bug detection. Int. J. Parallel Program. 2015, 43, 260–285. [Google Scholar] [CrossRef]
- Wu, T.; Yang, Y. Detecting android inter-app data leakage via compositional concolic walking. J. Autosoft. 2019. [Google Scholar] [CrossRef]
- Wu, Z.; Lu, K.; Wang, X.; Zhou, X.; Chen, C. Detecting harmful data races through parallel verification. J. Supercomput. 2015, 71, 2922–2943. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).