Stability Analysis of Darcy-Forchheimer Flow of Casson Type Nanofluid Over an Exponential Sheet: Investigation of Critical Points
Abstract
1. Introduction
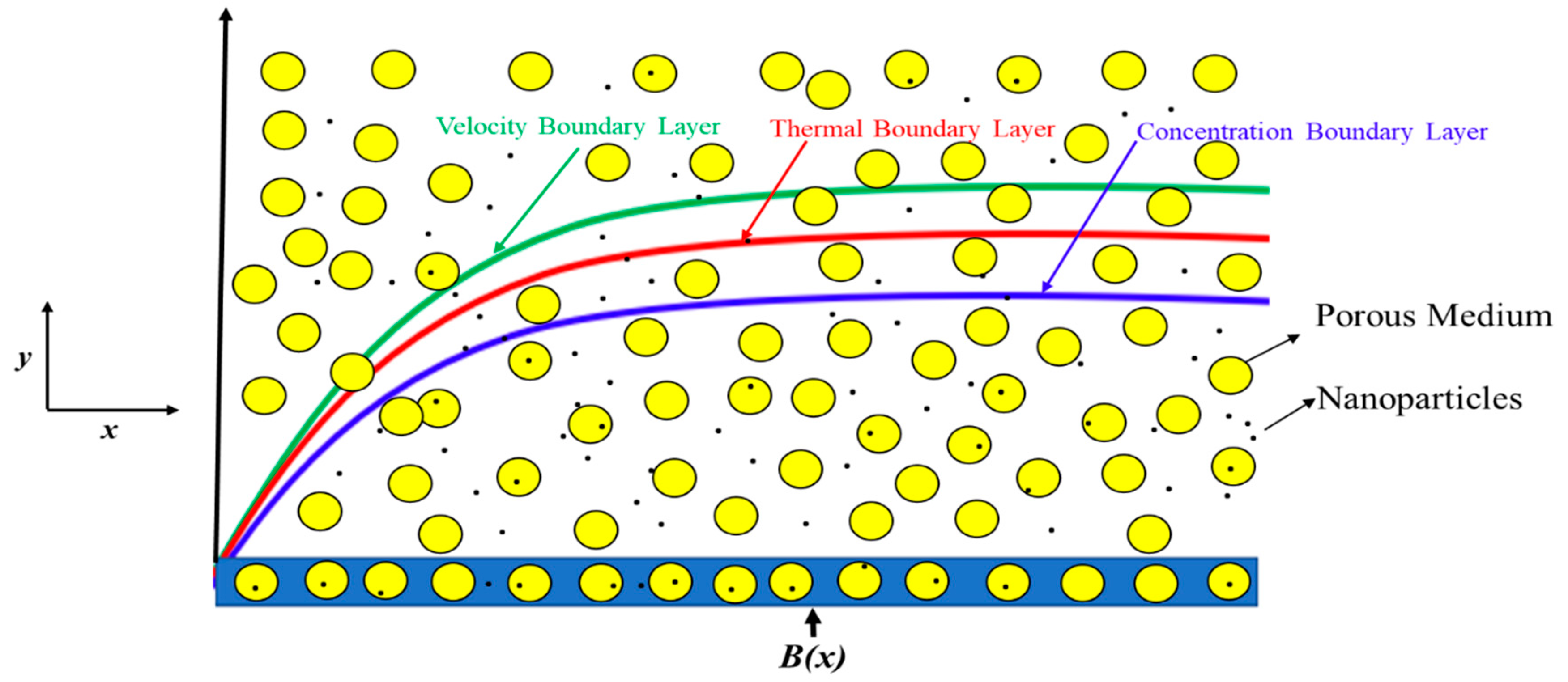
2. Mathematical Description of the Problem
3. Linear Stability Analysis
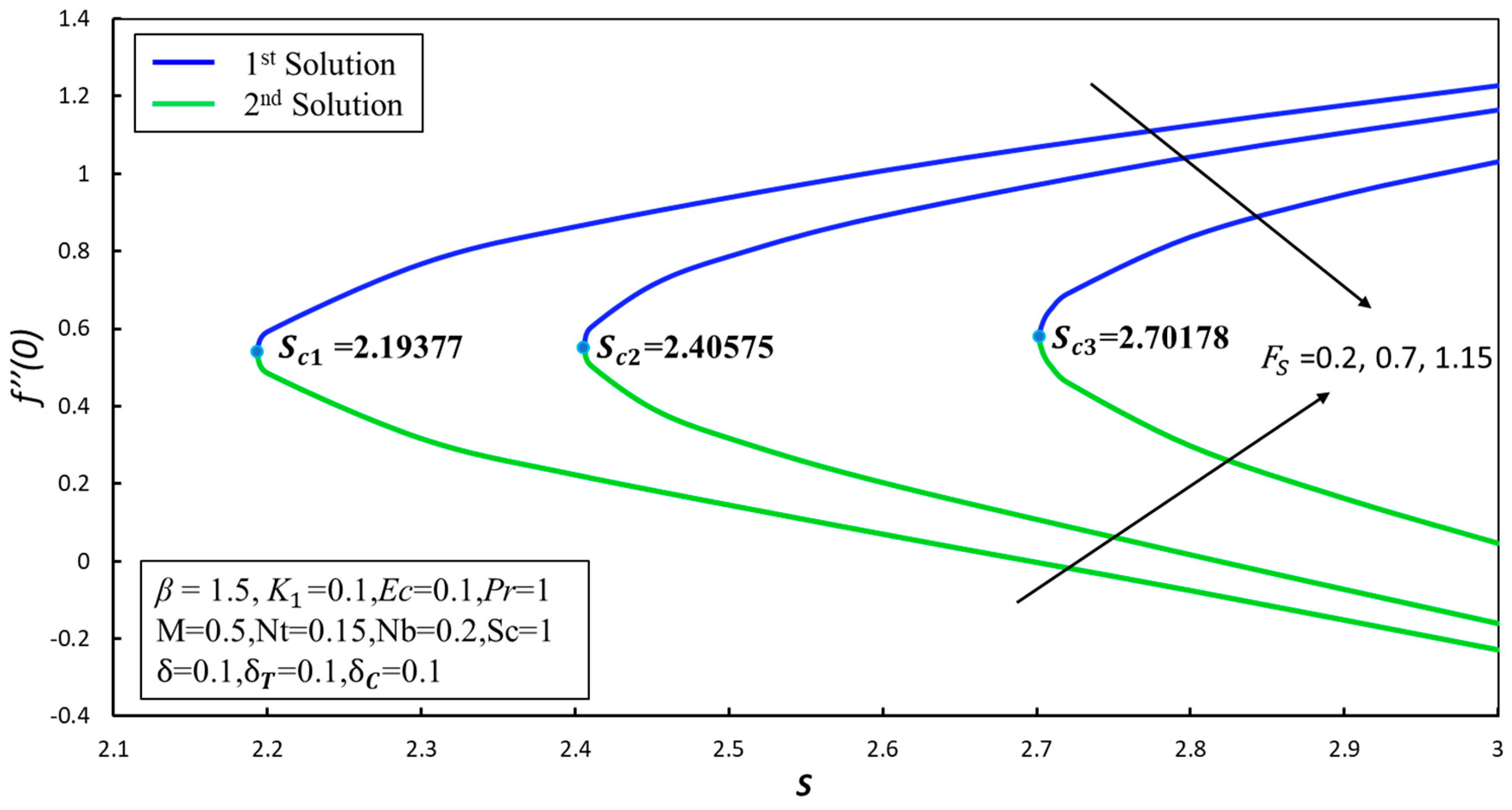
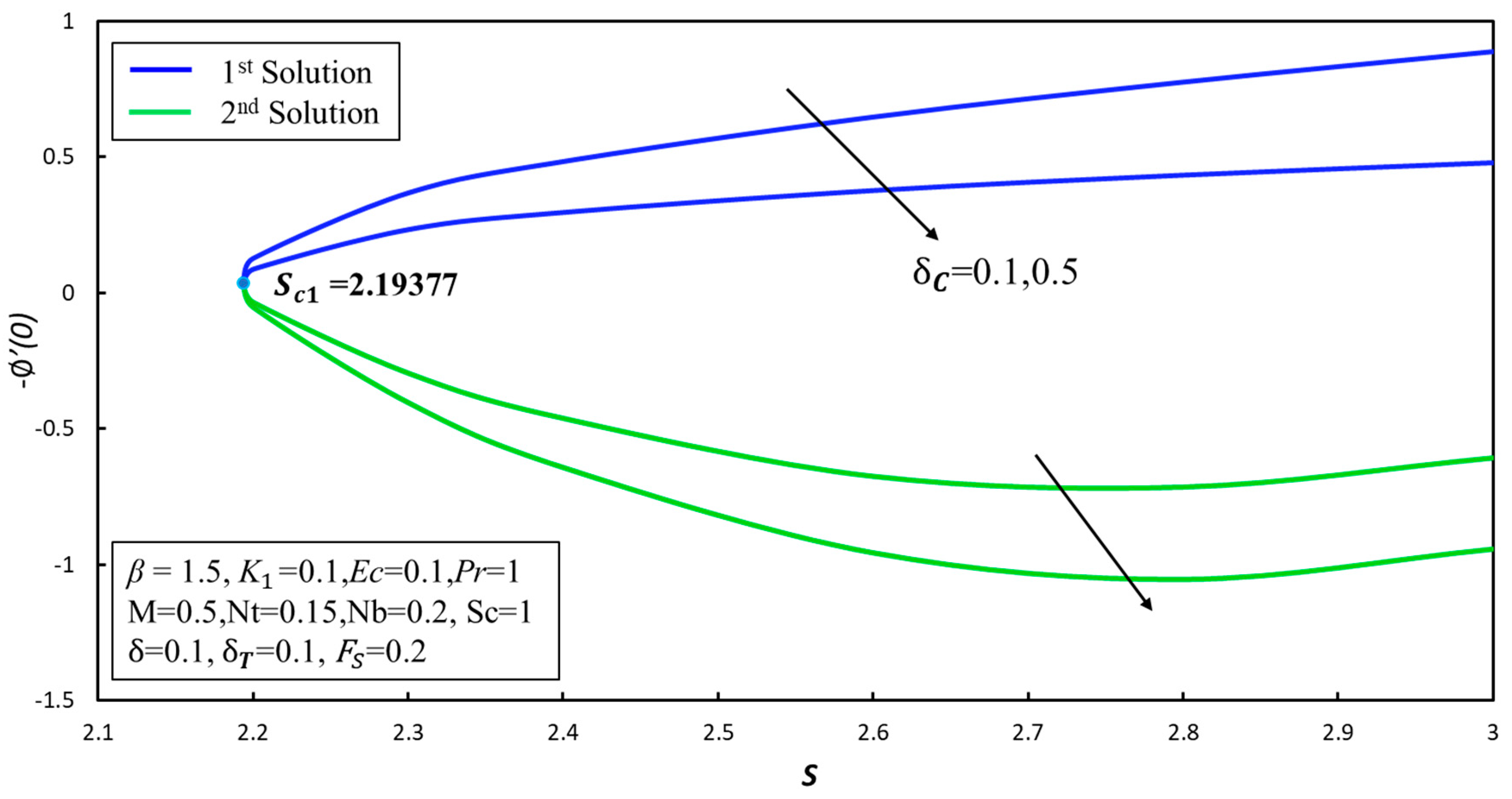
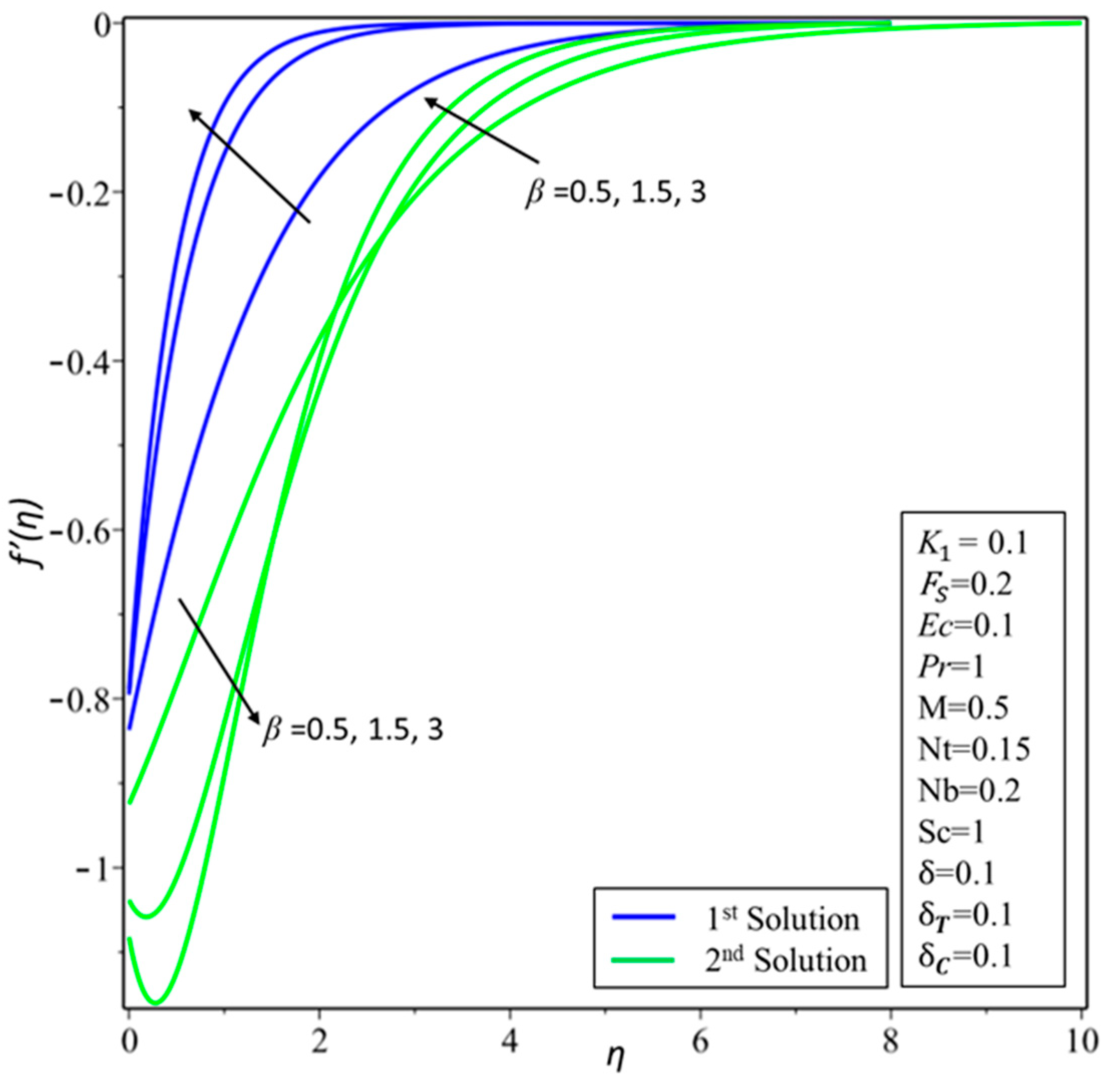
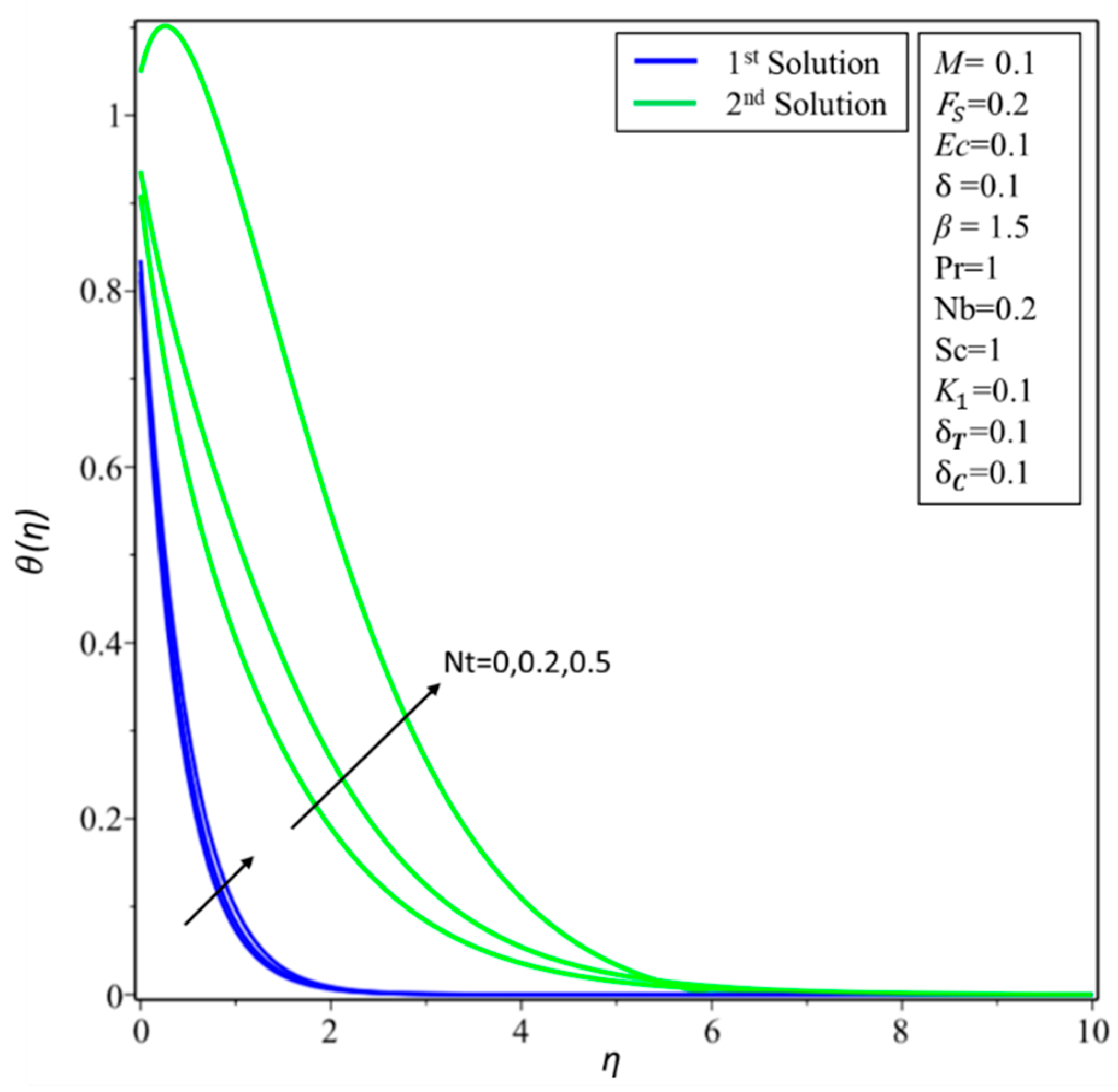
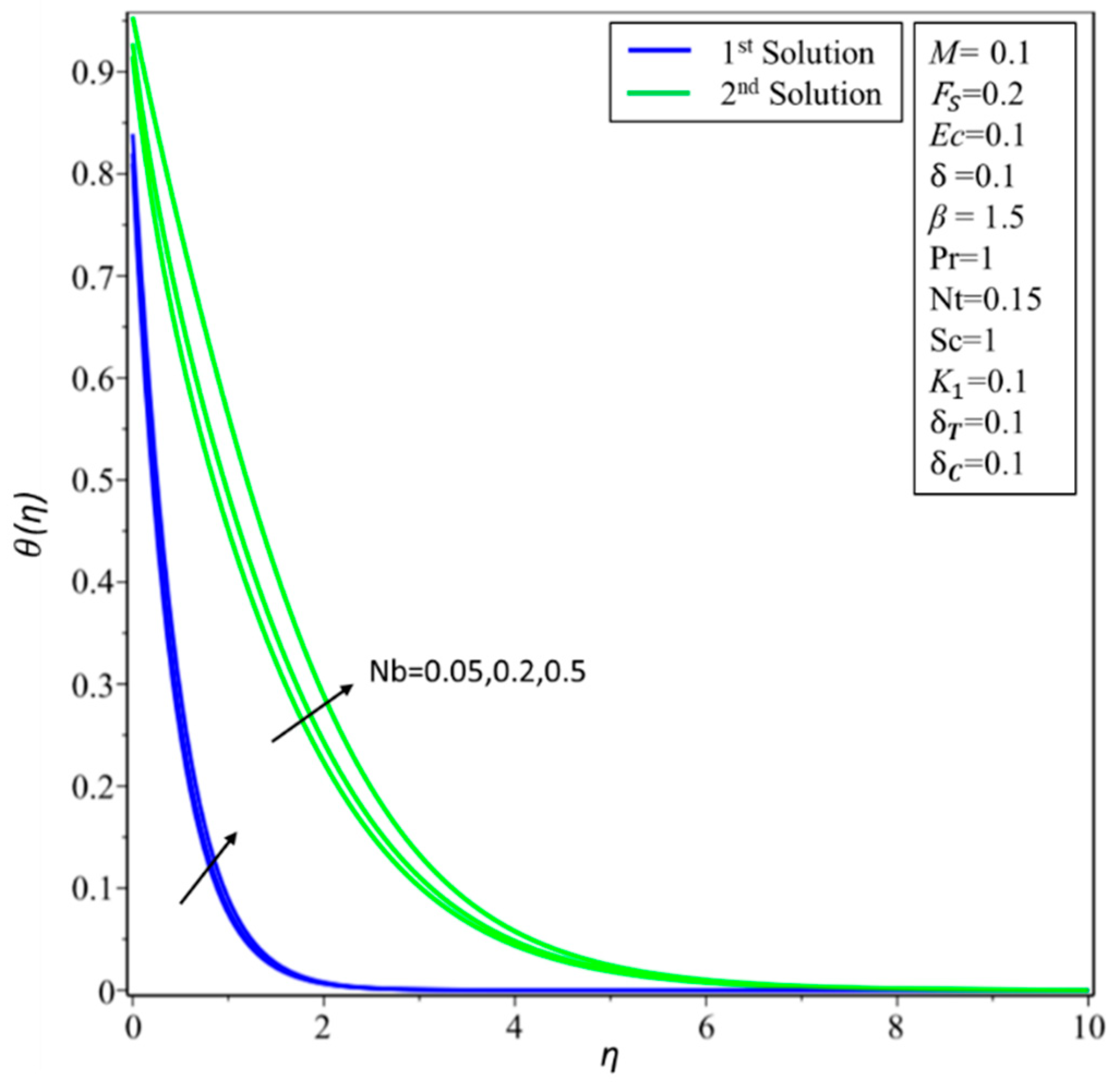
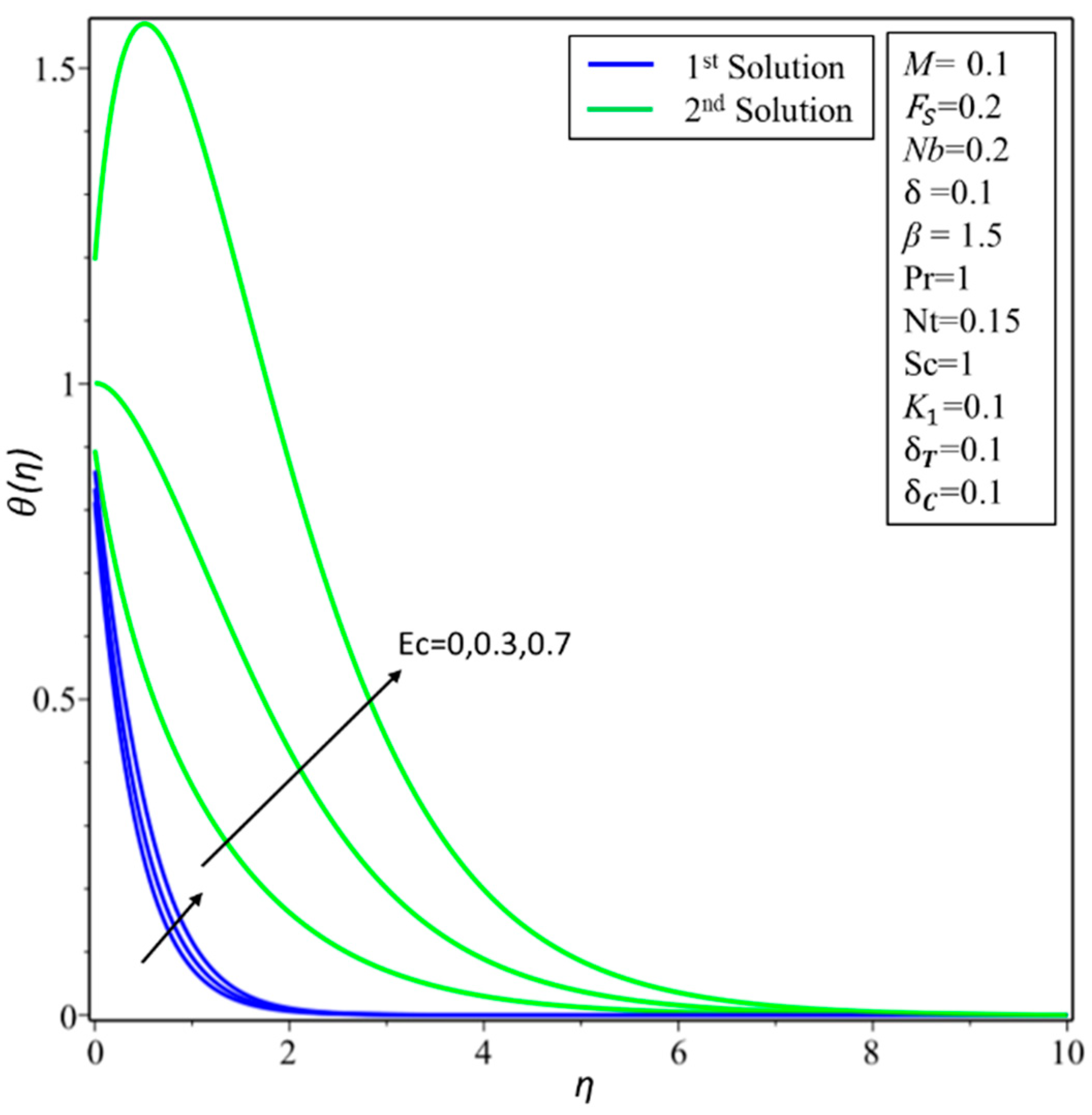
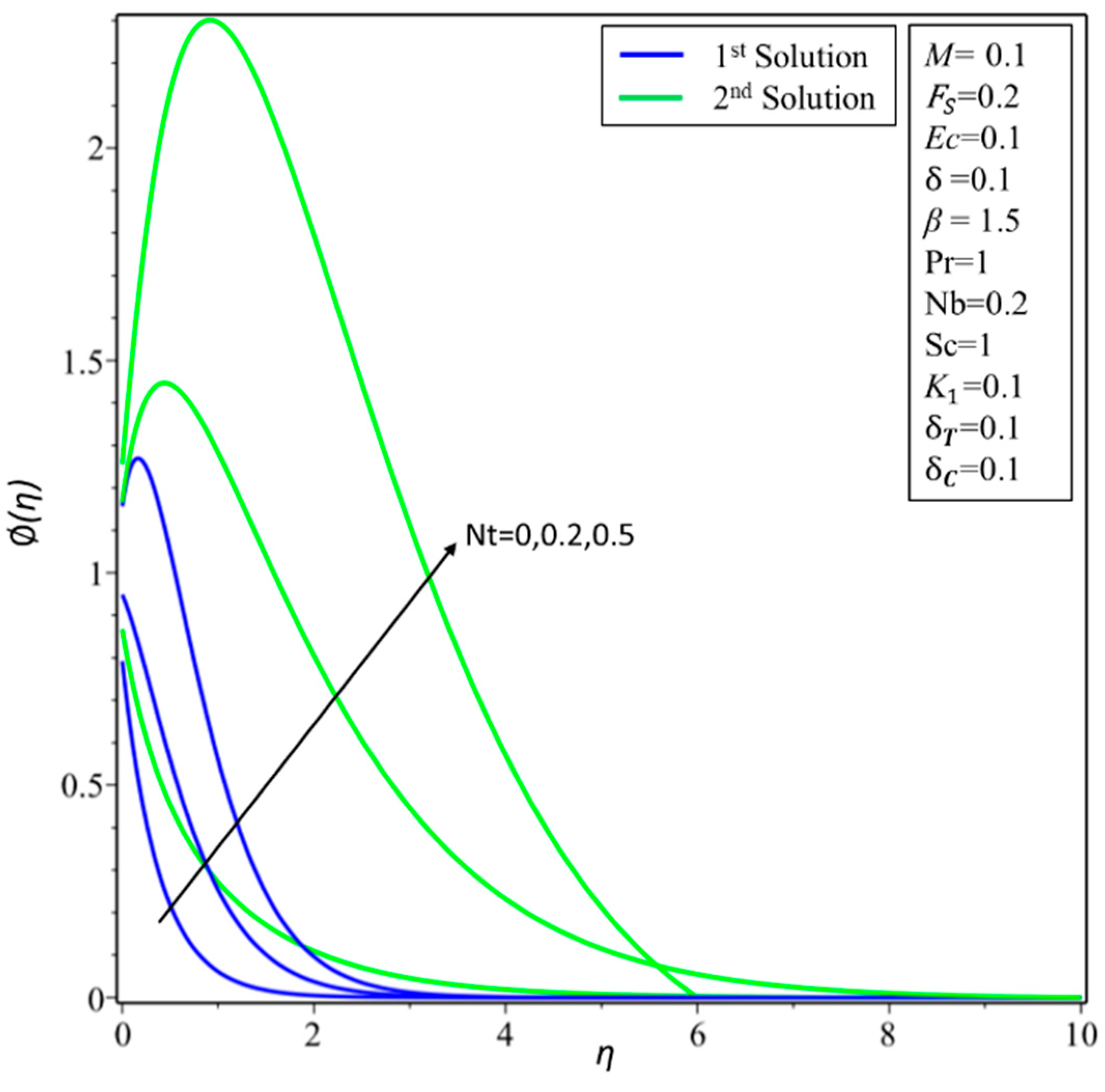
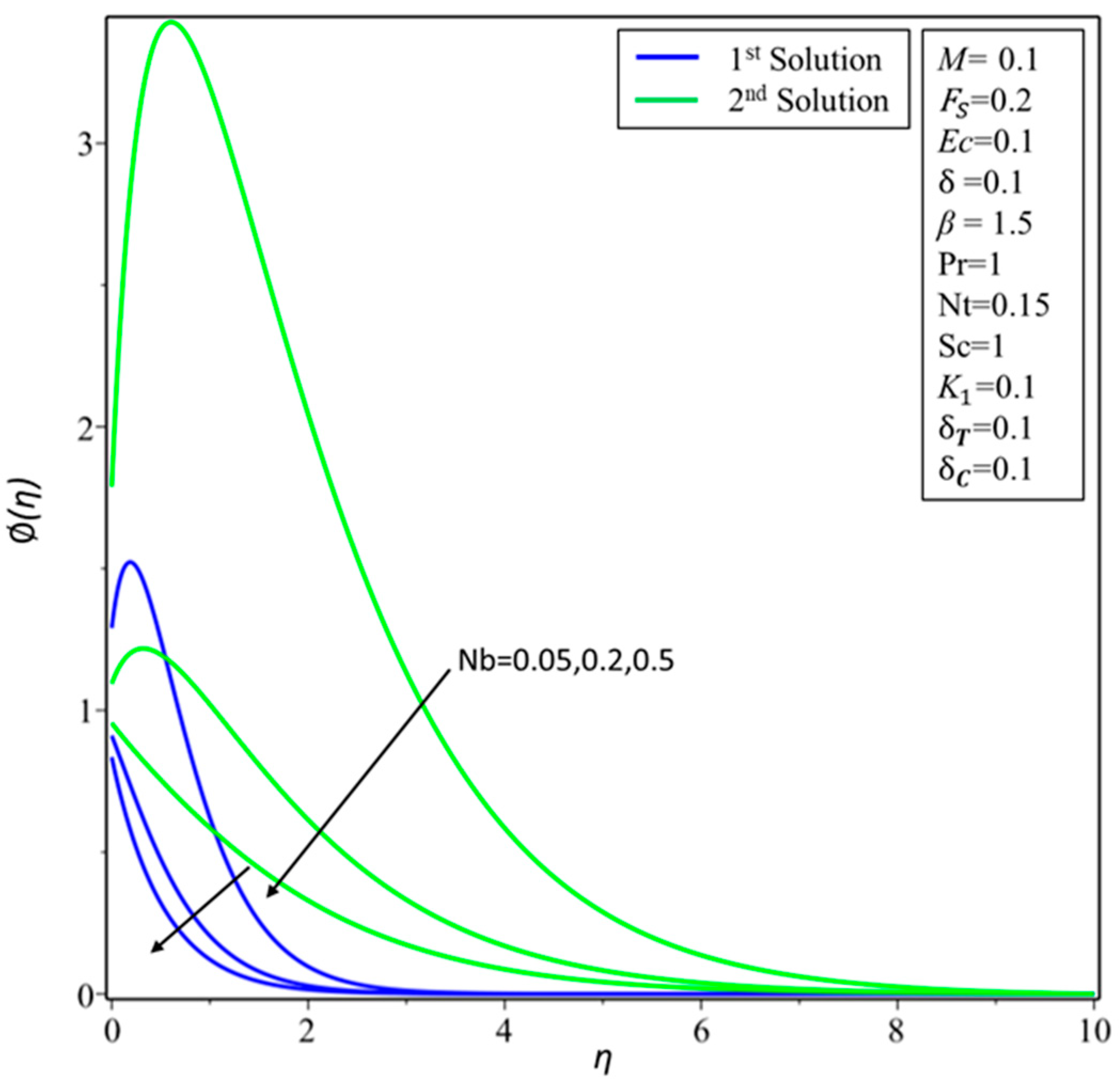
4. Result and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| u, v | velocity components | Ec | Eckert number |
| K | permeability of the porous medium | variable concentration at the sheet | |
| b | local inertia coefficient | local Reynolds number | |
| T | Temperature | skin friction coefficient | |
| a constant | local Nusselt number | ||
| variable temperature at the sheet | S | injunction/suction parameter | |
| ambient temperature | Greek letters | ||
| C | Concentration | Casson parameter | |
| a constant | smallest eigen value | ||
| ambient concentration | Stability transformed variable | ||
| Fluid’s yield stress | unknown eigen value | ||
| B(x) | magnetic field | stream function | |
| M | Hartmann number | Velocity slip | |
| Pr | Prandtl number | Thermal slip | |
| Brownian diffusion | Concentration slip | ||
| thermophoretic diffusion | Plastic dynamic viscosity | ||
| suction/injection velocity | Porosity | ||
| local Sherwood number | transformed variable | ||
| Brownian motion parameter | thermal diffusivity | ||
| thermophoresis parameter | The product of the component of deformation rate with itself | ||
| Schmidt number |
References
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: New York, NY, USA, 2006; Volume 3. [Google Scholar]
- Muskat, M. The Flow of Homogeneous Fluids through Porous Media. No. 532.5 M88. 1946. Available online: https://catalog.hathitrust.org/Record/009073808 (accessed on 30 December 2018).
- Bakar, S.A.; Arifin, N.M.; Nazar, R.; Ali, F.M.; Pop, I. Forced convection boundary layer stagnation-point flow in Darcy-Forchheimer porous medium past a shrinking sheet. Front. Heat Mass Transf. 2016, 7, 38. [Google Scholar]
- Hayat, T.; Muhammad, T.; Al-Mezal, S.; Liao, S.J. Darcy-Forchheimer flow with variable thermal conductivity and Cattaneo-Christov heat flux. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 2355–2369. [Google Scholar] [CrossRef]
- Muhammad, T.; Alsaedi, A.; Shehzad, S.A.; Hayat, T. A revised model for Darcy-Forchheimer flow of Maxwell nanofluid subject to convective boundary condition. Chin. J. Phys. 2017, 55, 963–976. [Google Scholar] [CrossRef]
- Hayat, T.; Saif, R.S.; Ellahi, R.; Muhammad, T.; Alsaedi, A. Simultaneous effects of melting heat and internal heat generation in stagnation point flow of Jeffrey fluid towards a nonlinear stretching surface with variable thickness. Int. J. Therm. Sci. 2018, 132, 344–354. [Google Scholar] [CrossRef]
- Alshomrani, A.S.; Ullah, M.Z. Effects of homogeneous-heterogeneous reactions and convective condition in Darcy-Forchheimer flow of carbon nanotubes. J. Heat Transf. 2019, 141, 012405. [Google Scholar] [CrossRef]
- Hayat, T.; Saif, R.S.; Ellahi, R.; Muhammad, T.; Ahmad, B. Numerical study for Darcy-Forchheimer flow due to a curved stretching surface with Cattaneo-Christov heat flux and homogeneous-heterogeneous reactions. Results Phys. 2017, 7, 2886–2892. [Google Scholar] [CrossRef]
- Seth, G.S.; Mandal, P.K. Hydromagnetic rotating flow of Casson fluid in Darcy-Forchheimer porous medium. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2018; Volume 192, p. 02059. [Google Scholar]
- Alarifi, I.M.; Abokhalil, A.G.; Osman, M.; Lund, L.A.; Ayed, M.B.; Belmabrouk, H.; Tlili, I. MHD Flow and Heat Transfer over Vertical Stretching Sheet with Heat Sink or Source Effect. Symmetry 2019, 11, 297. [Google Scholar] [CrossRef]
- Ellahi, R.; Riaz, A. Analytical solutions for MHD flow in a third-grade fluid with variable viscosity. Math. Comput. Model. 2010, 52, 1783–1793. [Google Scholar] [CrossRef]
- Ellahi, R.; Tariq, M.H.; Hassan, M.; Vafai, K. On boundary layer nano-ferroliquid flow under the influence of low oscillating stretchable rotating disk. J. Mol. Liq. 2017, 229, 339–345. [Google Scholar] [CrossRef]
- Hsiao, K.L. Combined electrical MHD heat transfer thermal extrusion system using Maxwell fluid with radiative and viscous dissipation effects. Appl. Therm. Eng. 2017, 112, 1281–1288. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Abelman, S.; Ganji, D.D. Numerical simulation of MHD nanofluid flow and heat transfer considering viscous dissipation. Int. J. Heat Mass Transf. 2014, 79, 212–222. [Google Scholar] [CrossRef]
- Charrier, E.E.; Pogoda, K.; Wells, R.G.; Janmey, P.A. Control of cell morphology and differentiation by substrates with independently tunable elasticity and viscous dissipation. Nat. Commun. 2018, 9, 449. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Kumar, R.; Shehzad, S.A.; Sheikholeslami, M. Rotating frame analysis of radiating and reacting ferro-nanofluid considering Joule heating and viscous dissipation. Int. J. Heat Mass Transf. 2018, 120, 540–551. [Google Scholar] [CrossRef]
- Reddy, M.; Reddy, S.; Rama, G. Micropolar fluid flow over a nonlinear stretching convectively heated vertical surface in the presence of Cattaneo-Christov heat flux and viscous dissipation. Front. Heat Mass Transf. (FHMT) 2017, 8, 20. [Google Scholar]
- Khan, M.I.; Hayat, T.; Khan, M.I.; Alsaedi, A. A modified homogeneous-heterogeneous reaction for MHD stagnation flow with viscous dissipation and Joule heating. Int. J. Heat Mass Transf. 2017, 113, 310–317. [Google Scholar] [CrossRef]
- Saqib, M.; Ali, F.; Khan, I.; Sheikh, N.A. Heat and mass transfer phenomena in the flow of Casson fluid over an infinite oscillating plate in the presence of first-order chemical reaction and slip effect. Neural Comput. Appl. 2018, 30, 2159–2172. [Google Scholar] [CrossRef]
- le Roux, C. Existence and uniqueness of the flow of second-grade fluids with slip boundary conditions. Arch. Ration. Mech. Anal. 1999, 148, 309–356. [Google Scholar] [CrossRef]
- Soltani, F.; Yilmazer, Ü. Slip velocity and slip layer thickness in flow of concentrated suspensions. J. Appl. Polym. Sci. 1998, 70, 515–522. [Google Scholar] [CrossRef]
- Khan, W.A.; Ismail, A.I.; Uddin, M.J. Melting and second order slip effect on convective flow of nanofluid past a radiating stretching/shrinking sheet. Propuls. Power Res. 2018, 7, 60–71. [Google Scholar]
- Alamri, S.Z.; Ellahi, R.; Shehzad, N.; Zeeshan, A. Convective radiative plane Poiseuille flow of nanofluid through porous medium with slip: An application of Stefan blowing. J. Mol. Liq. 2019, 273, 292–304. [Google Scholar] [CrossRef]
- Yunianto, B.; Tauviqirrahman, M.; Wicaksono, W.A. CFD analysis of partial slip effect on the performance of hydrodynamic lubricated journal bearings. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2018; Volume 204, p. 04014. [Google Scholar]
- Ellahi, R.; Hussain, F. Simultaneous effects of MHD and partial slip on peristaltic flow of Jeffery fluid in a rectangular duct. J. Magn. Magn. Mater. 2015, 393, 284–292. [Google Scholar] [CrossRef]
- Khan, M.I.; Hayat, T.; Waqas, M.; Khan, M.I.; Alsaedi, A. Entropy generation minimization (EGM) in nonlinear mixed convective flow of nanomaterial with Joule heating and slip condition. J. Mol. Liq. 2018, 256, 108–120. [Google Scholar] [CrossRef]
- Ullah, I.; Shafie, S.; Khan, I. Effects of slip condition and Newtonian heating on MHD flow of Casson fluid over a nonlinearly stretching sheet saturated in a porous medium. J. King Saud Univ. Sci. 2017, 29, 250–259. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Zeitschrift für angewandte Mathematik und Physik ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Miklavčič, M.; Wang, C. Viscous flow due to a shrinking sheet. Q. Appl. Math. 2006, 64, 283–290. [Google Scholar] [CrossRef]
- Naveed, M.; Abbas, Z.; Sajid, M.; Hasnain, J. Dual Solutions in Hydromagnetic Viscous Fluid Flow Past a Shrinking Curved Surface. Arab. J. Sci. Eng. 2018, 43, 1189–1194. [Google Scholar] [CrossRef]
- Jusoh, R.; Nazar, R.; Pop, I. Three-dimensional flow of a nanofluid over a permeable stretching/shrinking surface with velocity slip: A revised model. Phys. Fluids 2018, 30, 033604. [Google Scholar] [CrossRef]
- Othman, N.A.; Yacob, N.A.; Bachok, N.; Ishak, A.; Pop, I. Mixed convection boundary-layer stagnation point flow past a vertical stretching/shrinking surface in a nanofluid. Appl. Therm. Eng. 2017, 115, 1412–1417. [Google Scholar] [CrossRef]
- Khan, M.; Hafeez, A. A review on slip-flow and heat transfer performance of nanofluids from a permeable shrinking surface with thermal radiation: Dual solutions. Chem. Eng. Sci. 2017, 173, 1–11. [Google Scholar] [CrossRef]
- Naganthran, K.; Nazar, R.; Pop, I. Stability analysis of impinging oblique stagnation-point flow over a permeable shrinking surface in a viscoelastic fluid. Int. J. Mech. Sci. 2017, 131, 663–671. [Google Scholar] [CrossRef]
- Qing, J.; Bhatti, M.M.; Abbas, M.A.; Rashidi, M.M.; Ali, M.E.S. Entropy generation on MHD Casson nanofluid flow over a porous stretching/shrinking surface. Entropy 2016, 18, 123. [Google Scholar] [CrossRef]
- Rahman, M.M.; Roşca, A.V.; Pop, I. Boundary layer flow of a nanofluid past a permeable exponentially shrinking/stretching surface with second order slip using Buongiorno’s model. Int. J. Heat Mass Transf. 2014, 77, 1133–1143. [Google Scholar] [CrossRef]
- Rahman, M.M.; Rosca, A.V.; Pop, I. Boundary layer flow of a nanofluid past a permeable exponentially shrinking surface with convective boundary condition using Buongiorno’s model. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 299–319. [Google Scholar] [CrossRef]
- Yasin, M.H.M.; Ishak, A.; Pop, I. Boundary layer flow and heat transfer past a permeable shrinking surface embedded in a porous medium with a second-order slip: A stability analysis. Appl. Therm. Eng. 2017, 115, 1407–1411. [Google Scholar] [CrossRef]
- Raza, J.; Rohni, A.M.; Omar, Z. A note on some solutions of copper-water (cu-water) nanofluids in a channel with slowly expanding or contracting walls with heat transfer. Math. Comput. Appl. 2016, 21, 24. [Google Scholar] [CrossRef]
- Raza, J.; Rohni, A.M.; Omar, Z.; Awais, M. Rheology of the Cu-H2O nanofluid in porous channel with heat transfer: Multiple solutions. Phys. E: Low-Dimens. Syst. Nanostruct. 2017, 86, 248–252. [Google Scholar] [CrossRef]
- Raza, J.; Rohni, A.M.; Omar, Z. Rheology of micropolar fluid in a channel with changing walls: Investigation of multiple solutions. J. Mol. Liq. 2016, 223, 890–902. [Google Scholar] [CrossRef]
- Nakamura, M.; Sawada, T. Numerical study on the flow of a non-Newtonian fluid through an axisymmetric stenosis. J. Biomech. Eng. 1988, 110, 137–143. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]


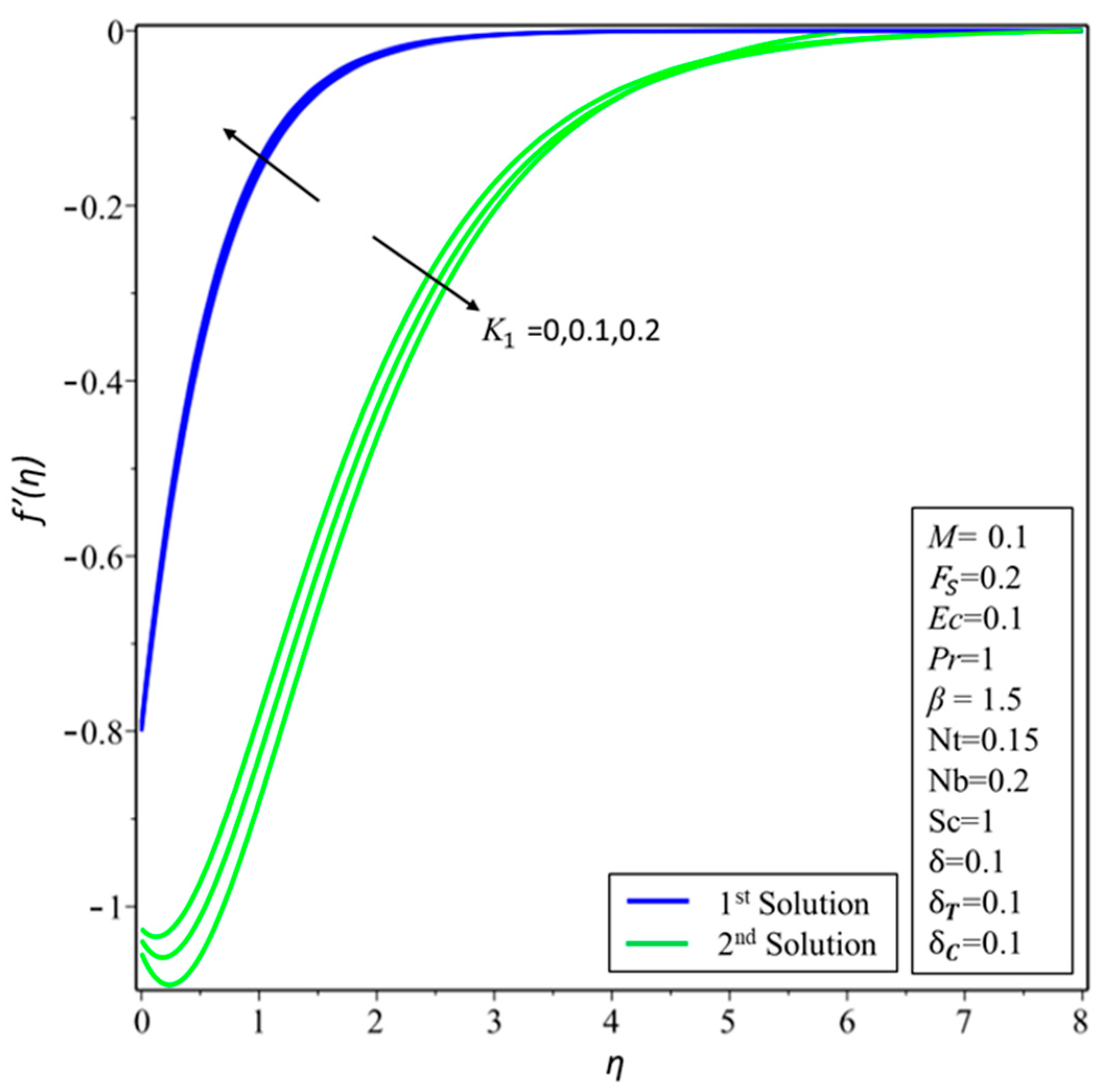

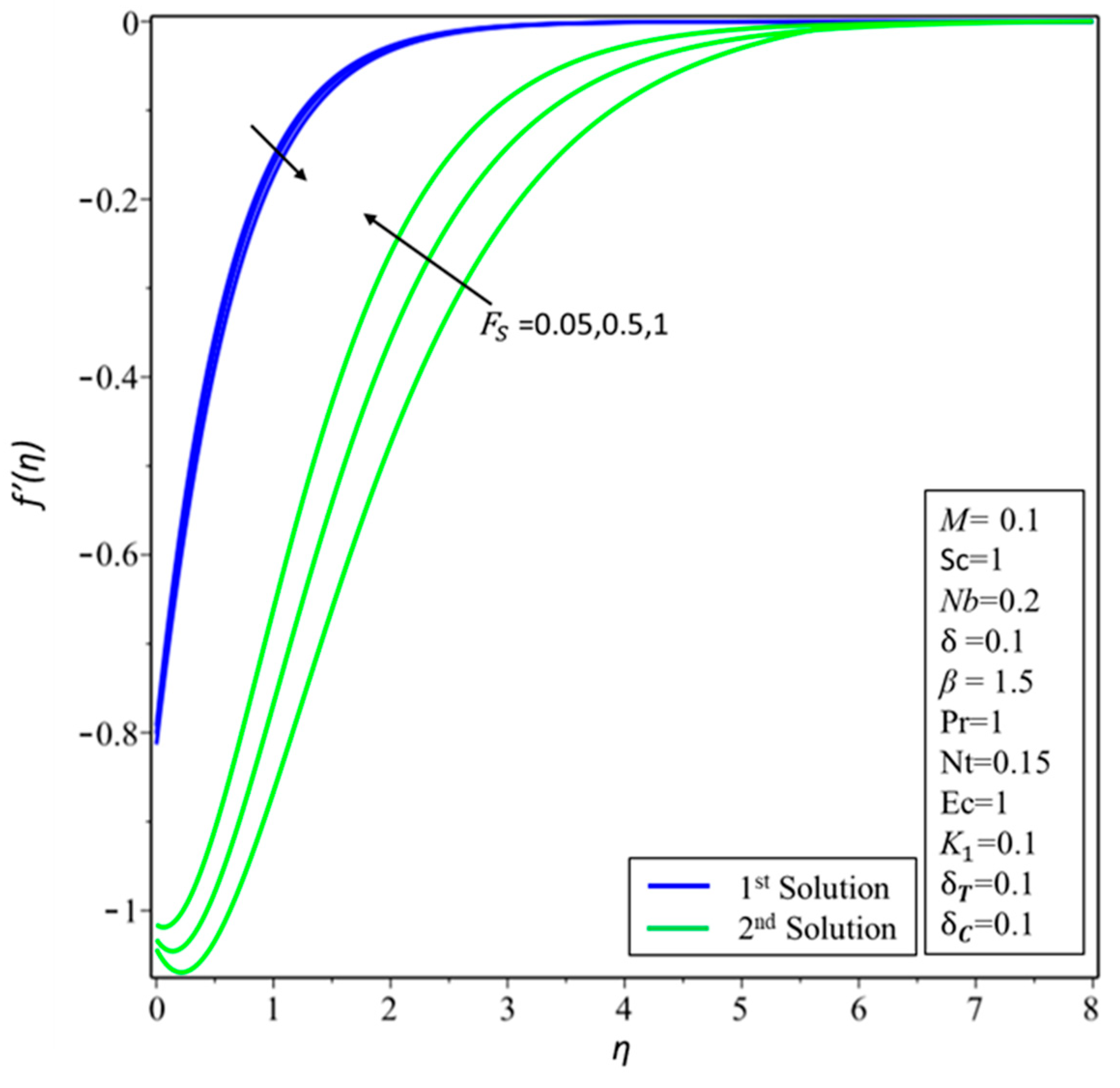
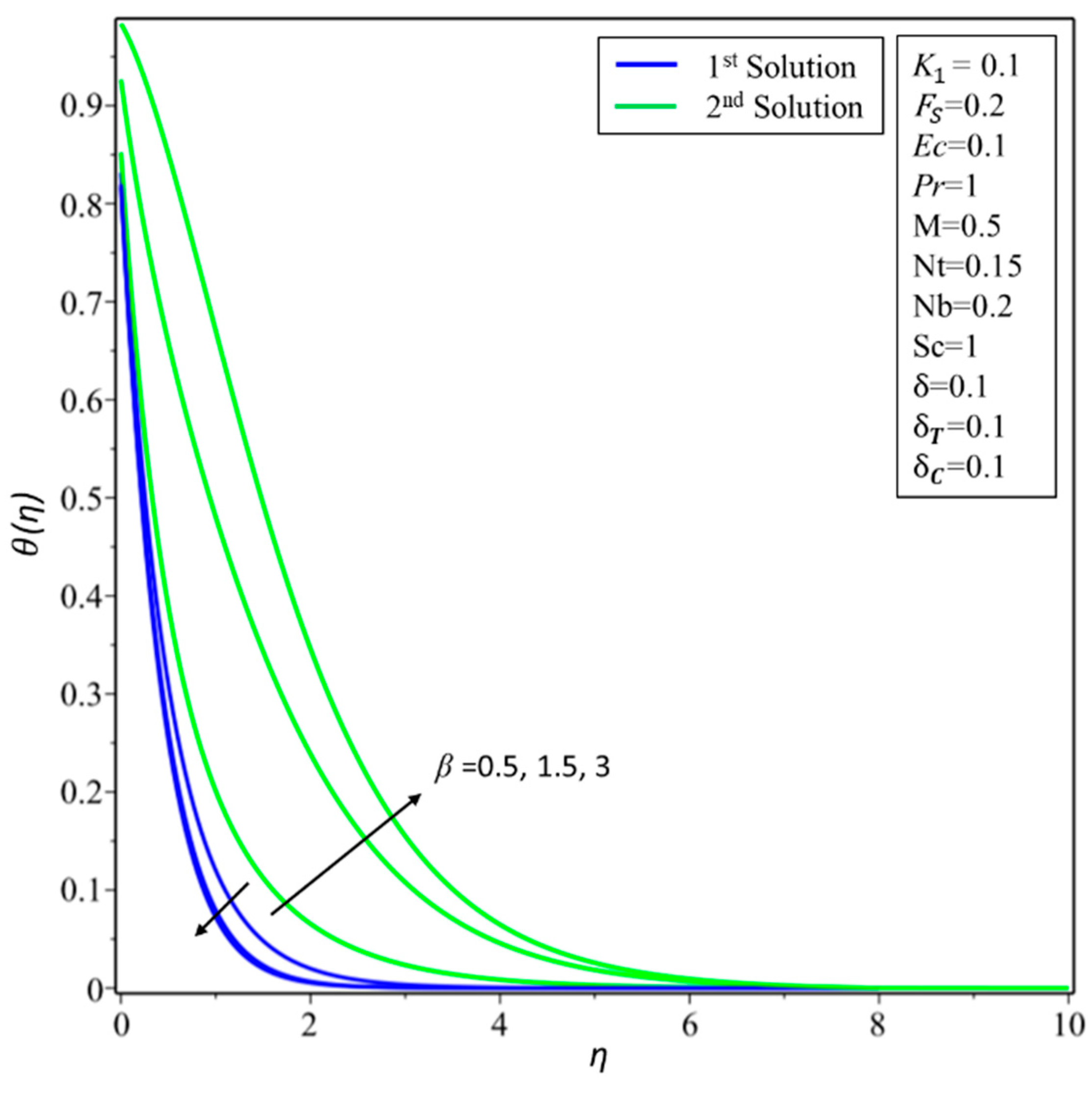
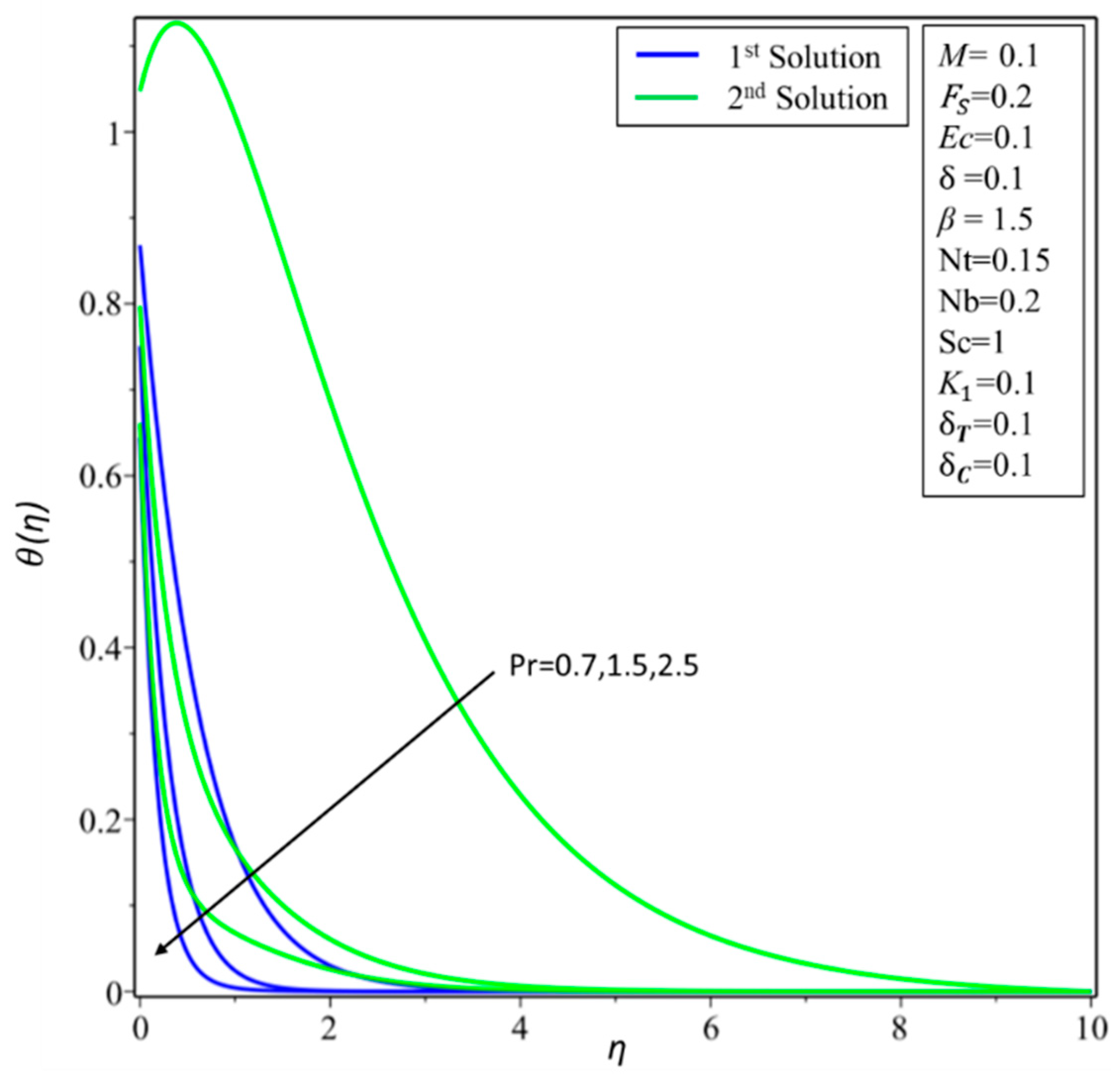

| M | |||
|---|---|---|---|
| bvp4c Method | Shooting Method | ||
| 0.5 | 0.1 | 1.636957 | 1.636908 |
| 0.2 | 1.651884 | 1.651959 | |
| 0.3 | 1.666407 | 1.666527 | |
| 0 | 0.1 | 1.552846 | 1.552775 |
| 1 | 1.707631 | 1.707671 | |
| 1.5 | 1.769173 | 1.769238 |
| M | |||
|---|---|---|---|
| First Solution | Second Solution | ||
| 0.5 | 0 | 0.87456 | −1.04592 |
| 0.1 | 0.73948 | −1.00248 | |
| 0.7 | 0 | 0.94310 | −1.294601 |
| 0.1 | 0.79092 | −1.12253 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali Lund, L.; Omar, Z.; Khan, I.; Raza, J.; Bakouri, M.; Tlili, I. Stability Analysis of Darcy-Forchheimer Flow of Casson Type Nanofluid Over an Exponential Sheet: Investigation of Critical Points. Symmetry 2019, 11, 412. https://doi.org/10.3390/sym11030412
Ali Lund L, Omar Z, Khan I, Raza J, Bakouri M, Tlili I. Stability Analysis of Darcy-Forchheimer Flow of Casson Type Nanofluid Over an Exponential Sheet: Investigation of Critical Points. Symmetry. 2019; 11(3):412. https://doi.org/10.3390/sym11030412
Chicago/Turabian StyleAli Lund, Liaquat, Zurni Omar, Ilyas Khan, Jawad Raza, Mohsen Bakouri, and I. Tlili. 2019. "Stability Analysis of Darcy-Forchheimer Flow of Casson Type Nanofluid Over an Exponential Sheet: Investigation of Critical Points" Symmetry 11, no. 3: 412. https://doi.org/10.3390/sym11030412
APA StyleAli Lund, L., Omar, Z., Khan, I., Raza, J., Bakouri, M., & Tlili, I. (2019). Stability Analysis of Darcy-Forchheimer Flow of Casson Type Nanofluid Over an Exponential Sheet: Investigation of Critical Points. Symmetry, 11(3), 412. https://doi.org/10.3390/sym11030412







