Effects MHD and Heat Generation on Mixed Convection Flow of Jeffrey Fluid in Microgravity Environment over an Inclined Stretching Sheet
Abstract
1. Introduction
2. Mathematical Formulation
3. Numerical Method
4. Results and Discussion
5. Conclusions
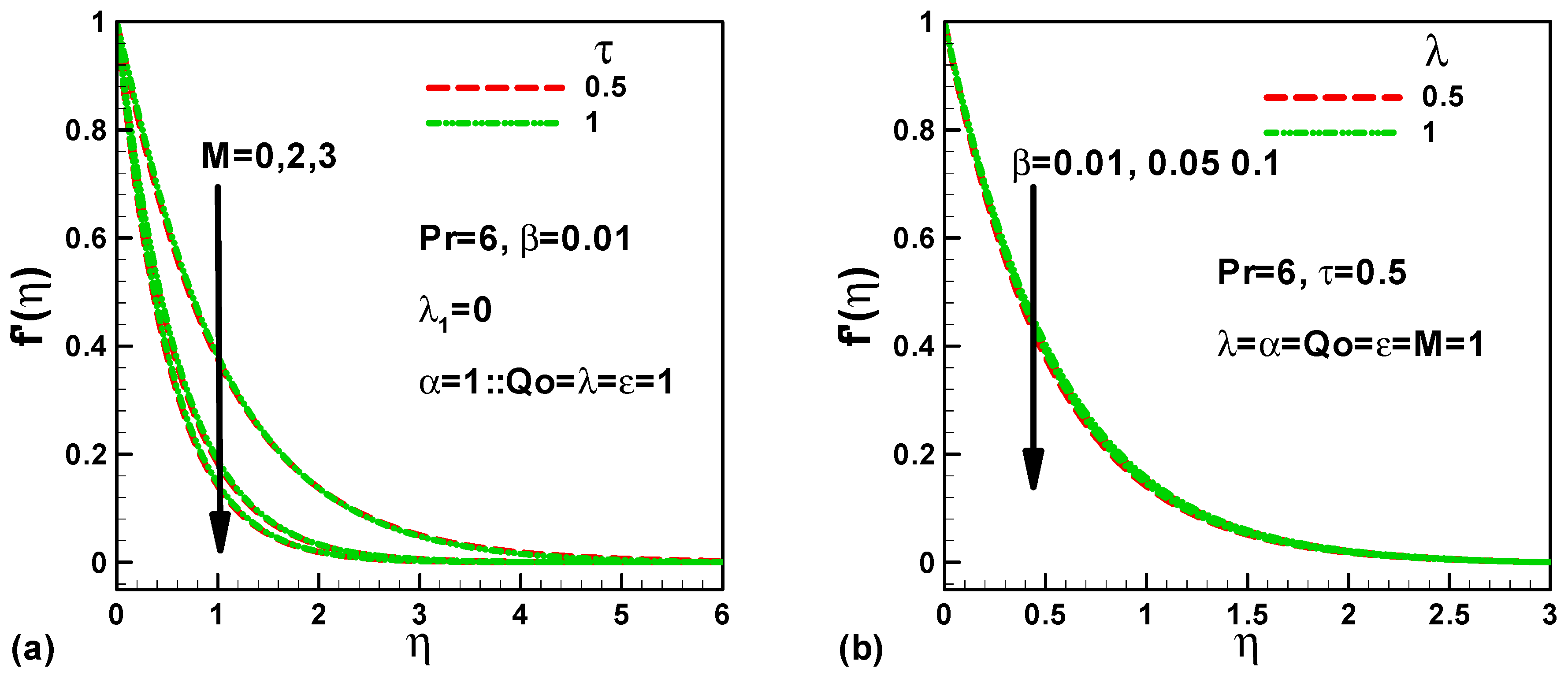
- The velocity profile is higher for dimensionless boundary layer thickness η = 0 then decreases significantly along the inclined stretching sheet to reach zero. In the absence of a magnetic field, the velocity profile is maximum and declines with the application of a magnetic field
- The temperature profile is higher for dimensionless boundary layer thickness η = 0 then decreases significantly along the inclined stretching sheet to reach zero. The thermal expansion coefficient and g-Jitter frequency have an insignificant effect on the temperature profile. Therefore, the thickness of the thermal boundary layer remains uniform in respect to the studied parameters.
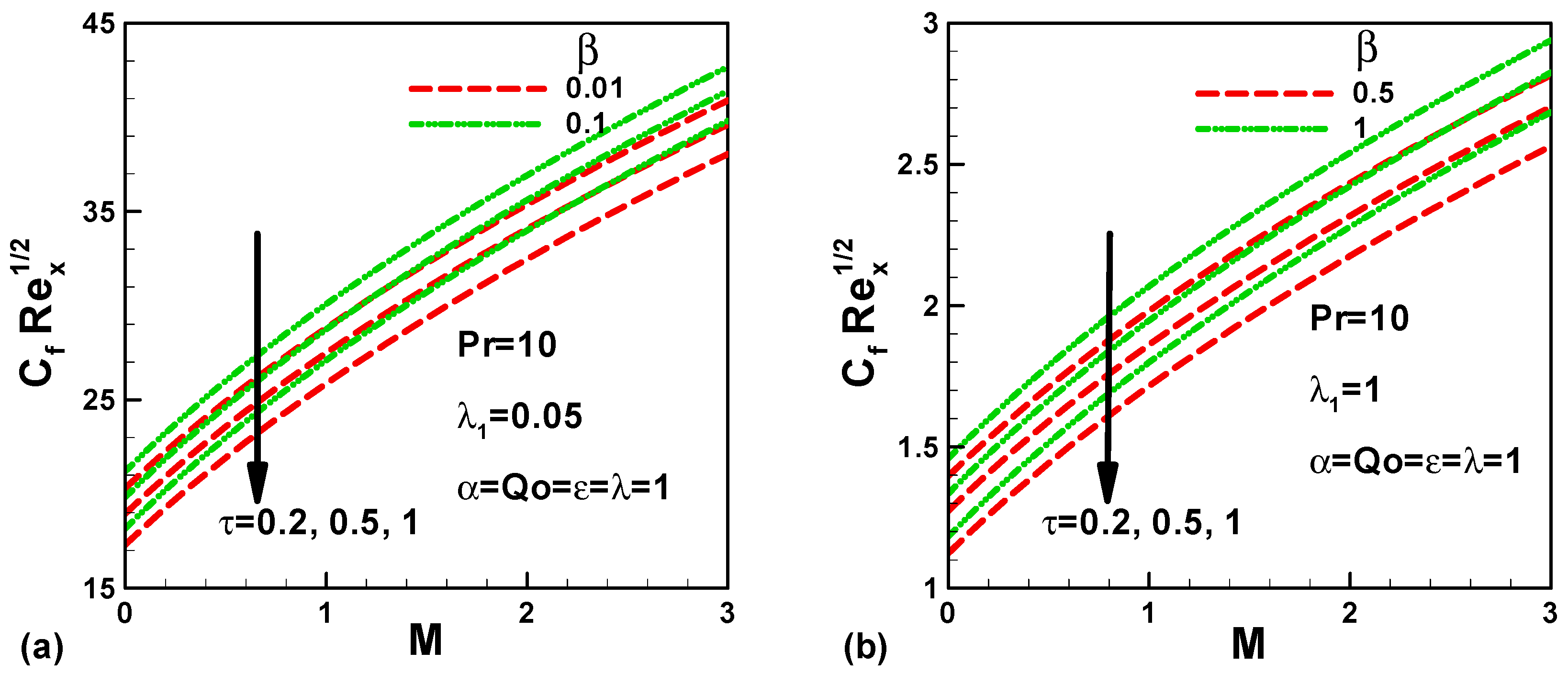
- The dimensionless skin friction increases with both magnetic field and thermal expansion whereas it lessens with g-Jitter frequency. The g-Jitter frequency period reduces skin friction; this effect can be physically elucidated by the fact that g-Jitter generates flow creating buoyancy forces due to the effect of the vibration frequency distribution and density gradients which results to increase the acceleration of the fluid flow.
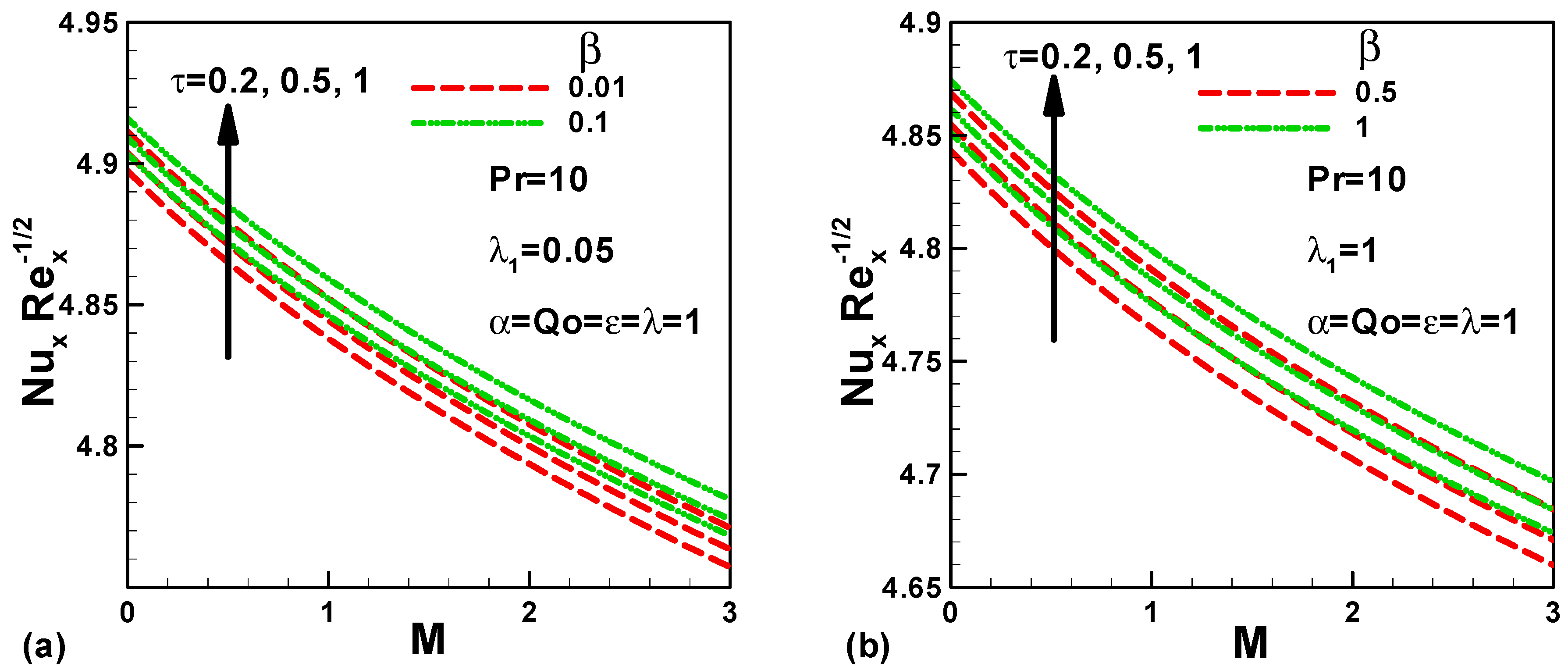
- The local Nusselt number increases with both the thermal expansion coefficient and g-Jitter frequency period. Whereas, it decreases with magnetic field. The Nusselt number at the inclined sheet surface with Jeffrey fluid and in microgravity environment lessens with magnetic field and augments with the thermal expansion coefficient and g-Jitter frequency period.
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Bi | Biot number |
| C | Nanoparticle volume fraction |
| Cp | Specific heat at constant pressure |
| Cf | Local skin-friction coefficient |
| Dn | Diffusivity of the microorganisms |
| DB | Brownian diffusion coefficient |
| DT | Thermophoretic diffusion coefficient of the microorganisms |
| Dimensionless velocity | |
| g | Gravitational acceleration |
| Local Grashof number | |
| hf | Convective heat transfer coefficient |
| k | Thermal conductivity |
| Le | Lewis number |
| Lb | Bioconvection Lewis number |
| Nb | Brownian motion number |
| Nr | Buoyancy ratio parameter |
| Nt | Thermophoresis number |
| Local Nusselt number | |
| n | Density of motile microorganisms |
| Nnx | Local density number |
| Pe | Bioconvection Péclet number |
| Pex | Local Péclet number |
| Pr | Prandtl number, ν/α |
| qw | Wall heat flux |
| r | Local radius of the truncated cone |
| Rax | Modified Rayleigh number |
| Rb | Bioconvection Rayleigh number |
| Shx | Local Sherwood number |
| T | Temperature |
| u | Velocity component in the x-direction |
| Ur | Reference velocity |
| v | Velocity component in the y-direction |
| wc | Maximum cell swimming speed |
| x | Streamwise coordinate |
| xo | Distance of the leading edge of truncated cone measured fromthe origin |
| x* | Distance measured from the leading edge of the truncated cone, x-xo |
| y | Transverse coordinate |
| α | Thermal diffusivity |
| β | Coefficient of thermal expansion |
| γ | Average volume of a microorganism |
| σ | Motile parameter |
| η | Pseudo-similarity variable |
| θ | Dimensionless temperature |
| ϕ | Dimensionless nanoparticle volume fraction |
| ψ | Stream function |
| χ | Dimensionless density of motile microorganisms |
| ξ | Dimensionless distance |
| μ | Dynamic viscosity |
| ν | Kinematic viscosity |
| Ω | Half angle of the truncated cone |
| ρf | Density of the fluid |
| ρf∞ | Density of the base fluid |
| ρp | Density of the particles |
| ρm∞ | Density of the microorganism |
| (ρc)f | Heat capacity of the fluid |
| (ρc)p | Effective heat capacity of the nanoparticle material |
| ρ | Density |
| ψ | Stream function |
| w | Condition at the wall |
| ∞ | Condition at infinity |
References
- Rawi, N.A.; Kasim, A.R.M.; Isa, M.; Shafie, S. G-Jitter induced mixed convection flow of heat and mass transfer past an inclined stretching sheet. J. Teknol. 2014, 71. [Google Scholar] [CrossRef]
- Shafie, S.; Amin, N.S.; Pop, I. G-Jitter free convection boundary layer flow of a micropolar fluid near a three-dimensional stagnation point of attachment. Int. J. Fluid Mech. Res. 2005, 32, 291–309. [Google Scholar] [CrossRef]
- Sharidan, S.; Amin, N.; Pop, I. G-Jitter mixed convection adjacent to a vertical stretching sheet. Microgravity-Sci. Technol. 2006, 18, 5–14. [Google Scholar] [CrossRef]
- Ramesh, K. Effects of viscous dissipation and Joule heating on the Couette and Poiseuille flows of a Jeffrey fluid with slip boundary conditions. Propuls. Power Res. 2018, 7, 329–341. [Google Scholar] [CrossRef]
- Hayat, T.; Waqas, M.; Khan, M.I.; Alsaedi, A. Impacts of constructive and destructive chemical reactions in magnetohydrodynamic (MHD) flow of Jeffrey liquid due to nonlinear radially stretched surface. J. Mol. Liq. 2017, 225, 302–310. [Google Scholar] [CrossRef]
- Selvi, R.K.; Muthuraj, R. MHD oscillatory flow of a Jeffrey fluid in a vertical porous channel with viscous dissipation. Ain Shams Eng. J. 2018, 9, 2503–2516. [Google Scholar] [CrossRef]
- Dalir, N. Numerical study of entropy generation for forced convection flow and heat transfer of a Jeffrey fluid over a stretching sheet. Alex. Eng. J. 2014, 53, 769–778. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Imtiaz, M.; Alsaedi, A. Homogeneous-heterogeneous reactions in nonlinear radiative flow of Jeffrey fluid between two stretchable rotating disks. Results Phys. 2017, 7, 2557–2567. [Google Scholar] [CrossRef]
- Khan, M.; Shahid, A.; Malik, M.Y.; Salahuddin, T. Thermal and concentration diffusion in Jeffery nanofluid flow over an inclined stretching sheet: A generalized Fourier’s and Fick’s perspective. J. Mol. Liq. 2018, 251, 7–14. [Google Scholar] [CrossRef]
- Reddy, P.B.A. Magnetohydrodynamic flow of a Casson fluid over an exponentially inclined permeable stretching surface with thermal radiation and chemical reaction. Ain Shams Eng. J. 2016, 7, 593–602. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D. Effects of thermal and solutal stratification on jeffrey magneto-nanofluid along an inclined stretching cylinder with thermal radiation and heat generation/absorption. Int. J. Mech. Sci. 2017, 131–132, 317–324. [Google Scholar] [CrossRef]
- Sandeep, N.; Sulochana, C. Momentum and heat transfer behaviour of Jeffrey, Maxwell and Oldroyd-B nanofluids past a stretching surface with non-uniform heat source/sink. Ain Shams Eng. J. 2018, 9, 517–524. [Google Scholar] [CrossRef]
- Ahmad, K.; Ishak, A. Magnetohydrodynamic (MHD) Jeffrey fluid over a stretching vertical surface in a porous medium. Propuls. Power Res. 2017, 6, 269–276. [Google Scholar] [CrossRef]
- Khan, M.I.; Waqas, M.; Hayat, T.; Alsaedi, A. Soret and Dufour effects in stretching flow of Jeffrey fluid subject to Newtonian heat and mass conditions. Results Phys. 2017, 7, 4183–4188. [Google Scholar] [CrossRef]
- Ghosh, P.; Ghosh, M.K. Streaming flows in differentially heated square porous cavity under sinusoidal g-jitter. Int. J. Therm. Sci. 2009, 48, 514–520. [Google Scholar] [CrossRef]
- Rouvreau, S.; Cordeiro, P.; Torero, J.L.; Joulain, P. Influence of g-jitter on a laminar boundary layer type diffusion flame. Proc. Combust. Inst. 2005, 30, 519–526. [Google Scholar] [CrossRef]
- Khoshnevis, A.; Ahadi, A.; Saghir, M.Z. On the influence of g-jitter and prevailing residual accelerations onboard International Space Station on a thermodiffusion experiment. Appl. Therm. Eng. 2014, 68, 36–44. [Google Scholar] [CrossRef]
- Kumar, A.; Gupta, V.K. Study of heat and mass transport in Couple-Stress liquid under G-jitter effect. Ain Shams Eng. J. 2018, 9, 973–984. [Google Scholar] [CrossRef]
- Bhadauria, B.S.; Singh, A. Through flow and G-jitter effects on chaotic convection in an anisotropic porous medium. Ain Shams Eng. J. 2018, 9, 1999–2013. [Google Scholar] [CrossRef]
- Shafie, S.; Amin, N.; Pop, I. G-Jitter free convection flow in the stagnation-point region of a three-dimensional body. Mech. Res. Commun. 2007, 34, 115–122. [Google Scholar] [CrossRef]
- Asif, M.; Haq, S.U.; Islam, S.; Khan, I.; Tlili, I. Exact solution of non-Newtonian fluid motion between side walls. Results Phys. 2018, 11, 534–539. [Google Scholar] [CrossRef]
- Agaie, B.G.; Khan, I.; Yacoob, Z.; Tlili, I. A novel technique of reduce order modelling without static correction for transient flow of non-isothermal hydrogen-natural gas mixture. Results Phys. 2018, 10, 532–540. [Google Scholar] [CrossRef]
- Tlili, I.; Hamadneh, N.N.; Khan, W.A. Thermodynamic Analysis of MHD Heat and Mass Transfer of Nanofluids Past a Static Wedge with Navier Slip and Convective Boundary Conditions. Arab. J. Sci. Eng. 2018, 1–13. [Google Scholar] [CrossRef]
- Khalid, A.; Khan, I.; Khan, A.; Shafie, S.; Tlili, I. Case study of MHD blood flow in a porous medium with CNTS and thermal analysis. Case Stud. Therm. Eng. 2018, 12, 374–380. [Google Scholar] [CrossRef]
- Khan, I.; Abro, K.A.; Mirbhar, M.N.; Tlili, I. Thermal analysis in Stokes’ second problem of nanofluid: Applications in thermal engineering. Case Stud. Therm. Eng. 2018, 12, 271–275. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Khan, I.; Tlili, I. Entropy generation in MHD mixed convection stagnation-point flow in the presence of joule and frictional heating. Case Stud. Therm. Eng. 2018, 12, 292–300. [Google Scholar] [CrossRef]
- Khan, Z.A.; Haq, S.U.; Khan, T.S.; Khan, I.; Tlili, I. Unsteady MHD flow of a Brinkman type fluid between two side walls perpendicular to an infinite plate. Results Phys. 2018, 9, 1602–1608. [Google Scholar] [CrossRef]
- Aman, S.; Khan, I.; Ismail, Z.; Salleh, M.Z.; Tlili, I. A new Caputo time fractional model for heat transfer enhancement of water based graphene nanofluid: An application to solar energy. Results Phys. 2018, 9, 1352–1362. [Google Scholar] [CrossRef]
- Khan, Z.; Khan, I.; Ullah, M.; Tlili, I. Effect of thermal radiation and chemical reaction on non-Newtonian fluid through a vertically stretching porous plate with uniform suction. Results Phys. 2018, 9, 1086–1095. [Google Scholar] [CrossRef]
- Imran, M.A.; Miraj, F.; Khan, I.; Tlili, I. MHD fractional Jeffrey’s fluid flow in the presence of thermo diffusion, thermal radiation effects with first order chemical reaction and uniform heat flux. Results Phys. 2018, 10, 10–17. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Pop, I. The effect of g-jitter on vertical free convection boundary-layer flow in porous media. Int. Commun. Heat Mass Transf. 2000, 27, 415–424. [Google Scholar] [CrossRef]
- Pandey, A.K.; Kumar, M. Natural convection and thermal radiation influence on nanofluid flow over a stretching cylinder in a porous medium with viscous dissipation. Alex. Eng. J. 2017, 56, 55–62. [Google Scholar] [CrossRef]
- Ashorynejad, H.R.; Sheikholeslami, M.; Pop, I.; Ganji, D.D. Nanofluid flow and heat transfer due to a stretching cylinder in the presence of magnetic field. Heat Mass Transf. 2013, 49, 427–436. [Google Scholar] [CrossRef]
- Buongiomo, J. Convective transport in nanofluids. ASME Trans. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Hayat, T.T.; Bibi, A.; Yasmin, H.H.; Alsaadi, F.E. Magnetic Field and Thermal Radiation Effects in Peristaltic Flow with Heat and Mass Convection. ASME. J. Therm. Sci. Eng. Appl. 2018, 10, 051018. [Google Scholar] [CrossRef]

| Ra | Hayat et al. [5] | Current |
|---|---|---|
| 1000 | 5.321 | 5.332 |
| 10,000 | 5.487 | 5.496 |
| 100,000 | 7.212 | 7.223 |
| 1,000,000 | 13.946 | 14.101 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tlili, I. Effects MHD and Heat Generation on Mixed Convection Flow of Jeffrey Fluid in Microgravity Environment over an Inclined Stretching Sheet. Symmetry 2019, 11, 438. https://doi.org/10.3390/sym11030438
Tlili I. Effects MHD and Heat Generation on Mixed Convection Flow of Jeffrey Fluid in Microgravity Environment over an Inclined Stretching Sheet. Symmetry. 2019; 11(3):438. https://doi.org/10.3390/sym11030438
Chicago/Turabian StyleTlili, Iskander. 2019. "Effects MHD and Heat Generation on Mixed Convection Flow of Jeffrey Fluid in Microgravity Environment over an Inclined Stretching Sheet" Symmetry 11, no. 3: 438. https://doi.org/10.3390/sym11030438
APA StyleTlili, I. (2019). Effects MHD and Heat Generation on Mixed Convection Flow of Jeffrey Fluid in Microgravity Environment over an Inclined Stretching Sheet. Symmetry, 11(3), 438. https://doi.org/10.3390/sym11030438




