Abstract
Neutrosophic extended triplet group is a new algebra structure and is different from the classical group. In this paper, the notion of generalized neutrosophic extended triplet group is proposed and some properties are discussed. In particular, the following conclusions are strictly proved: (1) an algebraic system is a generalized neutrosophic extended triplet group if and only if it is a quasi-completely regular semigroup; (2) an algebraic system is a weak commutative generalized neutrosophic extended triplet group if and only if it is a quasi-Clifford semigroup; (3) for each is a commutative generalized neutrosophic extended triplet group; (4) for each is a commutative neutrosophic extended triplet group if and only if , i.e., the factorization of n has only single factor.
1. Introduction
Groups are very important algebraic structures and have been applied in many fields, such as cryptology, engineering, physics, chemistry, etc. Recently, a new algebraic system, neutrosophic triplet group (NTG), is proposed by Smarandache and Ali in [1]. For an NTG , every element has its own neutral element (denote by ) satisfying condition , and there exits at least one opposite element (denote by ) in N relative to such that . Some further studies can be found in [2,3,4,5,6,7,8,9,10,11].
From the original definition of NTG, we can see that it is an extension of a group. However, it is different from a group. In NTG, the neutral element is different from the unit element of the classical algebraic system. By removing this restriction, an algebraic system, which is called neutrosophic extended triplet group (NETG), is proposed, and the classical group is regarded as a special case of NETG. Moreover, further studies of NETG can be found in [12,13,14,15,16,17,18] and some important results have been achieved.
For the algebraic system , ⊗ is the classical mod multiplication, where and is a positive integer. is only a commutative semigroup before NTG and NETG are introduced. Recently, properties of algebraic structure of in some special cases are studied in [19,20] by the point view of NTG. We can see that for some positive integers n, is a commutative NETG, but for some positive integers n, is not a commutative NETG. So, there are two problems, 1 What conditions can guarantee to be a NETG? 2 Is there a new algebraic system that makes is the algebraic system for each positive integer n? We will give positive answers for the two problems in this paper.
The paper is organized as follows. Section 2 gives the related work. In Section 3, the conditions which guarantee the algebraic system to be a NETG are deeply studied. In Section 4, the generalized neutrosophic extended triplet group (GNETG) is proposed and some properties and structure are discussed. Finally, the summary and future work are presented in Section 5.
2. Related Works
In this section, we will give the related research and results of the NETG. Some related notions are introduced at first. Let G be non-empty set, is a binary operation on G. If , implies , then is called a groupoid. A groupoid G is called a semigroup if satisfies associative law, i.e., ( . A semigroup G is called a group if there exists the unit element and for each element in G exists its inverse element.
Definition 1.
[11] Let N be a non-empty set together with a binary operation . Then, N is called a neutrosophic extended triplet set if for any , there exists a neutral of “a” (denote by ), and an opposite of “a”(denote by , such that , and:
The triplet is called a neutrosophic extended triplet.
Definition 2.
[11,15] Let be a neutrosophic extended triplet set. Then, N is called a neutrosophic extended triplet group (NETG), if the following conditions are satisfied:
(1) is well-defined, i.e., for any , one has .
(2) is associative, i.e., for all .
A NETG N is called a commutative NETG if for all .
From Definition 2, we can see that a NETG is an extension of the classical group. There are some important results about the properties and structure of a NETG. For examples, G is a NETG iff it is a completely regular semigroup, G is a singular NETG iff it is a generalized group, and so on. We introduce some related notions and results in the following. Figure 1 gives the relations of the NETG and other algebraic structures.
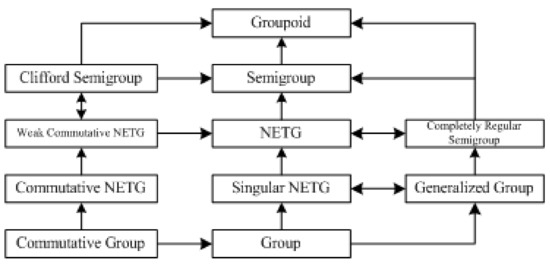
Figure 1.
The relations of NETG and other algebraic structures.
Proposition 1.
[15] be a NETG. We have:
- (1)
- is unique for any .
- (2)
- for any .
- (3)
- for any .
Definition 3.
[17] A NETG is said to be singular, if is unique for any .
Definition 4.
[21] A generalized group is a non-empty set admitting a binary operation called multiplication subject to the set of rules given below:
- (1)
- .
- (2)
- For each , there exists a unique such that .
- (3)
- For each , there exists such that .
Theorem 1.
[17] is a singular NETG iff is a generalized group.
Definition 5.
[15] Let be a NETG. Then N is called a weak commutative NETG if for all .
Definition 6.
[22] A semigroup is called regular if for any , there exists a unary operation on S such that
A semigroup S is called quasi-regular if for any , there exists a positive integer n such that is regular.
Definition 7.
[22] A semigroup is called completely regular if for any , there exists a unary operation on S such that
A semigroup S is called quasi-completely regular if for any , there exists a positive integer n such that is completely regular.
Proposition 2.
[22] Let be a semigroup. Then the following statements are equivalent:
- (1)
- S is completely regular;
- (2)
- every element of S lies in a subgroup of S;
- (3)
- every H-class in S is a group.
Definition 8.
[22] A semigroup is called Clifford semigroup, if it is completely regular and in which for any , such that
Proposition 3.
[22] Let be a semigroup. Then the following statements are equivalent:
- (1)
- S is Clifford semigroup;
- (2)
- S is a semilattice of groups;
- (3)
- S is regular, and the idempotents of S are central.
Theorem 2.
[18] Let be a groupoid. Then N is a NETG iff it is a completely regular semigroup.
Theorem 3.
[18] Let be a groupoid. Then N is a weak commutative NETG iff it is a Clifford semigroup.
3. The Relations of and NETG
Lemma 1.
In an algebra system , where Z is the integer set, we have for , holds iff holds.
Lemma 2.
For each positive integer , linear congruence equation has a solution iff , where is the greatest common divisor of a and b.
Proposition 4.
The solution of x for equation is , where .
Proof.
From Lemma 1, has a solution iff has a solution, and by Lemma 2, must have a solution being holds obviously. We will prove the solution to the equation is in the following.
Let , then there exist two integers and , such that and . If x satisfies the equation , we can get that , thus , i.e., , that is . Since , we have . Let , then, , that is .
On the other hand, being , that is , i.e., holds, so is the solution of equation . This tells us that the solution for equation is , where . □
Remark:
From Proposition 4, we can see that the solution of is just decided by the . If , then and have the same solution in .
Theorem 4.
In the algebra system , for each , has and iff .
Proof.
Necessity: In general, let and the neutral elements of exists, that is there are and such that and . That is the linear congruence equations and have solutions. Let and . From Proposition 4, . From Lemma 2, y has solution for equation iff , that is , which means .
Sufficiency: If , we should verify that there is x and y, such that and . From Proposition 4, has a solution and . From the given condition , we can infer that there exist , such that , which means , that is when . So there exists y, such that , which means if , thus for , has and . □
Example 1.

For , , the operation table as following Table 1. From Definition 1, we have , but and have not the neutral element and opposite element.

Table 1.
The operation table of .
We can get the above results by Theorem 4. Being , so from Theorem 4, and exist the neutral element and opposite element. In fact, from Proposition 4, being , i.e., they have the same greatest common divisor, so they have the same neutral element, that is . In the same way, has its neutral element and opposite element. However, , so and do not have the neutral element and opposite element.
Proposition 5.
In the algebra system , if the neutral element exists, then it is unique.
Proof.
In general, if and the neutral elements of exists, that is there are and such that and . Let and there are two integers and , such that .
By Proposition 4, the neutral element of has form , where , and from Theorem 4, there exists such that . Since , we have , which means there must exist such that , so the neutral element of exists.
In the following, we will show that if there exist two integers and , such that and , then .
From and , we have , i.e., . Being , then , that is .
From the above analysis, we can get that the neutral element of is unique in if it exists. □
Remark:
From Proposition 5, we can see that if the neutral element of exists, then it is unique. Let is the neutral element of , then we have that and are the neutrosophic extended triplets in .
Example 2.
For , . From the above results we have:
- (1)
- has not the neutral element and opposite element being . In fact, and do not have the neutral element and opposite element by Theorem 4 for the same reason.
- (2)
- and have the same neutral element being . In fact, and have the same neutral element, which is .
- (3)
- and have the same neutral element being .
- (4)
- and have the same neutral element .
- (5)
- has the neutral element .
- (6)
- We can see that the neutral element of each element is unique and explain that Proposition 5 is correct. Moreover, and are some neutrosophic extended triplets in , which verify the above Remark.
Theorem 5.
An algebra system is a NETG iff the factorization of n is a product of single factors, i.e., , where is a prime number.
Proof.
Necessity: Suppose that is a NETG, we verify the factorization of n is the product of a single factor and proof by contradiction.
Assume, the factorization of n is , and , such that . Without losing generality, let . We will prove and do not exist.
Because and , then
By Theorem 4, we have that and do not exist. This contradicts that is NETG. So, the factorization of n is a product of single factors if is a NETG.
Sufficiency: If the factorization of n is a product of some single factors, i.e., , where is a prime number. We will prove for each , and exist.
Let , because , so , i.e.,
From Theorem 4, has the neutral element and opposite element. From the arbitrariness of a, we can know that is a NETG if the factorization of n is a product of some single factors. □
Remark:
For an algebra system and , where is a prime number. From the above analysis, the number of different neutral elements in is .
Example 3.
For , , so each element in has its corresponding neutral element. From the above Remark, the number of different neutral elements in is . In fact, being different factors of 30 are , and 30. Thus, the different neutral elements are and respectively. In detail (just consider the neutral element):
- (1)
- and have the same neutral element, which is .
- (2)
- and have the same neutral element, which is .
- (3)
- and have the same neutral element, which is .
- (4)
- and have the same neutral element, which is .
- (5)
- and have the same neutral element, which is .
- (6)
- and have the same neutral element, which is .
- (7)
- has neutral element .
- (8)
- has neutral element .
4. GNETG and Quasi-Completely Regular Semigroup
Definition 9.
Let N be a non-empty set together with a binary operation . Then, N is called a generalized neutrosophic extended triplet set if for any , there exist at least a positive integer n, such that exists neutral element, denoted by , and opposite element, denoted by . The triplet is called a generalized neutrosophic extended triplet with degree n.
Definition 10.
Let is a generalized neutrosophic extended triplet set. Then, N is called a GNETG, if the following conditions are satisfied:
- (1)
- is well-defined, i.e., for any , .
- (2)
- is associative, i.e., for all .
A GNETG N is called a commutative generalized neutrosophic extended triplet group if for all .
Remark:
From Definition 9, it is obviously that a neutrosophic extended triplet is a generalized neutrosophic extended triplet with degree 1, so a neutrosophic extended triplet set is a generalized neutrosophic extended triplet set. Moreover, a NETG is a GNETG, but a GNETG is not a NETG in general.
Example 4.

Let , an operation on S is defined as in Table 2. We can see that and are neutrosophic extended triplets, but a does not exist the neutral element and opposite element. Thus, S is not a NETG. Moreover, has the neutral element and opposite element, so is a GNETG. and are generalized neutrosophic extended triplets with degree 2. We can infer that is a GNETG but not a NETG. Moreover, it is not a commutative GNETG being .

Table 2.
A GNETG of Example 4.
Example 5.
Consider , . From Theorem 4, we have:
- (1)
- and exist the neutral element and opposite element.
- (2)
- does not exist the neutral element and opposite element, but we can see that exists the neutral element and opposite element.
- (3)
- does not exist the neutral element and opposite element, but we can see that exists the neutral element and opposite element.
- (4)
- does not exist the neutral element and opposite element, but we can see that exists the neutral element and opposite element.
So is a generalized neutrosophic extended triplet set, but it is not a neutrosophic extended triplet set. Moreover, is a commutative GNETG. The following theorem shows that for each positive integer , is a commutative GNETG.
Theorem 6.
For each , there exists a positive integer m, such that has the neutral element and opposite element. That is, is commutative GNETG.
Proof.
If the factorization of n is a product of single factors, From Theorem 5, is a NETG, so has the neutral element and opposite element.
If , and , such that . For each , it is easy to get that there is a positive integer m, such that
that is has the neutral element and opposite element from Theorem 4. So, for each , there exists a positive integer m, such that has the neutral element and opposite element, i.e., is a commutative GNETG. □
Definition 11.
[22] Let be a semigroup, an element x in S is said to be periodic if there exists a positive integer n such that . S is pointwise periodic if each x in S is periodic.
Proposition 6.
Let be a pointwise periodic semigroup, then is a NETG, so it is a GNETG.
Proof.
Since is a pointwise periodic semigroup, so for each element x in a S, there exists a positive integer n such that .
If , then , so is a neutrosophic extended triplet.
If , so and , that is, is a neutrosophic extended triplet.
By the arbitrariness of x, we have is a NETG. Of course, it is a GNETG. □
Example 6.

Let , an operation on S is defined as following Table 3. Because , so is a pointwise periodic semigroup. Moreover, and are neutrosophic extended triplets, that is is a NETG.

Table 3.
A pointwise periodic semigroup of Example 6.
From Example 6, we can also see that if has zero element (c is the zero element in Example 6), then the neutral element of zero element is itself and the opposite element of zero element is every element in S.
Proposition 7.
Let is a GNETG, and is a generalized neutrosophic extended triplet with degree n. We have:
- (1)
- is unique.
- (1)
- .
Proof.
Assume , so , and there exists such that
We can obtain
We have . So is unique and . □
Proposition 8.
Let is a GNETG, and is a generalized neutrosophic extended triplet with degree n. Then
- (1)
- , for any .
- (2)
- for any .
- (3)
- .
- (4)
- , for any .
- (5)
- , for any .
Proof.
(1) For any , from Definition 9 and Proposition 7, we have
So , for any .
(2) For any , From Definition 9 and Proposition 7, we have
So for any .
(3) We prove firstly.
For any and ,
Moreover,
Thus, .
In the following we will prove .
It is obvious that when . If , by Proposition 7 we have:
Moreover, we can get
Thus, .
(4) For any , we have
Moreover,
Thus, (4) holds.
(5) Suppose , for each , from (4) we know that is unique. Applying (1), , that is,
By (3), . Thus, . □
Example 7.

Let , an operation on S is defined as following Table 4. Since and , so is a GNETG. We can get that (Corresponding to the results of Proposition 8):

Table 4.
A GNETG of Example 7.
- (1)
- Being , , that is, for any , .
- (2)
- Being , , that is, for any , .
- (3)
- Being , , that is, for any , .
- (4)
- For each element , , that is, for any , .
- (5)
- Being , that is, for any , .
Proposition 9.
Let be a commutative GNETG, then , there are two positive integers m andn such that the following hold:
- (1)
- .
- (2)
- .
Proof.
Being be a commutative GNETG, then for , there is a positive integer n, such that exists the neutral element and opposite element, denoted by and respectively. For , there is a positive integer m, such that exists the and opposite element, denoted by and respectively. So
in the same way, we have . That is:
Moreover, for any and , we can get,
Similarly, we have . That is:
Thus, we have
From this, by Proposition 7, we get: . Therefore, we get . □
Example 8.

Consider , which is a commutative GNETG from Example 5. Without losing generality, select and , then exist two positive integers 2 and 1, such that , so explain (1) of Proposition 9 is correct. Being and is a sub algebra structure of by Table 5. So, explain (2) of Proposition 9 is correct.

Table 5.
The operator table of in .
Example 9.
Apply the in Example 7, Since it is not a commutative GNETG, we can get that:
- (1)
- Being for each , and for each , so . On the other hand, , but does not exist, so the (1) of Proposition 9 does not hold.
- (2)
- Being , , , but does not exist, we can get that the (2) of Proposition 9 does not hold.
Theorem 7.
Let be a groupoid. Then N is a GNETG if and only if it is a quasi-completely regular semigroup.
Proof.
Necessity: Suppose N is a GNETG, from Definition 10, for each , there is a positive integer n, such that exists the neutral element and opposite element, denoted by and respectively. Set
by Proposition 8, is unique and we have
from Definition 7, N is a quasi-completely regular semigroup.
Sufficiency: If N is a completely quasi-regular semigroup. For any , there is a positive integer n and , such that and , set
then
From Definition 10, we have that N is a GNETG and . □
Example 10.
Apply in the Example 7, we know that it is a GNETG. We will show that it is a quasi-completely regular semigroup in the following.
For e, there exists an inverse element , such that , so e is completely regular. f and g are completely regular for the same reason. Moreover, being and , so and are completely regular, so is a quasi-completely regular semigroup by Definition 7.
Definition 12.
Let is a GNETG. N is called a weak commutative GNETG if there are two positive integers , such that for all .
Example 11.


Let , an operation on S is defined as following Table 6. Since and are neutrosophic extended triplets, but d does not exist the neutral element and opposite element. Thus, S is not a NETG. Moreover, exists the neutral element and opposite element, so is GNETG and is a generalized neutrosophic extended triplet with degree 2. We can infer that is a GNETG but not a NETG. Moreover, it is not a commutative GNETG being , we can show that it is a weak commutative GNETG.

Table 6.
The operation table of Example 11.
For , and f, there exist positive integers , and 1 respectively, so being . We know that , so . From Table 6, we can get the sub algebra system of as following Table 7, and is commutative. Thus, is a weak commutative GNETG.

Table 7.
The sub algebra system of S in Example 11.
Example 12.
Select the in Example 4, being for every , , , so . Thus, the in Example 4 is not weak commutative GNETG.
Proposition 10.
Let be a GNETG. Then is a weak commutative GNETG iff there are two positive integers n and m, such that N satisfies the following conditions:
- (1)
- , for all .
- (2)
- , for all .
Proof.
Necessity: If is a weak commutative GNETG, then there are two positive integers , such that and exist the neutral element and opposite element. So, from Proposition 7 and Definition 12, we have
Moreover,
Sufficiency: Suppose that N satisfies the conditions (1) and (2) above. Then:
From Definition 12 we know that is a weak commutative GNETG. □
Proposition 11.
Let be a weak commutative GNETG, then for , the following conditions are satisfied:
- (1)
- ;
- (2)
- .
Proof.
If , then there are two positive integers , such that and exist the neutral element and opposite element. We have
Similarly, we have . Moreover, for any and , we have:
Similarly, we have . So, we have . From this, we can get . Thus, we have . □
Example 13.

Let , an operation on S is defined as following Table 8. Being and , so is a GNETG. It is easy to verify is a weak commutative GNETG by Definition 12. We also can get:

Table 8.
The operation table of Example 13.
- (1)
- Being , and , so, .
- (2)
- Being , , , thus, .
Example 14.
Apply the in Example 4, Being it is not a weak commutative GNETG, we can get that:
- (1)
- Being , but , so, .
- (2)
- Being , , , thus, .
Definition 13.
A semigroup S is called a quasi-Clifford semigroup, if it is quasi-completely regular and for any , there are two positive integers such that
Theorem 8.
Let be a groupoid. Then N is a weak commutative GNETG iff it is a quasi-Clifford semigroup.
Proof.
Necessity: Suppose that N is a weak commutative GNETG. By Theorem 7, we know that N is a quasi-completely regular semigroup, then there are two positive integers , such that and exist the neutral element and opposite element. Set
For any , so we have
From Definition 13, we know that N is a quasi-Clifford semigroup.
Sufficiency: Assume that N is a quasi-Clifford semigroup, then there are two positive integers m and n, such that and are completely regular. Then there exists and . Set
Applying Definition 13, being we have , we can get that N is a weak commutative GNETG by Definition 12. □
Example 15.
Apply the in Example 11, Being it is a weak commutative GNETG from Example 11. We show that it is a quasi-Clifford semigroup. From Theorem 7, we can see that is a quasi-completely regular semigroup, we just show for any , there are two positive integers n and m such that .
From Example 11, for , and f, there exist positive integers , and 1 respectively, and set . For any , without losing generality, let , we can get . We can verify other cases, thus is a quasi-Clifford semigroup.
Example 16.
Apply the in Example 4, Being it is not a weak commutative GNETG from Example 12. We show that there exists , for any two positive integers n and m such that .
From Example 4, for any , and , but . That is for , there are not two positive integers such that . So is not a quasi-Clifford semigroup.
5. Conclusions
In the paper, from the perspective of semigroup theory, we deeply studied the GNETG and obtained some important results. We proved that the GNETG is equal to the quasi-completely regular semigroup, and the weak commutative GNETG is equal to the quasi-Clifford semigroup. Moreover, we investigated the relationship between and a NETG. All these results are interesting for exploring the structure characterization of GNETG. As the next research topics, we will explore the structure of some special GNETG and their relationships with related logic algebras. Moreover, we will discuss the integration of the related topics, such as the combination of neutrosophic set, fuzzy set, soft set and algebra systems [23,24].
Author Contributions
All authors have contributed equally to this paper.
Funding
This research was funded by National Natural Science Foundation of China (Grant No. 11501435), Instructional Science and Technology Plan Projects of China National Textile and Apparel Council (No. 2016073) and Scientific Research Program Funded by Shaanxi Provincial Education Department (Program No. 18JS042).
Acknowledgments
The authors would like to thank the reviewers for their many insightful comments and suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Smarandache, F.; Ali, M. Neutrosophic triplet group. Neural Comput. Appl. 2018, 29, 595–601. [Google Scholar] [CrossRef]
- Vasantha, W.B.; Kandasamy, I.; Smarandache, F. Neutrosophic Triplet Groups and Their Applications to Mathematical Modelling; EuropaNova: Brussels, Belgium, 2017; ISBN 978-1-59973-533-7. [Google Scholar]
- Smarandache, F. Hybrid Neutrosophic Triplet Ring in Physical Structures. Bull. Am. Phys. Soc. 2017, 62, 17. [Google Scholar]
- Bal, M.; Shalla, M.M.; Olgun, N. Neutrosophic Triplet Cosets and Quotient Groups. Symmetry 2017, 10, 126. [Google Scholar] [CrossRef]
- Smarandache, F.; Ali, M. Neutrosophic Triplet Ring and its Applications. In Proceedings of the 18th Annual Meeting of the APS Northwest Section, Pacific University, Forest Grove, OR, USA, 1–3 June 2017. [Google Scholar]
- Sahin, M.; Abdullah, K. Neutrosophic triplet normed space. Open Phys. 2017, 15, 697–704. [Google Scholar] [CrossRef]
- Jaiyeola, T.G.; Smarandache, F. Some results on neutrosophic triplet group and their applications. Symmetry 2018, 10, 202. [Google Scholar] [CrossRef]
- Şahin, M.; Kargın, A. neutrosophic triplet v-generalized metric space. Axioms 2018, 7, 67. [Google Scholar] [CrossRef]
- Ali, M.; Smarandache, F.; Khan, M. Study on the development of neutrosophic triplet ring and neutrosophic triplet field. Mathematics 2018, 6, 46. [Google Scholar] [CrossRef]
- Gulistan, M.; Nawaz, S.; Hassan, N. Neutrosophic triplet non-associative semihypergroups with application. Symmetry 2018, 10, 613. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophic Perspectives: Triplets, Duplets, Multisets, Hybrid Operators, Modal Logic, Hedge Algebras. And Applications; Pons Publishing House: Brussels, Belgium, 2017. [Google Scholar]
- Zhang, X.H.; Bo, C.X.; Smarandache, F.; Dai, J.H. New inclusion relation of neutrosophic sets with applications and related lattice structure. Int. J. Mach. Learn. Cybern. 2018, 9, 1753–1763. [Google Scholar] [CrossRef]
- Zhang, X.H.; Bo, C.X.; Smarandache, F.; Park, C. New operations of totally dependent-neutrosophic sets and totally dependent-neutrosophic soft sets. Symmetry 2018, 10, 187. [Google Scholar] [CrossRef]
- Zhang, X.H.; Wu, X.Y.; Smarandache, F.; Hu, M.H. Left (right)-quasi neutrosophic triplet loops (groups) and generalized BE-algebras. Symmetry 2018, 10, 241. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, Q.; Smarandache, F.; An, X. On Neutrosophic Triplet Groups: Basic Properties, NT-Subgroups, and Some Notes. Symmetry 2018, 10, 289. [Google Scholar] [CrossRef]
- Zhang, X.H.; Smarandache, F.; Liang, X.L. Neutrosophic Duplet Semi-Group and Cancellable Neutrosophic Triplet Groups. Symmetry 2017, 9, 275. [Google Scholar] [CrossRef]
- Zhang, X.H.; Wang, X.J.; Smarandache, F.; Jaíyéolá, T.G.; Liang, X.L. Singular neutrosophic extended triplet groups and generalized groups. Cognit. Syst. Res. 2018, in press. [Google Scholar] [CrossRef]
- Zhang, X.H.; Wu, X.Y.; Mao, X.Y.; Smarandache, F.; Park, C. On Neutrosophic Extended Triplet Groups (Loops) and Abel-Grassmann’s Groupoids (AG-Groupoids). J. Intell. Fuzzy Syst. 2019, in press. [Google Scholar]
- Vasantha, W.B.; Kandasamy, I.; Smarandache, F. A Classical Group of Neutrosophic Triplet Groups Using {Z2p, ×}. Symmetry 2018, 10, 193. [Google Scholar]
- Vasantha, W.B.; Kandasamy, I.; Smarandache, F. Neutrosophic Duplets of {Zpn, ×} and {Zpq, ×} and Their Properties. Symmetry 2018, 10, 344. [Google Scholar]
- Akinmoyewa, J.T. A study of some properties of generalized groups. Octogon Math. Mag. 2009, 17, 599–626. [Google Scholar]
- Howie, J.M. Fundamentals of Semigroup Theory; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Zhang, X.H. Fuzzy anti-grouped filters and fuzzy normal filters in pseudo-BCI algebras. J. Intell. Fuzzy Syst. 2017, 33, 1767–1774. [Google Scholar] [CrossRef]
- Zhang, X.H.; Park, C.; Wu, S.P. Soft set theoretical approach to pseudo-BCI algebras. J. Intell. Fuzzy Syst. 2018, 34, 559–568. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).