Abstract
Games are considered to be the most attractive and healthy event between nations and peoples. Soft expert sets are helpful for capturing uncertain and vague information. By contrast, neutrosophic set is a tri-component logic set, thus it can deal with uncertain, indeterminate, and incompatible information where the indeterminacy is quantified explicitly and truth membership, indeterminacy membership, and falsity membership independent of each other. Subsequently, we develop a combined approach and extend this concept further to introduce the notion of the neutrosophic cubic soft expert sets (NCSESs) by using the concept of neutrosophic cubic soft sets, which is a powerful tool for handling uncertain information in many problems and especially in games. Then we define and analyze the properties of internal neutrosophic cubic soft expert sets (INCSESs) and external neutrosophic cubic soft expert sets (ENCSESs), P-order, P-union, P-intersection, P-AND, P-OR and R-order, R-union, R-intersection, R-AND, and R-OR of NCSESs. The NCSESs satisfy the laws of commutativity, associativity, De Morgan, distributivity, idempotentency, and absorption. We derive some conditions for P-union and P-intersection of two INCSESs to be an INCSES. It is shown that P-union and P-intersection of ENCSESs need not be an ENCSES. The R-union and R-intersection of the INCSESs (resp., ENCSESs) need not be an INCSES (resp. ENCSES). Necessary conditions for the P-union, R-union and R-intersection of two ENCSESs to be an ENCSES are obtained. We also study the conditions for R-intersection and P-intersection of two NCSESs to be an INCSES and ENCSES. Finally, for its applications in games, we use the developed procedure to analyze the cricket series between Pakistan and India. It is shown that the proposed method is suitable to be used for decision-making, and as good as or better when compared to existing models.
1. Introduction
Researchers always try to discover methods to handle imprecise and vague information, which is not possible using classical set theory. In this regard, Zadeh gave the concept of fuzzy set [1], to cope with uncertainty. However, fuzzy sets were considered imperfect since it is not always easy to give an exact degree of membership to any element. To overcome this problem, the interval-valued fuzzy set was proposed by Turksen [2]. Atanassov [3] extended the notion of fuzzy sets to intuitionistic fuzzy sets by introducing the non-membership of an element with its membership in a set X, which were proven to be a better tool than fuzzy sets. Furthermore, the intuitionistic fuzzy sets are used in many directions [4]. Smarandache gave the notion of neutrosophic sets as a generalization of intuitionistic fuzzy sets and fuzzy sets [5]. The idea of neutrosophic sets are further expanded to different directions [6,7,8,9] by various researchers. Jun et al. [10] gave the idea of cubic set and it was characterized by interval-valued fuzzy set and fuzzy set, which is a more general tool to capture uncertainty and vagueness, since fuzzy set deals with single-value membership while interval-valued fuzzy set ranges the membership in the form of intervals. The hybrid platform provided by cubic set has the main advantage since it contains more information than a fuzzy set and interval-valued fuzzy set. By using this concept, different problems arising in several areas can be solved by choosing the finest choice by means of cubic sets as in the works of Abughazalah and Yaqoob [11], Rashid et al. [12], Gulistan et al. [13], Ma et al. [14], Naveed at al. [15], Gulistan et al. [16], Khan et al. [17,18], Yaqoob et al. [19], and Aslam et al. [20].
More recently, Jun et al. [21] gave the idea of neutrosophic cubic set and it was subsequently used in many areas by Khan et al. [22] and Gulistan et al. [23,24].
On the other hand, Molodtsov [25] introduced the concept of soft sets that can be seen as a new mathematical theory for dealing with uncertainty. It was applied to many different fields by Maji et al. [26] who later defined fuzzy soft set theory and some properties of fuzzy soft sets [27]. Hybrids of soft sets were further developed [28,29,30,31,32].
Alkhazaleh and Salleh in 2011 defined the concept of soft expert set in which the user could know the opinion of all the experts in one model and gave an application of this concept in the decision-making problem [33]. Arokia et al. [34] studied fuzzy parameterizations for decision-making in risk management systems via soft expert set. Arokia and Arockiarani [35] provided a fusion of soft expert set and matrix models. Alkhazaleh and Salleh [36] extended the concept of soft expert set in terms of fuzzy set and provided its application. Bashir and Salleh [37] provided the concept of fuzzy parameterized soft expert set. Bashir et al. [38] discussed possibility fuzzy soft expert set. Alhazaymeh et al. [39] provided the application of generalized vague soft expert set in decision-making. Broumi and Smarandache [40] extended the soft expert sets in terms of intuitionistic fuzzy sets. Abu Qamar and Hassan [41,42] presented the idea of Q-neutrosophic soft relation and its entropy measures of distance and similarity. Sahin et al. [43] gave the idea of neutrosophic soft expert sets while Uluçay et al. [44], introduced the concept of generalized neutrosophic soft expert set for multiple-criteria decision-making. Neutrosophic vague soft expert set theory was put forward by Al-Quran and Hassan [45] and developed it further to complex neutrosophic soft expert set [46,47]. Qayyum et al. [48] gave the idea of cubic soft expert sets for a more general approach. Ziemba and Becker [49] presented analysis of the digital divide using fuzzy forecasting, which is a new approach in decision-making.
Hence it is natural to extend the concept of expert sets to neutrosophic cubic soft expert sets for a more generalized approach. The major contribution of this paper is the development of neutrosophic cubic soft expert sets(NCSESs) by using the concept of neutrosophic cubic soft sets which generalizes the concept of fuzzy soft expert sets, intuitionistic soft expert sets, and cubic soft expert sets. We define and analyze the properties of internal neutrosophic cubic soft expert sets (INCSESs) and external neutrosophic cubic soft expert sets (ENCSESs), P-order, P-union, P-intersection, P-AND, P-OR, and R-order, R-union, R-intersection, R-AND, and R-OR of NCSESs. The NCSESs satisfy the laws of commutativity, associativity, De Morgan, distributivity, idempotentency, and absorption. We derive some conditions for P-union and P-intersection of two INCSESs to be an INCSES. It is shown that P-union and P-intersection of ENCSESs need not be an ENCSES. The R-union and R-intersection of the INCSESs (resp., ENCSESs) need not be an INCSES (resp. ENCSES). Necessary conditions for the P-union, R-union, and R-intersection of two ENCSESs to be an ENCSES are obtained. We also study the conditions for R-intersection and P-intersection of two NCSESs to be an INCSES and ENCSES. This paper is organized as follows. Section 2 will be on preliminaries, while Section 3 develops an approach to neutrosophic cubic soft expert set. We focus on the basic operations, namely P-order, R-order, P-containment, R-containment, P-union, P-intersection, R-union, R-intersection, complement, P-AND, P-OR, R-AND, and R-OR of NCSESs. Section 4 will present more results on NCSESs, followed by Section 5 on application in analyzing a cricket series. A comparison analysis will be discussed in Section 6 and a conclusion is drawn in Section 7.
2. Preliminaries
Here we recall some of the basic material from the literature to develop the new theory. For simplicity, the symbol stands for the soft expert set, N stands for the neutrosophic set, stands for the interval neutrosophic set and for the neutrosophic cubic sets.
In psychology, decision-making (also spelled decision-making) is regarded as the cognitive process resulting in the selection of a belief or a course of action among several alternative possibilities. Every decision-making process produces a final choice, which may or may not prompt action. Decision-making is the process of identifying and choosing alternatives based on the values, preferences, and beliefs of the decision-maker. Experts set is a technique used in decision-making problems, which is further extended to generalized forms, such as fuzzy experts set, intuitionistic fuzzy expert set, cubic expert sets, neutrosophic expert set and other hybrids. We begin by stating the definition of expert set.
Definition 1.
[33] Let U be a universe, E be a set of parameters, and X be a set of experts. Let disagree, agree} be a set of two valued opinion, and . A pair is called a soft expert set over U, where is a mapping given by where denotes the power set of U.
Definition 2.
[33] Two soft expert sets and over U, if
and if and only if as well as
Definition 3.
[33] Let E be a set of parameters and X be a set of experts. The NOT set of is defined by
Definition 4.
[33] The complement of a soft expert set is denoted by where is a mapping given by , for all
Definition 5.
[33] If in Definition 1 then is called agree soft expert set over U and it is denoted by
Definition 6.
[33] If in Definition 1 then is called disagree soft expert set over U and it is denoted by
Definition 7.
[33] The union of two soft expert sets and over U denoted by , is the soft expert set where , and for all
Definition 8.
[33] The intersection of two soft expert sets and over U denoted by , is the soft expert set where , and for all
Definition 9.
[33] If and are two soft expert sets over U then AND denoted by , is defined by
where , for all .
Definition 10.
[33] If and are two soft expert sets then OR denoted by is defined by
where , for all .
Definition 11.
[5] A neutrosophic set in X is the structure of the form
where such that
Definition 12.
[8] An interval neutrosophic set in X is the structure of the form
where such that
Definition 13.
[21] A neutrosophic cubic set in X is a pair where
is an interval neutrosophic set in X where and
is a neutrosophic set in X where
3. Neutrosophic Cubic Soft Expert Set
In this section, we develop an approach to neutrosophic cubic soft expert set which is a more general approach for soft expert set theory. We focus on the basic operations namely, P-order, R-order, P-containment, R-containment, P-union, P-intersection, R-union, R-intersection, complement, P-AND, P-OR, R-AND, and R-OR of neutrosophic cubic soft expert sets. The symbol stands for the neutrosophic cubic soft expert set.
Definition 14.
Let U be a finite set containing n alternatives, E be a set of criteria, X be a set of experts. A triplet is called neutrosophic cubic soft expert set over U, if and only if is a mapping into the set of all neutrosophic cubic set in U and defined as
where
such that
Example 1.
Let be the set of countries playing a cricket series, playing conditions, historic record} be the set of factors affecting the series, be the set of experts giving their expert opinion. Let Then the neutrosophic cubic soft expert set is given by
The function of the form denotes the range of values where the experts are sure to give certain membership to a certain element, denotes the range of values where the experts are hesitant and denotes the range of values where the experts are sure to give negative points to a certain element as a non-membership. Thus, experts have a wide range of scale to make their conclusion as compared to the previous defined versions of fuzzy sets. More specific in the current example is the function of the form which gives the expert opinion for the past performance of these two countries, gives the expert opinion for running series between these two countries and gives the expert opinion for the upcoming series between these two countries which is not to be held in the near future.
Definition 15.
A neutrosophic cubic soft expert set
over U is said to be:
- (i)
- Internal truth neutrosophic cubic soft experts set (briefly, ) if for all so that
- (ii)
- Internal indeterminacy neutrosophic cubic soft experts set (briefly, ) if for all so that
- (iii)
- Internal falsity neutrosophic cubic soft experts set (briefly, ) if for all so that
If a neutrosophic cubic soft expert set in satisfies (i), (ii), (iii), then it is known as internal neutrosophic cubic soft expert set in abbreviated as ().
Example 2.
Consider the Example 1. Then the internal neutrosophic cubic soft expert set is given by
Remark 1.
We can draw the following conclusion from Example 2;
(i) If the value of lies in the interval then it means that the respective team is going to maintain its progress in different time frames.
(ii) If the panel of experts consists of the internal panel (meaning that the experts are from the same country or same cricket board), then it is known as INCSESs.
Definition 16.
A neutrosophic cubic soft expert set
over U is said to be:
- (i)
- External truth neutrosophic cubic soft expert set (briefly, ) if for all we have
- (ii)
- External indeterminacy neutrosophic cubic soft expert set (briefly, ) if for all we have
- (iii)
- External falsity neutrosophic cubic soft expert set (briefly, ) if for all we have
If a neutrosophic cubic soft expert set over satisfies (i), (ii), (iii), then it is known as external neutrosophic cubic soft expert set in abbreviated as ().
Example 3.
Let U be the set of countries playing a one-day international (ODI) triangular series provided in Example 1, then the external neutrosophic cubic soft expert set is given by;
Remark 2.
We can draw the following conclusion from Example 3;
(i) If the value of does not lie in the interval then it means the respective team is not maintaining its progress in different time frames.
(ii) If the panel of experts consists of the external panel (meaning that the experts are not from the same country or same cricket board), then it is known as ENCSESs.
Our next discussion is to define some basic operations on neutrosophic cubic soft expert sets to get more insight of neutrosophic cubic soft expert sets.
Definition 17.
A over U is said to be P-order contained in another over U, denoted by
if
where condition implies that
Definition 18.
A over U is said to be R-order contained in another over U, denoted by
if
where condition implies that
Definition 19.
Two and over U is said to be equal which is denoted by
if
where condition implies that
Remark 3.
(a) We observe from Definitions 17–19, that for any two and over U;
(i) If and
then
(ii) If and
then
(b) Using Definitions 17–19, one can easily compare the performance of two cricket teams in different time frames.
Definition 20.
Let and be two in
Then we define (i) where
where
(ii) where
where
(iii) where
where
(iv) where
where
(v) The complement of a neutrosophic cubic soft expert set denoted by
Proposition 1.
Let , be in Then
- (i)
- If andthen
- (ii)
- Ifthen
- (iii)
- If andthen
- (iv)
- If andthen
- (v)
- If andthen ,
Proof.
The proof is straightforward. □
Theorem 1.
For any two and over U the following properties hold:
- (i)
- Idempotent law:
- (ii)
- Commutative law:
- (iii)
- Associative law:
- (iv)
- Distributive and De Morgan’s laws also true.
- (v)
- Involution law:
Proposition 2.
For any two and over U the following properties are equivalent:
- (i)
- (ii)
- (iii)
Proof.
By Definition 20, we have
as by hypothesis. Now for any since using Definition 17, implies that and for any where . Since and Thus
and So It is ok.
Hence □
(ii)⇒(iii) By Definition 20, we have
as and , by hypothesis. Now for any since by Definition 20, we have
this implies that
Thus, we have
Hence
(iii)⇒(i) By hypothesis we have
as and and Also
this implies that and for any .
Hence
Corollary 1.
If we take in the Proposition 2, then the following are equivalent:
- (i)
- (ii)
- (iii)
Proof.
The proof is straightforward. □
4. More on NCSESs
In this section, we discuss different types of union and intersection of the NCSESs and their related conditions.
1. The following example shows thatR-Union of twoinUneed not bein
Example 4.
Let and be two in where
and
Now by Definition 20, we have
As and
Hence is not a in U.
The following theorem gives the condition under which R-union of two in U is also a in U.
Theorem 2.
Let and be two in
where
and
such that
for all and Then is in U.
Proof.
By Definition 20, we know where
where
If or if then the result is trivial. If then
□
Since and are in U. So and Also
for all and Hence is in U.
2. The following example yields thatR-intersection of two need not be a.
Example 5.
Let and be two in where
and
Now by Definition 20, we have
As and
Hence is not a in U.
The following theorem gives the condition that R-intersection of two is to be a
Theorem 3.
Let and be two in
where and such that
for all and Then is a in U.
Proof.
Similar to the proof of the Theorem 2. □
3. The following example yields thatR-union of twoneed not be an.
Example 6.
Let and be two in where
and
Now by Definition 20, we have
As and
Hence R-union is not a in U.
The following theorem gives the condition that R-union of two to be a .
Theorem 4.
Let and be two in
where and such that
for all and Then is a in U.
Proof.
By Definition 20, we know where
where
If take
and
Then h is one of
If we choose or then
and so Thus
Hence
Now if then and so Assume then we have
So, we can write
For the case
which contradicted the fact that and be two in U. For the case
we have
Again, assume that then we have
or
For the case
which contradict and be two in U. For the case
we have
because
If or if then the result is trivial. Hence is a in
4. The following example shows thatR-intersection of twoneed not be.
Example 7.
Let and be two in where
and
Now by Definition 20, we have
As and Hence is not a in U.
The following theorem gives the condition that R-intersection of two is also a .
Theorem 5.
Let and be two in
where and such that
for all and Then is in U.
Proof.
Similar to the proof of Theorem 4. □
5. The following example shows thatP-union of twoneed not to be a.
Example 8.
Let and be two in where
and
Now by Definition 20, we have
As and
Hence P-union of and is not in
The following theorem gives the condition under which P-union of two is a .
Theorem 6.
Let and be two in
where and such that
for all and Then is a over
Proof.
Similar to the proof of Theorems 2 and 4. □
6. The following example shows thatP-intersection of twoneed not be a.
Example 9.
Let and be two in where
and
Now by Definition 20, we have
As and
Hence P-intersection of and is not in
Theorem 7.
Let be a family of internal cubic soft expert set () sets over for any . Then and are internal cubic soft expert set () sets over
Proof.
As be a family of internal generalized cubic soft expert set () over U so we have for each this implies that
and
Hence and are () over U. □
Theorem 8.
Let and be two in
where
and such that
for all and Then is also an and over
Proof.
Similar to the proof of Theorems 2 and 4. □
Theorem 9.
Let and be two in
where and
such that
for all and Then is a and over
Proof.
Similar to the proof of Theorems 2 and 4. □
Theorem 10.
Let , and be any two NCSESs in Then
- (i)
- ,
- (ii)
- (iii)
- ,
- (iv)
Proof.
The proof is straightforward. □
Next we define some more operations on NCSESs.
Definition 21.
For two neutrosophic cubic soft expert sets () and over U, P-AND is denoted as
where
Definition 22.
For any two and over U, R-AND is denoted as
where
Definition 23.
For any two and over U, P-OR is denoted as
where
Definition 24.
For any two and over U, R-OR is denoted as
where
Theorem 11.
Let , be a neutrosophic cubic soft expert sets in If , is an (resp., ). Then is (resp., ) respectively.
Proof.
Since , is an (resp., ) in so for any we have As
Hence is an . Also
Hence is an . □
5. Applications
In this section, we use NCSESs to construct an algorithm and applied it to a decision-making problem. The series between Pakistan and India remains a hot cake for cricket lovers and this cricket rivalry existed between them at the start of partition. The first series between the two teams took place in 1951–52, when Pakistan made a tour of India. India made a tour of Pakistan for the first time in 1954–55. Between 1962 and 1977, no cricket was played between the two countries owing to two major wars in 1965 and 1971. The 1999 Kargil War and the 2008 Mumbai terrorist attacks have also interrupted the game of cricket between the two nations. The growth of large expatriate populations from India and Pakistan across the world led to neutral venues such as the United Arab Emirates and Canada hosting several bilateral and multilateral ODI series involving the two teams. Tickets for The India-Pakistan match in the 2015 World Cup in Australia sold out in 12 min at the ticket counters.
We try to use NCSESs in India–Pakistan cricket rivalry to conclude which country is suffering more from the above mentioned conflicts.
For this we first define the neutrosophic cubic soft expert weight average operator () and score function.
Definition 25.
Let be a . Then neutrosophic cubic soft expert weight average operator () is denoted and define as
where is the weight of expert opinion, and
Definition 26.
Let be neutrosophic cubic soft expert value. A score function Q of is defined as , where
Decision-making problems have been studied using fuzzy soft sets. Now, we are going to present multicriteria neutrosophic cubic soft set in decision-making along with weights and score function. For this we propose the following algorithmic steps as pictured in Figure 1.
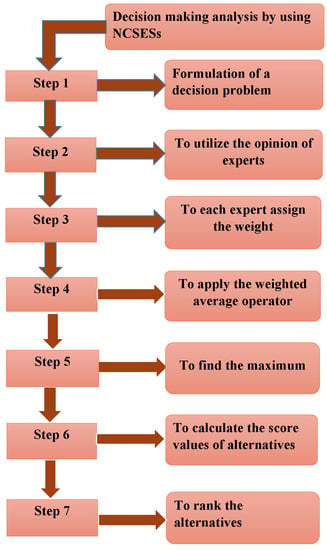
Figure 1.
Flow chart of NCSESs based on MADM Problem.
Step 1: Define a decision problem by inputting the neutrosophic cubic soft expert set
Step 2: Use the opinions of experts in the form of to determine the opinions regarding given criteria. Make a separate table for the opinion of each expert.
Step 3: Assign weight to each expert according to their expertise.
Step 4: Apply neutrosophic cubic soft expert weighted average operator to each above table and find the neutrosophic cubic soft expert weighted average corresponding to each attribute.
Step 5: Calculate the of
Step 6: Calculate the score of each
Step 7: Generate the non-increasing order of all the alternatives according to their scores.
Example 10.
Let be the set of countries playing a cricket series, Pakistan Cricket Board (PCB), The Board of Control for Cricket in India (BCCI), Bilateral relations between Pakistan and India} be the set of factors affecting the series, be the set of experts giving their expert opinion. The expert may consider the most burning parameter as “ICC’s Future Tours Programme (FTP)” when they are giving their opinion by considering three times of frames as past, present, and future.
Step 1: After a serious discussion, the committee constructed the following neutrosophic cubic soft expert set.
Step 2: Opinion of expert p
Opinion of expert q
Opinion of expert r
Step 3: Let be the weight vector assigned to the experts and r respectively.
Step 4: The neutrosophic cubic soft expert weighted average (NCSEWA) of each attribute is displayed in Table 1.

Table 1.
NCSEWA of each attribute.
Step 5: Calculate the of the first and second columns of Table 1 by using Definition 23. Thus we have
Step 6: Using Definition 26, we have .
Step 7: The score of the values corresponding to of implies the following order .
Thus, we can conclude that the country Pakistan is affected more by the factors, PCB, BCCI, Bilateral relations between Pakistan and India.
6. Comparison Analysis
In this paper, we extend the concept of soft expert sets to neutrosophic cubic soft expert sets. This new idea generalizes the different types of expert sets presented by Alkhazaleh and Salleh [33,36], Broumi and Smarandache [40], Qayyum et al. [48] and Sahin et al. [43].
1. If we consider only truth part or indeterminacy part or falsity part, then our model and the model presented by Qayyum et al. [48] coincides with each other.
2. Since NCSESs consists of interval neutrosophic soft expert soft sets and neutrosophic soft expert sets and if we consider only the part containing the neutrosophic soft expert sets then our model reduces to the model presented by Sahin et al. [43].
3. If we consider the part containing the interval neutrosophic soft expert soft sets, we get a special class of soft expert sets.
4. Similarly imposing some extra conditions to our model it will reduce it to those models presented by Alkhazaleh and Salleh [33,36], Broumi and Smarandache [40].
7. Conclusions
The model of NCSESs can be used in many decision-making problems and it will produce more reliable results as compared to the previously defined versions of soft expert sets. This paper is of introductory nature where we establish this new generalized theory of soft expert sets with its basic properties and provide an application. In future we shall apply this model to other areas to illustrate its novelty. We have defined different operations of NCSESs including different versions of NCSESs. We have designed aggregation operators and score functions of neutrosophic cubic soft expert value. We have also constructed an algorithm based on this new concept and applied the developed approach to a numerical example.
The substantial impact of our outcome for the research field is that we gave a generalized form of soft expert system which certainly improves the decision-making theory due to its wide range of values in the form of truth, indeterminacy, and falsity. We have not used any software for the decision-making, since the preliminary research is on a small scale. We intend to expand the research to a larger scale on an applied problem so that we can develop a software and related interface. We also intend to apply the developed approach to a variety of games, signature theory and others, since the nature of NCSESs enables us to deal with vague and inconsistent data. In decision-making theory, we often deal with data which are inconsistent and vague. Thus, ex-ante decision-making problems can also be handled easily through NCSESs. In future, arguments and modern theories linked to behavioral patterns could strengthen the idea of NCSESs, especially using aggregation operators and methods that effectively deal with the uncertainty and inaccuracy of the input data [49].
Author Contributions
All authors contributed equally.
Funding
Universiti Kebangsaan Malaysia- Grant No. GUP-2017-105.
Acknowledgments
We are indebted to Universiti Kebangsaan Malaysia for providing financial support under the grant GUP-2017-105.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zadeh, L.A. Fuzzy sets. Inform. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Turksen, I.B. Interval-valued fuzzy sets based on normal forms. Fuzzy Sets Syst. 1986, 20, 191–210. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.; Pasi, G.; Yager, R. Intuitionistic fuzzy interpretations of multi-criteria multi-person and multi-measurement tool decision making. Int. J. Syst. Sci. 2005, 36, 859–868. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field in Logics: Neutrosophic Logic. Neutrosophy, Neutrosophic Set, Neutrosophic Probability; American Reserch Press: Rehoboth, IL, USA, 1999. [Google Scholar]
- Smarandache, F. Neutrosophic set-a generalization of the intuitionistic fuzzy set. Int. J. Pure Appl. Math. 2005, 24, 287–297. [Google Scholar]
- De, S.K.; Beg, I. Triangular dense fuzzy neutrosophic sets. Neutrosophic Sets Syst. 2016, 13, 26–37. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.Q.; Sunderraman, R. Interval Neutrosophic Sets and Logic: Theory and Applications in Computing; Hexis: Phoenix, AZ, USA, 2005. [Google Scholar]
- Gulistan, M.; Nawaz, S.; Hassan, N. Neutrosophic triplet non-associative semihypergroups with application. Symmetry 2018, 10, 613. [Google Scholar] [CrossRef]
- Jun, Y.B.; Kim, C.S.; Yang, K.O. Cubic Sets. Ann. Fuzzy Math. Inform. 2012, 4, 83–98. [Google Scholar]
- Abughazalah, N.; Yaqoob, N. Applications of cubic structures to subsystems of finite state machines. Symmetry 2018, 10, 598. [Google Scholar] [CrossRef]
- Rashid, S.; Yaqoob, N.; Akram, M.; Gulistan, M. Cubic graphs with application. Int. J. Anal. Appl. 2018, 16, 733–750. [Google Scholar]
- Gulistan, M.; Yaqoob, N.; Vougiouklis, T.; Wahab, H.A. Extensions of cubic ideals in weak left almost semihypergroups. J. Intell. Fuzzy Syst. 2018, 34, 4161–4172. [Google Scholar] [CrossRef]
- Ma, X.L.; Zhan, J.; Khan, M.; Gulistan, M.; Yaqoob, N. Generalized cubic relations in Hv-LA-semigroups. J. Discret. Math. Sci. Cryptogr. 2018, 21, 607–630. [Google Scholar] [CrossRef]
- Yaqoob, N.; Gulistan, M.; Leoreanu-Fotea, V.; Hila, K. Cubic hyperideals in LA-semihypergroups. J. Intell. Fuzzy Syst. 2018, 34, 2707–2721. [Google Scholar] [CrossRef]
- Gulistan, M.; Khan, M.; Yaqoob, N.; Shahzad, M. Structural properties of cubic sets in regular LA-semihypergroups. Fuzzy Inf. Eng. 2017, 9, 93–116. [Google Scholar] [CrossRef]
- Khan, M.; Gulistan, M.; Yaqoob, N.; Hussain, F. General cubic hyperideals of LA-semihypergroups. Afr. Mat. 2016, 27, 731–751. [Google Scholar] [CrossRef]
- Khan, M.; Jun, Y.B.; Gulistan, M.; Yaqoob, N. The generalized version of Jun’s cubic sets in semigroups. J. Intell. Fuzzy Syst. 2015, 28, 947–960. [Google Scholar]
- Yaqoob, N.; Mostafa, S.M.; Ansari, M.A. On cubic KU-ideals of KU-algebras. ISRN Algebra 2013, 2013, 935905. [Google Scholar] [CrossRef]
- Aslam, M.; Aroob, T.; Yaqoob, N. On cubic Γ-hyperideals in left almost Γ-semihypergroups. Ann. Fuzzy Math. Inform. 2013, 5, 169–182. [Google Scholar]
- Jun, Y.B.; Smarandache, F.; Kim, C.S. Neutrosophic cubic sets. New Math. Nat. Comput. 2017, 13, 41–54. [Google Scholar] [CrossRef]
- Khan, M.; Gulistan, M.; Yaqoob, N.; Shabir, M. Neutrosophic cubic (α,β)-ideals in semigroups with application. J. Intell. Fuzzy Syst. 2018, 35, 2469–2483. [Google Scholar] [CrossRef]
- Gulistan, M.; Yaqoob, N.; Rashid, Z.; Smarandache, F.; Wahab, H.A. A study on neutrosophic cubic graphs with real life applications in industries. Symmetry 2018, 10, 203. [Google Scholar] [CrossRef]
- Gulistan, M.; Khan, A.; Abdullah, A.; Yaqoob, N. Complex neutrosophic subsemigroups and ideals. Int. J. Anal. Appl. 2018, 16, 97–116. [Google Scholar]
- Molodtsov, D.A. Soft set theory-first results. Comput. Math. Appl. 1999, 37, 19–31. [Google Scholar] [CrossRef]
- Maji, P.K.; Roy, A.R. Soft set theory. Comput. Math. Appl. 2003, 45, 555–562. [Google Scholar] [CrossRef]
- Maji, P.K.; Biswas, R.; Roy, A.R. Fuzzy soft sets. J. Fuzzy Math. 2001, 9, 589–602. [Google Scholar]
- Cagman, N.; Enginoglu, S.; Citak, F. Fuzzy soft set theory and its application. Iran. J. Fuzzy Syst. 2011, 8, 137–147. [Google Scholar]
- Feng, F.; Jun, Y.B.; Liu, X.; Li, L. An adjustable approach to fuzzy soft set based decision making. J. Comput. Appl. Math. 2010, 234, 10–20. [Google Scholar] [CrossRef]
- Gorzalczany, M.B. A method of inference in approximate reasoning based on interval valued fuzzy sets. Fuzzy Sets Syst. 1987, 21, 1–17. [Google Scholar] [CrossRef]
- Kong, Z.; Gao, L.; Wang, L. Comment on “A fuzzy soft set theoretic approach to decision making problems”. J. Comput. Appl. Math. 2009, 223, 540–542. [Google Scholar] [CrossRef]
- Roy, A.R.; Maji, P.K. A fuzzy soft set theoretic approach to decision making problems. J. Comput. Appl. Math. 2007, 203, 412–418. [Google Scholar] [CrossRef]
- Alkhazaleh, S.; Salleh, A.R. Soft expert sets. Adv. Decis. Sci. 2011, 2011, 757868. [Google Scholar] [CrossRef]
- Arokia Lancy, A.; Tamilarasi, C.; Arockiarani, I. Fuzzy parameterization for decision making in risk management system via soft expert set. Int. J. Innov. Res. Stud. 2013, 2, 339–344. [Google Scholar]
- Arokia Lancy, A.; Arockiarani, I. A fusion of soft expert set and matrix models. Int. J. Res. Eng. Technol. 2013, 2, 531–535. [Google Scholar]
- Alkhazaleh, S.; Salleh, A.R. Fuzzy soft expert set and its application. Appl. Math. 2014, 5, 1349–1368. [Google Scholar] [CrossRef]
- Bashir, M.; Salleh, A.R. Fuzzy parameterized soft expert set. Abstr. Appl. Anal. 2012, 2012, 25836. [Google Scholar] [CrossRef]
- Bashir, M.; Salleh, A.R. Possibility fuzzy soft expert set. Open J. Appl. Sci. 2012, 12, 208–211. [Google Scholar] [CrossRef]
- Alhazaymeh, K.; Hassan, N. Application of generalized vague soft expert set in decision making. Int. J. Pure Appl. Math. 2014, 93, 361–367. [Google Scholar] [CrossRef]
- Broumi, S.; Smarandache, F. Intuitionistic fuzzy soft expert sets and its application in decision making. J. New Theory 2015, 1, 89–105. [Google Scholar]
- Abu Qamar, M.; Hassan, N. Q-neutrosophic soft relation and its application in decision making. Entropy 2018, 20, 172. [Google Scholar] [CrossRef]
- Abu Qamar, M.; Hassan, N. Entropy measures of distance and similarity of Q-neutrosophic soft sets and some applications. Entropy 2018, 20, 672. [Google Scholar] [CrossRef]
- Sahin, M.; Alkhazaleh, S.; Ulucay, V. Neutrosophic soft expert sets. Appl. Math. 2015, 6, 116–127. [Google Scholar] [CrossRef]
- Uluçay, V.; Sahin, M.; Hassan, N. Generalized neutrosophic soft expert set for multiple-criteria decision-making. Symmetry 2018, 10, 437. [Google Scholar] [CrossRef]
- Al-Quran, A.; Hassan, N. Neutrosophic vague soft expert set theory. J. Intell. Fuzzy Syst. 2016, 30, 3691–3702. [Google Scholar] [CrossRef]
- Al-Quran, A.; Hassan, N. The complex neutrosophic soft expert set and its application in decision making. J. Intell. Fuzzy Syst. 2018, 34, 569–582. [Google Scholar] [CrossRef]
- Al-Quran, A.; Hassan, N. The complex neutrosophic soft expert relation and its multiple attribute decision-making method. Entropy 2018, 20, 101. [Google Scholar] [CrossRef]
- Qayyum, A.; Abdullah, S.; Aslam, M. Cubic soft expert sets and their application in decision making. J. Intell. Fuzzy Syst. 2016, 31, 1585–1596. [Google Scholar] [CrossRef]
- Ziemba, P.; Becker, J. Analysis of the digital divide using fuzzy forecasting. Symmetry 2019, 11, 166. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).