The Third and Fourth Kind Pseudo-Chebyshev Polynomials of Half-Integer Degree

Abstract

New sets of orthogonal functions, which correspond to the first, second, third, and fourth kind Chebyshev polynomials with half-integer indexes, have been recently introduced. In this article, links of these new sets of irrational functions to the third and fourth kind Chebyshev polynomials are highlighted and their connections with the classical Chebyshev polynomials are shown.

1. Introduction

In the second half of the XIX Century, Pafnuty Lvovich Chebyshev introduced two sets of polynomials, presently known as the first and second kind Chebyshev polynomials, which are actually a polynomial version of the circular sine and cosine functions. These polynomials have proved to be of fundamental importance in many questions of an applicative nature (see the classical book by T. Rivlin [1]). In fact, the roots of the first kind polynomials—the so called Chebyshev nodes—appear in approximation theory, since, by using these nodes, the relevant Gaussian quadrature rule realizes the highest possible degree of precision. Moreover, the resulting interpolation polynomial minimizes the Runge phenomenon. Furthermore, by expanding a continuous function in terms of first kind Chebyshev polynomials, the best approximation, with respect to the maximum norm, can be obtained. The second kind Chebyshev polynomials appear in the computation of powers of $2\times 2$ non-singular matrices [2]. For the same problem, in the case of powers of higher order matrices, an extension of these polynomials have been also introduced (see, e.g., [3,4]).

It is also useful to notice that Chebyshev polynomials represent an important tool in deriving integral representations [5,6], and that they can be generalized by using the properties and formalism of the Hermite polynomials [7]; for instance, by introducing multi-variable polynomials recognized as belonging to the Chebyshev family [8,9,10].

An excellent book on this subject is [11]. The importance of the Chebyshev polynomials in applications has been highlighted, in [12]. In a recent paper, the Chebyshev polynomials of the first and second kind have been shown to represent the real and imaginary part, respectively, of the complex Appell polynomials [13].

In a recent article [14], new sets of functions related to the classical Chebyshev polynomials have been introduced, in connections with the complex version of the Bernoulli spiral. Actually, the real and imaginary part of the Bernoulli spirals define the Rodhonea (or Grandi) curves of fractional index, which often appear in natural shapes [15]. This allows us to define two sets of functions corresponding to the first and second kind Chebyshev polynomials with fractional degree, called pseudo-Chebyshev polynomials (or pseudo-Chebyshev functions), as they are irrational functions. It was shown that, in the case of half-integer degree, the relevant pseudo-Chebyshev polynomials are orthogonal in the interval $(-1,1)$, with respect to the same weights of the Chebyshev polynomials of the same type.

In this article, by using the results of [16], we show the connections of the third and fourth kind pseudo-Chebyshev polynomials with the classical Chebyshev polynomials.

2. Definitions of Pseudo-Chebyshev Functions

The following polynomials $T_k\left(x\right)$, $U_k\left(x\right)$, $V_k\left(x\right)$, and $W_k\left(x\right)$ denote, respectively, the first, second, third, and fourth kind classical Chebyshev polynomials.

We have, by definition, for any integer k:

$$\begin{array}{c}{T}_{k+\frac{1}{2}}\left(x\right)=cos\left((k+\frac{1}{2})arccos\left(x\right)\right),\\ \sqrt{1-x^2}{U}_{k-\frac{1}{2}}\left(x\right)=sin\left((k+\frac{1}{2})arccos\left(x\right)\right),\\ \sqrt{1-x^2}{V}_{k+\frac{1}{2}}\left(x\right)=cos\left((k+\frac{1}{2})arccos\left(x\right)\right),\mathrm{and}\\ W_{k+\frac{1}{2}}\left(x\right)=sin\left((k+\frac{1}{2})arccos\left(x\right)\right).\end{array}$$

(1)

Note that definition (1) holds even for negative integer—that is, for $k+1/2<0$—according to the parity properties of the trigonometric functions.

The first, second, third, and fourth kind pseudo-Chebyshev functions are represented, in terms of the third and fourth kind Chebyshev polynomials, as follows:

$$\begin{array}{c}{T}_{k+\frac{1}{2}}\left(x\right)=\sqrt{\frac{1+x}{2}}{V}_k\left(x\right),\\ \sqrt{1-x^2}{U}_{k-\frac{1}{2}}\left(x\right)=\sqrt{\frac{1}{2(1+x)}}{W}_k\left(x\right),\\ \sqrt{1-x^2}{V}_{k+\frac{1}{2}}\left(x\right)=\sqrt{\frac{1}{2(1-x)}}{V}_k\left(x\right),\mathrm{and}\\ W_{k+\frac{1}{2}}\left(x\right)=\sqrt{\frac{1-x}{2}}{W}_k\left(x\right).\end{array}$$

(2)

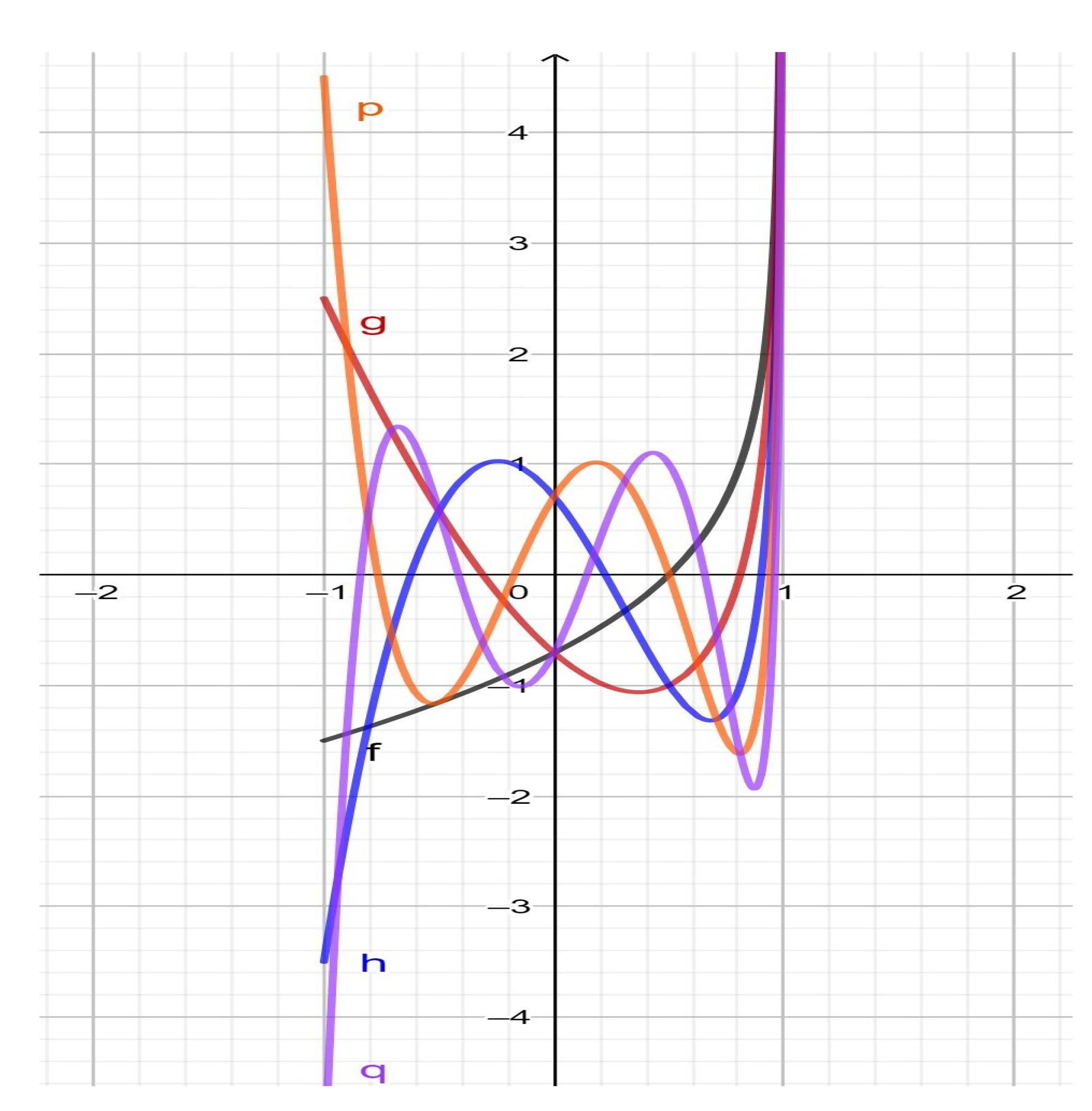
3. Properties of the First and Second Kind Pseudo-Chebyshev Functions

3.1. The First Kind Pseudo-Chebyshev $T_{k+1/2}$

In this section, we recall the main properties of the first kind pseudo-Chebyshev functions (their first few graphs are shown in Figure 1).

Recurrence relation

$$\left\{\begin{array}{c}{T}_{k+\frac{1}{2}}\left(x\right)=2x{T}_{k-\frac{1}{2}}\left(x\right)-T_{k-\frac{3}{2}}\left(x\right),\hfill \\ T_{\pm \frac{1}{2}}\left(x\right)=\sqrt{\frac{1+x}{2}}.\hfill \end{array}\right.$$

(3)

Differential equation

$$\begin{array}{c}(1-x^2)y^{″}-x{y}^{\prime }+{\left(k+\frac{1}{2}\right)}^{2}y=0.\end{array}$$

(4)

Orthogonality property

$$\begin{array}{c}{\displaystyle {\int }_{-1}^1{T}_{h+\frac{1}{2}}\left(x\right)T_{k+\frac{1}{2}}\left(x\right)\frac{1}{\sqrt{1-x^2}}dx=0,(h\ne k),}\end{array}$$

(5)

where h, k are integer numbers such that $h+k=2n$, $n=1,2,3,\cdots$,

$${\displaystyle {\int }_{-1}^1{T}_{k+\frac{1}{2}}^2\left(x\right)\frac{1}{\sqrt{1-x^2}}dx=\frac{\pi }{2}.}$$

(6)

3.2. The Second Kind Pseudo-Chebyshev $U_{k+1/2}$

In this section we recall the main properties of the second kind pseudo-Chebyshev functions (their first few graphs are shown in Figure 2).

Recurrence relation

$$\left\{\begin{array}{c}{U}_{k+\frac{1}{2}}\left(x\right)=2x{U}_{k-\frac{1}{2}}\left(x\right)-U_{k-\frac{3}{2}}\left(x\right),\hfill \\ U_{-\frac{1}{2}}\left(x\right)=\frac{1}{\sqrt{2(1+x)}},U_{\frac{1}{2}}\left(x\right)=\frac{2x+1}{\sqrt{2(1+x)}}.\hfill \end{array}\right.$$

(7)

Differential equation

$$\begin{array}{c}(1-x^2)y^{″}-3x{y}^{\prime }+\left(k-\frac{1}{2}\right)\left(k+\frac{3}{2}\right)y=0.\end{array}$$

(8)

Orthogonality property

$$\begin{array}{c}{\displaystyle {\int }_{-1}^1{U}_{h+\frac{1}{2}}\left(x\right)U_{k+\frac{1}{2}}\left(x\right)\sqrt{1-x^2}dx=0,(h\ne k),}\end{array}$$

(9)

where h, k are integer numbers such that $h+k=2n$, $n=1,2,3,\cdots$,

$${\displaystyle {\int }_{-1}^1{U}_{k+\frac{1}{2}}^2\left(x\right)\sqrt{1-x^2}dx=\frac{\pi }{2}.}$$

(10)

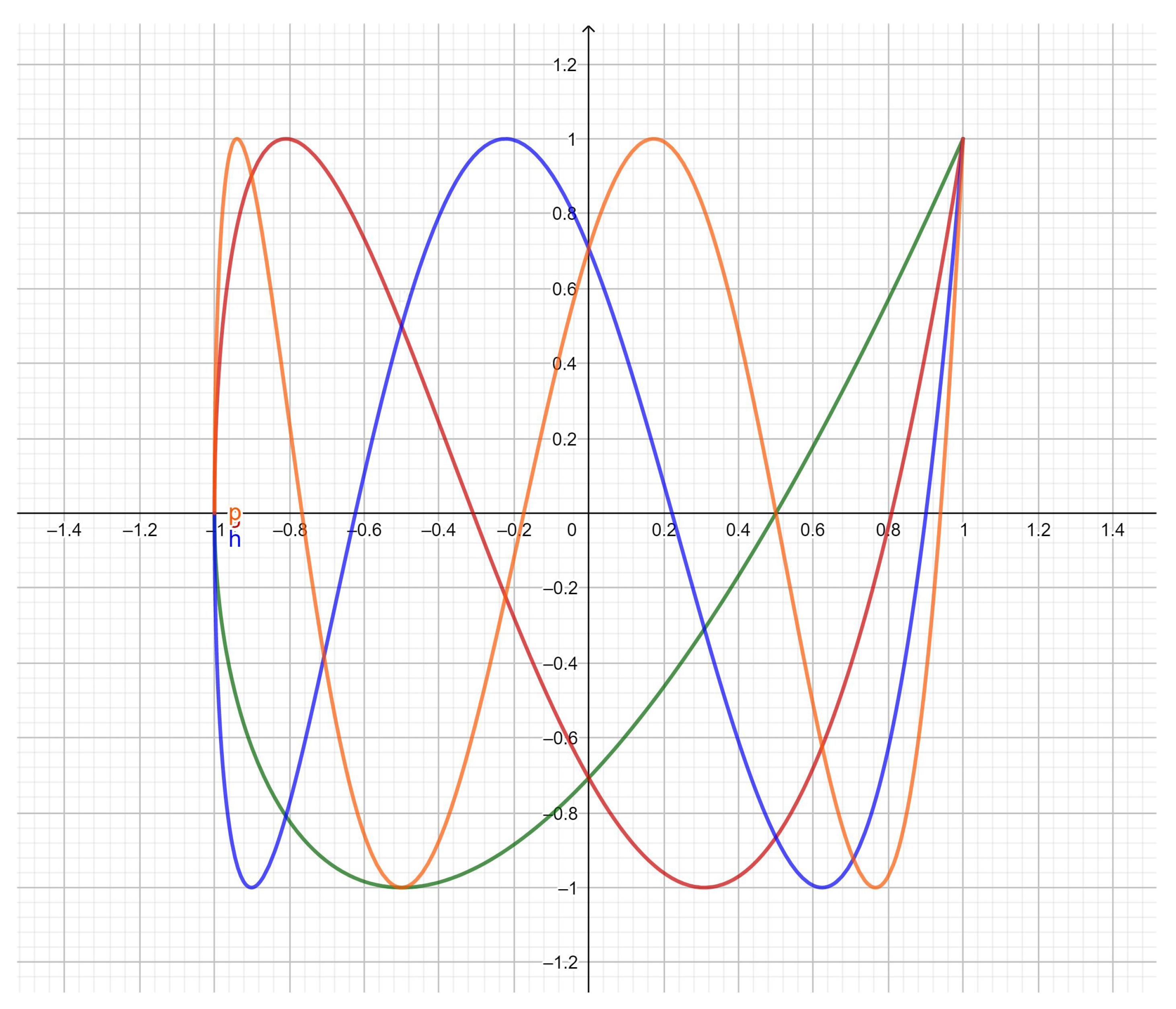
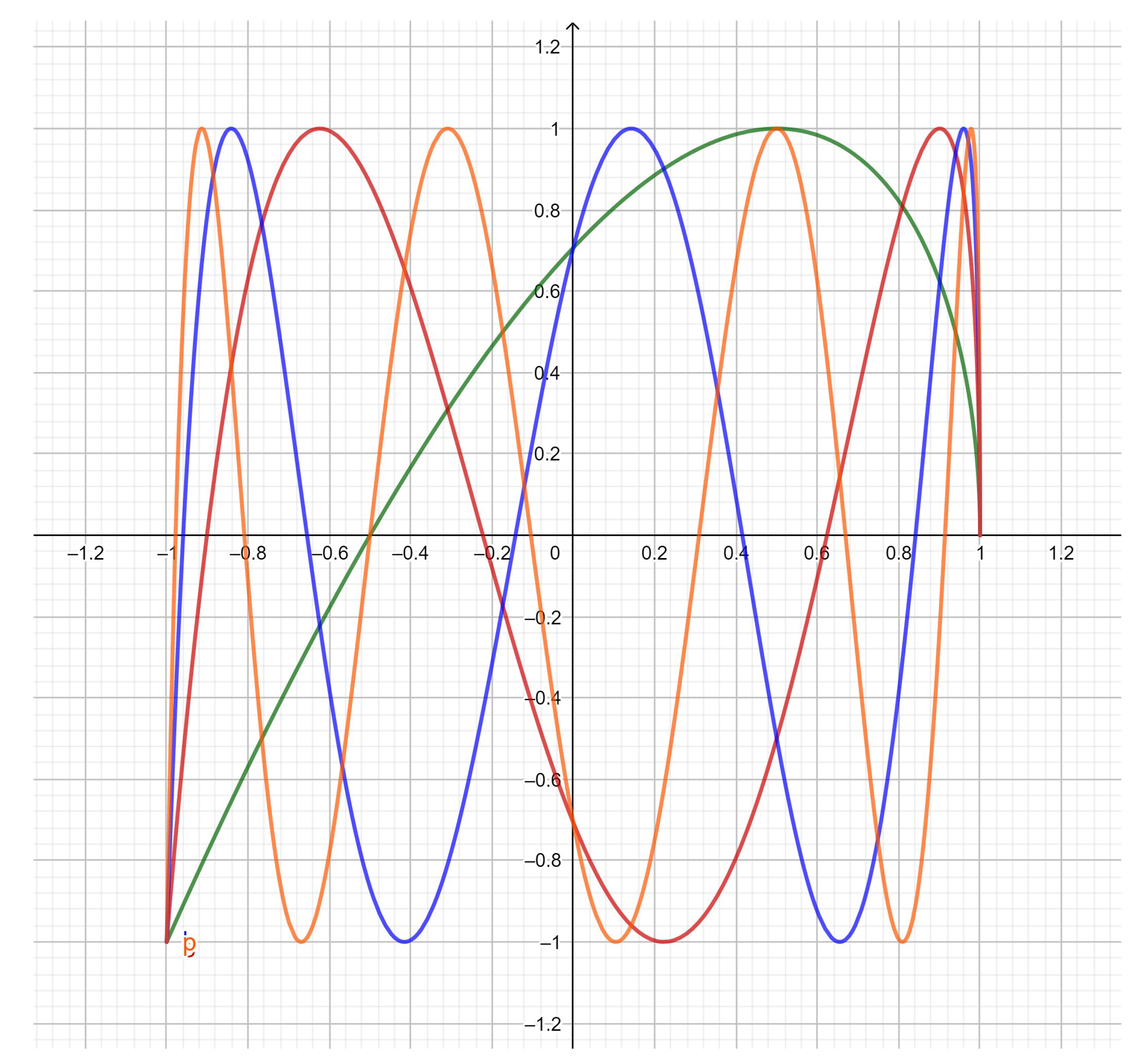
4. The Third and Fourth Kind Pseudo-Chebyshev Functions

The third and fourth kind Chebyshev polynomials have been also introduced, and studied by several authors (see [16,17,18]), because they can be applied in particular quadrature rules, where the singularity of the considered function appears at only one of the extrema ($+1$ or $-1$) of the integration interval (see [11]). Moreover, in a recent article, they have been used in the framework of solving high odd-order boundary value problems [17].

In what follows, we use the excellent survey by K. Aghigh, M. Masjed-Jamei, and M. Dehghan [16], which permits us to derive, in a straightforward way, the links among the pseudo-Chebyshev functions and the third and fourth kind Chebyshev polynomials.

In Figure 3 and Figure 4, graphs of the first few third and fourth kind pseudo-Chebyshev functions are shown.

4.1. The Third Kind Pseudo-Chebyshev $V_{k+1/2}$

Recurrence relation

$$\left\{\begin{array}{c}{V}_{k+\frac{1}{2}}\left(x\right)=2x{V}_{k-\frac{1}{2}}\left(x\right)-V_{k-\frac{3}{2}}\left(x\right),\hfill \\ V_{\pm \frac{1}{2}}\left(x\right)=\frac{1}{\sqrt{2(1-x)}}.\hfill \end{array}\right.$$

(11)

Differential equation

Theorem 1.

The third kind pseudo-Chebyshev functions $V_{k+1/2}\left(x\right)$ satisfy the differential equation:

$$\begin{array}{c}(1-x^2)y^{″}-3x{y}^{\prime }+\left(k-\frac{1}{2}\right)\left(k+\frac{3}{2}\right)y=0,\end{array}$$

(12)

so that the second and third kind pseudo-Chebyshev functions are solutions of the same differential equation.

Proof. 

Note that, from definition (1):

$$\begin{array}{c}{\displaystyle D_x{V}_{k+\frac{1}{2}}\left(x\right)={\displaystyle \frac{x}{1-x^2}}{V}_{k+\frac{1}{2}}\left(x\right)+\left(k+\frac{1}{2}\right)\frac{1}{1-x^2}{W}_{k+\frac{1}{2}}\left(x\right),}\\ {\displaystyle D_x^2{V}_{k+\frac{1}{2}}\left(x\right)=-\left[{\left(k+\frac{1}{2}\right)}^2-1\right]\frac{1}{1-x^2}{V}_{k+\frac{1}{2}}\left(x\right)+\frac{3x^2}{{(1-x^2)}^2}{V}_{k+\frac{1}{2}}\left(x\right)+}\\ {\displaystyle +3\left(k+\frac{1}{2}\right)\frac{x}{{(1-x^2)}^2}{W}_{k+\frac{1}{2}}\left(x\right),}\\ D_x^2{V}_{k+\frac{1}{2}}\left(x\right)-{\displaystyle \frac{3x}{1-x^2}}{D}_x{V}_{k+\frac{1}{2}}\left(x\right)=-\left[\left(k-\frac{1}{2}\right)\left(k+\frac{3}{2}\right)\right]V_{k+\frac{1}{2}}\left(x\right),\end{array}$$

so that Equation (12) follows. □

Orthogonality property

$${\int }_{-1}^1{V}_{h+\frac{1}{2}}\left(x\right)V_{k+\frac{1}{2}}\left(x\right)\sqrt{1-x^2}dx=0,(h\ne k),$$

(13)

where h, k are integer numbers such that $h+k=2n$, $n=1,2,3,\cdots$,

$$\begin{array}{c}\hfill {\displaystyle {\int }_{-1}^1{V}_{k+\frac{1}{2}}^2\left(x\right)\sqrt{1-x^2}dx=\frac{\pi }{2}.}\end{array}$$

(14)

4.2. The Fourth Kind Pseudo-Chebyshev $W_{k+1/2}$

Recurrence relation

$$\left\{\begin{array}{c}{W}_{k+\frac{1}{2}}\left(x\right)=2x{W}_{k-\frac{1}{2}}\left(x\right)-W_{k-\frac{3}{2}}\left(x\right),\hfill \\ W_{\pm \frac{1}{2}}\left(x\right)=\pm \sqrt{\frac{1-x}{2}}.\hfill \end{array}\right.$$

(15)

Differential equation

Theorem 2.

The fourth kind pseudo-Chebyshev functions $W_{k+1/2}\left(x\right)$ satisfy the differential equation:

$$\begin{array}{c}(1-x^2)y^{″}+x{y}^{\prime }+{\left(k+\frac{1}{2}\right)}^2(1-x^2)y=0.\end{array}$$

(16)

Proof. 

Note that

$$\begin{array}{c}{D}_x{W}_{k+\frac{1}{2}}\left(x\right)=-\left(k+\frac{1}{2}\right){(1-x^2)}^{-1/2}{T}_{k+\frac{1}{2}}\left(x\right),\\ D_x^2{W}_{k+\frac{1}{2}}\left(x\right)=-{\left(k+\frac{1}{2}\right)}^2{W}_{k+\frac{1}{2}}\left(x\right)-\left(k+\frac{1}{2}\right)x{(1-x^2)}^{-3/2}{T}_{k+\frac{1}{2}}\left(x\right)=\\ =-{\left(k+\frac{1}{2}\right)}^2{W}_{k+\frac{1}{2}}\left(x\right)-x{(1-x^2)}^{-1}{D}_x{W}_{k+\frac{1}{2}}\left(x\right),\end{array}$$

so that Equation (16) follows. □

Orthogonality property

$$\begin{array}{c}{\displaystyle {\int }_{-1}^1{W}_{h+\frac{1}{2}}\left(x\right)W_{k+\frac{1}{2}}\left(x\right)\frac{1}{\sqrt{1-x^2}}dx=0,(h\ne k),}\end{array}$$

(17)

where h, k are integer numbers such that $h+k=2n$, $n=1,2,3,\cdots$,

$${\int }_{-1}^1{W}_{k+\frac{1}{2}}^2\left(x\right)\frac{1}{\sqrt{1-x^2}}dx=\frac{\pi }{2}.$$

(18)

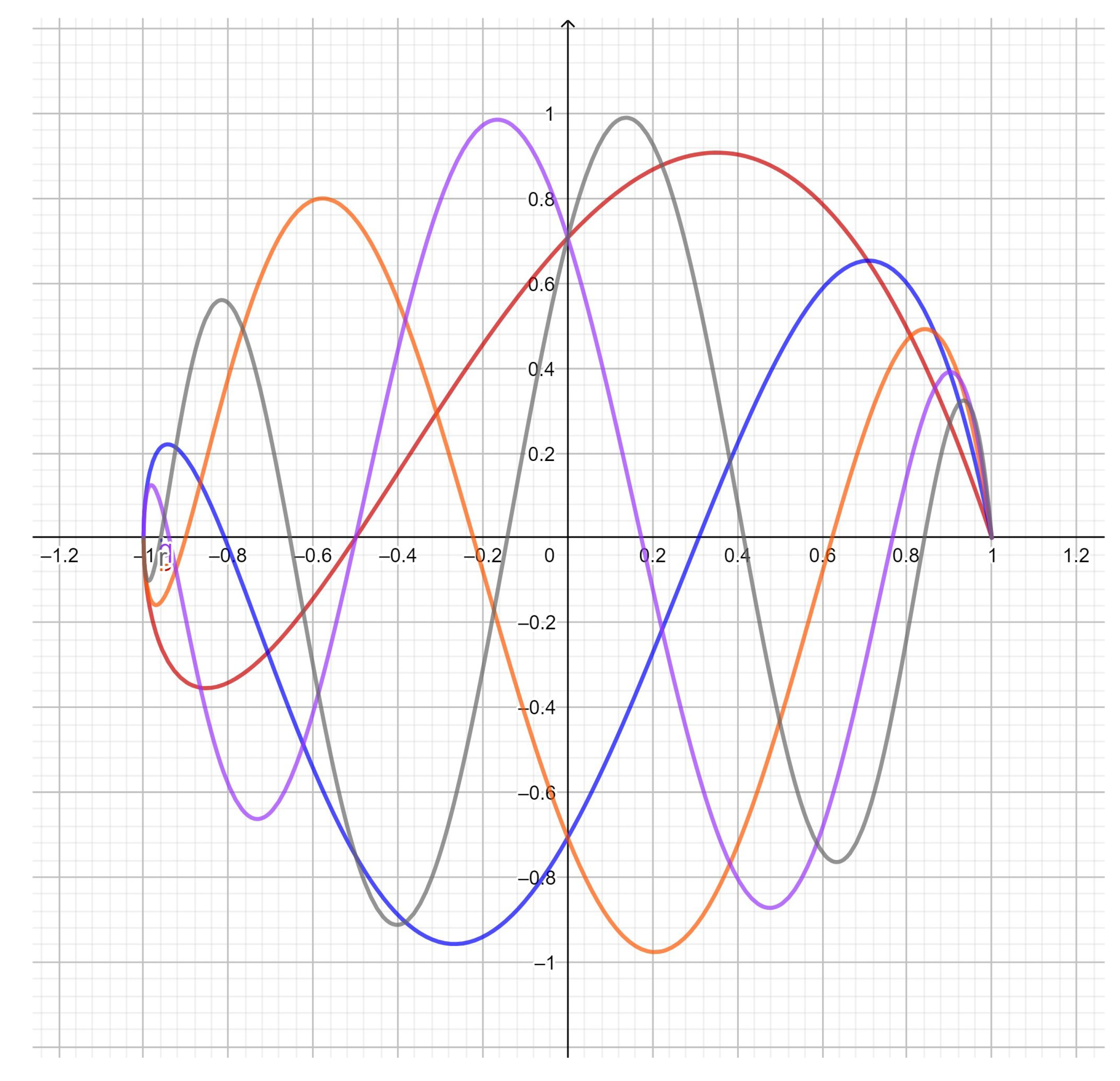
5. Further Properties of the Pseudo-Chebyshev Functions

5.1. Generating Functions

Theorem 3.

The generating functions of the pseudo-Chebyshev functions are given by:

$$\begin{array}{c}{\displaystyle {\displaystyle \sum _{k=0}^{\infty }}{T}_{k+\frac{1}{2}}\left(x\right)t^k=\sqrt{\frac{1+x}{2}}\frac{1-t}{1-2tx+t^2},}\\ {\displaystyle {\displaystyle \sum _{k=0}^{\infty }}{U}_{k-\frac{1}{2}}\left(x\right)t^k=\sqrt{\frac{1}{2(1+x)}}\frac{1+t}{1-2tx+t^2},}\\ {\displaystyle {\displaystyle \sum _{k=0}^{\infty }}{V}_{k+\frac{1}{2}}\left(x\right)t^k=\sqrt{\frac{1}{2(1-x)}}\frac{1-t}{1-2tx+t^2},and}\\ {\displaystyle {\displaystyle \sum _{k=0}^{\infty }}{W}_{k+\frac{1}{2}}\left(x\right)t^k=\sqrt{\frac{1-x}{2}}\frac{1+t}{1-2tx+t^2}.}\end{array}$$

(19)

Proof. 

Equations (19) follow from Definitions (2) by using the generating functions of the third and fourth Chebyshev polynomials, which are given below (see [16]):

$$\begin{array}{c}{\displaystyle \sum _{k=0}^{\infty }{V}_k\left(x\right)t^k=\frac{1-t}{1-2tx+t^2}\mathrm{and}}\\ {\displaystyle \sum _{k=0}^{\infty }{W}_k\left(x\right)t^k=\frac{1+t}{1-2tx+t^2}.}\end{array}$$

(20)

□

5.2. Explicit Forms

Theorem 4.

The explicit forms of the pseudo-Chebyshev functions are given by:

$$\begin{array}{c}{T}_{k+\frac{1}{2}}\left(x\right)=\sqrt{\frac{1+x}{2}}{\displaystyle \sum _{h=0}^k}{(-1)}^h\left(\genfrac{}{}{0pt}{}{2k+1}{2h}\right){\left(\frac{1-x}{2}\right)}^h{\left(\frac{1+x}{2}\right)}^{k-h},\\ U_{k-\frac{1}{2}}\left(x\right)=\sqrt{\frac{1}{2(1+x)}}{\displaystyle \sum _{h=0}^k}{(-1)}^h\left(\genfrac{}{}{0pt}{}{2k+1}{2h+1}\right){\left(\frac{1-x}{2}\right)}^h{\left(\frac{1+x}{2}\right)}^{k-h},\\ V_{k+\frac{1}{2}}\left(x\right)=\sqrt{\frac{1}{2(1-x)}}{\displaystyle \sum _{h=0}^k}{(-1)}^h\left(\genfrac{}{}{0pt}{}{2k+1}{2h}\right){\left(\frac{1-x}{2}\right)}^h{\left(\frac{1+x}{2}\right)}^{k-h},and\\ W_{k+\frac{1}{2}}\left(x\right)=\sqrt{\frac{1-x}{2}}{\displaystyle \sum _{h=0}^k}{(-1)}^h\left(\genfrac{}{}{0pt}{}{2k+1}{2h+1}\right){\left(\frac{1-x}{2}\right)}^h{\left(\frac{1+x}{2}\right)}^{k-h}.\end{array}$$

(21)

Proof. 

Recalling that

$$\begin{array}{c}cos\left(\frac{1}{2}arccos\left(x\right)\right)=\sqrt{\frac{1+x}{2}}\mathrm{and}sin\left(\frac{1}{2}arccos\left(x\right)\right)=\sqrt{\frac{1-x}{2}},\end{array}$$

(22)

we find:

$$\begin{array}{c}{\left[cos\left(\frac{1}{2}arccos\left(x\right)\right)+\mathrm{i}sin\left(\frac{1}{2}arccos\left(x\right)\right)\right]}^{2k+1}={\left(\sqrt{\frac{1+x}{2}}+\mathrm{i}\sqrt{\frac{1-x}{2}}\right)}^{2k+1},\end{array}$$

(23)

so that, by the binomial theorem, we find (see [16]):

$$\begin{array}{c}{\left(\sqrt{\frac{1+x}{2}}+\mathrm{i}\sqrt{\frac{1-x}{2}}\right)}^{2k+1}=\sqrt{\frac{1+x}{2}}{\displaystyle \sum _{h=0}^k}{(-1)}^h\left(\genfrac{}{}{0pt}{}{2k+1}{2h}\right){\left(\frac{1-x}{2}\right)}^h{\left(\frac{1+x}{2}\right)}^{k-h}\\ +\mathrm{i}\sqrt{\frac{1-x}{2}}{\displaystyle \sum _{h=0}^k}{(-1)}^h\left(\genfrac{}{}{0pt}{}{2k+1}{2h+1}\right){\left(\frac{1-x}{2}\right)}^h{\left(\frac{1+x}{2}\right)}^{k-h}.\end{array}$$

(24)

Therefore, recalling Definitions (2), Equation (21) follows. □

5.3. Location of Zeros

By Equation (1), the zeros of the pseudo-Chebyshev functions $T_{k+\frac{1}{2}}\left(x\right)$ and $V_{k+\frac{1}{2}}\left(x\right)$ are given by

$$\begin{array}{c}\hfill \begin{array}{c}{x}_{k,h}=cos\left({\displaystyle \frac{(2h-1)\pi }{2k+1}}\right),(h=1,2,\cdots ,k),\end{array}\end{array}$$

(25)

and the zeros of the pseudo-Chebyshev functions $U_{k+\frac{1}{2}}\left(x\right)$ and $W_{k+\frac{1}{2}}\left(x\right)$ are given by

$$\begin{array}{c}{x}_{k,h}=cos\left({\displaystyle \frac{2h\pi }{2k+1}}\right),(h=1,2,\cdots ,k).\end{array}$$

(26)

Furthermore, the $W_{k+\frac{1}{2}}\left(x\right)$ functions always vanish at the end of the interval [−1, 1].

5.4. Hypergeometric Representations

Theorem 5.

The hypergeometric representations of the pseudo-Chebyshev functions are given by:

$$\begin{array}{c}{T}_{k+\frac{1}{2}}\left(x\right)=\sqrt{\frac{1+x}{2}}{}_2{F}_1\left(-k,k+1,\frac{1}{2}|\frac{1-x}{2}\right),\\ U_{k-\frac{1}{2}}\left(x\right)=\frac{2k+1}{1+x}\sqrt{\frac{1}{2(1-x)}}{}_2{F}_1\left(-k,k+1,\frac{3}{2}|\frac{1-x}{2}\right),\\ V_{k+\frac{1}{2}}\left(x\right)=\frac{2k+1}{1-x}\sqrt{\frac{1}{2(1+x)}}{}_2{F}_1\left(-k,k+1,\frac{1}{2}|\frac{1-x}{2}\right),and\\ W_{k+\frac{1}{2}}\left(x\right)=(2k+1)\sqrt{\frac{1-x}{2}}{}_2{F}_1\left(-k,k+1,\frac{3}{2}|\frac{1-x}{2}\right).\end{array}$$

(27)

Proof. 

Equations (27) follow from the hypergeometric representations of the third and fourth kind Chebyshev polynomials (see [16]):

$$\begin{array}{c}{V}_k\left(x\right)={}_2{F}_1\left(-k,k+1,\frac{1}{2}|\frac{1-x}{2}\right),\\ W_k\left(x\right)=(2k+1){}_2{F}_1\left(-k,k+1,\frac{3}{2}|\frac{1-x}{2}\right),\end{array}$$

(28)

by using Definitions (2). □

5.5. Rodrigues-Type Formulas

Theorem 6.

The Rodrigues-type formulas for the pseudo-Chebyshev functions are given by:

$$\begin{array}{c}{\displaystyle T_{k+\frac{1}{2}}\left(x\right)={\displaystyle \frac{{(-1)}^k}{(2k-1)!!}}\sqrt{\frac{1-x}{2}}\frac{d^k}{d{x}^k}\left[{(1-x)}^{k-1/2}{(1+x)}^{k+1/2}\right],}\\ {\displaystyle U_{k-\frac{1}{2}}\left(x\right)={\displaystyle \frac{{(-1)}^k}{(2k-1)!!}}{\displaystyle \frac{1}{1-x}}\sqrt{\frac{1}{2(1+x)}}\frac{d^k}{d{x}^k}\left[{(1-x)}^{k+1/2}{(1+x)}^{k-1/2}\right],}\\ {\displaystyle V_{k+\frac{1}{2}}\left(x\right)={\displaystyle \frac{{(-1)}^k}{(2k-1)!!}}{\displaystyle \frac{1}{1+x}}\sqrt{\frac{1}{2(1-x)}}\frac{d^k}{d{x}^k}\left[{(1-x)}^{k-1/2}{(1+x)}^{k+1/2}\right],and}\\ {\displaystyle W_{k+\frac{1}{2}}\left(x\right)={\displaystyle \frac{{(-1)}^k}{(2k-1)!!}}\sqrt{\frac{1+x}{2}}\frac{d^k}{d{x}^k}\left[{(1-x)}^{k+1/2}{(1+x)}^{k-1/2}\right].}\end{array}$$

(29)

Proof. 

Equations (29) follow from the Rodrigues-type formulas of the third and fourth kind Chebyshev polynomials (see [16]):

$$\begin{array}{c}{\displaystyle V_k\left(x\right)={\displaystyle \frac{{(-1)}^k}{(2k-1)!!}}\sqrt{\frac{1-x}{1+x}}\frac{d^k}{d{x}^k}\left[{(1-x)}^{k-1/2}{(1+x)}^{k+1/2}\right],}\\ {\displaystyle W_k\left(x\right)={\displaystyle \frac{{(-1)}^k}{(2k-1)!!}}\sqrt{\frac{1+x}{1-x}}\frac{d^k}{d{x}^k}\left[{(1-x)}^{k+1/2}{(1+x)}^{k-1/2}\right].}\end{array}$$

(30)

by using Definitions (2). □

6. Links with First and Second Kind Chebyshev Polynomials

Theorem 7.

The pseudo-Chebyshev functions are connected with the first and second kind Chebyshev polynomials by means of the equations:

$$\begin{array}{c}{T}_{k+\frac{1}{2}}\left(x\right)=T_{2k+1}\left(\sqrt{\frac{1+x}{2}}\right)=T_{2k+1}\left(T_{1/2}\left(x\right)\right),\\ U_{k-\frac{1}{2}}\left(x\right)=\frac{1}{1+x}\sqrt{\frac{1}{2(1-x)}}{U}_{2k}\left(\sqrt{\frac{1+x}{2}}\right),\\ V_{k+\frac{1}{2}}\left(x\right)=\frac{1}{1-x^2}{T}_{2k+1}\left(\sqrt{\frac{1+x}{2}}\right)=\frac{1}{1-x^2}{T}_{k+\frac{1}{2}}\left(x\right),and\\ W_{k+\frac{1}{2}}\left(x\right)=\sqrt{\frac{1-x}{2}}{U}_{2k}\left(\sqrt{\frac{1+x}{2}}\right)=(1-x^2)U_{k-\frac{1}{2}}\left(x\right).\end{array}$$

(31)

Proof. 

The results follow from the equations:

$$\begin{array}{c}{V}_k\left(x\right)=\sqrt{\frac{2}{1+x}}{T}_{2k+1}\left(\sqrt{\frac{1+x}{2}}\right)\mathrm{and}\\ W_k\left(x\right)=U_{2k}\left(\sqrt{\frac{1+x}{2}}\right),\end{array}$$

(32)

(see [16]), by using Definitions (2). □

Remark 1.

Note that the first equation in (31) is a generalization of the known nesting property, satisfied by the first kind Chebyshev polynomials:

$$\begin{array}{c}{T}_m\left(T_n\left(x\right)\right)=T_{mn}\left(x\right).\end{array}$$

(33)

This property actually holds in general, independently of the indexes, as a consequence of the basic definition $T_k\left(x\right)=cos(karccos\left(x\right))$. Note that this composition identity still holds for the first kind Chebyshev polynomials in several variables [4].

7. Conclusions

We have derived the main properties satisfied by the first, second, third, and fourth kind pseudo-Chebyshev polynomials of half-integer degree, which are actually irrational functions. The relevant properties and graphs of these new functions have been derived from their link with the third and fourth kind classical Chebyshev polynomials.