Numerical Simulation of Partial Differential Equations via Local Meshless Method
Abstract
1. Introduction
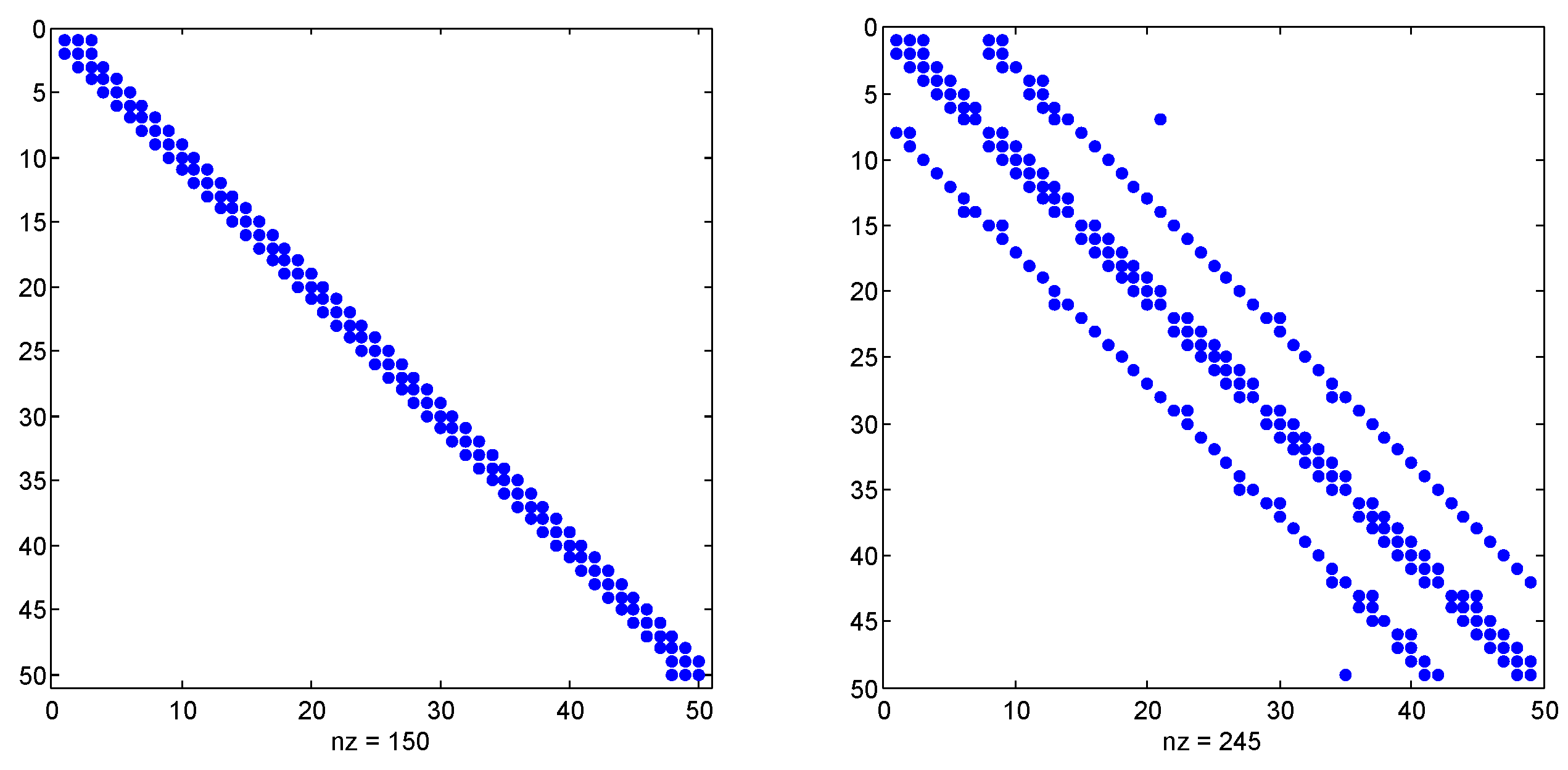
2. Implementation of Numerical Method
Local Meshless Method for KdVB Equation
3. Time Discretization
A -Weighted Technique for 2D Diffusion Equation
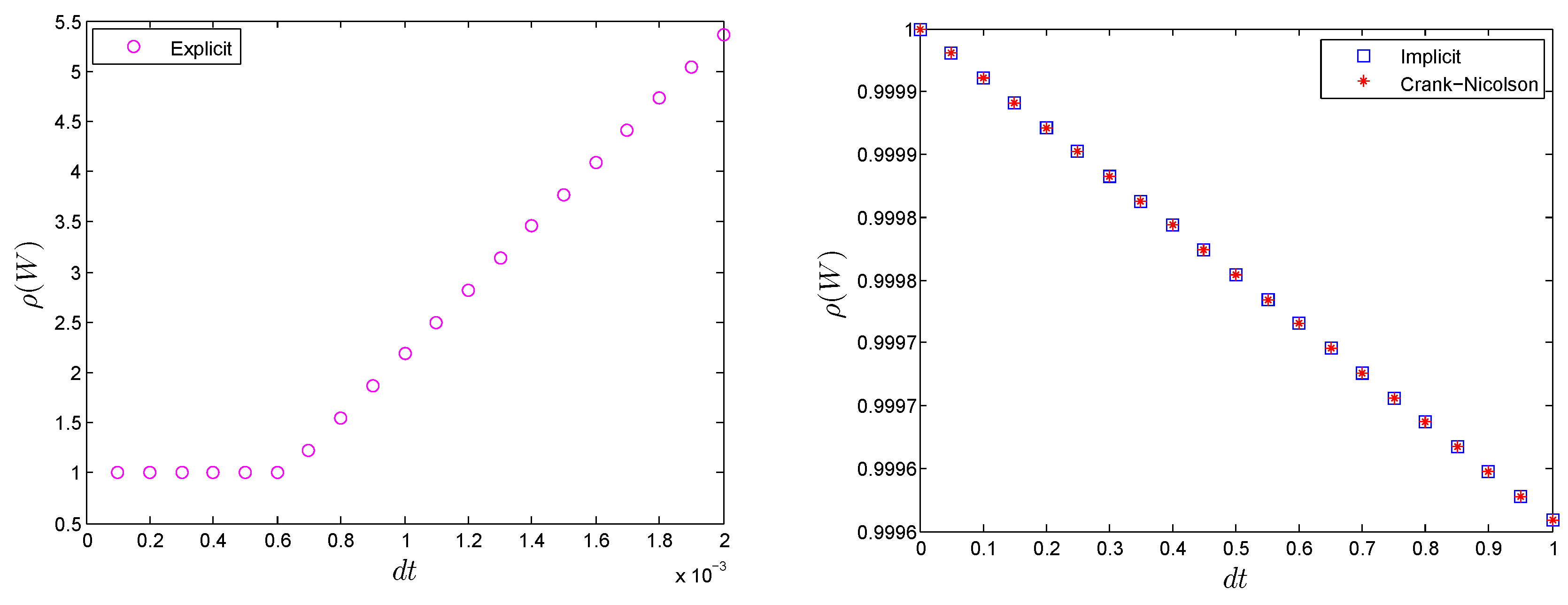
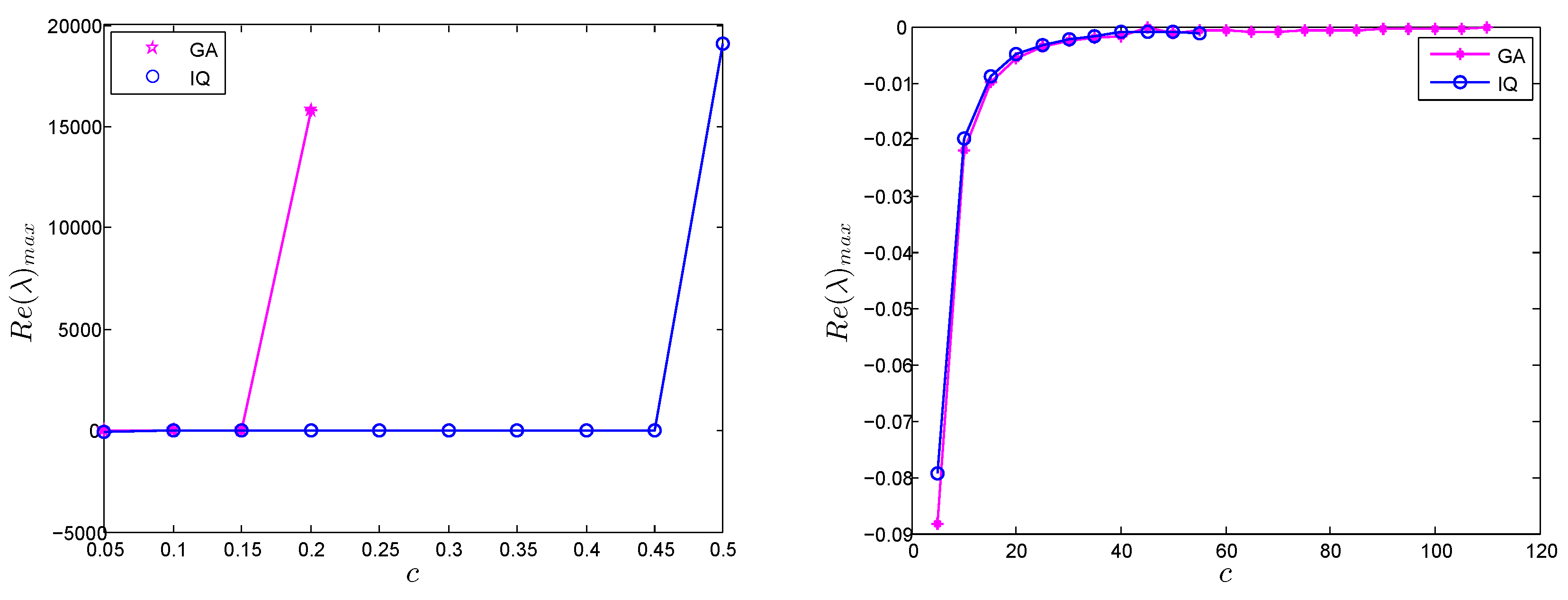
4. Stability Analysis
5. Numerical Analysis
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Su, C.H.; Gardner, C.S. Derivation of the Kortewege-de Vries and Burgers’ equation. J. Math. Phys. 1969, 10, 536–539. [Google Scholar] [CrossRef]
- Grad, H.; Hu, P.N. Unified shock profile in a plasma. J. Mech. Phys. Solids 1967, 10, 2596–2601. [Google Scholar] [CrossRef]
- Jonson, R.S. Shallow water waves in a viscous fluid-the undular bore. Phys. Fluids 1972, 15, 1993–1999. [Google Scholar] [CrossRef]
- Jonson, R.S. A nonlinear equation incorporating damping and dispersion. J. Math. Fluid Mech. 1970, 42, 49–60. [Google Scholar] [CrossRef]
- Sirajul, H.; Uddin, M. A mesh-free method for the numerical solution of the KdV-Burgers’ equation. Appl. Math. Model. 2009, 33, 3442–3449. [Google Scholar]
- Ali, A.; Mukhtar, S.; Hussain, I. A numerical meshless technique for the solution of some Burgers’ type equations. World Appl. Sci. J. 2011, 12, 1792–1798. [Google Scholar]
- Khater, A.H.; Temsah, R.S.; Hassan, M.M. Journal of computational and applied mathematics. J. Comput. Appl. Math. 2008, 222, 333–350. [Google Scholar] [CrossRef]
- Sajjadian, M. Numerical solutions of Korteweg-de Vries and Korteweg-de Vries-Burgers’ equations using computer programming. Int. J. Nonlinear Sci. 2013, 15, 69–79. [Google Scholar]
- Hepson, O.E.; Korkmaz, A.; Dag, I. Extended B-spline collocation method for KdV-Burgers’ equation. arXiv, 2017; arXiv:1701.02893. [Google Scholar]
- Arora, R.; Kumar, A. Solution of the coupled Drinfeld’s-Sokolov-Wilson (DSW) system by homotopy analysis method. Adv. Sci. Eng. Med. 2013, 5, 1105–1111. [Google Scholar] [CrossRef]
- Sirajul, H.; Hassan, N.; Tirmizi, S.I.A.; Usman, M. A Meshless Method of Lines for the Numerical Solution of Coupled Drinfeld’s-Sokolov-Wilson System; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Uddin, M.; Haq, S. Application of a numerical method using radial basis functions to nonlinear partial differential equations. Selcuk J. Appl. Math. 2011, 12, 77–93. [Google Scholar]
- Abbasbandy, S.; Shirzadi, A. MLPG method for two-dimensional diffusion equation with Neumann’s and non-classical boundary conditions. Appl. Numer. Math. 2011, 61, 170–180. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Ghehsareh, H.R.; Alhuthali, M.S.; Alsulami, H.H. Comparison of meshless local weak and strong forms based on particular solutions for a non-classical 2-D diffusion model. Eng. Anal. Bound. Elem. 2014, 39, 121–128. [Google Scholar] [CrossRef]
- Techapirom, T.; Luadsong, A. The MLPG with improved weight function for two-dimensional heat equation with non-local boundary condition. J. King Saud Univ. Sci. 2013, 25, 341–348. [Google Scholar] [CrossRef]
- Dehghan, M.; Salehi, R. The solitary wave solution of the two-dimensional regularized long-wave equation in fluids and plasmas. Comput. Phys. Commun. 2011, 182, 2540–2549. [Google Scholar] [CrossRef]
- Dehghana, M.; Abbaszadeha, M.; Mohebbib, A. The use of interpolating element-free Galerkin technique for solving 2D generalized Benjamin-Bona-Mahony-Burgers and regularized long-wave equations on non-rectangular domains with error estimate. J. Comput. Appl. Math. 2015, 286, 211–231. [Google Scholar] [CrossRef]
- Abdulloev, K.O.; Bogolubsky, I.L.; Makhankov, V.G. One more example of inelastic soliton interaction. Phys. Lett. 1976, 56, 427–428. [Google Scholar] [CrossRef]
- Bona, J.L.; Bryant, P.J. A mathematical model for long waves generated by wave makers in nonlinear dispersive systems. Proc. Camb. Philos. Soc. 1973, 73, 391–405. [Google Scholar] [CrossRef]
- Bhardwaj, D.; Shankar, R. A computational method for regularized long wave equation. Comput. Math. Appl. 2000, 40, 1397–1404. [Google Scholar] [CrossRef]
- Esen, A.; Kutluay, S. Application of a lumped Galerkin method to the regularized long wave equation. Appl. Math. Comput. 2006, 174, 833–845. [Google Scholar] [CrossRef]
- Gou, B.Y.; Cao, W.M. The Fourier pseudospectral method with a restrain operator for the RLW equation. Comput. Math. Appl. 1988, 74, 110–126. [Google Scholar]
- Raslan, K.R. A computational method for the regularized long wave equation. Appl. Math. Comput. 2005, 167, 1101–1118. [Google Scholar] [CrossRef]
- Roshan, T. A Petrov-Galerkin method for solving the generalized regularized long wave (GRLW) equation. Comput. Math. Appl. 2012, 63, 943–956. [Google Scholar] [CrossRef]
- Guo, P.F.; Zhang, L.W.; Liew, K.M. Numerical analysis of generalized regularized long wave equation using the element-free kp-Ritz method. Appl. Math. 2014, 240, 91–101. [Google Scholar] [CrossRef]
- Fischer, B.; Scholes, M. The pricing of options and corporate liabilities. J. Polit. Econ. 1973, 81, 637–654. [Google Scholar]
- Martín-Vaquero, J.; Khaliq, A.Q.M.; Kleefeld, B. Stabilized explicit Runge-Kutta methods for multi-asset American options. Comput. Math. Appl. 2014, 67, 1293–1308. [Google Scholar] [CrossRef]
- Nielsen, B.; Skavhaug, O.; Tveito, A. Penalty and front-fixing methods for the numerical solution of American option problems. J. Comput. Financ. 2002, 5, 69–97. [Google Scholar] [CrossRef]
- Fasshauer, G.E.; Khaliq, A.Q.M.; Voss, D.A. Using meshfree approximation for multi-asset American option problems. J. Chin. Inst. Eng. 2004, 27, 69–97. [Google Scholar] [CrossRef]
- Ahmad, I.; Khaliq, A.Q.M. Local RBF method for multi-dimensional partial differential equations. Comput. Math. Appl. 2017, 74, 292–324. [Google Scholar] [CrossRef]
- Rad, J.A.; Parand, K.; Ballestra, L.V. Pricing European and American options by radial basis point interpolation. Appl. Math. Comput. 2015, 251, 363–377. [Google Scholar] [CrossRef]
- Ahmad, I. A comparative analysis of local meshless formulation for multi-asset option models. Eng. Anal. Bound. Elem. 2016, 65, 159–176. [Google Scholar]
- Shen, Q. Local RBF-based differential quadrature collocation method for the boundary layer problems. Eng. Anal. Bound. Elem. 2010, 34, 213–228. [Google Scholar] [CrossRef]
- Aziz, I. Meshless methods for multivariate highly oscillatory Fredholm integral equations. Eng. Anal. Bound. Elem. 2015, 53, 100–112. [Google Scholar]
- Thounthong, P.; Khan, M.N.; Hussain, I.; Ahmad, I.; Kumam, P. Symmetric radial basis function method for simulation of elliptic partial differential equations. Mathematics 2018, 6, 327. [Google Scholar] [CrossRef]
- Luo, W.H.; Huang, T.Z.; Gu, X.M.; Liu, Y. Barycentric rational collocation methods for a class of nonlinear parabolic partial differential equations. Appl. Math. Lett. 2017, 68, 13–19. [Google Scholar] [CrossRef]
- Bianca, C.; Pennisi, M.; Motta, S.; Ragusa, M.A. Immune system network and cancer vaccine. AIP Conf. Proc. 2011, 1389, 945–948. [Google Scholar]
- Bianca, C.; Pappalardo, F.; Pennisi, M.; Ragusa, M.A. Persistence analysis in a Kolmogorov-type model for cancer-immune system competition. AIP Conf. Proc. 2013, 1558, 1797–1800. [Google Scholar]
- Gu, X.M.; Huang, T.Z.; Zhao, X.L.; Li, H.B.; Li, L. Strang-type preconditioners for solving fractional diffusion equations by boundary value methods. J. Comput. Appl. Math. 2015, 277, 73–86. [Google Scholar] [CrossRef]
- Beylkin, G.; Keiser, J.M.; Vozovoi, L. A new class of time discretization schemes for the solution of nonlinear PDEs. J. Comput. Phys. 1998, 147, 362–387. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer Science and Business Media: London, UK, 2000. [Google Scholar]
- Kosec, G.; Depolli, M.; Rashkovska, A.; Trobec, R. Super linear speedup in a local parallel meshless solution of thermo-fluid problem. Comput. Struct. 2014, 133, 30–38. [Google Scholar] [CrossRef]
- Ahmad, I. Local meshless method for PDEs arising from models of wound healing. Appl. Math. Model. 2017, 48, 688–710. [Google Scholar]
- Inc, M. On numerically doubly periodic wave solutions of the coupled Drinfeld’s-Sokolov-Wilson equation by the decomposition method. Appl. Math. Comput. 2006, 172, 421–430. [Google Scholar]
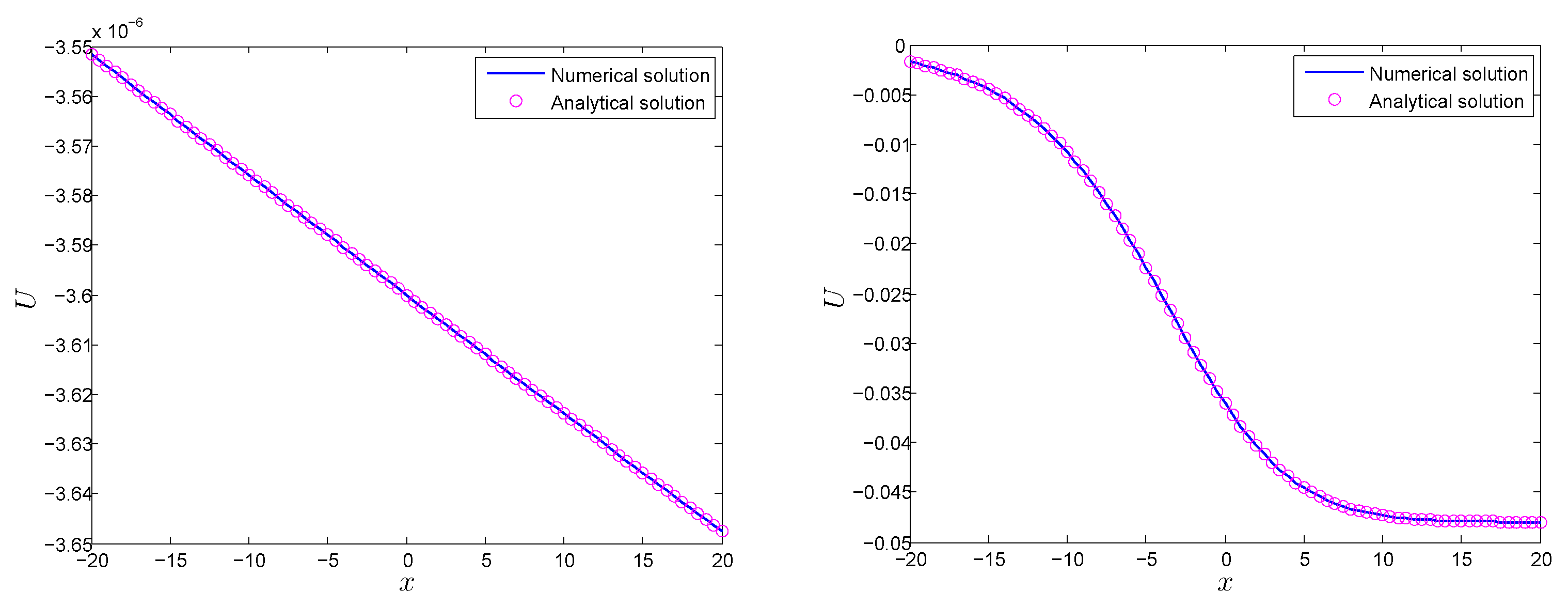
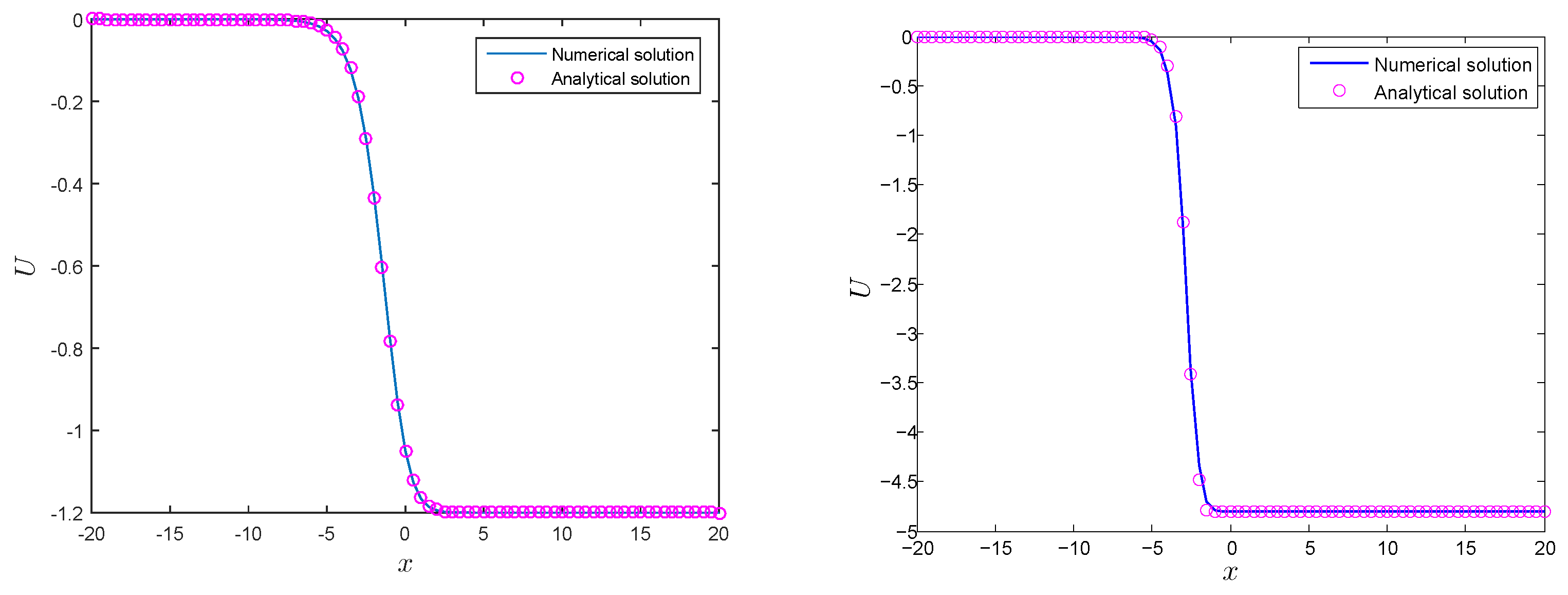
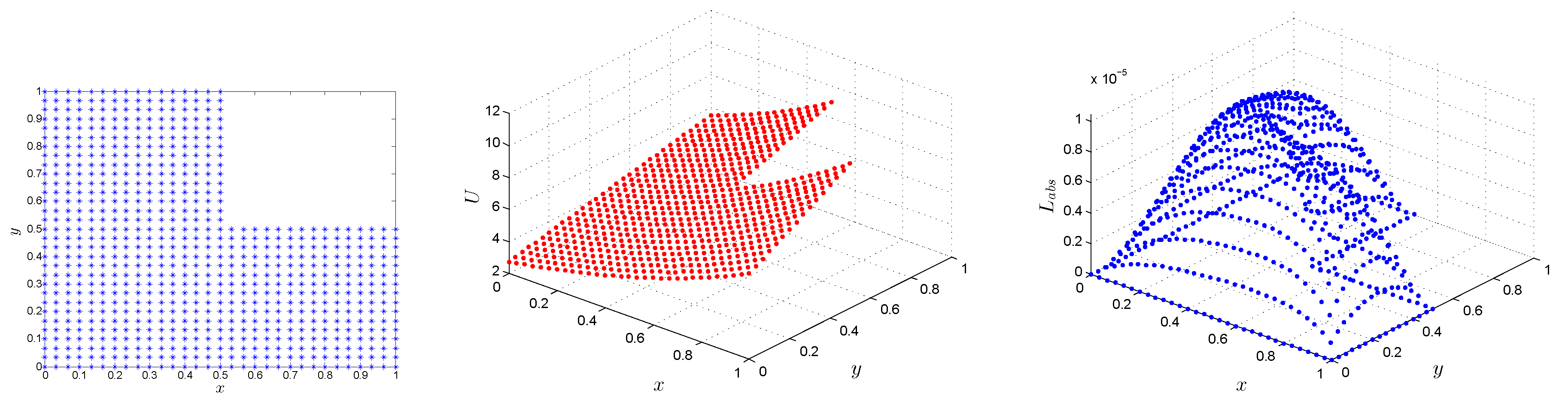
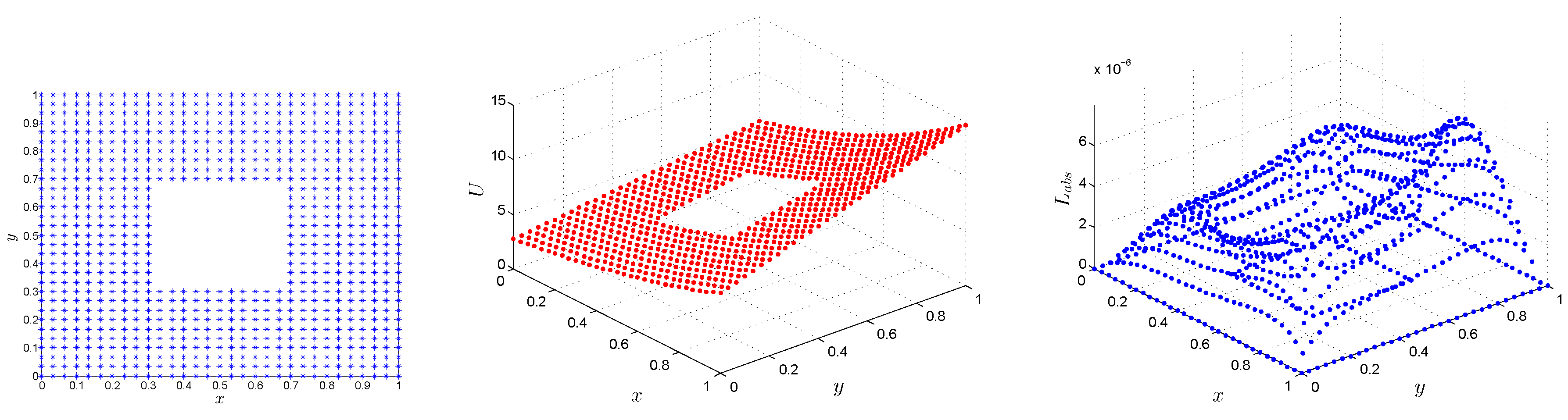

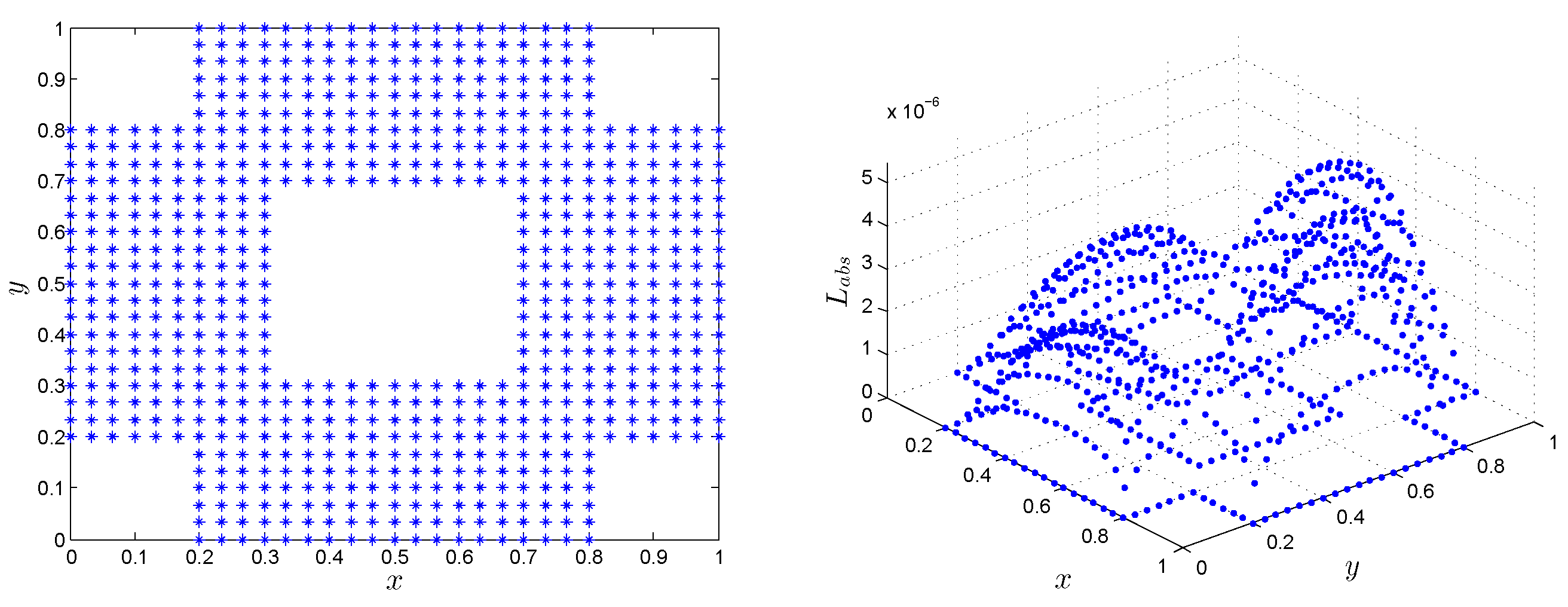
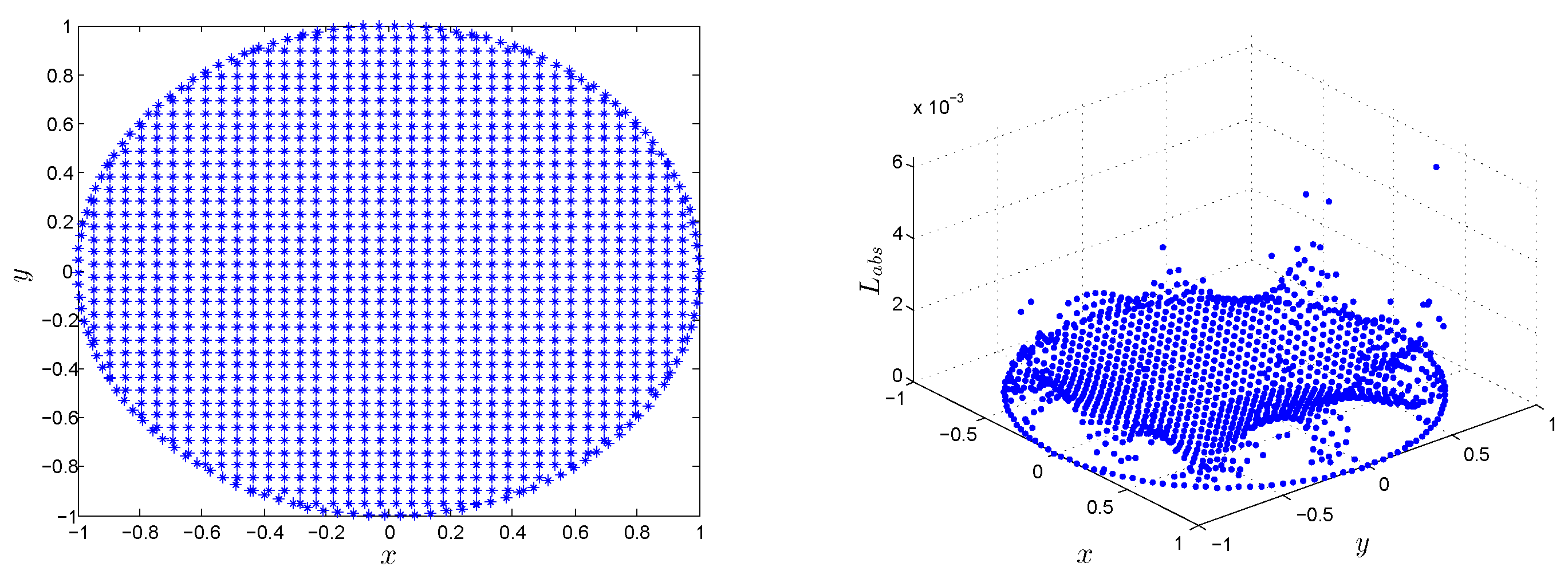

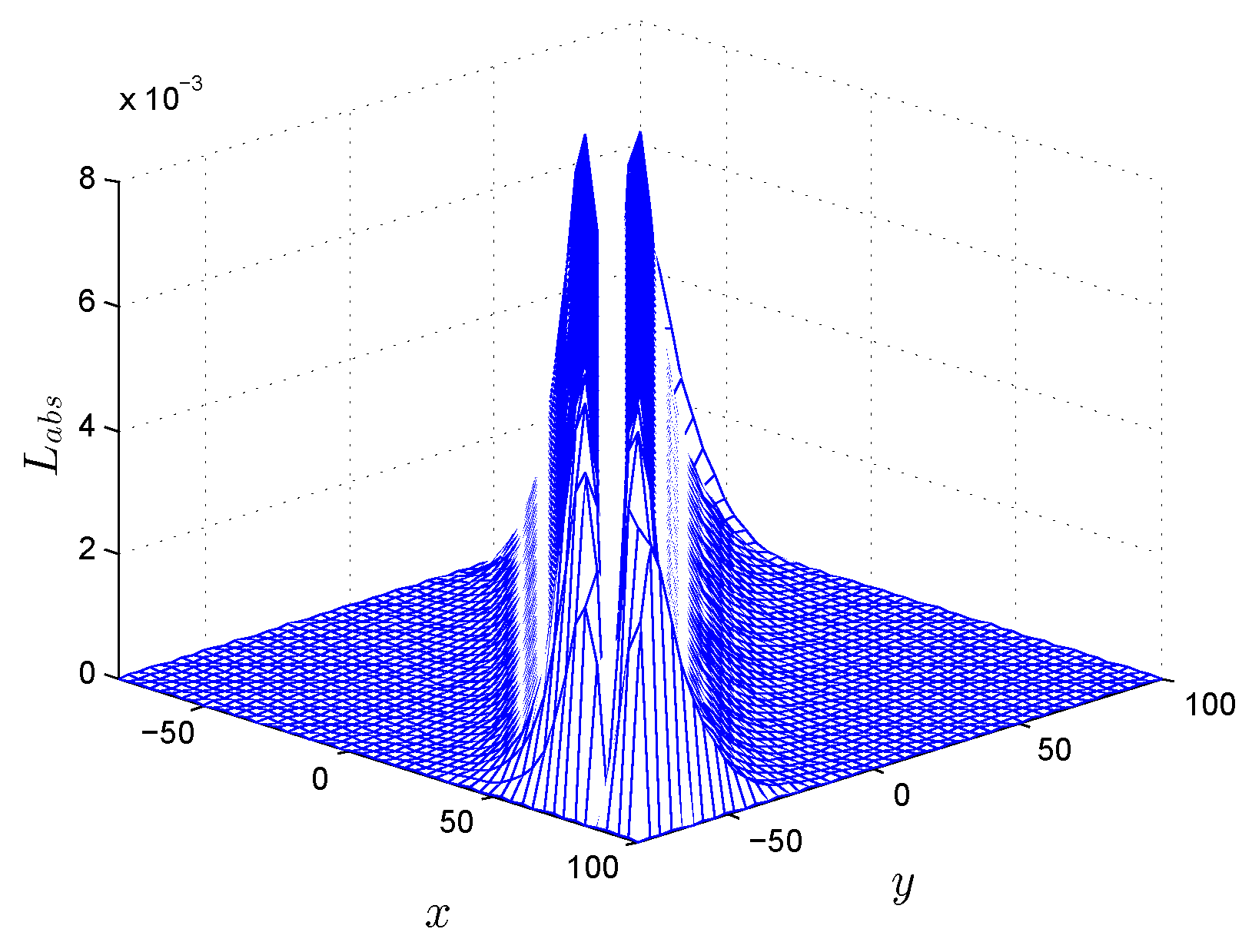
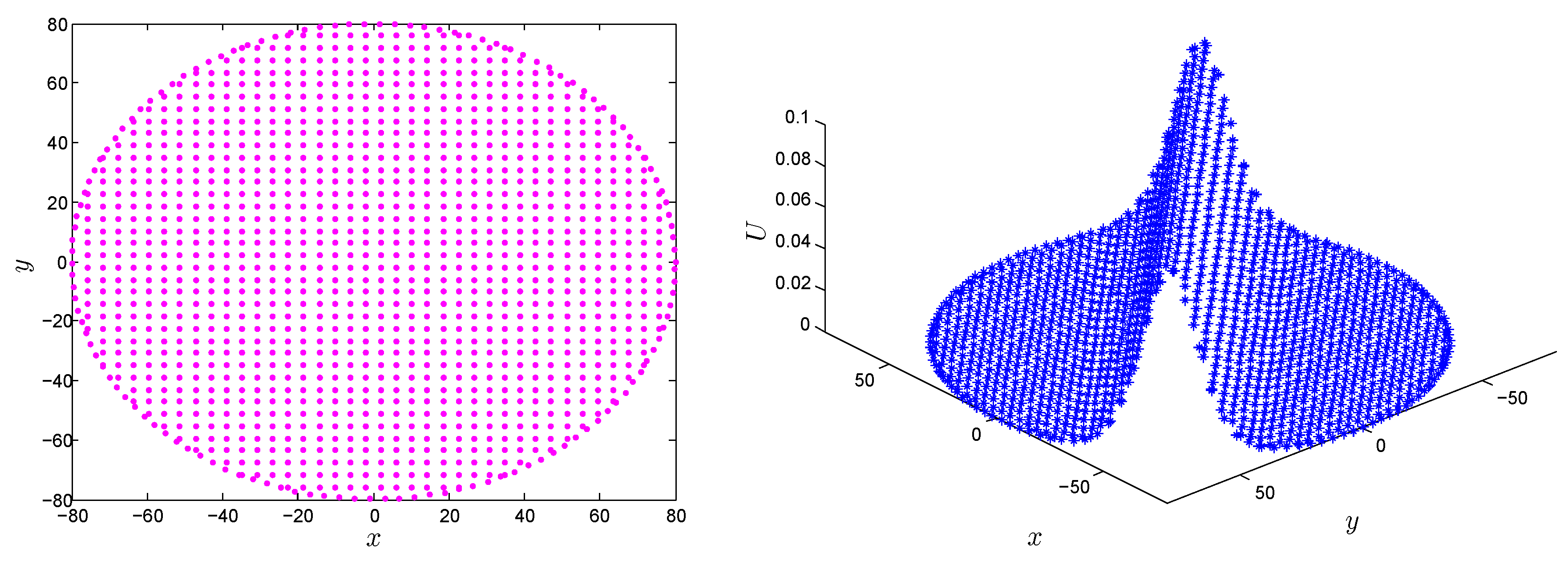
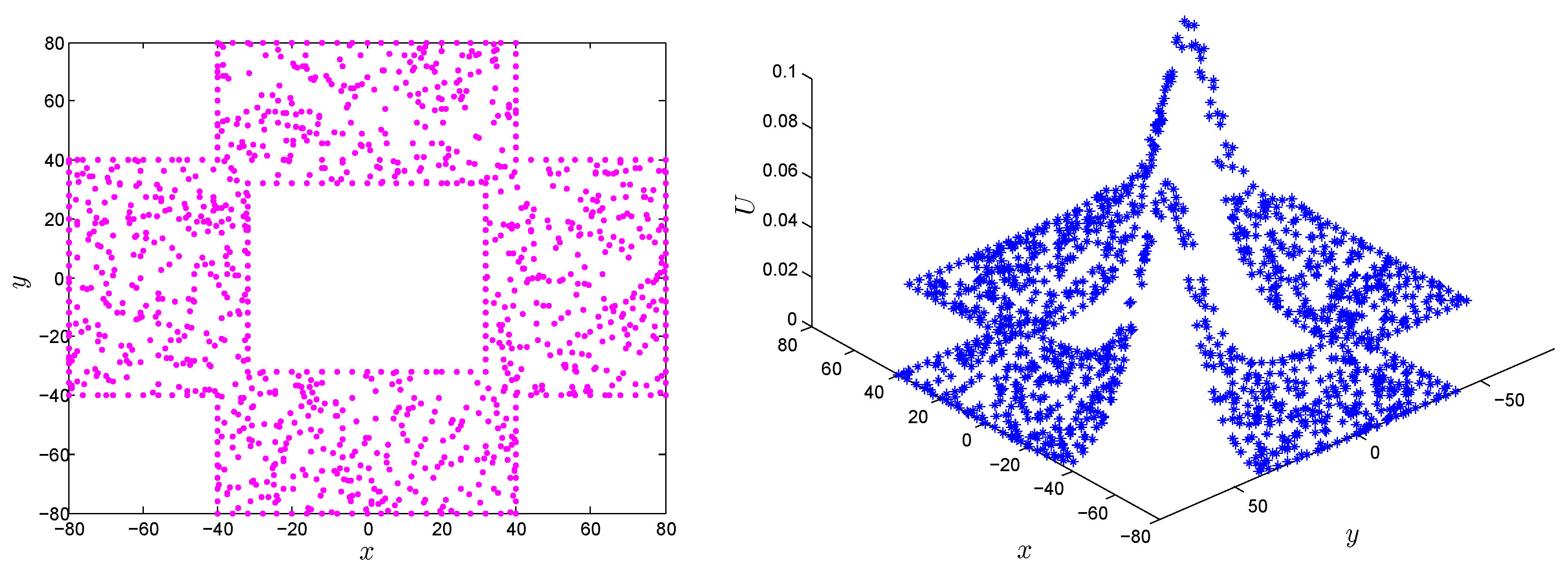
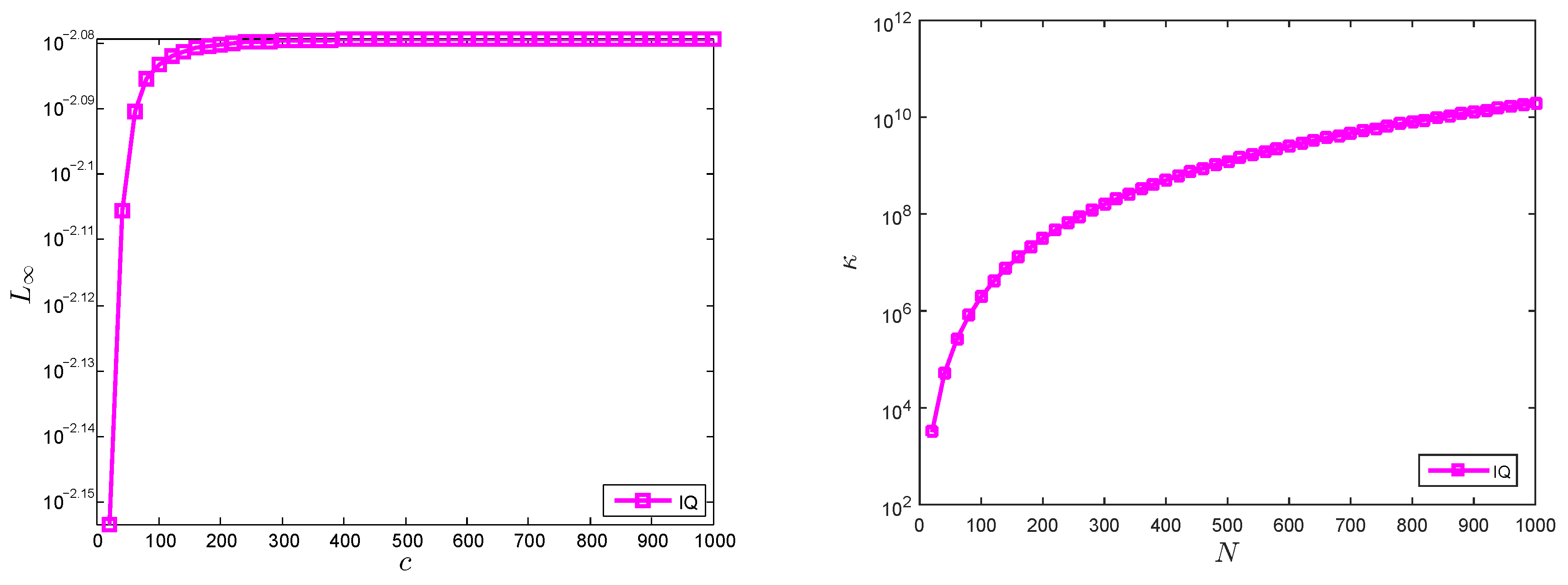
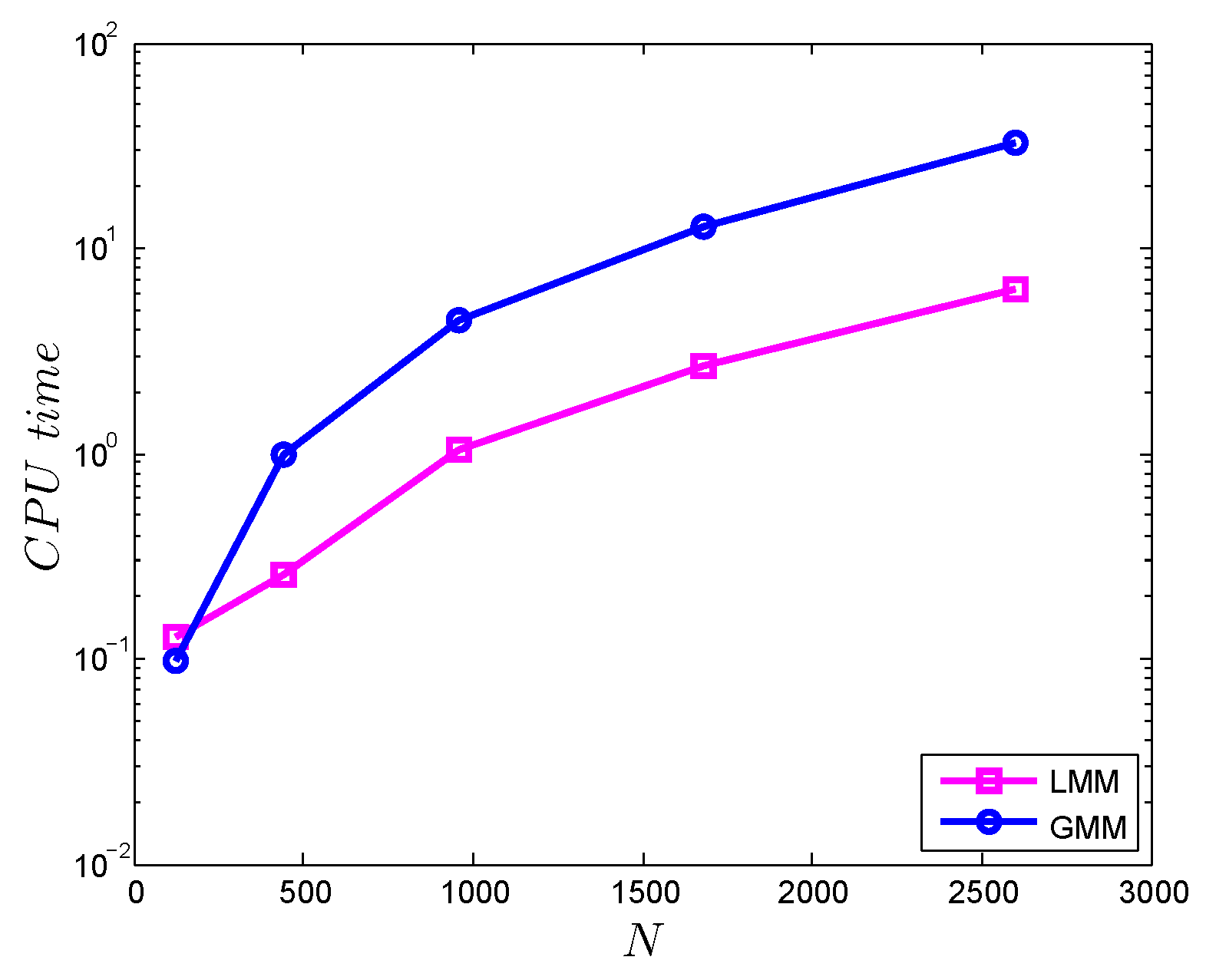
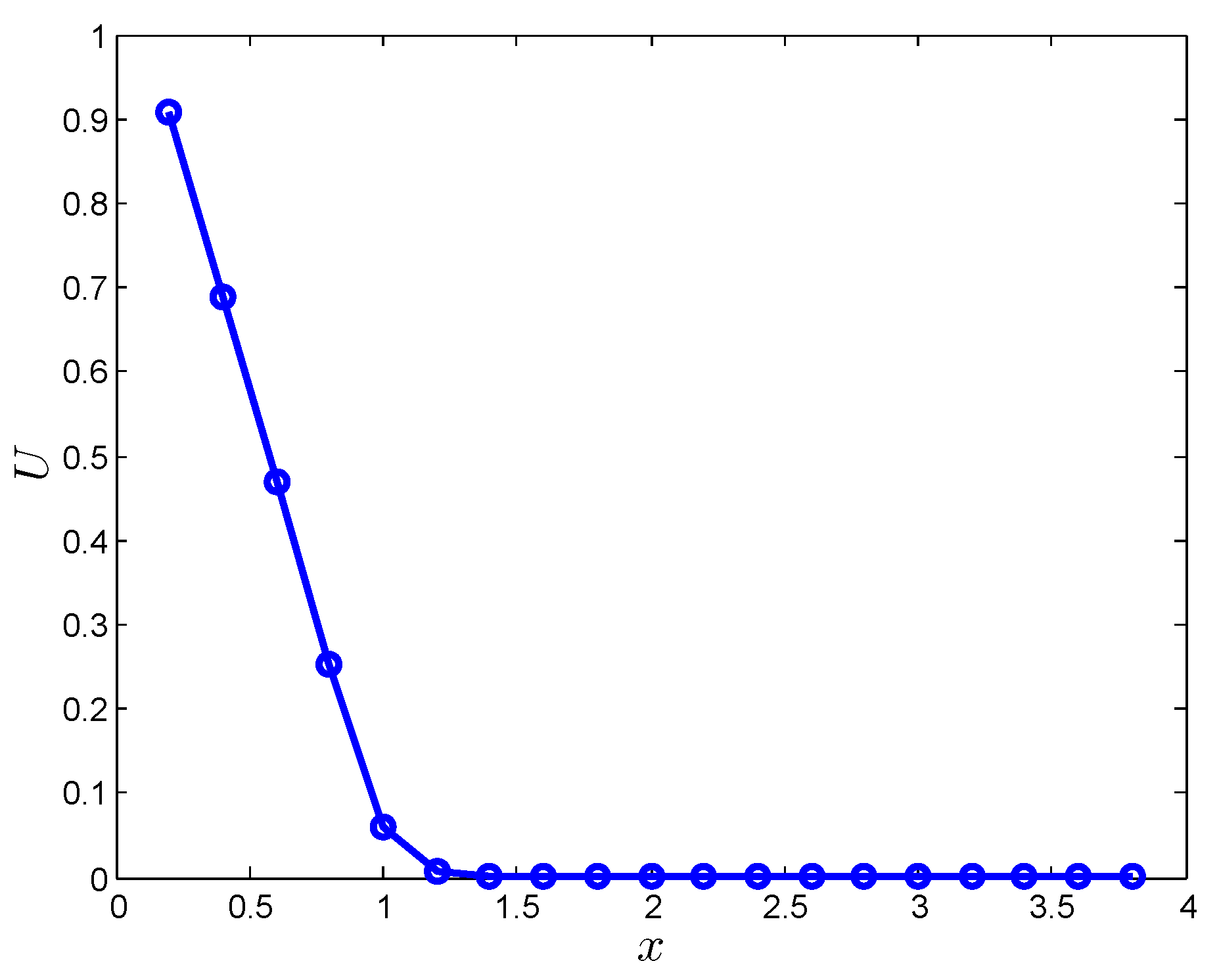
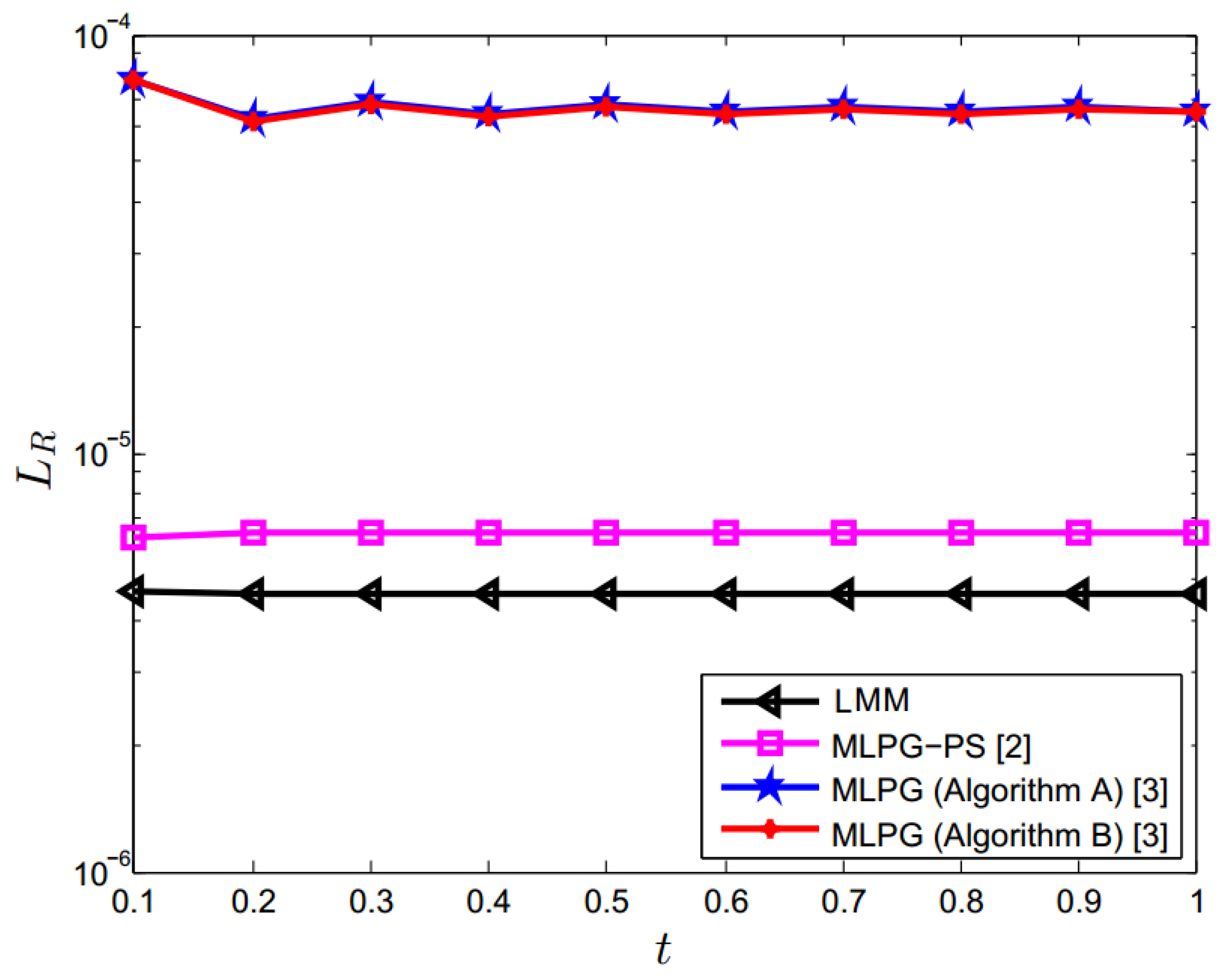
| t | LMM | LMM | [5] | [5] |
|---|---|---|---|---|
| 1 | 5.5555 × 10 | 2.8402 × 10 | 6.822 × 10 | 8.845 × 10 |
| 2 | 1.1110 × 10 | 5.6792 × 10 | 1.150 × 10 | 1.652 × 10 |
| 3 | 1.6661 × 10 | 8.5171 × 10 | 1.485 × 10 | 2.338 × 10 |
| 10 | 5.5441 × 10 | 2.8353 × 10 | 2.479 × 10 | 6.046 × 10 |
| 1 | 8.4705 × 10 | 1.5103 × 10 | 2.936 × 10 | 3.727 × 10 |
| 2 | 1.6937 × 10 | 3.0211 × 10 | 4.204 × 10 | 2.207 × 10 |
| 3 | 2.5400 × 10 | 4.5322 × 10 | 4.126 × 10 | 1.928 × 10 |
| 10 | 8.4535 × 10 | 1.5111 × 10 | 5.800 × 10 | 1.297 × 10 |
| 1 | 7.7105 × 10 | 1.1800 × 10 | 1.540 × 10 | 1.004 × 10 |
| 2 | 1.5374 × 10 | 2.3912 × 10 | 3.076 × 10 | 1.732 × 10 |
| 3 | 2.2987 × 10 | 3.6284 × 10 | 4.604 × 10 | 2.874 × 10 |
| 10 | 7.4772 × 10 | 1.2861 × 10 | 1.498 × 10 | 1.342 × 10 |
| t | CPU Time | ||||
|---|---|---|---|---|---|
| LMM | LMM | LMM | [8] | [8] | |
| 1 | 2.8316 × 10 | 3.1032 × 10 | 0.26 | 2.06127 × 10 | 4.62479 × 10 |
| 3 | 8.4947 × 10 | 9.3095 × 10 | 0.72 | 1.14705 × 10 | 9.14997 × 10 |
| 5 | 1.4158 × 10 | 1.5515 × 10 | 1.15 | 1.28565 × 10 | 1.21327 × 10 |
| 7 | 1.9821 × 10 | 2.1721 × 10 | 1.63 | 1.51656 × 10 | 1.45490 × 10 |
| 9 | 2.5484 × 10 | 2.7927 × 10 | 2.18 | 1.67755 × 10 | 1.66392 × 10 |
| x = 0.1 | x = 0.3 | x = 0.5 | ||||
|---|---|---|---|---|---|---|
| t | LMM | [11] | LMM | [11] | LMM | [11] |
| 0.1 | 4.44 × 10 | 4.5230 × 10 | 5.55 × 10 | 1.3291 × 10 | 6.10 × 10 | 6.6992 × 10 |
| 0.2 | 2.16 × 10 | 1.3524 × 10 | 1.22 × 10 | 1.3696 × 10 | 1.11 × 10 | 2.1989 × 10 |
| 0.3 | 5.21 × 10 | 2.2525 × 10 | 3.83 × 10 | 4.0690 × 10 | 2.16 × 10 | 2.3009 × 10 |
| 0.4 | 9.60 × 10 | 3.1523 × 10 | 7.71 × 10 | 6.7682 × 10 | 5.55 × 10 | 6.8008 × 10 |
| 0.5 | 1.53 × 10 | 4.0521 × 10 | 1.29 × 10 | 9.4666 × 10 | 1.03 × 10 | 1.1300 × 10 |
| x = 0.1 | x = 0.3 | x = 0.5 | ||||
|---|---|---|---|---|---|---|
| t | LMM | [11] | LMM | [11] | LMM | [11] |
| 0.1 | 7.81 × 10 | 2.2379 × 10 | 2.30 × 10 | 6.9696 × 10 | 3.82 × 10 | 1.2050 × 10 |
| 0.2 | 1.60 × 10 | 4.4328 × 10 | 4.64 × 10 | 1.3552 × 10 | 7.69 × 10 | 2.3025 × 10 |
| 0.3 | 2.46 × 10 | 6.6276 × 10 | 7.03 × 10 | 2.0134 × 10 | 1.15 × 10 | 3.3999 × 10 |
| 0.4 | 3.37 × 10 | 8.8225 × 10 | 9.46 × 10 | 2.6716 × 10 | 1.55 × 10 | 4.4973 × 10 |
| 0.5 | 4.31 × 10 | 1.1017 × 10 | 1.19 × 10 | 3.3298 × 10 | 1.95 × 10 | 5.5947 × 10 |
| c | U | V | c | U | V |
|---|---|---|---|---|---|
| 0.001 | 1.4629 × 10 | 3.0635 × 10 | 40 | 6.0559 × 10 | 1.2333 × 10 |
| 0.01 | 1.1800 × 10 | 2.0888 × 10 | 80 | 5.6560 × 10 | 1.1480 × 10 |
| 0.1 | 1.1655 × 10 | 2.2179 × 10 | 160 | 5.5559 × 10 | 1.1268 × 10 |
| 1 | 1.1747 × 10 | 2.0555 × 10 | 320 | 5.5265 × 10 | 1.1216 × 10 |
| 5 | 3.8443e × 10 | 1.0146 × 10 | 640 | 5.9097 × 10 | 1.1239 × 10 |
| 10 | 1.4029 × 10 | 3.0469 × 10 | 1000 | 9.0130 × 10 | 1.1524 × 10 |
| 20 | 7.6552 × 10 | 1.5794 × 10 | 1200 | 6.1639 × 10 | 1.1081 × 10 |
| 0.001 | 0.01 | 0.1 | 0.2 | 0.3 | |
|---|---|---|---|---|---|
| U | 2.8405 × 10 | 3.4306 × 10 | 3.5230 × 10 | 1.4130 × 10 | ⋯ |
| V | 5.2746 × 10 | 6.5458 × 10 | 9.1756 × 10 | 3.5451 × 10 | ⋯ |
| t | 1 | 5 | 10 | 15 | 20 |
|---|---|---|---|---|---|
| 6.8814 × 10 | 3.4458 × 10 | 7.0255 × 10 | 1.2374 × 10 | 2.0904 × 10 | |
| CPU time (in s) | 2.54 | 2.59 | 2.71 | 2.85 | 2.88 |
| N | P(1,1,1) | P(1.1,1.1,1.1) | CPU Time |
|---|---|---|---|
| 0.051746 | 0.0278333 | 7.6 | |
| 0.055708 | 0.021232 | 32.7 | |
| 0.058240 | 0.020440 | 128.9 | |
| 0.059639 | 0.020797 | 554.9 |
| N | at P(1,1,1) | at P(1.1,1.1,1.1) |
|---|---|---|
| 9.7425 × 10 | 2.0440 × 10 | |
| 6.4939 × 10 | 7.3929 × 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, I.; Riaz, M.; Ayaz, M.; Arif, M.; Islam, S.; Kumam, P. Numerical Simulation of Partial Differential Equations via Local Meshless Method. Symmetry 2019, 11, 257. https://doi.org/10.3390/sym11020257
Ahmad I, Riaz M, Ayaz M, Arif M, Islam S, Kumam P. Numerical Simulation of Partial Differential Equations via Local Meshless Method. Symmetry. 2019; 11(2):257. https://doi.org/10.3390/sym11020257
Chicago/Turabian StyleAhmad, Imtiaz, Muhammad Riaz, Muhammad Ayaz, Muhammad Arif, Saeed Islam, and Poom Kumam. 2019. "Numerical Simulation of Partial Differential Equations via Local Meshless Method" Symmetry 11, no. 2: 257. https://doi.org/10.3390/sym11020257
APA StyleAhmad, I., Riaz, M., Ayaz, M., Arif, M., Islam, S., & Kumam, P. (2019). Numerical Simulation of Partial Differential Equations via Local Meshless Method. Symmetry, 11(2), 257. https://doi.org/10.3390/sym11020257