1. Introduction
One of the most challenging problems in quantum mechanics is to find a consistent and natural way to connect it with classical physics. Over the years, many people have tried to find a way to make such a connection, and it has not been found to be a trivial task. For example, we can cite the work done by Klein [
1], where it was proven that the classical limit of quantum mechanics is not exactly Newtonian mechanics. There have been results, but only on specific systems under specific considerations. As far as we know, there is not a general way to connect both theories.
Having this in mind, we explore the possible physical statistical connection between an ultrarelativistic classical gas and a photon gas, which is a connection in the same context as the general problem stated above. Notice that for ultrarelativistic gases Hagedorn temperature must be taken into account [
2]. Furthermore, since we will deal with classical thermodynamics in equilibrium (thermostatics), we can avoid including the physical problems described in some theories of non-equilibrium relativistic thermodynamics as for example the extended relativistic thermodynamics [
3].
Let us start by reviewing the historical development of the solution for the well-known black-body radiation problem. In 1859, Kirchhoff stated that a black-body in thermal equilibrium should emit a radiation spectrum that does not depend on its shape or material. Thus, there must exist a universal function
that describes its energy density at a temperature
T and at a frequency interval
. Considering only thermodynamic aspects, Wien showed that such a function must obey [
4],
where
f was an unknown function; this is called now the Wien displacement law. With this result and trying to reproduce the experimental data available in his time, Wien proposed what is now called the Wien distribution law, which is written as:
where
c is the velocity of light in a vacuum,
h is Planck’s constant,
k is Boltzmann’s constant, and the subscript
W means Wien. When more experiments with more technological equipment were made, corresponding to the low frequency regime, the Wien distribution law failed. Instead, a distribution proposed by Rayleigh–Jeans, which was found using the energy equipartition theorem, appeared to be successful in this regime. This Rayleigh–Jeans distribution law can be written as:
where
means Rayleigh–Jeans. Finally, Planck studied the problem as a set of harmonic oscillators, and with this idea, he proposed the now called Planck distribution law, which is written as:
where
is an energy element, such that any oscillator can only have energies given by integer multiples of
, and
P means Planck. Using Equation (
1), it can be found that:
This result marks the birth of quantum mechanics.
We can see that the Wien law and Rayleigh–Jeans law are actually limits for the Planck distribution law on the high and low frequency regimes, respectively. However, we have to be careful with this relation. Many textbooks say that Planck’s work was derived using an extrapolating process with both distributions, which is wrong, because the Rayleigh–Jeans distribution law was not published until 1905 and Planck’s famous work was presented in a conference on 14 December 1900 [
4] and was published in 1901 [
5].
The question of what was the physical interpretation of Equation (
5) by Planck has been studied extensively. For a detailed study on these aspects, see [
4]. Apart from that, we know that the first physical interpretation of Equation (
5) as light quanta was given by Einstein [
6], proving that the entropy for the electromagnetic radiation has the same form as the entropy for a classical ideal gas. However, this work was done using the Wien distribution law; then, we can see that there is a difference in the concept of the photon for both distributions. Furthermore, Einstein used a probability distribution for Pquanta distributed on
N cells, of the form:
Equation (
6) corresponds to the number of possible combinations, whereas Planck used in [
5] a distribution of the form:
Then, we can see that the system described by the Wien distribution law is not exactly the same as the one described by Planck [
5]. This result motivates a further study of both systems.
Moving to a modern language, it is well known that we can study black-body radiation as an ideal quantum gas that obeys Bose–Einstein statistics. In the canonical ensemble, the partition function for such a gas is [
7]
where
is the energy of a photon in the
-state and
. Using this partition function, we can obtain the Helmholtz free energy
F using the well-known relation
, which in this case gives as a result:
where
U is the total energy of the system given by:
Using Equation (
9) and well-established thermodynamic relations, we can calculate the entropy
S, the pressure
P, the enthalpy
H, the Gibbs free energy
G, and the heat capacity at constant volume
, which in this case gives:
By using
, it can be proven that the chemical potential
for this gas of photons is:
We can obtain the mean value
N of photons in the gas with the expression:
Finally, it can be proven that the total energy in Equation (
10) satisfies the equation:
where “
a” is a constant. Equation (
14) represents the well-known Stefan–Boltzmann law.
Now that we have the statistical description of a photon gas, we are going to propose the conditions that need to be fulfilled in order to obtain a similar behavior from a classical ideal gas. The key idea to achieve this is to impose the condition (
12) on an ideal ultrarelativistic gas. This work is presented as follows. In
Section 2, we define the two different photon gases that we will use latter on, namely a Planck gas and a Wien gas, and we give the comparison between both of them. In
Section 3, we show that the comparison done in
Section 2 is similar to the comparison between an ultrarelativistic classical ideal gas with zero chemical potential and an ultrarelativistic boson gas. In
Section 4, we find that both comparisons are equivalent, and from this, we find that the ultrarelativistic classical gas can have a behavior identical to the Wien gas. In
Section 5, we find this kind of connection for two specific systems, namely between an evaporating gas and cavity radiation. In
Section 6, we analyze the density derived from this gas and obtain the type of gas particles that makes the former results physically consistent. We also analyze the Bose–Einstein condensation temperature to give a correct physical description. Finally, in
Section 7, we give our concluding remarks.
2. Photon Gas
Note that all the thermodynamic properties of the photon gas described in the Introduction have to do with the total energy, and it can be proven that all relations described for that gas (including the Stefan–Boltzmann law) are valid whether we use the Planck distribution law, Equation (
4), or the Wien distribution law, Equation (
2). Thus, we can consider two different photon gases with different “
a” constants, one whose total energy is derived using the Planck distribution law, namely “Planck gas”, and one whose energy is derived using Wien distribution law, namely “Wien gas”.
By using Equations (
4) and (
10), we obtain that the constant in the Stefan–Boltzmann law, Equation (
14) for the Planck gas, is [
7,
8],
whereas by using Equation (
2), we obtain for the Wien gas:
Doing the comparison between these two expressions, we find:
where
is the Riemann zeta function. By using these results and the relations previously found, we can compare all the thermodynamic properties of both gases, obtaining:
and:
This shows that although, as pointed out in the Introduction, for high frequencies, the Wien distribution function coincides with that of Planck, in the case of low frequencies until the maximum of each distribution, the density of the number of particles is larger in the case of the Planck distribution (see
Figure 1). Accordingly, this predicts a higher number of particles when all of the spectrum is considered.
3. Ultrarelativistic Ideal Gas
Let us consider now the comparison between two similar systems, a classical ultrarelativistic ideal gas and a boson ultrarelativistic ideal gas. We say that a gas is ultrarelativistic if the energy
E of every particle in the gas satisfies the relation:
where
p is the linear momentum of the particle and
m its mass. This model can be used to describe gases of particles without mass that moves at the velocity of light or particles whose energy is so big that their rest energy can be neglected. In this case, the temperature of the gas is also large, such that the following relation is fulfilled [
8]:
First, let us review the properties of the classical gas. For this gas, the partition function in the canonical ensemble is written as [
8]:
where
V is the volume,
N the number of particles, and the subscript
C means classical. By using the same procedure as in the Introduction, we find for this classical gas,
We can also calculate the total energy for this gas, obtaining the expression:
namely the energy of this gas is double that of the non-relativistic one. It can be shown that this gas still satisfies the ideal gas equation of state (
) [
8]. The factor of 3 in Equation (
24) shows that the equipartition theorem gives a different result for the non-relativistic and the ultrarelativistic cases of the ideal gas. The generalized equipartition theorem [
8,
9] may be applied to understand such a difference in the kinetic energy term. However, when general interaction potentials are considered, an interesting discussion on this issue can be seen in [
10] and the references therein.
As was mentioned in the Introduction, one important property of any photon gas is that the chemical potential is always zero, then if we want to be able to look for a connection with the quantum realm, we impose that this classical gas also has a zero chemical potential (or
). One might think that an ultrarelativistic gas with zero chemical potential could be similar to a Wien gas. Nevertheless, from the Boltzmann distribution function, there is no indication that makes us suspect that a classical ultrarelativistic gas with zero chemical potential can resemble a Wien or Planck gas (see
Appendix A). Therefore, the analysis must be done starting with the Jüttner distribution function. However, at first glance, since the expressions for the energy densities of an ultrarelativistic classical ideal gas and a non-relativistic ideal classical gas are similar, we could think that the similarity in this case does not also appear. Nevertheless, the functionality of the chemical potential for an ultrarelativistic gas permits finding that the similitude is not exact for a quantum system of neutrinos. Indeed, a comparison between the energy of a quantum system of neutrinos and the energy of an ultrarelativistic classical gas gives a factor of
, as can be seen at the end of
Appendix A (see the comment in
Section 7).
From Equation (
23), we obtain now that the number of particles is not constant, and it follows the relation:
Substituting into Equation (
24), we find:
we can see that now, the energy obeys the Stefan–Boltzmann law, Equation (
14), with:
which is half
. Substituting Equation (
25) and using the ideal gas law, we find that now, this gas satisfies the same relations derived for the photon gas in the last section, namely Relations (
9) and (
11). Thus, now our classical gas behaves like a kind of photon gas; which is a result that is not general for any relativistic ideal gas unless we constrain the chemical potential to vanish; that is: the result is valid if we maintain the relativistic ideal gas under the condition given by Equation (
25). Let us clarify that by this, we do not mean that some laboratory process has to be done in order to maintain this condition; rather, as there is not a physical reason that prohibits this condition to be fulfilled, we only expect it to happen for a particular gas in nature.
Furthermore, we know that the latter relations are valid also for the boson ultrarelativistic ideal gas, including the zero chemical potential because it costs no energy to increment the number of particles in the system [
8]. Taking the results of the analysis for this gas made in [
8] and comparing the results with the ones obtained above, we find the following proportions between the thermodynamic properties of the boson gas (
B) and the classical ideal gas (
C) with zero chemical potential or with chemical potential tending to zero.
and:
That is, the comparison between the gases of the previous section is completely analogous to the comparison of these two ultrarelativistic gases.
4. From Classical to Quantum
In order to find the connection we pursue, let us remind us of some results concerning the systems considered above. We know that Planck gas is actually an ultrarelativistic boson gas with an extra degree of freedom, namely the polarization of the photons. This extra degree of freedom results in duplicating the available number of states on the momentum space, and then, we can obtain the following relations:
With this result and by using Equations (
18), (
19), (
28), and (
29), we finally obtain:
Then, we see that the only difference between the resulting classical gas and the Wien gas is the polarization of the photons. Thus, if we start with a classical gas and impose the conditions of being relativistic and having zero chemical potential, then we would end up with a system with the same statistics as a photon gas, in particular, a Wien gas rather than a Planck gas. However, the statistics are different because for the the relativistic ideal gas with zero chemical potential, the distribution function depends on the classical momentum of the particles (see Equation (
40)), and for the Wien gas, the distribution function depends on the frequencies.
In order to understand why this effect occurs, let us make an extrapolation and calculate the corresponding energy of the “photon-like” bosons of this “resultant Wien-like gas”. Of course, this is not a canonical quantization, since it just represents the image of our relativistic classical ideal gas with zero chemical potential in a Wien gas. In order to do so, we start by considering that every single particle in the classical gas has a de Broglie wavelength associated with it given by:
Taking into consideration Equations (
20) and (
24), this becomes,
When we impose the conditions mentioned earlier, the particles of this gas will behave as photon-like bosons, whose wavelength will be the same as in Equation (
33). Then, the energy of each “photon-like” boson, by using Equation (
33), can be written as:
Since we start with an ultrarelativistic gas, the condition in Equation (
20) is fulfilled. Thus, the resulting energy for every “photon-like” boson satisfies:
i.e., every “photon-like” boson has an energy much greater than the rest energy of the particle, and it can be understood to correspond to the high frequency regime; then, our previous result makes sense.
5. The Connection of an Evaporating Gas with the Cavity Radiation
Let us consider a classical gas contained in a containerin a state of equilibrium, then we make a small hole (small enough to not perturb the equilibrium state and with a suitable procedure to maintain Equation (
25) as valid) and let particles flow to the outside; in such a manner, we define an evaporating gas. Had we a photon gas instead of the classical gas in the system described, we would obtain the well-known cavity radiation. Thus, the two systems are completely analogous, one in the classical realm and one in the quantum one.
We know that by construction, the radiation emitted for the cavity is black-body radiation; thus, the radiance of such system is written as [
11]:
where
is given by Equation (
15).
On the other hand, we can compute the number of particles leaving the hole per unit of time and area for the evaporating gas
with the relation [
8]:
where
N is the number of particles in the container,
V its volume, and
the mean velocity of the gas particles. Let us now consider that the gas in such system is a classical ideal ultrarelativistic gas as the one considered in
Section 3. Then, by using Equation (
25), we have:
Thus, if we want the “radiance” for such outgoing particles (i.e., energy per unit of time and area), we can simply multiply the expression in Equation (
38) by the mean value of the energy of every particle, that is by
, as was mentioned earlier, then comparing with Equation (
36), we obtain that the “radiance” for this classical gas
can be written as:
In order to compute the mean value of the velocity of the gas particles, we cannot use the Maxwell velocity distribution, because such a distribution is not compatible with special relativity. Instead, we use the Jüttner distribution [
12,
13,
14,
15], which was written originally in momentum space as:
where
n is the particle density in the reference frame at rest and
the Bessel function of second kind. With this, the number of available states in the momentum space is:
and taking into consideration that this gas satisfies Expression (
20), the latter can be written in the velocity space:
where as usual, we have defined:
Then, we can obtain the mean velocity:
which using Equation (
42) gives as the final result:
as we expected for this ultrarelativistic gas. Substituting Equation (
45) into Equation (
39), we obtain:
which can be written in terms of energies as:
Now, using the relations obtained earlier in Equation (
18), we finally find from this result:
which is one of the results obtained in
Section 3. Thus, we obtain that our previous results are consistent with these physical systems.
6. Physical Considerations
It has to be noted that the Jüttner distribution negates quantum effects on the system. Therefore, in order to use such a distribution, one of the requirements to avoid to consider quantum effects consists of assuring at first glance that the mean inter-particle distance
must be much bigger than the De Broglie distance
(
). In our case, taking into account that the chemical potential vanishes (and as a result, Equation (
25)), we arrive at:
and taking into account Equation (
33), we obtain:
Accordingly, in principle, quantum effects should be taken into account. However, in reality, what has to be satisfied is that the mean free path must be much bigger than the De Broglie wavelength (). We are going to see in the following that this condition can be satisfied.
One important aspect that we have to take into account in the procedure described in the previous sections is the range of temperatures in which it can occur and the physical conditions in which the system has to be. In particular, we can write Equation (
25) as:
where
is the particle density; from Equation (
51), we can find the density order of magnitude, so we can speak about an ultrarelativistic gas with the above conditions.
We know that the energy of a classical ideal relativistic gas is [
8]:
where
is the Bessel function of second order, and we define the variable:
The energy for the ultrarelativistic gas (see Equation (
24)) is reproduced in the limit given by Equation (
21). In order to obtain an order of magnitude for the temperature where we can consider the gas to be ultrarelativistic, we can compare Equation (
52) with Equation (
24). For a percentage difference of
, we obtain
, whereas for a percentage difference of
, we obtain
. If we suppose the gas to be made of hydrogen, we can substitute
, the proton mass in Equation (
53), and we obtain for the temperatures corresponding to the
difference and the
difference, respectively:
With these results, by substituting in Equation (
51), we obtain for the particle density the numerical values:
which are, of course, extremely large densities. Then, the above conditions cannot be fulfilled for a typical hydrogen gas. Moreover, the Hagedorn temperature for hadrons is about
[
2], and consequently, the hydrogen does not exist at temperatures of the order of
. Thus, we need particles that are much lighter than protons and that do not interact via electromagnetic forces (so we can still speak about an ideal gas). Such particles can only be neutrinos or neutrino pairs, as proposed by Landsberg [
16]. As we now know, there are three flavors of neutrinos [
17], but since they do not interact with one another, we can still speak about an ideal neutrino gas.
For neutrinos, we take
, where
[
17] is the current upper bound for the sum of the three neutrino masses. Using the same equations as above, we obtain the temperatures:
and the densities:
These results are not as extreme as those obtained for the hydrogen gas, and there is not a physical reason for avoiding the existence of such a system in nature. For neutrino pairs, we obtain one order of magnitude greater than the above results; thus, it is a possible system as well.
The results obtained in
Section 4 and
Section 5 were derived for classical ultrarelativistic particles; thus, they are valid for neutrinos (which are fermions), as well as for neutrino pairs (which are bosons [
16]), as long as we treat them as classical particles.
Observations of the cosmic microwave background suggest that neutrinos do not interact with themselves [
18] (no self-interaction). This implies that
is infinite, and consequently,
therefore, for these particles, no quantum effects have to be considered in this order of ideas.
Another effect that has to be considered is the pair production. Indeed, when relativistic temperatures () are present, pair production can take place. However, we are considering that particles are classical particles with an extra degree of freedom given by their spin; therefore, our previous analysis is consistent in this scenario as well. Moreover, since we are taking the chemical potential to be zero, this implies that there is equilibrium, and accordingly, we have a balance between the particles and the antiparticles. This is the interpretation of the zero chemical potential condition, namely an equilibrium in pair production. Then, it is consistent that the latter results were found in the canonical ensemble even when the number of particles was not constant, because as happens for photons, the zero chemical potential ensures that the results in the grand canonical ensemble are the same.
We take quantum effects only to be a contribution in the phase space from the particles spin, then if we consider classical particles with spin, Equation (
48) should be written as:
i.e., we only take the contribution to these classical results due to the spin
s being a spin degenerate factor
. Evidently, the only case where
is for
, which is possible for neutrinos. For neutrino pairs, we instead can only have
. Let us clarify that Equation (
63) does not imply that the statistics of the classical ideal gas is the same as that of the Wien gas. However, as we have mentioned in the last part of
Section 4, we can make an extrapolation and consider that the total energy of the classical gas comes from an energy distribution with the same form as the Wien distribution. With this in mind, in
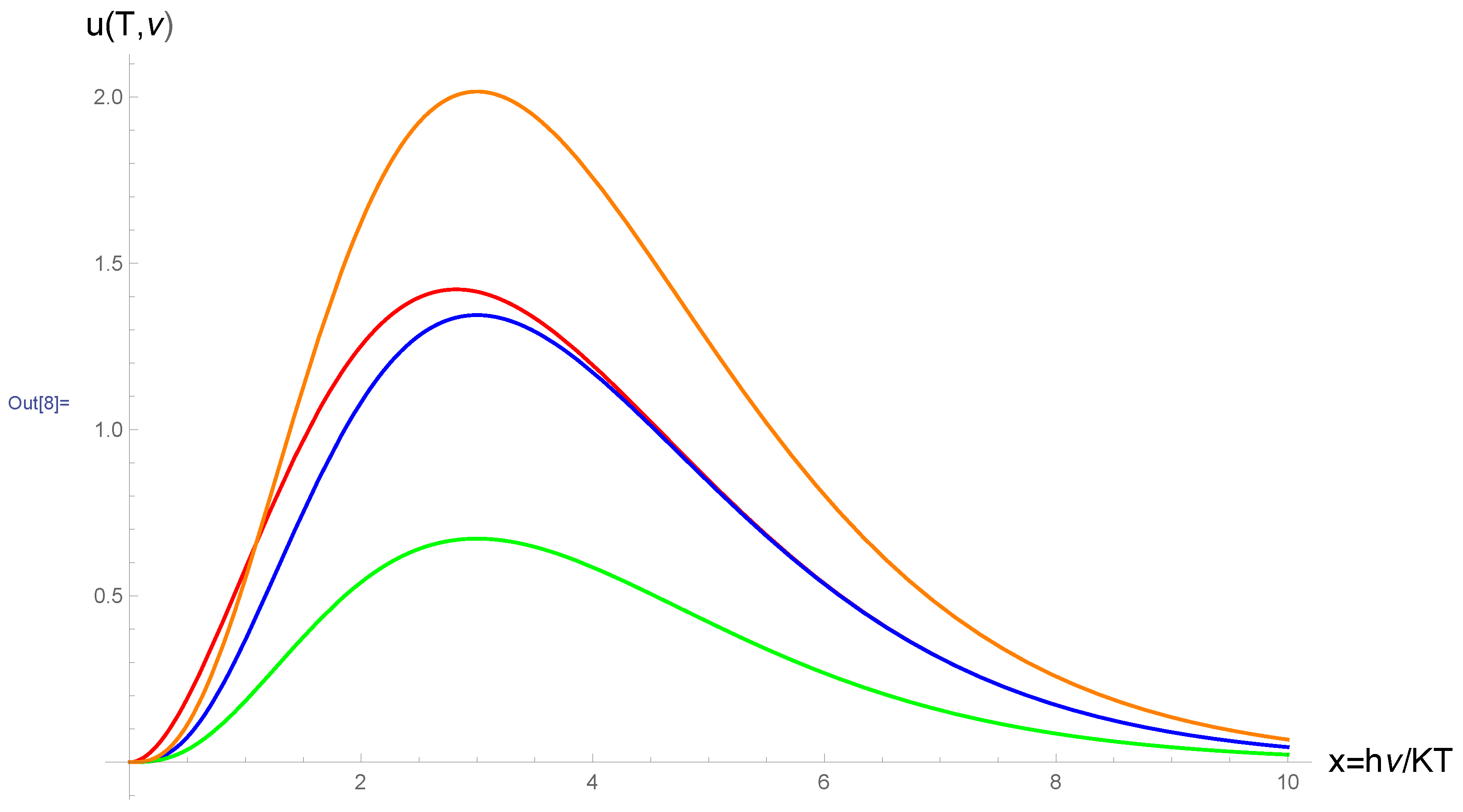
Figure 1, we show a comparison between the curves of
versus
for four cases: Planck distribution; Wien distribution (classical gas with
, i.e., neutrino gas); and the gases with
and
, i.e., neutrino pair gas.
Let us study now the relation between the temperature of our gas and the Bose condensation temperature in the case of neutrino pairs. For an ultrarelativistic ideal gas, the Bose condensation temperature
is given by the relation [
16]:
where
is the spin degeneracy. However, in the case of classical particles with spin, by taking into account the degeneracy, Equation (
25) changes to:
Accordingly, the temperature for a null chemical potential turns out to be:
Thus, by using Equation (
25), we find the relation between the condensation temperature and the actual temperature of the gas to be:
which proves that the temperature of our ultrarelativistic gas with zero chemical potential is always greater than the condensation temperature. Thus, the gas we are dealing with is never in a condensed state even if the chemical potential is zero.
This analysis was made only to show that in the boson case, the connection between classical and quantum gases is possible and consistent. If the resulting photon-like gas could have been condensed, there would not be a classical analogue for such a gas.
7. Concluding Remarks
It is very interesting that even though we used the simplest classical thermodynamic system, namely the ideal gas, it is still possible to find a pathway towards the quantum realm. By this, we mean that it is possible to obtain a gas with a statistic similar to that of a photon gas differing only in the spin degeneracy factor. This is achieved through the imposition of zero chemical potential to the relativistic ideal gas. After this, the resulting gas is very similar to a boson ultrarelativistic ideal gas, and it only differs from a Wien gas in the polarization factor in some cases, which for photons is two. In principle, the spin degeneracy of photons is
, but taking into account that the electromagnetic field is always transverse, we end up with
only. A more general case of connection between the ultrarelativistic ideal gas and the Wien photon gas is given by Equation (
63) (
), which as we have said earlier, for neutrinos with
gives
and for neutrino pairs with spin zero or one, and therefore with
, leads to
or
.
In summary, we have presented the conditions in which a classical ultrarelativistic ideal gas can present quantum behavior by imposing a zero value for the gas chemical potential. This procedure allows a nice connection between a classical evaporating gas system with the problem of cavity radiation. The resulting gas has properties close to those of a Wien gas. However, although in principle, no boson besides photons can have spin degeneracy two, the results are valid for a gas made of neutrinos treated as classical particles, and then, we have as a result a photon gas. Unfortunately, even in this case, as we have seen, the only possible way for a classical gas to go towards a quantum gas is the one that leads to a Wien gas. The actual photon gas (Planck gas) seems to be out of reach for the classical system.
A possible connection between neutrinos and light has been studied before in [
19]. Furthermore, the similarities between the behavior of a quantum system composed of neutrinos with zero chemical potential and vanishing mass and radiation has been studied in [
20], where they also found a relation of the same form as Equation (
47), but with a different constant, namely
. This result differs from ours only by a factor of
. The reason for this difference is that they took into account quantum effects produced by the fact that neutrinos are fermions, and thus, this can be understood as “quantum corrections” of our result (see
Appendix A for more details).