The Pentagonal Fuzzy Number:Its Different Representations, Properties, Ranking, Defuzzification and Application in Game Problems
Abstract
:1. Introduction
1.1. Uncertainty and Uncertainty Measure
- (i)
- The fact belongs to some certain interval
- (ii)
- The concept of the membership function is missing.
- (i)
- The conception of belongingness of the component has to be considered
- (ii)
- The concept of membership function is derived.
- (i)
- The conception of belongingness, or non-belongingness of the component has to be considered
- (ii)
- The concepts of the membership, or non-membership function are derived
- (i)
- The conception of truthfulness, falsity and indeterminacy of the component have to be considered
- (ii)
- The concept of membership function for truthfulness, falsity and indeterminacy are derived
1.2. Fuzzy Sets and Number
1.3. Interval-Valued Fuzzy Numbers (IVFNs)
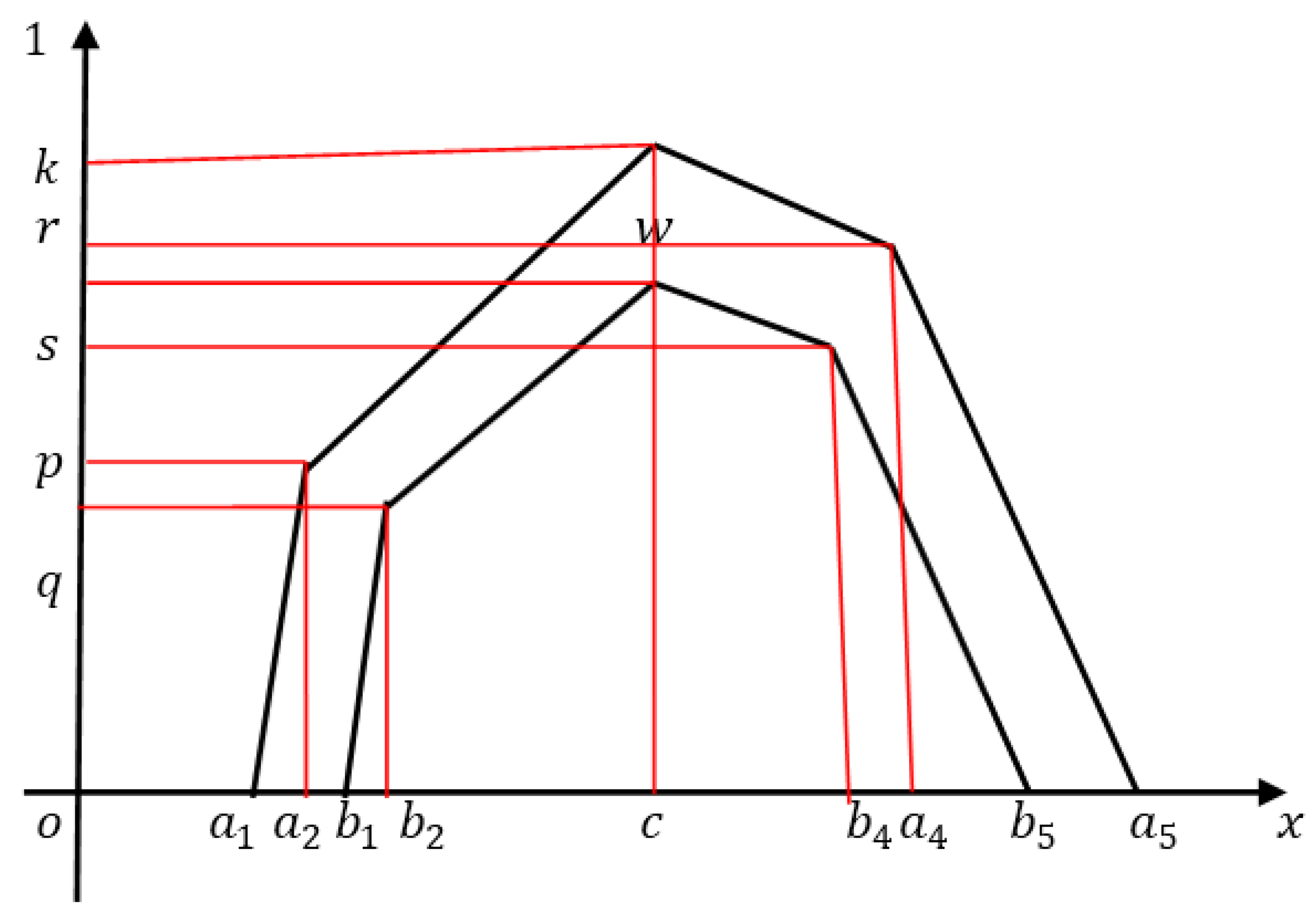
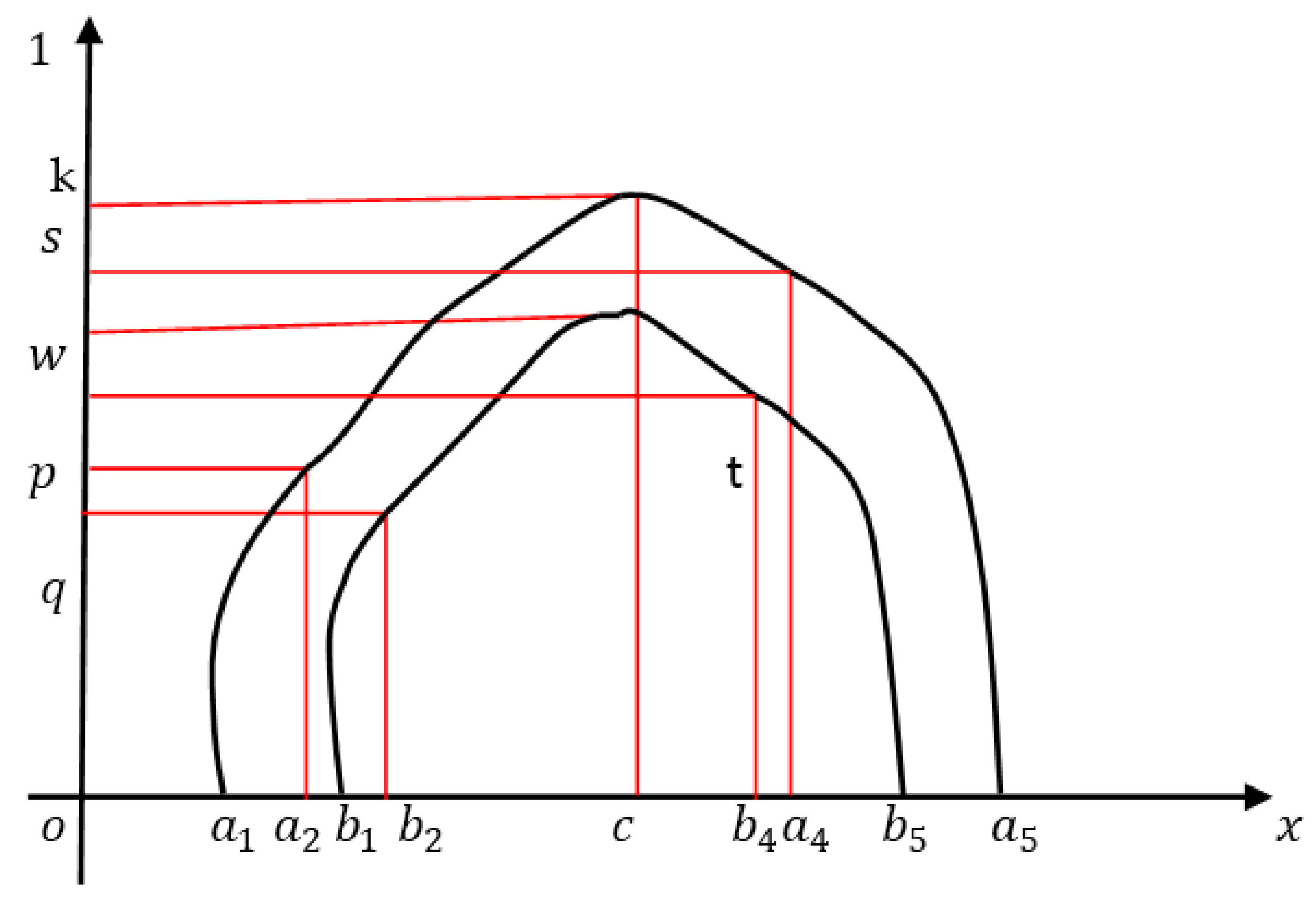
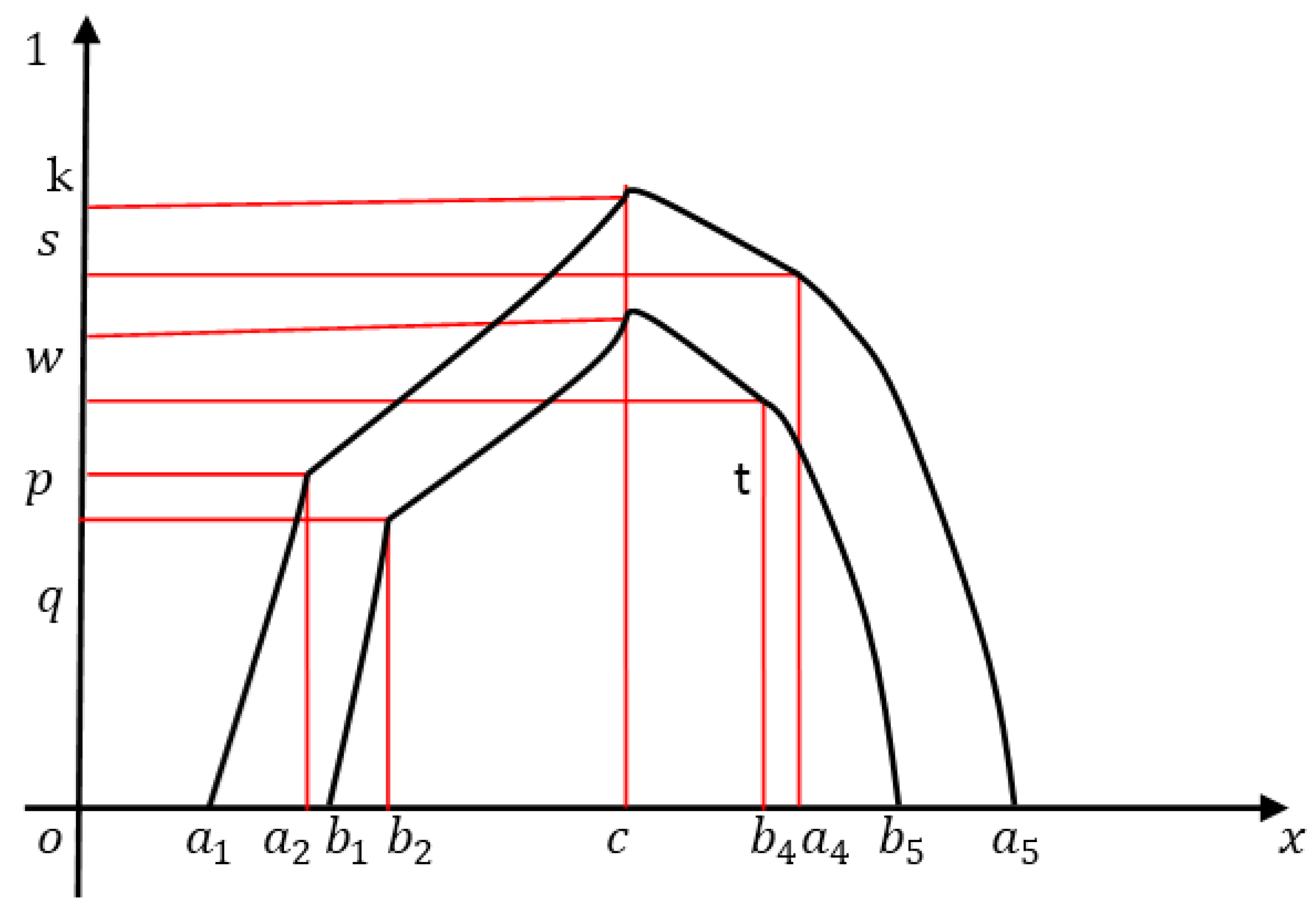
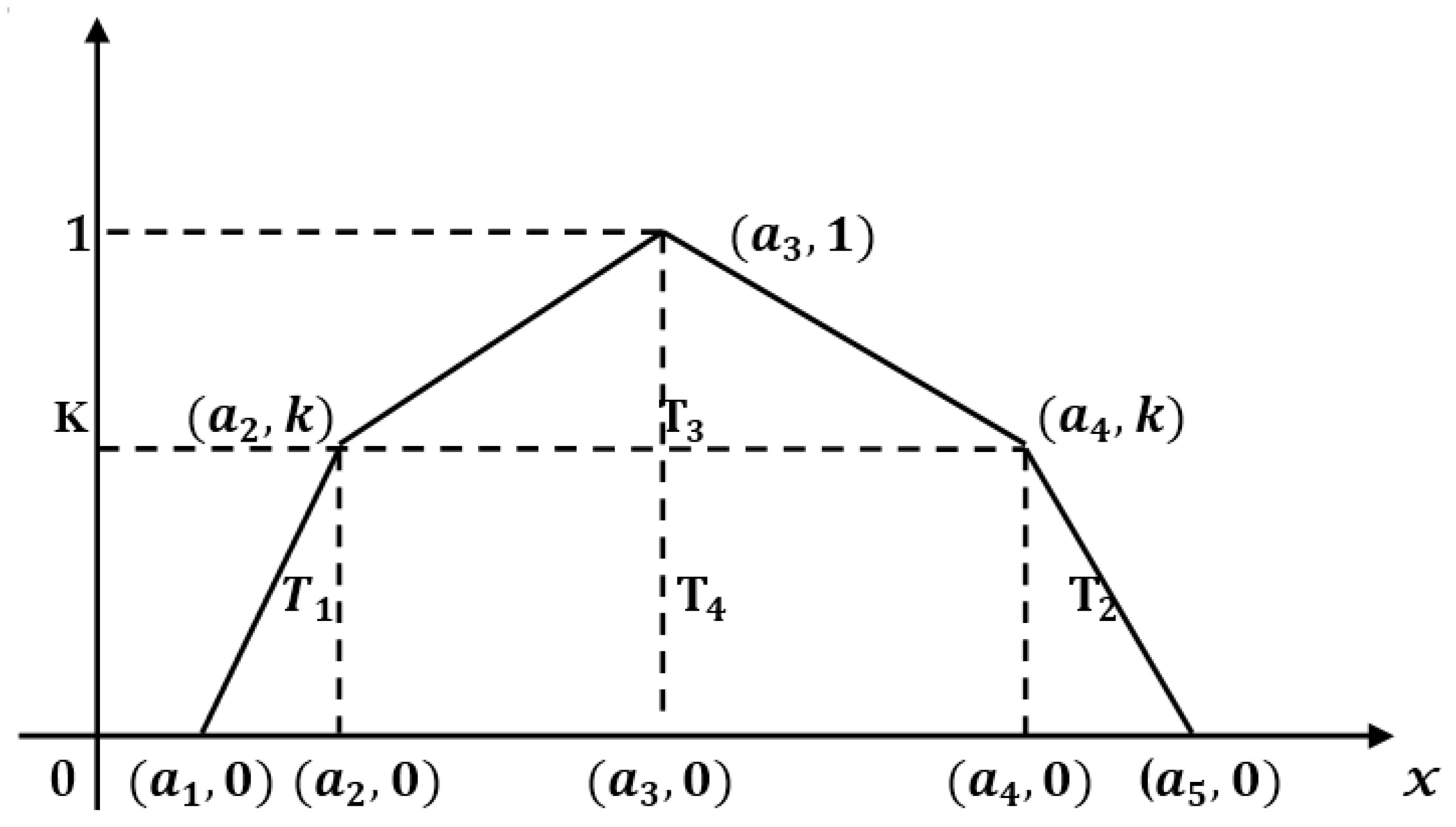
1.4. Pentagonal Fuzzy Numbers
1.5. Verbal Phrasesin Uncertainty Theory
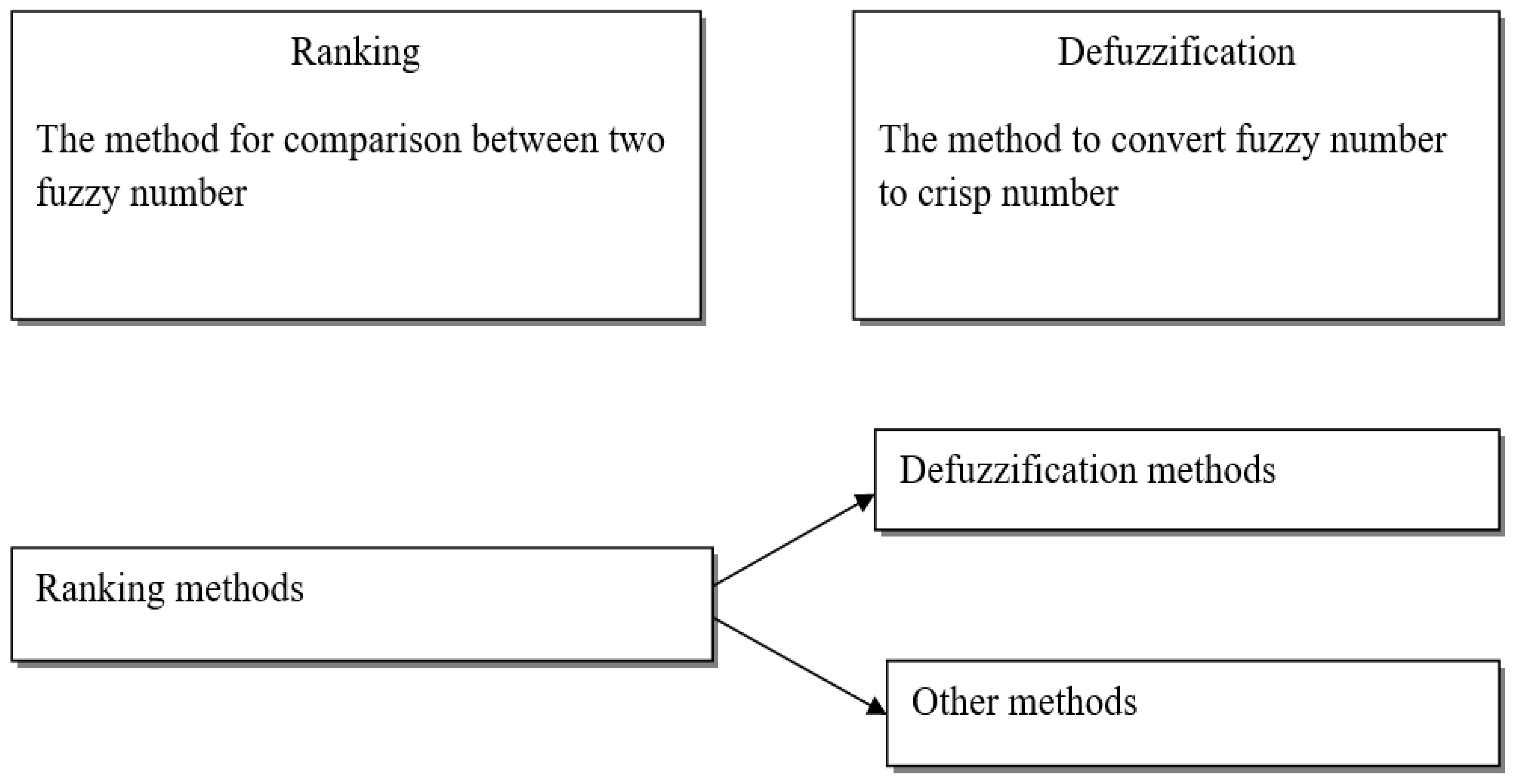
1.6. Ranking and Defuzzification
1.7. Motivation
1.8. Novelties
- (i)
- The development of different types of interval-valued PFN, i.e., symmetric linear PFN, asymmetric linear PFN, symmetric nonlinear PFN, and asymmetric nonlinear PFN were defined.
- (ii)
- The representation of the said PFNs in parametric form was defined.
- (iii)
- The ranking and defuzzification of PFN were done.
- (iv)
- The number was applied to a fuzzy game theory problem.
1.9. Structure of the Paper
2. Preliminaries
3. PFN and Its Different Representations
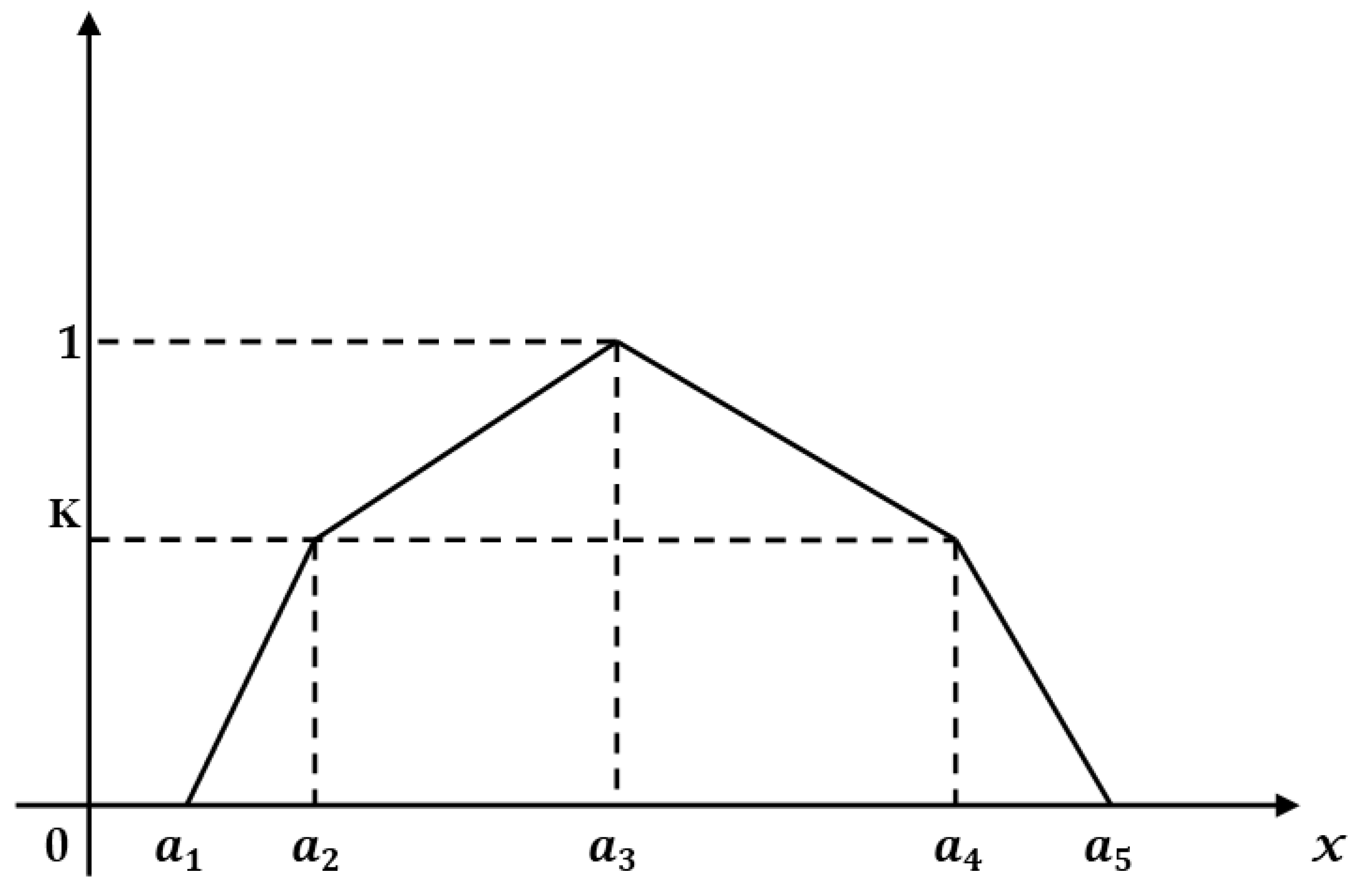
3.1. Linear PFN with Symmetry
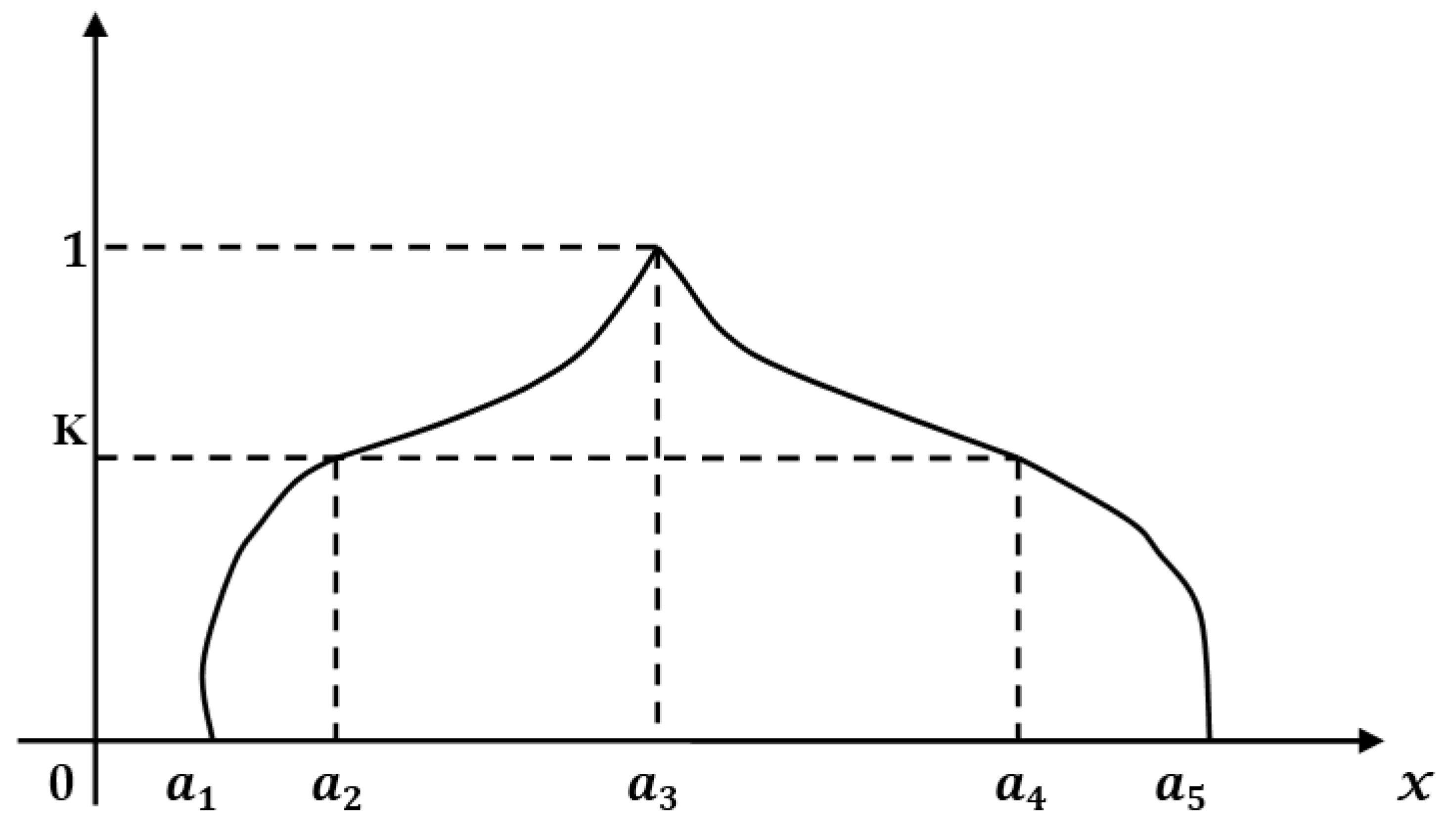
3.2. Non-Linear Pentagonal Fuzzy Number with Symmetry
4. Interval-Valued PFN
4.1. Linear Interval-Valued PFN
4.1.1. Linear Pentagonal Interval-Valued Fuzzy Number with Symmetry
4.1.2. The -Cut of a Linear Pentagonal Interval-Valued Fuzzy Number with Symmetry
4.1.3. Linear Pentagonal Interval-Valued Fuzzy Number with Asymmetry
4.1.4. The -Cut ofa Linear Pentagonal Interval-Valued Fuzzy Number with Asymmetry
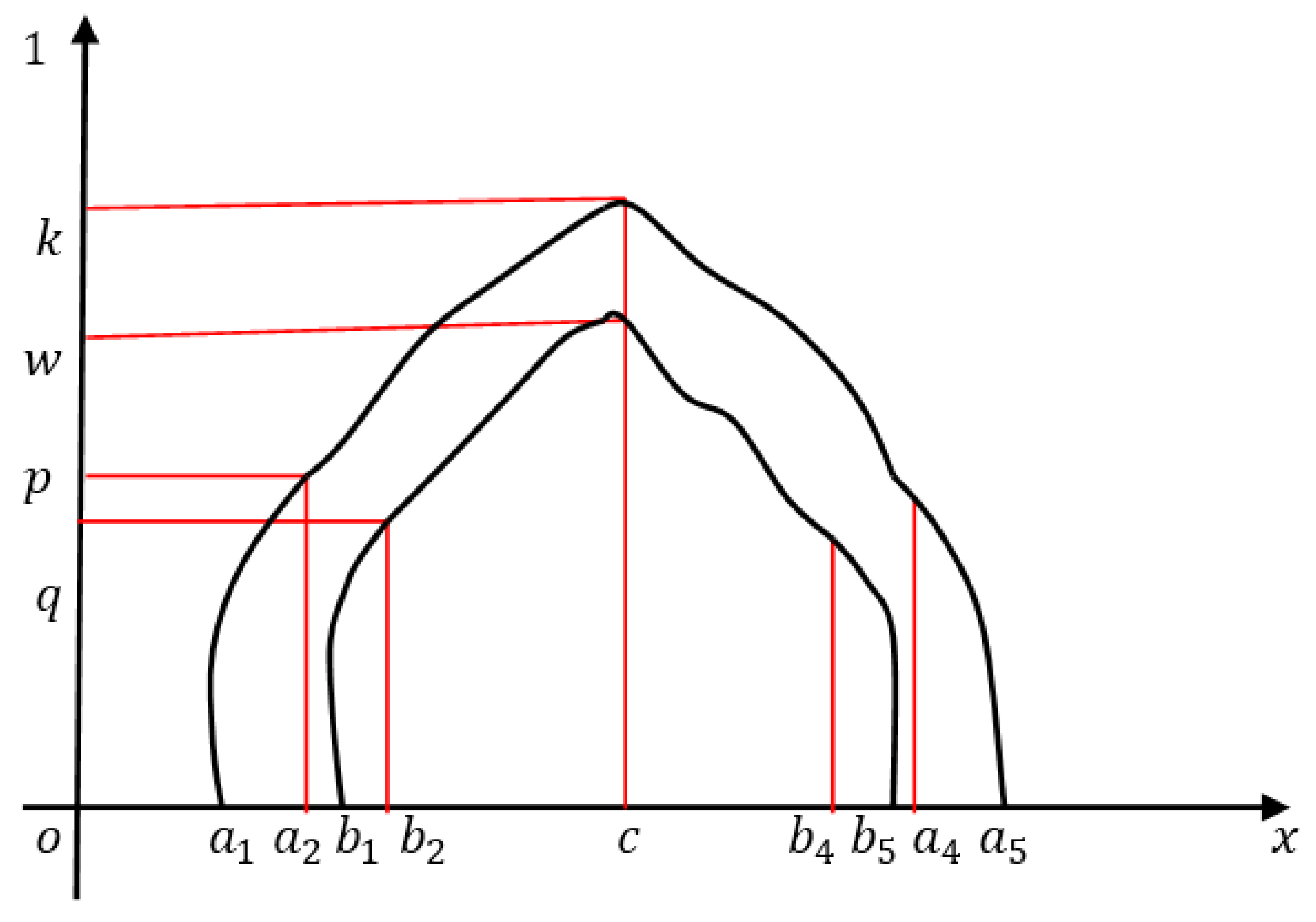
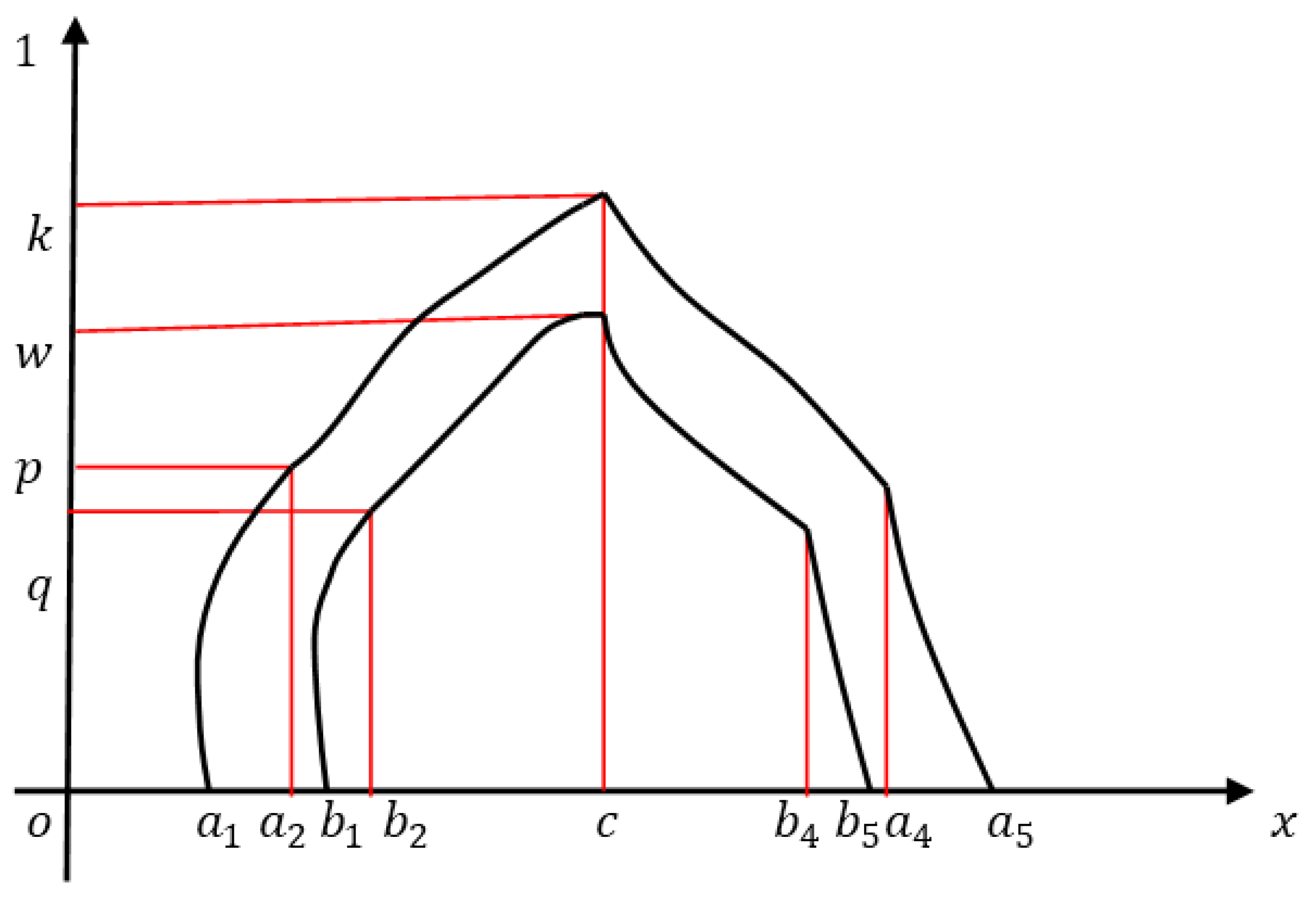
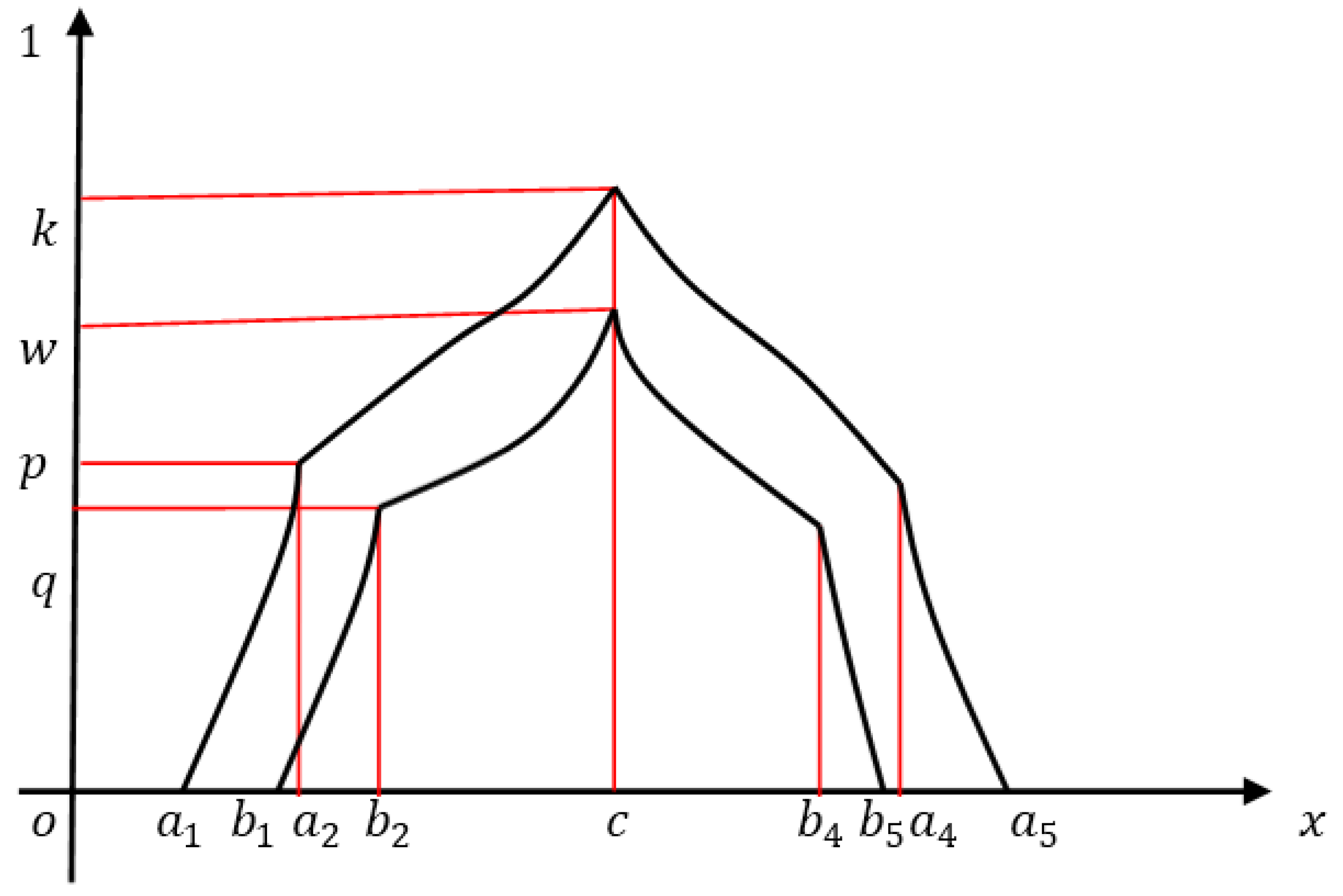
4.2. Non-Linear Interval-Valued Fuzzy NumberInterval-Valued Linear PFN with Symmetry
4.2.1. Non-Linear Pentagonal Interval-Valued Fuzzy Number with Symmetry
4.2.2. -Cut ofNon-Linear Pentagonal Interval-Valued Fuzzy Number with Symmetry
4.2.3. Non-Linear Pentagonal Interval-Valued Fuzzy Number with Asymmetry
4.2.4. -Cut ofNon-Linear Pentagonal Interval-Valued Fuzzy Number with Asymmetry
4.3. Verbal Phrase for the PFN and Interval-Valued PFN
VL-Very Low, L-Low, M-Medium, H-High, M-Medium, VH-Very High
VL-Very Low, L-Low, LM-Low Mean, HM-High Mean, H-High, VH-Very High;VL-Very Low, L-Low, LM-Low Mean, HM-High Mean, H-High, VH-Very High
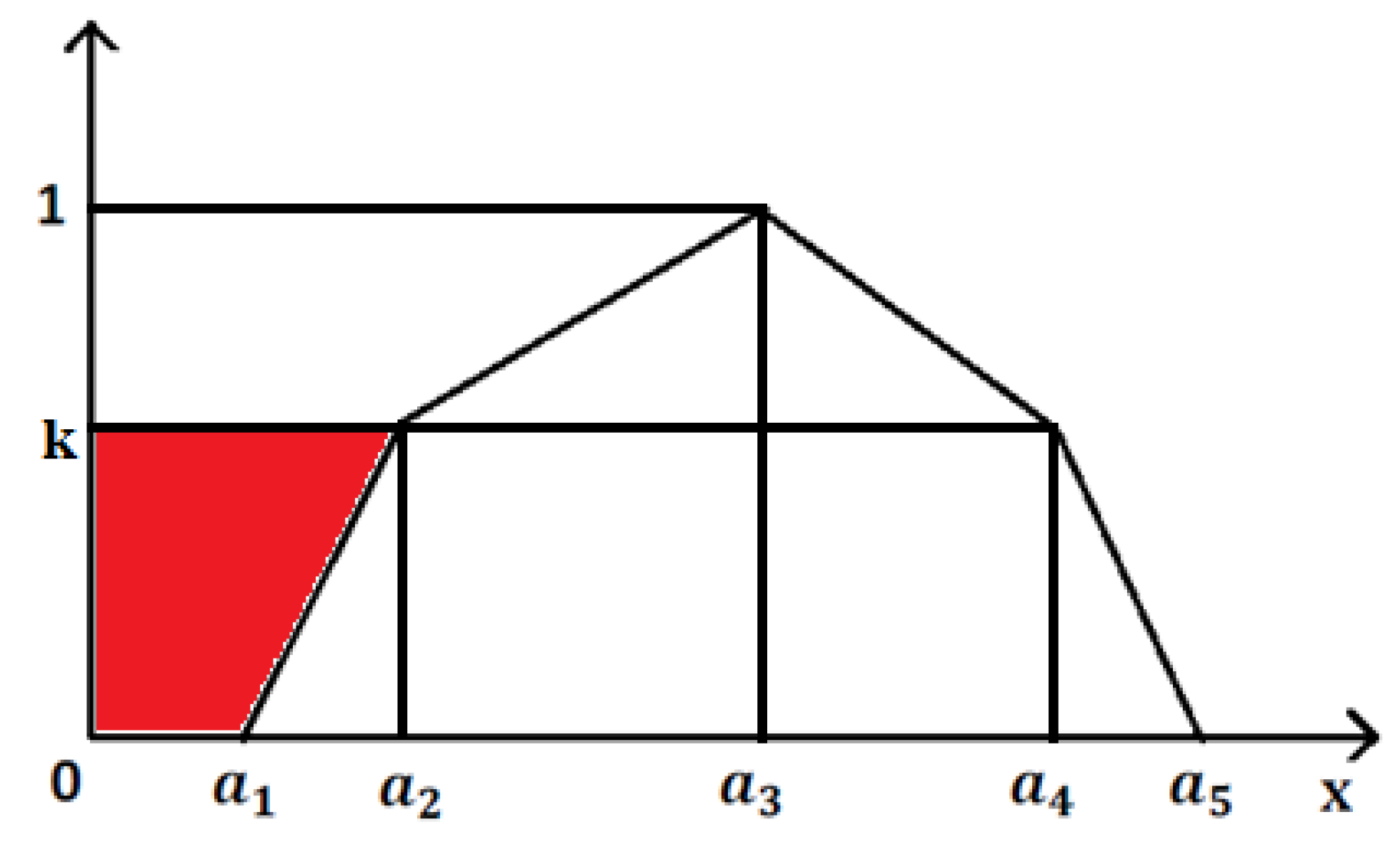
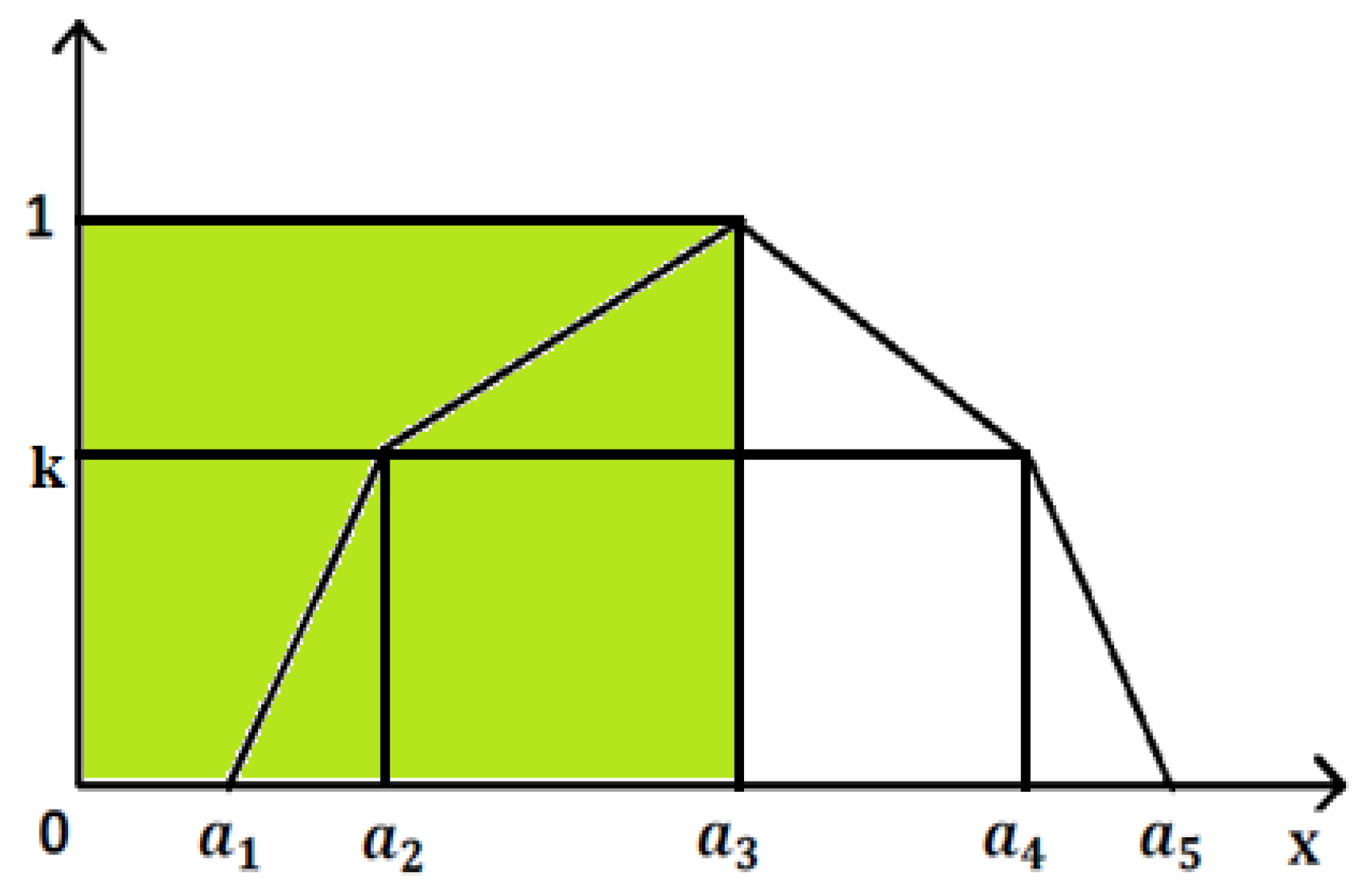
5. Defuzzification of Linear Symmetric PFN
5.1. The Defuzzification Method
- (i)
- Those who are not familiar with the fuzzy concept can relate to the result or solution.
- (ii)
- The crispified value of the fuzzy solutions is identified.
5.2. Defuzzification of Non-Linear Symmetric PFN Based on Centroid Method
5.3. Defuzzification of Linear Symmetric PFN Based on Mean of Alpha (α)-Cut Method
5.4. Defuzzification of Linear Symmetric PFN Based on Removalof Area Method for Linear Pentagonal Fuzzy Number
5.5. Comparison ofthe Above Three Defuzzification Methods
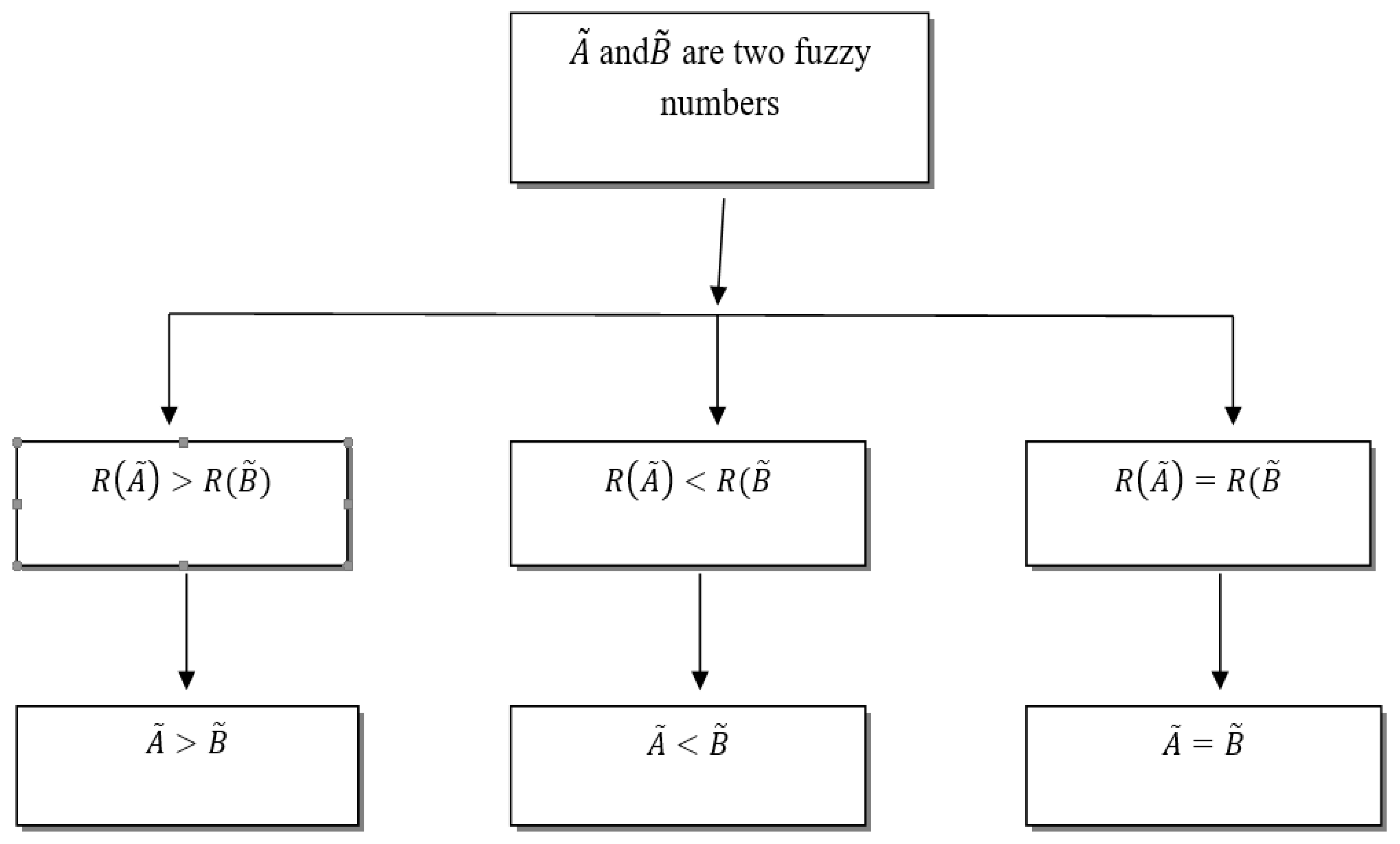
6. Ranking for the Pentagonal Fuzzy Number
6.1. Basic Concept of Ranking Fuzzy Numbers
6.2. Ranking of Pentagonal Fuzzy Numbers
6.3. Working Rule to Find the Ranking of a Pentagonal Fuzzy Number
6.4. Numerical Computation
7. Application of Pentagonal Fuzzy Number in a Game Problem in a Fuzzy Environment Using the Dominance Method
7.1. Operation for Solving a Game Problem Using Fuzzy
7.2. Numerical Problems
8. Conclusions and Scope of Future Research
- The expansion of the interval-valued pentagonal fuzzy numbers and functions, adds a new tool for modeling different aspects of science, engineering and other environmental studies.
- The classifications of linear and nonlinear membership functions provided an appropriate strategy for decision makers.
- Detailed illustrations of membership functions, -cuts and ranking, and defuzzification provide all the required information in one platform to model any real-world problem.
Author Contributions
Funding
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Chang, S.S.L.; Zadeh, L.A. On fuzzy mappings and control. IEEE Trans. Syst. Man Cybern. 1972, 2, 30–34. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Operations on fuzzy numbers. Int. J. Syst. Sci. 1978, 9, 613–626. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic Fuzzy Sets; VII ITKR’s Session: Sofia, Bulgarian, 1983. [Google Scholar]
- Smarandache, F. A Unifying Field in Logics Neutrosophy: Neutrosophic Probability; American Research Press: Rehoboth, DE, USA, 1998. [Google Scholar]
- Dubois, D.; Prade, H. Fundamental of Fuzzy Sets. In The Handbooks of Fuzzy Sets; Springer: New York, NY, USA, 2000; Volume 7. [Google Scholar]
- Guijun, W.; Xiaoping, L. The applications of interval-valued fuzzy numbers and interval distribution numbers. Fuzzy Sets Syst. 1998, 98, 331–335. [Google Scholar] [CrossRef]
- Wang, G.; Li, X. Correlation and information energy of interval-valued fuzzy number. Fuzzy Sets Syst. 2001, 103, 169–175. [Google Scholar] [CrossRef]
- Lin, F.T. Fuzzy job-shop scheduling based on ranking level (α,β) interval-valued fuzzy numbers. IEEE Trans. Fuzzy Syst. 2002, 10, 510–522. [Google Scholar]
- Wei, S.H.; Chen, S.M. A new approach for fuzzy risk analysis based on similarity measures of generalized fuzzy numbers. Expert Syst. Appl. 2009, 36, 589–598. [Google Scholar] [CrossRef]
- Kalaichelvi, A.; Malini, P.H.; Janofer, K. Application of interval fuzzy matrices and interval valued fuzzy soft sets in the analysis of/the factors influencing high scores in higher secondary examinations. Int. J. Math. Sci. Appl. 2012, 2, 777–780. [Google Scholar]
- Kumar, P.; Singh, S.B. Fuzzy fault tree analysis using level (?,?) interval-valued fuzzy numbers. Ind. Eng. Lett. 2015, 5, 36–42. [Google Scholar]
- Abirami, D.; Dinagar, D.S. On L-R type interval valued fuzzy numbers in critical path analysis. Int. J. Fuzzy Math. Arch. 2015, 6, 77–83. [Google Scholar]
- Su, J.-S. Fuzzy programming based on interval-valued fuzzy numbers and ranking. Int. J. Contemp. Math. Sci. 2007, 2, 393–410. [Google Scholar] [CrossRef]
- Bhatia, N.; Kumar, A. Sensitivity analysis for interval valued fully fuzzy linear programming problems. J. Appl. Res. Technol. 2012, 10, 871–884. [Google Scholar]
- Mondal, S.P. Differential equation with interval valued fuzzy number and its applications. Int. J. Syst. Assur. Eng. Manag. 2016, 7, 370–380. [Google Scholar] [CrossRef]
- Ebrahimnejad, A. A method for solvig linear programming with interval-valued fuzzy variables. RAIRO-Oper. Res. 2018, 52, 955–979. [Google Scholar] [CrossRef]
- Dahooie, J.H.; Zavadskas, E.K.; Abolhasani, M.; Vanaki, A.; Turskis, Z. A Novel Approach for Evaluation of Projects Using an Interval–Valued Fuzzy Additive Ratio Assessment (ARAS) Method: A Case Study of Oil and Gas Well Drilling Projects. Symmetry 2018, 10, 45. [Google Scholar] [CrossRef]
- Panda, A.; Pal, M. A study on pentagonal fuzzy number and its corresponding matrices. Pac. Sci. Rev. B Hum. Soc. Sci. 2015, 1, 131–139. [Google Scholar] [CrossRef]
- Anitha, P.; Parvathi, P. An Inventory Model with Stock Dependent Demand, two parameter Weibull Distribution Deterioration in a juzzy environment. In Proceedings of the 2016 Online International Conference on Green Engineering and Technologies (IC-GET), Hokkaido, Japan, 16–21 May 2016; pp. 1–8. [Google Scholar]
- Helen, R.; Uma, G. A new operation and ranking on pentagon fuzzy numbers. Int. J. Math. Sci. Appl. 2015, 5, 341–346. [Google Scholar]
- Siji, S.; Kumari, K.S. An Approach for Solving Network Problem with Pentagonal Intuitionistic Fuzzy Numbers Using Ranking Technique. Middle-East J. Sci. Res. 2016, 24, 2977–2980. [Google Scholar]
- Raj, A.V.; Karthik, S. Application of Pentagonal Fuzzy Number in Neural Network. Int. J. Math. Appl. 2016, 4, 149–154. [Google Scholar]
- Dhanamandand, K.; Parimaldevi, M. Cost analysis on a probabilistic multi objective-multi item inventory model using pentagonal fuzzy number. Glob. J. Appl. Math. Math. Sci. 2016, 9, 151–163. [Google Scholar]
- Pathinathan, T.; Ponnivalavan, K. Reverse order Triangular, Trapezoidal and Pentagonal Fuzzy Numbers. Ann. Pure Appl. Math. 2015, 9, 107–117. [Google Scholar]
- Ponnivalavan, K.; Pathinathan, T. Intuitionistic pentagonal fuzzy number. ARPN J. Eng. Appl. Sci. 2015, 10, 5446–5450. [Google Scholar]
- Christi, M.S.A.; Kasthuri, B. Transportation Problem with Pentagonal Intuitionistic Fuzzy Numbers Solved Using Ranking Technique and Russell’s Method. Int. J. Eng. Res. Appl. 2016, 6, 82–86. [Google Scholar]
- Mondal, S.P.; Mandal, M. Pentagonal fuzzy number, its properties and application in fuzzy equation. Future Comput. Inform. J. 2017, 2, 110–117. [Google Scholar] [CrossRef]
- Mondal, S.P.; Mandal, M.; Bhattacharya, D. Non-linear interval-valued fuzzy numbers and their application in difference equations. Granul. Comput. 2018, 3, 177–189. [Google Scholar] [CrossRef]
- Chu, T.C.; Huang, K.S.; Chang, T.M. COA defuzzification method for evaluating Cpk under fuzzy environments. J. Discret. Math. Sci.Cryptogr. 2004, 7, 271–280. [Google Scholar] [CrossRef]
- Perumal, L.; Nagi, F.H. Largest of maximum (LOM) method for switching fuzzy control system. Aust. J. Electr. Electron. Eng. 2008, 4, 167–178. [Google Scholar] [CrossRef]
- Tóth-Laufer, E.; Takács, M. The Effect of Aggregation and DefuzzificationMethod Selection on the Risk Level Calculation. In Proceedings of the 10th IEEE Jubilee International Symposium on Applied Machine Intelligence and Informatics, Herl’any, Slovakia, 26–28 January 2012. [Google Scholar]
- Mondal, S.P.; Khan, N.A.; Razzaq, O.A.; Tudu, S.; Roy, T.K. Adaptive strategies for system of fuzzy differential equation: Application of arms race model. J. Math. Comput. Sci. 2018, 18, 192–205. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Asady, B. Ranking of fuzzy numbers by sign distance. Inform. Sci. 2006, 176, 2405–2416. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Hajjari, T. A new approach for ranking of trapezoidal fuzzy numbers. Comput. Math. Appl. 2009, 57, 413–419. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Hajjari, T. An improvement on centroid point method for ranking of fuzzy numbers. J. Sci. IAU 2011, 78, 109–119. [Google Scholar]
- Asady, B. The revised method of ranking LR fuzzy number based on deviation degree. Expert Syst. Appl. 2010, 37, 5056–5060. [Google Scholar] [CrossRef]
- Chen, S.J.; Chen, S.M. A new method for handling multicriteria fuzzy decision making problems using FN-IOWA operators. Cybern. Syst. 2003, 34, 109–137. [Google Scholar] [CrossRef]
- Chen, S.J.; Chen, S.M. Fuzzy risk analysis based on the ranking of generalized trapezoidal fuzzy numbers. Appl. Intell. 2007, 26, 1–11. [Google Scholar]
- Chen, S.-M.; Chen, J.-H. Fuzzy risk analysis based on the ranking of generalized fuzzy numbers with different heights and different spreads. Expert Syst. Appl. 2009, 36, 6833–6842. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, Q. A TOPSIS-based centroid index ranking method of fuzzy numbers and its application in decision-making. Cybern. Syst. 2005, 36, 581–595. [Google Scholar]
- Deng, Y.; Zhu, Z.F.; Liu, Q. Ranking fuzzy numbers with an area method usingofgyration. Comput. Math. Appl. 2006, 51, 1127–1136. [Google Scholar] [CrossRef]
- Hajjari, T. Ranking of fuzzy numbers based on ambiguity degree. Aust. J. Basic Appl. Sci. 2011, 5, 62–69. [Google Scholar]
- Hajjari, T. On deviation degree methods for ranking fuzzy numbers. Aust. J. Basic Appl. Sci. 2011, 5, 750–758. [Google Scholar]
- Wang, Z.-X.; Liu, Y.-J.; Fan, Z.-P.; Feng, B. Ranking L-R fuzzy numbers based on deviation degree. Inform. Sci. 2009, 176, 2070–2077. [Google Scholar] [CrossRef]
- Chen, L.H.; Lu, H.W. An approximate approach for ranking fuzzy numbers based on left and right dominance. Comput. Math. Appl. 2001, 41, 1589–1602. [Google Scholar] [CrossRef]
- Chen, L.H.; Lu, H.W. The preference order of fuzzy numbers. Comput. Math. Appl. 2002, 44, 1455–1465. [Google Scholar] [CrossRef]
- Liu, X.W.; Han, S.L. Ranking fuzzy numbers with preference weighting function expectation. Comput. Math. Appl. 2005, 49, 1455–1465. [Google Scholar] [CrossRef]
- Cheng, C.H. A new approach for ranking fuzzy numbers by distance method. Fuzzy Sets Syst. 1998, 95, 307–317. [Google Scholar] [CrossRef]
- Chu, T.; Tsao, C. Ranking fuzzy numbers with an area between the centroid point and orginalpoint. Comput. Math. Appl. 2002, 43, 111–117. [Google Scholar] [CrossRef]
- Wang, Y.J.; Lee, H.S. The revised method of ranking fuzzy numbers with an area between the centroid and original points. Comput. Math. Appl. 2008, 55, 2033–2042. [Google Scholar] [CrossRef]
- Halgamuge, S.; Runkler, T.; Glesner, M. On the neural defuzzification methods. In Proceedings of the 5th IEEE International Conference on Fuzzy Systems, New Orleans, LA, USA, 8–11 September1996; pp. 463–469. [Google Scholar]
- Song, Q.; Leland, R.P. Adaptive learning defuzzificatin techniques and applications. Comput. Math. Appl. 1996, 81, 321–329. [Google Scholar]
- Yager, R.R. Knowledge-based defuzzification. Fuzzy Sets Syst. 1996, 80, 177–185. [Google Scholar] [CrossRef]
- Filev, D.P.; Yager, R.R. A generalized defuzzification method via BADD distributions. Int. J. Intell. Syst. 1991, 6, 687–697. [Google Scholar] [CrossRef]
- Jiang, T.; Li, Y. Generalized defuzzification strategies and their parameter learning procedure. IEEE Trans. Fuzzy Syst. 1996, 4, 64–71. [Google Scholar] [CrossRef]
- Ramon, E. Moore, Methods and Applications of Interval Analysis; Studies in Applied and Numerical Mathematics; SIAM: Philadelphia, PA, USA, 1979. [Google Scholar]








| Authors Information | Membership Function’s Type | Main Contribution in Theatrical Improvement | Application Area |
|---|---|---|---|
| Guijun and Xiaoping [7] | General fuzzy cases | Define IVFN and interval distribution number | Generalized pseudo-probability metric spaces and pseudo metric spaces |
| Anitha and Parvathi [8] | Correlation coefficient of IVFN | Properties of IVFN | Information energy |
| Lin [9] | Triangular Linear | Ranking using signed distance methods | Job-shop scheduling problem |
| Wei and Chen [10] | Trapezoidal Linear | Found similarity measures between two IVFN | Fuzzy risk analysis |
| Kalaichelvi et al. [11] | Not take the membership function concept | Extended the concept of IVFN to Soft IVFN | Fuzzy matrix theory |
| Kumar and Singh [12] | Triangular linear | Found the signed distance | Fuzzy fault tree |
| Abirami and Dinagar [13] | LR type | Found distance function | Project network |
| Su [14] | Triangular linear | Arithmetic operation and comparison | Linear programming problem |
| Bhatia and Kumar [15] | Triangular linear | Ranking for solving LPP | Linear programming problem |
| Mondal [16] | Triangular linear and non-linear | Arithmetic operation | Fuzzy differential equation |
| Ebrahimnejad [17] | Generalized trapezoidal linear | Arithmetic operation on LPP | Linear programming problem |
| Dahooie et al. [18] | Trapezoidal and triangular linear | Defuzzification and fuzzy additive ratio assessment method | Oil and gas well drilling projects |
| Authors Information | Membership Function’s Type | Main Contribution in Theatrical Improvement | Application Area |
|---|---|---|---|
| Panda and Pal [19] | Linear and symmetry on both end | exponent operation and arithmetic operation | Fuzzy matrix theory |
| Anitha and Parvathi [20] | Linear | Find expected crisp value | Inventory management |
| Helen and Uma [21] | Linear | Defining the parametric representation | Proofing the arithmetic operation and find the ranking |
| Siji and Kumari [22] | Linear membership, non-membership functions | Arithmetic operation and find the ranking | Networking problem |
| Raj and Karthik [23] | Linear | Arithmetic operation | Neural network problem |
| Dhanamand and Parimaldevi [24] | Linear | Find the ranking using circumcenter of centroids method | Multi item and multi -objective inventory management problem |
| Pathinathan and Ponnivalavan [25] | Reverse order linear | Arithmetic operation | Defining reverse order fuzzy number |
| Ponnivalavan and Pathinathan [26] | Linear membership, non-membership function | Arithmetic operation | Find score and accuracy function |
| Annie Christi and Kasthuri [27] | Linear membership, non-membership function | Arithmetic operation and ranking | Transportation problem |
| Mondal and Mandal [28] | Linear and non-linear | Define symmetric and asymmetric PFN | Fuzzy equation |
| Type of Uncertain Parameter | Verbal Phrase | Quantity Information | |
|---|---|---|---|
| Interval Number | [Low, High] | Example 1 | The height lies in the range [2000,3000] ft. |
| Example 2 | The car number is between the interval [1000,2000] cars | ||
| Triangular Fuzzy Number | [Low, Medium, High] | Example 1 | The height lies in the fuzzy number set [2010,2050,2150] ft |
| Example 2 | The car number is in the fuzzy number set [1000,1050,1200] cars | ||
| Trapezoidal Fuzzy Number | [Low, Low Mean, High Mean, High] | Example 1 | The height lies in the fuzzy number set [2000,2205,2705,2300] ft. |
| Example 2 | The car number is in the fuzzy number set [1000,1025,1075,1200] cars | ||
| Strategy | ||||
|---|---|---|---|---|
| (VL,M,H,M,L) | (VL,M,H,M,L) | (VL,M,H,M,L) | (VL,M,H,M,L) | |
| (VL,M,H,M,L) | (VL,M,H,M,L) | (VL,M,H,M,L) | (VL,M,H,M,L) | |
| (VL,M,H,M,L) | (VL,M,H,M,L) | (VL,M,H,M,L) | (VL,M,H,M,L) | |
| (VL,M,H,M,L) | (VL,M,H,M,L) | (VL,M,H,M,L) | (VL,M,H,M,L) |
| Strategy | ||||
|---|---|---|---|---|
| (VL,HM,VH,HM,L; L,LM,VH,H,VL) | (VL,HM,VH,HM,L; L,LM,VH,H,VL) | (VL,HM,VH,HM,L; L,LM,VH,H,VL) | (VL,HM,VH,HM,L; L,LM,VH,H,VL) | |
| (VL,HM,VH,HM,L; L,LM,VH,H,VL) | (VL,HM,VH,HM,L; L,LM,VH,H,VL) | (VL,HM,VH,HM,L; L,LM,VH,H,VL) | (VL,HM,VH,HM,L; L,LM,VH,H,VL) | |
| (VL,HM,VH,HM,L; L,LM,VH,H,VL) | (VL,HM,VH,HM,L; L,LM,VH,H,VL) | (VL,HM,VH,HM,L; L,LM,VH,H,VL) | (VL,HM,VH,HM,L; L,LM,VH,H,VL) | |
| (VL,HM,VH,HM,L; L,LM,VH,H,VL) | (VL,HM,VH,HM,L; L,LM,VH,H,VL) | (VL,HM,VH,HM,L; L,LM,VH,H,VL) | (VL,HM,VH,HM,L; L,LM,VH,H,VL) |
| No of Example | Value of k | Defuzzification Value by Centroid Method | Defuzzification Value by Mean of Alpha-Cut Method | Defuzzification Value by Removal-Area Method | |
|---|---|---|---|---|---|
| 1 | 1,1,1,1 | 3.00 | 3.00 | 2.6 | |
| 0.5 | 1,1,1,1 | 3.00 | 3.00 | 2.2 | |
| 0.3 | 2,2,2,2 | 1.0563 | 1.05 | 0.48 | |
| 0.2 | 1,1,1,1 | 0.00 | 0.00 | 0.112 |
| No. of Example | Components | Conclusion | ||
|---|---|---|---|---|
| Example 1 | Set-1 | (3.0,0.45) | ||
| Set-2 | (2.0,0.45) | |||
| Set-3 | (0.54,0.45) | |||
| Set-4 | (0.083,0.45) | |||
| Example 2 | Set-1 | (0.079,0.36) | ||
| Set-2 | (−0.79,0.36) | |||
| Set-3 | (−0.22,0.36) | |||
| Set-4 | (−0.067,0.36) |
| Strategy | B1 | B2 | B3 | B4 |
|---|---|---|---|---|
| A1 | (0,1,2,3,4;0.5) | (−1,0,1,2,3;0.5) | (2,3,4,5,6;0.5) | (−2,−1,0,1,2;0.5) |
| A2 | (1,2,3,4,5;0.5) | (2,3,4,5,6;0.5) | (0,1,2,3,4;0.5) | (2,3,4,5,6;0.5) |
| A3 | (2,3,4,5,6;0.5) | (0,1,2,3,4;0.5) | (2,3,4,5,6;0.5) | (−2,−1,0,1,2;0.5) |
| A4 | (−2,−1,0,1,2;0.5) | (2,3,4,5,6;0.5) | (−2,−1,0,1,2;0.5) | (6,7,8,9,10;0.5) |
| Strategy | B1 | B2 | B3 | B4 |
|---|---|---|---|---|
| A1 | 2 | 1 | 4 | 0 |
| A2 | 3 | 4 | 2 | 4 |
| A3 | 4 | 2 | 4 | 0 |
| A4 | 0 | 4 | 0 | 8 |
| Strategy | B1 | B2 | B3 | B4 |
|---|---|---|---|---|
| A2 | 3 | 4 | 2 | 4 |
| A3 | 4 | 2 | 4 | 0 |
| A4 | 0 | 4 | 0 | 8 |
| Strategy | B2 | B3 | B4 |
|---|---|---|---|
| A2 | 4 | 2 | 4 |
| A3 | 2 | 4 | 0 |
| A4 | 4 | 0 | 8 |
| Strategy | B3 | B4 |
|---|---|---|
| A2 | 2 | 4 |
| A3 | 4 | 0 |
| A4 | 0 | 8 |
| Strategy | B3 | B4 |
|---|---|---|
| A3 | 4 | 0 |
| A4 | 0 | 8 |
| Strategy | B1 | B2 | B3 | B4 |
|---|---|---|---|---|
| A1 | (1,2,3,4,5;0.5) | (0,1,2,3,4;0.5) | (3,4,5,6,7;0.5) | (−2,−1,0,1,2;0.5) |
| A2 | (2,3,4,5,6;0.5) | (3,4,5,6,7;0.5) | (1,2,3,4,5;0.5) | (3,4,5,6,7;0.5) |
| A3 | (3,4,5,6,7;0.5) | (1,2,3,4,5;0.5) | (3,4,5,6,7;0.5) | (−2,−1,0,1,2;0.5) |
| A4 | (−2,−1,0,1,2;0.5) | (2,3,4,5,6;0.5) | (−2,−1,0,1,2;0.5) | (7,8,9,10,11;0.5) |
| Strategy | B1 | B2 | B3 | B4 |
|---|---|---|---|---|
| A1 | 3 | 2 | 5 | 0 |
| A2 | 4 | 5 | 3 | 5 |
| A3 | 5 | 3 | 5 | 0 |
| A4 | 0 | 4 | 0 | 9 |
| Strategy | B1 | B2 | B3 | B4 |
|---|---|---|---|---|
| A1 | (2,3,4,5,6;0.5) | (2,3,4,5,6;0.5) | (4,5,6,7,8;0.5) | (-2,-1,0,1,2;0.5) |
| A2 | (3,4,5,6,7;0.5) | (4,5,6,7,8;0.5) | (3,4,5,6,7;0.5) | (4,5,6,7,8;0.5) |
| A3 | (4,5,6,7,8;0.5) | (2,3,4,5,6;0.5) | (4,5,6,7,8;0.5) | (-2,-1,0,1,2;0.5) |
| A4 | (-2,-1,0,1,2;0.5) | (4,5,6,7,8;0.5) | (-2,-1,0,1,2;0.5) | (8,9,10,11,12;0.5) |
| Strategy | B1 | B2 | B3 | B4 |
|---|---|---|---|---|
| A1 | 4 | 3 | 6 | 0 |
| A2 | 5 | 6 | 4 | 6 |
| A3 | 6 | 4 | 6 | 0 |
| A4 | 0 | 5 | 0 | 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chakraborty, A.; Mondal, S.P.; Alam, S.; Ahmadian, A.; Senu, N.; De, D.; Salahshour, S. The Pentagonal Fuzzy Number:Its Different Representations, Properties, Ranking, Defuzzification and Application in Game Problems. Symmetry 2019, 11, 248. https://doi.org/10.3390/sym11020248
Chakraborty A, Mondal SP, Alam S, Ahmadian A, Senu N, De D, Salahshour S. The Pentagonal Fuzzy Number:Its Different Representations, Properties, Ranking, Defuzzification and Application in Game Problems. Symmetry. 2019; 11(2):248. https://doi.org/10.3390/sym11020248
Chicago/Turabian StyleChakraborty, Avishek, Sankar Prasad Mondal, Shariful Alam, Ali Ahmadian, Norazak Senu, Debashis De, and Soheil Salahshour. 2019. "The Pentagonal Fuzzy Number:Its Different Representations, Properties, Ranking, Defuzzification and Application in Game Problems" Symmetry 11, no. 2: 248. https://doi.org/10.3390/sym11020248
APA StyleChakraborty, A., Mondal, S. P., Alam, S., Ahmadian, A., Senu, N., De, D., & Salahshour, S. (2019). The Pentagonal Fuzzy Number:Its Different Representations, Properties, Ranking, Defuzzification and Application in Game Problems. Symmetry, 11(2), 248. https://doi.org/10.3390/sym11020248









