Abstract
Based on the Rheological Paradigm, we extend the equations of state for relativistic spherically symmetric static neutron stars, taking into consideration the derivative of the matter pressure along the so-called director four-vector. The modified equations of state are applied to the model of a zero-temperature neutron condensate. This model includes one new parameter with the dimensionality of length, which describes the rheological type screening inside the neutron star. As an illustration of the new approach, we consider the rheological type generalization of the non-relativistic Lane–Emden theory and find numerically the profiles of the pressure for a number of values of the new guiding parameter. We have found that the rheological type self-interaction makes the neutron star more compact, since the radius of the star, related to the first null of the pressure profile, decreases when the modulus of the rheological type guiding parameter grows.
PACS:
04.20.-q; 04.40.-b; 04.40.Nr; 04.50.Kd
1. Introduction
Neutron stars play the key role in Modern Relativistic Astrophysics. These compact objects are, usually, rapidly rotating and have a strong magnetic field. Relativistic pulsars are the central elements of Pulsar Physics, and form the global system of lighthouses, giving us an effective tool for investigations of the Universe structure (see, e.g., [1,2,3,4]). The theory of the neutron star structure is based on the analysis of the so-called equations of state (EoS); various models of the EoS are well documented and applied to the theory of pulsar structure.
The most cited is the simplest model, which follows from the Lane and Emden model (see, e.g., [5] for details); it is appropriate for the non-relativistic non-rotating spherically symmetric objects with polytropic EoS. Nowadays, the Lane–Emden model plays the role of a censor for various modified theories of star’s structure: analogously with the requirement that every modified theory of gravity should have the Newtonian limit, one assumes that the theories of the star structure have to possess the appropriate Lane–Emden limit. In this sense, elaborating on a new rheological-type model of EoS in this paper, we compete below the analytical consideration by the analysis of an extension of this classical Lane–Emden model.
Relativistic models of neutron star structure use much more sophisticated versions of EoS (see, e.g., [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21] and references therein). From this diversity of models, one can formally distinguish, first, the models with hot and cold (degenerated) dense matter, second, the models with pure neutron and multi-species matter (quark, meson, hadronic, etc.), third, the models with nuclear interactions between hadronic species and self-interactions inside the neutron systems. In our work, we consider one-component dense degenerated neutron matter with internal self-interaction of the rheologic type.
Another trend in the modeling of the neutron star interior is connected with the so-called modified theories of gravity (see, e.g., [22,23,24,25,26,27,28,29,30] for modifications in the framework of the Einstein–aether theory, gravity, non-minimal theory). Below, we consider the rheological type EoS modifications in the standard Einstein theory of gravity.
One of the goals of the EoS modeling is connected with the problem of the neutron star compactness; to be more precise, the interest of astrophysicists is attracted to the mass/radius ratio, luminosity/radius ratio, etc. This interest was revived recently by the outstanding event encoded as GW170817 and GRB 170817A [31]: based on the observation of the binary neutron star merger, the status of constraints on the neutron star theory was renewed. The most sound consequence of this event is that the ratio of the velocities of the gravitational and electromagnetic waves is estimated to differ from one by the quantity about . In addition, the data processing has shown that, in order to recognize the start of the final stage of the merging of two neutron stars, i.e., to recognize the last moment when the stars can be identified as individual objects, one has to study in more detail the problem of the mass/radius ratio. In other words, the problem of the neutron star compactness remains important and significant for both observers and theoreticians. This is one of arguments, why below we consider the neutron star model with a new EoS of rheological type, and study the mass/radius ratio as the function of a new (rheological) parameter of state.
What is the novelty of our approach to the neutron star EoS modeling? We follow the Rheological Paradigm, according to which the response of the physical system on the external actions or on the internal evolutionary processes is nonlocal in space and/or in time. In particular, when the system is spatially homogeneous, the Rheological Paradigm recommends searching for the time delay of the response and memory effects; when the system is static, the response can appear far from the domain, in which the source of perturbation is located. In the context of modeling of the EoS for static spherically symmetric neutron stars, we assume, in fact, that the profile of the pressure , designed with respect to the radial variable r, is predetermined not only by the profiles of the particle number and temperature , but also by their directional derivatives.
What is the physical motivation of such a theory extension? Physics of complex media present us vivid examples of the so-called memory effects: one can distinguish, formally speaking, the fading memory and the shape memory of materials (see, e.g., [32,33], respectively). One deals with the fading memory, when one considers the evolutionary processes in media, and these effects demonstrate the presence of phenomena non-local in time. The shape memory effects are associated with spatially non-local phenomena. Clearly, one can see a symmetry in the temporal and spatial aspects of non-locality. Following the idea of this symmetry, we consider below the static generalization of rheologic type phenomena based on the similarity with the known dynamic rheologic phenomena.
Why we do believe that the idea of rheological type extension of the EoS can attract the attention of astrophysicists? There are at least three motives to think so. The first motive is that the rheological type self-interaction can make the profiles of the mass density and pressure steeper, i.e., for the same mass density at the center, for the same total mass and adiabatic index, the star radius can be smaller than the standard one. The second motive is connected with the idea to try to find new extrema in the profiles of the mass density and pressure; when the profiles are non-monotonic, one can speak about stratification and clusterization of the neutron star interior. The third motive is that the corresponding model becomes multi-parametric, the new parameters with the dimensionality of length acquire a natural explanation, thus simplifying the fitting of guiding parameters.
The paper is organized as follows. In Section 2, we recall the necessary elements of classical rheological approach and the idea of its generalization. In Section 3, we consider the formalism of extension of the rheological approach for the case of static spherically symmetric mass configuration. We apply the established formalism to the model of cold neutron condensate in Section 4. As an illustration, in SubSection 4.2, we consider the rheological type generalization of the known classical Lane–Emden model. Section 5 contains the discussion and the final section provides the conclusions.
2. Prologue: On the Rheological Type Extension of Time Dependent Constitutive Equations
In order to explain properly our approach to the theory of extended equations of state in the context of static neutron stars, we start with the analysis of the corresponding analogs given by the theory of spatially homogeneous systems admitting time delay of the response.
2.1. Classical Constitutive Equations in Rheology
The term Rheology was introduced by Bingham and Reiner in the 1920s; this branch of science studies various aspects of behavior of media possessing elasticity, viscosity and plasticity (see, e.g., [34,35]). Non-relativistic visco-elasticity started with the extension of the standard Hooke’s law
In the standard Hooke’s law is the stress tensor; describes the deformation tensor; the tensor includes 21 elastic moduli; Greek indices correspond to spatial values (say, in the Cartesian coordinates). The left-hand and right-hand sides are calculated at the same time t, thus the response of the medium was assumed to be instantaneous. When the medium is characterized by the delay of the response, one has to write this relationship for different moments of time, for instance, as:
where the parameter describes the time delay of the medium on the external action. If the processes develop rather slowly, one can present approximately the terms as ; for rapid processes, the decomposition is necessary, which include derivatives of the second, third, etc. orders. In the simplest case, we recover the extended constitutive equation
written by Maxwell [36] (here, the dot denotes the partial derivative with respect to time). The classical theory of thermo-visco-elasticity is well-elaborated and well-documented (see, e.g., [35,37,38]); we keep in mind the achievements in this sphere.
In the framework of relativistic physics Israel and Stewart have elaborated the model, indicated as Causal (Transient) Thermodynamics [39], which is based on the covariant extension of the Maxwell model of visco-elasticity, and uses the operator of convective derivative instead of time derivative . Here, Latin indices take values , and is the four-vector of macroscopic velocity of the medium. When the only scalar non-equilibrium pressure appears in the model (e.g., in the spatially isotropic medium), the constitutive equation for this quantity was presented in the following form:
Here, is the expansion scalar; is the bulk viscosity coefficient; is the relaxation parameter; and T is the medium temperature.
In the framework of relativistic cosmology, the rheological type extensions of the equations of state for the cosmic dark energy were used in the papers [40,41,42,43]; the corresponding link between the energy density and pressure P of the dark energy was chosen as follows:
The quantities and are the parameters of this linear model with the barotropic EoS.
2.2. Generalization of the Time Dependent EoS with Parametric Representation
The standard barotropic equations of state form a subclass of more general two-parameter class of EoS, which is characterized by the following relationships:
where and are given functions of two arguments, the particle number density n and temperature T. Using the non-relativistic concept of time delay, we assume that
In other words, the pressure at the time moment t is predetermined by the number density at the moment and by the temperature at the moment (generally, , since delay in particle migration and temperature transfer can be described by different laws). Similarly, the energy density at the time moment t is predetermined by the number density at the moment and by the temperature at the moment (generally, and ). For slow varying processes, the laws (7) give
3. The Formalism of the EoS Extension in the Framework of Static Models
3.1. The Standard Elements of the Model: Metric, Einstein Equations, and the Equation of Hydrostatic Equilibrium
In this subsection, we recover the well-known elements of the theory. We consider static spherically symmetric matter configurations, which are described by the metric
For the metric (10), only four Einstein’s equations are known to be non-trivial:
The prime denotes the derivative with respect to the radial variable r. Here, we introduced the energy density scalar W of the matter, longitudinal pressure and transversal pressure .
The direct consequence of (11) is the expression of through the integral of the function (when its profile is obtained):
where is usually associated with the mass inside the sphere of the radius r. The function can be formally found by integration of the equation
(when the profiles , and are known). As usual, instead of (13), we consider the consequence of the Bianchi identity , which in our context reads
Excluding the metric coefficients, we obtain the well-known standard equation of hydrostatic equilibrium:
In other words, (17) is the key equation of the problem. It will be solvable, when we add two equations of state, which connect and with W, directly in the scheme of barotropic equations of state, or in the parametric form as functions of the temperature and particle density .
3.2. Extended Equations of State for the Static Configurations
3.2.1. Convective and Directional Derivatives
The unit time-like velocity four-vector , which characterizes the medium motion, can be used as a tangent four-vector for reconstruction of the global reference frame with world-lines satisfying the equation . These world-lines form the system of time-like geodesics, when is normalized by unity and satisfies the requirements
The corresponding differential operator , the convective derivative, is widely used in relativistic theory of media, and the equation can be interpreted as the absence of acceleration in the medium velocity flow.
Analogously with the convective derivative, one can introduce the so-called directional derivative , where the unit space-like four-vector indicated as a director is defined as follows:
When we deal with the metric (10), the appropriate solutions for and are, respectively,
The scheme of generalization is very simple: we replace the convective derivatives with the directional ones.
3.2.2. Static Analogs of the Rheologically Extended Constitutive Equations
Now, we introduce the static spherically symmetric analogs of the rheological type equation of state. Our general ansatz is the following:
Here, ; the scalars , , , , , play the roles of specific correlation radii; they are the analogs of the relaxation parameters in the time dependent models. Clearly, when the pressure is isotropic, i.e., , we obtain only two extended equations.
4. The Model of Cold Isotropic Neutron Condensate
4.1. Extended Equation of Hydrostatic Equilibrium: The General Relativistic Model
Let us consider the model, in which the temperature is equal to zero, , the directional derivative of the temperature is vanishing, , and the pressure is of Pascal type, . For the standard model, the equation of state can be presented in the well-known one-parameter form (see, e.g., [5,6,44]):
The state parameter is assumed to be the function of the radial variable r. The critical value of the particle number density corresponds to the case, when the Fermi-momentum is equal to the quantity :
This parametrical representation of the EoS is known to be valid, when the energy density at the center, is less than a some critical value ; when , the neutron gas becomes instable and can be converted into the multi-component hadronic plasma (see, e.g., [4,6,7] for details).
Let us consider the extended model, based on the following assumption: , so that the energy density scalar is described by the same Equation (25). Then, keeping in mind the formula for directional derivative with (20), we can present the equation for the pressure in the following form
where the function is given by the Formula (24). In terms of the last equation can be written as follows:
Here, we introduce the function instead of . The equation of Hydrostatic Equilibrium (17) now takes the form
Thus, in order to find the profile we have to solve (30) into which we insert the function extracted from (29), the function given by (25) and the mass given by
obtained from (14). Then, we can extract from (30)
and exclude the integral by differentiation of (32). As a result, we obtain the equation
into which we have to insert given by (29). Clearly, it is the very sophisticated nonlinear differential equation of the third order for the quantity . This equation admits the numerical study only, and we optimistically hope to provide this analysis in a separate work. However, in order to demonstrate the capacities of the rheological type model under consideration, we complete our theoretical modeling by the study of the generalization of the classical Lane–Emden equation.
4.2. Rheological Type Generalization of the Non-Relativistic Lane–Emden Equation
In the context of study of the Fermi gas with , the term non-relativistic means that the Fermi-momentum is much less than the quantity , and, respectively, the particle number density is much less than the critical value:
Taking into account that in the non-relativistic limit, one can rewrite the Equation (32) in the quasi-Newtonian form:
where we have changed the function by the constant . Differentiation of this equation with respect to r gives the equation of the third order, which can be rewritten as the extended Lane–Emden equation with [5]
In this equation, we have introduced the generalized Lane–Emden function :
the dimensionless radial variable x:
and the dimensionless parameter :
4.2.1. Behavior of the Function near the Center
In terms of the generalized Lane–Emden function the function transforms into
thus providing the classical condition at the center, . We can now decompose the function in the vicinity of the center
and, to link the parameters , , , using the requirement that , which satisfies the equation (38), is regular at . In order to untwine the obtained coupled system, we consider the to be a small parameter, and put , the value, which corresponds to the Lane–Emden parameter for . Then, we obtain the reduced series of coupled relations:
Then, the leading order terms in the decomposition (43) form the function
Clearly, when , we recover the well-known Lane–Emden decomposition [5]. As for the conditions at the regular center, we obtain immediately from (45) that
When , the function has the maximum at , since and ; when the maximum disappears.
4.2.2. Behavior of the Pressure
In terms of the function the pressure P can be reconstructed, using (36) and (39)–(41), as follows:
where the convenient parameter is
Clearly, the pressure is regular at the center, since
As usual, the radius of the star, can be found as
where is the first null of the function . When , we have to analyze the equation , and obtain the value known from the Lane–Emden theory for the polytropic star with (see, e.g., [5]). When , the equation (see (47)) splits into two equations: and . The function is positive and is negative on the interval , thus there exists a new branch of solutions, when , and this new branch does not appear, when . For the case , the radius of the star decreases in comparison with the Lane–Emden value (see Figure 1).
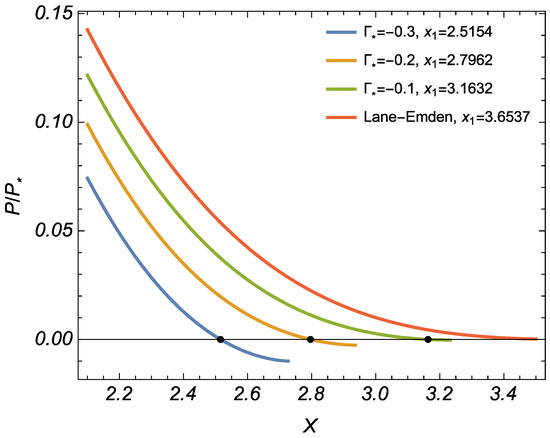
Figure 1.
Plot of the function in the domain of the first nulls; this plot depicts the profiles of the reduced pressure as the function of the dimensionless rheological parameter . For negative , the radius of the star, predetermined by the condition , becomes smaller than the radius predicted by the Lane–Emden theory; for positive there are no roots of the function .
4.2.3. The Mass/Radius Ratio
The total mass of the star can be obtained from (37) at . If we use the relation (40) for , extract the value from this equation, and then put it into (37), we obtain the so-called mass/radius ratio:
The Lane–Emden ratio coincides with (51), when . The values are visualized in the Table 1 for several values of the guiding parameter .

Table 1.
The value relates to the first zero of the function ; it determines the radius of the object and depends on the value of the guiding parameter . The function enters the mass/radius ratio (51). The case corresponds to the Lane–Emden model. For the fixed mass , the radius of the object, , decreases, if the modulus of the guiding parameter, , grows.
5. Conclusions
The main goal of this work is to establish the formalism of rheological type extension of the theory, which describes the interior of the static spherically symmetric relativistic compact objects. The key element of this extended model is formed by the rheologically generalized equations of state. For general cases, when the pressure tensor has a non-Pascal structure, the corresponding equations of state are obtained to be of the form (21)–(23). The extended equation of state for the neutron condensate with the Pascal type pressure is simplified to look like (28). When we deal with the extension of the non-relativistic Lane–Emden model, the modified EoS is presented by (47) with found from (38). In our model, the Equation of Hydrostatic Equilibrium has formally speaking the standard form (17); however, it converts into the sophisticated nonlinear differential equation of the third order, when we use the rheologically extended equations of state (see (33)).
In order to visualize analytically the capacities of the presented new model, we have considered the rheological type extension of the well-known Lane–Emden theory (see Subsection IVB). This extended model contains one dimensionless guiding parameter . The profiles of the pressure as the function of radial variable and of this guiding parameter demonstrate the following interesting features. First of all, the presence of the parameter allows the object to be extra-compact. Indeed, when is negative, the first null of the pressure profile, which gives the radius of the object , appears at the value of the radial variable less than for classical Lane–Emden prediction (see Figure 1). For positive , there are no new nulls of the equation . This fact can be interpreted as follows. Contrarily to the time delay in dynamic systems, for which the response appears later than the external impact took place, the rheological type “response” of the static system is localized closer to the center, in which the variation of the mass density occurred. The second interesting feature is that, when the total mass of the object is fixed, and the modulus of the guiding parameter, , increases, the radius of the neutron star becomes smaller (see (51) and Table 1). The third interesting feature is that the mass density and pressure profiles become non-monotonic. Indeed, according to the decomposition (45), valid near the center for small , there is the maximum at characterized by the value , which appears in the profile of , if the guiding parameter is negative. When , the maximum is placed at the center , so that the profile of remains monotonic for . The profile of the pressure behaves similarly. We emphasize once again that these features appear, since in the rheological type equation of state the pressure depends not only on the mass density, but also on the derivative of this quantity.
For the relativistic model with a strong gravitational field, arbitrary rheological parameter , and with the pressure expressed in terms of using (29), the Equation of Hydrostatic Equilibrium (33) supplemented by (25) becomes a nonlinear differential equation of the third order for the auxiliary function . In the classical theory of the neutron stars, when , the corresponding differential equation is of the second order. Thus, in the rheologic type model, we are faced with much more sophisticated mathematical problem, which guarantees the presence of new solutions, and probably, a number of surprises. In the near future, we hope to fulfil full-format numerical simulations for the nonlinear differential equation of the third order (33). We hope that in the full-format version of the model the extrema of the profiles , , will be found, thus describing the clusterization of the neutron star interior and modification of the mass/radius ratio. We also intend to consider the generalization of the nuclear EoS taking into account the rheological terms in (21)–(23). We are hoping that this work will bring us many new interesting results.
Author Contributions
Conceptualization, A.B.; methodology, A.B.; software, A.I. and A.K.; formal analysis, A.I. and A.K.; investigation, A.B.; writing—original draft preparation, A.B.; writing—review and editing, A.K. and L.G.
Funding
The research was funded by Committee on Science Ministry of Education and Science of the Republic of Armenia, grant number 18T-1C355.
Acknowledgments
The work was partially supported by the Program of Competitive Growth of Kazan Federal University and the grant 18T-1C355 of the Committee on Science Ministry of Education and Science of the Republic of Armenia.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Lyne, A.; Graham-Smith, F. Pulsar Astronomy; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Becker, W. Neutron Stars and Pulsars; Springer Science and Business Media: Berlin, Germany, 2009. [Google Scholar]
- Compact Stars: Nuclear Physics, Particle Physics and General Relativity; Springer Science and Business Media: Berlin, Germany, 2012.
- Sahakian, G.S. Physics of Neutron Stars; JINR: Dubna, Russia, 1995. (In Russian) [Google Scholar]
- Weinberg, S. Gravitation and Cosmology; Wiley and Sons: New York, NY, USA, 1972. [Google Scholar]
- Sahakian, G.S. Equilibrium Configurations of Degenerate Gaseous Masses; Israel Program for Scientific Translations, Jerusalem; Halsted (Wiley): New York, NY, USA, 1974. [Google Scholar]
- Grigoryan, L.S.; Sahakian, G.S. Theory of superdense matter and degenerate stellar configurations. Astrophys. Space Sci. 1983, 95, 305–356. [Google Scholar] [CrossRef]
- Sahu, P.K. Nuclear equation of state at high density and the properties of neutron stars. Phys. Rev. C 2000, 62, 045801. [Google Scholar] [CrossRef]
- Baldo, M.; Burgio, F. Microscopic Theory of the Nuclear Equation of State and Neutron Star Structure. Lect. Notes Phys. 2001, 578, 1–29. [Google Scholar]
- Shen, H. Complete relativistic equation of state for neutron stars. Phys. Rev. C 2002, 65, 035802. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.Y. Analytical representations of unified equations of state of neutron-star matter. Astron. Astrophys. 2004, 428, 191–197. [Google Scholar] [CrossRef]
- Ryu, C.Y.; Hyun, C.H.; Hong, S.W.; Kim, B.T. Kaon condensation and composition of neutron star matter in modified quark-meson coupling model. Phys. Rev. 2007, 75, 055804. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. Neutron Stars 1: Equation of State and Structure; Springer Science and Business Media: Berlin, Germany, 2007. [Google Scholar]
- Lattimer, J.M.; Prakash, M. Neutron Star Observations: Prognosis for Equation of State Constraints. Phys. Rept. 2007, 442, 109–165. [Google Scholar] [CrossRef]
- Blaschke, D.; Berdermann, J.; Lastowiecki, R. Hybrid neutron stars based on a modified PNJL model. Prog. Theor. Phys. Suppl. 2010, 186, 81–86. [Google Scholar] [CrossRef]
- Niu, Z.-M.; Gao, C.-Y. δ-meson effects on neutron stars in the modified quark-meson coupling model. Int. J. Mod. Phys. E 2010, 19, 2247–2263. [Google Scholar] [CrossRef]
- Miyatsu, T.; Cheoun, M.-K.; Saito, K. Equation of state for neutron stars in SU(3) flavor symmetry. Phys. Rev. C 2013, 88, 015802. [Google Scholar] [CrossRef]
- Nättilä, J.; Steiner, A.W.; Kajava, J.J.E.; Suleimanov, V.F.; Poutanen, J. Equation of state constraints for the cold dense matter inside neutron stars using the cooling tail method. Astron. Astrophys. 2016, 591, A25. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. The equation of state of hot, dense matter and neutron stars. Phys. Rep. 2016, 621, 127–164. [Google Scholar] [CrossRef]
- Lindblom, L. Causal representations of neutron-star equations of state. Phys. Rev. D 2018, 97, 123019. [Google Scholar] [CrossRef]
- Degenaar, N.; Suleimanov, V.F. Testing the equation of state of neutron stars with electromagnetic observations. arXiv, 2018; arXiv:1806.02833. [Google Scholar]
- Eling, C.; Jacobson, T.; Miller, M.C. Neutron stars in Einstein–aether theory. Phys. Rev. D 2009, 76, 042003. [Google Scholar] [CrossRef]
- Cooney, A.; DeDeo, S.; Psaltis, D. Neutron Stars in f(R) Gravity with Perturbative Constraints. Phys. Rev. D 2010, 82, 064033. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D. Maximal neutron star mass and the resolution of hyperon puzzle in modified gravity. Phys. Rev. D 2014, 89, 103509. [Google Scholar] [CrossRef]
- Cisterna, A.; Delsate, T.; Rinaldi, M. Neutron stars in general second order scalar-tensor theory: The case of non-minimal derivative coupling. Phys. Rev. D 2015, 92, 044050. [Google Scholar] [CrossRef]
- Doneva, D.D.; Yazadjiev, S.S.; Kokkotas, K.D. The I-Q relations for rapidly rotating neutron stars in f(R) gravity. Phys. Rev. D 2015, 92, 064015. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Farinelli, R.; Odintsov, S.D. The Mass-Radius relation for Neutron Stars in f(R) gravity. Phys. Rev. D 2016, 93, 023501. [Google Scholar] [CrossRef]
- Resco, M.A.; de la Cruz-Dombriz, A.; Llanes-Estrada, F.J.; Castrillo, V.Z. On neutron stars in f(R) theories: Small radii, large masses and large energy emitted in a merger. Phys. Dark Universe 2016, 13, 147–161. [Google Scholar] [CrossRef]
- Hendi, S.H.; Bordbar, G.H.; Eslam Panah, B.; Panahiyan, S. Modified TOV in gravity’s rainbow: Properties of neutron stars and dynamical stability conditions. J. Cosmol. Astropart. Phys. 2016, 09, 013. [Google Scholar] [CrossRef]
- Brax, P.; Davis, A.-C.; Jha, R. Neutron Stars in Screened Modified Gravity: Chameleon vs Dilaton. Phys. Rev. D 2017, 95, 083514. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. APJ Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Day, W.A. The Thermodynamics of Simple Materials with Fading Memory; Springer Tracts in Natural Philosophy; Springer: Berlin/Heidelberg, Germany, 1972; Volume 22. [Google Scholar]
- Otsuka, K.; Wayman, C.M. Shape Memory Materials; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Reiner, M. Advanced Rheology; H.K. Lewis and Co., Ltd.: London, UK, 1971. [Google Scholar]
- Rabotnov, Y.N. Elements of Hereditary Solid Mechanics; Mir Publishers: Moscow, Russia, 1980. [Google Scholar]
- Maxwell, J.C. On the dynamical theory of gases. Philos. Trans. R. Soc. Lond. 1867, 157, 49–88. [Google Scholar]
- Jou, D.; Casas-Vázquez, J.; Lebon, G. Extended Irreversible Thermodynamics; Springer: Berlin, Germany, 1996. [Google Scholar]
- Maugin, G.A. The Thermomechanics of Nonlinear Irreversible Behaviors. An Introduction; World Scientific: Singapore, 1999. [Google Scholar]
- Israel, W.; Stewart, J.M. Transient relativistic thermodynamics and kinetic theory. Ann. Phys. 1979, 118, 341–372. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. The new form of the equation of state for dark energy fluid and accelerating universe. Phys. Lett. B 2006, 639, 144–150. [Google Scholar] [CrossRef]
- Balakin, A.B.; Bochkarev, V.V. Archimedean-type force in a cosmic dark fluid. I. Exact solutions for the late-time accelerated expansion. Phys. Rev. D 2011, 83, 024035. [Google Scholar] [CrossRef]
- Balakin, A.B.; Bochkarev, V.V. Archimedean-type force in a cosmic dark fluid. II. Qualitative and numerical study of a multistage universe expansion. Phys. Rev. D 2011, 83, 024036. [Google Scholar] [CrossRef]
- Balakin, A.B.; Bochkarev, V.V. Archimedean-type force in a cosmic dark fluid. III. Big Rip, Little Rip and Cyclic solutions. Phys. Rev. D 2013, 87, 024006. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On massive neutron cores. Phys. Rev. 1939, 55, 374. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).