Analysis of the Digital Divide Using Fuzzy Forecasting
Abstract
:1. Introduction
2. Literature Review
3. Materials and Methods
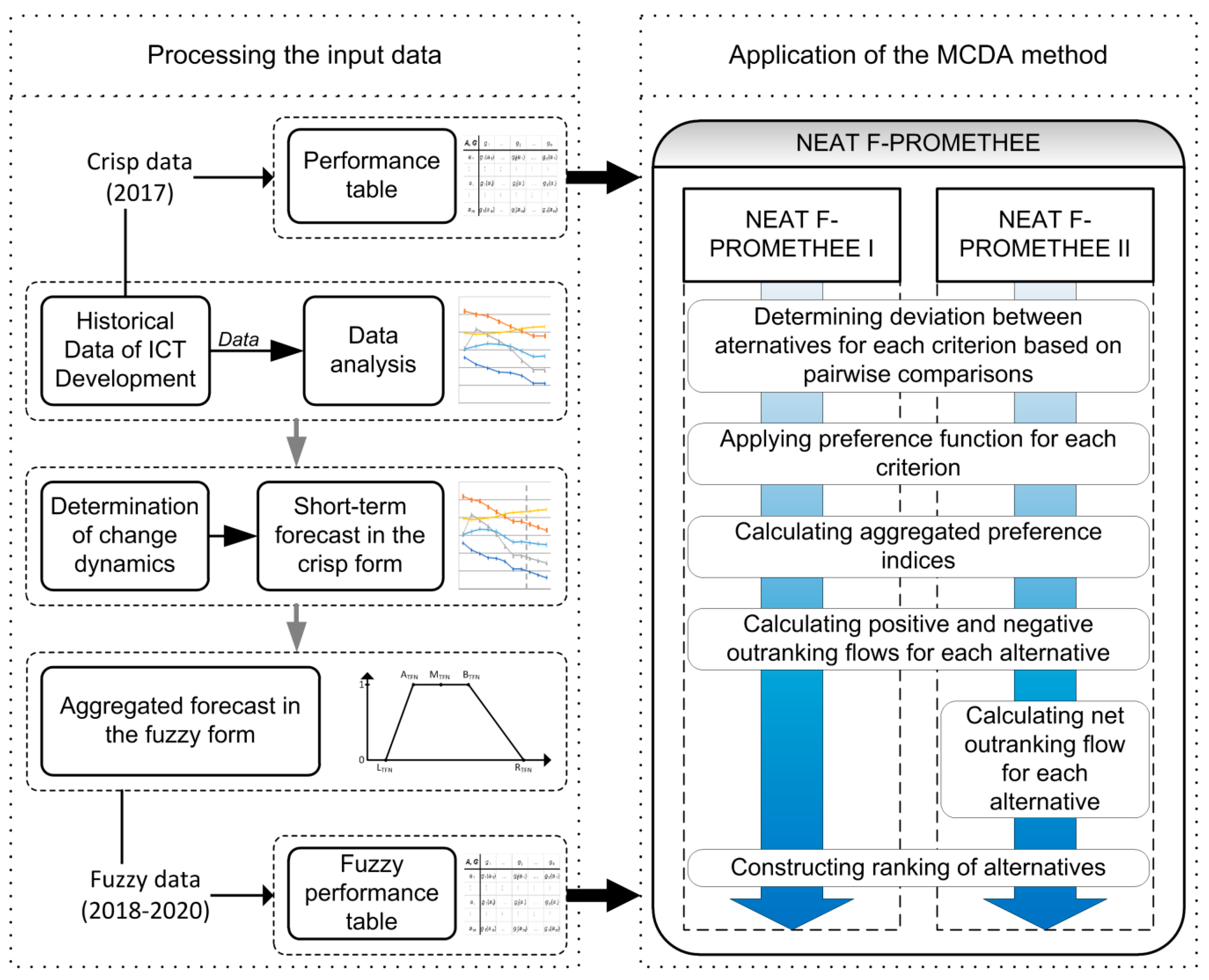
3.1. Methodological Framework
- obtaining partial historical data on the level of regional ICT development,
- defining the current level of ICT development in the countries studied,
- generating forecasts for individual ICT development indicators,
- blurring these forecasts,
- calculating the aggregate ICT development forecast for each of the countries studied.
3.2. Processing of Input Data
3.2.1. Data Sources
- Access indicators (ICT access, ):
- ○
- Fixed-telephone subscriptions per 100 inhabitants (FTL, ),
- ○
- Mobile-cellular subscriptions per 100 inhabitants (MCS, ),
- ○
- International Internet bandwidth Bit/s per Internet user (IIB, ),
- ○
- Percentage of households with computer (PHC, ),
- ○
- Percentage of households with Internet (PHI, ).
- Use indicators (ICT use, ):
- ○
- Percentage of individuals using the Internet (IU, ),
- ○
- Fixed-broadband subscriptions per 100 inhabitants (FBB, ),
- ○
- Active mobile-broadband subscriptions per 100 inhabitants (MBB, ).
- Skills indicators (ICT skills, ):
- ○
- Secondary gross enrolment ratio (SGE, ),
- ○
- Tertiary gross enrolment ratio (TGE, ),
- ○
- Mean years of schooling (MYS, ), which was introduced to ICT development index in 2014 (until 2013, Adult literacy rate—ALR was used). Therefore, the forecast for the MYS indicator was made on the basis of four-year data (2014–2017).
3.2.2. Chain Indices
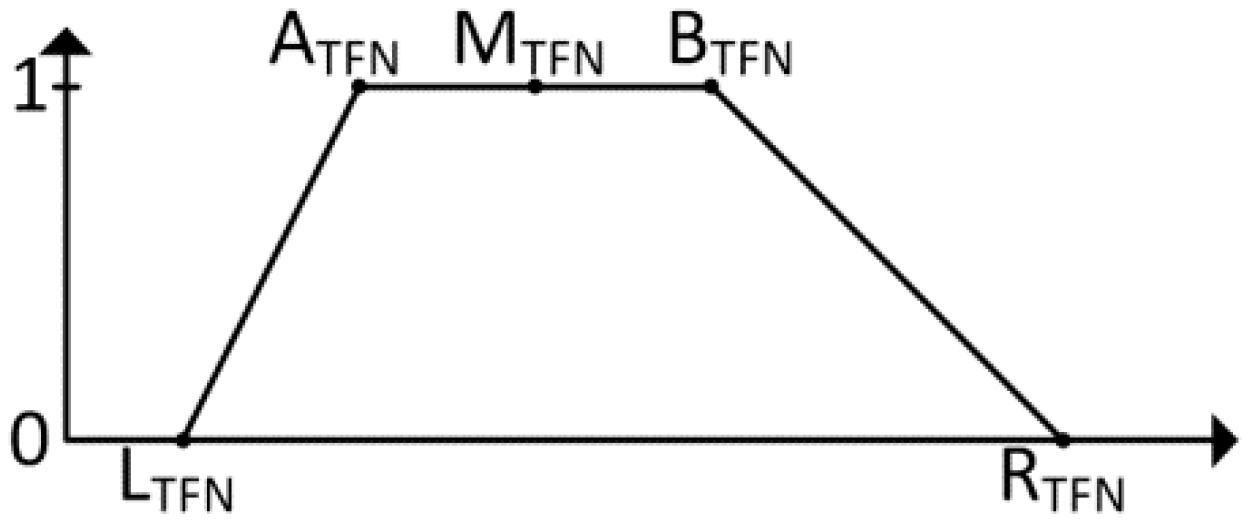
3.2.3. Generating Fuzzy Numbers
3.3. NEAT F-PROMETHEE Method
- determination of fuzzy deviation between the alternatives for individual criteria and pairwise comparisons,
- application of the preference function for each criterion,
- calculation of aggregate preference indices,
- calculation of positive and negative out ranking flows for each alternative,
- calculation of net outranking flow for each alternative (only NEAT F-PROMETHEE II),
- construction of the ranking of alternatives.
- the preference of alternative over takes place when and , while at least one of the inequalities must be strong,
- indifference between alternatives occurs when and ,
- incomparability between alternatives takes place when and , or when and .
- the alternative preference of over takes place when ,
- indifference between alternatives occurs when .
4. Results
4.1. Processing of Input Data
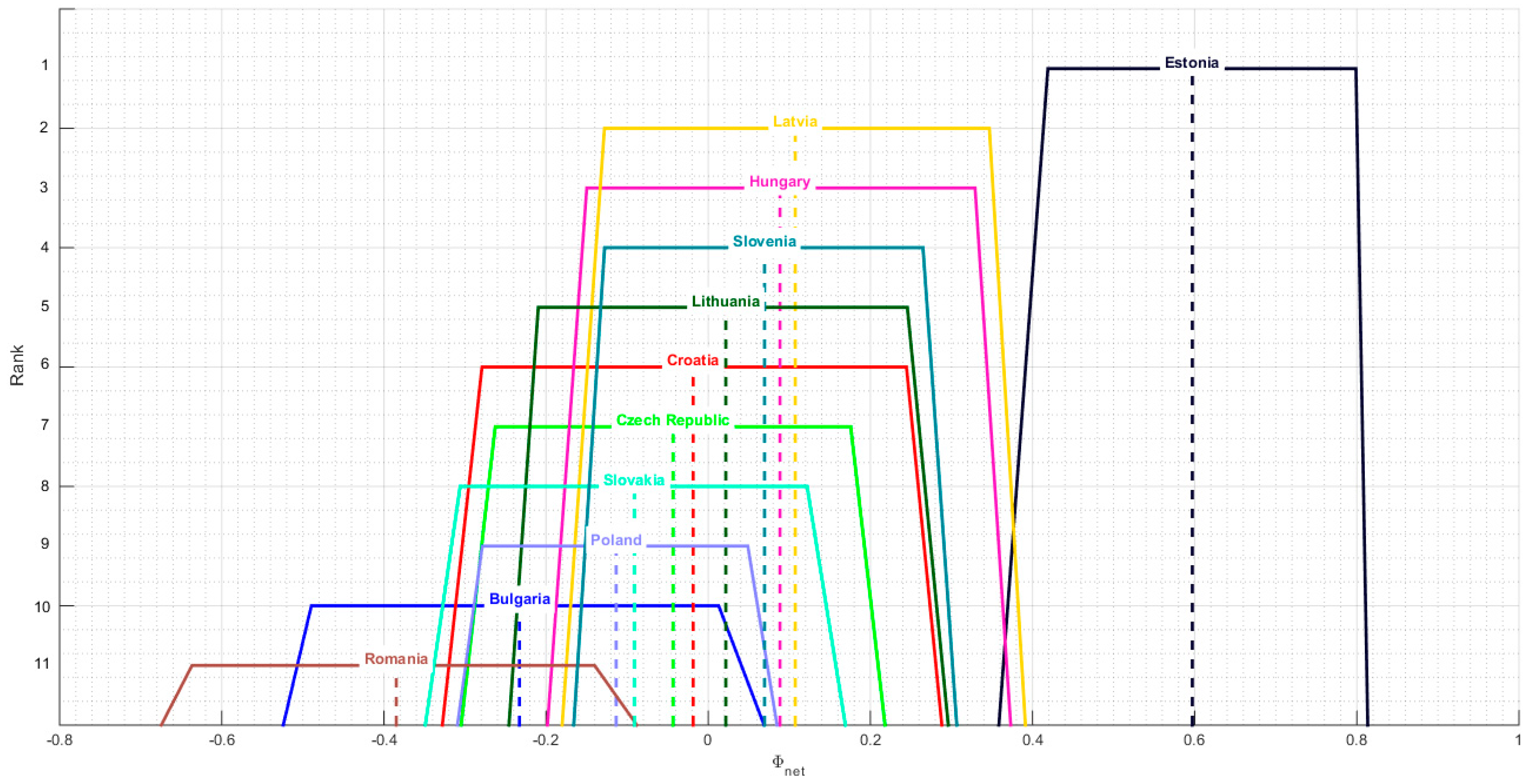
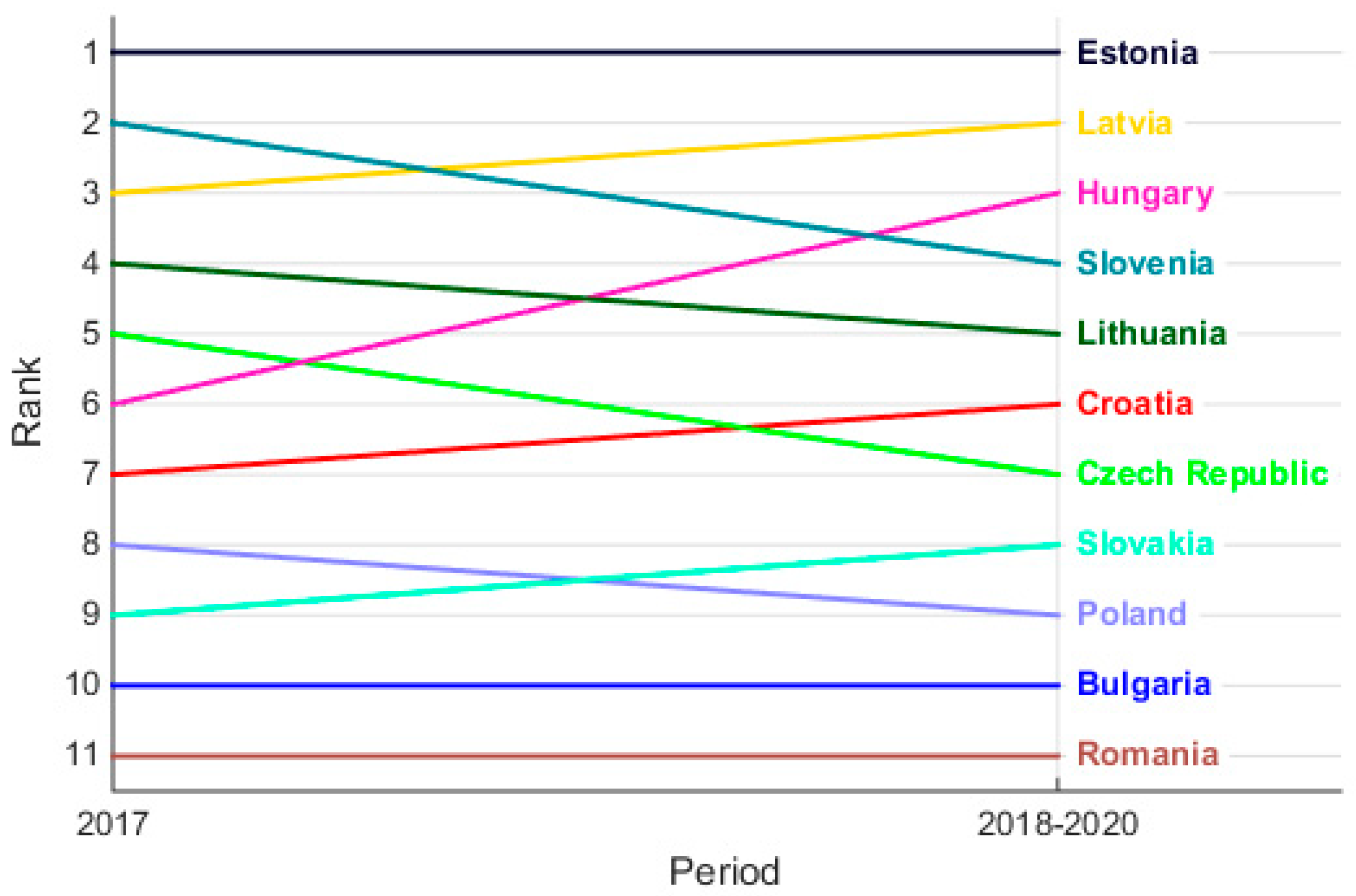
4.2. Evaluation and Forecast of Regional ICT Development Using the NEAT F-PROMETHEE Method
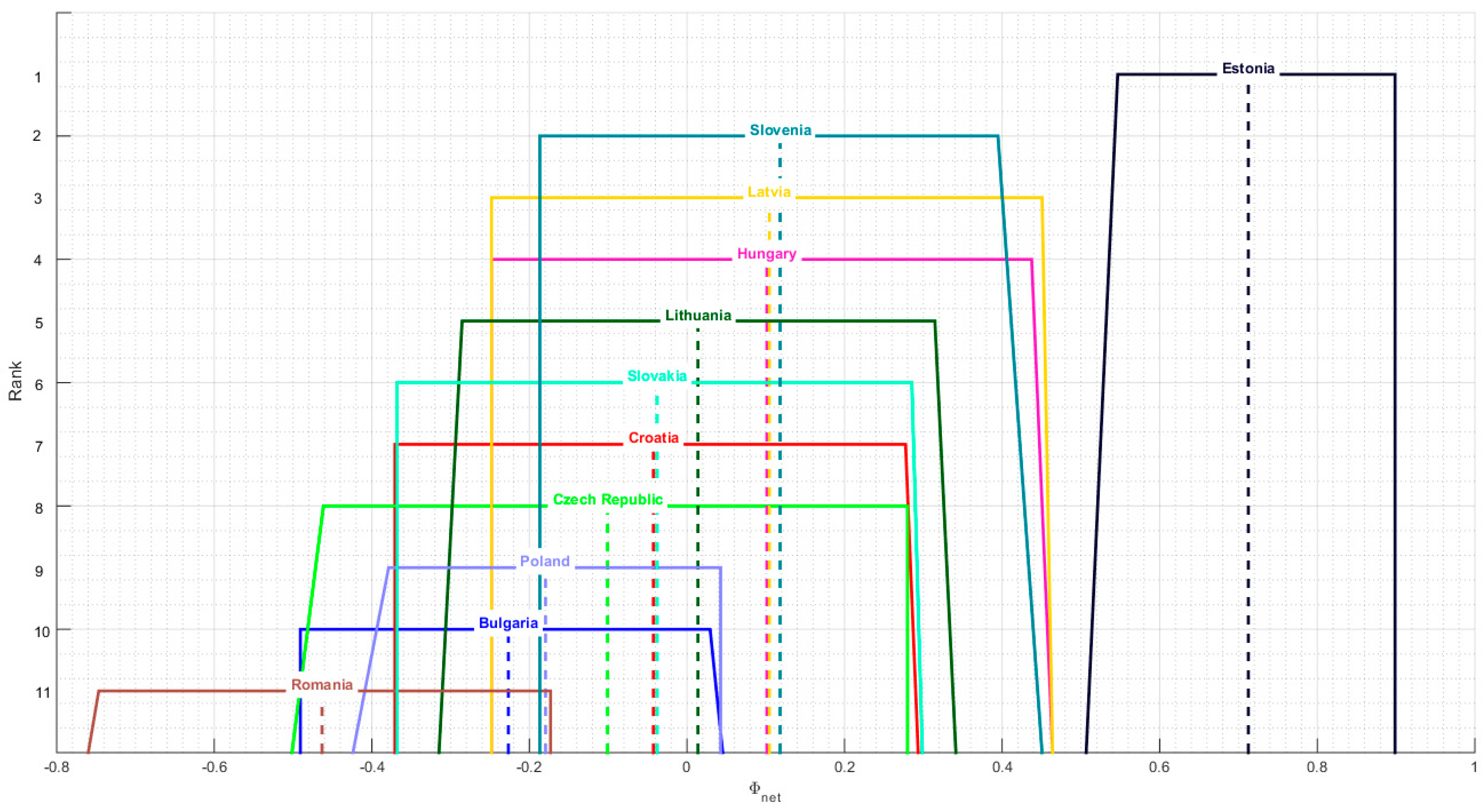
4.3. Testing the Resilience of Rankings to Changes in the Degree of Uncertainty of Preferences
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Values of Indicators in 2010–2017
| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | 136.1 | 140.7 | 148.1 | 145.2 | 132.4 | 129.3 | 127.2 | 127.2 |
| Croatia | 111.9 | 116.4 | 115.4 | 114.5 | 104.4 | 103.8 | 104.1 | 104.1 |
| Czech Republic | 121.7 | 121.6 | 126.8 | 131.3 | 129.5 | 115.6 | 115.5 | 115.5 |
| Estonia | 123.2 | 139.0 | 160.4 | 159.7 | 160.7 | 148.7 | 148.7 | 148.7 |
| Hungary | 120.3 | 117.3 | 116.1 | 116.4 | 118.1 | 118.9 | 119.1 | 119.1 |
| Latvia | 102.4 | 102.9 | 112.1 | 136.6 | 116.8 | 127.5 | 131.2 | 131.2 |
| Lithuania | 147.2 | 151.3 | 165.1 | 151.3 | 141.9 | 139.5 | 140.7 | 140.7 |
| Poland | 122.7 | 128.5 | 141.5 | 150.0 | 148.9 | 142.7 | 146.2 | 146.2 |
| Romania | 113.6 | 109.2 | 105.0 | 105.6 | 105.9 | 107.1 | 106.4 | 106.4 |
| Slovakia | 108.5 | 109.3 | 111.9 | 113.9 | 116.9 | 122.3 | 128.0 | 128.0 |
| Slovenia | 104.5 | 106.6 | 108.4 | 110.2 | 112.1 | 113.2 | 114.6 | 114.6 |
| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | 136.1 | 140.7 | 148.1 | 145.2 | 132.4 | 129.3 | 127.2 | 127.2 |
| Croatia | 111.9 | 116.4 | 115.4 | 114.5 | 104.4 | 103.8 | 104.1 | 104.1 |
| Czech Republic | 121.7 | 121.6 | 126.8 | 131.3 | 129.5 | 115.6 | 115.5 | 115.5 |
| Estonia | 123.2 | 139.0 | 160.4 | 159.7 | 160.7 | 148.7 | 148.7 | 148.7 |
| Hungary | 120.3 | 117.3 | 116.1 | 116.4 | 118.1 | 118.9 | 119.1 | 119.1 |
| Latvia | 102.4 | 102.9 | 112.1 | 136.6 | 116.8 | 127.5 | 131.2 | 131.2 |
| Lithuania | 147.2 | 151.3 | 165.1 | 151.3 | 141.9 | 139.5 | 140.7 | 140.7 |
| Poland | 122.7 | 128.5 | 141.5 | 150.0 | 148.9 | 142.7 | 146.2 | 146.2 |
| Romania | 113.6 | 109.2 | 105.0 | 105.6 | 105.9 | 107.1 | 106.4 | 106.4 |
| Slovakia | 108.5 | 109.3 | 111.9 | 113.9 | 116.9 | 122.3 | 128.0 | 128.0 |
| Slovenia | 104.5 | 106.6 | 108.4 | 110.2 | 112.1 | 113.2 | 114.6 | 114.6 |
| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | 35.1 | 38.0 | 52.3 | 54.9 | 57.9 | 59.0 | 60.2 | 60.2 |
| Croatia | 60.0 | 64.0 | 68.0 | 66.3 | 70.1 | 76.8 | 79.5 | 79.5 |
| Czech Republic | 64.1 | 69.0 | 67.3 | 73.9 | 78.5 | 73.1 | 75.6 | 75.6 |
| Estonia | 69.2 | 75.3 | 75.5 | 80.0 | 82.5 | 87.9 | 89.6 | 89.6 |
| Hungary | 66.4 | 71.8 | 71.4 | 73.1 | 74.0 | 75.0 | 76.4 | 76.4 |
| Latvia | 62.8 | 64.5 | 69.5 | 71.7 | 73.5 | 76.1 | 78.0 | 78.0 |
| Lithuania | 59.2 | 63.1 | 63.6 | 65.9 | 66.8 | 67.6 | 70.5 | 70.5 |
| Poland | 69.0 | 73.0 | 73.4 | 74.7 | 77.7 | 77.9 | 80.1 | 80.1 |
| Romania | 47.9 | 52.9 | 56.7 | 61.2 | 63.8 | 68.7 | 74.0 | 74.0 |
| Slovakia | 72.2 | 79.4 | 78.8 | 80.1 | 80.5 | 80.5 | 80.9 | 81.0 |
| Slovenia | 70.5 | 75.1 | 76.1 | 76.4 | 77.1 | 77.8 | 78.1 | 78.1 |
| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | 33.1 | 45.0 | 50.9 | 53.7 | 56.7 | 59.1 | 63.5 | 63.5 |
| Croatia | 56.5 | 61.4 | 66.4 | 64.6 | 68.4 | 76.7 | 77.2 | 77.3 |
| Czech Republic | 60.5 | 66.6 | 65.4 | 72.6 | 78.0 | 73.1 | 76.1 | 76.1 |
| Estonia | 67.8 | 70.8 | 75.0 | 80.3 | 82.9 | 87.7 | 86.2 | 86.2 |
| Hungary | 60.5 | 65.2 | 68.6 | 71.5 | 75.1 | 75.6 | 78.6 | 78.6 |
| Latvia | 59.8 | 63.6 | 68.7 | 71.6 | 73.4 | 76.0 | 77.3 | 77.3 |
| Lithuania | 60.6 | 61.8 | 61.6 | 64.7 | 66.0 | 68.3 | 71.7 | 71.8 |
| Poland | 63.4 | 66.6 | 70.5 | 71.9 | 74.8 | 75.8 | 80.4 | 80.5 |
| Romania | 42.2 | 47.4 | 53.8 | 58.1 | 60.5 | 67.7 | 72.4 | 72.4 |
| Slovakia | 67.5 | 70.8 | 75.4 | 77.9 | 78.4 | 79.5 | 80.5 | 80.5 |
| Slovenia | 68.1 | 72.6 | 73.9 | 75.6 | 76.8 | 77.6 | 78.4 | 78.4 |
| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | 46.2 | 51.0 | 51.9 | 53.1 | 55.5 | 56.7 | 59.8 | 59.8 |
| Croatia | 60.3 | 70.7 | 61.9 | 66.7 | 68.6 | 69.8 | 72.7 | 72.7 |
| Czech Republic | 68.8 | 73.0 | 73.4 | 74.1 | 79.7 | 75.7 | 76.5 | 76.5 |
| Estonia | 74.1 | 76.5 | 78.4 | 80.0 | 84.2 | 88.4 | 87.2 | 87.2 |
| Hungary | 53.0 | 59.0 | 70.6 | 72.6 | 76.1 | 72.8 | 79.3 | 79.3 |
| Latvia | 68.4 | 71.7 | 73.1 | 75.2 | 75.8 | 79.2 | 79.9 | 79.9 |
| Lithuania | 62.1 | 65.1 | 67.2 | 68.5 | 72.1 | 71.4 | 74.4 | 74.4 |
| Poland | 62.3 | 64.9 | 62.3 | 62.8 | 66.6 | 68.0 | 73.3 | 73.3 |
| Romania | 39.9 | 44.0 | 45.9 | 49.8 | 54.1 | 55.8 | 59.5 | 59.5 |
| Slovakia | 75.7 | 74.4 | 76.7 | 77.9 | 80.0 | 77.6 | 80.5 | 80.5 |
| Slovenia | 70.0 | 72.0 | 68.3 | 72.7 | 71.6 | 73.1 | 75.5 | 75.5 |
| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | 14.5 | 15.5 | 17.9 | 19.0 | 20.7 | 22.7 | 23.3 | 23.3 |
| Croatia | 18.3 | 19.5 | 20.7 | 21.5 | 23.0 | 23.2 | 24.6 | 24.6 |
| Czech Republic | 14.5 | 15.7 | 16.4 | 17.0 | 27.9 | 27.3 | 27.7 | 27.7 |
| Estonia | 25.1 | 27.1 | 25.5 | 26.5 | 28.9 | 30.0 | 31.1 | 31.1 |
| Hungary | 20.6 | 22.2 | 22.9 | 24.1 | 26.0 | 27.4 | 28.5 | 28.5 |
| Latvia | 19.3 | 20.4 | 23.3 | 24.7 | 24.7 | 24.8 | 25.6 | 25.6 |
| Lithuania | 20.6 | 22.1 | 21.1 | 22.0 | 26.7 | 27.8 | 28.7 | 28.7 |
| Poland | 13.0 | 14.4 | 15.6 | 15.6 | 18.9 | 19.0 | 19.2 | 19.2 |
| Romania | 14.0 | 15.4 | 16.1 | 17.3 | 18.6 | 19.8 | 20.7 | 20.7 |
| Slovakia | 12.7 | 13.6 | 14.7 | 15.5 | 21.8 | 23.3 | 24.5 | 24.5 |
| Slovenia | 23.7 | 24.8 | 24.3 | 25.0 | 26.8 | 27.4 | 28.3 | 28.3 |
| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | 8.0 | 14.5 | 48.5 | 58.6 | 66.4 | 81.3 | 88.4 | 88.4 |
| Croatia | 7.5 | 6.6 | 53.9 | 66.1 | 68.5 | 73.1 | 79.7 | 79.7 |
| Czech Republic | 34.1 | 43.1 | 52.1 | 54.4 | 66.7 | 72.0 | 76.0 | 76.0 |
| Estonia | 24.0 | 42.0 | 76.9 | 78.9 | 117.0 | 112.9 | 125.0 | 125.0 |
| Hungary | 7.8 | 13.2 | 24.2 | 27.5 | 34.0 | 39.8 | 44.5 | 44.5 |
| Latvia | 27.5 | 37.6 | 58.2 | 61.2 | 61.2 | 67.0 | 77.0 | 77.0 |
| Lithuania | 14.2 | 17.2 | 41.4 | 53.8 | 70.2 | 67.6 | 76.8 | 76.8 |
| Poland | 50.0 | 48.4 | 63.6 | 59.5 | 55.7 | 57.4 | 58.9 | 58.9 |
| Romania | 10.7 | 14.1 | 27.0 | 37.7 | 49.3 | 63.7 | 73.7 | 73.7 |
| Slovakia | 20.7 | 31.9 | 39.7 | 54.9 | 59.5 | 67.5 | 78.7 | 78.7 |
| Slovenia | 24.4 | 29.3 | 36.7 | 42.1 | 46.7 | 52.0 | 62.3 | 62.3 |
| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | 88.0 | 88.0 | 93.1 | 93.1 | 100.9 | 100.9 | 99.0 | 99.0 |
| Croatia | 95.3 | 95.3 | 98.4 | 98.4 | 98.4 | 98.4 | 99.0 | 99.0 |
| Czech Republic | 90.4 | 90.4 | 96.6 | 96.6 | 104.4 | 104.4 | 105.1 | 105.1 |
| Estonia | 103.6 | 103.6 | 107.1 | 107.1 | 108.6 | 108.6 | 115.2 | 115.2 |
| Hungary | 98.3 | 98.3 | 101.6 | 101.6 | 108.2 | 108.2 | 105.2 | 105.2 |
| Latvia | 95.2 | 95.2 | 97.7 | 97.7 | 110.5 | 110.5 | 115.4 | 115.4 |
| Lithuania | 98.0 | 98.0 | 105.9 | 105.9 | 105.4 | 105.4 | 106.8 | 106.8 |
| Poland | 97.0 | 97.0 | 97.7 | 97.7 | 108.7 | 108.7 | 108.7 | 108.7 |
| Romania | 95.1 | 95.1 | 95.0 | 95.0 | 97.9 | 97.9 | 92.3 | 92.3 |
| Slovakia | 89.4 | 89.4 | 93.9 | 93.9 | 91.8 | 91.8 | 91.9 | 91.9 |
| Slovenia | 97.1 | 97.1 | 97.6 | 97.6 | 110.9 | 110.9 | 110.7 | 110.7 |
| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | 53.0 | 53.0 | 62.7 | 62.7 | 70.8 | 70.8 | 73.9 | 73.9 |
| Croatia | 49.2 | 49.2 | 61.6 | 61.6 | 61.6 | 61.6 | 69.5 | 69.5 |
| Czech Republic | 60.7 | 60.7 | 64.2 | 64.2 | 65.4 | 65.4 | 66.0 | 66.0 |
| Estonia | 62.7 | 62.7 | 76.7 | 76.7 | 72.9 | 72.9 | 69.6 | 69.6 |
| Hungary | 61.7 | 61.7 | 59.6 | 59.6 | 57.0 | 57.0 | 50.9 | 50.9 |
| Latvia | 60.1 | 60.1 | 65.1 | 65.1 | 67.0 | 67.0 | 67.0 | 67.0 |
| Lithuania | 77.4 | 77.4 | 73.9 | 73.9 | 72.0 | 72.0 | 68.5 | 68.5 |
| Poland | 70.5 | 70.5 | 73.2 | 73.2 | 71.2 | 71.2 | 71.2 | 71.2 |
| Romania | 63.8 | 63.8 | 51.6 | 51.6 | 52.2 | 52.2 | 53.2 | 53.2 |
| Slovakia | 54.2 | 54.2 | 55.1 | 55.1 | 54.4 | 54.4 | 52.9 | 52.9 |
| Slovenia | 86.9 | 86.9 | 86.0 | 86.0 | 85.2 | 85.2 | 82.9 | 82.9 |
| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | - | - | - | - | 10.6 | 10.6 | 10.8 | 10.8 |
| Croatia | - | - | - | - | 11.0 | 11.0 | 11.2 | 11.2 |
| Czech Republic | - | - | - | - | 12.3 | 12.3 | 12.3 | 12.3 |
| Estonia | - | - | - | - | 12.5 | 12.5 | 12.5 | 12.5 |
| Hungary | - | - | - | - | 11.6 | 11.6 | 12.0 | 12.0 |
| Latvia | - | - | - | - | 11.5 | 11.5 | 11.7 | 11.7 |
| Lithuania | - | - | - | - | 12.7 | 12.7 | 12.7 | 12.7 |
| Poland | - | - | - | - | 11.9 | 11.9 | 11.9 | 11.9 |
| Romania | - | - | - | - | 10.6 | 10.6 | 10.8 | 10.8 |
| Slovakia | - | - | - | - | 12.1 | 12.1 | 12.2 | 12.2 |
| Slovenia | - | - | - | - | 12.1 | 12.1 | 12.1 | 12.1 |
Appendix B. Change Dynamics in 2011–2017 and Forecast of Indicators in 2018–2020
| Country | Change Dynamics in 2011–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | 1.03 | 1.05 | 0.98 | 0.91 | 0.98 | 0.98 | 1.00 | 0.99 | 126.01 | 124.80 | 123.61 |
| Croatia | 1.04 | 0.99 | 0.99 | 0.91 | 0.99 | 1.00 | 1.00 | 0.99 | 103.04 | 101.99 | 100.94 |
| Czech Republic | 1.00 | 1.04 | 1.04 | 0.99 | 0.89 | 1.00 | 1.00 | 0.99 | 114.61 | 113.75 | 112.90 |
| Estonia | 1.13 | 1.15 | 1.00 | 1.01 | 0.93 | 1.00 | 1.00 | 1.03 | 152.73 | 156.88 | 161.15 |
| Hungary | 0.98 | 0.99 | 1.00 | 1.01 | 1.01 | 1.00 | 1.00 | 1.00 | 118.94 | 118.77 | 118.60 |
| Latvia | 1.00 | 1.09 | 1.22 | 0.86 | 1.09 | 1.03 | 1.00 | 1.04 | 135.88 | 140.77 | 145.84 |
| Lithuania | 1.03 | 1.09 | 0.92 | 0.94 | 0.98 | 1.01 | 1.00 | 0.99 | 139.81 | 138.91 | 138.02 |
| Poland | 1.05 | 1.10 | 1.06 | 0.99 | 0.96 | 1.02 | 1.00 | 1.03 | 149.92 | 153.72 | 157.62 |
| Romania | 0.96 | 0.96 | 1.01 | 1.00 | 1.01 | 0.99 | 1.00 | 0.99 | 105.44 | 104.47 | 103.50 |
| Slovakia | 1.01 | 1.02 | 1.02 | 1.03 | 1.05 | 1.05 | 1.00 | 1.02 | 131.05 | 134.18 | 137.38 |
| Slovenia | 1.02 | 1.02 | 1.02 | 1.02 | 1.01 | 1.01 | 1.00 | 1.01 | 116.07 | 117.61 | 119.16 |
| Country | Change Dynamics in 2011–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | 1.03 | 1.38 | 1.18 | 1.26 | 1.13 | 1.15 | 1.00 | 1.15 | 203104.53 | 234557.56 | 270881.45 |
| Croatia | 0.96 | 1.88 | 1.08 | 1.43 | 0.98 | 2.09 | 1.00 | 1.28 | 152660.03 | 195919.13 | 251436.51 |
| Czech Republic | 1.32 | 1.12 | 1.09 | 1.00 | 1.45 | 1.12 | 1.00 | 1.15 | 207235.08 | 237671.20 | 272577.40 |
| Estonia | 1.05 | 1.09 | 1.09 | 0.98 | 6.07 | 1.21 | 1.00 | 1.37 | 289019.37 | 396267.11 | 543311.74 |
| Hungary | 1.00 | 1.28 | 1.59 | 1.49 | 0.36 | 11.48 | 1.00 | 1.44 | 222260.59 | 319192.59 | 458398.44 |
| Latvia | 1.44 | 1.33 | 1.14 | 1.38 | 0.23 | 11.57 | 1.00 | 1.34 | 331501.43 | 445514.74 | 598740.67 |
| Lithuania | 1.27 | 1.34 | 1.29 | 1.26 | 1.11 | 1.43 | 1.00 | 1.23 | 245140.53 | 302641.83 | 373630.90 |
| Poland | 1.07 | 1.36 | 1.34 | 1.10 | 0.97 | 1.06 | 1.00 | 1.12 | 93277.12 | 104451.00 | 116963.43 |
| Romania | 1.69 | 1.10 | 1.09 | 0.86 | 1.24 | 1.07 | 1.00 | 1.13 | 175170.43 | 197309.34 | 222246.27 |
| Slovakia | 1.02 | 0.97 | 0.98 | 1.27 | 2.77 | 1.27 | 1.00 | 1.23 | 64542.17 | 79573.10 | 98104.50 |
| Slovenia | 0.97 | 1.42 | 1.58 | 0.79 | 1.54 | 1.28 | 1.00 | 1.19 | 284834.13 | 339220.27 | 403990.88 |
| Country | Change Dynamics in 2011–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | 1.08 | 1.38 | 1.05 | 1.05 | 1.02 | 1.02 | 1.00 | 1.08 | 65.05 | 70.26 | 75.89 |
| Croatia | 1.07 | 1.06 | 0.98 | 1.06 | 1.10 | 1.04 | 1.00 | 1.04 | 82.70 | 86.09 | 89.61 |
| Czech Republic | 1.08 | 0.98 | 1.10 | 1.06 | 0.93 | 1.03 | 1.00 | 1.02 | 77.37 | 79.21 | 81.09 |
| Estonia | 1.09 | 1.00 | 1.06 | 1.03 | 1.07 | 1.02 | 1.00 | 1.04 | 92.95 | 96.44 | 100.06 |
| Hungary | 1.08 | 0.99 | 1.02 | 1.01 | 1.01 | 1.02 | 1.00 | 1.02 | 77.95 | 79.52 | 81.13 |
| Latvia | 1.03 | 1.08 | 1.03 | 1.03 | 1.04 | 1.02 | 1.00 | 1.03 | 80.48 | 83.01 | 85.62 |
| Lithuania | 1.07 | 1.01 | 1.04 | 1.01 | 1.01 | 1.04 | 1.00 | 1.03 | 72.23 | 74.05 | 75.92 |
| Poland | 1.06 | 1.01 | 1.02 | 1.04 | 1.00 | 1.03 | 1.00 | 1.02 | 81.83 | 83.59 | 85.39 |
| Romania | 1.10 | 1.07 | 1.08 | 1.04 | 1.08 | 1.08 | 1.00 | 1.06 | 78.70 | 83.73 | 89.09 |
| Slovakia | 1.10 | 0.99 | 1.02 | 1.00 | 1.00 | 1.00 | 1.00 | 1.02 | 82.28 | 83.64 | 85.02 |
| Slovenia | 1.07 | 1.01 | 1.00 | 1.01 | 1.01 | 1.00 | 1.00 | 1.01 | 79.19 | 80.35 | 81.53 |
| Country | Change Dynamics in 2011–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | 1.36 | 1.13 | 1.06 | 1.06 | 1.04 | 1.07 | 1.00 | 1.10 | 69.74 | 76.55 | 84.03 |
| Croatia | 1.09 | 1.08 | 0.97 | 1.06 | 1.12 | 1.01 | 1.00 | 1.05 | 80.78 | 84.47 | 88.33 |
| Czech Republic | 1.10 | 0.98 | 1.11 | 1.07 | 0.94 | 1.04 | 1.00 | 1.03 | 78.60 | 81.21 | 83.91 |
| Estonia | 1.04 | 1.06 | 1.07 | 1.03 | 1.06 | 0.98 | 1.00 | 1.03 | 89.20 | 92.31 | 95.53 |
| Hungary | 1.08 | 1.05 | 1.04 | 1.05 | 1.01 | 1.04 | 1.00 | 1.04 | 81.62 | 84.73 | 87.96 |
| Latvia | 1.06 | 1.08 | 1.04 | 1.03 | 1.04 | 1.02 | 1.00 | 1.04 | 80.19 | 83.18 | 86.29 |
| Lithuania | 1.02 | 1.00 | 1.05 | 1.02 | 1.03 | 1.05 | 1.00 | 1.02 | 73.50 | 75.30 | 77.14 |
| Poland | 1.05 | 1.06 | 1.02 | 1.04 | 1.01 | 1.06 | 1.00 | 1.03 | 83.23 | 86.12 | 89.10 |
| Romania | 1.12 | 1.14 | 1.08 | 1.04 | 1.12 | 1.07 | 1.00 | 1.08 | 78.20 | 84.47 | 91.24 |
| Slovakia | 1.05 | 1.06 | 1.03 | 1.01 | 1.01 | 1.01 | 1.00 | 1.03 | 82.57 | 84.68 | 86.84 |
| Slovenia | 1.07 | 1.02 | 1.02 | 1.02 | 1.01 | 1.01 | 1.00 | 1.02 | 80.02 | 81.65 | 83.31 |
| Country | Change Dynamics in 2011–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | 1.10 | 1.02 | 1.02 | 1.05 | 1.02 | 1.05 | 1.00 | 1.04 | 62.08 | 64.42 | 66.84 |
| Croatia | 1.17 | 0.88 | 1.08 | 1.03 | 1.02 | 1.04 | 1.00 | 1.03 | 74.67 | 76.69 | 78.77 |
| Czech Republic | 1.06 | 1.01 | 1.01 | 1.08 | 0.95 | 1.01 | 1.00 | 1.02 | 77.65 | 78.83 | 80.03 |
| Estonia | 1.03 | 1.02 | 1.02 | 1.05 | 1.05 | 0.99 | 1.00 | 1.02 | 89.30 | 91.41 | 93.56 |
| Hungary | 1.11 | 1.20 | 1.03 | 1.05 | 0.96 | 1.09 | 1.00 | 1.06 | 83.95 | 88.92 | 94.18 |
| Latvia | 1.05 | 1.02 | 1.03 | 1.01 | 1.04 | 1.01 | 1.00 | 1.02 | 81.68 | 83.51 | 85.39 |
| Lithuania | 1.05 | 1.03 | 1.02 | 1.05 | 0.99 | 1.04 | 1.00 | 1.03 | 76.32 | 78.32 | 80.36 |
| Poland | 1.04 | 0.96 | 1.01 | 1.06 | 1.02 | 1.08 | 1.00 | 1.02 | 75.02 | 76.79 | 78.59 |
| Romania | 1.10 | 1.04 | 1.08 | 1.09 | 1.03 | 1.07 | 1.00 | 1.06 | 63.00 | 66.70 | 70.61 |
| Slovakia | 0.98 | 1.03 | 1.02 | 1.03 | 0.97 | 1.04 | 1.00 | 1.01 | 81.19 | 81.90 | 82.62 |
| Slovenia | 1.03 | 0.95 | 1.06 | 0.98 | 1.02 | 1.03 | 1.00 | 1.01 | 76.32 | 77.15 | 77.99 |
| Country | Change Dynamics in 2011–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | 1.07 | 1.15 | 1.06 | 1.09 | 1.10 | 1.03 | 1.00 | 1.07 | 24.87 | 26.61 | 28.46 |
| Croatia | 1.07 | 1.06 | 1.04 | 1.07 | 1.01 | 1.06 | 1.00 | 1.04 | 25.69 | 26.80 | 27.96 |
| Czech Republic | 1.08 | 1.04 | 1.04 | 1.64 | 0.98 | 1.01 | 1.00 | 1.10 | 30.32 | 33.25 | 36.46 |
| Estonia | 1.08 | 0.94 | 1.04 | 1.09 | 1.04 | 1.04 | 1.00 | 1.03 | 32.03 | 33.02 | 34.05 |
| Hungary | 1.08 | 1.03 | 1.05 | 1.08 | 1.05 | 1.04 | 1.00 | 1.05 | 29.80 | 31.21 | 32.69 |
| Latvia | 1.06 | 1.14 | 1.06 | 1.00 | 1.00 | 1.03 | 1.00 | 1.04 | 26.70 | 27.81 | 28.96 |
| Lithuania | 1.07 | 0.95 | 1.04 | 1.21 | 1.04 | 1.03 | 1.00 | 1.05 | 30.09 | 31.55 | 33.08 |
| Poland | 1.11 | 1.08 | 1.00 | 1.21 | 1.01 | 1.01 | 1.00 | 1.06 | 20.32 | 21.49 | 22.73 |
| Romania | 1.10 | 1.05 | 1.07 | 1.08 | 1.06 | 1.05 | 1.00 | 1.06 | 21.87 | 23.12 | 24.44 |
| Slovakia | 1.07 | 1.08 | 1.05 | 1.41 | 1.07 | 1.05 | 1.00 | 1.10 | 26.87 | 29.51 | 32.41 |
| Slovenia | 1.05 | 0.98 | 1.03 | 1.07 | 1.02 | 1.03 | 1.00 | 1.03 | 28.97 | 29.70 | 30.46 |
| Country | Change Dynamics in 2011–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | 1.81 | 3.34 | 1.21 | 1.13 | 1.22 | 1.09 | 1.00 | 1.41 | 124.56 | 175.56 | 247.44 |
| Croatia | 0.88 | 8.17 | 1.23 | 1.04 | 1.07 | 1.09 | 1.00 | 1.40 | 111.77 | 156.67 | 219.61 |
| Czech Republic | 1.26 | 1.21 | 1.04 | 1.23 | 1.08 | 1.06 | 1.00 | 1.12 | 85.24 | 95.59 | 107.19 |
| Estonia | 1.75 | 1.83 | 1.03 | 1.48 | 0.96 | 1.11 | 1.00 | 1.27 | 158.28 | 200.36 | 253.64 |
| Hungary | 1.69 | 1.83 | 1.14 | 1.24 | 1.17 | 1.12 | 1.00 | 1.28 | 57.01 | 73.10 | 93.74 |
| Latvia | 1.37 | 1.55 | 1.05 | 1.00 | 1.09 | 1.15 | 1.00 | 1.16 | 89.17 | 103.30 | 119.67 |
| Lithuania | 1.21 | 2.41 | 1.30 | 1.30 | 0.96 | 1.14 | 1.00 | 1.27 | 97.74 | 124.40 | 158.32 |
| Poland | 0.97 | 1.31 | 0.94 | 0.94 | 1.03 | 1.03 | 1.00 | 1.02 | 60.26 | 61.68 | 63.14 |
| Romania | 1.32 | 1.91 | 1.40 | 1.31 | 1.29 | 1.16 | 1.00 | 1.32 | 97.12 | 127.96 | 168.58 |
| Slovakia | 1.54 | 1.24 | 1.38 | 1.08 | 1.13 | 1.17 | 1.00 | 1.21 | 95.30 | 115.34 | 139.59 |
| Slovenia | 1.20 | 1.25 | 1.15 | 1.11 | 1.11 | 1.20 | 1.00 | 1.14 | 71.17 | 81.37 | 93.02 |
| Country | Change Dynamics in 2011–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | 1.00 | 1.06 | 1.00 | 1.08 | 1.00 | 0.98 | 1.00 | 1.02 | 100.70 | 102.41 | 104.16 |
| Croatia | 1.00 | 1.03 | 1.00 | 1.00 | 1.00 | 1.01 | 1.00 | 1.01 | 99.54 | 100.08 | 100.63 |
| Czech Republic | 1.00 | 1.07 | 1.00 | 1.08 | 1.00 | 1.01 | 1.00 | 1.02 | 107.42 | 109.76 | 112.16 |
| Estonia | 1.00 | 1.03 | 1.00 | 1.01 | 1.00 | 1.06 | 1.00 | 1.02 | 116.94 | 118.72 | 120.53 |
| Hungary | 1.00 | 1.03 | 1.00 | 1.06 | 1.00 | 0.97 | 1.00 | 1.01 | 106.22 | 107.26 | 108.30 |
| Latvia | 1.00 | 1.03 | 1.00 | 1.13 | 1.00 | 1.04 | 1.00 | 1.03 | 118.57 | 121.87 | 125.26 |
| Lithuania | 1.00 | 1.08 | 1.00 | 1.00 | 1.00 | 1.01 | 1.00 | 1.01 | 108.14 | 109.48 | 110.84 |
| Poland | 1.00 | 1.01 | 1.00 | 1.11 | 1.00 | 1.00 | 1.00 | 1.02 | 110.48 | 112.29 | 114.14 |
| Romania | 1.00 | 1.00 | 1.00 | 1.03 | 1.00 | 0.94 | 1.00 | 1.00 | 91.85 | 91.45 | 91.05 |
| Slovakia | 1.00 | 1.05 | 1.00 | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 | 92.29 | 92.65 | 93.02 |
| Slovenia | 1.00 | 1.01 | 1.00 | 1.14 | 1.00 | 1.00 | 1.00 | 1.02 | 112.76 | 114.88 | 117.05 |
| Country | Change Dynamics in 2011–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | 1.00 | 1.18 | 1.00 | 1.13 | 1.00 | 1.04 | 1.00 | 1.05 | 77.53 | 81.31 | 85.26 |
| Croatia | 1.00 | 1.25 | 1.00 | 1.00 | 1.00 | 1.13 | 1.00 | 1.05 | 73.06 | 76.77 | 80.66 |
| Czech Republic | 1.00 | 1.06 | 1.00 | 1.02 | 1.00 | 1.01 | 1.00 | 1.01 | 66.82 | 67.62 | 68.44 |
| Estonia | 1.00 | 1.22 | 1.00 | 0.95 | 1.00 | 0.95 | 1.00 | 1.01 | 70.59 | 71.64 | 72.71 |
| Hungary | 1.00 | 0.97 | 1.00 | 0.96 | 1.00 | 0.89 | 1.00 | 0.97 | 49.48 | 48.13 | 46.82 |
| Latvia | 1.00 | 1.08 | 1.00 | 1.03 | 1.00 | 1.00 | 1.00 | 1.02 | 68.09 | 69.17 | 70.25 |
| Lithuania | 1.00 | 0.95 | 1.00 | 0.97 | 1.00 | 0.95 | 1.00 | 0.98 | 67.35 | 66.19 | 65.05 |
| Poland | 1.00 | 1.04 | 1.00 | 0.97 | 1.00 | 1.00 | 1.00 | 1.00 | 71.25 | 71.35 | 71.44 |
| Romania | 1.00 | 0.81 | 1.00 | 1.01 | 1.00 | 1.02 | 1.00 | 0.97 | 51.86 | 50.53 | 49.24 |
| Slovakia | 1.00 | 1.02 | 1.00 | 0.99 | 1.00 | 0.97 | 1.00 | 1.00 | 52.74 | 52.56 | 52.38 |
| Slovenia | 1.00 | 0.99 | 1.00 | 0.99 | 1.00 | 0.97 | 1.00 | 0.99 | 82.38 | 81.83 | 81.28 |
| Country | Change Dynamics in 2015–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | - | - | - | - | 1.00 | 1.02 | 1.00 | 1.01 | 10.87 | 10.94 | 11.00 |
| Croatia | - | - | - | - | 1.00 | 1.02 | 1.00 | 1.01 | 11.27 | 11.34 | 11.40 |
| Czech Republic | - | - | - | - | 1.00 | 1.00 | 1.00 | 1.00 | 12.30 | 12.30 | 12.30 |
| Estonia | - | - | - | - | 1.00 | 1.00 | 1.00 | 1.00 | 12.50 | 12.50 | 12.50 |
| Hungary | - | - | - | - | 1.00 | 1.03 | 1.00 | 1.01 | 12.14 | 12.27 | 12.41 |
| Latvia | - | - | - | - | 1.00 | 1.02 | 1.00 | 1.01 | 11.77 | 11.84 | 11.90 |
| Lithuania | - | - | - | - | 1.00 | 1.00 | 1.00 | 1.00 | 12.70 | 12.70 | 12.70 |
| Poland | - | - | - | - | 1.00 | 1.00 | 1.00 | 1.00 | 11.90 | 11.90 | 11.90 |
| Romania | - | - | - | - | 1.00 | 1.02 | 1.00 | 1.01 | 10.87 | 10.94 | 11.00 |
| Slovakia | - | - | - | - | 1.00 | 1.01 | 1.00 | 1.00 | 12.23 | 12.27 | 12.30 |
| Slovenia | - | - | - | - | 1.00 | 1.00 | 1.00 | 1.00 | 12.10 | 12.10 | 12.10 |
Appendix C. Forecasted Values of Indicators Aggregated to Fuzzy Numbers
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 123.61 | 123.83 | 125.79 | 126.01 | 124.81 | 0.98 |
| Croatia | 100.94 | 101.13 | 102.85 | 103.04 | 101.99 | 0.86 |
| Czech Republic | 112.90 | 113.05 | 114.45 | 114.61 | 113.75 | 0.70 |
| Estonia | 152.73 | 153.48 | 160.36 | 161.15 | 156.92 | 3.44 |
| Hungary | 118.60 | 118.63 | 118.91 | 118.94 | 118.77 | 0.14 |
| Latvia | 135.88 | 136.77 | 144.90 | 145.84 | 140.83 | 4.07 |
| Lithuania | 138.02 | 138.18 | 139.64 | 139.81 | 138.91 | 0.73 |
| Poland | 149.92 | 150.61 | 156.90 | 157.62 | 153.75 | 3.14 |
| Romania | 103.50 | 103.67 | 105.26 | 105.44 | 104.47 | 0.79 |
| Slovakia | 131.05 | 131.62 | 136.79 | 137.38 | 134.20 | 2.59 |
| Slovenia | 116.07 | 116.35 | 118.88 | 119.16 | 117.62 | 1.26 |
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 203104.53 | 208487.56 | 263874.80 | 270881.45 | 236181.18 | 27693.62 |
| Croatia | 152660.03 | 159576.52 | 240433.93 | 251436.51 | 200005.22 | 40428.70 |
| Czech Republic | 207235.08 | 212464.54 | 265857.91 | 272577.40 | 239161.23 | 26696.69 |
| Estonia | 289019.37 | 305295.40 | 513770.08 | 543311.74 | 409532.74 | 104237.34 |
| Hungary | 222260.59 | 236367.44 | 430200.31 | 458398.44 | 333283.87 | 96916.44 |
| Latvia | 331501.43 | 349094.86 | 568076.37 | 598740.67 | 458585.61 | 109490.76 |
| Lithuania | 245140.53 | 254585.54 | 359689.98 | 373630.90 | 307137.76 | 52552.22 |
| Poland | 93277.12 | 95222.14 | 114572.22 | 116963.43 | 104897.18 | 9675.04 |
| Romania | 175170.43 | 179012.06 | 217471.96 | 222246.27 | 198242.01 | 19229.95 |
| Slovakia | 64542.17 | 67013.34 | 94466.50 | 98104.50 | 80739.92 | 13726.58 |
| Slovenia | 284834.13 | 293974.69 | 391388.83 | 403990.88 | 342681.76 | 48707.07 |
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 65.05 | 65.97 | 74.83 | 75.89 | 70.40 | 4.43 |
| Croatia | 82.70 | 83.31 | 88.95 | 89.61 | 86.13 | 2.82 |
| Czech Republic | 77.37 | 77.70 | 80.74 | 81.09 | 79.22 | 1.52 |
| Estonia | 92.95 | 93.58 | 99.38 | 100.06 | 96.48 | 2.90 |
| Hungary | 77.95 | 78.23 | 80.84 | 81.13 | 79.54 | 1.30 |
| Latvia | 80.48 | 80.94 | 85.14 | 85.62 | 83.04 | 2.10 |
| Lithuania | 72.23 | 72.57 | 75.57 | 75.92 | 74.07 | 1.50 |
| Poland | 81.83 | 82.15 | 85.05 | 85.39 | 83.60 | 1.45 |
| Romania | 78.70 | 79.59 | 88.09 | 89.09 | 83.84 | 4.25 |
| Slovakia | 82.28 | 82.53 | 84.76 | 85.02 | 83.65 | 1.12 |
| Slovenia | 79.19 | 79.40 | 81.31 | 81.53 | 80.36 | 0.95 |
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 69.74 | 70.94 | 82.61 | 84.03 | 76.78 | 5.83 |
| Croatia | 80.78 | 81.44 | 87.61 | 88.33 | 84.53 | 3.08 |
| Czech Republic | 78.60 | 79.07 | 83.41 | 83.91 | 81.24 | 2.17 |
| Estonia | 89.20 | 89.76 | 94.93 | 95.53 | 92.34 | 2.58 |
| Hungary | 81.62 | 82.18 | 87.36 | 87.96 | 84.77 | 2.59 |
| Latvia | 80.19 | 80.73 | 85.71 | 86.29 | 83.22 | 2.49 |
| Lithuania | 73.50 | 73.83 | 76.80 | 77.14 | 75.31 | 1.48 |
| Poland | 83.23 | 83.76 | 88.54 | 89.10 | 86.15 | 2.39 |
| Romania | 78.20 | 79.32 | 89.97 | 91.24 | 84.64 | 5.33 |
| Slovakia | 82.57 | 82.96 | 86.44 | 86.84 | 84.70 | 1.74 |
| Slovenia | 80.02 | 80.31 | 83.00 | 83.31 | 81.66 | 1.34 |
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 62.08 | 62.50 | 66.39 | 66.84 | 64.45 | 1.94 |
| Croatia | 74.67 | 75.04 | 78.38 | 78.77 | 76.71 | 1.67 |
| Czech Republic | 77.65 | 77.86 | 79.81 | 80.03 | 78.83 | 0.97 |
| Estonia | 89.30 | 89.68 | 93.16 | 93.56 | 91.42 | 1.74 |
| Hungary | 83.95 | 84.84 | 93.19 | 94.18 | 89.02 | 4.18 |
| Latvia | 81.68 | 82.02 | 85.04 | 85.39 | 83.53 | 1.51 |
| Lithuania | 76.32 | 76.68 | 79.98 | 80.36 | 78.33 | 1.65 |
| Poland | 75.02 | 75.34 | 78.26 | 78.59 | 76.80 | 1.46 |
| Romania | 63.00 | 63.66 | 69.88 | 70.61 | 66.77 | 3.11 |
| Slovakia | 81.19 | 81.32 | 82.49 | 82.62 | 81.90 | 0.58 |
| Slovenia | 76.32 | 76.47 | 77.83 | 77.99 | 77.15 | 0.68 |
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 24.87 | 25.18 | 28.12 | 28.46 | 26.65 | 1.47 |
| Croatia | 25.69 | 25.89 | 27.74 | 27.96 | 26.81 | 0.93 |
| Czech Republic | 30.32 | 30.84 | 35.85 | 36.46 | 33.34 | 2.51 |
| Estonia | 32.03 | 32.21 | 33.86 | 34.05 | 33.03 | 0.82 |
| Hungary | 29.80 | 30.06 | 32.41 | 32.69 | 31.24 | 1.18 |
| Latvia | 26.70 | 26.90 | 28.74 | 28.96 | 27.82 | 0.92 |
| Lithuania | 30.09 | 30.35 | 32.80 | 33.08 | 31.58 | 1.22 |
| Poland | 20.32 | 20.53 | 22.49 | 22.73 | 21.51 | 0.98 |
| Romania | 21.87 | 22.09 | 24.19 | 24.44 | 23.14 | 1.05 |
| Slovakia | 26.87 | 27.34 | 31.86 | 32.41 | 29.60 | 2.26 |
| Slovenia | 28.97 | 29.10 | 30.32 | 30.46 | 29.71 | 0.61 |
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 124.56 | 132.12 | 232.93 | 247.44 | 182.52 | 50.40 |
| Croatia | 111.77 | 118.46 | 206.92 | 219.61 | 162.69 | 44.23 |
| Czech Republic | 85.24 | 87.04 | 104.97 | 107.19 | 96.01 | 8.96 |
| Estonia | 158.28 | 165.07 | 243.11 | 253.64 | 204.09 | 39.02 |
| Hungary | 57.01 | 59.58 | 89.65 | 93.74 | 74.62 | 15.03 |
| Latvia | 89.17 | 91.59 | 116.51 | 119.67 | 104.05 | 12.46 |
| Lithuania | 97.74 | 102.03 | 151.61 | 158.32 | 126.82 | 24.79 |
| Poland | 60.26 | 60.52 | 62.87 | 63.14 | 61.69 | 1.18 |
| Romania | 97.12 | 101.96 | 160.49 | 168.58 | 131.22 | 29.26 |
| Slovakia | 95.30 | 98.63 | 134.85 | 139.59 | 116.74 | 18.11 |
| Slovenia | 71.17 | 72.93 | 90.78 | 93.02 | 81.85 | 8.92 |
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 100.70 | 101.02 | 103.83 | 104.16 | 102.42 | 1.41 |
| Croatia | 99.54 | 99.64 | 100.53 | 100.63 | 100.08 | 0.44 |
| Czech Republic | 107.42 | 107.85 | 111.71 | 112.16 | 109.78 | 1.93 |
| Estonia | 116.94 | 117.26 | 120.20 | 120.53 | 118.73 | 1.47 |
| Hungary | 106.22 | 106.41 | 108.11 | 108.30 | 107.26 | 0.85 |
| Latvia | 118.57 | 119.17 | 124.63 | 125.26 | 121.90 | 2.73 |
| Lithuania | 108.14 | 108.39 | 110.59 | 110.84 | 109.49 | 1.10 |
| Poland | 110.48 | 110.81 | 113.80 | 114.14 | 112.30 | 1.49 |
| Romania | 91.05 | 91.13 | 91.78 | 91.85 | 91.45 | 0.32 |
| Slovakia | 92.29 | 92.35 | 92.95 | 93.02 | 92.65 | 0.30 |
| Slovenia | 112.76 | 113.14 | 116.65 | 117.05 | 114.90 | 1.75 |
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 77.53 | 78.21 | 84.52 | 85.26 | 81.37 | 3.16 |
| Croatia | 73.06 | 73.73 | 79.93 | 80.66 | 76.83 | 3.10 |
| Czech Republic | 66.82 | 66.96 | 68.29 | 68.44 | 67.63 | 0.66 |
| Estonia | 70.59 | 70.78 | 72.51 | 72.71 | 71.65 | 0.87 |
| Hungary | 46.82 | 47.06 | 49.23 | 49.48 | 48.14 | 1.08 |
| Latvia | 68.09 | 68.29 | 70.05 | 70.25 | 69.17 | 0.88 |
| Lithuania | 65.05 | 65.25 | 67.13 | 67.35 | 66.19 | 0.94 |
| Poland | 71.25 | 71.27 | 71.43 | 71.44 | 71.35 | 0.08 |
| Romania | 49.24 | 49.48 | 51.61 | 51.86 | 50.54 | 1.07 |
| Slovakia | 52.38 | 52.41 | 52.71 | 52.74 | 52.56 | 0.15 |
| Slovenia | 81.28 | 81.38 | 82.28 | 82.38 | 81.83 | 0.45 |
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 10.87 | 10.88 | 10.99 | 11.00 | 10.94 | 0.06 |
| Croatia | 11.27 | 11.28 | 11.39 | 11.40 | 11.34 | 0.06 |
| Czech Republic | 12.30 | 12.30 | 12.30 | 12.30 | 12.30 | 0.00 |
| Estonia | 12.50 | 12.50 | 12.50 | 12.50 | 12.50 | 0.00 |
| Hungary | 12.14 | 12.16 | 12.39 | 12.41 | 12.27 | 0.11 |
| Latvia | 11.77 | 11.78 | 11.89 | 11.90 | 11.84 | 0.06 |
| Lithuania | 12.70 | 12.70 | 12.70 | 12.70 | 12.70 | 0.00 |
| Poland | 11.90 | 11.90 | 11.90 | 11.90 | 11.90 | 0.00 |
| Romania | 10.87 | 10.88 | 10.99 | 11.00 | 10.94 | 0.06 |
| Slovakia | 12.23 | 12.24 | 12.29 | 12.30 | 12.27 | 0.03 |
| Slovenia | 12.10 | 12.10 | 12.10 | 12.10 | 12.10 | 0.00 |
References
- Cairncross, F. The Death of Distance 2.0: How the Communications Revolution Will Change Our Lives, 2nd ed.; Texere Publishing: London, UK, 2001; ISBN 978-1-58799-089-2. [Google Scholar]
- Redding, S.; Venables, A.J. Economic geography and international inequality. J. Int. Econ. 2004, 62, 53–82. [Google Scholar] [CrossRef]
- Bank, I.-A.D.; Chong, A. Development Connections: Unveiling the Impact of New Information Technologies, 2011th ed.; Palgrave Macmillan: New York, NY, USA, 2011; ISBN 978-0-230-11194-3. [Google Scholar]
- Forestier, E.; Grace, J.; Kenny, C. Can information and communication technologies be pro-poor? Telecommun. Policy 2002, 26, 623–646. [Google Scholar] [CrossRef]
- Graham, C. Strengthening Institutional Capacity in Poor Countries. Reducing Global Poverty; Brookings Institution: Washington, DC, USA, 2002. [Google Scholar]
- Cecchini, S.; Scott, C. Can information and communications technology applications contribute to poverty reduction? Lessons from rural India. Inf. Technol. Dev. 2003, 10, 73–84. [Google Scholar] [CrossRef]
- Pick, J.B.; Azari, R. Global digital divide: Influence of socioeconomic, governmental, and accessibility factors on information technology. Inf. Technol. Dev. 2008, 14, 91–115. [Google Scholar] [CrossRef]
- Barney, D. The Network Society, 1st ed.; Polity: Cambridge, UK, 2004; ISBN 978-0-7456-2668-0. [Google Scholar]
- Castells, M. The Internet Galaxy: Reflections on the Internet, Business, and Society, 1st ed.; Oxford University Press: Oxford, UK, 2003; ISBN 978-0-19-925577-1. [Google Scholar]
- Hüsing, T.; Selhofer, H. The digital divide index—A measure of social inequalities in the adoption of ICT. In Proceedings of the Paper to IST 2002 Conference, Copenhagen, Denmark, 4–6 November 2002; pp. 1273–1286. [Google Scholar]
- Fuchs, C.; Horak, E. Informational Capitalism and the Digital Divide in Africa. Masaryk Univ. J. Law Technol. 2008, 1, 11–32. [Google Scholar]
- Kubielas, S.; Olender-Skorek, M. ICT modernization in Central and Eastern Europe: a Schumpeterian catching up perspective. Int. Econ. Econ. Policy 2014, 11, 115–136. [Google Scholar] [CrossRef]
- ITU Measuring the Information Society Reports 2010–2017. Available online: https://www.itu.int/en/ITU-D/Statistics/Pages/publications/mis2017.aspx (accessed on 22 August 2018).
- Ziemba, P.; Wątróbski, J.; Zioło, M.; Karczmarczyk, A. Using the PROSA Method in Offshore Wind Farm Location Problems. Energies 2017, 10, 1755. [Google Scholar] [CrossRef]
- Pelenc, J.; Ballet, J.; Dedeurwaerdere, T. Weak Sustainability versus Strong Sustainability; Brief for GSDR United Nations: Fontainebleau, France, 2015. [Google Scholar]
- Becker, J.; Becker, A.; Sulikowski, P.; Zdziebko, T. ANP-based analysis of ICT usage in Central European enterprises. Procedia Comput. Sci. 2018, 126, 2173–2183. [Google Scholar] [CrossRef]
- White, L.; Lee, G.J. Operational research and sustainable development: Tackling the social dimension. Eur. J. Oper. Res. 2009, 193, 683–692. [Google Scholar] [CrossRef]
- Diaz-Balteiro, L.; González-Pachón, J.; Romero, C. Measuring systems sustainability with multi-criteria methods: A critical review. Eur. J. Oper. Res. 2017, 258, 607–616. [Google Scholar] [CrossRef]
- Ziemba, P.; Jankowski, J.; Wątróbski, J. Online Comparison System with Certain and Uncertain Criteria Based on Multi-criteria Decision Analysis Method. In Proceedings of the Computational Collective Intelligence, Nicosia, Cyprus, 27–29 September 2017; Nguyen, N.T., Papadopoulos, G.A., Jędrzejowicz, P., Trawiński, B., Vossen, G., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 579–589. [Google Scholar]
- Ziemba, P. NEAT F-PROMETHEE—A new fuzzy multiple criteria decision making method based on the adjustment of mapping trapezoidal fuzzy numbers. Expert Syst. Appl. 2018, 110, 363–380. [Google Scholar] [CrossRef]
- Ziemba, P.; Jankowski, J.; Wątróbski, J. Dynamic Decision Support in the Internet Marketing Management. In Transactions on Computational Collective Intelligence XXIX; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; pp. 39–68. ISBN 978-3-319-90286-9. [Google Scholar]
- Ziemba, P.; Wątróbski, J.; Karczmarczyk, A.; Jankowski, J.; Wolski, W. Integrated approach to e-commerce websites evaluation with the use of surveys and eye tracking based experiments. In Proceedings of the 2017 Federated Conference on Computer Science and Information Systems (FedCSIS), Prague, Czech Republic, 3–6 September 2017; pp. 1019–1030. [Google Scholar]
- Campbell, D. Can the digital divide be contained? Int. Labour Review 2001, 140, 119–141. [Google Scholar] [CrossRef]
- Norris, P. Digital Divide: Civic Engagement, Information Poverty and the Internet World-Wide; Cambridge University Press: Cambridge, UK, 2001; Volume 5, ISBN 978-0-521-00223-3. [Google Scholar]
- Warschauer, M. Technology and Social Inclusion: Rethinking the Digital Divide; The MIT Press: Cambridge, MA, USA, 2004; ISBN 978-0-262-73173-7. [Google Scholar]
- Gumpert, G.; Drucker, S. The Perfections of Sustainability and Imperfections in the Digital Community: Paradoxes of Connection and Disconnection. In Proceedings of the Digital Cities III, Information Technologies for Social Capital: Cross-Cultural Perspectives, Amsterdam, The Netherlands, 18–19 September 2003; van den Besselaar, P., Koizumi, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 369–379. [Google Scholar]
- White, D.S.; Gunasekaran, A.; Shea, T.P.; Ariguzo, G.C. Mapping the global digital divide. Int. J. Bus. Inf. Syst. 2011, 7, 207–219. [Google Scholar] [CrossRef]
- OECD. Understanding the Digital Divide; Organization for Economic Cooperation and Development (OECD): Paris, France, 2001. [Google Scholar]
- Jahanmir, S.F.; Cavadas, J. Factors affecting late adoption of digital innovations. J. Bus. Res. 2018, 88, 337–343. [Google Scholar] [CrossRef]
- Leaning, M. Chapter One—Integrating Media and Information Literacy. In Media and Information Literacy; Leaning, M., Ed.; Chandos Publishing: Cambridge, UK, 2017; pp. 3–14. ISBN 978-0-08-100170-7. [Google Scholar]
- Warren, M. The digital vicious cycle: Links between social disadvantage and digital exclusion in rural areas. Telecommun. Policy 2007, 31, 374–388. [Google Scholar] [CrossRef]
- James, J. Sharing mobile phones in developing countries: Implications for the digital divide. Technol. Forecast. Soc. Chang. 2011, 78, 729–735. [Google Scholar] [CrossRef]
- James, J. The ICT Development Index and the digital divide: How are they related? Technol. Forecast. Soc. Chang. 2012, 79, 587–594. [Google Scholar] [CrossRef]
- Petrović, M.; Bojković, N.; Anić, I.; Petrović, D. Benchmarking the digital divide using a multi-level outranking framework: Evidence from EBRD countries of operation. Gov. Inf. Q. 2012, 29, 597–607. [Google Scholar] [CrossRef]
- Coria, S.R.; Mondragón-Becerra, R.; Pérez-Meza, M.; Ramírez-Vásquez, S.K.; Martínez-Peláez, R.; Barragán-López, D.; Ávila-Barrón, O.R. CT4RDD: Classification trees for research on digital divide. Expert Syst. Appl. 2013, 40, 5779–5786. [Google Scholar] [CrossRef]
- Khalid, M.S.; Pedersen, M.J.L. Digital Exclusion in Higher Education Contexts: A Systematic Literature Review. Procedia Soc. Behav. Sci. 2016, 228, 614–621. [Google Scholar] [CrossRef]
- Scheerder, A.; van Deursen, A.; van Dijk, J. Determinants of Internet skills, uses and outcomes. A systematic review of the second- and third-level digital divide. Telemat. Inform. 2017, 34, 1607–1624. [Google Scholar] [CrossRef]
- Vicente Cuervo, M.R.; López Menéndez, A.J. A multivariate framework for the analysis of the digital divide: Evidence for the European Union-15. Inf. Manag. 2006, 43, 756–766. [Google Scholar] [CrossRef]
- Polat, R.K. Digital exclusion in Turkey: A policy perspective. Gov. Inf. Q. 2012, 29, 589–596. [Google Scholar] [CrossRef]
- Park, S.R.; Choi, D.Y.; Hong, P. Club convergence and factors of digital divide across countries. Technol. Forecast. Soc. Chang. 2015, 96, 92–100. [Google Scholar] [CrossRef]
- Cruz-Jesus, F.; Vicente, M.R.; Bacao, F.; Oliveira, T. The education-related digital divide: An analysis for the EU-28. Comput. Hum. Behav. 2016, 56, 72–82. [Google Scholar] [CrossRef]
- Szeles, M.R. New insights from a multilevel approach to the regional digital divide in the European Union. Telecommun. Policy 2018, 42, 452–463. [Google Scholar] [CrossRef]
- Kyriakidou, V.; Michalakelis, C.; Sphicopoulos, T. Digital divide gap convergence in Europe. Technol. Soc. 2011, 33, 265–270. [Google Scholar] [CrossRef]
- Srinuan, C.; Srinuan, P.; Bohlin, E. An analysis of mobile Internet access in Thailand: Implications for bridging the digital divide. Telemat. Inform. 2012, 29, 254–262. [Google Scholar] [CrossRef]
- Prieger, J.E. The broadband digital divide and the economic benefits of mobile broadband for rural areas. Telecommun. Policy 2013, 37, 483–502. [Google Scholar] [CrossRef]
- Pick, J.B.; Nishida, T. Digital divides in the world and its regions: A spatial and multivariate analysis of technological utilization. Technol. Forecast. Soc. Chang. 2015, 91, 1–17. [Google Scholar] [CrossRef]
- Chipeva, P.; Cruz-Jesus, F.; Oliveira, T.; Irani, Z. Digital divide at individual level: Evidence for Eastern and Western European countries. Gov. Inf. Q. 2018, 35, 460–479. [Google Scholar] [CrossRef]
- Rockmann, R.; Gewald, H.; Haug, M. Equal Access for Everyone? A Digital Divide Cascade for Retired Senior Citizens; ECIS: Portsmouth, UK, 2018. [Google Scholar]
- Van Dijk, J.A.G.M. The Evolution of the Digital Divide. Stand Alone 2012, 15, 57–75. [Google Scholar]
- Haselhorst, P. Bridging the Digital Divide. Available online: https://www.digitalethics.org/essays/bridging-digital-divide (accessed on 13 January 2019).
- Wątróbski, J.; Jankowski, J.; Ziemba, P. Multistage performance modelling in digital marketing management. Econ. Sociol. 2016, 9, 101–125. [Google Scholar] [CrossRef] [PubMed]
- ITU Measuring the Information Society Report 2009. Available online: https://www.itu.int/en/ITU-D/Statistics/Pages/publications/mis2009.aspx (accessed on 3 September 2018).
- Eurostat Glossary: Chain Index. Available online: http://ec.europa.eu/eurostat/statistics-explained/index.php/Glossary:Chain_index (accessed on 22 August 2018).
- Crawley, M.J. The R Book, 2nd ed.; A John Wiley & Sons: Silwood Park, UK, 2012; ISBN 978-0-470-97392-9. [Google Scholar]
- Sobczyk, M. Statystyka. Podstawy Teoretyczne, Przykłady—Zadania; Wyd. UMCS: Lublin, Poland, 1998. [Google Scholar]
- Brans, J.-P.; De Smet, Y. PROMETHEE Methods. In Multiple Criteria Decision Analysis: State of the Art Surveys; Greco, S., Ehrgott, M., Figueira, J.R., Eds.; International Series in Operations Research & Management Science; Springer: New York, NY, USA, 2016; pp. 187–219. ISBN 978-1-4939-3094-4. [Google Scholar]
- Souter, D. Inside the Information Society: How the Digital Divide has Changed. Available online: https://www.apc.org/en/blog/inside-information-society-how-digital-divide-has-changed (accessed on 13 January 2019).
- Ziemba, P.; Jankowski, J.; Wątróbski, J.; Becker, J. Knowledge Management in Website Quality Evaluation Domain. In Proceedings of the Computational Collective Intelligence, Madrid, Spain, 21–23 September 2015; Núñez, M., Nguyen, N.T., Camacho, D., Trawiński, B., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 75–85. [Google Scholar]
- Ziemba, P.; Jankowski, J.; Wątróbski, J.; Wolski, W.; Becker, J. Integration of domain ontologies in the repository of website evaluation methods. In Proceedings of the 2015 Federated Conference on Computer Science and Information Systems (FedCSIS), Lodz, Poland, 13–16 September 2015; pp. 1585–1595. [Google Scholar]
- Ziemba, P.; Wątróbski, J.; Jankowski, J.; Wolski, W. Construction and Restructuring of the Knowledge Repository of Website Evaluation Methods. In Information Technology for Management; Ziemba, E., Ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 29–52. [Google Scholar]
- Convertino, M.; Muñoz-Carpena, R.; Chu-Agor, M.L.; Kiker, G.A.; Linkov, I. Untangling drivers of species distributions: Global sensitivity and uncertainty analyses of MaxEnt. Environ. Model. Softw. 2014, 51, 296–309. [Google Scholar] [CrossRef]
- Convertino, M.; Muñoz-Carpena, R.; Kiker, G.A.; Perz, S.G. Design of optimal ecosystem monitoring networks: hotspot detection and biodiversity patterns. Stoch. Environ. Res. Risk Assess. 2015, 29, 1085–1101. [Google Scholar] [CrossRef]

| Country | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Bulgaria | 29.7 | 31.0 | 29.3 | 26.9 | 25.3 | 23.3 | 21.0 | 21.0 |
| Croatia | 42.4 | 40.1 | 37.9 | 36.8 | 36.7 | 34.7 | 33.9 | 33.9 |
| Czech Republic | 22.9 | 20.9 | 19.9 | 18.7 | 18.6 | 17.7 | 15.6 | 15.6 |
| Estonia | 36.0 | 35.1 | 34.7 | 33.1 | 31.7 | 30.3 | 29.0 | 29.0 |
| Hungary | 29.8 | 29.4 | 29.7 | 29.9 | 30.3 | 31.2 | 31.5 | 31.6 |
| Latvia | 23.6 | 23.0 | 24.3 | 23.4 | 19.6 | 17.5 | 18.2 | 18.2 |
| Lithuania | 22.1 | 21.9 | 22.3 | 20.7 | 19.5 | 18.7 | 17.8 | 17.8 |
| Poland | 20.0 | 18.1 | 15.6 | 13.9 | 12.6 | 23.7 | 24.5 | 24.5 |
| Romania | 20.9 | 21.9 | 21.4 | 21.8 | 21.1 | 19.8 | 19.1 | 19.1 |
| Slovakia | 20.1 | 19.3 | 17.9 | 17.7 | 16.8 | 15.9 | 15.1 | 15.1 |
| Slovenia | 44.9 | 42.9 | 40.1 | 38.2 | 37.1 | 36.2 | 35.1 | 35.1 |
| Country | Change Dynamics in 2011–2017 | Average Dynamics | Value Forecast | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | ||
| Bulgaria | 1.04 | 0.95 | 0.92 | 0.94 | 0.92 | 0.90 | 1.00 | 0.95 | 19.94 | 18.97 | 18.05 |
| Croatia | 0.95 | 0.95 | 0.97 | 1.00 | 0.95 | 0.98 | 1.00 | 0.97 | 32.80 | 31.76 | 30.76 |
| Czech Republic | 0.91 | 0.95 | 0.94 | 0.99 | 0.95 | 0.88 | 1.00 | 0.95 | 14.72 | 13.93 | 13.19 |
| Estonia | 0.98 | 0.99 | 0.95 | 0.96 | 0.96 | 0.96 | 1.00 | 0.97 | 28.15 | 27.30 | 26.47 |
| Hungary | 0.99 | 1.01 | 1.01 | 1.01 | 1.03 | 1.01 | 1.00 | 1.01 | 31.81 | 32.07 | 32.33 |
| Latvia | 0.97 | 1.06 | 0.96 | 0.84 | 0.89 | 1.04 | 1.00 | 0.96 | 17.50 | 16.86 | 16.24 |
| Lithuania | 0.99 | 1.02 | 0.93 | 0.94 | 0.96 | 0.95 | 1.00 | 0.97 | 17.22 | 16.70 | 16.18 |
| Poland | 0.91 | 0.86 | 0.89 | 0.91 | 1.88 | 1.03 | 1.00 | 1.03 | 25.16 | 25.89 | 26.65 |
| Romania | 1.05 | 0.98 | 1.02 | 0.97 | 0.94 | 0.96 | 1.00 | 0.99 | 18.86 | 18.61 | 18.38 |
| Slovakia | 0.96 | 0.93 | 0.99 | 0.95 | 0.95 | 0.95 | 1.00 | 0.96 | 14.47 | 13.89 | 13.33 |
| Slovenia | 0.96 | 0.93 | 0.95 | 0.97 | 0.98 | 0.97 | 1.00 | 0.97 | 33.91 | 32.74 | 31.61 |
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 18.05 | 18.22 | 19.76 | 19.94 | 18.99 | 0.77 |
| Croatia | 30.76 | 30.94 | 32.61 | 32.80 | 31.78 | 0.83 |
| Czech Republic | 13.19 | 13.32 | 14.58 | 14.72 | 13.95 | 0.63 |
| Estonia | 26.47 | 26.62 | 27.99 | 28.15 | 27.31 | 0.69 |
| Hungary | 31.81 | 31.86 | 32.28 | 32.33 | 32.07 | 0.21 |
| Latvia | 16.24 | 16.36 | 17.38 | 17.50 | 16.87 | 0.51 |
| Lithuania | 16.18 | 16.28 | 17.13 | 17.22 | 16.70 | 0.42 |
| Poland | 25.16 | 25.29 | 26.51 | 26.65 | 25.90 | 0.61 |
| Romania | 18.38 | 18.42 | 18.81 | 18.86 | 18.62 | 0.20 |
| Slovakia | 13.33 | 13.43 | 14.36 | 14.47 | 13.90 | 0.47 |
| Slovenia | 31.61 | 31.81 | 33.69 | 33.91 | 32.75 | 0.94 |
| Country | FTL | MCS | IIB | PHC | PHI | IU | FBB | MBB | SGE | TGE | MYS |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bulgaria | 21.0 | 127.2 | 175,869.19 | 60.2 | 63.5 | 59.8 | 23.3 | 88.4 | 99.0 | 73.9 | 10.8 |
| Croatia | 33.9 | 104.1 | 118,952.58 | 79.5 | 77.3 | 72.7 | 24.6 | 79.7 | 99.0 | 69.5 | 11.2 |
| Czech Republic | 15.6 | 115.5 | 180,696.61 | 75.6 | 76.1 | 76.5 | 27.7 | 76.0 | 105.1 | 66.0 | 12.3 |
| Estonia | 29.0 | 148.7 | 210,797.71 | 89.6 | 86.2 | 87.2 | 31.1 | 125.0 | 115.2 | 69.6 | 12.5 |
| Hungary | 31.6 | 119.1 | 154,764.78 | 76.4 | 78.6 | 79.3 | 28.5 | 44.5 | 105.2 | 50.9 | 12.0 |
| Latvia | 18.2 | 131.2 | 246,665.68 | 78.0 | 77.3 | 79.9 | 25.6 | 77.0 | 115.4 | 67.0 | 11.7 |
| Lithuania | 17.8 | 140.7 | 198,564.36 | 70.5 | 71.8 | 74.4 | 28.7 | 76.8 | 106.8 | 68.5 | 12.7 |
| Poland | 24.5 | 146.2 | 83,298.59 | 80.1 | 80.5 | 73.3 | 19.2 | 58.9 | 108.7 | 71.2 | 11.9 |
| Romania | 19.1 | 106.4 | 155,515.59 | 74.0 | 72.4 | 59.5 | 20.7 | 73.7 | 92.3 | 53.2 | 10.8 |
| Slovakia | 15.1 | 128.0 | 52,350.51 | 81.0 | 80.5 | 80.5 | 24.5 | 78.7 | 91.9 | 52.9 | 12.2 |
| Slovenia | 35.1 | 114.6 | 239,167.56 | 78.1 | 78.4 | 75.5 | 28.3 | 62.3 | 110.7 | 82.9 | 12.1 |
| Country | FTL | MCS | IIB | PHC | PHI | IU | FBB | MBB | SGE | TGE | MYS |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bulgaria | (18.05, 18.22, 19.76, 19.94) | (123.61, 123.83, 125.79, 126.01) | (203104.53, 208487.6, 263874.8, 270881.45) | (65.05, 65.97, 74.83, 75.89) | (69.74, 70.94, 82.61, 84.03) | (62.08, 62.5, 66.39, 66.84) | (24.87, 25.18, 28.12, 28.46) | (124.56, 132.12, 232.93, 247.44) | (100.7, 101.02, 103.83, 104.16) | (77.53, 78.21, 84.52, 85.26) | (10.87, 10.88, 10.99, 11) |
| Croatia | (30.76, 30.94, 32.61, 32.8) | (100.94, 101.13, 102.85, 103.04) | (152660.03, 159576.5, 240433.93, 251436.51) | (82.7, 83.31, 88.95, 89.61) | (80.78, 81.44, 87.61, 88.33) | (74.67, 75.04, 78.38, 78.77) | (25.69, 25.89, 27.74, 27.96) | (111.77, 118.46, 206.92, 219.61) | (99.54, 99.64, 100.53, 100.63) | (73.06, 73.73, 79.93, 80.66) | (11.27, 11.28, 11.39, 11.4) |
| Czech Republic | (13.19, 13.32, 14.58, 14.72) | (112.9, 113.05, 114.45, 114.61) | (207235.08, 212464.5, 265857.91, 272577.4) | (77.37, 77.7, 80.74, 81.09) | (78.6, 79.07, 83.41, 83.91) | (77.65, 77.86, 79.81, 80.03) | (30.32, 30.84, 35.85, 36.46) | (85.24, 87.04, 104.97, 107.19) | (107.42, 107.85, 111.71, 112.16) | (66.82, 66.96, 68.29, 68.44) | (12.3, 12.3, 12.3, 12.3) |
| Estonia | (26.47, 26.62, 27.99, 28.15) | (152.73, 153.48, 160.36, 161.15) | (289019.37, 305295.4, 513770.08, 543311.74) | (92.95, 93.58, 99.38, 100.06) | (89.2, 89.76, 94.93, 95.53) | (89.3, 89.68, 93.16, 93.56) | (32.03, 32.21, 33.86, 34.05) | (158.28, 165.07, 243.11, 253.64) | (116.94, 117.26, 120.2, 120.53) | (70.59, 70.78, 72.51, 72.71) | (12.5, 12.5, 12.5, 12.5) |
| Hungary | (31.81, 31.86, 32.28, 32.33) | (118.6, 118.63, 118.91, 118.94) | (222260.59, 236367.4, 430200.31, 458398.44) | (77.95, 78.23, 80.84, 81.13) | (81.62, 82.18, 87.36, 87.96) | (83.95, 84.84, 93.19, 94.18) | (29.8, 30.06, 32.41, 32.69) | (57.01, 59.58, 89.65, 93.74) | (106.22, 106.41, 108.11, 108.3) | (46.82, 47.06, 49.23, 49.48) | (12.14, 12.16, 12.39, 12.41) |
| Latvia | (16.24, 16.36, 17.38, 17.5) | (135.88, 136.77, 144.9, 145.84) | (331501.43, 349094.9, 568076.37, 598740.67) | (80.48, 80.94, 85.14, 85.62) | (80.19, 80.73, 85.71, 86.29) | (81.68, 82.02, 85.04, 85.39) | (26.7, 26.9, 28.74, 28.96) | (89.17, 91.59, 116.51, 119.67) | (118.57, 119.17, 124.63, 125.26) | (68.09, 68.29, 70.05, 70.25) | (11.77, 11.78, 11.89, 11.9) |
| Lithuania | (16.18, 16.28, 17.13, 17.22) | (138.02, 138.18, 139.64, 139.81) | (245140.53, 254585.5, 359689.98, 373630.9) | (72.23, 72.57, 75.57, 75.92) | (73.5, 73.83, 76.8, 77.14) | (76.32, 76.68, 79.98, 80.36) | (30.09, 30.35, 32.8, 33.08) | (97.74, 102.03, 151.61, 158.32) | (108.14, 108.39, 110.59, 110.84) | (65.05, 65.25, 67.13, 67.35) | (12.7, 12.7, 12.7, 12.7) |
| Poland | (25.16, 25.29, 26.51, 26.65) | (149.92, 150.61, 156.9, 157.62) | (93277.12, 95222.14, 114572.22, 116963.43) | (81.83, 82.15, 85.05, 85.39) | (83.23, 83.76, 88.54, 89.1) | (75.02, 75.34, 78.26, 78.59) | (20.32, 20.53, 22.49, 22.73) | (60.26, 60.52, 62.87, 63.14) | (110.48, 110.81, 113.8, 114.14) | (71.25, 71.27, 71.43, 71.44) | (11.9, 11.9, 11.9, 11.9) |
| Romania | (18.38, 18.42, 18.81, 18.86) | (103.5, 103.67, 105.26, 105.44) | (175170.43, 179012.1, 217471.96, 222246.27) | (78.7, 79.59, 88.09, 89.09) | (78.2, 79.32, 89.97, 91.24) | (63, 63.66, 69.88, 70.61) | (21.87, 22.09, 24.19, 24.44) | (97.12, 101.96, 160.49, 168.58) | (91.05, 91.13, 91.78, 91.85) | (49.24, 49.48, 51.61, 51.86) | (10.87, 10.88, 10.99, 11) |
| Slovakia | (13.33, 13.43, 14.36, 14.47) | (131.05, 131.62, 136.79, 137.38) | (64542.17, 67013.34, 94466.5, 98104.5) | (82.28, 82.53, 84.76, 85.02) | (82.57, 82.96, 86.44, 86.84) | (81.19, 81.32, 82.49, 82.62) | (26.87, 27.34, 31.86, 32.41) | (95.3, 98.63, 134.85, 139.59) | (92.29, 92.35, 92.95, 93.02) | (52.38, 52.41, 52.71, 52.74) | (12.23, 12.24, 12.29, 12.3) |
| Slovenia | (31.61, 31.81, 33.69, 33.91) | (116.07, 116.35, 118.88, 119.16) | (284834.13, 293974.7, 391388.83, 403990.88) | (79.19, 79.4, 81.31, 81.53) | (80.02, 80.31, 83, 83.31) | (76.32, 76.47, 77.83, 77.99) | (28.97, 29.1, 30.32, 30.46) | (71.17, 72.93, 90.78, 93.02) | (112.76, 113.14, 116.65, 117.05) | (81.28, 81.38, 82.28, 82.38) | (12.1, 12.1, 12.1, 12.1) |
| Group of Criteria | Group of Indicators | Group Weight | Criterion | Indicator | Criterion Weight | Aggregated Weight | Preference Threshold | |
|---|---|---|---|---|---|---|---|---|
| Current State | Forecast | |||||||
| G1 | ICT access | 0.4 | C1 | FTL | 0.2 | 0.08 | 14.26 | 14.23 |
| C2 | MCS | 0.2 | 0.08 | 29.05 | 35.46 | |||
| C3 | IIB | 0.2 | 0.08 | 116679.03 | 226113.21 | |||
| C4 | PHC | 0.2 | 0.08 | 13.83 | 12.79 | |||
| C5 | PHI | 0.2 | 0.08 | 11.16 | 8.75 | |||
| G2 | ICT use | 0.4 | C6 | IU | 0.333 | 0.133 | 15.95 | 15.46 |
| C7 | FBB | 0.333 | 0.133 | 6.92 | 7.33 | |||
| C8 | MBB | 0.333 | 0.133 | 38.42 | 86.72 | |||
| G3 | ICT skills | 0.2 | C9 | SGE | 0.333 | 0.066 | 15.52 | 18.87 |
| C10 | TGE | 0.333 | 0.066 | 18.8 | 22.6 | |||
| C11 | MYS | 0.333 | 0.066 | 1.24 | 1.16 | |||
| Country | IDI Rank | ||||||
|---|---|---|---|---|---|---|---|
| Bulgaria | 0.1594 | 10 | 0.4866 | 10 | −0.3272 | 10 | 10 |
| Croatia | 0.2068 | 9 | 0.2914 | 7 | −0.0845 | 7 | 4 |
| Czech Republic | 0.2219 | 7 | 0.2094 | 5 | 0.0124 | 5 | 6 |
| Estonia | 0.6955 | 1 | 0.0199 | 1 | 0.6755 | 1 | 1 |
| Hungary | 0.2503 | 5 | 0.2734 | 6 | −0.0231 | 6 | 8 |
| Latvia | 0.2947 | 3 | 0.1584 | 3 | 0.1363 | 3 | 3 |
| Lithuania | 0.2858 | 4 | 0.2002 | 4 | 0.0855 | 4 | 5 |
| Poland | 0.2304 | 6 | 0.3166 | 9 | −0.0862 | 8 | 9 |
| Romania | 0.0607 | 11 | 0.5542 | 11 | −0.4935 | 11 | 11 |
| Slovakia | 0.2087 | 8 | 0.3086 | 8 | −0.0999 | 9 | 7 |
| Slovenia | 0.3531 | 2 | 0.1483 | 2 | 0.2047 | 2 | 2 |
| Country | |||
|---|---|---|---|
| Bulgaria | (0.0882,0.1012,0.2957,0.3252) | (0.2564,0.2829,0.5907,0.6124) | (−0.5241, −0.4894,0.0128,0.0688) |
| Croatia | (0.1285,0.1453,0.4214,0.4494) | (0.1613,0.1769,0.4243,0.4564) | (−0.3279, −0.2790,0.2444,0.2881) |
| Czech Republic | (0.1190,0.1314,0.3252,0.3526) | (0.1345,0.1495,0.3940,0.4238) | (−0.3047, −0.2626,0.1757,0.2180) |
| Estonia | (0.4492,0.4898,0.8107,0.8241) | (0.0106,0.0117,0.0709,0.0907) | (0.3584,0.4189,0.7989,0.8134) |
| Hungary | (0.1823,0.1998,0.4595,0.4888) | (0.1158,0.1304,0.3496,0.3806) | (−0.1983, −0.1498,0.3291,0.3730) |
| Latvia | (0.1757,0.1929,0.4459,0.4774) | (0.0862,0.0991,0.3209,0.3559) | (−0.1802, −0.1280,0.3467,0.3912) |
| Lithuania | (0.1637,0.1762,0.3950,0.4274) | (0.1313,0.1494,0.3858,0.4095) | (−0.2457, −0.2096,0.2455,0.2960) |
| Poland | (0.1536,0.1638,0.3028,0.3190) | (0.2342,0.2540,0.4425,0.4629) | (−0.3093, −0.2786,0.0487,0.0848) |
| Romania | (0.0211,0.0287,0.2447,0.2737) | (0.3617,0.3848,0.6653,0.6957) | (−0.6746, −0.6366, −0.1401, −0.0879) |
| Slovakia | (0.1088,0.1214,0.3342,0.3707) | (0.2014,0.2123,0.4273,0.4578) | (−0.3489, −0.3059,0.1219,0.1692) |
| Slovenia | (0.1950,0.2083,0.3724,0.3982) | (0.0917,0.1075,0.3361,0.3609) | (−0.1658, −0.1278,0.2648,0.3065) |
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 0.2027 | 10 | 0.4356 | 10 | −0.2328 | 10 |
| Croatia | 0.2862 | 6 | 0.3048 | 7 | −0.0186 | 6 |
| Czech Republic | 0.2322 | 9 | 0.2756 | 6 | −0.0434 | 7 |
| Estonia | 0.6432 | 1 | 0.0462 | 1 | 0.5971 | 1 |
| Hungary | 0.3327 | 2 | 0.2442 | 4 | 0.0884 | 3 |
| Latvia | 0.3231 | 3 | 0.2157 | 2 | 0.1073 | 2 |
| Lithuania | 0.2907 | 5 | 0.2691 | 5 | 0.0216 | 5 |
| Poland | 0.2348 | 7 | 0.3484 | 9 | −0.1135 | 9 |
| Romania | 0.1422 | 11 | 0.5269 | 11 | −0.3847 | 11 |
| Slovakia | 0.2340 | 8 | 0.3248 | 8 | −0.0909 | 8 |
| Slovenia | 0.2936 | 4 | 0.2241 | 3 | 0.0694 | 4 |
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 0.3599 | 10 | 0.6333 | 10 | −0.2733 | 10 |
| Croatia | 0.4293 | 9 | 0.5706 | 9 | −0.1413 | 9 |
| Czech Republic | 0.4413 | 7 | 0.5586 | 7 | −0.1173 | 7 |
| Estonia | 0.9266 | 1 | 0.0733 | 1 | 0.8533 | 1 |
| Hungary | 0.4746 | 6 | 0.5253 | 6 | −0.0506 | 6 |
| Latvia | 0.6066 | 3 | 0.3933 | 3 | 0.2133 | 3 |
| Lithuania | 0.5319 | 4 | 0.4680 | 4 | 0.0639 | 4 |
| Poland | 0.4359 | 8 | 0.5640 | 8 | −0.1280 | 8 |
| Romania | 0.1773 | 11 | 0.8159 | 11 | −0.6386 | 11 |
| Slovakia | 0.4987 | 5 | 0.5013 | 5 | −0.0026 | 5 |
| Slovenia | 0.6106 | 2 | 0.3893 | 2 | 0.2212 | 2 |
| Country | ||||||
|---|---|---|---|---|---|---|
| Bulgaria | 0.3866 | 10 | 0.6133 | 10 | −0.2266 | 10 |
| Croatia | 0.4786 | 7 | 0.5213 | 7 | −0.0426 | 7 |
| Czech Republic | 0.4495 | 8 | 0.5504 | 8 | −0.1008 | 8 |
| Estonia | 0.8562 | 1 | 0.1437 | 1 | 0.7124 | 1 |
| Hungary | 0.5507 | 4 | 0.4492 | 4 | 0.1014 | 4 |
| Latvia | 0.5523 | 3 | 0.4476 | 3 | 0.1046 | 3 |
| Lithuania | 0.5069 | 5 | 0.4930 | 5 | 0.0139 | 5 |
| Poland | 0.4102 | 9 | 0.5897 | 9 | −0.1795 | 9 |
| Romania | 0.2683 | 11 | 0.7316 | 11 | −0.4632 | 11 |
| Slovakia | 0.4810 | 6 | 0.5189 | 6 | −0.0379 | 6 |
| Slovenia | 0.5590 | 2 | 0.4409 | 2 | 0.1181 | 2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ziemba, P.; Becker, J. Analysis of the Digital Divide Using Fuzzy Forecasting. Symmetry 2019, 11, 166. https://doi.org/10.3390/sym11020166
Ziemba P, Becker J. Analysis of the Digital Divide Using Fuzzy Forecasting. Symmetry. 2019; 11(2):166. https://doi.org/10.3390/sym11020166
Chicago/Turabian StyleZiemba, Paweł, and Jarosław Becker. 2019. "Analysis of the Digital Divide Using Fuzzy Forecasting" Symmetry 11, no. 2: 166. https://doi.org/10.3390/sym11020166
APA StyleZiemba, P., & Becker, J. (2019). Analysis of the Digital Divide Using Fuzzy Forecasting. Symmetry, 11(2), 166. https://doi.org/10.3390/sym11020166





