Abstract
Multibody system dynamics is already a well developed branch of theoretical, computational and applied mechanics. Thousands of documents can be found in any of the well-known scientific databases. In this work it is demonstrated that multibody system dynamics is built of many thematic communities. Using the Elsevier’s abstract and citation database SCOPUS, a massive amount of data is collected and analyzed with the use of the open source visualization tool Gephi. The information is represented as a large set of nodes with connections to study their graphical distribution and explore geometry and symmetries. A randomized radial symmetry is found in the graphical representation of the collected information. Furthermore, the concept of modularity is used to demonstrate that community structures are present in the field of multibody system dynamics. In particular, twenty-four different thematic communities have been identified. The scientific production of each community is analyzed, which allows to predict its growing rate in the next years. The journals and conference proceedings mainly used by the authors belonging to the community as well as the cooperation between them by country are also analyzed.
1. Introduction
Since the amazing designs of Leonardo da Vinci to our days, the complexity of the mechanisms that man has used has only increased. Lighter materials, more economical designs, harder operating conditions, etc., are some of the objectives that the mechanical engineers of our days face. Fortunately, the level of difficulty that we face today is a reflection of the degree of development that has been achieved in mechanical engineering.
A mechanism can be understood as a set of solids interconnected with the purpose of transferring movements and/or forces from a source to an output [1]. The study of mechanisms has traditionally been dealt with by the theory of machines and mechanisms. However, the complexity in the design of mechanisms seems to be unlimited and, therefore, the interest in this branch of mechanics has been growing over time. In a multibody system, the subject of study of multibody system dynamics, in general, one can find rigid and flexible solids interconnected by ideal or non-ideal kinematic joints and subjected to the action of external forces and/or movement restrictions.
The first textbook entirely dedicated to the dynamics of multibody systems appeared in 1977 and was written by Wittenburg [2]. The computational approach seems to be a common characteristic of the works that fall within multibody system dynamics (MBS) and one that confers a character not always present in the whole field of the theory of machines and mechanisms.
In 1977, supported by the IUTAM (international union of theoretical and applied mechanics), the first international symposium on multibody system dynamics (MBS) was held in Munich. It might be said that another important milestone was the big international conference around the MBS that took place in Iowa City in 1983, organized by the NATO advanced study institute. In our days there are many institutions that concentrate their interest on the MBS and in almost all conferences on mechanical engineering a session on MBS is included. The interest continues to grow in such a way that nowadays the already consolidated techniques of the MBS are exported to many fields of technology, such as the dynamics of railway vehicles [3], satellites [4], or nano and micro-mechanical systems [3,5]. In 1997, the international journal Multibody System Dynamics was born including in its first number two review articles signed by A. Shabana [6] and W. Schielen [3] where a journey through the history of the MBS is made and some of the applications that were most beginning to arouse interest were pointed out. In 2007, Werner Schiehlen [7] retrospectively looked at the first ten years of life of the journal Multibody System Dynamics, identifying a multibody system dynamics community and pointing out the research trends during that decade. Today, there are two international journals, Multibody System Dynamics and Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, fully dedicated to MBS and many others that accept contributions from this field. The present paper proposes a step forward in the characterization of the MBS network. By using an automated paper metadata extraction tool, together with visualization and programming tools, a massive amount of documents will be analyzed to look for thematic communities that have grown inside the MBS network around certain topics. This will allow to understand which are the topics in which the research activity is more intense and to find communities that might be unknown for many members of the MBS network. In addition, once the communities are defined this paper aims at studying the activity trends along time.
The tools developed by MBS are supported by the most elementary laws of physics. In fact, already d’Alembert in 1743 [8] raised the equations of a system of rigid bodies subject to certain constraints, where the concept of reaction forces was already included. However, the first systematic analysis of a system of interconnected bodies was made by Lagrange in 1788 [8] laying the bases of what is today known as analytical mechanics. The equations of the first and second kind presented by Lagrange [8] constituted the DAE systems (differential algebraic equations) and ODE (ordinary differential equations) that describe the motion of a multibody system. Unfortunately, at that time there were no numerical techniques nor computers that would allow to obtain the solution of any system. Today, the complexity of the equations of motion has motivated the search for procedures that allow them to be obtained with the least possible effort. A wide review of these procedures can be found in the work of H. Bremer [9].
The development of computer science and numerical techniques has been, therefore, of central importance for the consolidation of the MBS. Several general-purpose programs for the analysis and simulation of multibody systems such as ADAMS, RECURDYN or DADS have been released to the market. In addition, there are open source simulation codes that might be used in MBS applications. Multibody system dynamics follows a continuous development and simultaneously offers tools in an excellent state of maturity.
In a multibody system, the absolute motion of a solid with respect to a reference, which is defined by a set of absolute coordinates, can be considered as the superposition of large rotations and deformations. This motion with respect to the inertial reference is mathematically defined by the time evolution of a set of variables. If a body is rigid, there is a minimum of six variables that completely define its spatial motion. In addition, the motion of a rigid body can be described by a larger set of variables that satisfies certain relationships. Such relationships translate into mathematical constraint equations that are solved together with the system differential equations of motion. Nevertheless, if the bodies are flexible the number of degrees of freedom is in principle infinite. The concept of symmetry has been used many times to find simplified and computationally efficient multibody models, either rigid or flexible, in vehicle dynamics, biomechanics and other fields of application.
The dynamics of the rigid bodies included in a certain multibody system can be described by different sets of coordinates. In some cases it is possible to use the Lagrange equations of the second kind, that is, using a minimum set of coordinates equal to the number of degrees of freedom [8]. In such a case, one talks about ’independent coordinates’. However, the use of this type of coordinate is not systematic and, therefore, the programming of the equations of motion is reduced to some particular cases.
Using a larger set of variables to obtain the equations of motion usually leads to less cumbersome mathematical equations [10]. The dynamic problem can be formulated according to Lagrange’s equations of the first kind, which constitutes a system of differential algebraic equations, and the set of coordinates are called ’dependent’.
Within dependent coordinates, ’relative’, ’reference point coordinates’ or ’Cartesian’ coordinates are used. Relative coordinates refer to position or orientation of any body with respect to another one to which it is connected [11]. On the other hand, the reference point or Cartesian coordinates refer the position and orientation of each body to a global frame [12]. In general, reference point coordinates contain the components of a vector of position and a set of angles or angular parameters that define the orientation of a body reference frame in the global frame.
During the 1980s, a new methodology for a rigid multibody system based on fully Cartesian coordinates appeared. Such coordinates were known as ’natural coordinates’ [13,14]. Unlike reference point coordinates, which include angles or angular parameters [15], the natural coordinates are composed of vectors of position of material points or vectors that define trajectories in solids [13], that is, exclusively Cartesian coordinates. The method of natural coordinates allows sharing coordinates between different solids since, in general, such coordinates belong to points or vectors that define the kinematic joints that connect solids to each other. This feature results in a significant reduction in the total number of coordinates required to model a mechanism. Unda et al. [16] performed a comparative study between the use of natural coordinates and the point of reference, concluding that the number of natural coordinates is always lower than that of the reference point coordinates.
The dynamics of flexible multibody systems (FMBS) has been a subject of major interest over time. In 2003, Wasfy and Noor [5] published an exhaustive bibliographic review (including 877 references) of the work carried out in the field of flexible MBS. In that reference, the different formulations for FMBS are classified into three groups according to the type of reference frames used to define the system variables. These three groups are the methods that use a floating frame of reference, those that use co-rotational reference frames and those that use the inertial frame only. The description of the deformation that a flexible body undergoes during general motion usually requires the use of a large number of coordinates. There are many approaches that have been successfully used in MBS, each one characterized by a certain choice of coordinates, measurement of deformations, etc.
The floating frame of reference formulation (FFR) appeared in the 1960s as a result of the research carried out in the field of machine dynamics, aerospace applications and the finite element method [6]. As a logical extension of the formulations based on reference point coordinates, the FFR uses the description of the motion of a moving reference frame linked to the flexible body to represent large rotations. The motion of such a reference frame can be described using any of the coordinate sets used for rigid solids. The most used set of coordinates has been the reference point coordinates [17]. Moreover, the natural coordinates are successfully employed to describe the motion of the floating frame of reference [18]. In the FFR, deformation has been described by different techniques such as the modal expansion [18] or the finite element method [17]. The FFR is mainly appropriate for applications where deformations are small, although non-linear effects such as geometric stiffening could also be addressed in this formulation [19]. In addition, the FFR allows the use of component mode synthesis [17] to reduce the number of system coordinates.
Co-rotational formulations use a frame of reference, called the co-rotational frame, which follows approximately the rigid body motion of each finite element. In this sense, this formulation differs from the FFR, which uses a single reference system for all the elements of the same body. This procedure was initially used by Belitschko and Hsieh [20] to triangular plate elements and two-dimensional beam elements. One can follow different criteria to define the co-rotational frame in which its motion does not need to coincide with the motion of any point of the finite element. This formulation made possible the use of non-isoparametric elements by incremental procedures, given that these elements can only describe small rotations. When using this approach, the use of integration methods that conserve energy and momentum is important, especially when the number of time increments used in the integration is large [20]. In co-rotational approaches, geometrically non-linear effects are incorporated automatically. However, component mode synthesis is not easily applicable.
Methods based on inertial coordinates use a single reference frame to describe the general motion of the flexible body. All variables are defined in the global inertial frame. The first applications of this kind of method in MBS are the works of Simo [21] and Simo and Vu-Quoc [22,23]. In the formulation of Simo [22], the position of an arbitrary point in an element is obtained by interpolation of the position vectors of the nodes and the rotations of the extreme sections. It is possible to use a similar description in which, instead of interpolating rotations that define the orientation of the cross section reference frame, one interpolates the vectors of the element frame itself [14,24]. This description must include non-linear constraints that ensure orthogonality and normality of the frame vectors. Both formulations, that of Simo [21,22] and Avello [24], fit within the so-called ’large rotation vector formulations’.
The formulation in absolute nodal coordinates, the absolute nodal coordinate formulation (ANCF) [17,25,26], also uses a set of coordinates defined in an inertial reference frame. This formulation was originally developed using a local reference frame to measure the deformations of the finite elements [17,27], so it could be considered as a co-rotational method. However, subsequent works on this formulation focused on the use of the inertial reference frame as the unique frame to measure deformations in the finite elements [28,29,30,31]. For this reason, non-linear deformation measures such as Green–Lagrange stress tensor where introduced. From these works on, the ANCF can be considered a fully inertial method. The identifying characteristic of the ANCF is the use of partial derivatives of the nodal position vector with respect to the geometrical parameters of the elements, also called slopes, as nodal variables, instead of small or large rotations [17]. The element mass matrix is constant in most of the developed elements and no terms appear due to centrifugal or Coriolis inertial forces in the equations of motion. The ANCF lacks some of the problems associated with incremental formulations related to the description of rigid body inertia [32]. From the work of Omar and Shabana [29], finite isoparametric elements are parametrized as surfaces, in two-dimensional models, or volumes [30,31,33]. In beam or plate elements, shear and cross-section deformations are inherently included. The use of a non-linear deformation measure as the tensor of Green–Lagrange together with the volumetric description of the kinematics of beam elements gave rise to an inaccurate displacement field due to several numerical locking effects [34,35]. With time, many of these numerical shortcomings were overcome. Over the years, many researchers have contributed to the development of the ANCF, see, for instance, references [36,37,38], and many applications have been dealt with by this formulation. An extensive review on the use and application of the ANCF can be found in Gerstmayr et al. [39].
After briefly introducing some important issues of the multibody system dynamics, the work described in this document is outlined as follows. In order to analyze the presence of thematic communities within the field of multibody system dynamics, a massive amount of data has been collected from Scopus, the well acknowledged abstract and citation database owned by Elsevier. This information is gathered with the help of a bot as explained in the next section. This information is processed in a visualization software called Gephi [40], which is specially designed to explore large networks. The information is represented as a large set of nodes with connections to study their graphical distribution and explore geometry and symmetries. A randomized radial symmetry is found in the graphical representation of the collected information. The main results of the analysis are the detection of a main community and a number of thematic communities, twenty-four of which are identified. A summary and conclusions drawn from the analysis are included in the last section.
2. Methodology
This section explains the methodology followed in this work to obtain and analyze the information on scientific publications in the field of multibody system dynamics. The methodology consists of two main steps. In the first step, specific software is used to gather the information from the literature, in particular the relevant information from the publications indexed in Scopus. In the second step, all the data obtained is processed to determine the relationship between the different elements and graphically identify the different scientific collaboration networks.
2.1. Automatically Gathering Information
The information was obtained from the Scopus database. Elsevier’s Scopus was chosen because of its extensive coverage of peer-reviewed journals, being slightly higher in number than that of Web of Science [41]. To get the information, the research network bot (ResNetBot) [42] was used. ResNetBot is a software for the automatic extraction of information from Scopus and has previously been used in bibliometric studies in different scientific fields [43,44]. ResNetBot makes use of the API interface of Scopus to obtain information from articles, authors and institutions. The way this bot works is shown in the flowchart of Figure 1, which is divided into three phases:
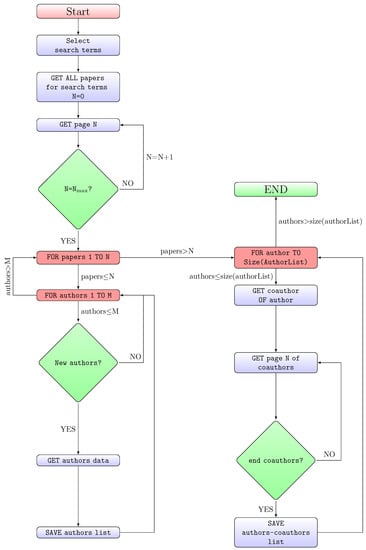
Figure 1.
Flowchart of the implementation of ResNetBot.
- (1)
- Get publication data. In the first phase ResNetBot obtains information from all publications (journal papers, conference proceedings and books) that contain the words ’multibody’ or ’multi-body’ in the title, abstract or keywords and are stored in the bot database.
- (2)
- Get author data. For each unique author identification number (Author ID) extracted in the previous phase, ResNetBot obtains and stores the information available in Scopus about the author: Affiliations, publications and dates, number of citations and h-index.
- (3)
- Collect collaboration networks. For each Author ID, the bot gets the Author IDs from the co-authors it has collaborated with, along with their affiliation, city and country.
Analyzing the papers that include the words ‘multibody’ or ‘multi-body’ in the abstract, keywords or title does not lead to the complete set of documents that could be included in the field of multibody system dynamics. In fact, a significant number of papers published in the journal Multibody System Dynamics do not meet this criterion. This research does not claim to be an analysis of the complete literature on multibody system dynamics. Instead, this research aims at collecting a sufficiently large amount of documents so that the different communities detected would be represented. According to the large number of documents that are analyzed (see following sections) the objective seems to have been fulfilled.
The data collected by ResNetBot is structured according to its corresponding field and is stored as a set of plain-text files using the JavaScript Object Notation (JSON) format [45]. Because the Scopus database contains a large amount of information from different sources, it is common to find inconsistencies in the data [46,47]. Thus, for example, when checking the keywords obtained from publications, one can find different expressions such as ’multi-body system dynamics’, ’multibody system dynamics’ or ’dynamics of multibody systems’ with the same meaning. To resolve this inconsistency some of the refining algorithms of the OpenRefine software [48] have been applied, including the nearest neighbor and key collision methods [49,50,51]. Finally, all collected and refined information is organized in spreadsheets and stored in a local database.
2.2. Graphical Detection of Communities
Within a set of data (nodes) with common characteristics, a community consists of a group of nodes that are more interconnected with each other than with the rest of nodes in the network. The problem of community detection therefore seeks to identify those nodes that, for a given special relationship, are connected in a denser way [52,53]. In bibliometric analysis the nodes may be the publications, and the connections the citations between them. Thus, a community could be determined as those groups of publications that are most cited in between them. In a different analysis the nodes may be the authors and the connections between them indicate that they have collaborated in some publication (they are co-authors). In this case a community will be identified as that group of authors who carry out more research together.
Given the large amount of data collected by ResNetBot, to help identify the presence of communities it is necessary to process the information using statistical analysis and graph-based visualization tools. The graphical representation will make it possible to visually identify the relationship between the nodes in the network. A node is represented as a point or vertex and the relationships between two nodes are shown with a line or edge joining both nodes. Graph-based visualization software includes several powerful visualization tools that allow detailed analysis and interpretation of graphical results. In this work, the open-source graph visualization tool Gephi [40] has been used.
Among others features, Gephi allows to modify the size of the nodes and the thickness of the edges according to some characteristics defined by the user, to group in the space the nodes that are more interconnected and to use different colors to identify in a fast way the relation between them and the presence of communities. For the detection of communities within the data network, Gephi uses modularity. Modularity [54] applies objective functions for the detection of communities and provides numerical values that represent the accuracy of the community structure. Together with the graphical visualization of the results, Gephi also offers a comprehensive statistical analysis of the data.
3. Analysis of Scientific Production and Community Detection
In order to find a sufficiently large amount of data that could be representative of the scientific work and authors related to multibody system dynamics, Scopus was used. An advanced query was launched, giving as a result a list of 20,050 papers including the words ’multibody’ or ’multi-body’ either in the title or in the abstract or in the keywords. The query was formulated as follows
(AUTHKEY(multibod*) OR AUTHKEY(multi-bod*) OR ABS(multibod*) OR ABS(multi-bod*) OR TITLE(multibod*) OR TITLE(multi-bod*)).
This query was launched at the end of July 2019 and included documents from 1953 to 2020. As explained in the previous section, all the information was downloaded with the help of the ResNetBot.
In order to process all the information in the visualization software Gephi, a list of nodes was generated, a node being a published document which is visible in SCOPUS. It must be recalled that SCOPUS includes journal papers, conference proceedings and books. A list of connections or edges between the nodes is generated by using the reference of the papers. Therefore, a document appears in the graph connected to all the documents it cites as well as to those documents that cite it. Loading the nodes and the relations, one can extract a lot of information from this massive amount of data.
3.1. Detection of a Main MBS Community
The first important result that can be visualized in Gephi is that not all the documents should be included in the MBS community. To explain this issue, Figure 2 is used. Figure 2a is the result of visualizing the 20,050 nodes with their relations. The layout tool ForceAtlas2 was used to distribute the documents using the concept of gravity to generate attraction between the nodes. Once this is done, Figure 2a appears showing that there is a large amount of papers, distributed in a ring shaped area that are not connected to the central community. This may be because these papers do not use the words ’multibody’ or ’multi-body’ in the same sense as the members of the community, and, in fact, they do not cite papers that belong to the main community. Therefore, a main community called the multibody system community or MBS community is detected and shown for the first time in Figure 2b, where the unconnected documents (those in the ring) have been filtered.

Figure 2.
(a) Graph of all papers including either ’multibody’ or ’multi-body’ in the title, abstract or keywords; (b) graph of all the papers in the left picture showing connection (citations) between them.
According to the previous procedure, after filtering, the MBS community detected has a total of 11,511 documents.
In order to understand the most important topics that describe the community, the keywords of all the documents were collected. Using a Python subroutine, they were all translated to the lower case and the singular forms. A total of 36,774 keywords were collected. Then, the function ’Counter’ from the module ’Collections’ was used to count the number of appearances of all keywords. Table 1 shows the most utilized keywords in the document analyzed. From a view to the list of keywords, one may conclude that:

Table 1.
List of most commonly used keywords.
- The most used keyword is multibody dynamics.
- Multibody systems documents are mainly concerned with dynamics.
- Simulation is a key issue in the community.
- Flexibility appears as a top issue in the community.
- It is interesting that one of the well known approaches for flexible multibody systems, the absolute nodal coordinate formulation, has achieved a high position in the rank, showing the large development that this formulation achieved in the last years.
- ‘Vehicle dynamics’, ‘optimization’ and ‘friction’ are highly important issues according to their position in the rank of used keywords.
3.2. Detection of Thematic Communities
Within the main MBS community, one can find some thematic communities by analyzing the modularity class of all the papers included in it. The modularity tool in Gephi, which relays the algorithm from Blondel et al. [55], also known as the Louvain method, has been run with a resolution parameter value of 1.0, finding 32 communities with different sizes. Modularity is a scale value that measures the density of relations (citations) inside communities to relations outside communities. All these communities are shown in Figure 3 in different colors. The 32 detected communities have different sizes (number of papers included) ranging from 1103 for the biggest one to 4 for the smallest one. Since such small sizes do not seem to realistically define a community, only the first 24 detected communities have been analyzed in this work. The smallest of these 24 communities includes 152 papers, which allow one to understand the goal of such a community. In what follows, the 24 analyzed communities have been numbered from the largest (comm-1) to the smallest (comm-24).

Figure 3.
Graph of the detected communities inside the main multibody system dynamics (MBS) community.
Figure 3 shows a representation of the main MBS community and the 32 thematic communities. The community layout, that is, the distribution of individuals, was obtained by using the ForceAtlas2 algorithm included in Gephi. This algorithm uses the concept of gravity to calculate the attraction of the individuals. In the figure, all papers that cite one another are connected by an edge. The shape of the thematic communities is also meaningful. For a shape, size and distribution analysis of the communities, the selected 24 communities were plotted separately using the same reference frame in Appendix A. It may be noted that the shapes of the different communities are quite different. For example, there are some communities that are well concentrated in areas of the main MBS community, while others are spread and overlap with each other. This behavior might be a consequence of the main topics of the community being either too specific or too general. The ones dealing with general topics are connected to documents of other (maybe many) communities and therefore are most likely to appear spread.
Once the communities are automatically identified by the modularity class tool, a careful review of the documents included in each community allows the identification of the main goals. It is interesting that every community usually has a number of highly cited documents, which is represented with a larger circle in Figure 3. The size is proportional to the number of relations (citations). In view of these goals, a representative name is given to each thematic community. The twenty-four identified communities are presented as follows.
- comm-1
- Flexible multibody systems in general. This is the largest community in terms of published documents, with a total of 1103. The documents in it cover many aspects related with the flexibility in the presence of large rotations and deformations. Significant attention has been paid in this community to the pioneering work of Kane et al. [56] about centrifugal stiffening in rotating beams. A very complete review of the work in this community was carried out by Noor and Wasfy [5].
- comm-2
- Railway. This community, with 1027 documents, deals with the dynamics of railway systems in general. There are many documents that focus on the problem of wheel/rail contact. As a highly cited reference, the work of Shabana et al. [57] presents an elastic contact method which seems to be highly efficient for simulation purposes.
- comm-3
- Absolute nodal coordinate formulation. Interestingly, a well structured community devoted to the development and application of the absolute nodal coordinate formulation is found with 963 documents. According to the shape and location of this community, see Appendix A, the documents are clearly attracted by the documents of this community but also by some of the flexible multibody systems in general. A particular book by Shabana [17] is a highly cited document. There is an extensive review of the work done by this community by Gerstmyer et al. [39].
- comm-4
- Contact and non-ideal joints. A community dedicated to contact problems with 890 references is found. This community is easily identified by the modularity class tool and appears well concentrated, see green community in Appendix A. Many documents have paid attention to elastic or continuous contact models with the work of Lankarani and Nikravesh [58] and Machado et al. [59] as highly visible references. Clearance in joints is also a highly investigated topic within this community.
- comm-5
- Computational aspects of differential algebraic equations (DAE). The particular numerical problems presented in differential algebraic equations (DAE) have attracted many researchers over time. Problems such as the numerical fulfillment of constraint equations, the numerical stability of integrators, etc., are present in this community with 841 documents. The review work of Bauchau and Laulusa [60] and the one about projection methods by Bayo and Ledesma [61] are highly cited within this community.
- comm-6
- Optimization and sensitivity. Optimization and sensitivity analysis in multibody systems deserves the interest of many researchers because of their benefits for design. The work of D. Bestle [62] has been a pioneer in this community and counts 592 references in our analysis.
- comm-7
- Two-wheelers. The dynamics of motorcycles and bicycles have been a specific topic of research for many authors of the multibody system network. The work of Cossalter and Lot [63] about a motorcycle multibody model is a remarkable reference that identifies the goals of this community well. An already old review by W. Kortüm [64] has received many citations from documents from a community that includes 525 works.
- comm-8
- Biomechanics. The use of multibody dynamics techniques in biomechanics has experienced a huge development in recent years, with even the release of proprietary (AnyBody) as well as open software (OpenSim) highly extended in the community which, counts 517 documents. Multibody models for biomechanics usually include the dynamics of the biological actuators and are redundantly actuated, requiring the use of optimization methods. A highly cited work is the one by Damsgaard et al. [65] where the software AnyBody is presented to the community. Some of the results of the authors of this community have served as a basis for other applied and fundamental investigations, see, for example references [66,67].
- comm-9
- Accurate and efficient integrators. This community of 459 documents is mainly devoted to the development of efficient and accurate numerical integrators. The documents belonging to this community are well connected to those in the flexible multibody systems in general and the absolute nodal coordinate formulation communities. The topic of energy and momentum conserving numerical methods is one that is more present among the documents of this community. The work of Bauchau [68] and Betsch [69] have received many citations from the community.
- comm-10
- Robots as multibody systems. This community with 429 documents is concerned mainly with the applications of multibody systems techniques to robotics, including robots with flexible linkages, trajectory planning through optimization or the use of recursive formulations. There appears a highly cited book by A. Jain [70] that exemplifies the goals of this community.
- comm-11
- The vibration and transfer matrix method. Multibody systems containing elastic or restoring forces are susceptible of vibration. Linear and non-linear equations of motion are many times obtained with the methods of multibody systems. The transfer matrix method, which is connected to vibrating systems and extended by Rui et al. [71] to general multibody systems has a high impact in the works belonging to this community, which counts 421 documents.
- comm-12
- Aeronautic applications. The methods of multibody systems have encountered a large development and application in aeronautics as reflects this community with 406 documents. Problems of aeroelasticity, modeling of specific parts as rotors, landing gears, etc., or the stability of flight are presented in the documents of this community. The work of Masarati et al. [72] has been highly cited within the community.
- comm-13
- Marine applications. A total of 401 documents are encountered in this community, where hydrodynamic interaction, floatation and drift issues are of interest and are analyzed together with multibody models. There is a recent review of applications of MBS to ships and offshore structures by Lee and Roh [73].
- comm-14
- Powertrain elements. This community counts 399 documents that are mainly devoted to important aspects of powertrain dynamics as explained by Novotny and Pistek [74]. The high angular speeds in powertrain systems together with the flexibility of some components were the causes for the application of MBS techniques in this field, giving birth to a specific community. The dynamics of crankshafts is a topic of high interest in this community.
- comm-15
- Road vehicle dynamics. Multibody system dynamics has encountered a large application in vehicle system dynamics. The existence of this community with 321 documents probes this fact. The generation of a full vehicle multibody model with detailed suspension systems or the analysis of ride comfort or handling are hot topics in this community. The book by Blundell and Harty [75] is a highly cited reference in the community.
- comm-16
- Wind turbines. The analysis and simulation of wind turbines is the subject of many papers from this community of 308 documents. Within it, the modeling and simulation of gear box dynamics is a hot topic as reported by Helsen et al. [76]. In addition, modal analysis and aeroelasticity issues are also accounted for in many documents.
- comm-17
- Complex terrain and tracked vehicles. A community with 301 documents dedicated to the modeling and simulation of tracked vehicles has also been found. Among others, the work of Rubinstein and Hitron [77] has received many citations. Due to the special nature of this kind of vehicle, this community pays great attention to the modeling of complex terrains.
- comm-18
- Non-smooth contact. This community of 258 documents in our analysis focuses also on contact, but with a slightly different hint related to the discretization of the contact surfaces. Non matching discretizations are studied with the help of the concept of dual Lagrange multiplier space, see reference [78]. In general, the works found in this community are strongly related with the finite element method in multibody contact situations, see Laursen and Simo [79], with geometric problems arising from the different discretizations of the contact surfaces. Friction and frictionless situations are considered with a focus on the formulation of equations and constraints more than on the frictional phenomenon.
- comm-19
- Space applications. There appeared a community with 227 documents that applies the methods of multibody system dynamics to space problems as attitude control of satellites or assembly of space structures by robotic manipulators. Control issues both for linear and nonlinear multibody systems are important in this kind of application, and is most of the time realized by autonomous systems. As an example, the work of Umetani and Yoshida [80] has a significant impact in the community.
- comm-20
- Friction. A community with a size of 196 documents around friction is found. Since friction requires contact, this community is related with both the contact and non-ideal joints (comm-4) and the non-smooth contact (comm-18) communities. It might make sense to group together the three mentioned communities into a large one (1295 documents). However, the particular hint of this community seems to be the friction phenomenon itself and for this reason the entity of the community has been respected. Complementary problems have been useful for the modeling of friction forces as, for example, reported by Anitescu and Potra [81].
- comm-21
- Flapping wings. A community with a size of 182 documents mainly focused on the analysis and modeling of flapping wings has been detected. Within this community one may find documents dealing with insect flight, micro aerial vehicles or different kinds of ornithopters, see reference [82]. Flapping wings are modeled as flexible structures for which the methods of flexible multibody systems encountered a challenging application.
- comm-22
- Accident reconstruction. Multibody system dynamics has been successfully applied to the reconstruction of accidents. Among other studies the kind of accident due to impacts of vehicle/pedestrian or falls are the most common. The dynamic simulation has been used to evaluate potential injuries as well as safety conditions. For example, in the highly cited document by Crocetta et al. [83] the influence of the vehicle front-end design on pedestrian ground impact is investigated. This community counts 169 documents in this analysis.
- comm-23
- Fatigue and life assessment. A community of 162 documents with the fatigue of materials as a main issue has been detected. Flexible multibody dynamics methods have proven to be useful for the evaluation of alternating stresses that can be used together with fatigue failure criteria for life assessment of components. As an example, the work of Dietz et al. [84] in the context of railway dynamics has received many citations.
- comm-24
- Computer numerical control (CNC) machining. This is the smallest community analyzed in this paper, with a size of 152 documents. Machining by computer numerical control (CNC) units is also fertile soil for application of multibody system dynamics. In this community, the evaluation of geometrical errors in the trajectory of the tool and their compensation are of major importance. CNC machines have different designs, with many axes and large mobility, that are successfully modeled with multibody system dynamics techniques. As a highly representative reference, one may take the work of Zhu et al. [85].
As a consequence of the common aspects of the documents of each community, by examining a list of the most used keywords one may also understand the goals of each community. Table 2, Table 3, Table 4 and Table 5 show the most used fifteen keywords in each community. In order to find a more meaningful list of keywords for each community, the keywords ’multibody’, ’multibody dynamics’, ’multibody system’ and ’multibody system dynamics’ were excluded.

Table 2.
List of most commonly used keywords in communities 1 to 6. The number of appearances of the keyword is included in parenthesis.

Table 3.
List of most commonly used keywords in communities 7 to 12. The number of appearances of the keyword is included in parenthesis.

Table 4.
List of most commonly used keywords in communities 13 to 18. The number of appearances of the keyword is included in parenthesis.

Table 5.
List of most commonly used keywords in communities 19 to 24. The number of appearances of the keyword is included in parenthesis.
3.3. Activity of the Communities along the Time
Once the communities have been introduced, it is easy to analyze the activity of each community. In this work, the activity is measured by the number of documents published per year in the community. This was done again by using the Counter subroutine of Python Collections library. The period analyzed comprises the years from 1970 to 2018. While some information is available for 2019 and 2020, these years were excluded from the analysis because the information is not complete. To reduce the noise in the trend lines of each community, a moving average using the numbers of two consecutive years was used. Figure 4 shows the trend lines obtained for the twenty-four communities.
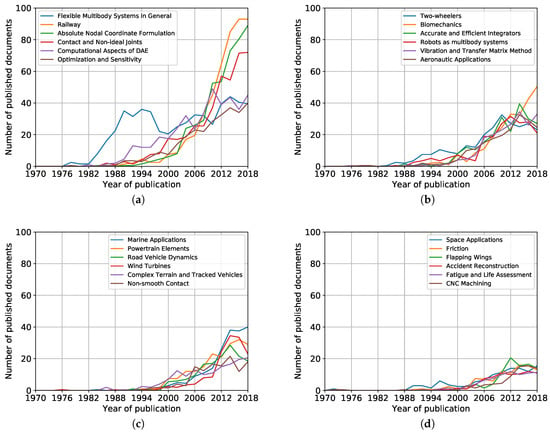
Figure 4.
Activity of the communities measured as the number of journal papers per year: (a) comm-1 to comm-6; (b) comm-7 to comm-12; (c) comm-13 to comm-18; and (d) comm-19 to comm-24.
In general, Figure 4 shows a continuous increase in the number of published documents in all communities. From a look at Figure 4a, one may see that Flexible Multibody Systems in General was the first community to grow with a great interest in the eighties and early nineties. While it continues with moderate activities, other communities as Railways, Absolute Nodal Coordinate Formulation and Contact and Non-ideal Joints show a large activity and growing trend for the coming years. From Figure 4b, it is interesting how Two-wheelers was an early developed community that nowadays follows a moderate activity. The growing activity of the Biomechanics community predicts an increasing interests for the near future. From Figure 4c,d, the increasing activities of Marine Applications and Space Applications are remarkable.
3.4. Most Used Journals by MBS Community Members
Gephi allows an easy analysis of which journals prefer to use the authors of the MBS network. The analysis was done as follows. The total of 11,511 documents were filtered by type, selecting only journal publications. In this way, a total of 7579 journal publications were considered. Table 6 shows the percentages of the 7579 journal publications that were published in the fifteen most used journals. From a view to the table, it remains clear that the main journal is Multibody System Dynamics, which since 1997 has consolidated as a highly reputable journal. The position in the rank of two journals from the context of vehicle dynamics (SAE Technical Papers and Vehicle System Dynamics) is remarkable. With percentages close to 2.5%, a third group of journals is composed of Nonlinear Dynamics, Journal of Computational and Nonlinear Dynamics and Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics.

Table 6.
List of the fifteen journals that have published more papers belonging to the MBS community.
3.5. Most Used Conference Proceedings by MBS Community Members
In a similar manner, the most used conference proceedings were analyzed. The total of 11,511 documents were filtered by type, selecting only conference proceeding publications. In this way, a total of 3236 conference proceeding publications was considered. Table 7 shows the percentages of the 3236 documents that were published in the fifteen most used conference proceedings.

Table 7.
List of the fifteen conference proceedings that have published more papers belonging to the MBS community.
From Table 7 it can be concluded that the Proceedings of the ASME Design Engineering Technical Conference together with the very successful Proceedings of the ECCOMAS Thematic Conference on Multibody Dynamics are the leading options in terms of number of published documents. However, it must be clarified that ASME publishes within the Proceedings of the ASME Design Engineering Technical Conference articles from conferences organized from 2001 to today. The presence in the rank of the Proceedings of the International Offshore and Polar Engineering Conference or Proceedings of the International Astronautical Congress are understood from the existence of thematic communities that have an affinity with the topic of these conferences. For the sake of comparison, the percentage of papers published in the proceedings of some serial conferences were analyzed next. To do that, all editions of the ASME Design Engineering Technical Conferences were grouped together. The same thing was done for all editions of the Proceedings of the ECCOMAS Thematic Conference on Multibody Dynamics and the Proceedings of the International Astronautical Congress, IAC and the results are shown together in Table 8. The percentage shown is calculated from the total number of conference proceeding papers.

Table 8.
Conference proceedings grouped by series that have published a significant amount of papers of MBS community.
3.6. Analysis of Collaborations of Authors by Country
As explained in Section 2, all the authors that have published a document including the words ’multibody’ or ’multi-body’ in the title, abstract or keywords were considered. The information of a total of 30,502 authors was gathered and analyzed. This massive amount of information is represented in Figure 5a where the layout algorithm ForceAtlas2 has been used to find a meaningful representation. As mentioned before, the ForceAtlas2 layout is based on the concept of gravity, which is used to generate attraction between connected nodes. On the contrary, non-connected nodes generate repulsion between each other. As may be seen in the figure, there is a group of authors represented in green near the center of the graph that show no connection with surrounding authors. The same situation is shown for a group represented in gray near the mid-south part of the graph. Both groups of authors are strongly attracted between them but unconnected to the rest of the nodes. In addition, there are small clusters of authors allocated at the outermost part of the graph. Again, the giant component filter of Gephi has been used to separate the large network of authors contributing to the MBS communities. The MBS network is represented independently in Figure 5b. Once the main network of authors, which counts 9148 authors, is obtained, it will be redistributed with the ForceAtlas2 layout. The result is shown in Figure 6 where each color represents a different country. It must be emphasized that the affiliation considered for each author is the current (or last) one. The analysis presented does not take into account that an author might have had a different affiliation in the past. Therefore, the results shown in this section may be considered as a current picture of the community.

Figure 5.
(a) Graph of all authors who have published a paper including the word ’multibody’ in the title, abstract or keywords; (b) graph of all authors in the left picture that are included to the MBS network.
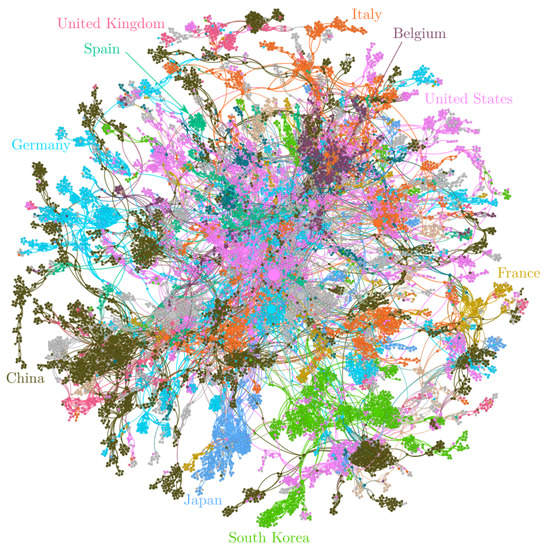
Figure 6.
Graph of authors network by country of affiliation after redistribution.
The shape and location of the different countries in Figure 6 is interesting. Note that when a color is too concentrated in a small area, it means that the authors of that country are mainly working within them, that is without international cooperation. This is approximately the case of South Korea and Japan, which at the same time show large percentages of authors in Table 9. This table shows the percentage of authors that belong to the twenty countries with the largest number of researchers in the network. The top ten countries have been colored in Figure 6. On the other hand, the authors of United States (purple color) are spread all along the graph, which means this country has a large international cooperation. In Figure 6, there are some nodes that have a comparatively large size. The size in the graph is proportional to the number of connections of the node. In this way, the largest node in the graph is in purple color and corresponds to Prof. A. Shabana. It must be mentioned that there is a certain amount of nodes in gray. They all belong to the rest of the countries not included in the top ten.

Table 9.
Table of the twenty most active countries in MBS according to the total number of researches that have published at least one document.
4. Summary and Conclusions
This work contains an analysis of a massive amount of information about publications and authors in the multibody system dynamics community. The information was gathered automatically by a dedicated bot that connects to the SCOPUS database. The amount of authors and documents considered are 30,502 and 20,050, respectively. The query to SCOPUS was launched in July 2019. This massive amount of data is treated with the software Gephi, which allows for filtering and detecting communities. The modularity class was used to detect a high number of communities within the multibody system dynamics network. Each community was commented on and a representative reference was given for each one. Once the communities were detected, the scientific production of each community was studied chronologically. The most used journals and conference proceedings were obtained. Finally, the cooperation of authors was studied by country. The main conclusions of this work are enumerated as follows:
- ResNetBot was highly efficient at collecting a huge amount of data from the abstract and citation database, SCOPUS. Such an amount of data could be analyzed by using the software Gephi.
- There appear to be 32 communities from the analysis of the modularity. In this paper, only the 24 largest communities were studied. The community detection carried out showed a reasonable result since the documents conforming to a community have meaningful similarities and common objectives.
- The five largest communities are flexible multibody systems in general, railway, absolute nodal coordinate formulation, contact and non-ideal joints, computational aspects of DAE.
- The recent activity analyzed by communities predicts an increasing interest in railway, absolute nodal coordinate formulation, contact and non-ideal joints and biomechanics.
- The fifteen journals most used for publishing by researchers were obtained, with the journal Multibody System Dynamics being the one that has published the largest number of papers from the analyzed network.
- The fifteen conference proceedings most used for publishing by researchers were obtained. The list included conferences from fields like astronautical sciences or offshore engineering.
- Authors from many countries are contributing to the multibody system dynamics communities. The most active countries in the network have been found. Their cooperation was analyzed, obtaining interesting patterns of collaborations in the graph.
As could be checked, the multibody system community continues to grow and attract researchers. Its formalisms and techniques have been applied in many fields from railway to the simulation of the flight of ornithopters or the reconstruction of accidents.
Author Contributions
D.G.-V. performed the literature review and article writing. D.G.-V., A.A., J.L.-M. and F.G.M. analyzed the data using community detection methods. D.G.-V., A.A., J.L.-M. and F.G.M.: Research idea, article writing, and formatting; they jointly contributed to the structure and aims of the manuscript, paper drafting, editing, and review. All authors have read and approved the final manuscript.
Funding
This research has been supported in part by the Ministry of Science, Innovation and Universities at the University of Almería under the program "Proyectos de I+D de Generacion de Conocimiento" of the national program for the generation of scientific and technological knowledge and strengthening of the R+D+I system with grant number PGC2018-098813-B-C33.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Fingerprint Images of all Detected Communities
This section shows a picture of each one of the twenty-four analysed communities, where the shape, distribution and size of each one can be appreciated (Figure A1 and Figure A2).
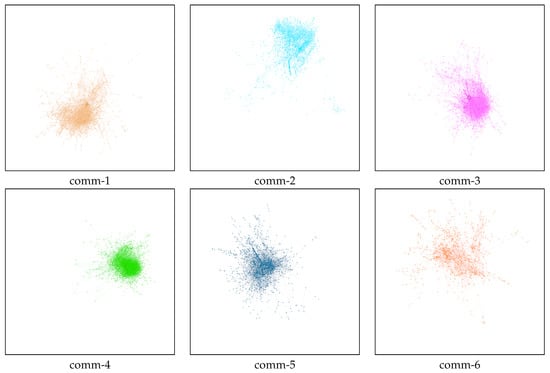
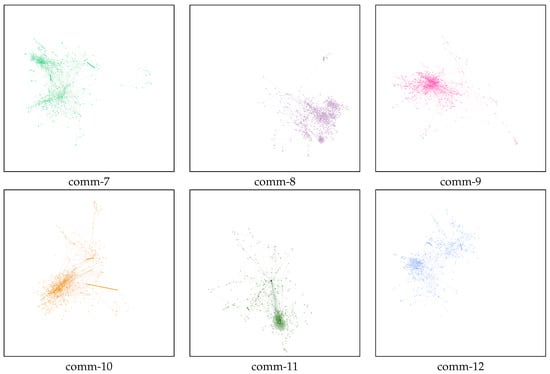
Figure A1.
Graph of the first group of the twelve most crowded communities (in order from left to right and top to bottom).


Figure A2.
Graph of the second group of the twelve most crowded communities (in order from left to right and top to bottom).
References
- Erdman, A.G.; Sandor, G.N. Diseño de Mecanismos, Análisis y Síntesis, tercera ed.; Prentice Hall: México city, Mexico, 1998. [Google Scholar]
- Wittenburg, J. Dynamics of Systems of Rigid Bodies; Teubner: Stuttgart, Germany, 1977. [Google Scholar]
- Schiehlen, W. Multibody system dynamics: Roots and perspectives. Multibody Syst. Dyn. 1997, 1, 149–188. [Google Scholar] [CrossRef]
- Valverde, J.; Escalona, J.; Mayo, J.; Domínguez, J. Dynamic analysis of a light structure in outer space: Short Electrodynamic Tether. Multibody Syst. Dyn. 2003, 10, 125–146. [Google Scholar] [CrossRef]
- Wasfy, T.M.; Noor, A.K. Computational strategies for flexible multibody systems. Appl. Mech. Rev. 2003, 56, 553–613. [Google Scholar] [CrossRef]
- Shabana, A.A. Flexible multibody dynamics: Review of past and recent developments. Multibody Syst. Dyn. 1997, 1, 189–222. [Google Scholar] [CrossRef]
- Schiehlen, W. Research trends in multibody system dynamics. Multibody Syst. Dyn. 2007, 18, 3–13. [Google Scholar] [CrossRef]
- Gantmájer, F. Mecánica Analítica; MIR: Moscú, Russia, 1996. [Google Scholar]
- Bremer, H. On the dynamics of elastic multibody systems. Appl. Mech. Rev. 1999, 52, 275–303. [Google Scholar] [CrossRef]
- Nikravesh, P.E. Computer-Aided Analysis of Mechanical Systems; Prentice-Hall International, Inc.: Upper Saddle River, NJ, USA, 1988. [Google Scholar]
- Paul, B.; Krajcinovic, K. Computer analysis of machines with planar motion: Part 1—Kinematics; Part 2—Dynamics. ASME J. Appl. Mech. 1970, 37, 697–712. [Google Scholar] [CrossRef]
- Haug, E. Elements and Methods of Computational Dynamics. In Computer Aided Analysis and Optimization of Mechanical System Dynamics; Haug, E., Ed.; Springer: Berlin/Heidelberg, Germany, 1984; pp. 3–38. [Google Scholar]
- García de Jalón, J.; Unda, J.; Avello, A.; Jiménez, J. Dynamic analysis of three-dimensional mechanisms in natural coordinates. ASME J. Mech. Transm. Autom. Des. 1987, 109, 460–465. [Google Scholar] [CrossRef]
- García de Jalón, J.; Bayo, E. Kinematic and Dynamic Simulation of Multibody Systems—The Real-Time Challenge; Springer: New York, NY, USA, 1993. [Google Scholar]
- Shabana, A. Computational Dynamics, 2nd ed.; Wiley-Interscience: New York, NY, USA, 2001. [Google Scholar]
- Unda, J.; de Jalón, J.G.; Losantos, F.; Enparantza, R. A comparative study on some different formulations of the dynamic equations of constrained mechanical systems. ASME J. Mech. Transm. Autom. Des. 1987, 109, 466–474. [Google Scholar] [CrossRef]
- Shabana, A. Dynamics of Multibody Systems; Cambriedge University Press: New York, NY, USA, 1998. [Google Scholar]
- Vukasovic, N.; Celigüeta, J.; de Jalón, J.G. Flexible multibody dynamics based on a fully cartesian system of support coordinates. ASME J. Mech. Des. 1993, 115, 294–299. [Google Scholar] [CrossRef]
- Mayo, J. Análisis Geométricamente No Lineal en Dinámica de Mecanismos Flexibles. Ph.D. Thesis, Escuela Técnica Superior de Ingenieros Industriales, Universidad de Sevilla, Sevilla, Spain, 1993. [Google Scholar]
- Belytschko, T.; Hsieh, B. Non-linear transient finite element analysis with convected co-ordinates. Int. J. Numer. Methods Eng. 1973, 7, 255–271. [Google Scholar] [CrossRef]
- Simo, J. A finite strain beam formulation. The three-dimensional dynamic problem. Part I. Comput. Methods Appl. Mech. Eng. 1985, 49, 55–70. [Google Scholar] [CrossRef]
- Simo, J.; Vu-Quoc, L. A three-dimensional finite-strain rod model. Part II: Computational aspects. Comput. Methods Appl. Mech. Eng. 1986, 58, 79–116. [Google Scholar] [CrossRef]
- Simo, J.; Vu-Quoc, L. On the dynamics of flexible beams under large overall motions-The plane case: Part I and Part II. ASME J. Appl. Mech. 1986, 53, 849–863. [Google Scholar] [CrossRef]
- Avello, A. Dinámica de Mecanismos Flexibles con Coordenadas Cartesianas y Teoría de Grandes Deformaciones. Ph.D. Thesis, Universidad de Navarra, San Sebastian, Spain, 1990. [Google Scholar]
- Shabana, A.A.; Hussien, H.; Escalona, J.L. Application of the absolute nodal coordinate formulation to large rotation and large deformation problems. ASME J. Mech. Des. 1998, 120, 188–195. [Google Scholar] [CrossRef]
- Shabana, A. Computer implementation of the absolute nodal coordinate formulation for flexible multibody dynamics. Nonlinear Dyn. 1998, 16, 293–306. [Google Scholar] [CrossRef]
- Berzeri, M.; Campanelli, M.; Shabana, A. Definition of the elastic forces in the finite-element absolute nodal coordinate formulation and the floating frame of reference formulation. Multibody Syst. Dyn. 2001, 5, 21–54. [Google Scholar] [CrossRef]
- Berzeri, M.; Shabana, A.A. Development of simple models for the elastic forces in the absolute nodal co-ordinate formulation. J. Sound Vib. 2000, 235, 539–565. [Google Scholar] [CrossRef]
- Omar, M.; Shabana, A. A two-dimensional shear deformable beam for large rotation and deformation problems. J. Sound Vib. 2001, 243, 565–573. [Google Scholar] [CrossRef]
- Yakoub, R.; Shabana, A. Three dimensional absolute nodal coordinate formulation for beam elements: Implementation and Applications. ASME J. Mech. Des. 2001, 123, 614–621. [Google Scholar] [CrossRef]
- Shabana, A.; Yakoub, R. Three-dimensional absolute nodal coordinate formulation for beam elements: Theory. ASME J. Mech. Des. 2001, 123, 606–613. [Google Scholar] [CrossRef]
- Shabana, A.A. Finite element incremental approach and exact rigid body inertia. ASME J. Mech. Des. 1996, 118, 171–178. [Google Scholar] [CrossRef]
- Mikkola, A.; Shabana, A. A non-incremental finite element procedure for the analysis of large deformation of plates and shells in mechanical system applications. Multibody Syst. Dyn. 2003, 9, 283–309. [Google Scholar] [CrossRef]
- Sopanen, J.; Mikkola, A. Description of elastic forces in absolute nodal coordinate formulation. Nonlinear Dyn. 2003, 34, 53–74. [Google Scholar] [CrossRef]
- Sopanen, J.; Mikkola, A. Studies on the Stiffness Properties of the Absolute Nodal Coordinate Formulation for Three-dimensional Beams. In Proceedings of the ASME DETC and CIE Conference; American Society of Mechanical Engineers Digital Collection: Little Falls, NJ, USA, 2003. [Google Scholar]
- Kerkkanen, K.S.; Sopanen, J.T.; Mikkola, A. A geometrically nonlinear beam element for multibody applications. J. Mech. Des. Trans. ASME 2005, 127, 621–630. [Google Scholar]
- Dufva, K.; Sopanen, J.; Mikkola, A. A two-dimensional shear deformable beam element based on the absolute nodal coordinate formulation. J. Sound Vib. 2005, 280, 719–738. [Google Scholar] [CrossRef]
- Dufva, K.; Sopanen, J.; Mikkola, A. Three-dimensional beam element based on a cross-sectional coordinate system approach. Nonlinear Dyn. 2005, in press. [Google Scholar] [CrossRef]
- Gerstmayr, J.; Sugiyama, H.; Mikkola, A. Review on the absolute nodal coordinate formulation for large deformation analysis of multibody systems. J. Comput. Nonlinear Dyn. 2013, 8. [Google Scholar] [CrossRef]
- Bastian, M.; Heymann, S.; Jacomy, M. Gephi: An Open Source Software for Exploring and Manipulating Networks. In Proceedings of the Third International AAAI Conference on Weblogs and Social Media, San Jose, CA, USA, 17–20 May 2009. [Google Scholar]
- De la Cruz-Lovera, C.; Perea-Moreno, A.J.; de la Cruz-Fernández, J.L.; Alvarez-Bermejo, J.; Manzano-Agugliaro, F. Worldwide research on energy efficiency and sustainability in public buildings. Sustainability 2017, 9, 1294. [Google Scholar] [CrossRef]
- Montoya, F.G.; Alcayde, A.; Baños, R.; Manzano-Agugliaro, F. A fast method for identifying worldwide scientific collaborations using the Scopus database. Telemat. Inform. 2018, 35, 168–185. [Google Scholar] [CrossRef]
- Montoya, F.; Baños, R.; Alcayde, A.; Montoya, M.; Manzano-Agugliaro, F. Power quality: Scientific collaboration networks and research trends. Energies 2018, 11, 2067. [Google Scholar] [CrossRef]
- Alcayde, A.; G Montoya, F.; Baños, R.; Perea-Moreno, A.J.; Manzano-Agugliaro, F. Analysis of Research Topics and Scientific Collaborations in Renewable Energy Using Community Detection. Sustainability 2018, 10, 4510. [Google Scholar] [CrossRef]
- Oracle. Json. Available online: http://www.json.org (accessed on 24 July 2018).
- Valderrama-Zurián, J.C.; Aguilar-Moya, R.; Melero-Fuentes, D.; Aleixandre-Benavent, R. A systematic analysis of duplicate records in Scopus. J. Informetr. 2015, 9, 570–576. [Google Scholar] [CrossRef]
- Franceschini, F.; Maisano, D.; Mastrogiacomo, L. Empirical analysis and classification of database errors in Scopus and Web of Science. J. Informetr. 2016, 10, 933–953. [Google Scholar] [CrossRef]
- Google. OpenRefine. Available online: http://openrefine.org (accessed on 24 July 2018).
- Baxter, R.; Christen, P.; Churches, T. A comparison of fast blocking methods for record linkage. In Proceedings of the ACM SIGKDD’03 Workshop on Data Cleaning, Record Linkage, and Object Consolidation, Washington, DC, USA, 27 August 2003; pp. 25–27. [Google Scholar]
- Jin, L.; Li, C.; Mehrotra, S. Efficient record linkage in large data sets. In Proceedings of the Eighth International Conference on Database Systems for Advanced Applications (DASFAA 2003), Kyoto, Japan, 26–28 March 2003; pp. 137–146. [Google Scholar]
- Cavnar, W.; Trenkle, J. N-gram-based text categorization. In Proceedings of the SDAIR-94, 3rd Annual Symposium on Document Analysis and Information Retrieval, Las Vegas, NV, USA, 11–13 April 1994; pp. 161–175. [Google Scholar]
- Abidin, A.F.; Mohamed, A.; Shareef, H. Intelligent detection of unstable power swing for correct distance relay operation using S-transform and neural networks. Expert Syst. Appl. 2011, 38, 14969–14975. [Google Scholar] [CrossRef]
- Montoya, F.G.; Alcayde, A.; Sánchez, P.; Gil, C.; Montoya, M.; Gómez, J. Comparative analysis of power variables in high performance embedded and x86 architectures using GNU/Linux. Comput. Electr. Eng. 2011, 37, 541–549. [Google Scholar] [CrossRef]
- Newman, M.E.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef]
- Blondel, V.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast Unfolding of Communities in Large Networks. J. Stat. Mech. Theory Exp. 2008, 2008. [Google Scholar] [CrossRef]
- Kane, T.; Ryan, R.; Banerjee, A. Dynamics of a cantilever beam attached to a moving base. J. Guid. Control Dyn. 1987, 10, 139–151. [Google Scholar] [CrossRef]
- Shabana, A.; Zaazaa, K.; Escalona, J.; Sany, J. Development of elastic force model for wheel/rail contact problems. J. Sound Vib. 2004, 269, 295–325. [Google Scholar] [CrossRef]
- Lankarani, H.; Nikravesh, P. Contact force model with hysteresis damping for impact analysis of multibody systems. J. Mech. Transm. Autom. Des. 1990, 112, 369–376. [Google Scholar] [CrossRef]
- Machado, M.; Moreira, P.; Flores, P.; Lankarani, H. Compliant contact force models in multibody dynamics: Evolution of the Hertz contact theory. Mech. Mach. Theory 2012, 53, 99–121. [Google Scholar] [CrossRef]
- Bauchau, O.; Laulusa, A. Review of contemporary approaches for constraint enforcement in multibody systems. J. Comput. Nonlinear Dyn. 2008, 3, 1–8. [Google Scholar] [CrossRef]
- Bayo, E.; Ledesma, R. Augmented Lagrangian and mass-orthogonal projection methods for constrained multibody dynamics. Nonlinear Dyn. 1996, 9, 113–130. [Google Scholar] [CrossRef]
- Bestle, D. Analyzing and optimizing multibody systems. Mech. Struct. Mach. 1992, 20, 67–92. [Google Scholar] [CrossRef]
- Cossalter, V.; Lot, R. A motorcycle multi-body model for real time simulations based on the natural coordinates approach. Veh. Syst. Dyn. 2002, 37, 423–447. [Google Scholar] [CrossRef]
- Kortüm, W. Review of Multibody Computer, Codes for Vehicle system Dynamics. Veh. Syst. Dyn. 1993, 22, 3–31. [Google Scholar] [CrossRef]
- Damsgaard, M.; Rasmussen, J.; Christensen, S.; Surma, E.; de Zee, M. Analysis of musculoskeletal systems in the AnyBody Modeling System. Simul. Model. Pract. Theory 2006, 14, 1100–1111. [Google Scholar] [CrossRef]
- Zagrodny, B.; Ludwicki, M.; Wojnicz, W.; Mrozowski, J.; Awrejcewicz, J. Cooperation of mono-and bi-articular muscles: Human lower limb. J. Musculoskelet. Neuronal Interact. 2018, 18, 176–182. [Google Scholar]
- Wojnicz, W.; Zagrodny, B.; Ludwicki, M.; Awrejcewicz, J.; Wittbrodt, E. A two dimensional approach for modelling of pennate muscle behaviour. Biocybern. Biomed. Eng. 2017, 37, 302–315. [Google Scholar] [CrossRef]
- Bauchau, O. Computational Schemes for Flexible, Nonlinear Multi-Body Systems. Multibody Syst. Dyn. 1998, 2, 169–225. [Google Scholar] [CrossRef]
- Betsch, P. The discrete null space method for the energy consistent integration of constrained mechanical systems. Part I: Holonomic constraints. Comput. Methods Appl. Mech. Eng. 2005, 194, 5159–5190. [Google Scholar] [CrossRef]
- Jain, A. Robot and Multibody Dynamics: Analysis and Algorithms; Springer: Berlin, Germany, 2011; pp. 1–510. [Google Scholar] [CrossRef]
- Rui, X.; Wang, G.; Zhang, J. Transfer Matrix Method for Multibody Systems: Theory and Applications; Wiley: Hoboken, NJ, USA, 2017; pp. 1–732. [Google Scholar] [CrossRef]
- Masarati, P.; Morandini, M.; Mantegazza, P. An efficient formulation for general-purpose multibody/multiphysics analysis. J. Comput. Nonlinear Dyn. 2014, 9. [Google Scholar] [CrossRef]
- Lee, H.W.; Roh, M.I. Review of the multibody dynamics in the applications of ships and offshore structures. Ocean Eng. 2018, 167, 65–76. [Google Scholar] [CrossRef]
- Novotny, P.; Pistek, V. New efficient methods for powertrain vibration analysis. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2010, 224, 611–629. [Google Scholar] [CrossRef]
- Blundell, M.; Harty, D. The Multibody Systems Approach to Vehicle Dynamics; Elsevier: Amsterdam, The Netherlands, 2014; pp. 1–741. [Google Scholar] [CrossRef]
- Helsen, J.; Vanhollebeke, F.; Marrant, B.; Vandepitte, D.; Desmet, W. Multibody modelling of varying complexity for modal behaviour analysis of wind turbine gearboxes. Renew. Energy 2011, 36, 3098–3113. [Google Scholar] [CrossRef]
- Rubinstein, D.; Hitron, R. A detailed multi-body model for dynamic simulation of off-road tracked vehicles. J. Terramech. 2004, 41, 163–173. [Google Scholar] [CrossRef]
- Wohlmuth, B.; Krause, R. Monotone multigrid methods on nonmatching grids for nonlinear multibody contact problems. SIAM J. Sci. Comput. 2003, 25, 324–347. [Google Scholar] [CrossRef]
- Laursen, T.; Simo, J. A continuum-based finite element formulation for the implicit solution of multibody, large deformation-frictional contact problems. Int. J. Numer. Methods Eng. 1993, 36, 3451–3485. [Google Scholar] [CrossRef]
- Umetani, Y.; Yoshida, K. Resolved Motion Rate Control of Space Manipulators with Generalized Jacobian Matrix. IEEE Trans. Robot. Autom. 1989, 5, 303–314. [Google Scholar] [CrossRef]
- Anitescu, M.; Potra, F. Formulating Dynamic Multi-Rigid-Body Contact Problems with Friction as Solvable Linear Complementarity Problems. Nonlinear Dyn. 1997, 14, 231–247. [Google Scholar] [CrossRef]
- Pfeiffer, A.; Lee, J.S.; Han, J.H.; Baier, H. Ornithopter Flight Simulation Based on Flexible Multi-Body Dynamics. J. Bionic Eng. 2010, 7, 102–111. [Google Scholar] [CrossRef]
- Crocetta, G.; Piantini, S.; Pierini, M.; Simms, C. The influence of vehicle front-end design on pedestrian ground impact. Accid. Anal. Prev. 2015, 79, 56–69. [Google Scholar] [CrossRef] [PubMed]
- Dietz, S.; Netter, H.; Sachau, D. Fatigue life prediction of a railway bogie under dynamic loads through simulation. Veh. Syst. Dyn. 1998, 29, 385–402. [Google Scholar] [CrossRef]
- Zhu, S.; Ding, G.; Qin, S.; Lei, J.; Zhuang, L.; Yan, K. Integrated geometric error modeling, identification and compensation of CNC machine tools. Int. J. Mach. Tools Manuf. 2012, 52, 24–29. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).