Optimal Parameter Selection in Robotic Belt Polishing for Aeroengine Blade Based on GRA-RSM Method
Abstract
1. Introduction
2. Experiment Procedure
2.1. Experimental Design
2.2. Experimental Materials and Experimental Preparation
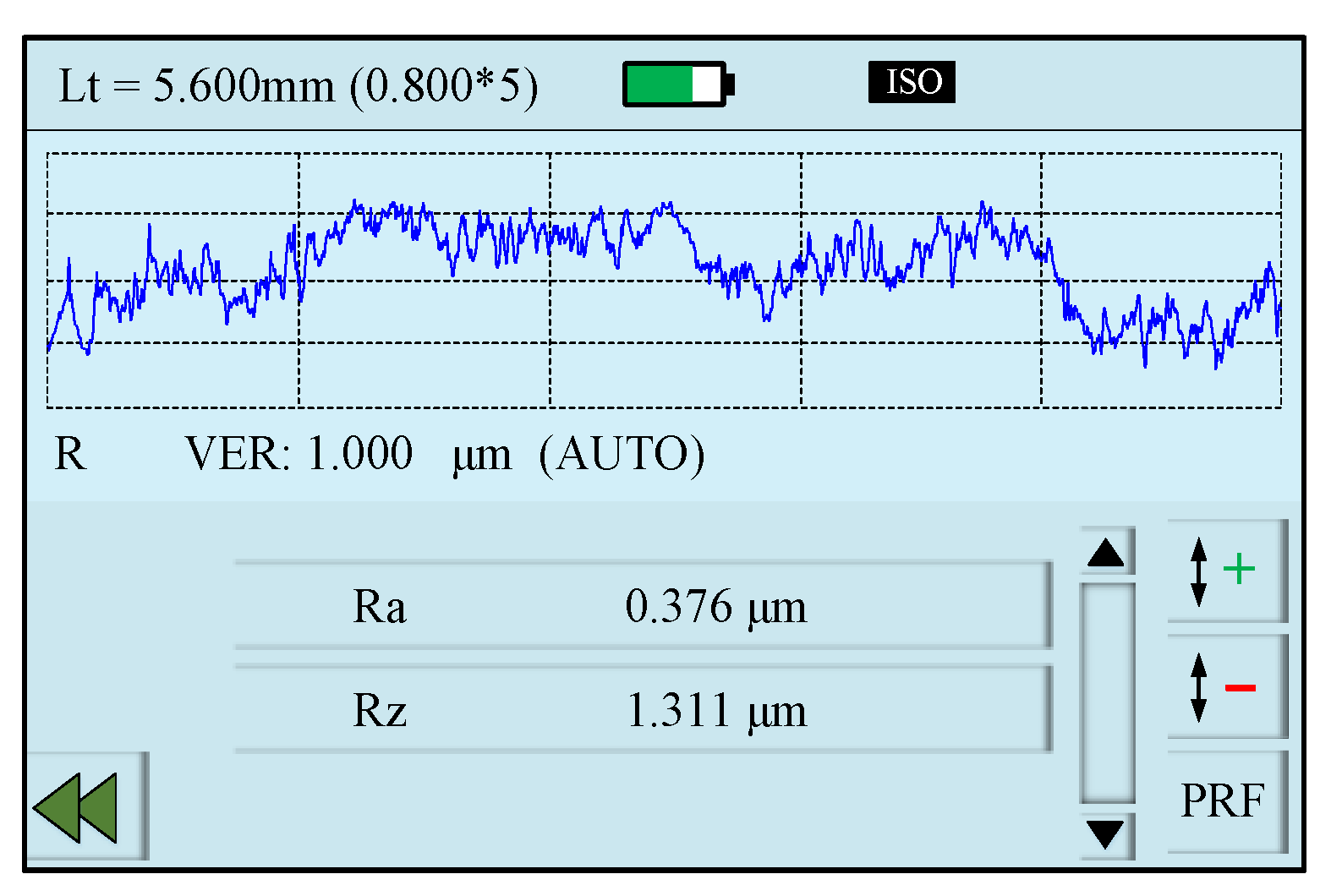
2.3. Measurement Methods
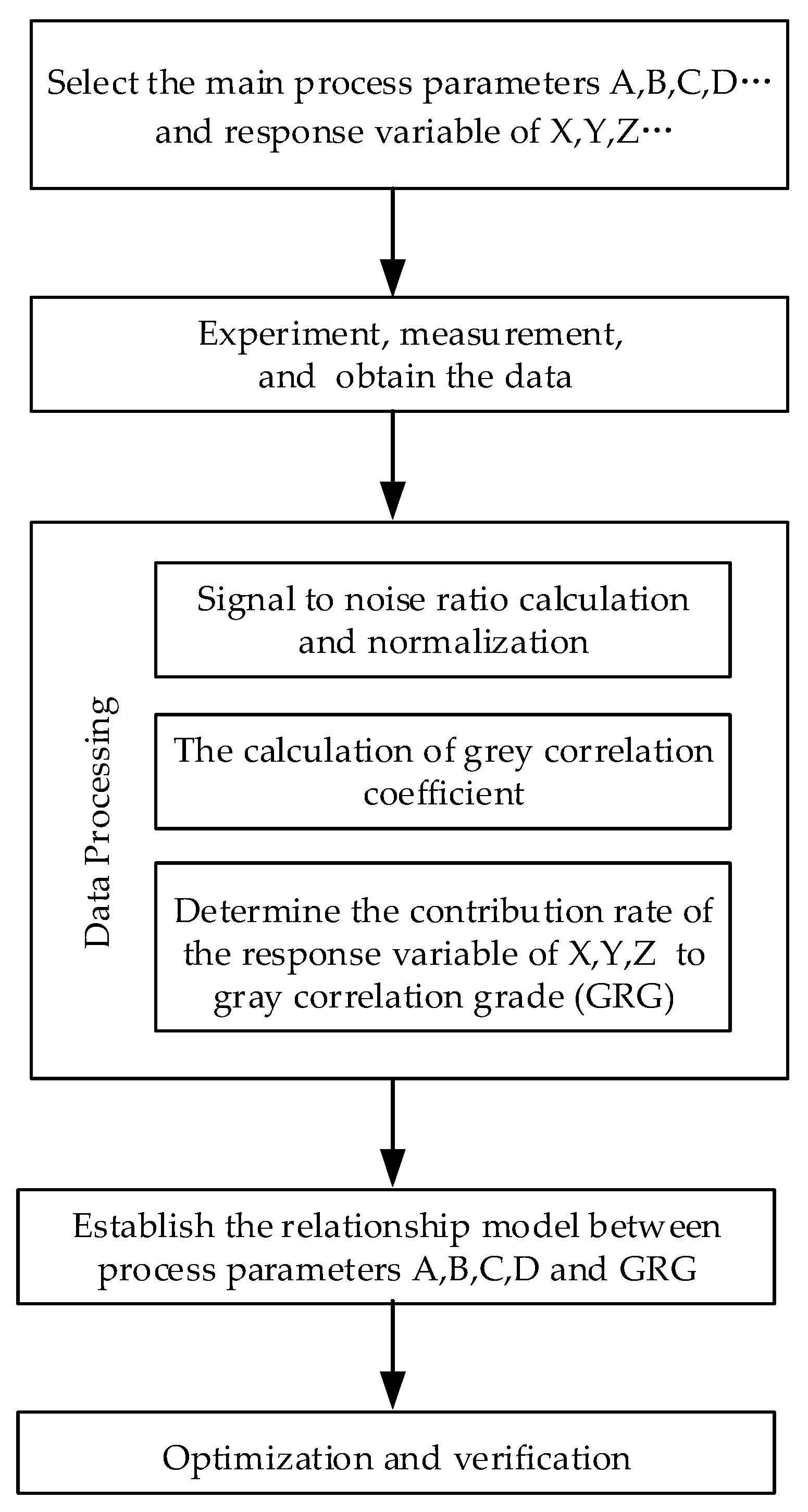
3. Multiobjective Optimization Method
4. Results and Discussion
4.1. Effect of Polishing Parameters on a Single Response Variable
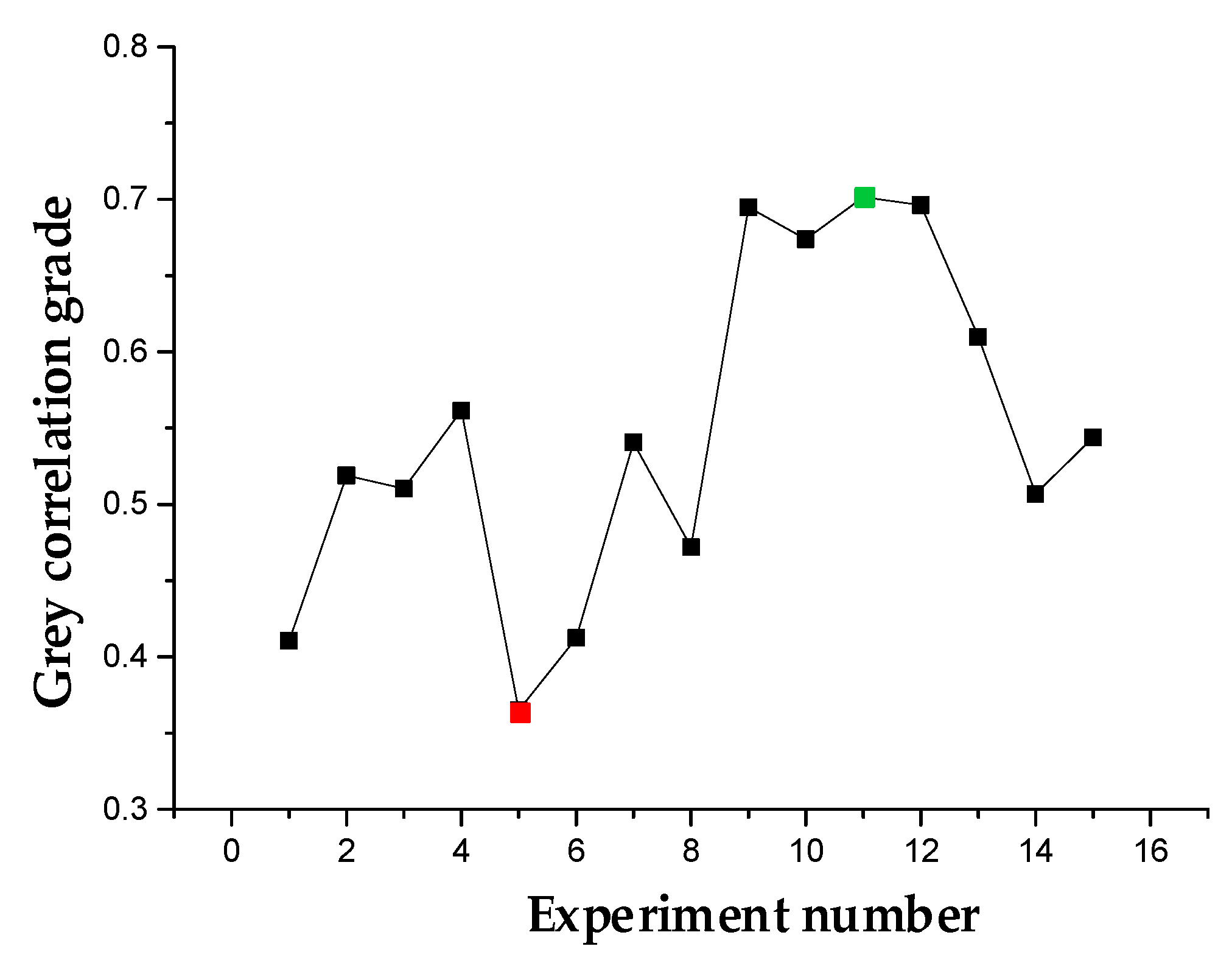
4.2. Gray Correlation Analysis
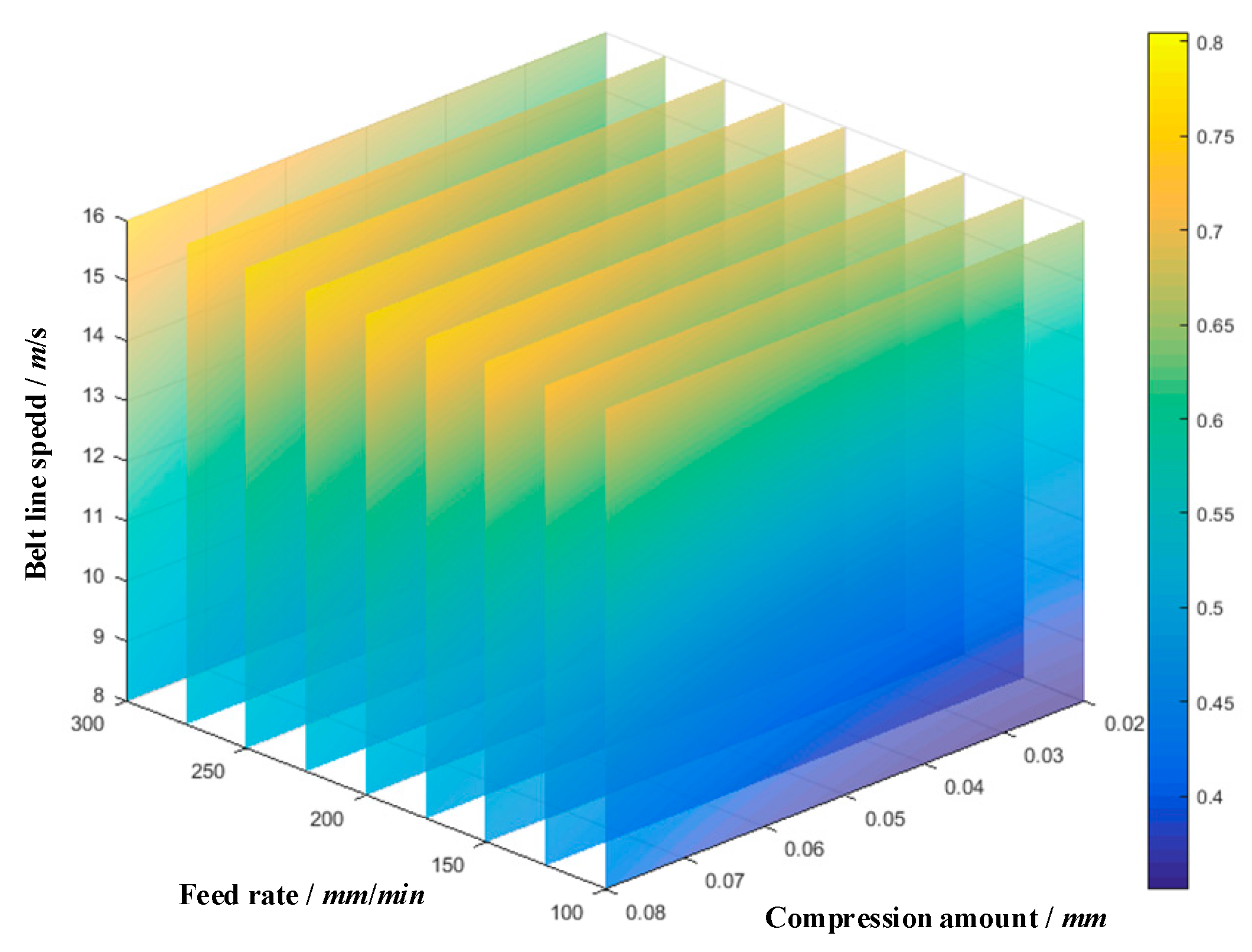
4.3. Model Establishment
− 3.05046 × 10−5 vf × vs + 5.42413 × 10−5 ap × vs − 3.62566×10−6 vf2 + 15.99582 ap2
+ 1.85397 × 10−3 vs2
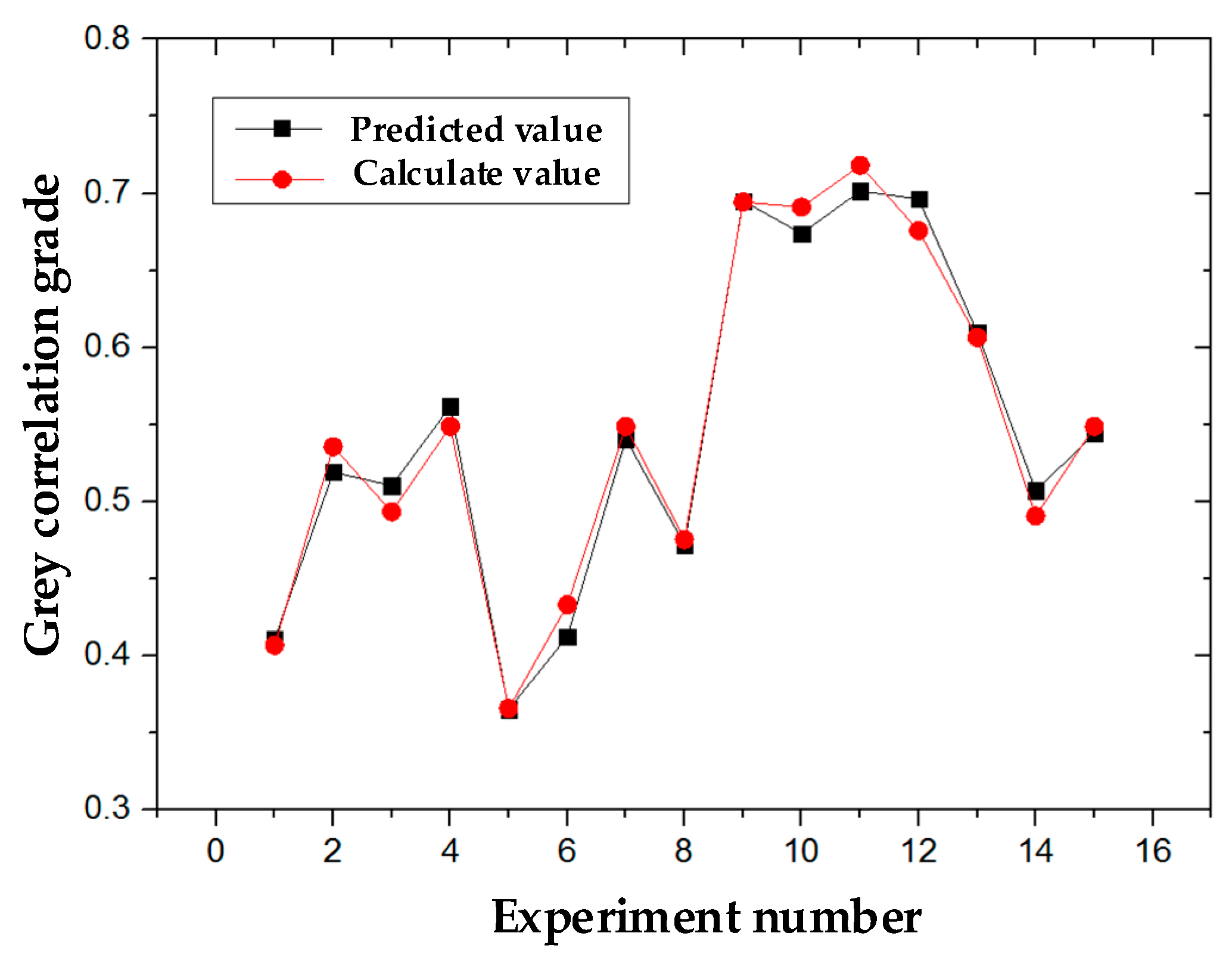
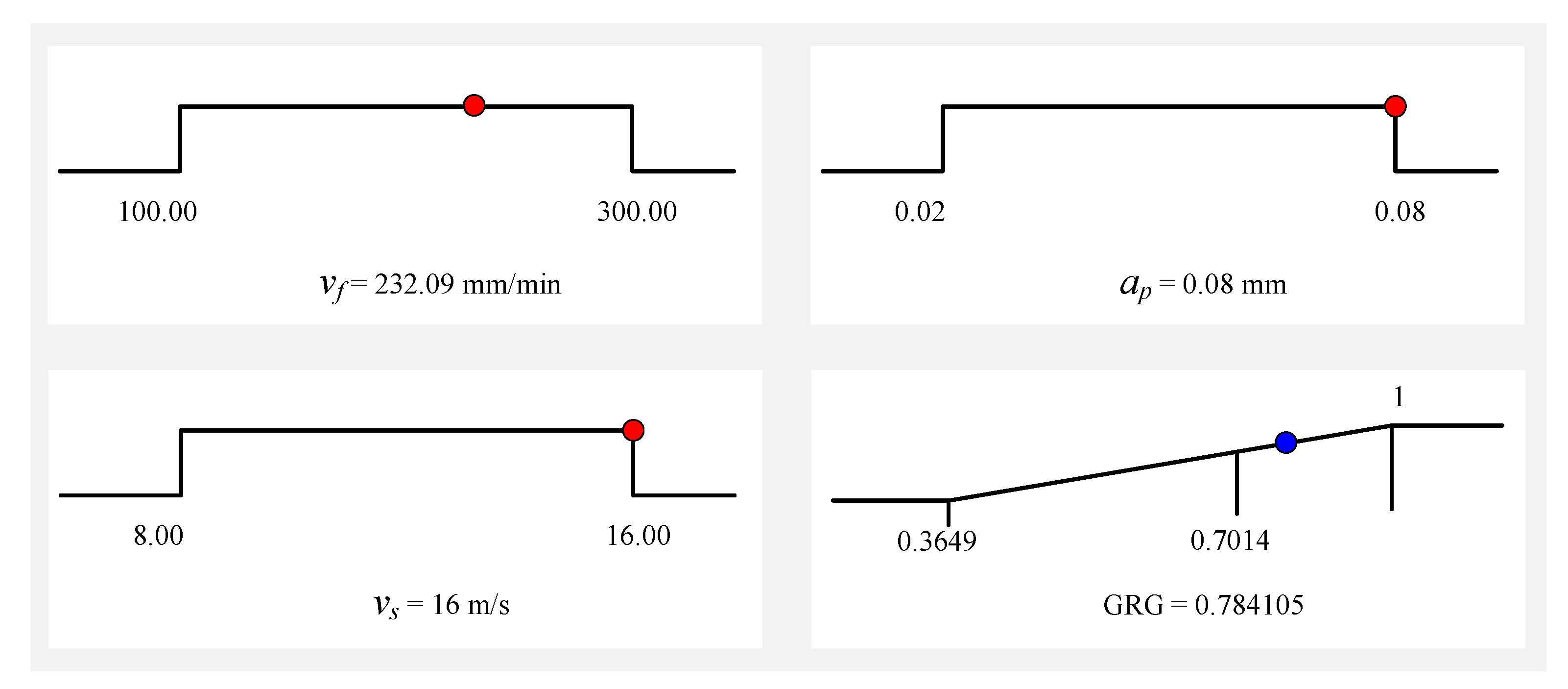
4.4. Optimal Gray Correlation Prediction
4.5. Verification
5. Conclusions
- In the robotic belt polishing for aeroengine blades, the main parameters influencing the aeroengine blade polishing include feed rate vf, compression amount ap, and belt line speed vs. The belt line speed vs is the main process parameter affecting material removal rates and surface roughness.
- The results of principal component analysis show that surface roughness is the priority principal component, then followed by material removal rate. The corresponding contribution rates were 54.6% and 45.4%, respectively. The proposed GRA-RSM method can effectively predict the optimal setting of process parameters in the robotic belt polishing for aeroengine blades, then achieving the important aim of reducing the surface roughness, and improving the material removal rate simultaneously.
- For the maximum grey correlation grade, which increased by 10.96%, the optimum polishing parameter combination was selected as follows: the feed rate vf is 232.09 mm/min, the compression amount ap is 0.08 mm, and the belt line speed vs is 16m/s. Finally, the surface roughness was reduced by 6.29%, and the material removal rate was increased by 16.11%.
Author Contributions
Funding
Conflicts of Interest
References
- Moumen, M.; Chaves-Jacob, J.; Bouaziz, M.; Linares, J.M. Optimization of pre-polishing parameters on a 5-axis milling machine. Int. J. Adv. Manuf. Technol. 2016, 85, 443–454. [Google Scholar] [CrossRef]
- Huang, H.; Gong, Z.M.; Chen, X.Q.; Zhou, L. Robotic grinding and polishing for turbine-vane overhaul. J. Mater. Process. Technol. 2002, 127, 140–145. [Google Scholar] [CrossRef]
- Márquez, J.J.; Pérez, J.M.; Rıos, J.; Vizán, A. Process modeling for robotic polishing. J. Mater. Process. Technol. 2005, 159, 69–82. [Google Scholar] [CrossRef]
- Xiao, G.; Huang, Y. Equivalent self-adaptive belt grinding for the real-R edge of an aero-engine precision-forged blade. Int. J. Adv. Manuf. Technol. 2016, 83, 1697–1706. [Google Scholar] [CrossRef]
- Xiao, G.; Huang, Y. Micro-stiffener surface characteristics with belt polishing processing for titanium alloys. Int. J. Adv. Manuf. Technol. 2019, 100, 349–359. [Google Scholar] [CrossRef]
- Xiao, G.; Huang, Y.; Wang, J. Path planning method for longitudinal micromarks on blisk root-fillet with belt grinding. Int. J. Adv. Manuf. Technol. 2018, 95, 797–810. [Google Scholar] [CrossRef]
- Xiao, G.; Huang, Y.; Fei, Y. On-machine contact measurement for the main-push propeller blade with belt grinding. Int. J. Adv. Manuf. Technol. 2016, 87, 1713–1723. [Google Scholar] [CrossRef]
- Xiao, G.; Huang, Y.; Yang, Y.H.; Yi, H. Workpiece surface integrity of GH4169 Nickel-based Superalloy when employing abrasive belt grinding method. Adv. Mater. Res. 2014, 936, 1252–1257. [Google Scholar] [CrossRef]
- Huo, W.G.; Xu, J.H.; Fu, Y.C.; Qi, H.J.; Shao, J. Investigation of surface integrity on dry grinding Ti6Al4V alloy with super-abrasive wheels. J. Shan. Univ. 2012, 42, 100–104. [Google Scholar]
- Bigerelle, M.; Gautier, A.; Hagege, B.; Favergeon, J.; Bounichane, B. Roughness characteristic length scales of belt finished surface. J. Mater. Process. Technol. 2009, 209, 6103–6116. [Google Scholar] [CrossRef]
- Wu, S.; Kazerounian, K.; Gan, Z.; Sun, Y. A material removal model for robotic belt grinding process. Mach. Sci. Technol. 2014, 18, 15–30. [Google Scholar] [CrossRef]
- Song, Y.; Liang, W.; Yang, Y. A method for grinding removal control of a robot belt grinding system. J. Intell. Manuf. 2012, 23, 1903–1913. [Google Scholar] [CrossRef]
- Wang, P.; Zhu, Z.; Wang, Y. A novel hybrid MCDM model combining the SAW, TOPSIS and GRA methods based on experimental design. Inform. Sci. 2016, 345, 27–45. [Google Scholar] [CrossRef]
- Verma, R.; Singh, N.P. GRA based network selection in heterogeneous wireless networks Wireless. Pers. Commun. 2013, 72, 1437–1452. [Google Scholar] [CrossRef]
- Du, S.; Chen, M.; Xie, L.; Wang, X. Optimization of process parameters in the high-speed milling of titanium alloy TB17 for surface integrity by the Taguchi-Grey relational analysis method. Adv. Mech. Eng. 2016, 8, 1–12. [Google Scholar] [CrossRef]
- Xiao, G.; Huang, Y. Two-Level Static Floatation Tool Used in Belt Grinding for Root Fillet of Titanium Alloy Blade. IEEE Access 2019, 7, 28663–28671. [Google Scholar] [CrossRef]
- Chen, Z.; Shi, Y.; Lin, X. Evaluation and improvement of material removal rate with good surface quality in TC4 blisk blade polishing process. J. Adv. Mech. Des. Syst. Manuf. 2018, 12, 1–12. [Google Scholar] [CrossRef]
- Kang, C.; Shi, Y.; He, X.; Yu, T.; Deng, B.; Zhang, H.; Sun, P. Multi-response optimization of T300/epoxy prepreg tape-wound cylinder by grey relational analysis coupled with the response surface method. Mater. Res. Exp. 2017, 4, 1–13. [Google Scholar] [CrossRef]
- Ray, A. Optimization of process parameters of green electrical discharge machining using principal component analysis (PCA). Int. J. Adv. Manuf. Technol. 2016, 87, 1299–1311. [Google Scholar]


| Experimental Parameters | Symbol | Units | Levels of Experimental Parameters | ||
|---|---|---|---|---|---|
| Level 1 | Level 2 | Level 3 | |||
| Feed rate | vf | mm/min | 100 | 200 | 300 |
| Compression | ap | mm | 0.02 | 0.05 | 0.08 |
| Belt line speed | vs | m/s | 8 | 12 | 16 |
| Number | Experiment Parameters | SR | MRR | ||||
|---|---|---|---|---|---|---|---|
| vf | ap | vs | Ra (μm) | S/N | Zw (mm²/min) | S/N | |
| 1 | 200 | 0.02 | 8 | 0.415 | 7.6390 | 0.0123 | −38.2019 |
| 2 | 100 | 0.08 | 12 | 0.448 | 6.9744 | 0.0374 | −28.5426 |
| 3 | 200 | 0.08 | 8 | 0.527 | 5.5638 | 0.0428 | −27.3711 |
| 4 | 200 | 0.05 | 12 | 0.383 | 8.3360 | 0.0337 | −29.4474 |
| 5 | 100 | 0.05 | 8 | 0.558 | 5.0673 | 0.0181 | −34.8464 |
| 6 | 300 | 0.05 | 8 | 0.543 | 5.3040 | 0.0262 | −31.6340 |
| 7 | 200 | 0.05 | 12 | 0.407 | 7.8081 | 0.0351 | −29.0939 |
| 8 | 100 | 0.02 | 12 | 0.413 | 7.6810 | 0.0234 | −32.6157 |
| 9 | 300 | 0.05 | 16 | 0.394 | 8.0901 | 0.0574 | −24.8218 |
| 10 | 200 | 0.02 | 16 | 0.311 | 10.1448 | 0.0193 | −34.2889 |
| 11 | 200 | 0.08 | 16 | 0.413 | 7.6810 | 0.0701 | −23.0856 |
| 12 | 100 | 0.05 | 16 | 0.347 | 9.1934 | 0.0457 | −26.8017 |
| 13 | 300 | 0.08 | 12 | 0.476 | 6.4479 | 0.0547 | −25.2403 |
| 14 | 300 | 0.02 | 12 | 0.403 | 7.8939 | 0.0281 | −31.0259 |
| 15 | 200 | 0.05 | 12 | 0.421 | 7.5144 | 0.0381 | −28.3815 |
| Chemical Composition | Al | V | Fe | Si | C | N | H | O | Other |
|---|---|---|---|---|---|---|---|---|---|
| % | 5.5–6.8 | 3.5–4.5 | ≤0.30 | ≤0.15 | ≤0.10 | ≤0.05 | ≤0.01 | ≤0.20 | 0.11 |
| Source | Process Parameters | ||
|---|---|---|---|
| vf | ap | vs | |
| SR | |||
| Level 1 | 7.2290 | 8.3397 | 5.8935 |
| Level 2 | 7.8124 | 7.3305 | 7.5222 |
| Level 3 | 6.9340 | 6.6668 | 8.7773 |
| Max-min | 0.8785 | 1.6729 | 2.8838 |
| Rank | 3 | 2 | 1 |
| Optimal level | A2 | B1 | C3 |
| MRR | |||
| Level 1 | −30.7016 | −34.0331 | −33.0134 |
| Level 2 | −29.9815 | −29.2895 | −29.1924 |
| Level 3 | −28.1805 | −26.0599 | −27.2495 |
| Max-min | 2.5211 | 7.9732 | 5.7639 |
| Rank | 3 | 1 | 2 |
| Optimal level | A3 | B3 | C3 |
| Number | Deviation Sequence Δ0i | Gray Relational Coefficients | Gray Relational Grades | ||
|---|---|---|---|---|---|
| SR | MRR | SR | MRR | ||
| 1 | 0.4935 | 1.0000 | 0.5033 | 0.3333 | 0.4105 |
| 2 | 0.6244 | 0.3610 | 0.4447 | 0.5807 | 0.5190 |
| 3 | 0.9022 | 0.2835 | 0.3566 | 0.6382 | 0.5103 |
| 4 | 0.3562 | 0.4209 | 0.5840 | 0.5430 | 0.5616 |
| 5 | 1.0000 | 0.7780 | 0.3333 | 0.3912 | 0.3649 |
| 6 | 0.9534 | 0.5655 | 0.3440 | 0.4693 | 0.4124 |
| 7 | 0.4602 | 0.3975 | 0.5207 | 0.5571 | 0.5406 |
| 8 | 0.4852 | 0.6304 | 0.5075 | 0.4423 | 0.4719 |
| 9 | 0.4047 | 0.1149 | 0.5527 | 0.8132 | 0.6949 |
| 10 | 0.0000 | 0.7411 | 1.0000 | 0.4029 | 0.6740 |
| 11 | 0.4852 | 0.0000 | 0.5075 | 1.0000 | 0.7014 |
| 12 | 0.1874 | 0.2458 | 0.7274 | 0.6704 | 0.6963 |
| 13 | 0.7281 | 0.1425 | 0.4071 | 0.7782 | 0.6097 |
| 14 | 0.4433 | 0.5253 | 0.5300 | 0.4877 | 0.5069 |
| 15 | 0.5181 | 0.3503 | 0.4911 | 0.5880 | 0.5440 |
| Principal Component | Eigenvalue | Contribution |
|---|---|---|
| SR | 1.0924 | 54.6% |
| MRR | 0.90476 | 45.4% |
| Total | 100% |
| Initial Factor Setting | Optimal Process Condition | Improvement | ||
|---|---|---|---|---|
| Prediction | Validation | |||
| vf | 200 mm/min | 232.09 mm/min | 232.09 mm/min | |
| ap | 0.08 mm | 0.08 mm | 0.08 mm | |
| vs | 16 m/s | 16 m/s | 16 m/s | |
| SR | 0.413 μm | 0.387 μm | 6.29% | |
| MRR | 0.0701 mm²/min | 0.0814 mm²/min | 16.11% | |
| GRG | 0.7014 | 0.7841 | 0.7783 | 10.96% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Shi, Y.; Chen, Z.; Yu, T.; Zhao, P.; Shirinzadeh, B. Optimal Parameter Selection in Robotic Belt Polishing for Aeroengine Blade Based on GRA-RSM Method. Symmetry 2019, 11, 1526. https://doi.org/10.3390/sym11121526
Guo J, Shi Y, Chen Z, Yu T, Zhao P, Shirinzadeh B. Optimal Parameter Selection in Robotic Belt Polishing for Aeroengine Blade Based on GRA-RSM Method. Symmetry. 2019; 11(12):1526. https://doi.org/10.3390/sym11121526
Chicago/Turabian StyleGuo, Jian, Yaoyao Shi, Zhen Chen, Tao Yu, Pan Zhao, and Bijan Shirinzadeh. 2019. "Optimal Parameter Selection in Robotic Belt Polishing for Aeroengine Blade Based on GRA-RSM Method" Symmetry 11, no. 12: 1526. https://doi.org/10.3390/sym11121526
APA StyleGuo, J., Shi, Y., Chen, Z., Yu, T., Zhao, P., & Shirinzadeh, B. (2019). Optimal Parameter Selection in Robotic Belt Polishing for Aeroengine Blade Based on GRA-RSM Method. Symmetry, 11(12), 1526. https://doi.org/10.3390/sym11121526






