Abstract
In this paper, non-Fourier heat conduction in a cylinder with non-homogeneous boundary conditions is analytically studied. A superposition approach combining with the solution structure theorems is used to get a solution for equation of hyperbolic heat conduction. In this solution, a complex origin problem is divided into, different, easier subproblems which can actually be integrated to take the solution of the first problem. The first problem is split into three sub-problems by setting the term of heat generation, the initial conditions, and the boundary condition with specified value in each sub-problem. This method provides a precise and convenient solution to the equation of non-Fourier heat conduction. The results show that at low times (t = 0.1) up to about r = 0.4, the contribution of T1 and T3 dominate compared to T2 contributing little to the overall temperature. But at r > 0.4, all three temperature components will have the same role and less impact on the overall temperature (T).
1. Introduction
In recent years, some studies have focused on the deviation from the classical Fourier heat transfer equation. In the classical theory of conduction heat transfer based on Fourier’s law, the thermal heat flux is a linear relationship with the gradient of temperature and the heat wave propagation speed is assumed to be unlimited (Equation (1)).
where is the coefficient of thermal conductivity and is temperature. When this equation is combined into the balance equation of energy,
The classical parabolic heat conduction equation is derived,
where , , and are thermal diffusivity, density, and specific heat, respectively. Also, the effect of any thermal disturbance on the medium is instantaneously sensed through the entire molecular network. In the majority of engineering applications such as material processing (welding, cutting, forming, etc.), applying high power laser radiation, cryogenic applications, and materials which experience the high heat transfer rates [1,2,3,4], this equation is very useful. However, at very low times and very high thermal fluxes and very low temperatures close to absolute zero, the Fourier law has poor accuracy, and considering the effects of non-Fourier in describing the heat dissipation process and prediction of temperature distribution, non-Fourier are more reliable in these situations. Fourier’s failure to exactly predict the temperature field in sufficiently high heat flux and low temperature engineering usages is because it assumes that thermal energy transport is occurring at an infinite propagation speed [2,5]. As a result, a more advanced method, in the situation of the thermal waves finite propagation speed, is required to analyze the high temperature gradients. Usually, when the infinite propagation speed was assumed, the temperature was calculated more than its actual values and it causes some errors in temperature prediction.
A modified equation of non-Fourier heat flux has been developed by Cattaneo [6] and Vernotte [7] in the present form,
where is known thermal relaxation time. If the relaxation time ignores, , the law of the non-Fourier model is converted to the Fourier law. The energy equation is derived as follow,
In the Equation (5), expresses the rate of internal generation of energy. Inserting Equation (4) into Equation (5), the equation of hyperbolic heat transfer, containing source the term, derived,
where the source term is . Different solution procedures for Equation (6) with different boundary and initial conditions for finite media can be found in literature.
The analytical, numerical, and experimental methods were used in many researches for analysis and calculating the rate of heat transfer in applied physics problems [8,9,10]. Using the heat sources such as lasers and microwaves at very small times of applying the heat or high frequencies has a great deal of application in analytical physics, applied sciences, and engineering. In fast and short processes and rapid and concentrated conduction heat transfer, the order of space and time is very small. So, the law of Fourier equation which assumed that heat propagates at an infinite velocity, cannot be used [11].
Ozisik and Vick [12] studied the heat propagation in a semi-infinite body with a volumetric source of energy by solving the thermal wave equation. They found that the classical Fourier’s law was no longer suitable in obtaining the temperature field at short times. Jiang [13] applied the method of Laplace transform to study the hyperbolic conduction heat transfer in a hollow sphere whose boundaries are affected by a sudden change in temperature. Moosaie [14] solved, analytically, the equation of non-Fourier heat conduction for a finite body with an arbitrary initial condition and insulated boundaries. His results showed that the time needed for reaching steady state situation is enhanced with rising the relaxation time . Moosaie [15] investigated a finite body subjected to an arbitrary non-periodic surface disturbance. Their obtained solution is such that for a given non-periodic disturbance, analytically if possible, but in general numerically is a straight forward computational task. Ahmadikia and Riesmanian [16] presented an analytical method for solving the hyperbolic heat transfer in a blade under periodic boundary conditions applying the Laplace transform approach. The findings showed that in small blades under rapid phenomena, temperature behavior is the non-Fourier wave form. Bamdad et al. [17] studied the non-fluoride effects at extended surfaces. Their results showed that for all fins at the start times, the point of discontinuity is time, relaxation time, and cross-section of the dependent fin. In addition, the cross-sectional effects on the amplitude of the heat wave reflecting from the tip of the fin are such that there is no reflected heat wave in the fins with concave shape. Lam and Fang [18] presented an analytical method to investigate the heat conduction in a slab applied by various boundary conditions. They indicated that the solution accuracy depends on the terms number which were applied in the Fourier series expansion process.
Liu et al. [19] surveyed the non-Fourier heat conduction characteristics in the oil/water emulsions experimentally. Their results showed that in the ratio of time lag less than one, no thermal waves exist for oil/water emulsions.
The analysis of non-Fourier heat conduction in infinite hollow cylinders subjected to a heat source, which is a function of time, was investigated by Daneshjou et al. [20]. They used the Laplace transform method and demonstrated that their approach is valuable in correctness and exactness. Ma et al. [21] studied the C-V wave model for a plate which is irradiated by a non-Gaussian laser pulse. The method of mode superposition was applied for solving the equation. They discussed the dependence of the wave velocity on relaxation time. The influence of scanning and wave velocity on the temperature field was also presented. Wankhade et al. [22] investigated the heat transfer response of wet fins using the models of Fourier and non-Fourier. The method of separation of variables was applied, and the results showed a considerable deviation in temperature response using the non-Fourier heat conduction compared to the Fourier model. Also, the effect of fin surface conditions was studied. Han and Peddieson [23] investigated the Non-Fourier one-dimensional unsteady equation in a body for medium speeds less than (sub-critical), equal to (critical), and greater than (super-critical) the thermal wave speed. Liu et al [24] studied a hyperbolic lattice Boltzmann method (HLBM) compare to the parabolic lattice Boltzmann method (PLBM) to survey the non-Fourier effects. The results show that the electron temperatures simulated by the two-step HLBM/PLBM and two-temperature models are not much different from each other and both of them coincide with the experimental data.
Review of this research indicated that various solutions are studied in different works. In each study, different features of non-Fourier heat conduction were investigated and, therefore, various results were established which could be useful in its position. However, the shortage of a general problem with nonzero initial conditions and boundary conditions with internal heat generation in these studies is observed. In this study, an exact solution is presented to non-Fourier heat conduction in a cylinder with nonzero initial and boundary conditions. As it will be mentioned later, analytical solutions of this problem were obtained by applying the theory of solution structure combined with the superposition method. This approach can be used for obtaining the heat transfer in many physical applications which solved by different methods [25,26,27,28,29,30,31].
2. Formulation
2.1. Hyperbolic Heat Conduction
According to the Figure 1, we assume a cylinder composed of a homogenous heat conducting material with different boundary conditions at both sides: A symmetry boundary condition in the cylinder’s central line and convection in the cylinder surface (r = R) with ambient.
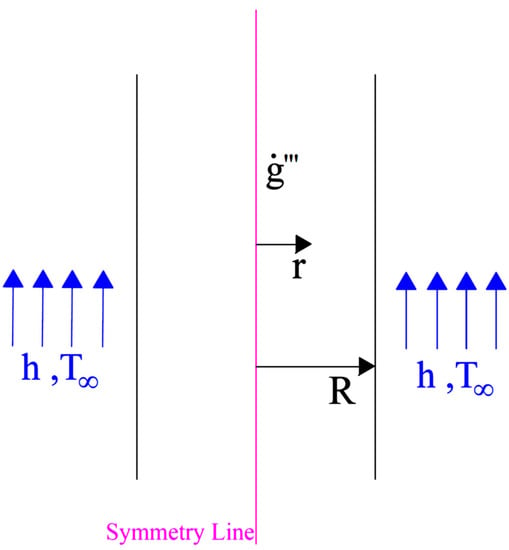
Figure 1.
A schematic illustration of the problem.
The heat is conducted through the cylinder in r-direction, where one dimensional heat conduction dominates. This problem was solved for L/r > 10 and a one-dimensional assumption for this problem is reasonable. For simplifying the solution, by using the following parameters, we can non-dimensionalize the governing equations,
Combining the Equations (4)–(6) with Equation (7), we can derive the non-dimensional form of non-Fourier heat conduction equations as follows,
where as a total internal heat generation in system can be determined as follows,
For the problem situation, the boundary conditions are defined as follows,
is the dimensionless ambient temperature and is the convection heat transfer coefficient.
The initial conditions are considered to be,
These conditions can be derived from Equation (9). In Equations (14) and (15), and are dimensionless initial condition function and dimensionless initial rate of temperature change function, respectively.
In this paper, as an internal energy generation will be defined as [11],
or
where
where is the absorption coefficient, is the amplitude of laser density, and is the solid surface reflectivity. This model assumes no spatial variations of in the plane perpendicular to the laser beam.
2.2. Solution Structure Theorems and Superposition Approach
One of the famous and most widely used techniques for solving some types of heat conduction equations is the superposition method. This method can be used for solving the linear heat transfer problems with non-homogenous conditions. In this method, an origin problem is split into different easier subproblems which can be integrated to take a solution to the original problem. The method of superposition relies upon the assumption that the original problem (Equation (10)) can be divided into three subproblems by setting the heat generation term (Equation (11)), the initial conditions (Equations (14) and (15)), and the boundary conditions (Equations (12) and (13)) to different values in each subproblem:
Solutions to these subproblems are assigned as , , and sequentially. Therefore, the general solution to the first equation (Equation (10)) is the sum of subproblems one through three, which is
It can be seen that , , and illustrated the independent contributions of the initial rate of temperature variation, initial condition, and internal heat generation to the temperature field, respectively. Subproblems one to three can be simply solved by applying the solution structure theorems [18] once the solution to subproblem one is known. By using the solution structure theorems, the solutions of subproblems one to three can be determined as follows:
where will be obtained by using the Fourier method. and can be simply derived by using the solution structure theorem. It means that only the solution of subproblem one is needed to obtain the solutions to subproblems two and three. Finally, the general solution to the first heat conduction equation is the sum of subproblems one to three.
2.3. Formulation of the Problem
In the literature, there are a few non-Fourier heat conduction problems with different boundary conditions but most of them are limited to boundaries with zero temperature or the insulated boundaries. In this study, we obtain the general analytical solution to hyperbolic heat conduction in a cylinder composed of a homogenous heat conducing material with different boundary conditions at both sides: A symmetry boundary condition in the cylinder’s central line and the convection boundary condition in the cylinder surface (r = R) with ambient.
Let us first consider the solution to subproblem one. This subproblem is solved with the condition . As a result, the equation of this subproblem and the initial conditions and boundary conditions are as bellow:
Using the Fourier series expansion theory, the general form of solution of equation is,
Now, by using the solution structure theorems, we have
where
and are the first order Bessel functions and was obtained by solving the Equation (34).
Also,
Ultimately, the temperature field within the slab can be obtained as,
3. Results and Discussions
In this paper, the temperature field in a one dimensional cylinder with non-zero initial and boundary condition are examined. The values , , , and were selected. It can be concluded that all the profiles of temperature from to are in the infinite series form. By using a relative error test, we can write:
where and are two consecutive partial sums for the temperature, and is the relative error for this study. We showed that the original partial differential equation is split into three subproblems, subproblems one through three demonstrating the contributions of initial rate of change in temperature, initial condition, and internal heat generation, which are given by Equations (31) to (35), respectively.
It can be noted from these equations that all the temperature profiles from to are in the form of an infinite series.
Figure 2 shows the contribution of different components of temperature at various times for a one dimensional cylinder with non-zero initial and boundary condition. According to the Figure 2a, it can be seen that at small times (t = 0.1) up to about r = 0.4, the contribution of and dominate compared to which contributes little to the overall temperature. But at r > 0.4, all three temperature components will have the same role and less impact on the overall temperature.
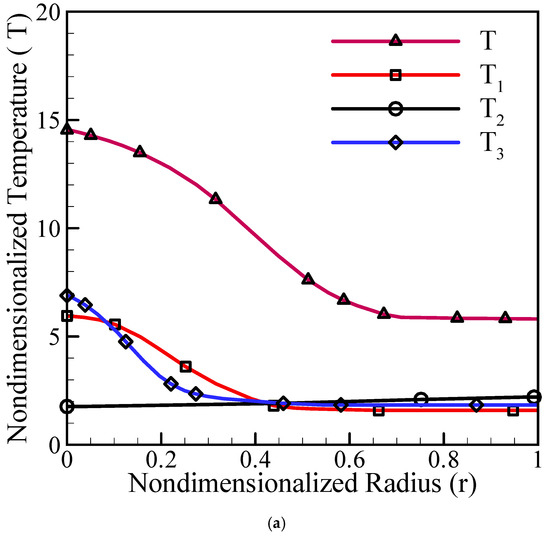
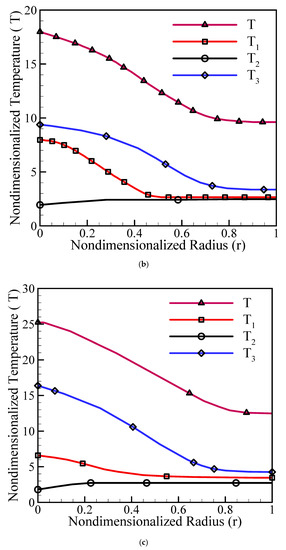
Figure 2.
Contribution of temperature components at t = 0.1 (a), t = 0.5 (b), and t = 1 (c).
Figure 2b shows that still does not have much effect on the overall temperature and acts approximately uniformly with a constant value. and still have a downward trend, but , because of is related to the temperature component of internal heat generation, is dominant.
The downward trend of and will be continued to r = 0.5 and r = 0.8, respectively. After these points, significant variations were not seen. Also, in the areas near the center of the cylinder, where the source term generates the energy, the overall temperature has larger values compared to its values at t = 0.1.
As time increases Figure 2c, the contribution of to the overall temperature is less. Also, the effects of on the overall temperature near to the center of the cylinder are decreased. This means that the effects of initial rate of temperature change have been remarkable, only, at the small times and with increasing the time the effects were not impressive. Due to the fact that the internal heat generation is time and space dependent, the values of in areas close to the center of the cylinder have increased dramatically and will have the greatest impact on the overall temperature ().
Figure 3a illustrates the temperature temporal trend at low times. As time arises, temperatures of cylinder’s center (r = 0) enhance because of absorption of more energy compared to the other places. However, the boundary of cylinder surface remains relatively unchanged and keeps its initial temperature. According to the Figure 3b, with enhancing the time, the surface boundary temperature became affected by the entering energy, hence increasing the temperatures at a slower rate occurred. The temperature throughout the cylinder will continue to increase toward equilibrium between the center and the surface of the cylinder. This trend was shown in Figure 3c.
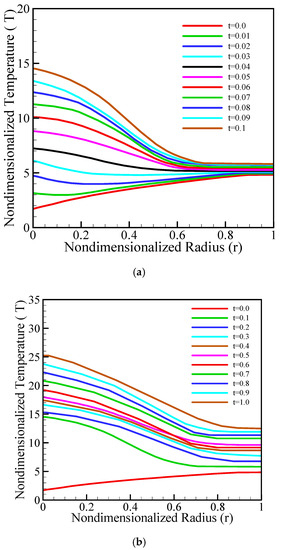
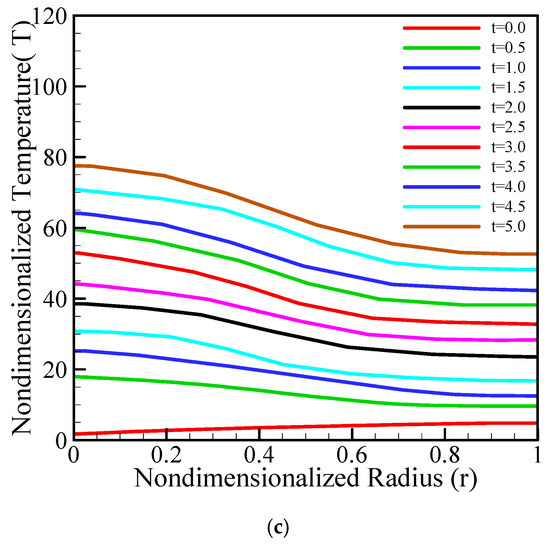
Figure 3.
Temperature distributions from t = 0 to t = 0.1 (a), t = 0.0 to t = 1 (b), and t = 1 to t = 5 (c).
4. Conclusions
In this paper the analytical solution of non-Fourier heat conduction in a cylinder composed of a homogenous material with different boundary conditions: A symmetry boundary condition in the cylinder’s central line and the convection in the cylinder surface (r = R) with ambient is investigated.
We conclude that the obtained results provide an accurate, convenient, and useful solution to the non-Fourier equation, which is usable for analyses of various engineering applications.
The key findings and conclusions from the present solution are as follows:
At small times (t = 0.1) up to about r = 0.4, the contribution of and dominate compared to contributing little to the overall temperature.
At t = 0.5, does not have much effect on the overall temperature and acts approximately uniformly with a constant value.
At t = 0.5, and have a downward trend, but is dominant.
At t = 1, the effects of on the overall temperature near to the center of the cylinder are decreased.
At low times, by enhancing the time, temperatures at the center of the cylinder (r = 0) enhance.
At big times, the temperature throughout the cylinder will continue to increase.
Author Contributions
The contributions of each author in preparing this paper has been clearly identified as bellow, In the writing the article all authors had contributions. The literature review was performed by R.K. and S.M.A. All equations were derived and checked by M.A. (Mohammad Akbari) The results and discussion was prepared by M.A. (Masoud Afrand) According to the reviewer comments, all of the authors prepared the revision format of the manuscript. Ultimately, final approval of the article was done by R.K., M.A. (Mohammad Akbari) and M.A. (Masoud Afrand).
Funding
This research received no external funding.
Conflicts of Interest
The authors of this article certify that they have NO affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in the manuscript entitled “Analytical Solution of Heat Conduction in a Symmetrical Cylinder Using the Solution Structure Theorem and Superposition Technique ”.
Abbreviations
| Nomenclature | |
| Thermal Wave Propagation Speed, m/s | |
| Specific Heat, J/kg K | |
| Total Internal Heat Generation in System | |
| Reference Laser Power Density, | |
| Dimensionless Internal Heat Generation | |
| Transmitted Energy Strength | |
| Internal Heat Generation, | |
| Laser peak Power Density, | |
| Thermal Conductivity, | |
| Convection Heat Transfer Coefficient, | |
| Dimensionless Convection Heat Transfer Coefficient | |
| Heat Flux, c | |
| Dimensionless Heat Flux, | |
| Dimensionless Source Term | |
| Surface Reflectivity of the Solid | |
| Dimensionless Time, | |
| Time, s | |
| Dimensionless Temperature, | |
| Dimensionless Ambient Temperature, | |
| Temperature, K | |
| Ambient Temperature, K | |
| r-coordinate, m | |
| Dimensionless Space Coordinate, | |
| Greek symbols | |
| Thermal Diffusivity , | |
| Eigen Value, | |
| Relative Error | |
| Dimensionless Absorption Coefficient, | |
| Density () | |
| Relaxation Time , s | |
| Dimensionless Initial Condition Function | |
| Dimensionless Initial rate of Temperature Change Function | |
| Dummy Index | |
References
- Dabby, F.W.; Paek, U.-C. High-intensity laser-induced vaporization and explosion of solid material. IEEE J. Quantum Electron. 1972, 8, 106–111. [Google Scholar] [CrossRef]
- Yeung, W.K.; Lam, T.T. Thermal analysis of anisotropic thin-film superconductors. Adv. Electron. Packag. 1999, 26, 1261–1268. [Google Scholar]
- Lundell, J.H.; Dickey, R.R. Vaporization of graphite in the temperature range of 4000 to 4500 K. In Proceedings of the NASA Ames Research Center, Moffett Field, CA, USA, 26–28 January 1976; pp. 76–166. [Google Scholar]
- Robin, J.E.; Nordin, P. Enhancement of CW laser melt-through of opaque solid materials by supersonic transverse gas flow. Appl. Phys. Lett. 1975, 26, 289–292. [Google Scholar] [CrossRef]
- Chen, J.K.; Tzou, D.Y.; Beraun, J.E. Numerical investigation of ultrashort laser damage in semiconductors. Int. J. Heat Mass Transf. 2005, 48, 501–509. [Google Scholar] [CrossRef]
- Cattaneo, C. Sur une former de l’equation de la chaleur elinant le paradoxe d’une propagation instance. Comptes Rendus Acad. Sci. 1958, 247, 431–432. [Google Scholar]
- Vernotte, P. Les paradoxes de la theories continue de l’equation de la chaleur. Comptes Rendus Acad. Sci. 1958, 246, 3154–4155. [Google Scholar]
- Wang, B.L.; Han, J.C.; Sun, Y.G. A finite element/finite difference scheme for the non-classical heat conduction and associated thermal stresses. Finite Elem. Anal. Des. 2012, 50, 201–206. [Google Scholar] [CrossRef]
- Lee, H.L.; Chen, W.L.; Chang, W.J.; Wei, E.J.; Yang, Y.C. Analysis of dual-phase-lag heat conduction in short-pulse laser heating of metals with a hybrid method. Appl. Therm. Eng. 2013, 52, 275–283. [Google Scholar] [CrossRef]
- Mishra, S.C.; Sahai, H. Analysis of non-Fourier conduction and radiation in a cylindrical medium using lattice Boltzmann method and finite volume method. Int. J. Heat Mass Transf. 2013, 61, 41–55. [Google Scholar] [CrossRef]
- Qui, T.; Juhasz, T.; Suarez, C.; Bron, W.; Tien, C. Femto second laser heating of multi-layer II experiments. Int. J. Heat Mass Transf. 1994, 37, 2799–2808. [Google Scholar]
- Ozisik, M.; Vick, B. Propagation and Reflection of Thermal Waves in a Finite Medium. Int. J. Heat Mass Transf. 1984, 27, 1845–1855. [Google Scholar] [CrossRef]
- Jiang, F. Solution and analysis of hyperbolic heat propagation in hollow spherical objects. Heat Mass Transf. 2006, 42, 1083–1091. [Google Scholar] [CrossRef]
- Moosaie, A. Non Fourier heat conduction in a finite medium with insulated boundaries and arbitrary initial condition. Int. Commun. Heat Mass Transf. 2008, 35, 103–111. [Google Scholar] [CrossRef]
- Moosaie, A. Non Fourier heat conduction in a finite medium subjected to arbitrary non-periodic surface disturbance. Int. Commun. Heat Mass Transf. 2008, 35, 376–383. [Google Scholar] [CrossRef]
- Ahmadikia, H.; Rismanian, M. Analytical solution of non-Fourier heat conduction problem on a fin under periodic boundary conditions. J. Mech. Sci. Technol. 2011, 25, 2919–2926. [Google Scholar] [CrossRef]
- Bamdad, K.; Azimi, A.; Ahmadikia, H. Thermal performance analysis of arbitrary-profile fins with non-fourier heat conduction behavior. J. Eng. Math. 2012, 76, 181–193. [Google Scholar] [CrossRef]
- lam, T.T.; Fong, E. Application of solution structure theorem to non-Fourier heat conduction problems: Analytical Approach. Int. J. Heat Mass Transf. 2011, 54, 1–11. [Google Scholar] [CrossRef]
- Liu, F.; Chen, Q.; Kang, Z.; Pan, W.; Zhang, D.; Wang, L. Non-Fourier heat conduction in oil-in-water emulsions. Int. J. Heat Mass Transf. 2019, 135, 323–330. [Google Scholar] [CrossRef]
- Daneshjou, K.; Bakhtiari, M.; Parsania, H.; Fakoor, M. Non-Fourier heat conduction analysis of infinite 2D orthotropic FG hollow cylinders subjected to time-dependent heat source. Appl. Therm. Eng. 2016, 98, 582–590. [Google Scholar] [CrossRef]
- Ma, J.; Sun, Y.; Yang, J. Analytical solution of non-Fourier heat conduction in a square plate subjected to a moving laser pulse. Int. J. Heat Mass Transf. 2017, 115, 606–610. [Google Scholar] [CrossRef]
- Wankhade, P.A.; Kundu, B.; Das, R. Establishment of non-Fourier heat conduction model for an accurate transient thermal response in wet fins. Int. J. Heat Mass Transf. 2018, 126, 911–923. [Google Scholar] [CrossRef]
- Hana, S.; Peddieson, J. Non-Fourier heat conduction/convection in moving medium. Int. J. Therm. Sci. 2018, 130, 128–139. [Google Scholar] [CrossRef]
- Liu, Y.; Li, L.; Lou, Q. A hyperbolic lattice Boltzmann method for simulating non-Fourier heat conduction. Int. J. Heat Mass Transf. 2019, 131, 772–780. [Google Scholar] [CrossRef]
- Kalbasi, R.; Afrand, M.; Alsarraf, J.; Tran, M.D. Studies on optimum fins number in PCM-based heat sinks. Energy 2019, 171, 1088–1099. [Google Scholar] [CrossRef]
- Li, Z.; Al-Rashed, A.A.; Rostamzadeh, M.; Kalbasi, R.; Shahsavar, A.; Afrand, M. Heat transfer reduction in buildings by embedding phase change material in multi-layer walls: Effects of repositioning, thermophysical properties and thickness of PCM. Energy Convers. Manag. 2019, 195, 43–56. [Google Scholar] [CrossRef]
- Li, Z.; Shahsavar, A.; Al-Rashed, A.A.; Kalbasi, R.; Afrand, M.; Talebizadehsardari, P. Multi-objective energy and exergy optimization of different configurations of hybrid earth-air heat exchanger and building integrated photovoltaic/thermal system. Energy Convers. Manag. 2019, 195, 1098–1110. [Google Scholar] [CrossRef]
- Nadooshan, A.A.; Kalbasi, R.; Afrand, M. Perforated fins effect on the heat transfer rate from a circular tube by using wind tunnel: An experimental view. Heat Mass Transf. 2018, 54, 3047–3057. [Google Scholar] [CrossRef]
- Salimpour, M.R.; Kalbasi, R.; Lorenzini, G. Constructal multi-scale structure of PCM-based heat sinks. Contin. Mech. Thermodyn. 2017, 29, 477–491. [Google Scholar] [CrossRef]
- Shanazari, E.; Kalbasi, R. Improving performance of an inverted absorber multi-effect solar still by applying exergy analysis. Appl. Therm. Eng. 2018, 143, 1–10. [Google Scholar] [CrossRef]
- Yari, M.; Kalbasi, R.; Talebizadehsardari, P. Energetic-exergetic analysis of an air handling unit to reduce energy consumption by a novel creative idea. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 3959–3975. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).