Large-Eddy Simulation of an Asymmetric Plane Diffuser: Comparison of Different Subgrid Scale Models
Abstract
1. Introduction
2. SGS Models
2.1. Smagorinsky Model (SM)
2.2. Standard Dynamic Smagorinsky Model (DSM)
2.3. Standard One-Equation Model (OM)
2.4. One-Equation Dynamic Model (ODM)
2.5. One-Equation Vreman Model (OVM)
3. Computational Method
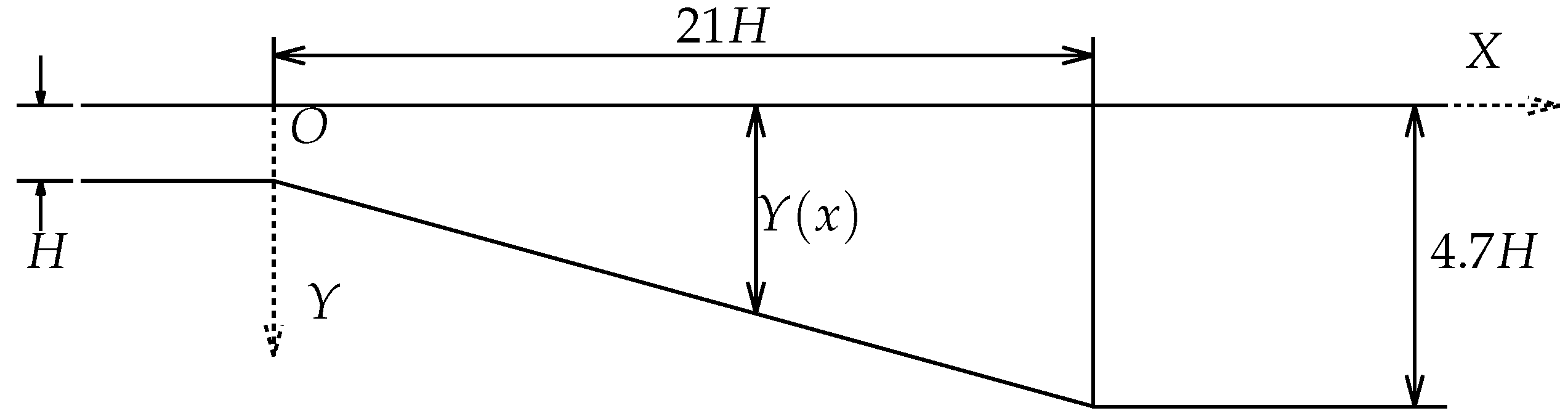
3.1. Domain Size and Boundary Condition
3.2. Computational Meshes
3.3. Solution Strategy
4. Results and Discussion
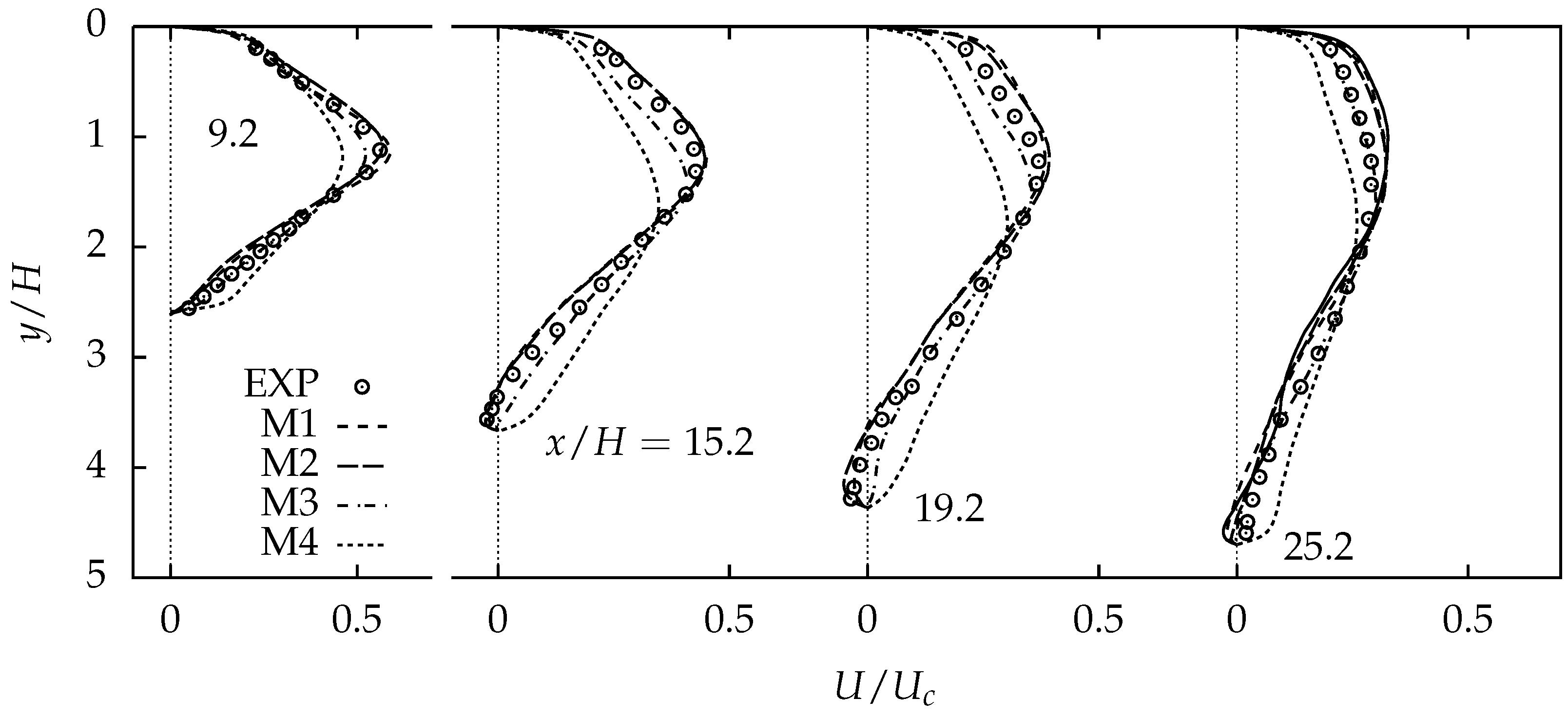
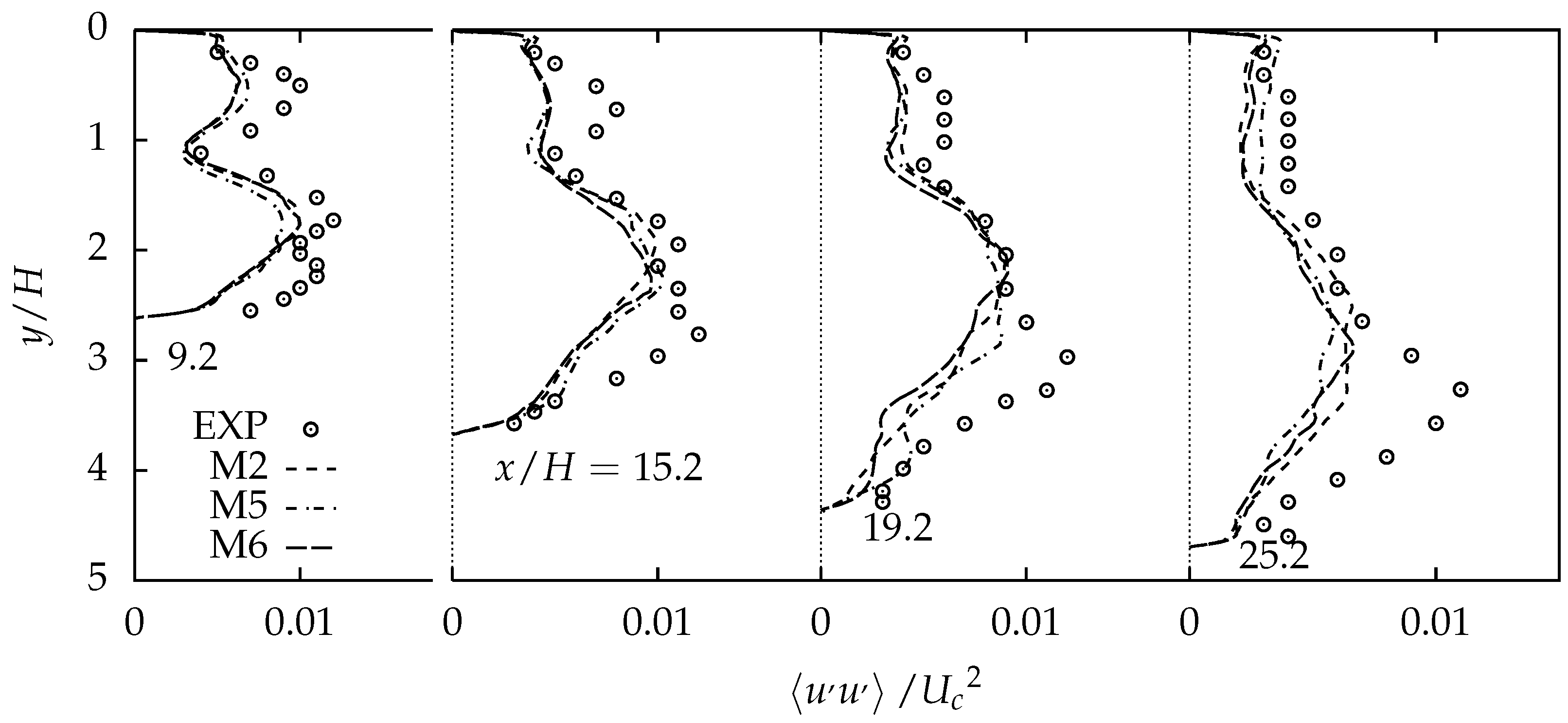
4.1. Comparison of Mesh Resolution
4.2. Comparison of Subgrid Modeling
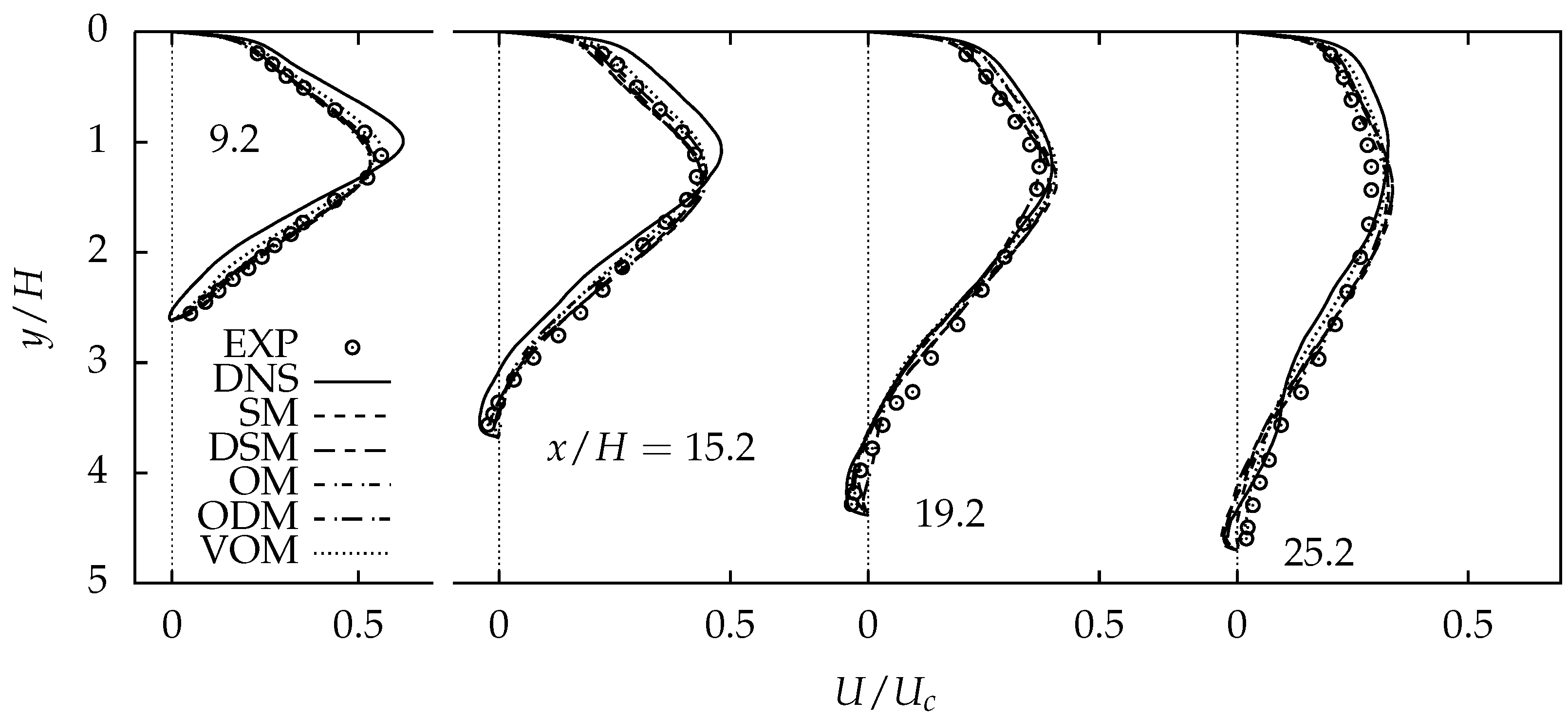
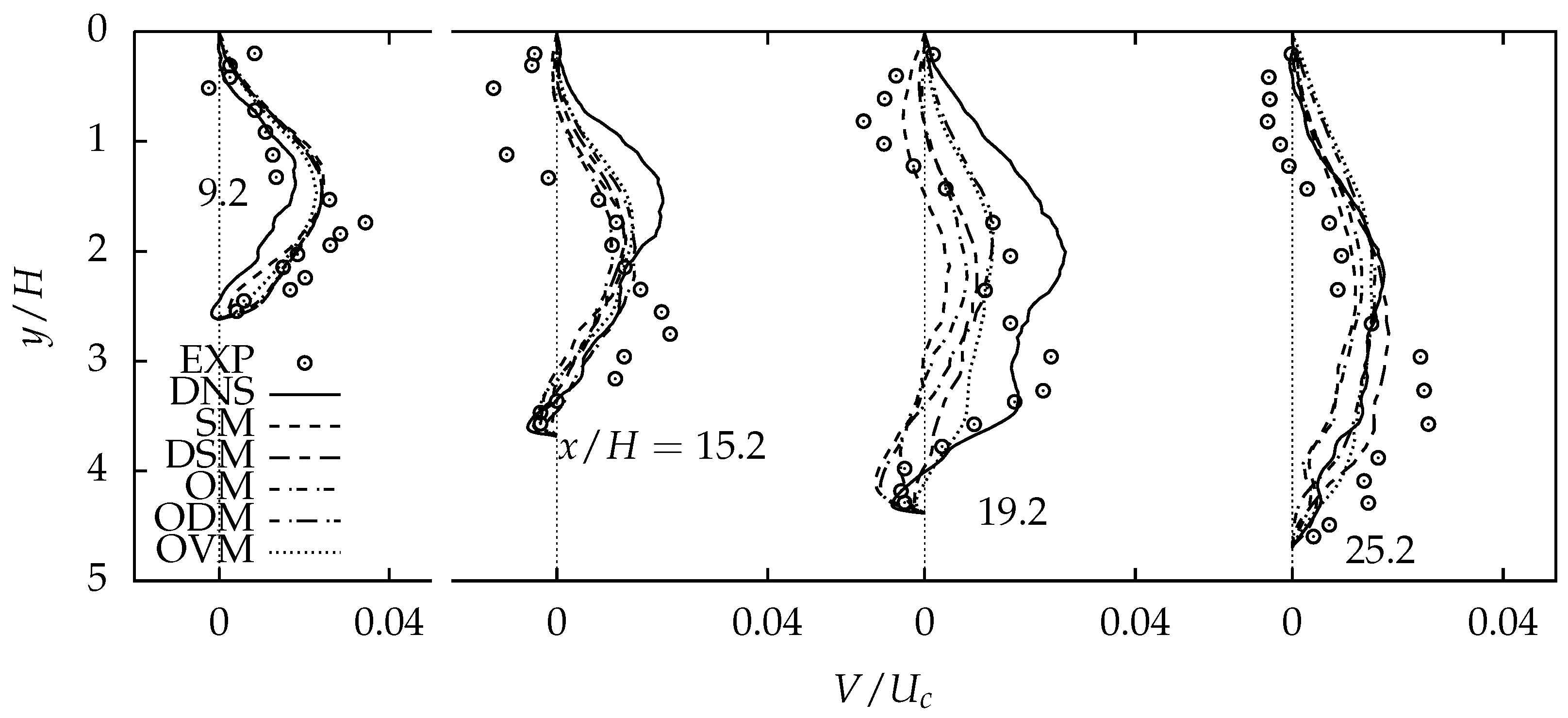
4.2.1. Comparison of Mean Properties
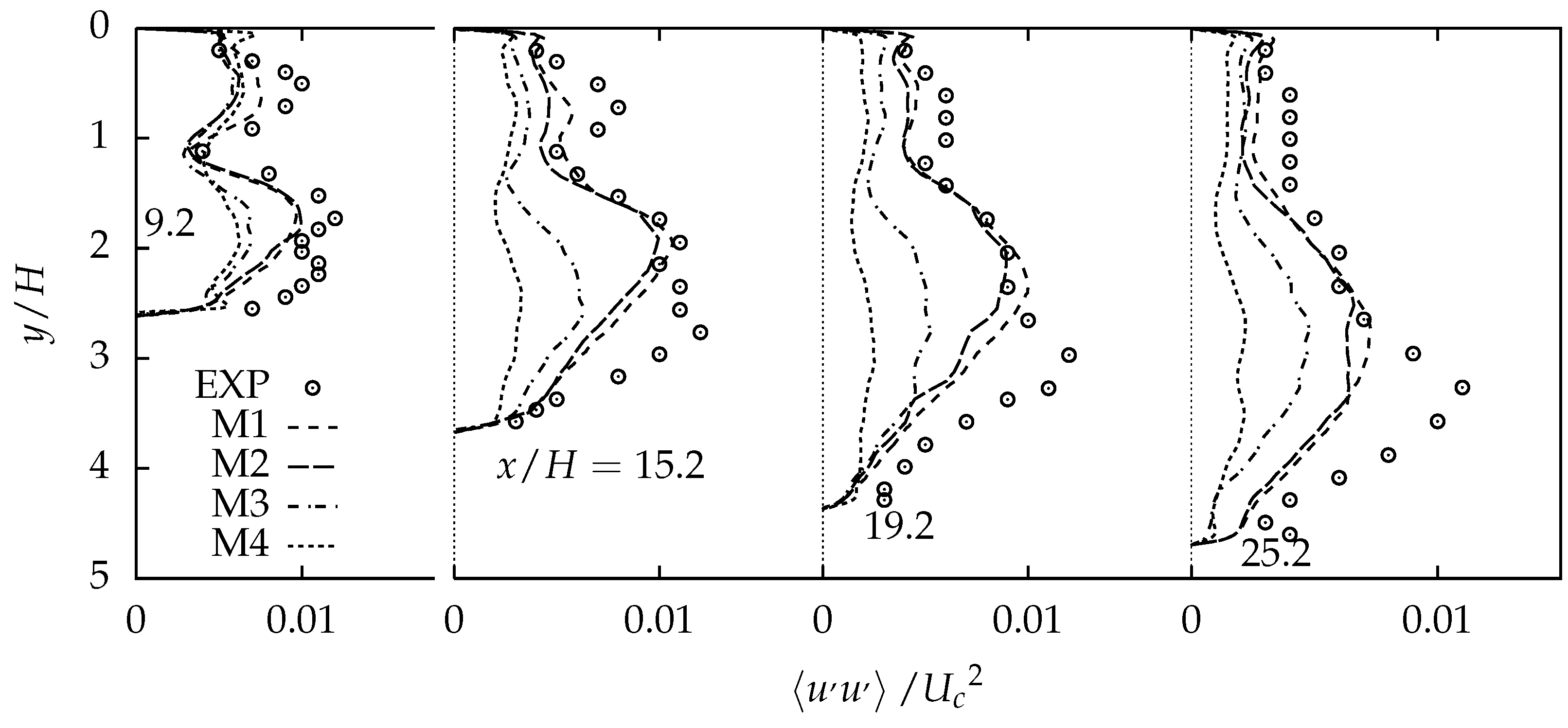
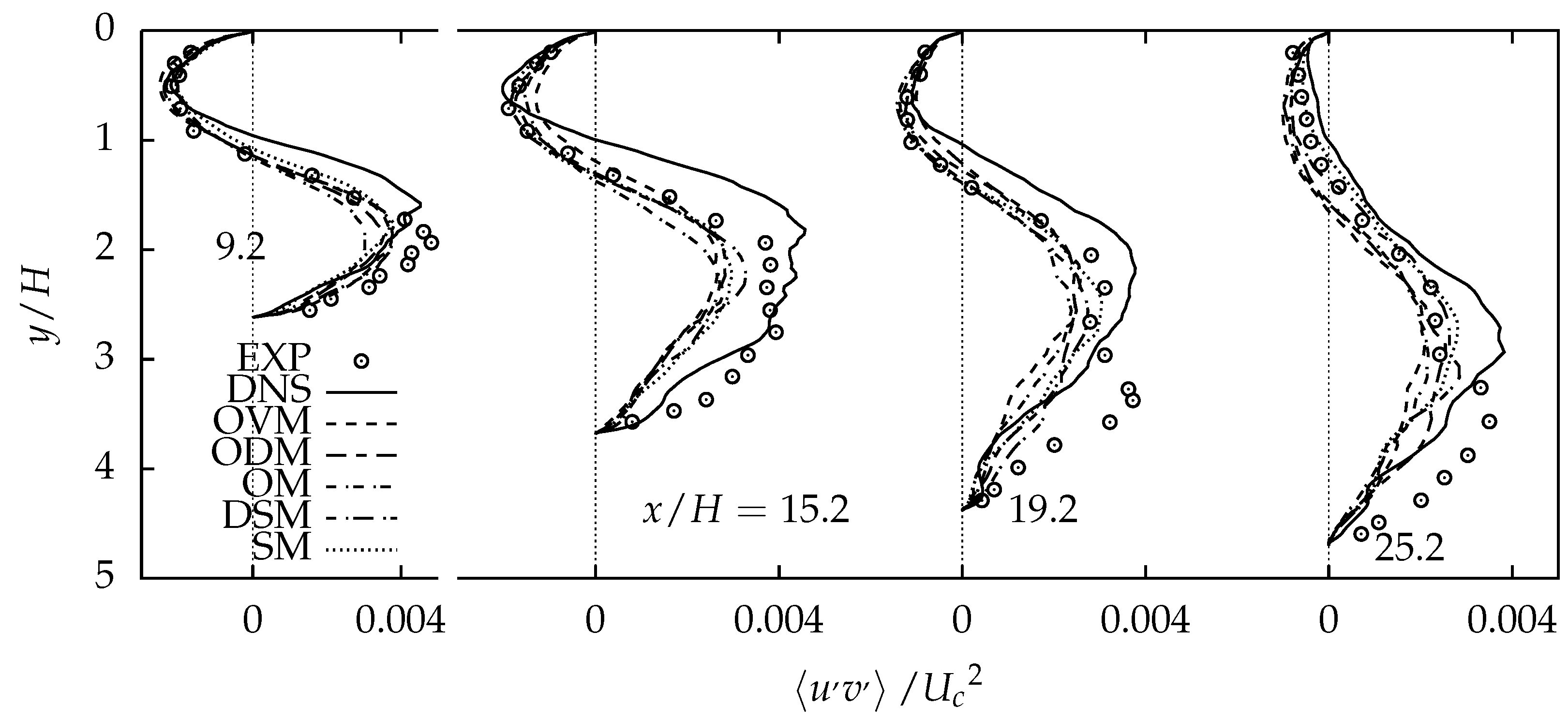
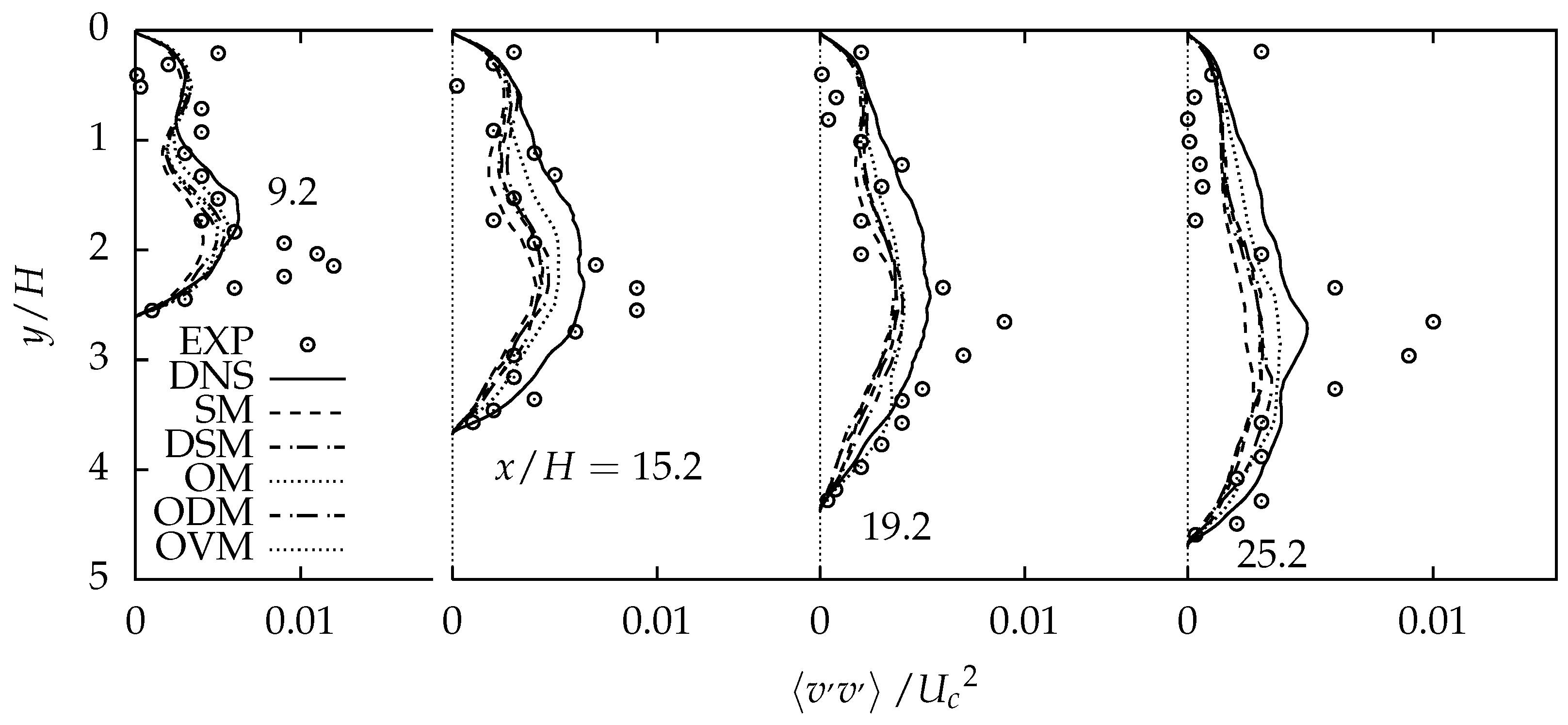
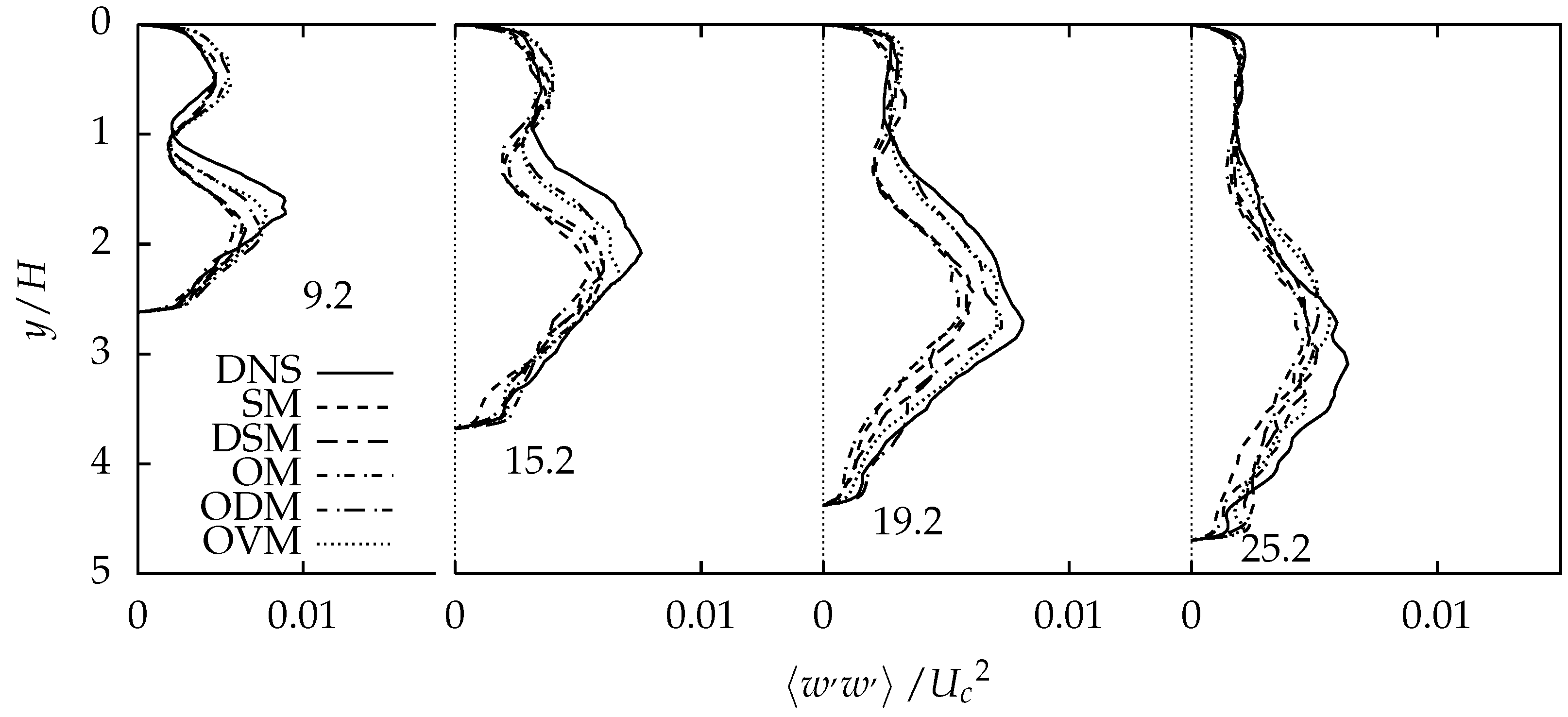
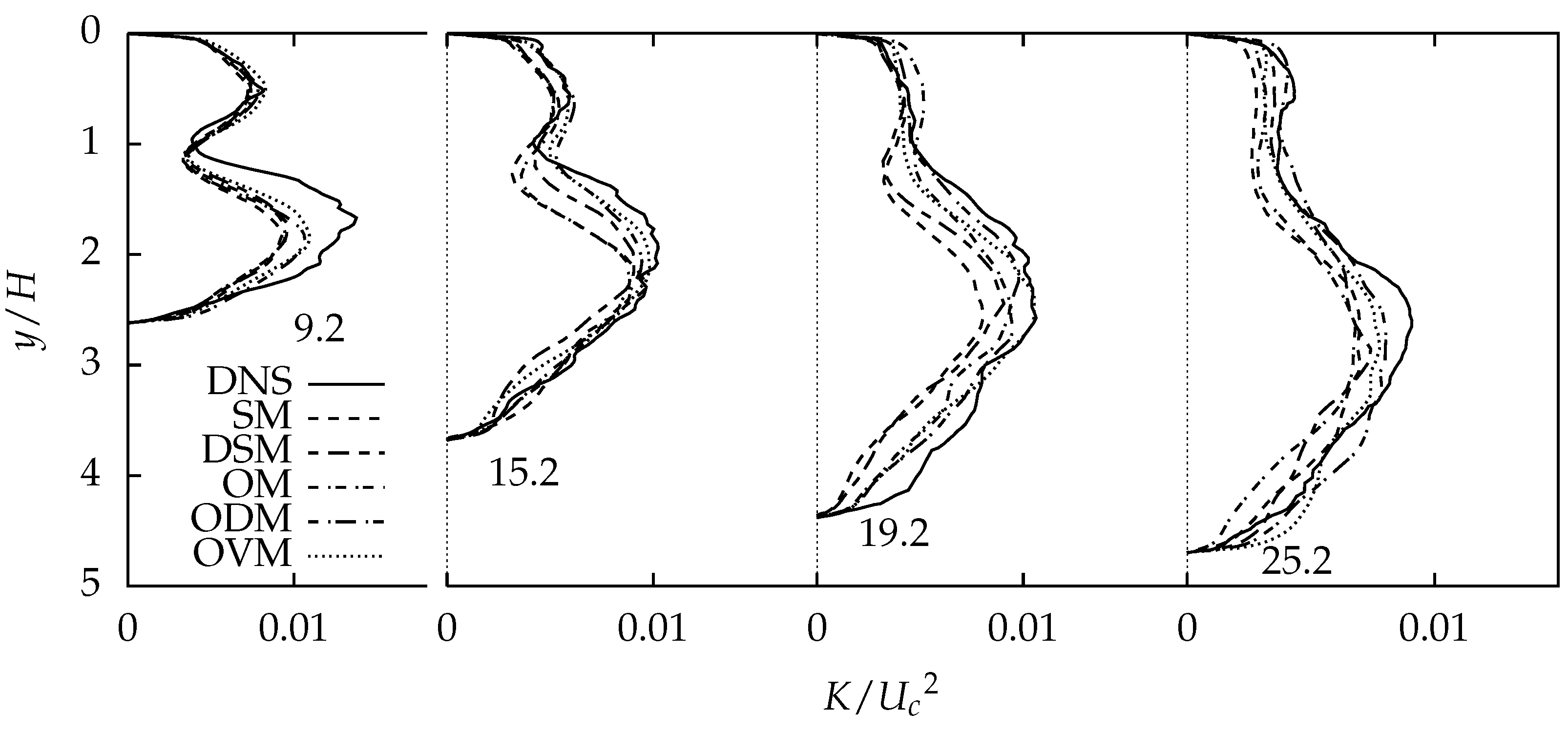
4.2.2. Comparison of Turbulent Stresses and Resolved Turbulent Kinetic Energy
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational fluid dynamics |
| DNS | Direct numerical simulation |
| DSM | Standard dynamic Smagorinsky model |
| LES | Large eddy simulation |
| N-S | Navier–Stokes |
| ODM | One-equation dynamic model |
| OM | Standard one-equation model |
| OVM | One-equation Vreman model |
| RANS | Reynolds-averaged Navier–Stokes simulation |
| SGS | subgrid scale |
| SM | Smagorinsky model |
Appendix A. Determination of the Distance from the Wall Measured in Wall Units in the Diffuser Flow for Smagorinsky Model
References
- Sayles, E.L.; Eaton, J.K. Sensitivity of an asymmetric, three-dimensional diffuser to inlet condition perturbations. Int. J. Heat Fluid Flow 2014, 49, 100–107. [Google Scholar] [CrossRef]
- Azad, R.S. Turbulent flow in a conical diffuser: A review. Exp. Fluid Sci. 1996, 13, 318–337. [Google Scholar] [CrossRef]
- Obi, S.; Aoki, K.; Masuda, S. Experimental and computational study of turbulent separating flow in an asymmetric plane diffuser. In Proceedings of the Ninth Symposium on Turbulent Shear Flows, Hyoto, Japan, 16–18 August 1993; p. 305-1. [Google Scholar]
- Kim, J.; Moin, P.; Moser, R. Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 1987, 177, 133–166. [Google Scholar] [CrossRef]
- Ohta, T.; Kajishima, T. Analysis of non-steady separated turbulent flow in an asymmetric plane diffuser by direct numerical simulations. J. Fluid Sci. Technol. 2010, 5, 515–527. [Google Scholar] [CrossRef]
- Kaltenbach, H.J.; Fatica, M.; Mittal, R.; Lund, T.S.; Moin, P. Study of flow in a planar asymmetric diffuser using large-eddy simulation. J. Fluid Mech. 1999, 390, 151–185. [Google Scholar] [CrossRef]
- Durbin, P.A. Separated flow computations with the k-epsilon-v-squared model. AIAA J. 1995, 33, 659–664. [Google Scholar] [CrossRef]
- Iaccarino, G. Predictions of a turbulent separated flow using commercial CFD codes. J. Fluids Eng. 2001, 123, 819–828. [Google Scholar] [CrossRef]
- El-Behery, S.M.; Hamed, M.H. A comparative study of turbulence models performance for separating flow in a planar asymmetric diffuser. Comput. Fluids 2011, 44, 248–257. [Google Scholar] [CrossRef]
- Schneider, H.; von Terzi, D.; Bauer, H.J.; Rodi, W. Reliable and accurate prediction of three-dimensional separation in asymmetric diffusers using large-eddy simulation. J. Fluids Eng. 2010, 132, 031101. [Google Scholar] [CrossRef]
- Abe, K.I.; Ohtsuka, T. An investigation of LES and Hybrid LES/RANS models for predicting 3-D diffuser flow. Int. J. Heat Fluid Flow 2010, 31, 833–844. [Google Scholar] [CrossRef]
- Schluter, J.; Wu, X.; Pitsch, H. Large-Eddy Ssimulations of a Separated Plane Diffuser. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005; p. 672. [Google Scholar]
- Kobayashi, H.; Ham, F.; Wu, X. Application of a local SGS model based on coherent structures to complex geometries. Int. J. Heat Fluid Flow 2008, 29, 640–653. [Google Scholar] [CrossRef]
- Taghinia, J.; Rahman, M.M.; Siikonen, T.; Agarwal, R.K. One-equation sub-grid scale model with variable eddy-viscosity coefficient. Comput. Fluids 2015, 107, 155–164. [Google Scholar] [CrossRef]
- Shuai, S.; Agarwal, R.K. A One-Equation Turbulence Model Based on k-kL Closure. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 1879. [Google Scholar]
- Sagaut, P. Large Eddy Simulation for Incompressible Flows: An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Geramny, 2006. [Google Scholar]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Lilly, D.K. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A 1992, 4, 633–635. [Google Scholar] [CrossRef]
- Yoshizawa, A. A statistically-derived subgrid model for the large-eddy simulation of turbulence. Phys. Fluids 1982, 25, 1532–1538. [Google Scholar] [CrossRef]
- Kajishima, T.; Nomachi, T. One-equation subgrid scale model using dynamic procedure for the energy production. J. Appl. Mech. 2006, 73, 368–373. [Google Scholar] [CrossRef]
- Yoshizawa, A.; Horiuti, K. A statistically-derived subgrid-scale kinetic energy model for the large-eddy simulation of turbulent flows. J. Phys. Soc. Jpn. 1985, 54, 2834–2839. [Google Scholar] [CrossRef]
- Horiuti, K. Large eddy simulation of turbulent channel flow by one-equation modeling. J. Phys. Soc. Jpn. 1985, 54, 2855–2865. [Google Scholar] [CrossRef]
- Okamoto, M.; Shima, N. Investigation for the One-Eaquation-Type Subgrid Model with Eddy-Viscosity Expression Including the Shear-Damping Effect. JSME Int. J. Ser. B 1999, 42, 154–161. [Google Scholar] [CrossRef]
- Vreman, A.W. An eddy-viscosity subgrid-scale model for turbulent shear flow: Algebraic theory and applications. Phys. Fluids 2004, 16, 3670–3681. [Google Scholar] [CrossRef]
- Park, N.; Lee, S.; Lee, J.; Choi, H. A dynamic subgrid-scale eddy viscosity model with a global model coefficient. Phys. Fluids 2006, 18, 125109. [Google Scholar] [CrossRef]
- You, D.; Moin, P. A dynamic global-coefficient subgrid-scale eddy-viscosity model for large-eddy simulation in complex geometries. Phys. Fluids 2007, 19, 065110. [Google Scholar] [CrossRef]
- You, D.; Moin, P. A dynamic global-coefficient subgrid-scale model for large-eddy simulation of turbulent scalar transport in complex geometries. Phys. Fluids 2009, 21, 045109. [Google Scholar] [CrossRef]
- Obi, S.; Ohizumi, H.; Aoki, K.; Masuda, S. Turbulent separation control in a plane asymmetric diffuser by periodic perturbation. Eng. Turbul. Model. Exp. 1993, 633–642. [Google Scholar] [CrossRef]
- Kajishima, T.; Ohta, T.; Okazaki, K.; Miyake, Y. High-order finite-difference method for incompressible flows using collocated grid system. JSME Int. J. Ser. B 1998, 41, 830–839. [Google Scholar] [CrossRef]
- Ohta, T. DNS of turbulent channel flow subjected to the acceleration. Trans. Jpn. Soc. Mech. Eng. Ser. B 2004, 70, 1–8. [Google Scholar] [CrossRef]
- Tang, H.; Lei, Y.; Fu, Y. Noise Reduction Mechanisms of an Airfoil with Trailing Edge Serrations at Low Mach Number. Appl. Sci. 2019, 9, 3784. [Google Scholar] [CrossRef]
- Tamura, A.; Kikuchi, K.; Takahashi, T. Residual cutting method for elliptic boundary value problems. J. Comput. Phys. 1997, 137, 247–264. [Google Scholar] [CrossRef]
- Buice, C.U.; Eaton, J.K. Experimental Investigation of Flow Through an Asymmetric Plane Diffuser. Center for Turbulence Research Annual Research Briefs 1995, 117–120. [Google Scholar] [CrossRef][Green Version]
- Dean, R.B. Reynolds number dependence of skin friction and other bulk flow variables in two-dimensional rectangular duct flow. J. Fluids Eng. 1978, 100, 215–223. [Google Scholar] [CrossRef]

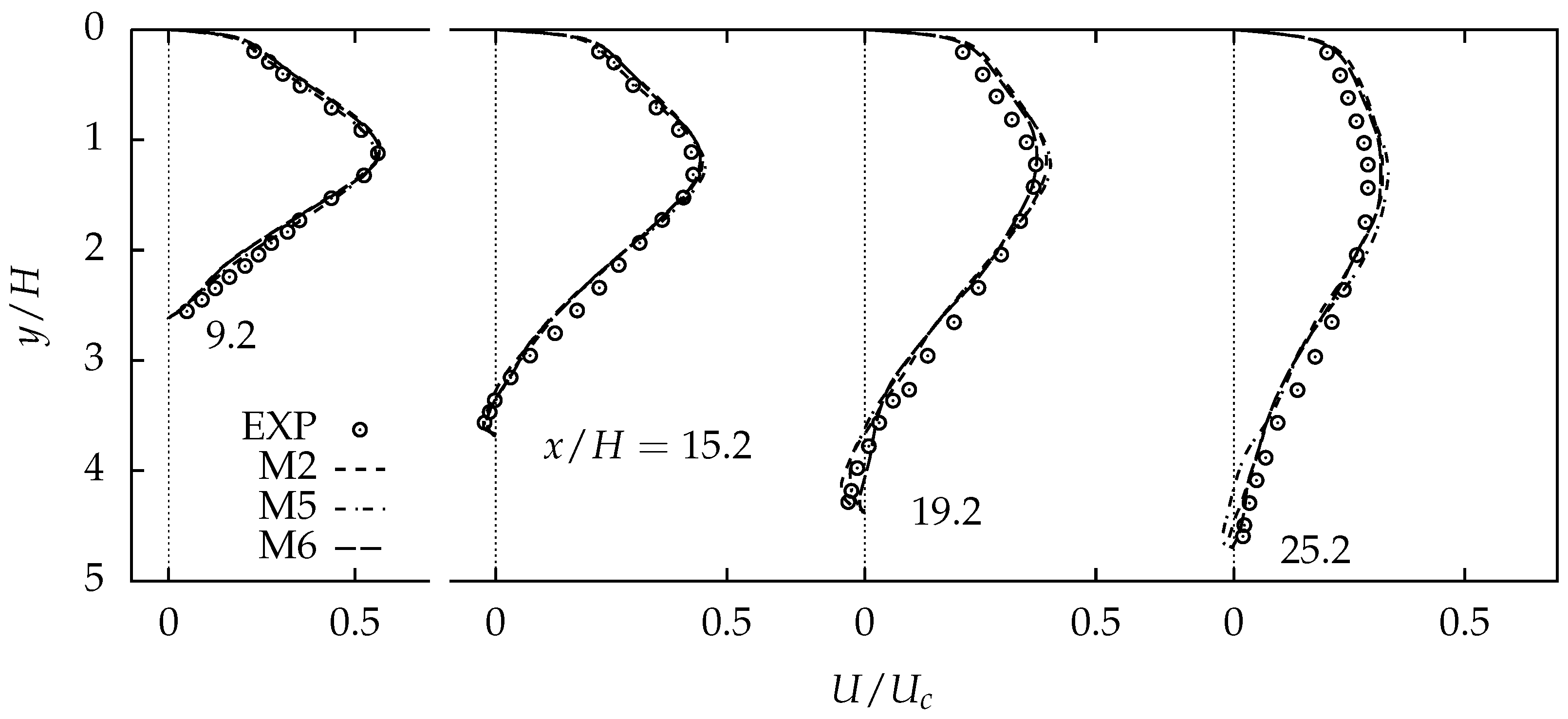

| Case | ||||||||
|---|---|---|---|---|---|---|---|---|
| DNS | 320 | 1200 | 160 | 320 | 20.15 | 20.15 | 0.50 | 9.77 |
| M1 | 160 | 600 | 80 | 160 | 40.30 | 40.30 | 1.04 | 19.54 |
| M2 | 128 | 480 | 80 | 160 | 50.38 | 50.38 | 1.04 | 19.54 |
| M3 | 128 | 360 | 80 | 160 | 50.38 | 67.17 | 1.04 | 19.54 |
| M4 | 128 | 300 | 80 | 160 | 50.38 | 80.6 | 1.04 | 19.54 |
| M5 | 128 | 480 | 160 | 160 | 50.38 | 50.38 | 0.50 | 19.54 |
| M6 | 128 | 372 | 80 | 160 | 50.38 | 50.38–100.76 | 1.04 | 19.54 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, H.; Lei, Y.; Li, X.; Fu, Y. Large-Eddy Simulation of an Asymmetric Plane Diffuser: Comparison of Different Subgrid Scale Models. Symmetry 2019, 11, 1337. https://doi.org/10.3390/sym11111337
Tang H, Lei Y, Li X, Fu Y. Large-Eddy Simulation of an Asymmetric Plane Diffuser: Comparison of Different Subgrid Scale Models. Symmetry. 2019; 11(11):1337. https://doi.org/10.3390/sym11111337
Chicago/Turabian StyleTang, Hui, Yulong Lei, Xingzhong Li, and Yao Fu. 2019. "Large-Eddy Simulation of an Asymmetric Plane Diffuser: Comparison of Different Subgrid Scale Models" Symmetry 11, no. 11: 1337. https://doi.org/10.3390/sym11111337
APA StyleTang, H., Lei, Y., Li, X., & Fu, Y. (2019). Large-Eddy Simulation of an Asymmetric Plane Diffuser: Comparison of Different Subgrid Scale Models. Symmetry, 11(11), 1337. https://doi.org/10.3390/sym11111337





