A Method for Constructing Supervised Topic Model Based on Term Frequency-Inverse Topic Frequency

Abstract

Supervised topic modeling has been successfully applied in the fields of document classification and tag recommendation in recent years. However, most existing models neglect the fact that topic terms have the ability to distinguish topics. In this paper, we propose a term frequency-inverse topic frequency (TF-ITF) method for constructing a supervised topic model, in which the weight of each topic term indicates the ability to distinguish topics. We conduct a series of experiments with not only the symmetric Dirichlet prior parameters but also the asymmetric Dirichlet prior parameters. Experimental results demonstrate that the result of introducing TF-ITF into a supervised topic model outperforms several state-of-the-art supervised topic models.

1. Introduction

A topic model is a probabilistic generation model to find the representative topic of a document, with latent semantic analysis (LSA) [1], probabilistic latent semantic analysis (PLSA) [2] and latent Dirichlet allocation (LDA) [3] examples of classical topic models. However, these models are unsupervised, making the number and the content of topics difficult to control. As a result, a supervised topic model is proposed.

Supervised topic models have been successfully applied in the fields of tag recommendation [4,5] and document classification [6,7] in recent years. Furthermore, supervised topic models have been applied to various document-related tasks, and more successfully than unsupervised models. To the best of our knowledge, a supervised LDA was the prototype of the supervised topic model [8], which used variational methods to handle intractable posterior expectations. Since then, several supervised topic models have been proposed, e.g., discriminative LDA [9], a discriminative variation of LDA in which a class-dependent linear transformation is introduced in the topic mixture proportions. Maximum entropy discrimination LDA [10] utilizes the max-margin principle to train supervised topic models and estimate predictive topic representations that are arguably more suitable for prediction. The above methods train a single topic for documents.

It is well-known that a document with only one topic is inappropriate; for example, a document on sport medicine includes both sport and medical topics. This paper studies supervised topic models for multiple topics. Labeled LDA (L-LDA) [11] is a classical supervised topic model that matches the topics to the labels in the document. The number of topics is determined by the metadata of the document (such as labels), and topic terms have a better way to interpret topics. Partially labeled LDA [12] makes use of the learning machinery of topic models to discover the hidden topics within each label, as well as unlabeled, corpus-wide latent topics. Nonparametric labeled LDA [13] uses a mixture of random measures as a base distribution of the hierarchical Dirichlet process framework with good effect. Dependency-LDA [14] further considers the label frequency and label dependency observed in the training data for constructing the supervised topic model.

Although supervised topic models have been studied extensively, most neglect the fact that topic terms have the ability to distinguish topics. Zou et al. [15] proved that a term weight with a more discriminative knowledge of topics is important.

In this paper, we propose a term frequency-inverse topic frequency (TF-ITF) method for constructing a supervised topic model, in which the weight of each topic term has the ability to distinguish topics.

The rest of the paper is organized as follows: the background knowledge of the research is reviewed in Section 2. Section 3 describes a term frequency-inverse topic frequency (TF-ITF) method for constructing a supervised topic model in detail. The experiments of our proposed method are conducted in Section 4. This paper is concluded in Section 5.

In order to make the proposed method easier to describe and understand, we summarize the notation needed in our formulation in

Table 1. Notations description.

Notation	Description
$w$	Term
$c$	Topic
$d$	Document $d$
$n$	Number of terms in document $d$
$N_i$	The $\mathrm{i}$th term of document $\mathrm{d}$
$p\left(w\right)$	The term $w$ probability in corpus
$\beta$	The Dirichlet prior parameter
$\eta$	The scale coefficient
$\gamma$	The smoothing factor
$C$	Number of topics in corpus
$C_w$	Number of topics for Term $w$
$SN$	The sampling number matrix of topic-term
$\Phi$	The probability matrix of topic-term
${\Phi }^{weight}$	The weight matrix of topic-term
${\Phi }^{\prime }$	The final generated probability matrix of topic-term

.

2. Background

In this section, we review some representative works on supervised topic models in detail, including L-LDA [11], Dependency-LDA [14] and CF-weight-LDA [15]. Then we analyze the limitations of the related works in the generation process of topic terms.

2.1. L-LDA (Labeled Latent Dirichlet Allocation)

L-LDA is an extension of the unsupervised LDA model. In order to contain the supervision, it applies a 1:1 correspondence between topics and labels. In addition to labels, keywords of scientific papers and categories of news are also considered as topics. L-LDA assumes that each document $d$ is restricted to a multinomial distribution ${\theta }_d$ over labels which are part of the corpus. Each label is represented as a topic $c$ that is a multinomial distribution ${\Phi }_c$ over the terms. The generative process for the algorithm is shown in

Table 2. Generative process of labeled latent Dirichlet allocation (L-LDA).

Steps	Description
1	For each topic $c\in C$:
2	Generate the multinomial topic distributions over vocabulary ${\Phi }_c~Dirichlet\left({\beta }_c\right)$
3	End for
4	For each document $d\in D$:
5	Generate the multinomial topic distributions over document ${\theta }_d~Dirichlet\left({\alpha }_d\right)$ according to the label set of each document $d$
6	For each term $W_{d,n}\in d$:
7	Generate topic $Z_{d,n}~Multinomial\left({\theta }_d\right)$
8	Generate term $W_{d,n}~Multinomial\left({\Phi }_{Z_{d,n}}\right)$
9	End for
10	End for

.

It should be noted that it first samples a document topic distribution ${\theta }_d$ from a symmetric Dirichlet prior ${\alpha }_d$ of each document $d$.

The whole process of L-LDA contains topic constraints, which is different from LDA. More detailed descriptions of L-LDA are presented in the literature [11].

2.2. Dependency-LDA (Dependency Latent Dirichlet Allocation)

Dependency-LDA further considers the label frequency and label dependency observed in the training data using an asymmetric document-label Dirichlet prior [15], as defined by Equation (1):

$$\alpha =\left[{\eta }_d\frac{N_{d,1}}{M_d}+{\alpha }_d, {\eta }_d\frac{N_{d,2}}{M_d}+{\alpha }_d,\dots {\eta }_d\frac{N_{d,i}}{M_d}+{\alpha }_d,\dots ,{\eta }_d\frac{N_{d,C}}{M_d}+{\alpha }_d\right]$$

(1)

The generative process for the algorithm is shown in

Table 3. Generative process of Dependency-LDA.

Steps	Description
1	for each topic $c\in C$:
2	Generate the multinomial topic distributions over label ${\Phi }_c~Dirichlet\left({\beta }^{\prime }\right)$
3	End for
4	for each label $l\in L$:
5	Generate the multinomial topic distributions over vocabulary ${\phi }_l~Dirichlet\left(\beta \right)$
6	End for
7	for each document $d\in D$:
8	Generate the multinomial topic distributions over document ${\theta }_d{}^{\prime }~Dirichlet\left({\alpha }^{\prime }\right)$
9	for each label $i\in \left\{1,2,\dots ,M_d\right\}$:
10	Generate the topic $Z^{\prime }{}_{d,i}~Multinomial\left({\theta }_d{}^{\prime }\right)$
11	Generate the label $c^{\prime }{}_{d,i}~Multinomial\left({\Phi }_{Z^{\prime }d,i}\right)$ according to the label set of each document $d$
12	End for
13	Compute the asymmetric Dirichlet prior $\alpha$ using Equation (1)
14	Generate the multinomial topic distributions over document ${\theta }_d~Dirichlet\left(\alpha \right)$
15	For each term $W_{d,n}\in d$:
16	Generate topic $Z_{d,n}~Multinomial\left({\theta }_d\right)$
17	Generate term $W_{d,n}~Multinomial\left({\phi }_{Z_{d,n}}\right)$
18	End for
19	End for

.

More detailed descriptions of Dependency-LDA are presented in the literature [14].

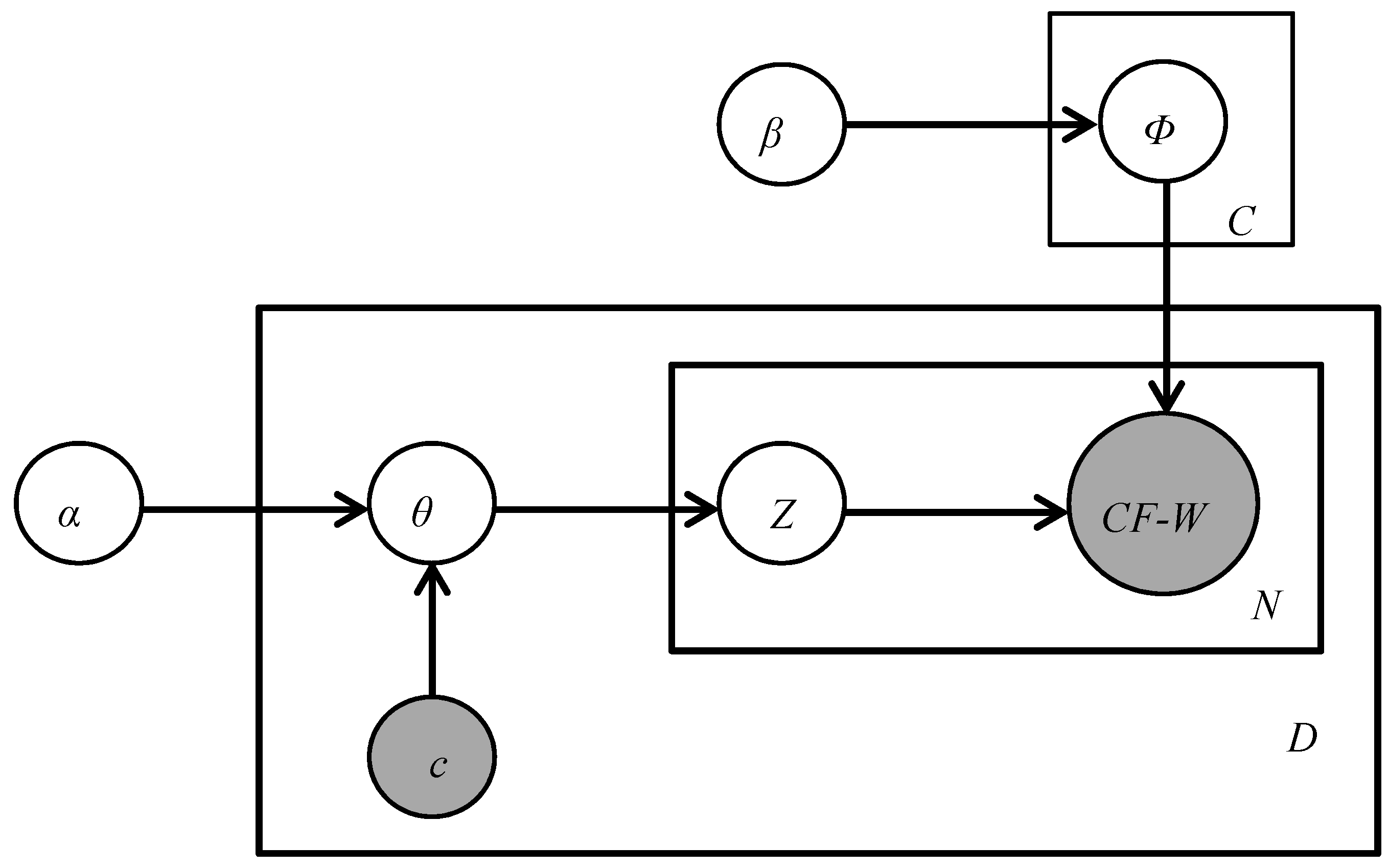
2.3. CF-Weight LDA (CF-Weight Latent Dirichlet Allocation)

Zou et al. [15] proved that a term weight with a more discriminative knowledge of topics is important. Each term is weighted by the corresponding CF-weight, which is based on the class frequency as follows:

$$CF-Weigh{t}_v=\eta log\left(\frac{C}{C{F}_v}\right)+\gamma$$

(2)

where $C{F}_v$ is the topic frequency of term $v$, i.e., the number of labels where term $v$ has occurred in the training data; $C$ is the total number of labels; $\eta$ is the scale coefficient; and $\gamma$ is the smoothing factor. A term with a higher (lower) class frequency will correspond to a smaller (larger) CF-weight; according to Equation (2), the model of CF-weight LDA is shown in Figure 1.

In Figure 1, the two observable parts of the grey filled areas, $c$ and $CF-W$, are explicit variables that indicate labels and weighted terms, respectively. Blank nodes are implicit variables and unobservable. The goal of CF-weight LDA model training is to estimate all $C$ label-word distributions $\Phi$. Given observed data $CF-W$, this is achieved by approximating the posterior distribution of latent variables $P(\Phi ,\theta ,z|CF-W,\alpha ,\beta )$.

In the Gibbs sampler algorithm, the probability of term $w_{d,n}$ in the topic $c$ is given by Equation (3):

$$P\left(Z_{d,n}=c|w_{d,n},Z_d^{-n},\alpha ,\beta \right)\propto \frac{S{N}_{d,c}^{-n}+\alpha }{S{N}_d^{-n}+\left|y_d\right|\alpha }·\frac{S{N}_{c,w_{d,n}}^{-n}+\beta }{S{N}_c^{-n}+V\beta }$$

(3)

where $S{N}_{d,c}$ and $S{N}_d$ are the number of terms with CF-weights assigned to topic $c$ and the total number of terms with CF-weights in document $d$, respectively; $S{N}_{c,w_{d,n}}$ and $S{N}_c$ are the number of terms $w_{d,n}$ with CF-weights assigned to topic $c$ and the total number of terms with CF-weights assigned to topic $c$, respectively; the superscript $–n$ is a quantity except for the term token in position $n$; $\alpha$ and $\beta$ are Dirichlet prior parameters, and $y_d$ is the total number of labels of document $d$.

More detailed descriptions of CF-weight LDA are presented in the literature [15].

Although accomplishments have been achieved in existing research works for supervised topic models, unfortunately, two limitations exist:

(1)

The L-LDA and Dependency-LDA supervised topic models achieve correspondence between topics of document and multiple labels. The topic of each document is not the only one. However, they neglect the weight of terms by the topic frequency knowledge.

(2)

The CF-weight LDA supervised topic model uses the weight of terms with topic frequency knowledge. Nevertheless, the term frequency in the topic is neglected, and the calculating formula for the weight of terms reflects the poor ability of distinguishing topics without certain judgment conditions, for example, the perplexity value of the topic model.

To address the problems mentioned above, we propose a method for constructing a supervised topic model based on term frequency-inverse topic frequency to achieve a better topic model.

3. Proposed Method

The Gibbs sampler, a Markov chain Monte Carlo (MCMC) algorithm, which can approximately obtain a sequence of observations with a specified multivariate probability distribution, is used in this paper, since direct sampling is difficult [16]. The topic distribution of terms in each loop is updated in Gibbs sampling [17], which is more flexible compared with the maximum likelihood estimation method.

Firstly, each document is preprocessed through tokenization, lemmatization and deletion of unsuitable terms; secondly, the sampling number matrix of topic-term $SN$ is generated by the Gibbs sampler. The principle of Gibbs sampling is simple, effective and easy to implement quickly, which is why Gibbs sampling is used to construct the topic model in this step.

When the perplexity value of the topic model tends to be stable, the sampling number matrix of topic-term $SN$ is calculated and output. Based on $SN$, we can obtain the probability matrix of topic-term $\Phi$. The probability of term $v$ of topic $c$ is ${\Phi }_{c,v}$:

$${\Phi }_{c,v}=\frac{S{N}_{c,v}+\beta }{S{N}_c+V\beta }$$

(4)

where $S{N}_{c,v}$ is the number of terms $v$ assigned to topic $c$; $S{N}_c$ is the total number of all terms assigned to topic $c$; $V$ is the total number of terms in the corpus; and $\beta$ is the initial parameter.

The perplexity is a measurement of how well a probability distribution or probability model predicts a sample. It may be used to compare probability models. A low perplexity indicates the probability distribution is good at predicting the sample [18]. For a data set $D$, perplexity is defined by the following equation:

$$Perplexity\left(D\right)=exp\left(-\frac{{\sum }_{d=1}^M\mathit{log}p\left(w_d\right)}{{\sum }_{d=1}^M{N}_d}\right)$$

(5)

where $M$ denotes the number of documents in the data set, $w_d$ is a term, and $N_d$ is the number of terms in a given document $d$ [19].

When the perplexity value decreases and gradually becomes stable, the training of topic model is completed. The probability matrix of topic-term $\Phi$ can be calculated by Equation (4).

Next, we calculate the weight matrix of the topic-term ${\Phi }^{weight}$. The calculation method is enlightened by TF-IDF (term frequency-inverse document frequency), a numerical statistic which can reflect how important a term is to a document in a corpus from information retrieval fields [20]. Similarly, in topic model fields, the importance of a term in a topic can be expressed by its weight. In this paper, we propose a term frequency-inverse topic frequency (TF-ITF) method for calculating the weight matrix of the topic-term ${\Phi }^{weight}$. The calculation of weights is mainly in two parts:

(1)

Term frequency: Term frequency is the number of times the term has appeared in the topic. Higher values of the term frequency indicate that the term can represent the topic better.

(2)

Inverse topic frequency: Inverse topic frequency is a measure of the importance of a term. The less number of topics in which the term has occurred indicates the term can distinguish topics better.

Based on term frequency and inverse topic frequency, the equation of term frequency-inverse topic frequency is as follows:

$${\Phi }_{c,v}^{weight}=\eta \ast \left[\frac{S{N}_{c,v}}{S{N}_c}\ast log\left(\frac{C}{C_v}\right)\right]+\gamma$$

(6)

where ${\Phi }_{c,v}^{weight}$ is the weight of the term $v$ in topic $c$; $S{N}_{c,v}$ denotes the number of terms $v$ occurring in the topic $c$; $S{N}_c$ is the total number of terms in topic $c$; $S{N}_{c,v}/S{N}_c$ denotes the term frequency; $C_v$ is the number of topics in which term $v$ has occurred in the training data; $C$ is the total number of topics; $\eta$ is the scale coefficient, where $\eta \ge$ 1 generally and $\gamma$ is the smoothing factor, where $\gamma \le$ 0.01 to avoid the situation that the weight is equal to 0.

The elements of ${\Phi }^{weight}$ and $\Phi$ are multiplied to generate the final probability matrix of topic-term ${\Phi }^{\prime }$ as follows:

$${\Phi }^{\prime }={\Phi }^{weight}. \ast \Phi$$

(7)

To sum up, the training steps of the proposed method are as follows:

Step 1.

Set the appropriate Dirichlet prior parameters α and $\beta$, and set the number of topics $T$ according to the label set of the corpus.

Step 2.

Choose a topic at random for each term in the corpus.

Step 3.

Loop through each term in the corpus, and use Equation (3) to calculate the probability of each term in all topics.

Step 4.

Repeat step 3 until the Gibbs sampling algorithm converges, which means the perplexity value of documents is stable. Calculate the probability matrix of topic-term $\Phi$ by Equation (4).

Step 5.

Calculate the weight matrix of topic-term ${\Phi }^{weight}$ by Equation (6).

Step 6.

Generate the final probability matrix of topic-term ${\Phi }^{\prime }$ by Equation (7).

4. Experimental Results and Analysis

In this section, we conduct experiments to verify the efficiency of the proposed method on a real dataset. Performance improvement of our approach is compared with state-of-the-art supervised topic models.

4.1. Experiment Environment

The experiments were executed on a personal computer with an AMD FX-Series CPU FX-8350 @4.0 GHz, the processor having eight physical computing cores, 16 GB DDR3 RAM memory @1600 MHz. The machine was running Windows7 on 64 bits, TensorFlow 1.4.0 with CPU support only and Python 3.6.

4.2. Dataset

To demonstrate the efficiency of our proposed method, we use a benchmark dataset: the Reuters Corpus-10,788 dataset is based on a large number of Reuters news reports and is widely used in research of natural language processing, recommendation systems, and information retrieval. The Reuters Corpus-10,788 dataset is obtained readily by the Python natural language processing toolkit. The dataset has 10,788 documents that contain about 1,300,000 terms and 90 topics. Based on a randomized approach, experimental data consists of 3000 documents from the Reuters Corpus-10,788 dataset.

4.3. Evaluation Metrics

The final generated probability matrix of topic-term ${\Phi }^{\prime }$ is an important experimental result that is estimated by predicting the topics of test documents. For a test document, firstly, we construct the term frequency vector of the document, and then calculate the similarity between the test document and each topic of the final generated probability matrix of topic-term ${\Phi }^{\prime }$ using a cosine measure in sequence. Finally, the output is sorted in descending order according to the similarity value. The hit ratio of the topics for a test document is the final prediction accuracy. The measurement is shown as follows.

$$Precision=\frac{TP}{TP+FP}$$

(8)

where $Precision$ is the precision of topics for a test document, $TP$ is the number of true topics, and $FP$ is the number of false topics.

For example, the topics of test document “test/18,609” are “grain, sugar, rice”, while our method predicted the first three topics of test document “test/18,609” as “sugar, money-fx, rice”, with a hit ratio of 66.7%. The final result is the average precision of topics in test documents, as defined by Equation (9):

$$Precisio{n}_{avg}=\frac{{\sum }_1^{N}Precision}{N}$$

(9)

where $Precisio{n}_{avg}$ is the average precision of topics for test documents, and N is the number of test documents.

It is important to note that the purpose of our method is to evaluate the effect of the supervised topic models by predicting the precision of the topics for the documents, so as to verify the explanatory ability of the supervised topic models.

4.4. Baseline Methods

To assess the efficiency of our proposed approach, three state-of-the-art methods of constructing supervised topic models were compared with our method. A classic supervised topic model L-LDA is proposed in [11], denoted by L-LDA₂₀₀₉, that uses a symmetric document-label Dirichlet prior. Dependency-LDA uses an asymmetric document-label Dirichlet prior in [14], denoted by D-LDA₂₀₁₂. On the basis of these two methods, we propose a term frequency-inverse topic frequency method for constructing supervised topic models, denoted by L-LDA_TF-ITF and D-LDA_TF-ITF. In addition, the importance of a term weight with more discriminative knowledge of the topic was proved for another method [15], based on L-LDA and denoted by CFW-LDA₂₀₁₈. All methods trained topic models using Gibbs sampling.

4.5. Comparison with Baseline Methods

In the process of experiment, this paper sets Dirichlet prior parameters $\alpha$ as 0.001 and $\beta$ as 0.001 for all methods. The parameters of CF-weight LDA are the same as with our method: $\eta$ is set to 50 and $\gamma$ is set to 0.001 according to the existing research.

Table 4. The experimental results.

Methods	Precision
L-LDA2009	48.61%
D-LDA2012	47.49%
CFW-LDA2018	52.46%
L-LDATF-ITF	53.76%
D-LDATF-ITF	47.93%

shows the experimental results in the Reuters Corpus-10,788 dataset.

As shown in Table 4, for the baseline method of supervised topic model with symmetric Dirichlet prior parameters, L-LDA₂₀₀₉, the corresponding improved method, L-LDA_TF-ITF, performs better than L-LDA₂₀₀₉ by 5.15%. At the same time, for the baseline method of supervised topic model with asymmetric Dirichlet prior parameters, D-LDA₂₀₁₂, the corresponding improvement method, D-LDA_TF-ITF, performs better than D-LDA₂₀₁₂ by 0.44%. The accuracy benefits from the weight of the topic term.

In addition, L-LDA_TF-ITF performs better than CFW-LDA₂₀₁₈ by 1.3% under the same conditions. CFW-LDA₂₀₁₈ uses the weight of terms by the topic frequency knowledge. Nevertheless, the term frequency of the topic is neglected, and the calculating formula for weight of terms reflects the poor ability to distinguish topics without certain judgment conditions. To summarize, it is verified that the method proposed in this paper trains a more effective supervised topic model that has better topic interpretation.

5. Conclusions

In this paper, we have highlighted that most supervised topic models neglect the use of terms with the significant ability to distinguish topics. In order to overcome this limitation, we introduce a term frequency-inverse topic frequency (TF-ITF) method for constructing supervised topic models, so that every topic term has a weight, thereby providing the ability to distinguish between topics. Experimental results demonstrate that the method for constructing supervised topic models based on TF-ITF outperforms several state-of-the-art supervised topic models.

As future work, we plan to at least further explore the following two directions. Although the Gibbs sampling technique is fast to implement and easy to understand, we intend to obtain a better topic model by using a variational autoencoder, which is a powerful technique for learning latent representations. We will also apply our constructed supervised topic model in information retrieval, recommender systems, text classification, and other fields, to achieve better performance.