Block Cipher in the Ideal Cipher Model: A Dedicated Permutation Modeled as a Black-Box Public Random Permutation
Abstract
:1. Introduction
1.1. Pseudorandom Permutation and Pseudorandom Function with BBB
1.2. Our Construction
2. Preliminaries
2.1. Notations
2.2. Security Definition
2.3. H-Coefficient Technique
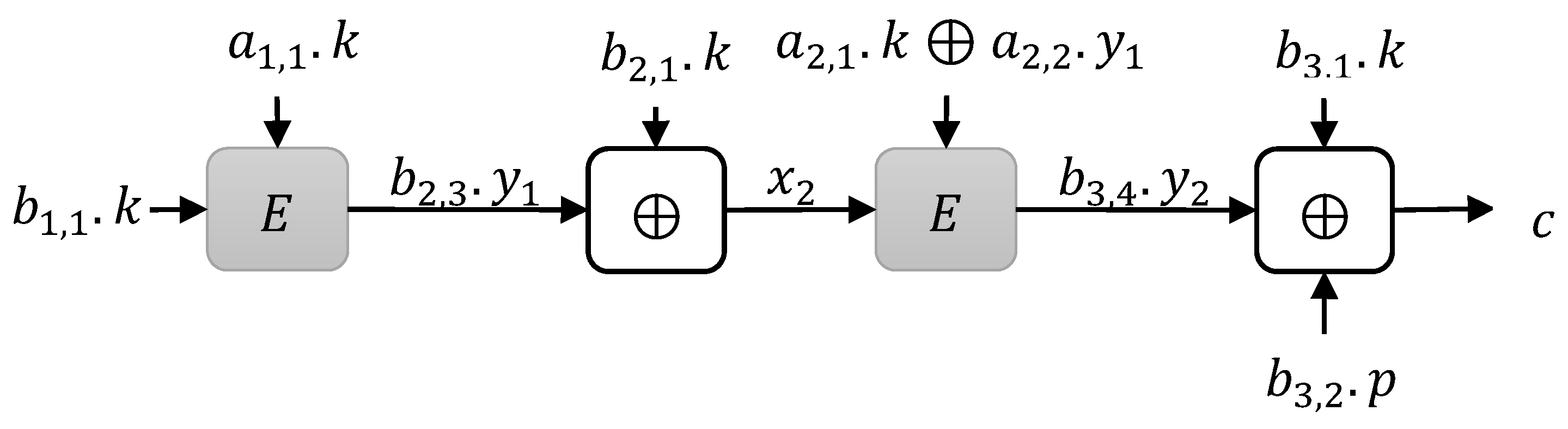
3. Construction Limitations
| Algorithm 1 |
| input: |
| Output: |
|
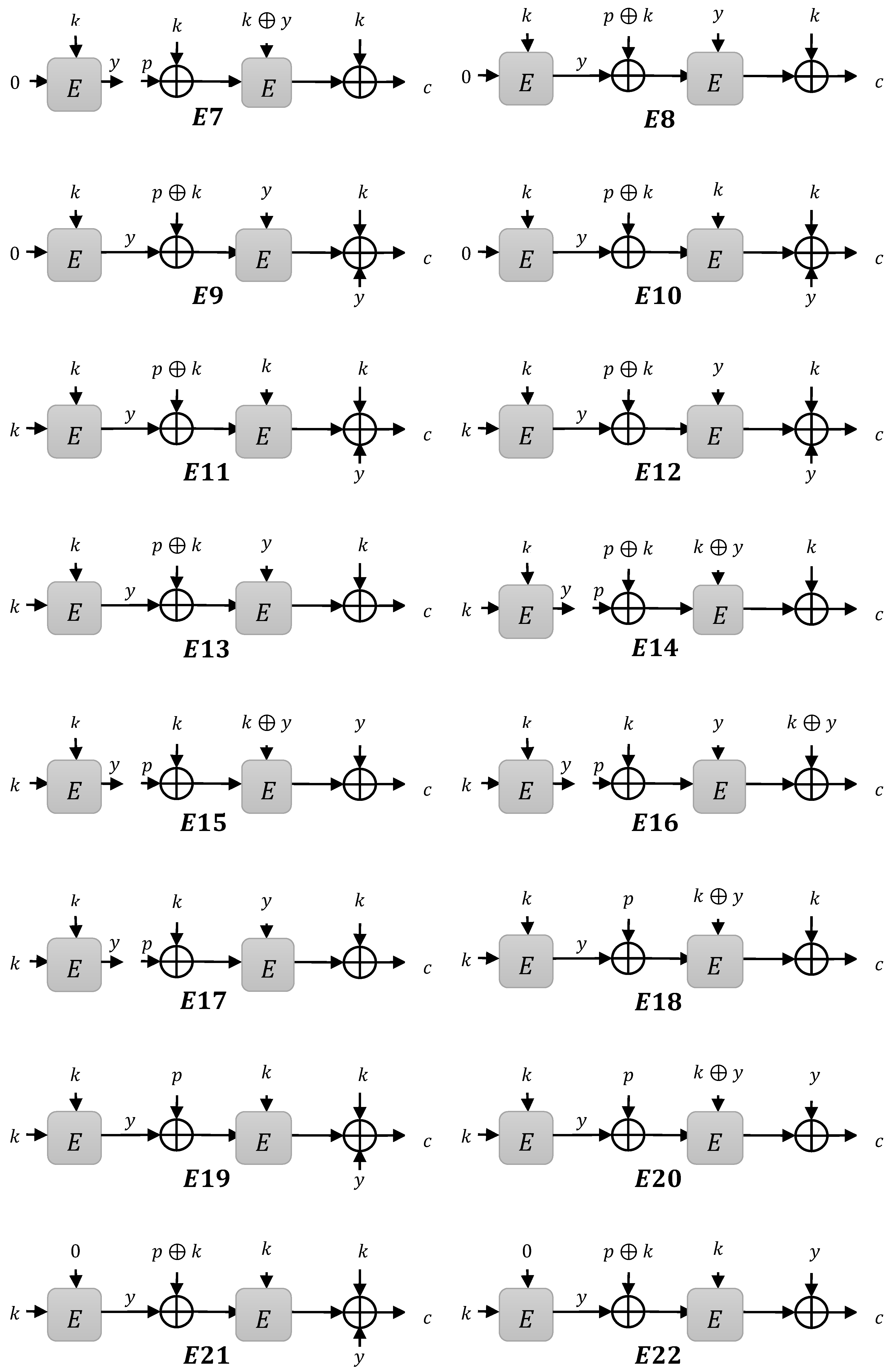
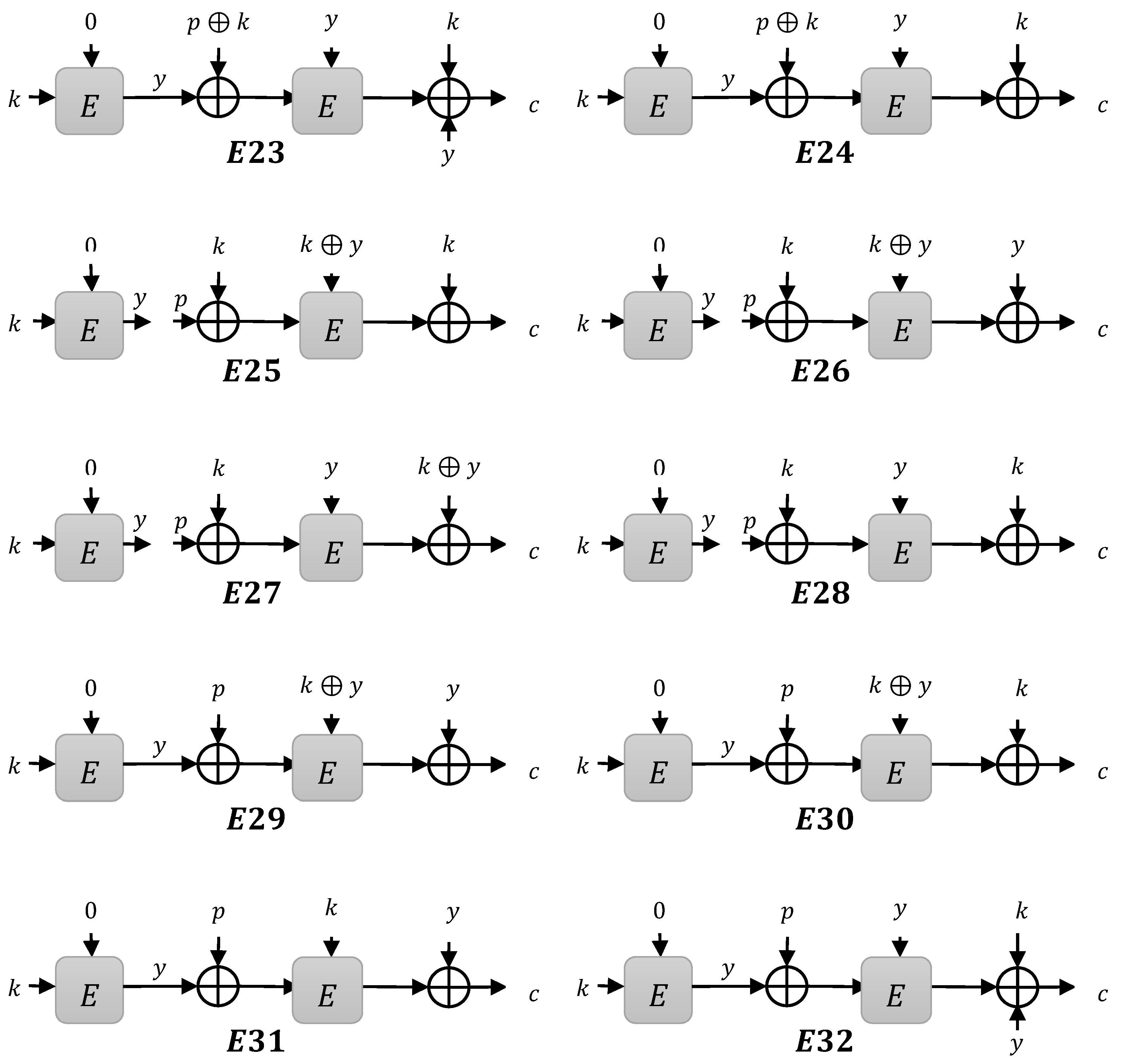
3.1. Instances
- Type 1 instances: when is XOR to compute
- Type 2 instances: when is XOR to compute
- Type 3 instances: when is XOR to compute
3.1.1. Type 1 Instances
3.1.2. Type 2 Instances
3.1.3. Type 3 Instances
4. Security Proof
4.1. Bad Events
4.2.
- (a)
- such that ;
- (b)
- such that ;
- (c)
- and such that
- (d)
- and such that
4.3. Ratio for
Author Contributions
Funding
Conflicts of Interest
References
- Iwata, T. New Blockcipher Modes of Operation with Beyond the Birthday Bound Security. In International Workshop on Fast Software Encryption; Springer: Berlin/Heidelberg, Germany, 2006; pp. 310–327. [Google Scholar]
- Patarin, J. Mirror theory and cryptography. Appl. Algebra Eng. Commun. Comput. 2017, 28, 321–338. [Google Scholar] [CrossRef]
- Iwata, T.; Mennink, B.; Vizár, D. Cenc is optimally secure. IACR Cryptol. ePrint Arch. 2016, 2016, 1087. [Google Scholar]
- Bellare, M.; Desai, A.; Jokipii, E.; Rogaway, P. A concrete security treatment of symmetric encryption. In Proceedings of the 38th Annual Symposium on Foundations of Computer Science, Miami Beach, FL, USA, 20–22 October 1997; pp. 394–403. [Google Scholar]
- Bellare, M.; Guérin, R.; Rogaway, P. Xor macs: New methods for message authentication using finite pseudorandom functions. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 1995; pp. 15–28. [Google Scholar]
- Bernstein, D.J. How to stretch random functions: The security of protected counter sums. J. Cryptol. 1999, 12, 185–192. [Google Scholar] [CrossRef]
- McGrew, D.A.; Viega, J. The security and performance of the galois/counter mode (gcm) of operation. In International Conference on Cryptology in India; Springer: Berlin/Heidelberg, Germany, 2004; pp. 343–355. [Google Scholar]
- Patarin, J. A Proof of Security in O(2n) for the Xor of Two Random Permutations. In International Conference on Information Theoretic Security; Springer: Berlin/Heidelberg, Germany, 2008; pp. 232–248. [Google Scholar]
- Patarin, J. Luby-rackoff: 7 rounds are enough for 2n(1−ε) security. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2003; pp. 513–529. [Google Scholar]
- Patarin, J. On linear systems of equations with distinct variables and small block size. In International Conference on Information Security and Cryptology; Springer: Berlin/Heidelberg, Germany, 2005; pp. 299–321. [Google Scholar]
- Patarin, J. Introduction to mirror theory: Analysis of systems of linear equalities and linear non equalities for cryptography. IACR Cryptol. ePrint Arch. 2010, 2010, 287. [Google Scholar]
- Daemen, J.; Rijmen, V. Rijndael/aes. Encycl. Cryptogr. Secur. 2005, 520–524. [Google Scholar] [CrossRef]
- Bogdanov, A.; Knudsen, L.R.; Leander, G.; Paar, C.; Poschmann, A.; Robshaw, M.J.; Seurin, Y.; Vikkelsoe, C. Present: An ultra-lightweight block cipher. In International Workshop on Cryptographic Hardware and Embedded Systems; Springer: Berlin/Heidelberg, Germany, 2007; pp. 450–466. [Google Scholar]
- De Canniere, C.; Dunkelman, O.; Knežević, M. Katan and ktantan—A family of small and efficient hardware-oriented block ciphers. In International Workshop on Cryptographic Hardware and Embedded Systems; Springer: Berlin/Heidelberg, Germany, 2009; pp. 272–288. [Google Scholar]
- Guo, J.; Peyrin, T.; Poschmann, A.; Robshaw, M. The led block cipher. In International Workshop on Cryptographic Hardware and Embedded Systems; Springer: Berlin/Heidelberg, Germany, 2011; pp. 326–341. [Google Scholar]
- Impagliazzo, R.; Rudich, S. Limits on the provable consequences of one-way permutations (invited talk). In Proceedings on Advances in Cryptology; Springer: Berlin/Heidelberg, Germany, 1990; pp. 8–26. [Google Scholar]
- Hall, C.; Wagner, D.; Kelsey, J.; Schneier, B. Building prfs from prps. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 1998; pp. 370–389. [Google Scholar]
- Bellare, M.; Rogaway, P. The security of triple encryption and a framework for code-based game-playing proofs. In Annual International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 2006; pp. 409–426. [Google Scholar]
- Chang, D.; Nandi, M. A short proof of the prp/prf switching lemma. IACR Cryptol. ePrint Arch. 2008, 2008, 78. [Google Scholar]
- Bellare, M.; Krovetz, T.; Rogaway, P. Luby-rackoff backwards: Increasing security by making block ciphers non-invertible. In International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 1998; pp. 266–280. [Google Scholar]
- Lucks, S. The sum of prps is a secure prf. In International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 2000; pp. 470–484. [Google Scholar]
- Lim, C.H.; Korkishko, T. Mcrypton–a lightweight block cipher for security of low-cost rfid tags and sensors. In International Workshop on Information Security Applications; Springer: Berlin/Heidelberg, Germany, 2005; pp. 243–258. [Google Scholar]
- Wu, W.; Zhang, L. Lblock: A Lightweight Block Cipher; Springer: Berlin/Heidelberg, Germany, 2011; pp. 327–344. [Google Scholar]
- Borghoff, J.; Canteaut, A.; Güneysu, T.; Kavun, E.B.; Knezevic, M.; Knudsen, L.R.; Leander, G.; Nikov, V.; Paar, C.; Rechberger, C.; et al. Prince—A Low-Latency Block Cipher for Pervasive Computing App. Lications; Springer: Berlin/Heidelberg, Germany, 2012; pp. 208–225. [Google Scholar]
- Beaulieu, R.; Treatman-Clark, S.; Shors, D.; Weeks, B.; Smith, J.; Wingers, L. The simon and speck lightweight block ciphers. In Proceedings of the 52nd ACM/EDAC/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 8–12 June 2015; pp. 1–6. [Google Scholar]
- Beierle, C.; Jean, J.; Kölbl, S.; Leander, G.; Moradi, A.; Peyrin, T.; Sasaki, Y.; Sasdrich, P.; Sim, S.M. The skinny family of block ciphers and its low-latency variant mantis. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2016; pp. 123–153. [Google Scholar]
- Bellare, M.; Impagliazzo, R. A tool for obtaining tighter security analyses of pseudorandom function based constructions, with app. lications to prp to prf conversion. IACR Cryptol. ePrint Arch. 1999, 1999, 24. [Google Scholar]
- Patarin, J. Security in O(2n) for the xor of two random permutations\-proof with the standard h technique. IACR Cryptol. ePrint Arch. 2013, 2013, 368. [Google Scholar]
- Cogliati, B.; Lampe, R.; Patarin, J. The indistinguishability of the xor of $$ k $$ permutations. In International Workshop on Fast Software Encryption; Springer: Berlin/Heidelberg, Germany, 2014; pp. 285–302. [Google Scholar]
- Dai, W.; Hoang, V.T.; Tessaro, S. Information-theoretic indistinguishability via the chi-squared method. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2017; pp. 497–523. [Google Scholar]
- Bhattacharya, S.; Nandi, M. Revisiting variable output length xor pseudorandom function. IACR Trans. Symmetric Cryptol. 2018, 2018, 314–335. [Google Scholar]
- Yasuda, K. A new variant of pmac: Beyond the birthday bound. In Annual Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2011; pp. 596–609. [Google Scholar]
- Datta, N.; Dutta, A.; Nandi, M.; Paul, G.; Zhang, L. Single key variant of PMAC_plus. IACR Trans. Symmetric Cryptol. 2017, 2017, 268–305. [Google Scholar]
- Naito, Y. Blockcipher-based macs: Beyond the birthday bound without message length. In International Conference on the Theory and App.lication of Cryptology and Information Security; Springer: Berlin/Heidelberg, Germany, 2017; pp. 446–470. [Google Scholar]
- Gilboa, S.; Gueron, S. The advantage of truncated permutations. In International Symposium on Cyber Security Cryptography and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2019; pp. 111–120. [Google Scholar]
- Cogliati, B.; Seurin, Y. Ewcdm: An efficient, beyond-birthday secure, nonce-misuse resistant mac. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2016; pp. 121–149. [Google Scholar]
- Mennink, B.; Neves, S. Encrypted davies-meyer and its dual: Towards optimal security using mirror theory. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2017; pp. 556–583. [Google Scholar]
- Mennink, B.; Neves, S. Optimal prfs from blockcipher designs. IACR Trans. Symmetric Cryptol. 2017, 228–252. [Google Scholar]
- Chen, Y.L.; Lambooij, E.; Mennink, B. How to build pseudorandom functions from public random permutations. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2019; pp. 266–293. [Google Scholar]
- Beaulieu, R.; Shors, D.; Smith, J.; Treatman-Clark, S.; Weeks, B.; Wingers, L. Simon and speck: Block ciphers for the internet of things. IACR Cryptol. ePrint Arch. 2015, 2015, 585. [Google Scholar]
- Chen, S.; Steinberger, J. Tight security bounds for key-alternating ciphers. In Annual International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 2014; pp. 327–350. [Google Scholar]
- Even, S.; Mansour, Y. A construction of a cipher from a single pseudorandom permutation. J. Cryptol. 1997, 10, 151–161. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nawaz, Y.; Wang, L. Block Cipher in the Ideal Cipher Model: A Dedicated Permutation Modeled as a Black-Box Public Random Permutation. Symmetry 2019, 11, 1485. https://doi.org/10.3390/sym11121485
Nawaz Y, Wang L. Block Cipher in the Ideal Cipher Model: A Dedicated Permutation Modeled as a Black-Box Public Random Permutation. Symmetry. 2019; 11(12):1485. https://doi.org/10.3390/sym11121485
Chicago/Turabian StyleNawaz, Yasir, and Lei Wang. 2019. "Block Cipher in the Ideal Cipher Model: A Dedicated Permutation Modeled as a Black-Box Public Random Permutation" Symmetry 11, no. 12: 1485. https://doi.org/10.3390/sym11121485
APA StyleNawaz, Y., & Wang, L. (2019). Block Cipher in the Ideal Cipher Model: A Dedicated Permutation Modeled as a Black-Box Public Random Permutation. Symmetry, 11(12), 1485. https://doi.org/10.3390/sym11121485



