Modified Advanced Encryption Standard Algorithm for Information Security

Abstract

The wide acceptability of Advanced Encryption Standard (AES) as the most efficient of all of the symmetric cryptographic techniques has further opened it up to more attacks. Efforts that were aimed at securing information while using AES is still being undermined by the activities of attackers This has further necessitated the need for researchers to come up with ways of enhancing the strength of AES. This article presents an enhanced AES algorithm that was achieved by modifying its SubBytes and ShiftRows transformations. The SubBytes transformation is modified to be round key dependent, while the ShiftRows transformation is randomized. The rationale behind the modification is to make the two transformations round key dependent, so that a single bit change in the key will produce a significant change in the cipher text. The conventional and modified AES algorithms are both implemented and evaluated in terms avalanche effect and execution time. The modified AES algorithm achieved an avalanche effect of 57.81% as compared to 50.78 recorded with the conventional AES. However, with 16, 32, 64, and 128 plain text bytes, the modified AES recorded an execution time of 0.18, 0.31, 0.46, and 0.59 ms, respectively. This is slightly higher than the results obtained with the conventional AES. Though a slightly higher execution time in milliseconds was recorded with the modified AES, the improved encryption and decryption strength via the avalanche effects measured is a desirable feat.

1. Introduction

The advancement in Information and Communication Technology (ICT) has made internet one of the major mediums through which information is being shared in this 21st century. However, the confidentiality, integrity, and availability of information shared over public network still remains an open issue [1]. Information hiding techniques using watermarking and steganography as well as cryptography have been widely explored to ensure the security of information transmitted over an unsecured network. With emphasis on cryptography, information security is guaranteed by making a secret message unreadable to a third party, but accessible by the sender and recipient alone while using one or more secret keys. Cryptographic techniques could be symmetric—if the same key is used for encryption and decryption or asymmetric—if different keys are used for encryption and decryption [2]. Symmetric cryptographic techniques are the most appropriate when a large amount of data is to be secured [3]. Of the available symmetric cryptographic techniques, such as Data Encryption Standard (DES), Triple DES, and Advanced Encryption Standard (AES), AES is the most common and widely used [4]. However, several attacks that aimed at undermining the strength of AES algorithm have been reported in the literature. Differential fault analysis attacks that inject faults into AES structure with the aim of retrieving the secret information were reported in [5], while cache timing attack, which uses side channel information, such as power consumption statistics, timing information, and cache contents to infer the unknown key used in data encryption, was reported in [6]. Most recently, related-key differential attacks was reported in [7]. In this attack, the cryptanalyst queries the block ciphers with plaintext pairs to deduce the secret key that was used. Similarly, cipher strength analysis carried out by cipher analysts have revealed that with the current trend of increasing computational power, eight out of ten rounds of AES has been brute forced successfully and soonest the remaining two rounds may be broken [8]. This has called for the need to urgently explore techniques that could further strengthen the AES algorithm. Therefore, this article introduces an enhanced AES algorithm that was achieved by modifying its SubBytes and ShiftRows transformations. The rationale behind the modification is to make the two transformations round key dependent, so that a change to any bit of the key will result to a significant change in the cipher text. The rest of the paper is organized, as follows: Section 2 explained the existing AES algorithm, its structure, and various transformation stages. A review of recent works as regards AES modification was carried out in Section 3, while the proposed methodology was explained in details in Section 4. The result of the modified AES algorithm, its performance evaluation using avalanche effect, execution time is presented in Section 5. A comparative analysis of the modified AES with those that were obtained from existing works is also presented in Section 5. The study’s conclusion is provided in Section 6.

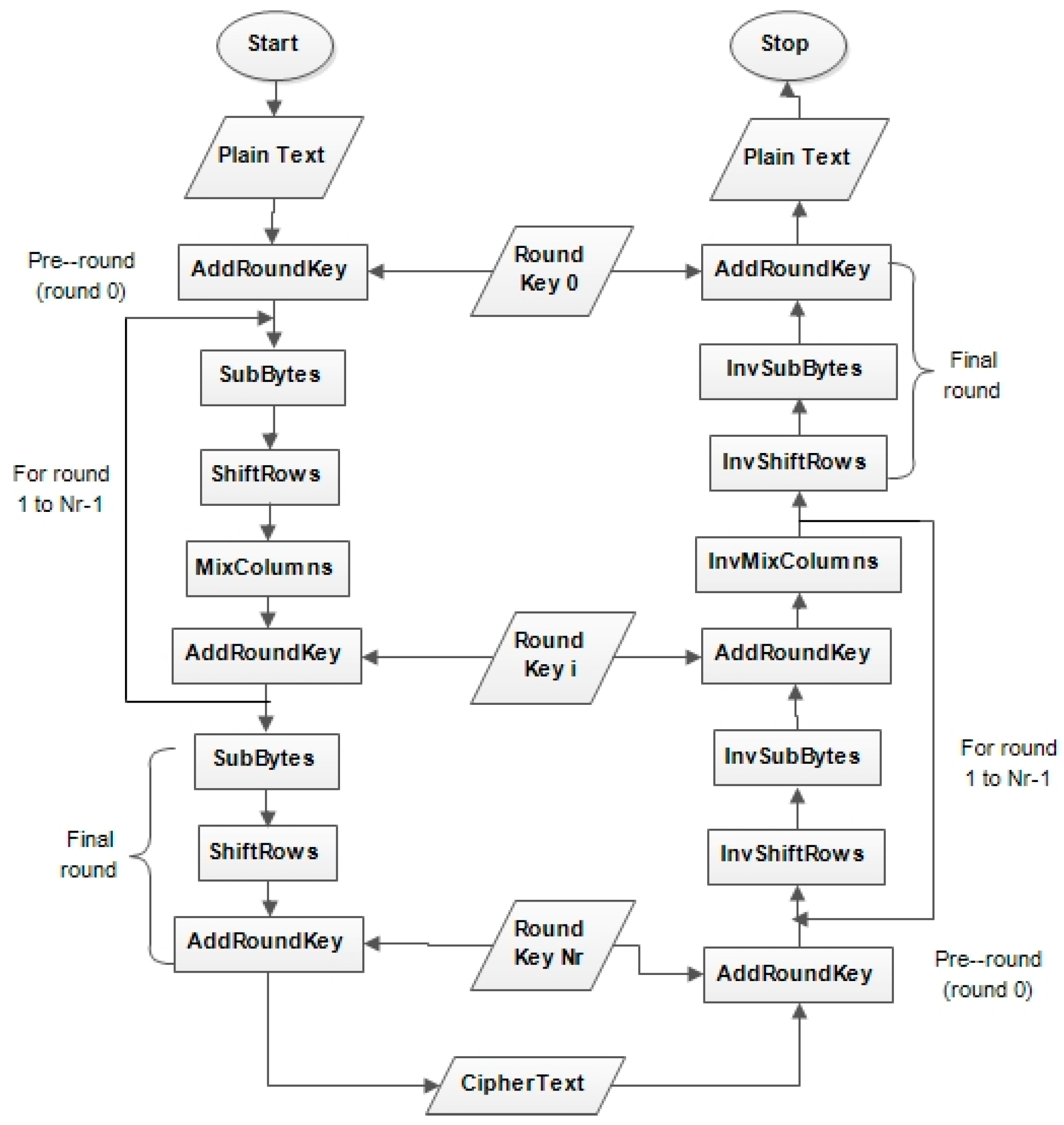
2. Existing AES Algorithm

The AES algorithm is a symmetric key algorithm that was established as the standard for encrypting digital data by the US National Institute for Standard and Technology (NIST). It is an iterative round block cipher that works on 128bit plaintext using three different key lengths 128, 192, and 256 bits [9]. The key length determines the number of encryption and decryption rounds to be performed which could be 10, 12, and 14 rounds for 128, 192, and 256-bit key length, respectively. It is believed that the larger the key length, the higher the cryptographic strength [9]. The AES algorithm consists of four invertible transformations: SubBytes, ShiftRows MixColumns, and AddRoundKey, as shown in Figure 1.

All of these transformations are performed in all the encryption rounds, except the final round, where the MixColumns transformation is omitted to make the encryption and decryption scheme symmetric, these transformations are described below:

(i)

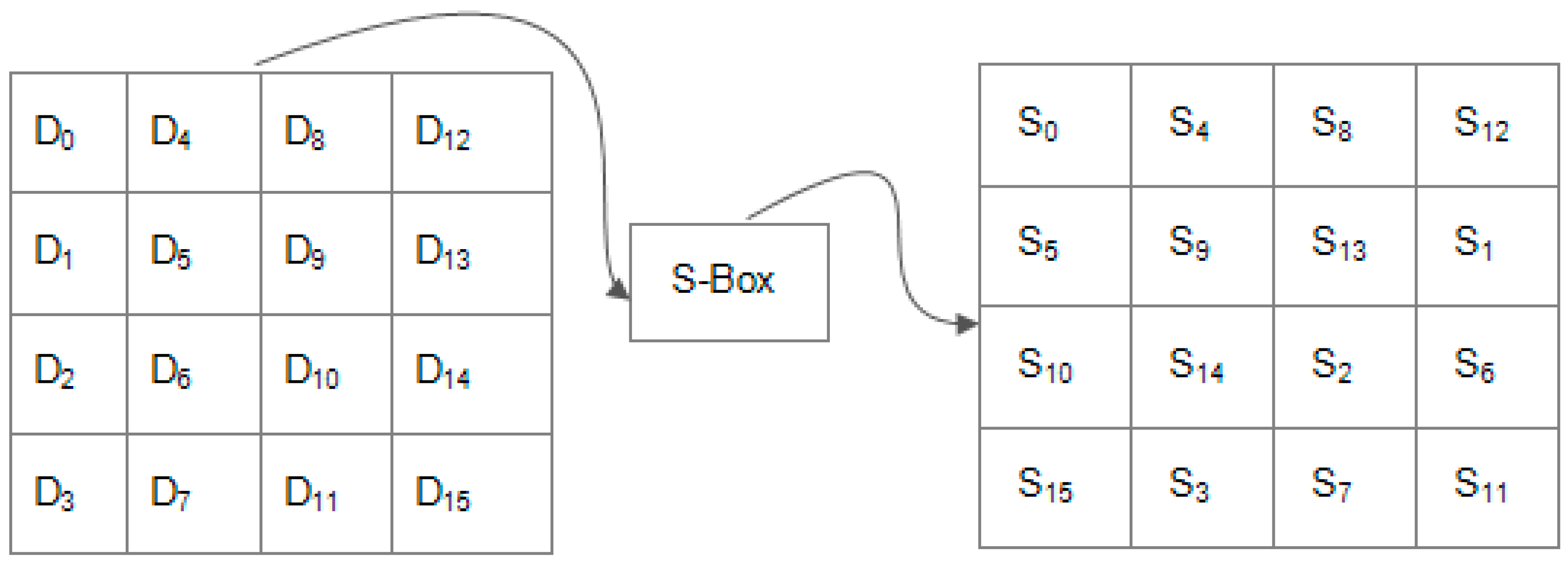
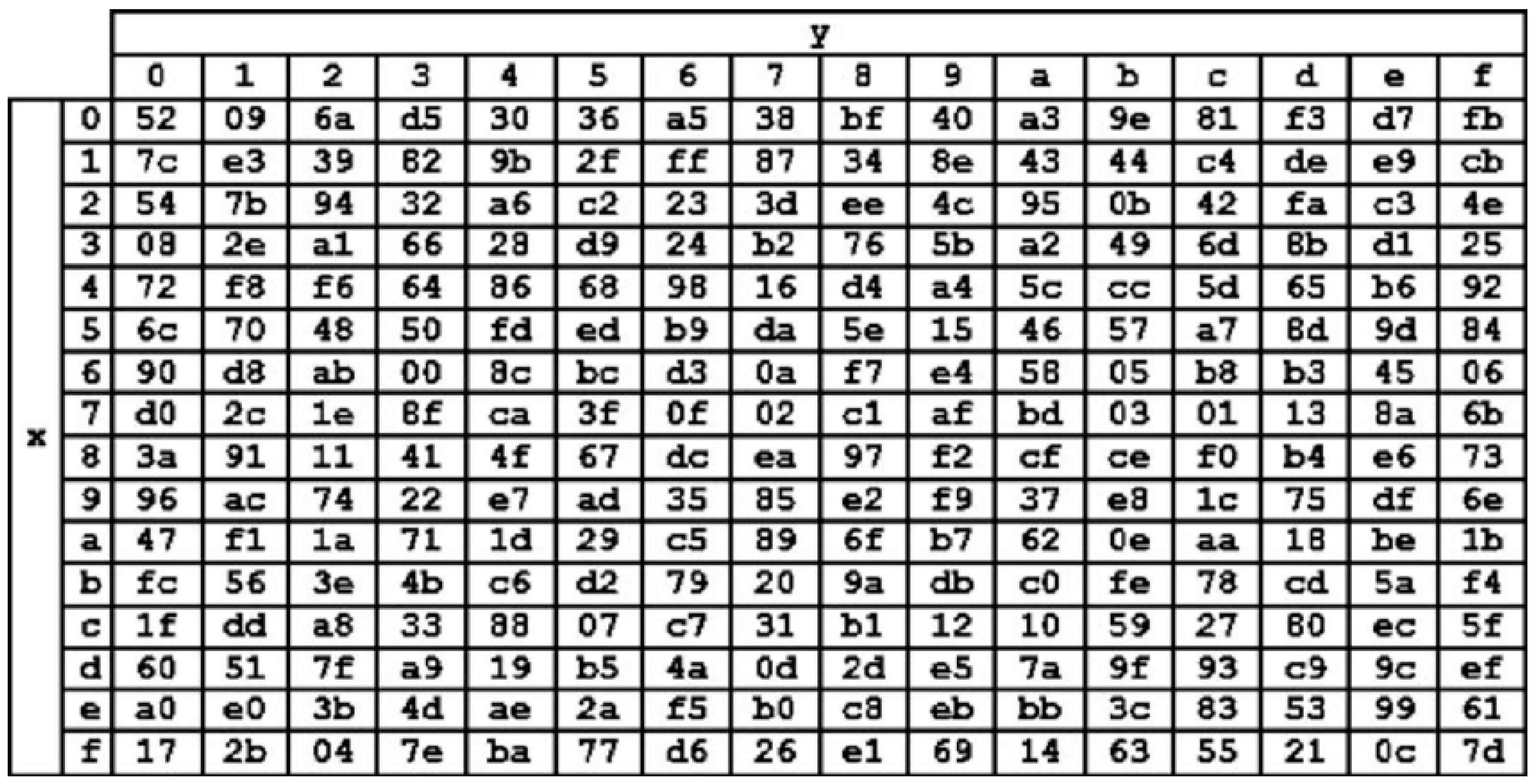
SubBytes Transformation: as shown in Figure 2, SubBytes transformation is the only non-linear and invertible byte transformation that replaces each byte of the input data block (D0, …, D15) by the row (first 4-bits) and column (second 4-bits) of a 16 × 16 Substitution Box (S-Box). The S-Box, as shown in Figure 3, has special mathematical properties that ensure that changes in individual state bits propagate quickly across the cipher text, which introduces confusion. Inverse substitution table (InvS-Box) is used during decryption to undo the effect of the SubBytes transformation.

(ii)

ShiftRows Transformation: This manipulates the rows of the state by using a certain offset to shift the bytes in each row, as shown in Figure 4. This is carried out to ensure that the columns of the state are not independently encrypted. During this operation, the first row remains unchanged, while one-byte, two-byte, and three-byte circular shift operation is performed on the second, third, and fourth rows, respectively. For the decryption process, the first row remains unchanged, while the other rows are shifted to the right based on the same offset used to shift them to the left during encryption process

(iii)

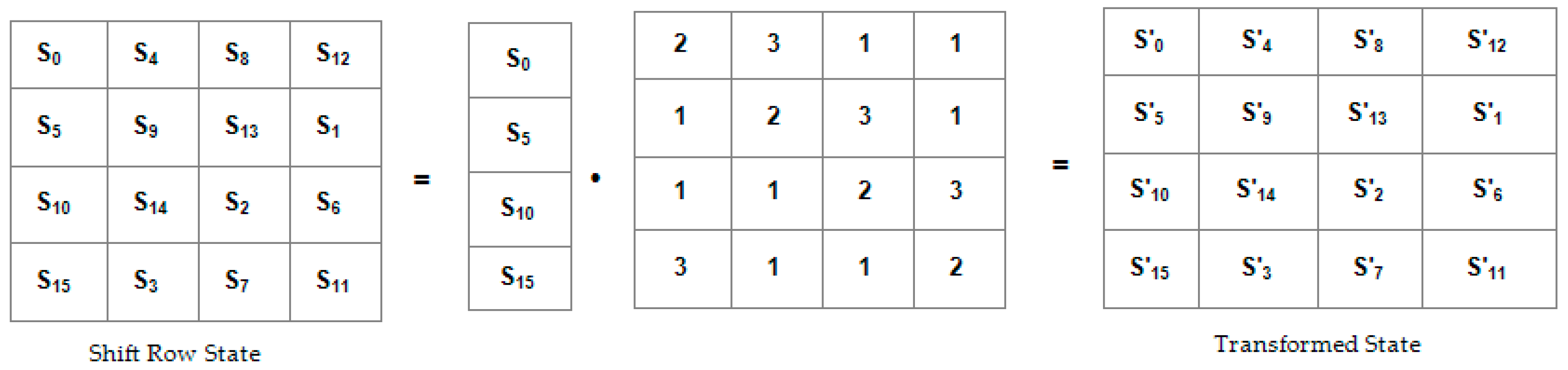
MixColumns Transformation: This is a linear diffusion process that sees the columns of the state as coefficients of polynomial of order x⁷. It manipulates all the columns of the state by carrying out multiplication and addition operation on their bytes. Exclusive OR (XOR) is used for the addition operation while modulo $m(x)=x^8+x^4{x}^3+x+1$ is used for the multiplication operation. As shown in Figure 5, each column of the state obtained from shiftrow transformation is multiplied by a mixing matrix to obtain the transformed matrix. With this manipulation, the initial setting of the cipher text is changed, such that no bytes look similar. Inverse MixColumns is used to undo this transformation during the decryption process.

(iv)

AddRoundKey Transformation: This is the last transformation that will be done for each round. As shown in Figure 6, an addition operation between the bytes of the transformed state and the round key is carried out while using XOR.

3. Related Works

Several research efforts have been directed at improving AES algorithm. A modified version of AES that is specifically designed to handle the unique features of image encryption and decryption was proposed in [11]. MixColumns transformation in the conventional AES was replaced with bit permutation. The computed number of pixel change rate and the unified average change intensity revealed that the modified AES is more sensitive to differential attack. Authors in [12] made the various attacks that have been targeted at undermining the strength of AES known. Among these is fault injection attacks that could be used to reveal AES key. Therefore, they proposed randomizing the key generation process of AES as a way out. This led to a higher avalanche effect in the modified AES. Additionally, it was envisaged that an increase in the number of rounds of AES could make the algorithm more secured in [13]. The assumption was validated by increasing the rounds of AES from 10 to 16. The results obtained revealed that the modified AES requires a higher computational time when compared to the conventional AES. An attempt to reduce the complexity path of AES was made in [14]. The complexity observed was as a result of redundant logical functions in the MixColumn transformation of AES. These logical functions were eradicated in the modified version of AES. After evaluating the modified AES, a 13.6% reduction in LUTs, 10.93% slice reduction, and a 1.19% reduction in delay consumption were achieved. Similarly, the low diffusion rate encountered by the conventional AES at the early cipher and key schedule rounds was addressed in [15]. XOR operation was added between the SubBytes and ShiftRow transformation processes, while modulo addition was added between the ShiftRow and MixColumn operations. The avalanche effect measured achieved a 61.98% increase in diffusion for the round 1 and 14.79% and 13.87% increase in diffusion for round 2 and 3, respectively. Furthermore, the increase in computational speed of computing systems is a sign that AES algorithm could be broken. Therefore, the use of the system’s Media Access Control (MAC) Address as an additional key to shuffle the substitution box and shift row stage of the conventional AES algorithm was proposed in [16]. They permuted the six-bytes MAC Address to produce two 4 × 4 matrices (W₁ and W₂). Each of the matrices was then XORed with the original key K to obtain $Sortke{y}_1=W_1 ⨁ K$ and $Sortke{y}_2=W_2 ⨁ K$. Sortkey₁ and Sortkey₂ were then used as row and column respectively in the S-Box to substitute the state. Though, breaking the modified AES will be more complex than the conventional AES, a higher execution time was recorded with the modified AES. Authors in [16] were of the opinion that S-Box and Mix Columns are the most energy consuming stages in encryption and decryption processes of the AES algorithm. They therefore proposed a one-dimensional S-Box construction aimed at reducing AES energy consumption. The S-Box was constructed from a formulated affine transformation equation in Galois Field (2⁴). The proposed method proved to be more efficient than conventional AES with 18.35% efficiency rate when compared to conventional AES.

Additionally, the need to reduce the energy consumption of AES so as to make them suitable for smart devices was explored in [17]. A Lorenz attractor which coupled three nonlinear differential equation was employed to formulate a one-dimensional substitution box used by the modified AES. This yielded a low energy consuming AES was achieved with a better latency and packet transmission rate. Authors in [18] also observed that cryptanalysts have been exploiting the static nature of the contents of S-Boxes. Therefore, a dynamic S-Box was created from the exsting S-Box and round keys, such that, for round_i, the first byte of the round key ($key\left[i\right]=roundKe{y}_i\left[0, 0\right]$) is XORed with all of the bytes of the original S-Box, as shown in Equation (1):

$$DynamicSBo{x}_i\left[x,y\right]=SBox\left[x,y\right]⨁key\left[i\right]$$

(1)

The dynamic S-Box was then used to perform sub byte operation for that round. Comparative analysis carried out revealed that the new technique out performed the original AES in terms of the avalanche effect though the execution time is doubled. Similarly, a modified AES algorithm that was obtained by increasing the key length and the number of rounds was introduced in [19]. They are of the opinion that an increase in the key length and number of rounds could further strengthen the AES algorithm. The key length was increased to 320 bits, while the number of rounds was increased to sixteen. The modification led to a higher execution time when compared to the original AES algorithm, but lesser than 3DES. Additionally, the authors in [20] observed that most AES attacks target the secret key used for the encryption and decryption. To this effect, the Genetic Algorithm (GA) was employed to generate a secret key to be used for encryption and decryption purposes. Using text and audio data for encryption, less encryption and decryption time was observed when compared to the conventional 128 bit AES algorithm. Similarly, Elliptic Curve Cryptography (ECC) was employed in [21] to generate irreversible random numbers used as AES secret keys. X and Y coordinates used for random number generation improved the entropy of the random numbers generated. Security analysis carried out showed that the proposed technique is extremely sensitive to key changes and is also resistive to certain attacks. Furthermore, a dynamic key and S-box generation approach to the conventional AES algorithm was introduced in [22]. The dynamic key was generated by using the system time function that randomly generates the secret key using the time recorded when the user logs into the system. In the same way, the initial S-Box was transformed into a dynamic one with the aid of the dynamic random key generated. In a similar manner, Pseudo-Noise (PN) sequence generator was employed in [23] to produce dynamic S-box values and initial secret keys needed for encryption and decryption. Since the initial secret keys were internally generated, the seed value is difficult to deduce by an attacker, therefore, the modified AES algorithm was impenetrable by brute force attack. The modified AES algorithm also yielded a high encryption quality, an avalanche effect of 60%, a throughput of 3.039 Gbps, and a latency of 10 clock cycles.

4. Proposed Methodology

This section presents the methodology adopted in this study in detail.

4.1. Modified SubBytes Transformation

AES SubBytes transformation was modified to make it round key dependent; this is to ensure that a change in the key is easily discovered in the cipher text. To achieve that, the 16 bytes round key was used to obtain four eight-bit keys $XORke{y}_0, XORke{y}_1, XORke{y}_2, XORke{y}_3$ by XORing all the bytes of the corresponding row ($Ro{w}_i$) in the round key matrix, as shown in Equation (2). After obtaining the $XORkeys$, each $XORke{y}_i$ as shown in Equations (3)–(6) was then added to all of the bytes in the corresponding row ($Ro{w}_i$) of the state matrix before substituting the values in the S-Box. Mathematically, given the state S and a round key K, represented as a 4 × 4 matrices:

S=	S 0,0	S 0,1	S 0,2	S 0,3	and K =	K0,0	K0,1	K0,2	K0,3
	S 1,0	S 1,1	S 1,2	S 1,3		K1,0	K1,1	K1,2	K1,3
	S 2,0	S 2,1	S 2,2	S 2,3		K2,0	K2,1	K2,2	K2,3
	S 3,0	S 3,1	S 3,2	S 3,3		K3,0	K3,1	K3,2	K3,3

$$XORke{y}_i= K_{i,0} ⨁ K_{i,1} ⨁ K_{i,2} ⨁ K_{i,3},\mathrm{where}i=0to3$$

(2)

Alternatively,

$$XORke{y}_0= K_{0,0} ⨁ K_{0,1} ⨁ K_{0,2} ⨁ K_{0,3}$$

(3)

$$XORke{y}_1= K_{1,0} ⨁ K_{1,1} ⨁ K_{1,2} ⨁ K_{1,3}$$

(4)

$$XORke{y}_2= K_{2,0} ⨁ K_{2,1} ⨁ K_{2,2} ⨁ K_{2,3}$$

(5)

$$XORke{y}_3= K_{3,0} ⨁ K_{3,1} ⨁ K_{3,2} ⨁ K_{3,3}$$

(6)

The new state matrix, S′ was obtained while using Equation (7).

$$S{\prime }_{i,j}=S_{i,j} ⨁ XORke{y}_i,\mathrm{where}j=0to3\mathrm{where}i\mathrm{ranges}\mathrm{from}0to3$$

(7)

The operation can be seen clearly from the matrix below:

S ’ =	S 0,0 ⨁ Key0	S 0,1 ⨁ Key0	S 0,2 ⨁ Key0	S 0,3 ⨁ Key0
	S 1,0 ⨁ Key1	S 1,1 ⨁ Key1	S 1,2 ⨁ Key1	S 1,3 ⨁ Key1
	S 2,0 ⨁ Key2	S 2,1 ⨁ Key2	S 2,2 ⨁ Key2	S 2,3 ⨁ Key2
	S 3,0 ⨁ Key3	S 3,1 ⨁ Key3	S 3,2 ⨁ Key3	S 3,3 ⨁ Key3

The resultant state matrix S′ is given as follows:

S′=	S’0,0	S’0,1	S’0,2	S’0,3
	S’1,0	S’1,1	S’1,2	S’1,3
	S’2,0	S’2,1	S’2,2	S’2,3
	S’3,0	S’3,1	S’3,2	S’3,3

After obtaining the new state matrix S′, the bytes are then substituted in the substitution table (S-Box) using normal SubBytes operation, as shown in Equation (8):

$$S{\prime }_{i,j}=SubstitutionBox[S{\prime }_{i,j}],\mathrm{where}j=0to3\mathrm{for}\mathrm{every}i=0to3$$

(8)

4.2. Modified Inverse SubBytes Transformation

To obtain the modified inverse SubBytes operation, the SubBytes transformation was proved to be invertible, as shown in Equation (9). Given two polynomials $f(x) \mathrm{and} f(k)$ operating in Galois Field 2⁸ (GF (2⁸)), such that:

$$f(h)=f(x) ⨁ f(k),\mathrm{and}f(x)=(f(x) \oplus f(k))\oplus f(k)=f(h) ⨁f(k)$$

(9)

The proof is given, as follows:

Given two hexadecimal numbers ED (11101101 in binary) and BF (10111111 in binary), the number x, which is the XOR of ED and BF can be obtained by adding BF to ED while using and exclusive OR operation. The operation is shown, as follows:

ED and BF can be expressed in terms of polynomial $f(x) \mathrm{and} f(k)$, respectively, in Galois Field 2⁸ (GF (2⁸)) as:

$$f(x)=x^7+x^6+x^5+x^3+x^2+1=ED$$

(10)

$$f(k)=x^7+x^5+x^4+x^3+x^2+x^1+1=BF$$

(11)

Therefore,

$$\begin{array}{l}f(h)=f(x) ⨁ f(k)=x^7+x^6+x^5+x^3+x^2+1 ⨁x^7 +x^5+x^4+x^3+x^2+x^1+1\\ = x^6+x^4+x^1\end{array}$$

(12)

$f(h)=x^6+x^4+x^1=01010010$ in binary, and 52 in hexadecimal. To prove that $f(x)=(f(x)\oplus f(k))\oplus f(k)=f(h)⨁f(k)$, using the polynomials $f(h)⨁f(k)$, we obtain:

$$f(x)=f(h) ⨁f(k)=x^6+x^4+ x^1 ⨁x^7+x^5+x^4+x^3+x^2+x^1+1= x^7+x^6+x^5+x^3+x^2+1$$

(13)

Since $f(x)=(f(x) \oplus f(k))\oplus f(k)=f(h) ⨁f(k)$, the SubBytes operation is proven to be invertible.

During the inverse SubBytes operation, the substitution is done before XORing the state matrix with the $XORkeys$ using

$$S{\prime }_{i,j}=InverseSubstitutionBox[S{\prime }_{i,j}],\mathrm{where}j=0to3,\mathrm{for}\mathrm{every}i=0to3$$

(14)

The matrix S′ is then obtained after the substitution as:

S ’ =	S’0,0	S’0,1	S’0,2	S’0,3
	S’1,0	S’1,1	S’1,2	S’1,3
	S’2,0	S’2,1	S’2,2	S’2,3
	S’3,0	S’3,1	S’3,2	S’3,3

Hence, the original state S is obtained by XORing the S′ matrix with the $XORkeys$ using Equation (15):

$$S_{i,j}=S{\prime }_{i,j} ⨁ XORke{y}_i,\mathrm{where}j=0\mathit{to}3\mathrm{for}\mathrm{each}i\mathrm{from}0\mathit{to}3$$

(15)

The inverse SubBytes operation is shown in the matrix below:

S =	S’ 0,0 ⨁ Key0	S’ 0,1 ⨁ Key0	S’ 0,2 ⨁ Key0	S’ 0,3 ⨁ Key0
	S’ 1,0 ⨁ Key1	S’ 1,1 ⨁ Key1	S’ 1,2 ⨁ Key1	S’ 1,3 ⨁ Key1
	S’ 2,0 ⨁ Key2	S’ 2,1 ⨁ Key2	S’ 2,2 ⨁ Key2	S’ 2,3 ⨁ Key2
	S’ 3,0 ⨁ Key3	S’ 3,1 ⨁ Key3	S’ 3,2 ⨁ Key3	S’ 3,3 ⨁ Key3

The resultant matrix S, which is the original state is obtained, as follows:

S =	S0,0	S0,1	S0,2	S0,3
	S1,0	S1,1	S1,2	S1,3
	S2,0	S2,1	S2,2	S2,3
	S3,0	S3,1	S3,2	S3,3

The proof above shows that the SubBytes operation is invertible, since

$SubstitutionBox[S_{i,j}⨁XORke{y}_i\left]=InverseSubstitutionBox[{S^{\prime }}_{i,j}\right]⨁XORke{y}_i$,

where j = 0 to 3, for each i from 0 to 3.

4.3. Modified ShiftRows Transformation

Modification to the ShiftRows operation was achieved by randomizing the entire operation. In the conventional AES algorithm, the ShiftRows operation depends on a fixed number, called the offset, which determines the number of byte position(s) each row of the state will be shifted. With this modification, the operation does not have to depend on the fixed offset, it now depends on a number, called the Rank Number (RNo), which is obtained by manipulating each row of the state matrix with the corresponding row of the round key matrix. The rows of the state are shifted based on the rank number obtained. To obtain the rank number using a state matrix S and a round key matrix K, the following steps were adopted:

S=	S 0,0	S 0,1	S 0,2	S 0,3	and K =	K0,0	K0,1	K0,2	K0,3
	S 1,0	S 1,1	S 1,2	S 1,3		K1,0	K1,1	K1,2	K1,3
	S 2,0	S 2,1	S 2,2	S 2,3		K2,0	K2,1	K2,2	K2,3
	S 3,0	S 3,1	S 3,2	S 3,3		K3,0	K3,1	K3,2	K3,3

• Step 1: Each row (Rowi) of the state matrix was added to the corresponding row in the round key matrix using XOR to obtain a 4-byte vector called State-Key (SKey) vector.
• Step 2: The four-byte of the State-Key vector are then XORed together to obtain an 8-bit value called the Rank Value (RVal).
• Step 3: The eight-bit Rank Value (RVali) is then stored in corresponding Rowi of the state matrix.
• Step 4: Steps 1–3 will be repeated for the remaining rows Row1 to Row3
• Step 5: Attach Rank Number (RNo) to the Rank Values obtained in Step 3 above for each of the rows of the state (Row0 to Row3) in ascending order with the minimum rank value having 1 as the rank number while the maximum rank value has 4 as the Rank Number.

The above steps can be mathematically expressed, as follows:

The State–Key (SKey) vector is obtained using Equation (16), such that:

$$SKe{y}_i=((S_{i,0} ⨁ K_{i,0}), (S_{i,1} ⨁ K_{i,1}), (S_{i,2} ⨁ K_{i,2}), (S_{i,3} ⨁ K_{i,3}))$$

(16)

Equation (16) can be further reduced into Equation (17), such that:

$$SKe{y}_i=(S{K}_{i,0}, S{K}_{i,1},S{K}_{i,2},S{K}_{i,3}),\mathrm{where}S{K}_{i,j}=S_{i,j} ⨁ K_{i,j}$$

(17)

Alternatively, Equation (17) can be decomposed into Equations (18)–(20):

$$SKe{y}_0=(S{K}_{0,0}, S{K}_{0,1},S{K}_{0,2},S{K}_{0,3})$$

(18)

$$SKe{y}_1=(S{K}_{1,0}, S{K}_{1,1},S{K}_{1,2},S{K}_{1,3})$$

(19)

$$SKe{y}_2=(S{K}_{2,0}, S{K}_{2,1},S{K}_{2,2},S{K}_{2,3})$$

(20)

$$SKe{y}_3=(S{K}_{3,0}, S{K}_{3,1},S{K}_{3,2},S{K}_{3,3})$$

(21)

The Rank Values (RVals) are then obtained using Equation (22), such that:

$$RVa{l}_i=(S{K}_{i,0} ⨁ S{K}_{i,1} ⨁ S{K}_{i,2} ⨁ S{K}_{i,3}),\mathrm{where}i=0\mathit{to}3$$

(22)

Alternatively, Equation (22), which is generic, can further be broken into four independent equations representing each row of the state shown in Equations (23)–(26):

$$RVa{l}_0= S{K}_{0,0} ⨁ S{K}_{0,1} ⨁ S{K}_{0,2} ⨁ S{K}_{0,3}$$

(23)

$$RVa{l}_1= S{K}_{1,0} ⨁ S{K}_{1,1} ⨁ S{K}_{1,2} ⨁ S{K}_{1,3}$$

(24)

$$RVa{l}_2= S{K}_{2,0} ⨁ S{K}_{2,1} ⨁ S{K}_{2,2} ⨁ S{K}_{2,3}$$

(25)

$$RVa{l}_3= S{K}_{30} ⨁ S{K}_{3,1} ⨁ S{K}_{3,2} ⨁ S{K}_{3,3}$$

(26)

After obtaining the Rank Values (RVals), Rank Number (RNo) is then attached to these values in ascending order, with RNo of 1 being attached to the smallest RVal, while RNo of 4 is attached to the biggest RVal.

Lastly, each row of the state is then shifted $RNo-1$ positions to the left. This means that the row with RNo = 1 is not shifted, the one with RNo = 2 is shifted one-byte position to the left, followed by the row with RNo = 3, which is shifted two-byte position to the left, and lastly, the row with the highest rank number, RNo = 4 is shifted three-byte position to the left.

Table 1. Relationship Between Rank Number and Number of Byte Position to Shift Each Row in Modified ShiftRows Operation of the Enhanced AES.

S/No	Rank Number (RNo)	No. of Byte Position to Shift (RNo-1)
1	1	0
2	2	1
3	3	2
4	4	3

displays the above statements.

Given the state matrix S and round key matrix K, the modified ShiftRows operation is described below:

S =	4D	87	F2	97	and K =	11	55	75	A1
	EC	6E	4C	90		1F	44	53	CA
	4A	C3	46	E7		83	E6	90	3D
	8C	D8	95	A6		D4	31	77	9F

The State-Key (SKey) vectors are obtained, as follows:

$$SKe{y}_0=((4D ⨁ 11), (87 ⨁ 55), (F2 ⨁ 75), (97 ⨁ A1))=(5\mathrm{C},\mathrm{D}2,87,36)$$

$$SKe{y}_1=((EC ⨁ 1F), (6E ⨁ 44), (4C ⨁ 53), (90 ⨁ CA))=(\mathrm{F}3,2\mathrm{A},1\mathrm{F},5\mathrm{A})$$

$$SKe{y}_2=((4A ⨁ 83), (C3 ⨁ E6), (46 ⨁ 90), (E7 ⨁ 3D))=(\mathrm{C}9,25,\mathrm{D}6,\mathrm{DA})$$

$$SKe{y}_3=((8C ⨁ D4), (D8 ⨁ 31), (95 ⨁ 77), (A6 ⨁ 9F))=(58,\mathrm{E}9,\mathrm{E}2,39)$$

The Rank Values (RVals) are then obtained, as follows:

$$RVa{l}_0= 5\mathrm{C}⨁\mathrm{D}2⨁87⨁36=3F$$

$$RVa{l}_1= \mathrm{F}3⨁2\mathrm{A}⨁1\mathrm{F}⨁5\mathrm{A}=9C$$

$$RVa{l}_2= \mathrm{C}9⨁25⨁\mathrm{D}6⨁\mathrm{DA}=E0$$

$$RVa{l}_3= 58⨁\mathrm{E}9⨁\mathrm{E}2⨁39=6A$$

Table 2. Rank Values with their Corresponding Rank Numbers.

S/No	RVals	Value (Hex)	Value (Dec)	RNos	State Row No
1	RVal0	3F	63	1	0
2	RVal1	9C	156	3	1
3	RVal2	E0	224	4	2
4	RVal3	6A	106	2	3

depicts the Rank Values (RVals), their corresponding Rank Numbers (RNos), and state row number.

From Table 2, based on the rank numbers that were obtained for each row, the corresponding row will have to shift one less than the RNo value of that row. Row 0 will not shift, Row 1 will have to shift two-byte position to the left, row 2 will have to shift three-byte position to the left, and finally row 3 will have to shift one-byte position to the left. After performing these ShiftRows operations on the above state while using the state and the round key matrices S and K, the state matrix obtained is given as S and S′ for state matrix before and after the modified ShiftRows operation, respectively:

S =	4D	87	F2	97	S’ =	4D	87	F2	97
	EC	6E	4C	90		4C	90	EC	6E
	4A	C3	46	E7		E7	4A	C3	46
	8C	D8	95	A6		D8	95	A6	8C

4.4. Modified Inverse ShiftRows Transformation

The rank number computation for the modified InvShiftRows operation remains the same as that of modified ShiftRows operation since the round keys are read in reverse order during decryption process. The only difference is the direction to which the rows of the state matrix are shifted. For the inverse, the rows are shifted to the right based on the rank number.

4.5. Evaluating the Performance of the Modified AES

The strength of a cryptographic algorithm can be determined by measuring its diffusion and confusion property while using the avalanche effect. The term avalanche effect was first used by Horst Feistel in his article titled “Cryptography and Computer Privacy” published in 1973. Later, the concept was identified as Shannon’s property of confusion. The avalanche effect is used to measure the amount of randomness (non-linearity) of hash functions and cryptographic algorithm, especially block ciphers, such as Data Encryption Standard (DES) and Advance Encryption Standard (AES). The avalanche effect to some extent, tries to reflect the intuitive idea of high non-linearity. Meaning that, a small change in either the plaintext or the key (by flipping a single bit), propagates and significantly produces changes in the output (at least half the output bits [24]. Strict Avalanche Criterion (SAC) test of a cryptographic algorithm is conducted by comparing two encrypted texts before and after complementing some bits of the original plain text or encryption key. This is achieved by obtaining the Hamming Distance between the two encrypted text represented as vectors $x=(x_1, x_2,x_3,\dots , x_n)$ and $y=(y_1,y_2,y_3,\dots ,y_n)$. x is generated before flipping any bit of the plain text or encryption key, while y is generated after randomly flipping one bit of the plain text or encryption key. The Hamming Distance should be, on average, $\frac{n}{2}$. This implies that SAC is satisfied if, whenever a single bit in the input is complemented, each of the output bit changes with at least 50% probability.

Mathematically,

$$\forall x_i, y_i:H(x_i,y_i)=1,Average(h(f(x_i), f(y_i)))=\frac{n}{2}$$

Where $i=0, 1, 2,\dots , n-1$ and $h=Hamming Distance$. The Hamming Distance for two vectors $x, y\in T$, where T belong to the set {0, 1} defined as the number of positions h $(where 0\le h\le n)$ where the vectors differ. Alternatively, it can be defined as the number of ones (1s) of the vector $z=x\oplus y$ [25]. Given two vectors $b=(b_1, b_2,b_3,\dots b_n)$ and $b\prime =(b{\prime }_1, b{\prime }_2,b{\prime }_3,\dots b{\prime }_n)$, where b is a binary representation of the cipher text obtained before flipping a bit in the encryption key, and b’ is the binary representation of the cipher text that is obtained after flipping a single bit in the encryption key. The resultant vector $z$, which is the binary representation of the result obtained after adding b and b′ using exclusive OR (XOR) operation, represent the hamming distance vector.

$$z=((b_1 ⨁ b{\prime }_1), (b_{2 }⨁ b{\prime }_2), (b_3 ⨁ b{\prime }_3),\dots ,(b_n ⨁ b{\prime }_n))$$

Using the vector z, the hamming distance h, can be obtained as the number of 1’s in the vector z. The avalanche effect can now be computed as the number of 1’s in the z vector divided by the total number of elements n, in the vector, that is,

$$Avalanche Effect= \frac{Hamming Distance (h)}{Number of Elements in z(n)}$$

Let $x=1101001010111001$ and $y=1011011001010010$

$$\begin{gathered} \begin{array}{r}1101001010111001\\ \underset{¯}{⨁\hspace{1em}1011011001010010}\end{array} \\ z=x ⨁ y = 0110010011101011 \end{gathered}$$

The Hamming Distance, $h = 9 \mathrm{and} Number of Elements in z vector, n = 16$. The Hamming distance satisfies the condition $0\le h\le n$, since $0\le 9\le 16$. Hence,

$$Avalanche Effect=\frac{Hamming Distance (h)}{Number of Elements in z (n)}=\frac{9}{16}=0.5625$$

$$Avalanche Effect=0.5625*100=56.25\%$$

Avalanche effect could also be computed using Equation (27) such that:

$$Avalanche Effect=\frac{No. of bits differs in two cipher texts}{Total No. of bits in cipher text}\times 100\%.$$

(27)

If a cryptographic algorithm does not exhibit a significant degree of avalanche effect (at least 50%), then that algorithm has poor randomization. Thus, cryptanalysts can make predictions about the input, only being given the output. This may be enough to partially or worst, completely break the algorithm. In addition to the avalanche effect, the time taken for encryption and decryption were also measured.

5. Results and Discussion

The modified AES and the conventional AES were evaluated in terms of the avalanche effect and execution time (encryption/decryption time). The avalanche effect is a desirable property of block ciphers that ensures a single bit flip in input text produces at least 50% change in the output text. Execution time refers to the time taken by the algorithm to encrypt or decrypt a given input text.

5.1. Measuring the Avalanche Effect

The avalanche effect of the modified AES was carried out while using a short plain text and a 0.5 MB text file. The text file was encrypted with two different keys: key1 (original key) and key2 (obtained by flipping single bit (112th bit) of key1 from 0 to 1).

5.1.1. Avalanche Effect with a Short Plain Text File

A short plain text: I Love Unilorin! with hexadecimal values: 49 20 4C 6F 76 65 20 55 6E 69 6C 6F 72 69 6E 21 was first used to measure the avalanche effect of the modified and conventional AES. The plain text was encrypted with two different keys: key1 (original key) and key2 (obtained by flipping single bit (112th bit) of key1 from 0 to 1). Based on the computed results in

Table 3. Avalanche Effect Test Result Obtained After Flipping Single Bit in the Secret Key.

AES Name	Secret Key (Plain)	Secret Key (Hex)	Cipher Text (Hex)	Avalanche Effect
Conventional AES	dKro9Wahme#dHrn7	64 4B 72 6F 39 57 61 68 6D 65 23 64 48 72 6E 37	83 4A A0 CB 25 78 FD FB 5D 14 24 BD 32 CD E0 00	0.5078125 (50.78123%)
	dKro9Wahme#dHsn7	64 4B 72 6F 39 57 61 68 6D 65 23 64 48 73 6E 37	BB 87 74 9F 78 20 28 D8 40 1D DE 6C F7 41 3A E7
Modified AES	dKro9Wahme#dHrn7	64 4B 72 6F 39 57 61 68 6D 65 23 64 48 72 6E 37	D6 BA 33 8A C3 61 3A 74 B5 FB EB A4 EA 97 B1 10	0.578125 (57.8125%)
	dKro9Wahme#dHsn7	64 4B 72 6F 39 57 61 68 6D 65 23 64 48 73 6E 37	5D 2D A4 39 11 04 95 C8 2E 17 D3 7F 5C 43 22 86

, the modified AES achieved higher avalanche effect as compared to the conventional AES algorithm. The conventional AES achieved an avalanche effect of 50.7812%, while that of the Modified AES is 57.8125%. This means that, more than 57% of the bits that made up the cipher text changes after encryption by flipping just a single bit (112th bit) in the secret key while using the Modified AES as compared to less than 51% changes when the conventional AES was used.

Table 4. Avalanche Effect Test Result Obtained After Flipping Single Bit in the Plain Text.

AES Name	Secret Key	Plain Text	Plain Text (Hex)	Cipher Text (Hex)	Avalanche Effect
Conventional AES	dKro9Wahme#dHrn7	I Love Unilorin!	49 20 4C 6F 76 65 20 55 6E 69 6C 6F 72 69 6E 21	83 4A A0 CB 25 78 FD FB 5D 14 24 BD 32 CD E0 00	0.4921875 (49.21875%)
		I Love Unimorin!	49 20 4C 6F 76 65 20 55 6E 69 6D 6F 72 69 6E 21	F2 96 36 B1 6A FA 68 D2 C4 4A DF 2D BA 64 CA A9
Modified AES		I Love Unilorin!	49 20 4C 6F 76 65 20 55 6E 69 6C 6F 72 69 6E 21	D6 BA 33 8A C3 61 3A 74 B5 FB EB A4 EA 97 B1 10	0.5625 (56.25%)
		I Love Unimorin!	49 20 4C 6F 76 65 20 55 6E 69 6D 6F 72 69 6E 21	6B CC 92 7D 1E C2 74 B4 E7 EB 7E 0A D1 CA 67 6F

presents the avalanche effect that was obtained after flipping a single bit in the plain text. From the result, the modified AES achieved an avalanche effect of 56.25% when compared to 49.21875% achieved by the conventional AES algorithm. This signifies that, more than 56% of the bits that made up the cipher text changes after encryption by flipping just a single bit (88th bit) in the plain text while using the Modified AES as compared to less than 50% changes when the conventional AES was used.

5.1.2. Avalanche Effect with a 0.5 mb Text File

In addition to the short plain text file, a 0.5 mb text file was also used to measure the avalanche effect of the modified AES. As documented in

Table 5. Avalanche Effect Test Result Obtained After Flipping Single Bit in the Secret Key.

AES Name	Secret Key (Plain)	Secret Key (Hex)	File Size	Avalanche Effect
Conventional AES	dKro9Wahme#dHrn7	64 4B 72 6F 39 57 61 68 6D 65 23 64 48 72 6E 37	0.5 MB	0.49973 (49.973%)
	dKro9Wahme#dHsn7	64 4B 72 6F 39 57 61 68 6D 65 23 64 48 73 6E 37
Modified AES	dKro9Wahme#dHrn7	64 4B 72 6F 39 57 61 68 6D 65 23 64 48 72 6E 37	0.5 MB	0.563625 (56.3625%)
	dKro9Wahme#dHsn7	64 4B 72 6F 39 57 61 68 6D 65 23 64 48 73 6E 37

, the conventional AES achieved an avalanche effect of 49.973%, while that of the Modified AES is 56.3625%. This means that more than 56% of the bits that made up the cipher text changed after encryption when the 112th bit in the secret key was flipped. This showed that the modified AES achieved a higher avalanche effect when compared to the conventional AES algorithm.

Table 6. Avalanche Effect Test Result Obtained After Flipping Single Bit in the Plain Text.

AES Name	Secret Key	File Size	Avalanche Effect
Conventional AES	dKro9Wahme#dHrn7	0.5 MB	0.504715 (50.4715%)
Modified AES	dKro9Wahme#dHrn7	0.5 MB	0.55735 (55.735%)

presents the avalanche effect test result that was obtained after flipping a single it in the plain text. From the result, the modified AES achieved an avalanche effect of 55.735% as compared to 50.4715% achieved by the conventional AES algorithm. This signifies that more than 55% of the bits that made up the cipher text changes after encryption by randomly flipping just a single bit (3751st bit) in the plain text while using the Modified AES as compared to 50.4% changes when the conventional AES was used.

5.2. Measuring the Execution Time

The execution time is a function of the time that is taken to convert a plain text to a cipher text (encryption time) and the time that is needed to convert the cipher text back to the plain text (decryption time). The encryption time and decryption time is expected to be small in order to have a responsive and fast system. Furthermore, the execution time depends to some extent on the configuration of the system used. Therefore, the execution time reported was carried out on a laptop with the following configuration:

(i)

4.00 GB Random Access Memory (RAM).

(ii)

500 GB Hard Disk Drive (HDD).

(iii)

Intel(R) Core i3 Processor clocking @ 2.27 GHz Dual Core.

(iv)

A 64 bit Microsoft Windows 10 Pro Operating System.

Table 7. Execution Time Test Result.

Plain Text Size	AES Name	Avrg. Encryption Time (ms)	Avrg. Decryption Time (ms)
16 Byte	Conventional AES	0.1215	0.1637
	Modified AES	0.1658	0.1789
32 Byte	Conventional AES	0.2156	0.2232
	Modified AES	0.2976	0.3114
64 Byte	Conventional AES	0.4154	0.3326
	Modified AES	0.4564	0.4626
128 Byte	Conventional AES	0.4333	0.4076
	Modified AES	0.6984	0.5911
0.5 mb	Conventional AES	1769.85	1684.17
	Modified AES	2359.65	2269.32

presents the execution time test results in milliseconds (ms), which was obtained by computing the average encryption/decryption time after encrypting/decrypting the same input text while using the same key five times.

The above result indicates that the modified AES has a slight increase in the encryption and decryption time when compared to the conventional AES algorithm.

5.3. Comparative Analysis of Computed Results with Existing Works

A comparative analysis of the results that were obtained with those presented in existing works was carried out. This was a little bit of tasking, as there is no standard performance metrics that are widely and generally acceptable by all researchers in this regard. While some measured the performance of their modified AES version using text files of different sizes, some used images and video files. However, most authors employed execution time as their performance metrics while few used avalanche effect. As presented in

Table 8. Execution Time Comparison.

S/N	Author	Test Data	Execution Time		Difference (s)
			Conventional AES (s)	Modified AES (s)
1.	[11]	256 × 256 image	12.1760	11.4190	0.7570
2.	[16]	16 bytes text file	0.0113	0.2414	−0.2301
3.	[24]	Three 256 × 256 coloured images	86.5342	9.0000	77.5342
4.	[26]	4.45MB image	3.7390	3.6490	0.0900
5.	[27]	128 × 128 image	0.2330	0.0840	0.1490
6.	[28]	Image files	41.4573	18.9419	22.5154
7.	[29]	16 bytes text file	1.9259	1.8749	0.0510
8.	[30]	Text File	0.2467	0.2461	0.0006
9.	[31]	Text File	0.6000	0.6010	−0.0010
10.	[32]	Plain text	6.2100	6.1700	0.0400
11.	[33]	256 × 256 image of 192 KB	6.4430	6.3490	−0.0940
Proposed Technique		16 bytes text file	0.0713	0.1723	−0.1010

, the proposed technique recorded a slightly higher execution time in seconds than the conventional AES. Though this may not be clearly noticeable in real life application, yet it is significant.

Table 9. Avalanche Effect Comparison.

S/N	Author	Avalanche Effect		Difference (%)
		Conventional AES (%)	Modified AES (%)
1.	[12]	15.81	24.31	8.50
2.	[32]	50.78	52.34	1.56
3.	[34]	49.21	52.34	3.13
4.	[34]	47.7	58.59	10.89
Proposed Technique		49.973	56.3625	6.3895

presents a comparison of the avalanche effect of the modified AES with those that are available in existing literature. Few researchers have employed the avalanche effect to measure the performance of their algorithms. Therefore, it is recommended that more researchers should use it, as it is a desirable property of encryption algorithms. The proposed technique achieved a higher avalanche effect when compared to the Conventional AES. The difference obtained is higher than that obtained in [32,34].

6. Conclusions

The proposed method attempts to strengthen the conventional AES algorithm by making the SubBytes transformation round key dependent and randomizing the ShiftRows transformation. This is to ensure that a single bit change in either the key or the plain text produces significant changes in the cipher text, thereby increasing its avalanche effect. The modified algorithm is evaluated in terms of avalanche effect and execution time and the results that were obtained revealed that the modified AES achieved a higher avalanche effect with a slight increase in the execution time. The high avalanche effect recorded, as further shown that the conventional AES can still be strengthened and it is recommended that more researchers should use the avalanche effect as a performance evaluation metric.