Second-Order Sliding Mode Formation Control of Multiple Robots by Extreme Learning Machine
Abstract
:1. Introduction
- An architecture that combines second-order sliding mode control and the extreme learning machine technique is investigated.
- The closed-loop stability of this combination is presented in the sense of Lyapunov.
- Some numerical results for different formation patterns are demonstrated to support the combination.
2. Formation Model
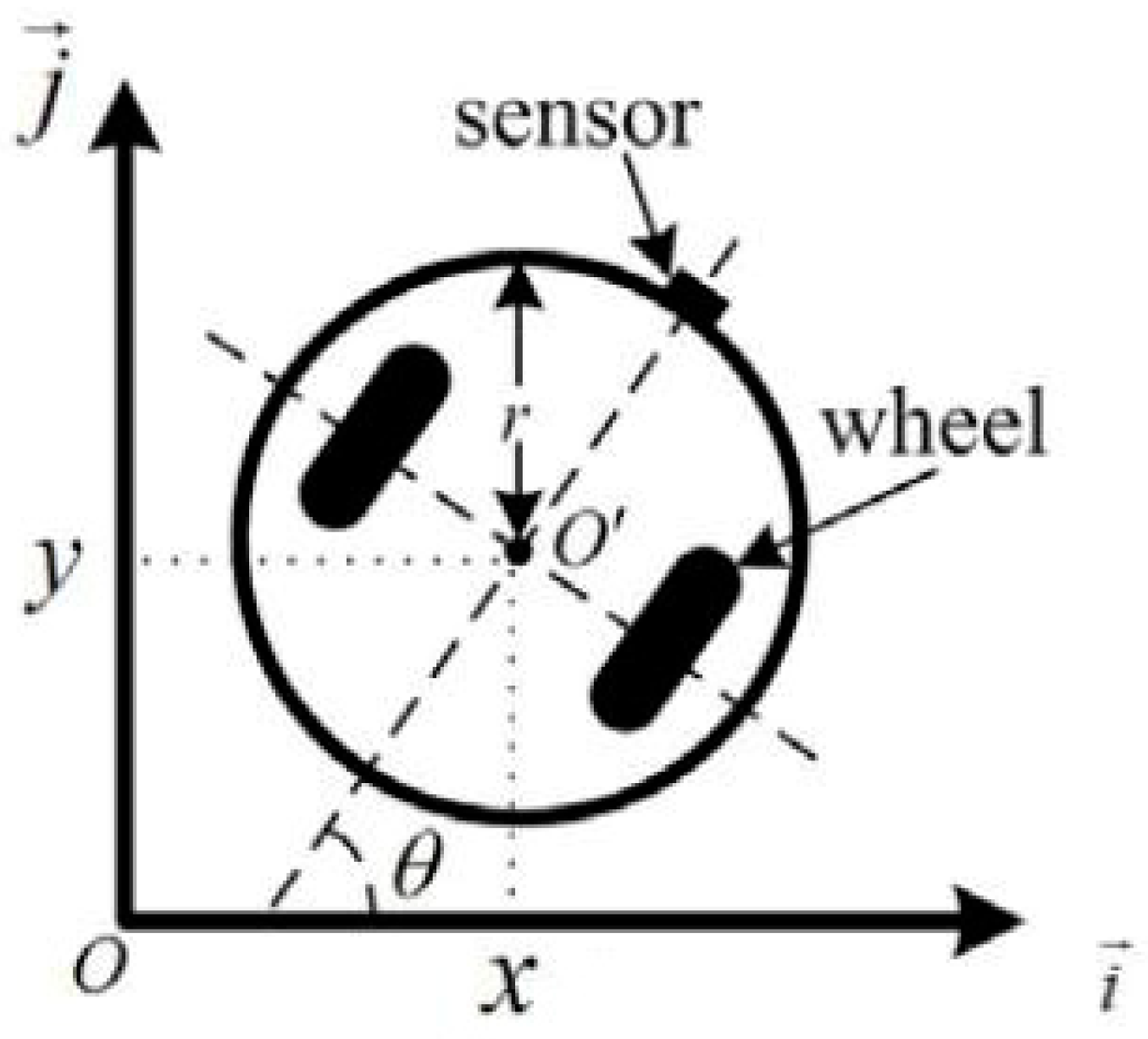
2.1. A Single Robot
2.2. A Leader–Follower Pair
3. Formation Control Design
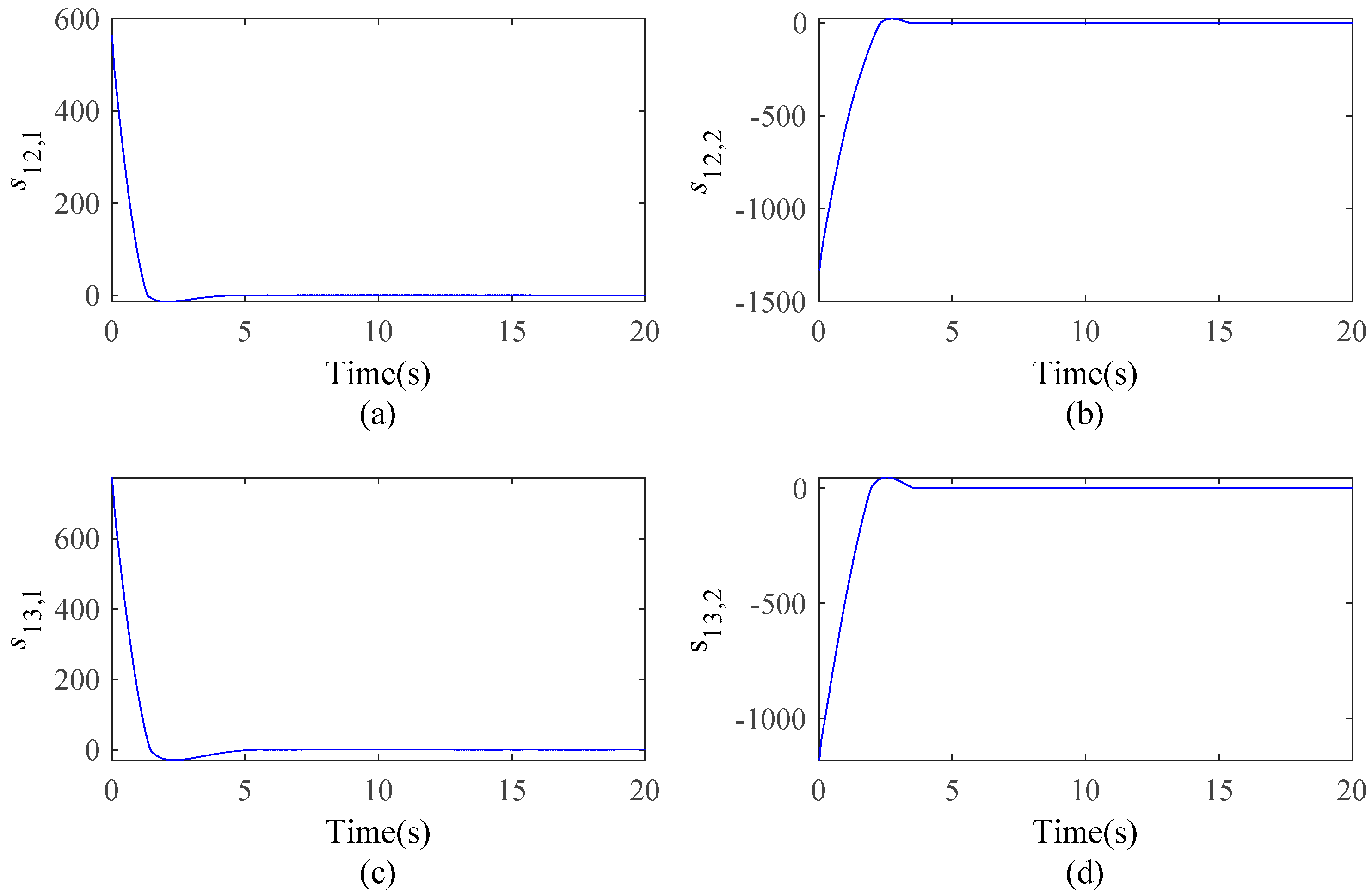
3.1. Sliding Surfaces and Input–Output Dynamics
3.2. Super-Twisting Sliding Mode Control Design
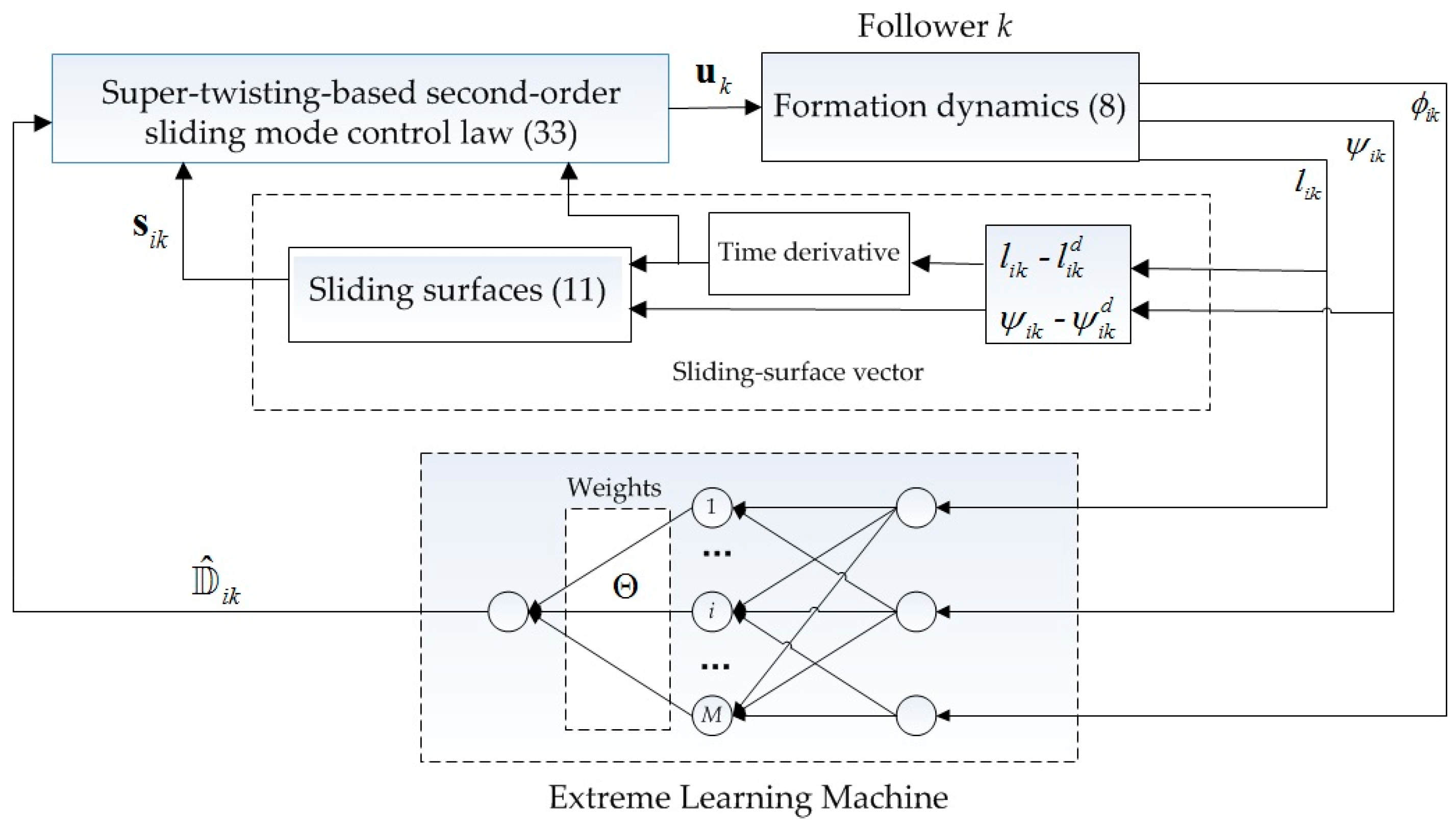
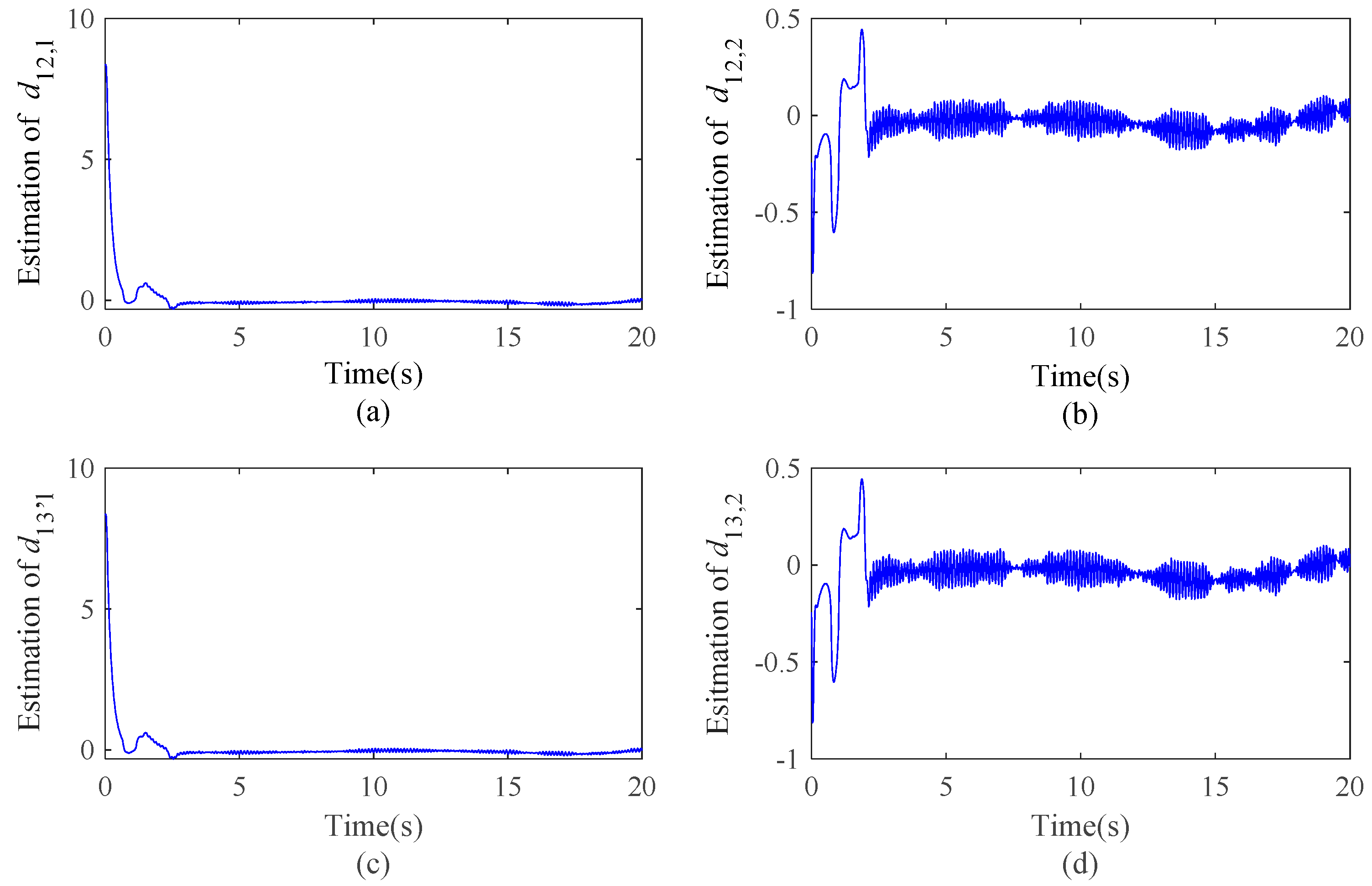
3.3. Super-Twisting Sliding Mode Control Design via ELM
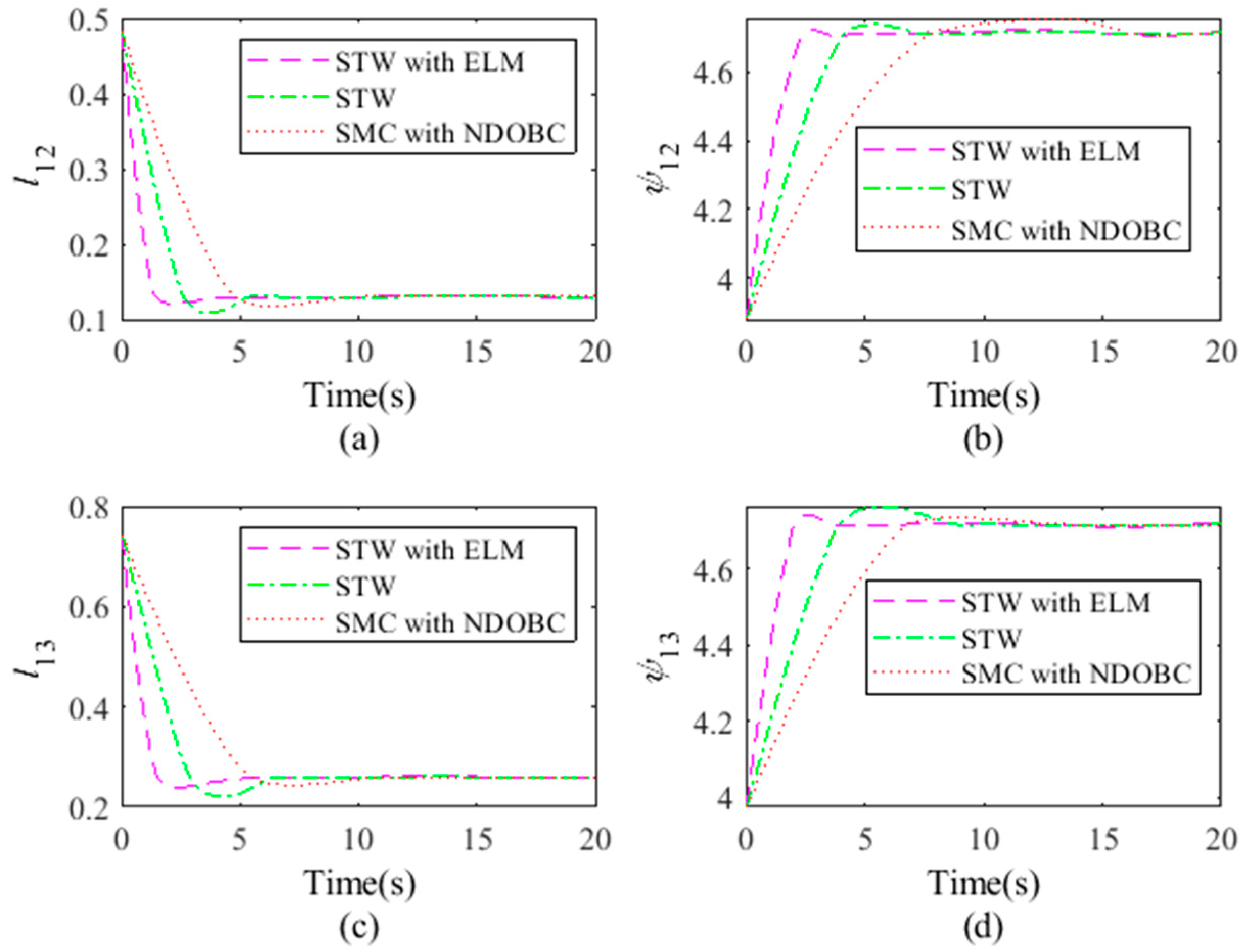
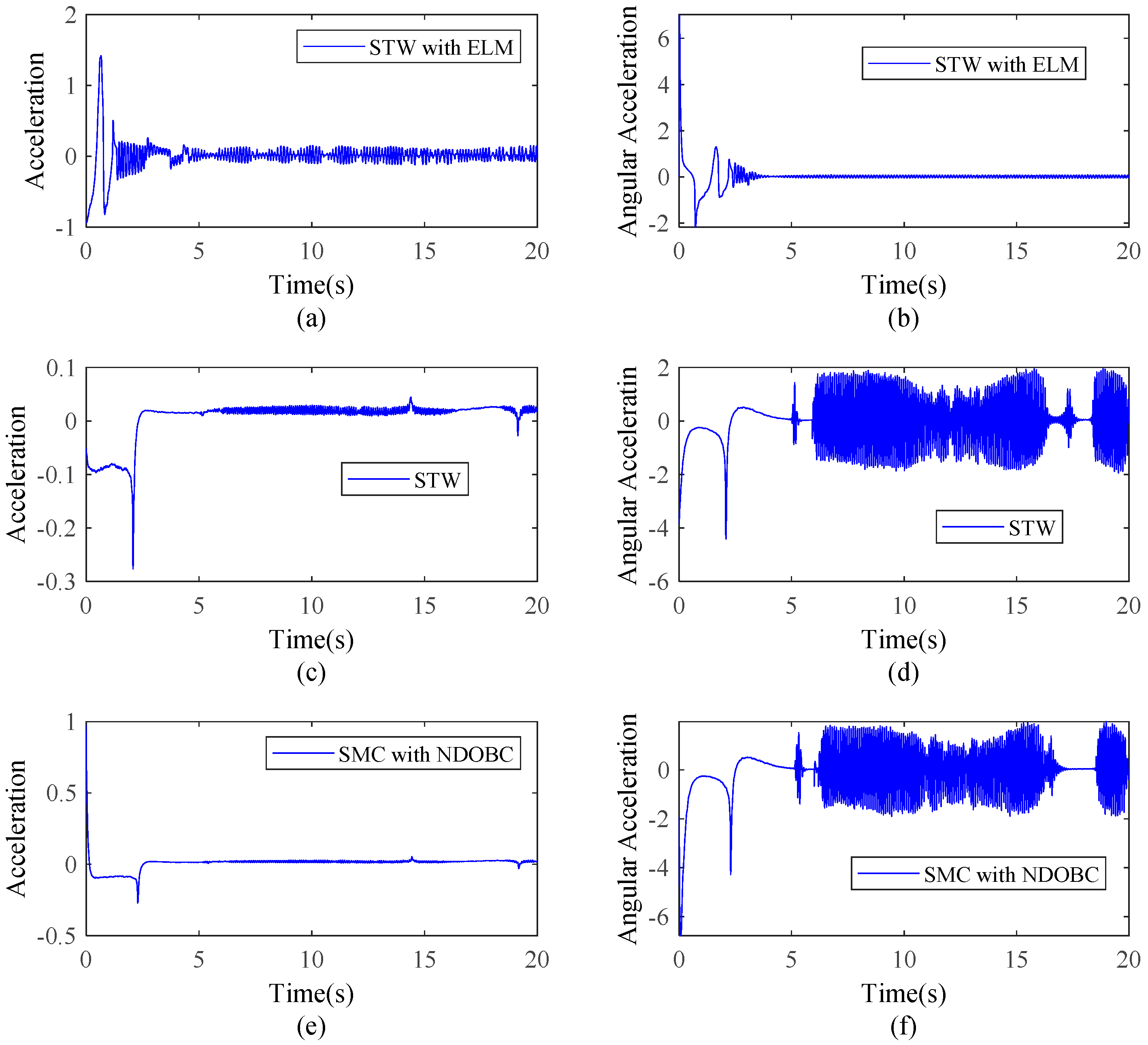
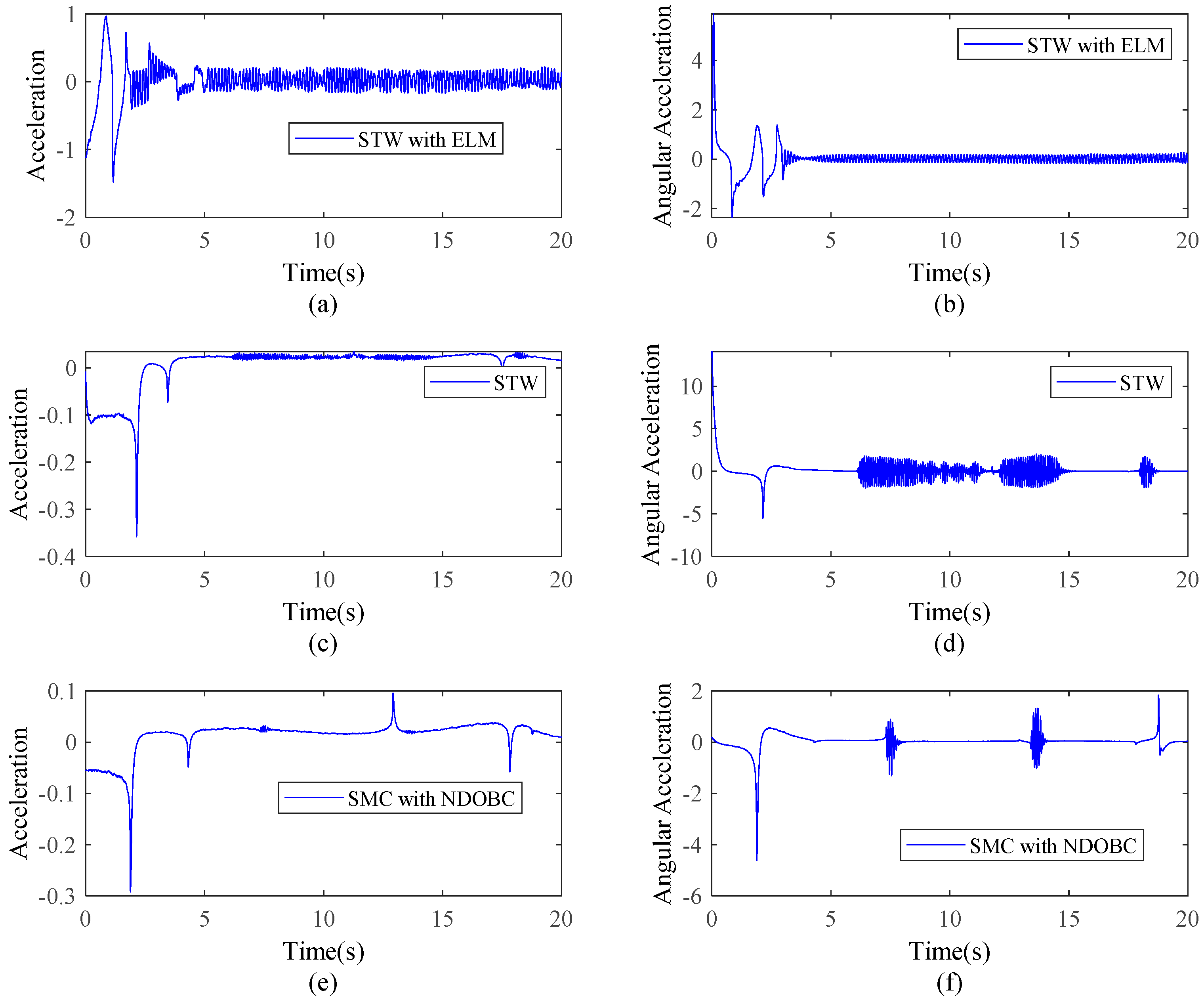
4. Simulation Results
4.1. Multirobot Platform
4.2. Formation Tasks
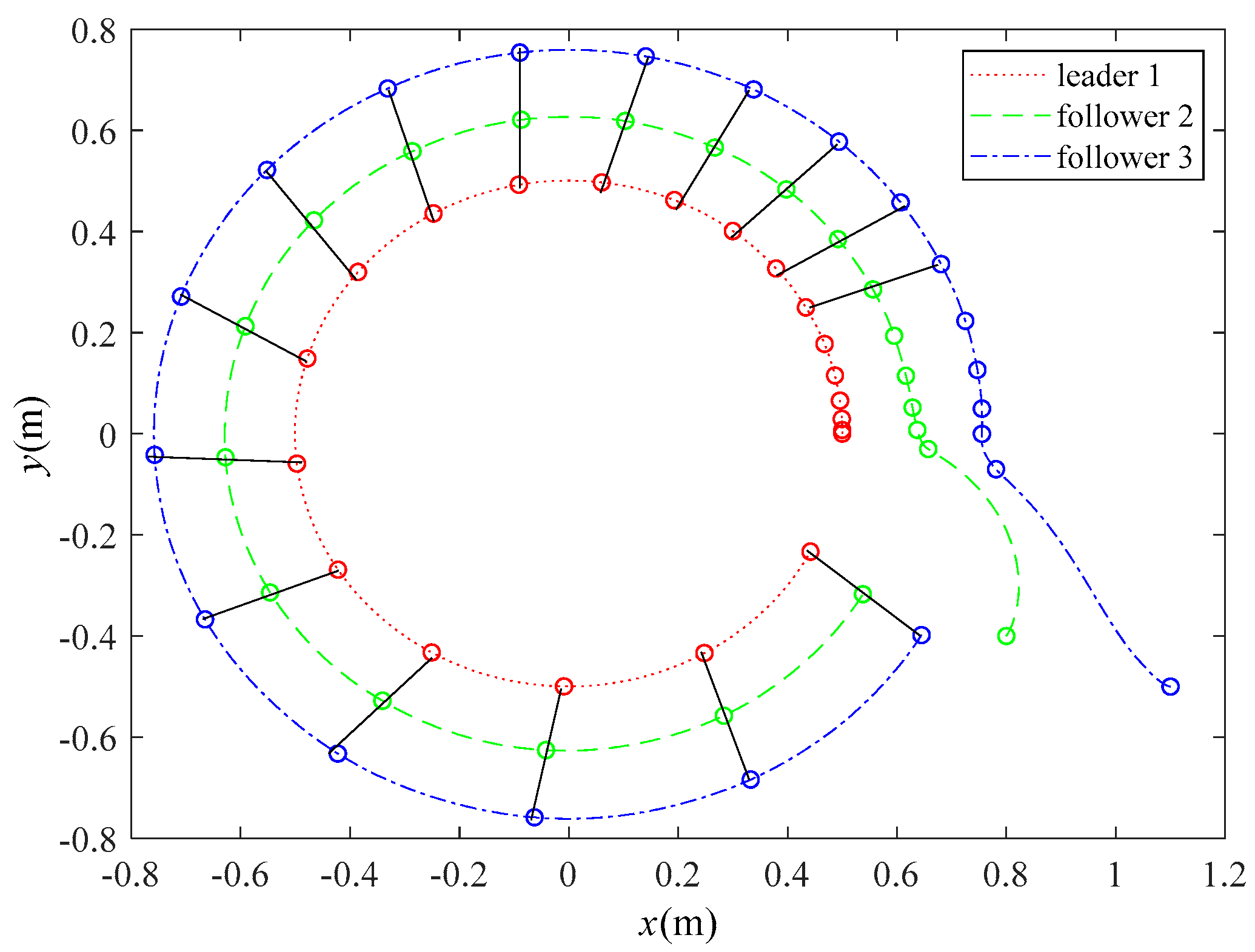
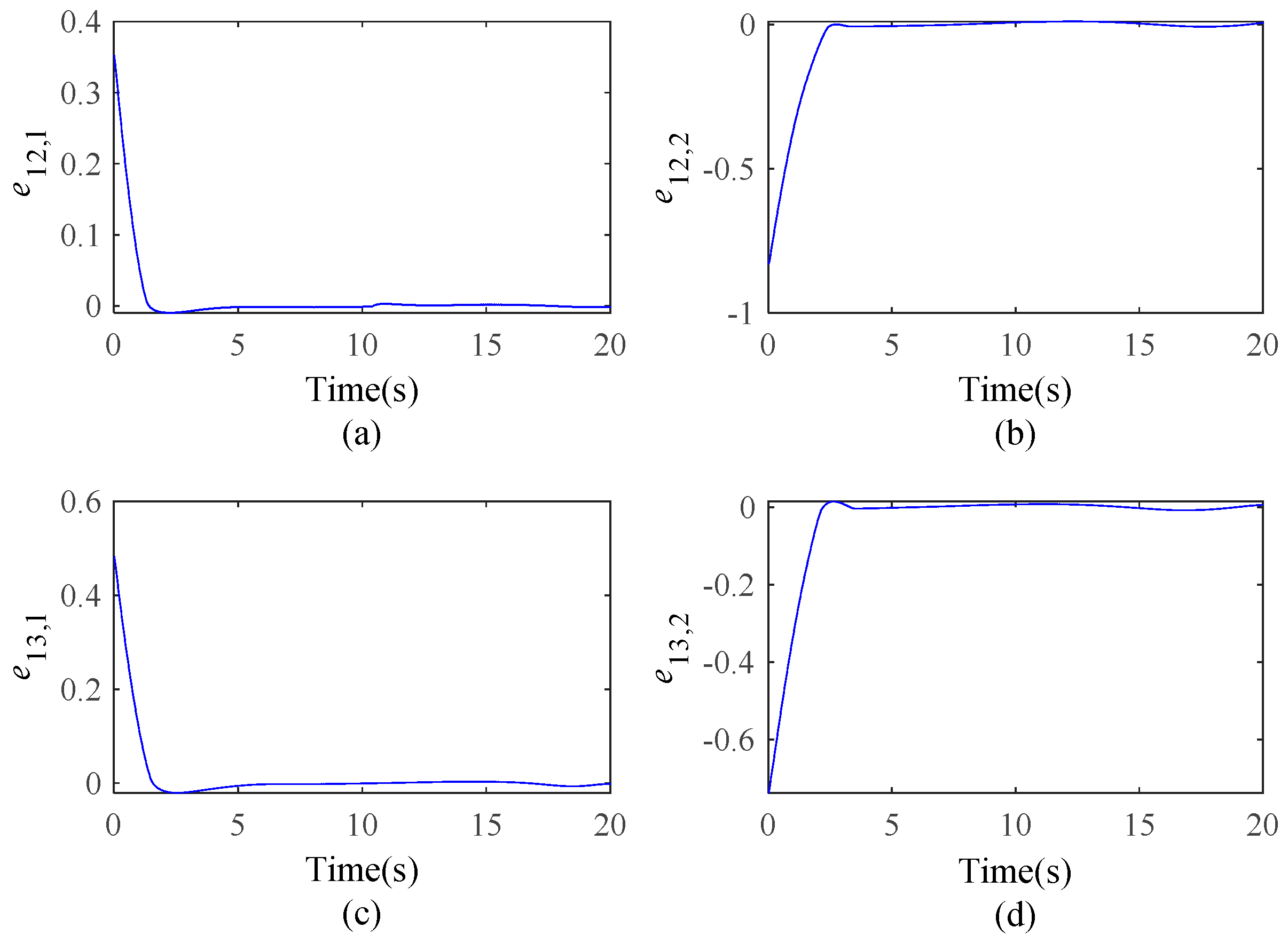
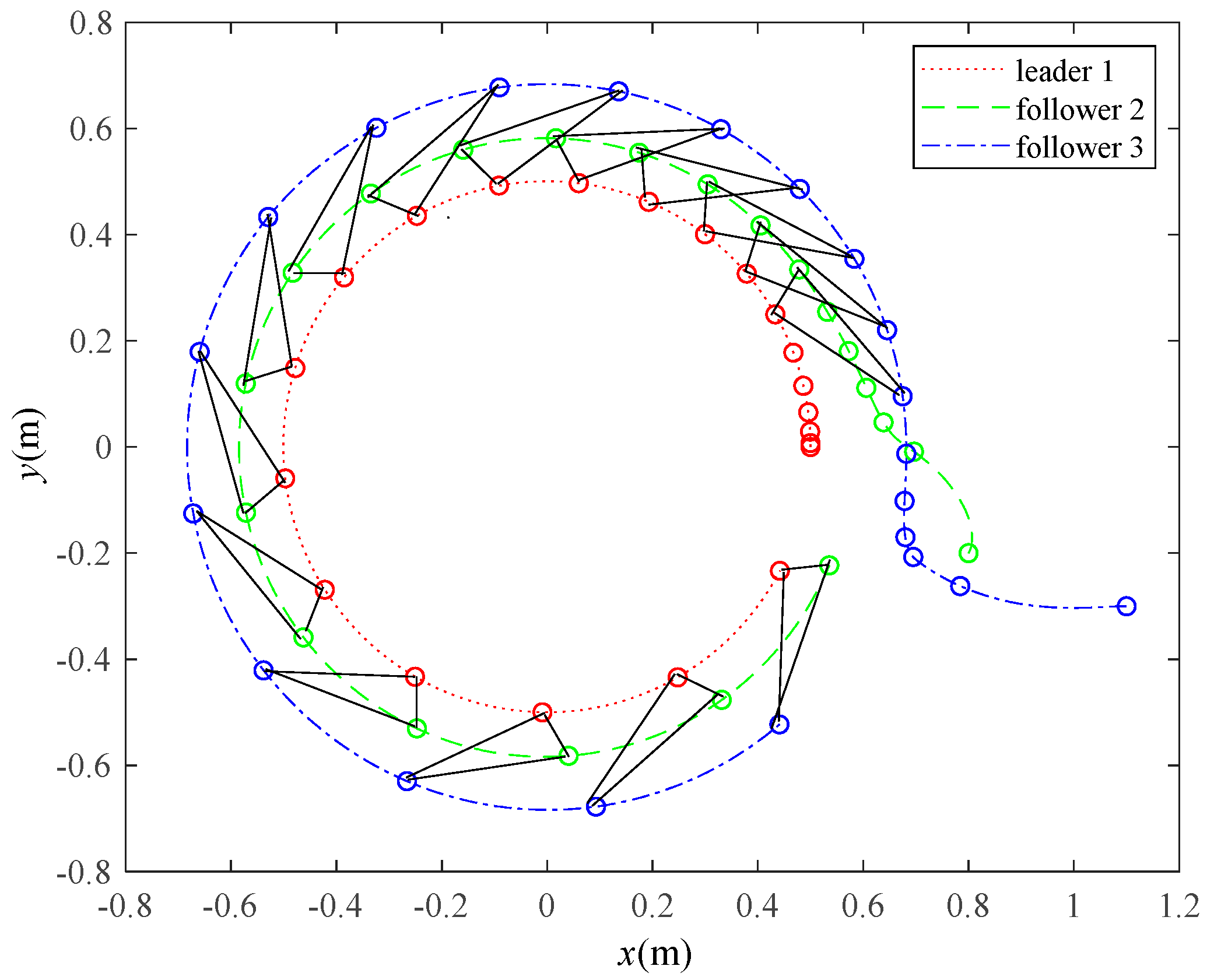
4.2.1. String Formation Moving Along a Circular Trajectory
4.2.2. Triangular Formation Moving in a Circular Trajectory
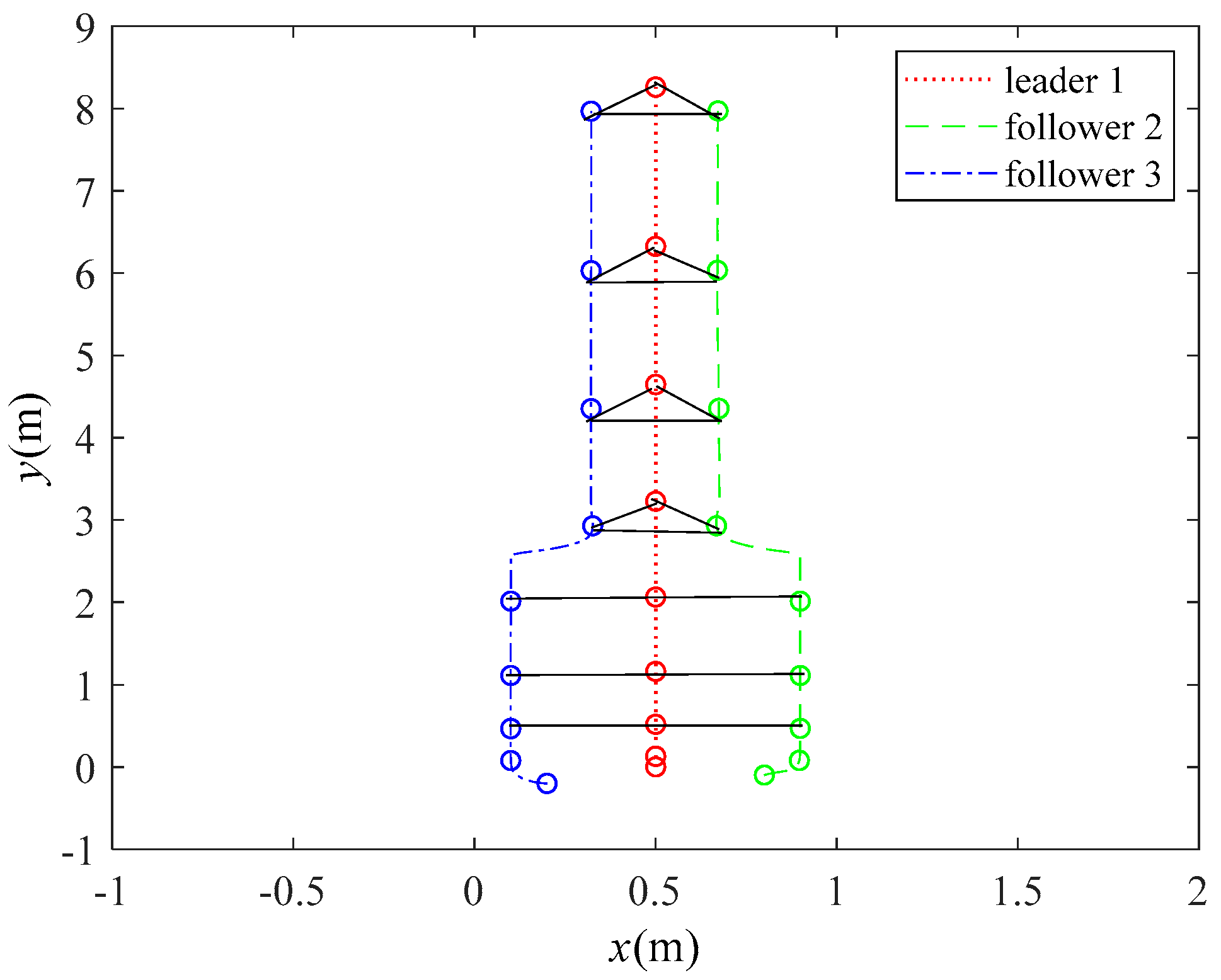
4.2.3. Maneuvers from a String Formation to a Triangular One
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ren, W.; Sorensen, N. Distributed coordination architecture for multi-robot formation control. Robot. Auton. Syst. 2008, 56, 324–333. [Google Scholar] [CrossRef]
- Dai, Y.Y.; Qian, D.W.; Lee, S. Multiple robots motion control to transport an object. Filomat 2018, 32, 1547–1558. [Google Scholar] [CrossRef]
- Chu, P.M.; Cho, S.; Fong, S.; Park, Y.W.; Cho, K. 3D Reconstruction framework for multiple remote robots on cloud system. Symmetry 2017, 9, 55. [Google Scholar] [CrossRef]
- Qian, D.W.; Xi, Y.F. Leader-Follower formation maneuvers for multi-robot systems via derivative and integral terminal sliding mode. Appl. Sci. 2018, 8, 1045. [Google Scholar] [CrossRef]
- Qian, D.W.; Zhang, G.G.; Chen, J.R.; Wang, J.; Wu, Z.M. Coordinated formation design of multi-robot systems via an adaptive-gain super-twisting sliding mode method. Appl. Sci. 2019, 9, 4315. [Google Scholar] [CrossRef]
- Yoo, S.J.; Park, B.S. Connectivity preservation and collision avoidance in networked nonholonomic multi-robot formation systems: Unified error transformation strategy. Automatica 2019, 103, 274–281. [Google Scholar] [CrossRef]
- Qian, D.W.; Tong, S.W.; Li, C.D. Observer-based leader-following formation control of uncertain multiple agents by integral sliding mode. Bull. Pol. Acad. Sci. Tech. Sci. 2017, 65, 35–44. [Google Scholar] [CrossRef]
- Qian, D.W.; Tong, S.W.; Guo, J.R.; Lee, S.G. Leader-follower-based formation control of non-holonomic mobile robots with mismatched uncertainties via integral sliding mode. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2015, 229, 559–569. [Google Scholar] [CrossRef]
- Yao, X.Y.; Ding, H.F.; Ge, M.F. Formation-containment control for multi-robot systems with two-layer leaders via hierarchical controller-estimator algorithms. J. Frankl. Inst. Eng. Appl. Math. 2018, 355, 5272–5290. [Google Scholar] [CrossRef]
- Park, M.J.; Kwon, O.M.; Ryu, J.H. A Katz-centrality-based protocol design for leader-following formation of discrete-time multi-agent systems with communication delays. J. Frankl. Inst. 2018, 355, 6111–6131. [Google Scholar] [CrossRef]
- Sun, N.; Wu, Y.; Chen, H.; Fang, Y. Antiswing cargo transportation of underactuated tower crane systems by a nonlinear controller embedded with an integral term. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1387–1398. [Google Scholar] [CrossRef]
- Qian, D.W.; Tong, S.W.; Lee, S.G. Fuzzy-Logic-based control of payloads subjected to double-pendulum motion in overhead cranes. Autom. Constr. 2016, 65, 133–143. [Google Scholar] [CrossRef]
- Liu, Y.; Jia, Y.M. Robust formation control of discrete-time multi-agent systems by iterative learning approach. Int. J. Syst. Sci. 2015, 46, 625–633. [Google Scholar] [CrossRef]
- Jin, X. Nonrepetitive leader-follower formation tracking for multiagent systems with LOS range and angle constraints using iterative learning control. IEEE Trans. Cybern. 2019, 49, 1748–1758. [Google Scholar] [CrossRef] [PubMed]
- Nascimento, T.P.; Conceicao, A.G.S.; Moreira, A.P. Multi-Robot nonlinear model predictive formation control: The obstacle avoidance problem. Robotica 2016, 34, 549–567. [Google Scholar] [CrossRef]
- Li, C.D.; Yi, J.Q.; Wang, H.K.; Zhang, G.Q.; Li, J.Q. Interval data driven construction of shadowed sets with application to linguistic word modeling. Inf. Sci. 2020, 507, 503–521. [Google Scholar] [CrossRef]
- Li, C.D.; Gao, J.L.; Yi, J.Q.; Zhang, G.Q. Analysis and design of functionally weighted single-input-rule-modules connected fuzzy inference systems. IEEE Trans. Fuzzy Syst. 2018, 26, 56–71. [Google Scholar] [CrossRef]
- Qian, D.W.; Tong, S.W.; Li, C.D. Leader-following formation control of multiple robots with uncertainties through sliding mode and nonlinear disturbance observer. ETRI J. 2016, 38, 1008–1018. [Google Scholar] [CrossRef]
- Qian, D.W.; Li, C.D.; Lee, S.G.; Ma, C. Robust formation maneuvers through sliding mode for multi-agent systems with uncertainties. IEEE CAA J. Autom. Sin. 2018, 5, 342–351. [Google Scholar] [CrossRef]
- Nair, R.R.; Karki, H.; Shukla, A.; Behera, L.; Jamshidi, M. Fault-Tolerant formation control of nonholonomic robots using fast adaptive gain nonsingular terminal sliding mode control. IEEE Syst. J. 2018, 13, 1006–1017. [Google Scholar] [CrossRef]
- Utkin, V.I. Discussion aspects of high-order sliding mode control. IEEE Trans. Autom. Control. 2016, 61, 829–833. [Google Scholar] [CrossRef]
- Uppal, A.A.; Alsmadi, Y.M.; Utkin, V.I.; Bhatti, A.I.; Khan, S.A. Sliding mode control of underground coal gasification energy conversion process. IEEE Trans. Control Syst. Technol. 2018, 26, 587–598. [Google Scholar] [CrossRef]
- Utkin, V.I.; Poznyak, A.S. Adaptive sliding mode control with application to super-twist algorithm: Equivalent control method. Automatica 2013, 49, 39–47. [Google Scholar] [CrossRef]
- Tian, C.; Li, C.D.; Zhang, G.; Lv, Y.S. Data driven parallel prediction of building energy consumption using generative adversarial nets. Energy Build. 2019, 186, 230–243. [Google Scholar] [CrossRef]
- Yang, Q.M.; Ge, S.S.; Sun, Y.X. Adaptive actuator fault tolerant control for uncertain nonlinear systems with multiple actuators. Automatica 2015, 60, 92–99. [Google Scholar] [CrossRef]
- Peng, W.; Li, C.D.; Zhang, G.; Yi, J.Q. Interval type-2 fuzzy logic based transmission power allocation strategy for lifetime maximization of WSNs. Eng. Appl. Artif. Intell. 2020. [Google Scholar] [CrossRef]
- Huang, G.B.; Wang, D.H.; Lan, Y. Extreme learning machines: A survey. Int. J. Mach. Learn. Cybern. 2011, 2, 107–122. [Google Scholar] [CrossRef]
- Wu, S.B.; Cao, W.H. Parametric model for microwave filter by using multiple hidden layer output matrix extreme learning machine. IET Microw. Antennas Propag. 2019, 13, 1889–1896. [Google Scholar] [CrossRef]
- Yu, Y.L.; Xu, M.X.; Gu, J. Vision-based traffic accident detection using sparse spatio-temporal features and weighted extreme learning machine. IET Intell. Transp. Syst. 2019, 13, 1417–1428. [Google Scholar] [CrossRef]
- Wong, P.K.; Gao, X.H.; Wong, K.I.; Vong, C.M.; Yang, Z.X. Initial-training-free online sequential extreme learning machine based adaptive engine air-fuel ratio control. Int. J. Mach. Learn. Cybern. 2019, 10, 2245–2256. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, D.; Zhang, G.; Wang, J.; Wu, Z. Second-Order Sliding Mode Formation Control of Multiple Robots by Extreme Learning Machine. Symmetry 2019, 11, 1444. https://doi.org/10.3390/sym11121444
Qian D, Zhang G, Wang J, Wu Z. Second-Order Sliding Mode Formation Control of Multiple Robots by Extreme Learning Machine. Symmetry. 2019; 11(12):1444. https://doi.org/10.3390/sym11121444
Chicago/Turabian StyleQian, Dianwei, Guigang Zhang, Jian Wang, and Zhimin Wu. 2019. "Second-Order Sliding Mode Formation Control of Multiple Robots by Extreme Learning Machine" Symmetry 11, no. 12: 1444. https://doi.org/10.3390/sym11121444
APA StyleQian, D., Zhang, G., Wang, J., & Wu, Z. (2019). Second-Order Sliding Mode Formation Control of Multiple Robots by Extreme Learning Machine. Symmetry, 11(12), 1444. https://doi.org/10.3390/sym11121444



