1. Introduction
All digraphs considered in this paper are finite without loops and multiple arcs, and we refer to [
1] for notation and graph-theoretical terminology not defined here. In a digraph
D with vertex set
and arc set
,
u is said to be an
in-neighbor of
v if
. For a vertex
, denote
be the
open in-neighborhood of
v. The
closed in-neighborhood of
v is
. In all cases above, we omit the subscript
D when the digraph
D is clear from the context. For
,
denotes the subdigraph induced by
S.
For two digraphs
and
, the
Cartesian product is the digraph with vertex set
and
if and only if
and
or
and
, where
for
. We use
to present that
and
are isomorphic. The sets of vertices of the directed path
and the directed cycle
are denoted by
and
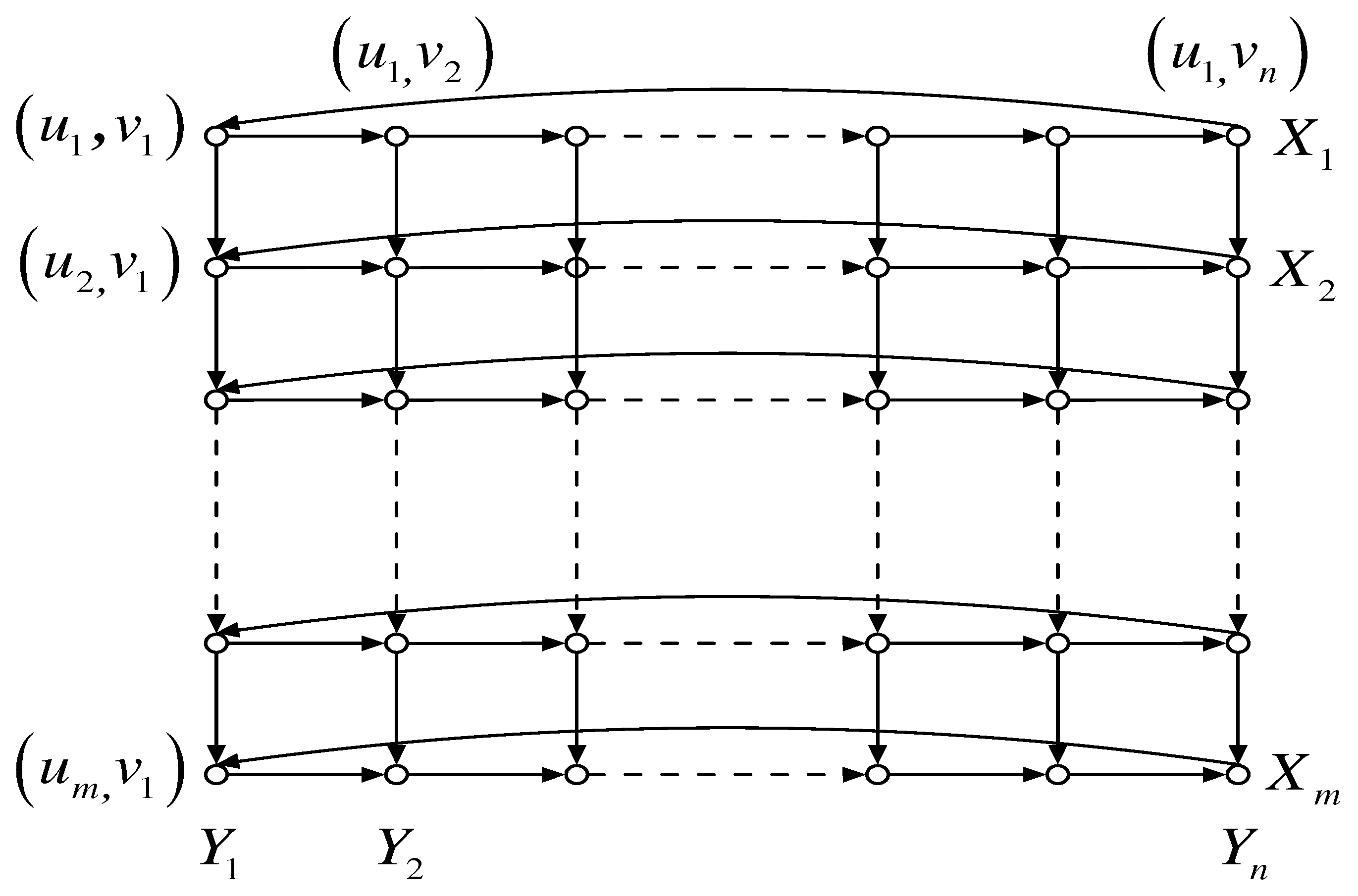
, respectively. Furthermore, in the Cartesian product
(see
Figure 1), let
for
and let
for
. In fact,
and
are isomorphic to the directed cycle
and the directed path
, respectively. Throughout this paper, for each vertex
in
, the subscript
i is taken modulo
n. Hence, if
and
k is the smallest positive integer such that
, then
.
Domination and its variations in graphs have been widely investigated as they have many applications in the real word and other disciplines such as computer networks and location theory, see [
2,
3,
4,
5]. The signed domination is one variation of domination and is now well studied in the literature. The study of signed domination of undirected graphs was initiated by Dunbar et al. in [
6]. Then, many authors paid much attention to signed domination of graphs, see [
7,
8,
9,
10,
11,
12,
13,
14,
15] and elsewhere. The signed domination of graph has some applications, for example, this concept can also serve as a model of social networks in which global decisions must be made similar to that exhibited in [
10]. In [
16], Zelinka generalizes this concept to digraphs. For a two-valued function
, the
weight of
f is
. Formally, a two-valued function
is said to be a
signed dominating function (SDF) if
for each vertex
. The
signed domination number of
D, denoted by
, is the minimum weight among all signed dominating functions of
D. Signed domination of digraphs was studied by several authors including [
16,
17,
18]. Throughout this paper, if
f is a signed dominating function of
D, then we let
P and
M denote the sets of those vertices in
D which are assigned under
f the value 1 and
, respectively. Hence
and
.
Product graphs are considered in order to gain global information from the factor graphs [
19]. Many interesting wireless networks are based on product graphs with simple factors, such as paths and cycles. In particular, any square grid (resp., torus) is the Cartesian product of two paths (resp., cycles) [
20]. The domination numbers of Cartesian product of two directed paths (resp., cycles) have been recently determined by several authors [
21,
22,
23,
24,
25,
26,
27]. Even more recently, Zhang and Shaheen [
28] determined the exact value of signed domination number
on Cartesian product
and
for any
and
, and Wang et al. [
29] solved the remaining cases.
In this paper, we continue to study the signed domination number of and obtain its exact value for any positive integers m and n.
2. Signed Domination Number of
In this section we determine the exact values of signed domination number of Cartesian product
for any
and
. Notice that
. In [
16], Zelinka obtained that
. Thus, in what follows, we may assume that
in the Cartesian product
. We begin with one lemma that will be useful in the proof of our main results.
Lemma 1. Let f be a SDF of. The following statements are true:
- (1)
.
- (2)
For,.
- (3)
For,.
- (4)
For,.
Proof. The statements (1) and (2) are trivial by the definition of SDF.
(3) If , then for some integer . Suppose on the contrary that there exists some such that . Then at least one of and holds. Without loss of generality, assume that , where . By the definition of SDF, . Thus , a contradiction. Therefore, . For the cases that or , one can reach the same contradictions by applying the argument similar to that above. Consequently, the statement (3) is true.
(4) If
, then
for some integer
. Assume that
is false for
. Then there exists some
such that
. Hence it follows that at least one of
,
and
is true. Suppose that
, where
. Then
and
by the definition of SDF. Thus
, which is a contradiction. This implies that either
or
. Without loss of generality, assume that
, where
. Let
, where
. If
, then
. By the statement (2),
, a contradiction again. So
. Let
,
, and
, where
. By the definition of SDF,
. Since
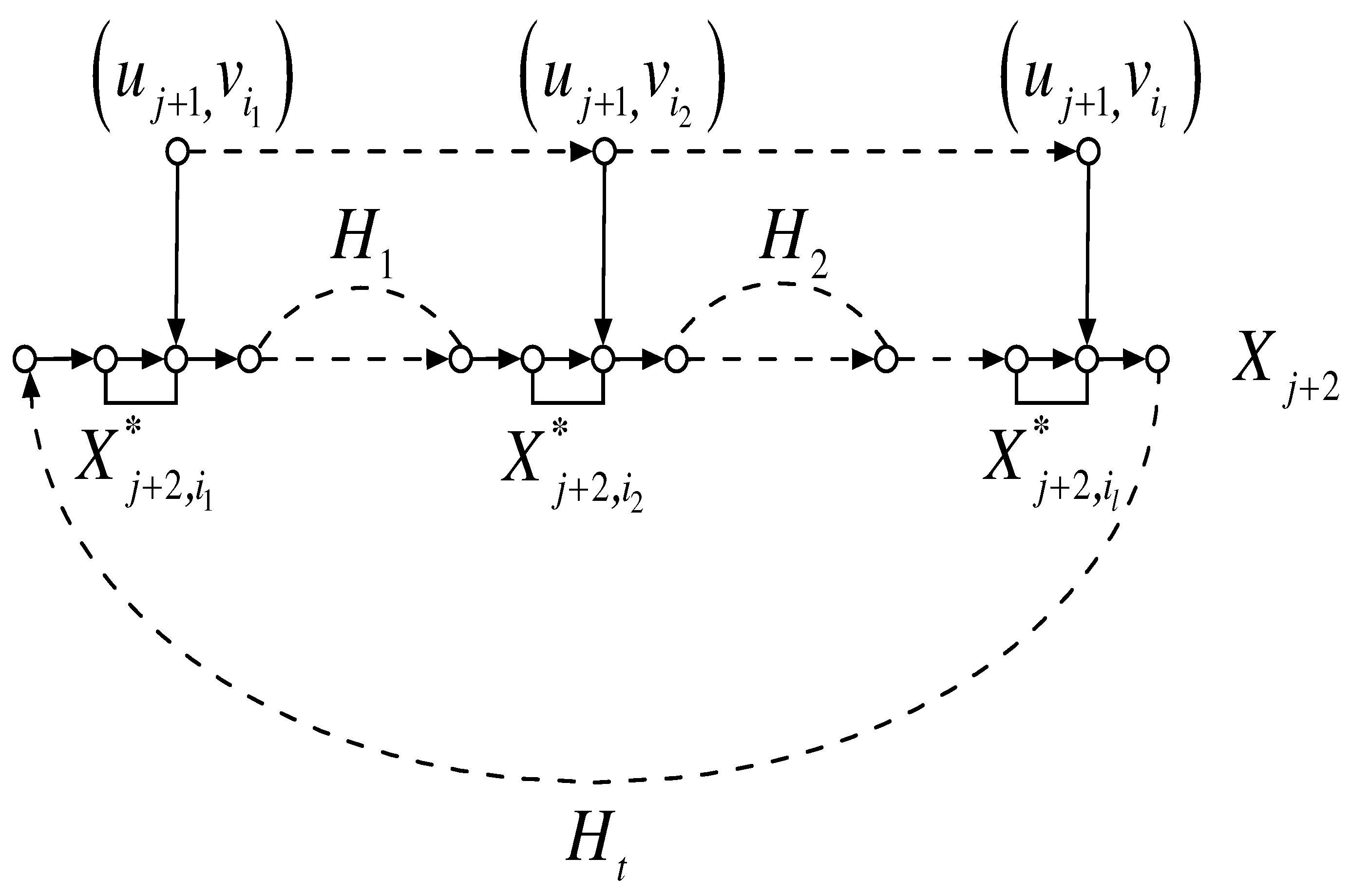
, it follows that
would be divided into some directed segments (that is, these directed segments are all isomorphic to directed paths) by
l pairs of vertices
,
,…,
. Without loss of generality, assume that there are
t such directed segments, denoted by
, where
(The directed segments
’s of
are shown in
Figure 2). Then each segment
contains at most
vertices which are assigned under
f the value
by the definition of SDF, where
. Thus
as
. Notice that
, that is,
. Then
, which is a contradiction. Consequently, the statement (4) is true for the case when
. By a similar argument above, one can obtain the same contradictions for the cases when
or
. Hence the statement (4) holds. This completes the proof of Lemma 1. □
Next we shall give our main results in this paper. The methods to prove the following theorems are similar. First we present the upper bound on by constructing signed dominating function for with weight attaining the upper bound, then we establish the lower bound on by Lemma 1, moreover, the lower bound coincides with the upper bound. Thus the exact value of is determined.
Proof. Let . Define by assigning to each vertex of the value while to each vertex of the value 1. It is easy to check that f is a SDF of with weight . If (, respectively), then (, respectively), and (, respectively) by Lemma 1 (1) and (2). This implies that (, respectively) when (, respectively). This completes the proof of Theorem 1. □
Theorem 2. For any integerssuch that, Proof. Suppose that for some integer . We next consider the following cases to complete the proof of Theorem 2.
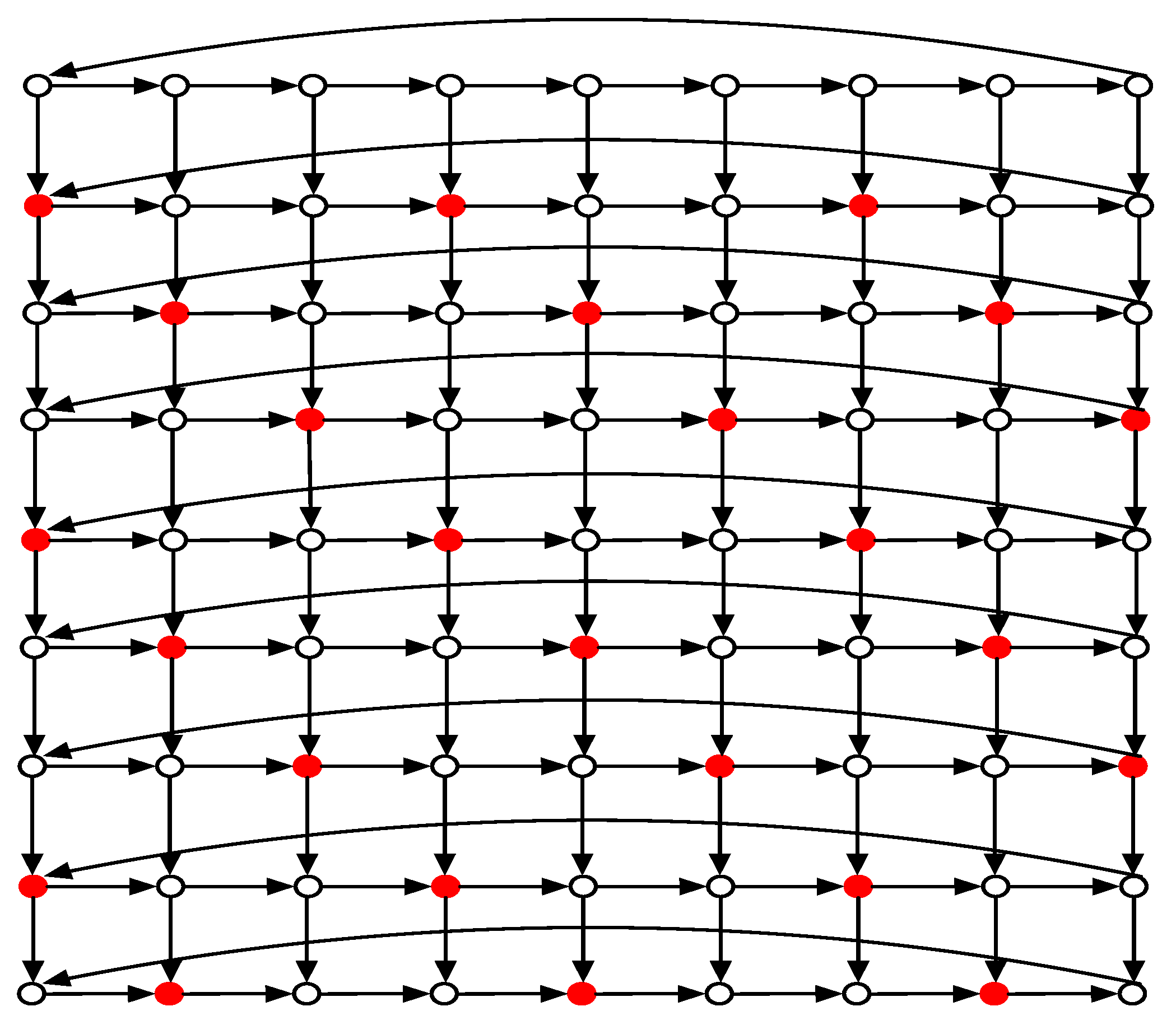
Case 1.. Then
for some integer
. We first show that
by constructing a SDF of
with weight
. Let
,
for
, and
for
. Define
by assigning to each vertex of
the value
while to each vertex of
the value 1. It is easy to verify that
f is a SDF of
with weight
(The SDF
f of
is shown in
Figure 3). Thus
. By Lemma 1 (3) and (4), we have
and
for every
, and so
from Lemma 1 (1). Then
, which implies that
.
Case 2.. Then
for some integer
. We first prove that
by establishing a SDF of
with weight
. Set
,
and
for
. Define
as follows: each vertex of
is assigned the value
while each vertex of
is assigned the value 1. It is not hard to see that
g is a SDF of
with weight
(The SDF
g of
can be obtained by restricting
f defined in Case 1 on
, which is depicted in
Figure 3). Thus
. For each
, it follows from Lemma 1 (4) that
. According to Lemma 1 (1), we have
. Hence
. This implies that
.
Case 3.. Then
for some integer
. We first demonstrate that
by giving a SDF of
with weight
. We write
for
,
and
for
. Assigning to all vertices of
the value
and to all other vertices the value 1, we produce a SDF
h of
with weight
(The SDF
h of
can be obtained by restricting
f defined in Case 1 (see
Figure 3) to
). So
. According to Lemma 1 (3) and (4), we obtain
,
and
for every
. This means that
by Lemma 1 (1). Therefore,
, implying that
. This completes the proof of Theorem 2. □
Theorem 3. For any positive integerssuch that, Proof. Suppose that for some integer . We first prove that Theorem 3 is true when . Let for . Define by assigning to each vertex of the value while to each vertex of the value 1. It is easy to check that f is a SDF of with weight . Then or when or . By Lemma 1 (1) and (3), if (, respectively), then we have (, respectively), and so (, respectively). This implies that or when or . We next assume that and proceed the proof of Theorem 3 by considering two cases.
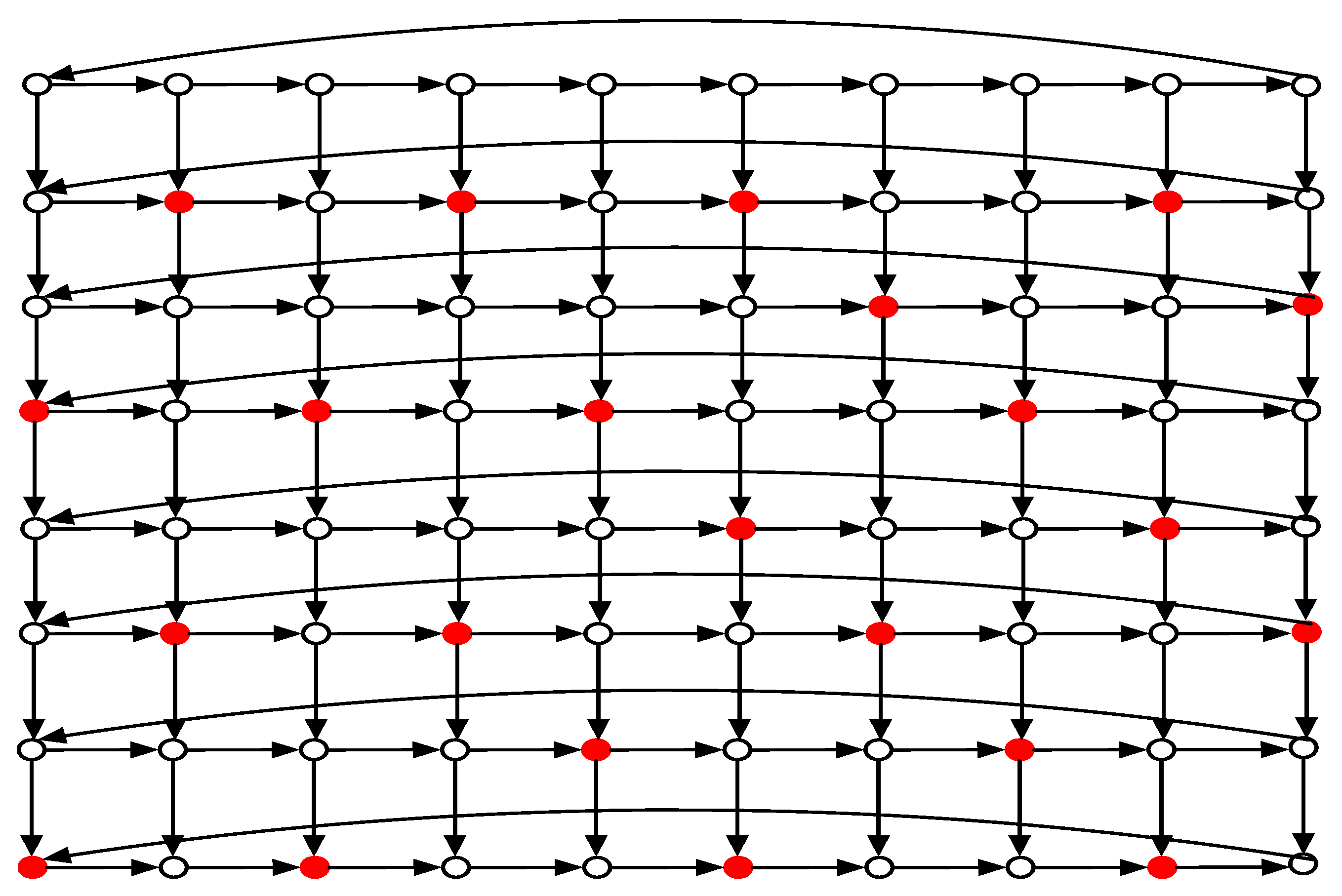
Case 1.. Then
for some integer
. We first show that
by constructing a SDF of
with weight
. Set
for
and
for
. Define
as follow: each vertex of
is assigned the value
while each vertex of
is assigned the value 1. It is not hard to verify that
g is a SDF of
with weight
(The SDF
g of
is shown in
Figure 4). Thus
. By Lemma 1 (3) and (4), we have
and
for every
, and so
from Lemma 1 (1). Then
, which implies that
.
Case 2.. Then
for some integer
. We first demonstrate that
by establishing a SDF of
with weight
. We write
for
and
for
. Assigning to all vertices of
the value
, and to all other vertices the value 1, we produce a SDF
h of
with weight
(The SDF
h of
can be obtained by restricting
g defined in Case 1 (see
Figure 4) to
). So
. For every
, it follows from Lemma 1 (3) that
. This derives that
by Lemma 1 (1). Therefore,
, implying that
. This completes the proof of Theorem 3. □
Theorem 4. For any positive integerssuch that, Proof. Suppose that for some integer . We first show that Theorem 4 is true when . Define by assigning to each vertex of the value while to each vertex of the value 1. It is easy to check that f is a SDF of with weight . Then or when or . By Lemma 1 (1) and (3), if (, respectively), then we have (, respectively), and so (, respectively). This implies that or when or . We next assume that and consider two cases to complete the proof of Theorem 4.
Case 1.. Then
for some integer
. We first prove that
by constructing a SDF of
with weight
. Let
for
and
for
. Define
as follow: each vertex of
is assigned the value
while each vertex of
is assigned the value 1. It is not hard to verify that
g is a SDF of
with weight
(The SDF
g of
is shown in
Figure 5). Thus
. By Lemma 1 (3) and (4), we have
and
for every
. So
according to Lemma 1 (1). Then
, which implies that
.
Case 2.. Then
for some integer
. We first demonstrate that
by establishing a SDF of
with weight
. We write
for
and
for
. Assigning to all vertices of
the value
, and to all other vertices the value 1, we produce a SDF
h of
with weight
(The SDF
h of
can be obtained by restricting
g defined in Case 1 (see
Figure 5) to
). So
. For every
, it follows from Lemma 1 (3) that
. This means that
by Lemma 1 (1). Therefore,
, implying that
. This completes the proof of Theorem 4. □