Hyperhomographies on Krasner Hyperfields

Abstract

In this paper, we introduce generalized homographic transformations as hyperhomographies over Krasner hyperfields.These particular algebraic hyperstructues are quotient structures of classical fields modulo normal groups. Besides, we define some hyperoperations and investigate the properties of the derived hypergroups and $H_v$-groups associated with the considered hyperhomographies. They are equipped hyperhomographies obtained as quotient sets of nondegenerate hyperhomographies modulo a special equivalence. Thus the symmetrical property of the equivalence relations plays a fundamental role in this constructions.

1. Introduction

In a recently published paper [1], the authors have initiated the study of elliptic hypercurves defined on Krasner hyperfields, generalizing the elliptic curves over fields. The main idea consists in substituting the field with a hyperfield, in particular with the associated quotient Krasner hyperfield. The power of this algebraic hyperstructure has been already used in solving different problems in affine algebraic schemes [2], theory of arithmetic functions [3], tropical geometry [4], algebraic geometry [5], etc. The quotient Krasner hyperfield is practically the quotient $\overline{F}=F/G$ of a classical field F by any normal subgroup G of the multiplicative part $(F\setminus \{0\},·)$. It was introduced by Krasner in 1983 [6] and investigated from the hyperalgebraic point of view mostly by Massouros [7] around 1985. In this new environment, the definition of an elliptic curve over a field F can be naturally extended to the definition of an elliptic hypercurve over a quotient Krasner hyperfield. Besides the group operation on the set of elliptic curves is extended to a hyperoperation on a family of elliptic hypercurves. The properties of the associated hypergroup have been investigated also in relation with the Berardi’s cryptographic system [8].

The study developed in this paper goes in the same direction as our recent study. This time we extend a particular quadratic equation in two variables from a field F to a Krasner hyperfield $F/G$. It is well known that a conic section, which is a curve obtained as the intersection between the surface of a cone and a plane, can be algebraically represented as a quadratic equation with coefficients in a filed, i.e., $g(x,y)=a{x}^2+bxy+c{y}^2+dx+ey+f=0$. If $a=c=0$ and $b\ne 0$, the equation $g(x,y)=0$ models a homographic transformation. Generally, after a suitable change of variables, a homographic transformation $y=\frac{ax+b}{cx+d}$, with $ad-bc\ne 0$, can be written in the form $(X-A)(Y-B)=1$, where $X=x$, $Y=\frac{1}{\alpha }y$, where $\alpha =\frac{bc-ad}{c^2}\ne 0$, $A=-\frac{d}{c}$, and $B=\frac{a}{\alpha c}$ are elements in the field F. Equivalently, a homography transformation is given by a function $y=f_{a,b}\left(x\right)=b+\frac{1}{x-a}$, with $a,b$ elements in a field F. The aim of this paper is to generalize the homography transformation from the field F to the Krasner hyperfield $\overline{F}$. First, we generalize the reduced quadratic forms on Krasner hyperfields. This investigation leads us to introduce the notion of conic hypersection on a Krasner hyperfield. Secondly, using hyperconics, we define some hyperoperations and the associated hyperstructures give us the possibility of studying simultaneously some conics. As in our previous research paper [1], the results can be also applied in cryptography in relation with the Berardi’s cryptographic system [8].

2. Preliminaries

We recall here some basic notions of conics and hyperstructures theory also we fix the notations used in this paper. We assign the readers to these topics in the following fundamental books [9,10,11].

2.1. Conic Sections

A conic is a plane affine curve of degree 2, defined by an irreducible polynomial $g(x,y)=a{x}^2+bxy+c{y}^2+dx+ey+f=0$ with coefficients in a field F. Based on the number of the points at infinity (this number can be 2, 1, or 0), the irreducible conics are divided in three categories: hyperbola, parabola and ellipse. Certain sets of points on curves can form an algebraic structure, and till now it is very well known the group structure. Generally the group low on conics is defined over a field F, following the rule illustrated in Figure 1 or Figure 2. In particular, if we take $\mathcal{O}$ an arbitrary point on the conic, then for two arbitrary points p and q on the conic, their sum $p+q$ is obtained as the second point of the intersection with the conic of the parallel line through $\mathcal{O}$ to the line joining p and q. In this case $\mathcal{O}$ is the identity element of the group.

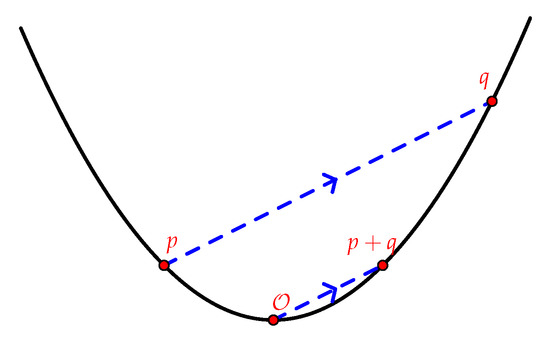
Figure 1. Addition between two points on a curve when the identity element belongs to the curve.

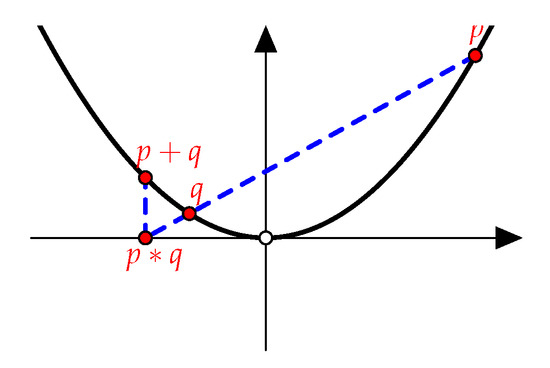
Figure 2. Addition between two points on a curve when the identity element is at infinity.

If we consider now that the identity element $\mathcal{O}$ is at infinity, then the sum $p+q$ of two arbitrary points p and q on the conic is the image on the conic of the point obtained as intersection with the x-axis of the line passing through p and q, as shown in Figure 2.

Example 1.

Consider $f\left(x\right)=x^2$ over the finite field $F={\mathbb{Z}}_5$. Then we have a parabola in F and the Cayley table of its points $Q_{{}_f}\left(F\right)=\{\mathcal{O},(1,1),(2,4),(3,4),(4,1)\}$ where, $\mathcal{O}=(0,0)$ is the identity element of the group, is as follows.

If we take the identity element $\mathcal{O}$ at infinity, then the group operation is calculated as in the following Cayley table:

The geometrical interpretation of the associativity of the group law is equivalent with a special case of Pascal’s theorem, which is a very special case of Bezout’s theorem.

Theorem 1.

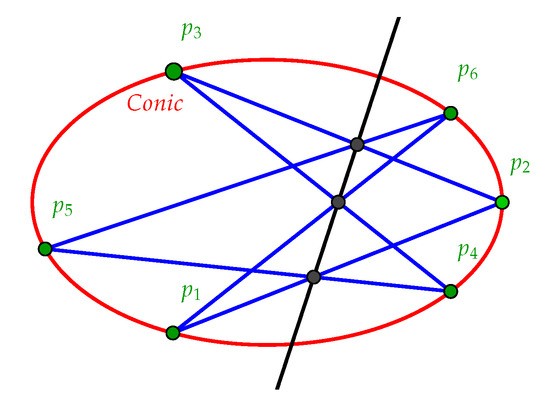
For any conic and any six points $p_1,p_2,\dots ,p_6$ on it, the opposite sides of the resulting hexagram, extended if necessary, intersect at points lying on some straight line. More specifically, let $L(p,q)$ denote the line through the points p and q. Then the points $L(p_1,p_2)\cap L(p_4,p_5)$, $L(p_2,p_3)\cap L(p_5,p_6)$, and $L(p_3,p_4)\cap L(p_6,p_1)$ lie on a straight line, called the Pascal line of the hexagon (see Figure 3).

Figure 3. Pascal’s theorem.

2.2. Krasner Hyperrings and Hyperfields

In this section we briefly recall the main definitions and properties of hyperrings and hyperfields, focussing on the concept of Krasner hyperfield.

Let H be a non-empty set and ${\mathcal{P}}^{\ast }\left(H\right)$ be the set of all non-empty subsets of H. Let ∘ be a hyperoperation (or join operation) on H, that is, a function from the cartesian product $H\times H$ into ${\mathcal{P}}^{\ast }\left(H\right).$ The image of the pair $(a,b)\in H\times H$ under the hyperoperation ∘ in ${\mathcal{P}}^{\ast }\left(H\right)$ is denoted by $a\circ b$. The join operation can be extended in a natural way to subsets of H as follows: for non-empty subsets $A,B$ of H, define $A\circ B={\displaystyle \bigcup _{a\in A,b\in B}}a\circ b$. The notation $a\circ A$ is used for $\left\{a\right\}\circ A$ and $A\circ a$ for $A\circ \left\{a\right\}$. Generally, we mean $H^k=H\times H\times \dots \times H$ (k times), for all $k\in \mathbb{N}$ and also the singleton $\left\{a\right\}$ is identified with its element a. The hyperstructure $(H,\circ )$ is called a semihypergroup if the hyperoperation is associative, i.e., $(a\circ b)\circ c=a\circ (b\circ c)$ for all $a,b,c\in H$, which means that

$${\displaystyle \bigcup _{u\in a\circ b}}u\circ c={\displaystyle \bigcup _{v\in b\circ c}}a\circ v.$$

A semihypergroup $(H,\circ )$ is called a hypergroup if the reproduction law holds: $a\circ H=H\circ a=H$, for all $a\in H$.

Definition 1.

Let $(H,\circ )$ be a hypergroup and $\varnothing \ne K\subset H$. We say that $(K,\circ )$ is a subhypergroup of H, denoted by $K\le H,$ if for all $x\in K$ we have $K\circ x=K=x\circ K$.

An element $e_r$ (respectively $e_l$) of H is called a right identity (respectively left identity $e_l$) if for all $a\in H$, $a\in a\circ e_r$ (respectively $a\in e_l\circ a$). An element e is called a two side identity, or for simplicity an identity if, for all $a\in H$, $a\in a\circ e\cap e\circ a.$ A right identity $e_r$ (resp. left identity $e_l$) of H is called a scalar right identity (respectively scalar left identity) if for all $a\in H$, $a=a\circ e_r$ (respectively $a=e_l\circ a$). An element e is called a scalar identity if for all $a\in H$, $a=a\circ e=e\circ a.$ An element $a^{\prime }\in H$ is called a right inverse (respectively left inverse) of a in H if $e_r\in a\circ a^{\prime }$, for some right identity $e_r$ in H (respectively $e_l\in a^{\prime }\circ a$, for some left identity $e_l$). An element $a^{\prime }\in H$ is called an inverse of $a\in H$ if $e\in a^{\prime }\circ a\cap a\circ a^{\prime },$ for some identity e in $H.$ We denote the set of all right inverses, left inverses and inverses of $a\in H$ by $i_r\left(a\right),$ $i_l\left(a\right),$ and $i\left(a\right),$ respectively. In addition, if H has a scalar identity, and the inverse of $a\in H$ exists, we indicate it by $a^{-1}.$

Definition 2.

A hypergroup H is called reversible, if the following conditions hold:

(i) 

H has at least one identity e;

(ii) 

every element x of H has at least one inverse, that is $i\left(x\right)\ne \varnothing$;

(iii) 

$x\in y\circ z$ implies that $y\in x\circ z^{\prime }$ and $z\in y^{\prime }\circ x$, where $z^{\prime }\in i\left(z\right)$ and $y^{\prime }\in i\left(y\right)$.

Definition 3.

Suppose that $(H,·)$ and $(K,\circ )$ are two hypergroups. A function $f:H\to K$ is called a homomorphism if $f(a·b)\subseteq f\left(a\right)\circ f\left(b\right),$ for all a and b in H. We say that f is a good homomorphism if for all a and b in H, there is $f(a·b)=f\left(a\right)\circ f\left(b\right)$. Moreover, $(H,·)$ and $(K,\circ )$ are isomorphic, denoted by $H\cong K$, if f is a bijective good homomorphism.

An exhaustive review for the theory of hypergroups appears in [9], while the book [12] contains a wealth of applications. The more general algebraic structure that satisfies the ring-like axioms is the hyperring. There are different kinds of hyperrings. The most general one, introduced by Vougiouklis [13], has both addition and multiplication defined as hyperoperations. If only the multiplication is a hyperoperation, then we talk about multiplicative hyperrings [14,15]. If only the addition + is a hyperoperation and the multiplication · is a usual operation, then we say that R is an additive hyperring. A special case of this type is the hyperring introduced by Krasner [6]. An exhaustive review for the theory of hyperrings appears in [16,17,18,19].

Definition 4

([6]). A Krasner hyperring is an algebraic structure $(R,+,·)$ which satisfies the following axioms:

(1) 

$(R,+)$ is a canonical hypergroup, i.e.,

(i) 

for every $x,y,z\in R,x+(y+z)=(x+y)+z,$

(ii) 

for every $x,y\in R,x+y=y+x,$

(iii) 

there exists $0\in R$ such that $0+x=\left\{x\right\}$ for every $x\in R$,

(iv) 

for every $x\in R$ there exists a unique element $x^{\prime }\in R$ such that $0\in x+x^{\prime }$; (we shall write $-x$ for $x^{\prime }$ and we call it the opposite of x.)

(v) 

$z\in x+y$ implies that $y\in z-x$ and $x\in z-y$.

(2) 

$(R,·)$ is a semigroup having zero as a bilaterally absorbing element, i.e., $x·0=0·x=0$.

(3) 

The multiplication is distributive with respect to the hyperoperation +.

A Krasner hyperring $(R,+,·)$ is called commutative, if $(R,·)$ is a commutative semigroup with unit element, i.e., a monoid. A Krasner hyperring is called a Krasner hyperfield, if the multiplicative part $(R\setminus \{0\},·)$ is a group.

In the following we recall the first construction of a Krasner hyperfield, as a quotient structure of a classical field by a normal subgroup. Let $(F,+,·)$ be a field and G be a normal subgroup of $(F^{\ast },·),$ where $F^{\ast }=F\setminus \left\{0\right\}.$ Take $\frac{F}{G}=\{aG\mid a\in F\}$ with the hyperoperation and the multiplication defined by:

(i)

$aG\oplus bG=\left\{cG\right|c\in aG+bG\},$

(ii)

$aG\odot bG=abG,$

for all $aG,bG\in \frac{F}{G}$. Then $(\frac{F}{G},\oplus ,\odot )$ is a hyperfield. From now on, we denote $\overline{a}=aG,$ for all $aG\in \frac{F}{G}$ and the constructed hyperfield $(\frac{F}{G},\oplus ,\odot )$ by $\overline{F},$ and call it the Krasner hyperfield. Moreover, we denote the inverse of $\overline{a}$ relative to ⊕ by $⊝\overline{a}$ and, for $\overline{a}\ne \overline{0},$ the multiplicative inverse ${\overline{a}}^{-1}$ by ${\displaystyle \frac{1}{\overline{a}}}$. Besides, we will use the notation $\overline{S}=\left\{\overline{s}\right|s\in S\}$ and $\overline{T}=\left\{\overline{t}\right|t\in T\}$ for all $S\subseteq F,T\subseteq F^2$.

3. Hyperhomographies

In this section we define the notion of hyperhomography on a Krasner hyperfield, as a quotient structure of a classical field by a normal subgroup. Using it, we introduce some hyperoperations and investigate the properties of the associated hypergroups.

Definition 5.

Let $\overline{F}$ be the Krasner hyperfield associated with the field F and $(\overline{A},\overline{B})\in {\overline{F}}^2$. Define the generalized homography transformation on F as $\overline{1}\in (\overline{x}⊝\overline{A})\odot (\overline{y}⊝\overline{B})$ on $\overline{F}$, and call it the hyperhomography relation. We call the set $H_{\overline{A},\overline{B}}\left(\overline{F}\right)=\{(\overline{x},\overline{y})\in {\overline{F}}^2\mid \overline{1}\in (\overline{x}⊝\overline{A})\odot (\overline{y}⊝\overline{B})\}$ hyperhomography, while $H_{a,b}\left(F\right)=\{(x,y)\in F^2\mid y=f_{a,b}\left(x\right)=b+\frac{1}{x-a}\}$ is a homography, for all $a\in \overline{A}$ and $b\in \overline{B}$.

Notice that the hyperhomography $H_{\overline{A},\overline{B}}\left(\overline{F}\right)$ is a generalization of a homography $H_{a,b}\left(F\right)$, because $(x,y)\in H_{a,b}\left(F\right)$ is equivalent with $y=f_{a,b}\left(x\right)=b+\frac{1}{x-a}$, i.e., $(x-a)(y-a)=1$. The classical operations on the field F have been extended to the hyperoperation ⊕ and operation ⊙ on $\overline{F}$, where by $\overline{x}⊝\overline{A}$ we denote the hyperaddition between $\overline{x}$ and the opposite of $\overline{A}$ with respect to the hyperoperation ⊕. Besides, since the result of a hyperoperation is a set, the equality relation in the definition of a homography is substitute by a "belongingness" relation in the definition of a hyperhomography.

Moreover denote $H_{\overline{A},\overline{B}}\left(F\right)={\displaystyle \bigcup _{a\in \overline{A},b\in \overline{B}}}{H}_{a,b}\left(F\right)$ and $H_{a,b}\left(\overline{F}\right)=\overline{H_{a,b}\left(F\right)}=\{(\overline{x},\overline{y})\mid (x,y)\in H_{a,b}\left(F\right)\}$, for all $a\in \overline{A},b\in \overline{B}.$ It follows that $\overline{H_{\overline{A},\overline{B}}\left(F\right)}={\displaystyle \bigcup _{a\in \overline{A},b\in \overline{B}}}{H}_{a,b}\left(\overline{F}\right)$.

Theorem 2.

The relation between homographies and hyperhomographies is given by the following identity $H_{\overline{A},\overline{B}}\left(\overline{F}\right)=\overline{H_{\overline{A},\overline{B}}\left(F\right)}.$

Proof. 

$(\Leftarrow )$. Let $\overline{(x,y)}\in \overline{H_{\overline{A},\overline{B}}\left(F\right)},$ thus there exists $(a,b)\in \overline{A}\times \overline{B}$, such that $\overline{(x,y)}=(\overline{x},\overline{y})\in H_{a,b}\left(\overline{F}\right)$, hence $(x{g}_1,y{g}_2)\in H_{a,b}\left(F\right)$ for some $g_1,g_2\in G$. Then $(x{g}_1-a)(y{g}_2-b)=1$ and the following implications hold:

$$\begin{array}{cc}\hfill 1=(x{g}_1-a)(y{g}_2-b)& ⟹\left\{\begin{array}{cc}\overline{1}\hfill & =\overline{(x{g}_1-a)(y{g}_2-b)}\hfill \\ \hfill & =\overline{(x{g}_1-a)}\odot \overline{(y{g}_2-b)}\hfill \\ \hfill & \subseteq (\overline{x}-\overline{a})\odot (\overline{y}-\overline{b})\hfill \\ \hfill & =(\overline{x}⊝\overline{a})\odot (\overline{y}⊝\overline{b})\hfill \end{array}\right.\hfill \\ \hfill & ⟹\overline{1}\in (\overline{x}⊝\overline{A})\odot (\overline{y}⊝\overline{B})\hfill \\ \hfill & ⟹(\overline{x},\overline{y})\in H_{\overline{A},\overline{B}}\left(\overline{F}\right)\hfill \\ \hfill & ⟹\overline{(x,y)}\in H_{\overline{A},\overline{B}}\left(\overline{F}\right),\hfill \end{array}$$

so

$$\overline{H_{\overline{A},\overline{B}}\left(F\right)}\subseteq H_{\overline{A},\overline{B}}\left(\overline{F}\right).$$

$(\Rightarrow )$. Conversely, suppose that $(\overline{x},\overline{y})\in H_{\overline{A},\overline{B}}\left(\overline{F}\right),$ then the following implications hold, too:

$$\begin{array}{ll}(\overline{x},\overline{y})\in H_{\overline{A},\overline{B}}\left(\overline{F}\right)& ⟹\overline{1}\in (\overline{x}⊝\overline{A})\odot (\overline{y}⊝\overline{B})\\ & ⟹\overline{1}\in (\overline{x}\oplus \overline{(-A)})\odot (\overline{y}\oplus \overline{(-B)})\\ & ⟹\overline{1}\in \overline{(x-\overline{A})}\odot \overline{(y-\overline{B})}\\ & ⟹\overline{1}\in \overline{(x-\overline{A})(y-\overline{B})}\\ & ⟹\overline{1}=\overline{(x-a)(y-b)},forsome(a,b)\in \overline{A}\times \overline{B}\\ & ⟹\overline{1}=\overline{(x-a)}\odot \overline{(y-b)}\\ & ⟹\overline{(y-b)}={\overline{(x-a)}}^{-1}\\ & ⟹\overline{(y-b)}=\overline{{(x-a)}^{-1}}\\ & ⟹\overline{(y-b)}=\overline{\left({\displaystyle \frac{1}{x-a}}\right)}\\ & ⟹(y-b)g={\displaystyle \frac{1}{x-a}}forsomeg\in G\\ & ⟹yg=b^{\prime }+{\displaystyle \frac{1}{x-a}},b^{\prime }=bg\in \overline{B}\\ & ⟹(x,yg)\in H_{a,b^{\prime }}\left(F\right)\\ & ⟹(\overline{x},\overline{y})=\overline{(x,gy)}\in \overline{H_{a,b^{\prime }}\left(F\right)}=H_{a,b^{\prime }}\left(\overline{F}\right)\\ & ⟹(\overline{x},\overline{y})\in {\displaystyle \bigcup _{a\in \overline{A},b\in \overline{B}}}{H}_{a,b}\left(\overline{F}\right),\\ & ⟹(\overline{x},\overline{y})\in \overline{H_{\overline{A},\overline{B}}\left(F\right)},\end{array}$$

therefore $H_{\overline{A},\overline{B}}\left(\overline{F}\right)\subseteq \overline{H_{\overline{A},\overline{B}}\left(F\right)}$ and consequently $H_{\overline{A},\overline{B}}\left(\overline{F}\right)=\overline{H_{\overline{A},\overline{B}}\left(F\right)}$. □

Thanks to Theorem 2, we call the set $H_{\overline{A},\overline{B}}\left(F\right)$ the hyperhomography on F, while the set $H_{a,b}\left(\overline{F}\right)$ is a homography on $\overline{F}$.

Example 2.

Let $F={\mathbb{Z}}_5$ be the field of all integers modulo $5$ and $G=\{1,4\}⩽F^{\ast }$. Thus the quotient set $F^{\ast }/G$ is $\overline{F}=\left\{\overline{0},\overline{1},\overline{2}\right\}$ and the hyperaddition $\oplus$ and the multiplication $\odot$ are defined on $\overline{F}$ as follows:where $\overline{0}=\left\{0\right\}$, $\overline{1}=\{1,4\}$ and $\overline{2}=\{2,3\}$.

Consider now the hyperhomography

$$H_{\overline{0},\overline{1}}\left(\overline{F}\right)=\{(\overline{x},\overline{y})\in {\overline{F}}^2|\overline{1}\in \overline{x}\odot (\overline{y}⊝\overline{1})\}=\{(\overline{1},\overline{0}),(\overline{1},\overline{2}),(\overline{2},\overline{1}),(\overline{2},\overline{2})\},$$

and the homographies

$$H_{0,1}\left(F\right)=\{(x,y)\in F^2\mid y=1+{\displaystyle \frac{1}{x}}\}=\{(1,2),(2,4),(3,3),(4,0)\},$$

$$H_{0,4}\left(F\right)=\{(x,y)\in F^2\mid y=4+{\displaystyle \frac{1}{x}}\}=\{(1,0),(2,2),(3,1),(4,3)\}.$$

Then it follows that

$$H_{0,1}\left(\overline{F}\right)=\overline{H_{0,1}\left(F\right)}=\{(\overline{1},\overline{0}),(\overline{1},\overline{2}),(\overline{2},\overline{1}),(\overline{2},\overline{2})\}=\overline{H_{0,4}\left(F\right)}=H_{0,4}\left(\overline{F}\right)$$

and therefore

$$H_{\overline{0},\overline{1}}\left(\overline{F}\right)=H_{0,1}\left(\overline{F}\right)\cup H_{0,4}\left(\overline{F}\right),$$

as stated by Theorem 2.

Definition 6.

A hyperhomography $H_{{}_{\overline{A},\overline{B}}}\left(F\right)$ in $F^2$ is called nondegenerate, if the following conditions hold, respectively:

(i) 

for all $a\in \overline{A},b\in \overline{B}$, if $\nu =a-b^{-1}\in F$, then $(\nu ,0)$ can be omitted from $H_{a,b}\left(F\right)$,

(ii) 

for all $a,c\in \overline{A}$ and $b,d\in \overline{B},$ there is $H_{a,b}\left(F\right)\cap H_{c,d}\left(F\right)\ne \varnothing ⟹H_{a,b}\left(F\right)=H_{c,d}\left(F\right),$

(iii) 

for all $a\in \overline{A},b\in \overline{B},$ the element $(a,\infty )$ can be added to $H_{a,b}\left(F\right),$ where ∞ is an element outside of $F.$

By consequence, under the same conditions, also $H_{{}_{\overline{A},\overline{B}}}\left(\overline{F}\right)=\overline{H_{\overline{A},\overline{B}}\left(F\right)}$ is called a nondegenerate hyperhomography in ${\overline{F}}^2$.

For a nondegenerate hyperhomography in $F^2$, we fix some new notations: $F_{{}_{\infty }}=F\cup \{\infty \}$, ${\overline{F}}_{{}_{\infty }}=\overline{F}\cup \{\infty \}$ and $\overline{(a,\infty )}=(\overline{a},\infty )$, for any $a\in F$.

Example 3.

If we go back to Example 2 and use the concepts in Definition 6, then we can omit $(4,0)$ from $H_{0,1}\left(F\right)$ and $(1,0)$ from $H_{0,4}\left(F\right)$, respectively, and add in both sets the element $(0,\infty )$. Then $H_{0,1}\left(F\right)=\{(0,\infty ),(1,2),(2,4),(3,3)\}$ and $H_{0,4}\left(F\right)=\{(0,\infty ),(2,2),(3,1),(4,3)\}$ are nondegenerate homographies, while $H_{\overline{0},\overline{1}}\left(\overline{F}\right)=\{(0,\infty ),(\overline{1},\overline{2}),(\overline{2},\overline{1}),(\overline{2},\overline{2})\}$ is a nondegenerate hyperhomography with the property $H_{\overline{0},\overline{1}}\left(\overline{F}\right)=H_{0,1}\left(\overline{F}\right)\cup H_{0,4}\left(\overline{F}\right)$ where,

$$H_{0,1}\left(\overline{F}\right)=\overline{H_{0,1}\left(F\right)}=\{(\overline{0},\overline{\infty }),(\overline{1},\overline{2}),(\overline{2},\overline{4}),(\overline{3},\overline{3})\}=\{(0,\infty ),(\overline{1},\overline{2}),(\overline{2},\overline{1}),(\overline{2},\overline{2})\},$$

$$H_{0,4}\left(\overline{F}\right)=\overline{H_{0,4}\left(F\right)}=\{(\overline{0},\overline{\infty }),(\overline{2},\overline{2}),(\overline{3},\overline{1}),(\overline{4},\overline{3})\}=\{(0,\infty ),(\overline{2},\overline{2}),(\overline{2},\overline{1}),(\overline{1},\overline{2})\}.$$

Definition 7.

Let $H_{\overline{A},\overline{B}}\left(F\right)$ be a nondegenerate hyperhomography in $F^2$. Setting $f_{a,b}\left(a\right)=\infty$, we obtain that $(a,\infty )=(a,f_{a,b}\left(a\right))\in H_{a,b}\left(F\right)$. Define

$${\mathcal{G}}_{a,b}^x=\left\{\begin{array}{cc}\left\{x\right\},& \mathit{if}G=\left\{1\right\}\hfill \\ \{x,2a-x\},& \mathit{if}G\ne \left\{1\right\},b=0\hfill \\ \{y\in F|y=x\mathrm{or}(x-\nu )(y-\nu )={(a-\nu )}^2\},& \mathit{if}G\ne \left\{1\right\},b\ne 0,\hfill \end{array}\right.$$

for all $x\in F\setminus \left\{\nu \right\}$ and $(a,b)\in \overline{A}\times \overline{B}$, where $\nu =a-b^{-1}$.

Moreover set $\widehat{X}=\{\widehat{x}\mid x\in X\}$, where $\widehat{x}=(x,f_{a,b}\left(x\right))$, for all $(a,b)\in \overline{A}\times \overline{B}$ and $x\in X\subseteq F$.

Corollary 1.

Let $H_{\overline{A},\overline{B}}\left(F\right)$ be a nondegenerate hyperhomography in $F^2$ and G be a normal subgroup of $F^{\ast }$. If $G\ne \left\{1\right\}$ and $0\ne b\in \overline{B}$, then ${\mathcal{G}}_{a,b}^x=\{x,\frac{(ab-1)x+a(2-ab)}{bx+(1-ab)}\}.$

Proof. 

According to Definition 7, if $G\ne \left\{1\right\}$ and $0\ne b\in \overline{B}$, then $y=x$ or $(x-a+\frac{1}{b})(y-a+\frac{1}{b})=\frac{1}{b^2}$. In the second case, solving the equation we get $y=\frac{(ab-1)x+a(2-ab)}{bx+(1-ab)}$. □

In the following, for a nondegenerate hyperhomography in $F^2$, we define the lines passing through two points.

Definition 8.

Let $H_{\overline{A},\overline{B}}\left(F\right)$ be a nondegenerate hyperhomography in $F^2$. For all $a\in \overline{A},b\in \overline{B}$ and $\widehat{x_i},\widehat{x_j}\in H_{a,b}\left(F\right)$, define $L_0=\{(x,0)\mid x\in F\}$ and

$$L_{a,b}({\widehat{x}}_i,{\widehat{x}}_j)=\left\{\begin{array}{cc}\{(x,y)\in F^2|y-f_{a,b}\left(x_i\right)=\frac{f_{a,b}\left(x_j\right)-f_{a,b}\left(x_i\right)}{x_j-x_i}(x-x_i)\},\hfill & x_i\ne x_j,a\notin \{x_i,x_j\}\hfill \\ \{(x,y)\in F^2|y-f_{a,b}\left(x_i\right)=f_{a,b}^{\prime }\left(x_i\right)(x-x_i)\},\hfill & x_i=x_j\ne a\hfill \\ \left\{(x,y)\right|y\in F_{{}_{\infty }},x\in \{x_i,x_j\},x=a\iff y=\infty \},\hfill & x_i\ne x_j,a\in \{x_i,x_j\}\hfill \\ \left\{(a,y)\right|y\in F_{{}_{\infty }}\},\hfill & x_i=x_j=a,\hfill \end{array}\right.$$

where $f_{a,b}^{{}^{\prime }}$ means the formal derivative of $f_{a,b}$. In addition we call $L_{a,b}({\widehat{x}}_i,{\widehat{x}}_j)$ the line passing through the points ${\widehat{x}}_i$ and ${\widehat{x}}_j.$ Intuitively, for each $a\in F$, the line passing through $(a,\infty )$ is a vertical line. In other words, $(a,\infty )$ plays an asymptotic extension role for $f_{a,b}$.

Taking two arbitrary points ${\widehat{x}}_i,{\widehat{x}}_j$ on the homography $H_{a,b}\left(F\right)$, define $x_i{•}_{{}_{ab}}{x}_j$ by $L_0\cap L_{a,b}(\widehat{x_i},\widehat{x_j})=\left\{(x_i{•}_{{}_{ab}}{x}_j,0)\right\}.$ Using the definition of the lines $L_{a,b}(\widehat{x_i},\widehat{x_j})$ and $L_0$, for $x_i\ne a\ne x_j$ we have

$$y=0,y-f_{a,b}\left(x_i\right)=m(x-x_i)⟹x=x_i-\frac{f_{a,b}\left(x_i\right)}{m}$$

where, $m=\left\{\begin{array}{cc}\frac{f_{a,b}\left(x_j\right)-f_{a,b}\left(x_i\right)}{x_j-x_i},\hfill & \mathrm{if}{x}_i\ne x_j\hfill \\ f_{a,b}^{\prime }\left(x_i\right),\hfill & \mathrm{if}{x}_i=x_j\hfill \end{array}\right.=\left\{\begin{array}{cc}\frac{-1}{(x_i-a)(x_j-a)},\hfill & \mathrm{if}{x}_i\ne x_j\hfill \\ \frac{-1}{{(x_i-a)}^2},\hfill & \mathrm{if}{x}_i=x_j\hfill \end{array}\right.=\frac{-1}{(x_i-a)(x_j-a)}\in F^{\ast }$ and hence $x=x_i{•}_{{}_{ab}}{x}_j\in F.$ If $x_i$ or $x_j$ are equal to $a,$ according to Definition 8, we have

$$L_0\cap L_{a,b}(\widehat{x_i},\widehat{x_j})=\left\{\begin{array}{cc}\left\{(x_i,0)\right\},\hfill & \mathrm{if}{x}_i\ne a=x_j\hfill \\ \left\{(x_j,0)\right\},\hfill & \mathrm{if}{x}_i=a\ne x_j\hfill \\ \left\{\right(a,0\left)\right\},\hfill & \mathrm{if}{x}_i=a=x_j\hfill \end{array}\right.⟹x_i{•}_{{}_{ab}}{x}_j=\left\{\begin{array}{cc}{x}_i,\hfill & \mathrm{if}{x}_i\ne a=x_j\hfill \\ x_j,\hfill & \mathrm{if}{x}_i=a\ne x_j\hfill \\ a,\hfill & \mathrm{if}{x}_i=a=x_j\hfill \end{array}\right.⟹x_i{•}_{{}_{ab}}{x}_j\in F.$$

Thus $\mid L_0\cap L_{a,b}(\widehat{x_i},\widehat{x_j})\mid =1$ and $x_i{•}_{{}_{ab}}{x}_j$ is well defined, therefore we have

$$\widehat{x_i{•}_{{}_{ab}}{x}_j}=(x_i{•}_{{}_{ab}}{x}_j,f_{a,b}\left(x_i{•}_{{}_{ab}}{x}_j\right)).$$

We will better illustrate the above defined notions in the following example.

Example 4.

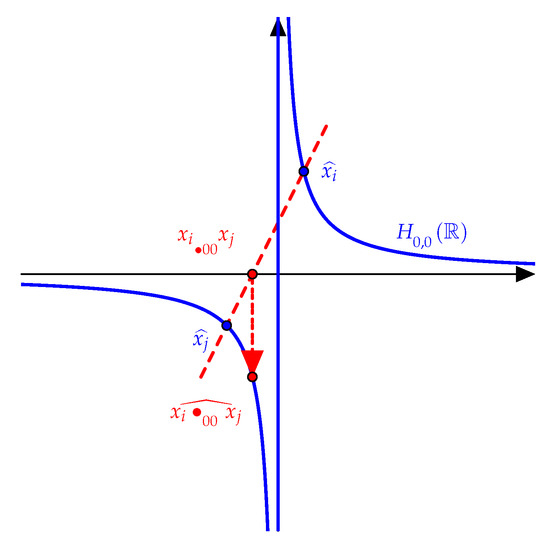
Consider the field $F=\mathbb{R}$ and the homography transformation $f_{{}_{0,0}}\left(x\right)=\frac{1}{x}$ over F, so its graph is the hyperbola $H_{0,0}\left(\mathbb{R}\right)$ represented below in Figure 4. Taking on $H_{0,0}\left(\mathbb{R}\right)$ two arbitrary points ${\widehat{x}}_i=(x_i,f_{{}_{0,0}}\left(x_i\right))$ and ${\widehat{x}}_j=(x_j,f_{{}_{0,0}}\left(x_j\right))$, we draw the line $L_{0,0}({\widehat{x}}_i,{\widehat{x}}_j)$ passing through ${\widehat{x}}_i$ and ${\widehat{x}}_j$. Then $x_i{•}_{{}_{00}}{x}_j=L_0\cap L_{0,0}({\widehat{x}}_i,{\widehat{x}}_j)$, where $L_0$ is the x-axis. Then we obtain the point $\widehat{x_i{•}_{{}_{00}}{x}_j}=(x_i{•}_{{}_{00}}{x}_j,f_{0,0}\left(x_i{•}_{{}_{00}}{x}_j\right))$ on the hyperbola $H_{0,0}\left(\mathbb{R}\right)$.

Figure 4. Hyperbola $H_{0,0}\left(\mathbb{R}\right)$.

Proposition 1.

Let $H_{\overline{A},\overline{B}}\left(F\right)$ be a nondegenerate hyperhomography in $F^2,$ and $\widehat{x_i},\widehat{x_j}\in H_{a,b}^2\left(F\right)$. Then, it follows that

$$x_i{•}_{{}_{ab}}{x}_j=b{x}_i{x}_j-(ab-1)(x_i+x_j-a).$$

Proof. 

Based on Definition 8 and on the fact that $f_{a,b}\left(x\right)=b+\frac{1}{x-a}$ and $f_{a,b}^{\prime }\left(x\right)=-\frac{1}{{(x-a)}^2}$, by simple computations, we obtain

$$\begin{array}{cc}\hfill x_i{•}_{{}_{ab}}{x}_j& =\left\{\begin{array}{cc}{\displaystyle \frac{x_i{f}_{{}_{a,b}}\left(x_j\right)-x_j{f}_{{}_{a,b}}\left(x_i\right)}{f_{{}_{a,b}}\left(x_j\right)-f_{{}_{a,b}}\left(x_i\right)}}\hfill & x_i\ne x_j,a\notin \{x_i,x_j\},\hfill \\ x_i-{\displaystyle \frac{f_{{}_{a,b}}\left(x_i\right)}{f_{{}_{a,b}}^{{}^{\prime }}\left(x_i\right)}}\hfill & x_i=x_j\ne a,\hfill \\ x_i\hfill & x_i\ne a=x_j,\hfill \\ x_j\hfill & x_j\ne a=x_i,\hfill \\ a\hfill & x_i=a=x_j\hfill \end{array}\right.\hfill \\ \hfill & =\left\{\begin{array}{cc}{x}_i+(x_i-a)(x_j-a)(b+\frac{1}{x_i-a})\hfill & x_i\ne x_j,a\notin \{x_i,x_j\}\hfill \\ x_i+(x_i-a)(x_i-a)(b+\frac{1}{x_i-a})\hfill & x_i=x_j\ne a\hfill \\ x_i\hfill & x_i\ne a=x_j\hfill \\ x_j\hfill & x_j\ne a=x_i\hfill \\ a\hfill & x_i=a=x_j\hfill \end{array}\right.\hfill \\ \hfill & =\left\{\begin{array}{cc}b{x}_i{x}_j-(ab-1)(x_i+x_j-a)\hfill & x_i\ne x_j,a\notin \{x_i,x_j\},\hfill \\ b{x}_i^2-(ab-1)(2x_i-a)\hfill & x_i=x_j\ne a,\hfill \\ x_i\hfill & x_i\ne a=x_j,\hfill \\ x_j\hfill & x_j\ne a=x_i,\hfill \\ a\hfill & x_i=a=x_j.\hfill \end{array}\right.\hfill \\ \hfill & =b{x}_i{x}_j-(ab-1)(x_i+x_j-a).\hfill \end{array}$$

 □

Remark 1. 

$(H_{a,b}\left(F\right),{•}_{{}_{ab}})$ is a homography group, for all $(a,b)\in \overline{A}\times \overline{B}$. Moreover, notice that "${•}_{{}_{ab}}$" is the group operation on the homography $H_{a,b}\left(F\right).$

On a nondegenerate hyperhomography $H_{\overline{A},\overline{B}}\left(F\right)$ in $F^2$ we introduce the equivalence relation “∼” by considering

$$(x,y)\sim (x^{\prime },y^{\prime })⟺\left\{\begin{array}{c}x=x^{\prime },\hfill \\ y=y^{\prime }\notin \{\infty \},\hfill \end{array}\right.\mathrm{or}y,y^{\prime }\in \{\infty \}$$

and denote the set of the equivalence classes of $H_{\overline{A},\overline{B}}\left(F\right)$ and $H_{a,b}\left(F\right)$ by ${\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right)$ and ${\mathcal{H}}_{a,b}\left(F\right)$, respectively. It follows that ${\displaystyle \frac{(x,y)}{\sim }}=\left\{\begin{array}{cc}(x,y),\hfill & \mathrm{if}x\notin \overline{A}\hfill \\ (\overline{A},\infty ),\hfill & \mathrm{if}x\in \overline{A}.\hfill \end{array}\right.$

Furthermore, if we introduce the notation $\mathcal{O}=\overline{A}$ and $\widehat{\mathcal{O}}=(\mathcal{O},\infty ).$ We will have $\overline{\mathcal{O}}=\mathcal{O}$, $\overline{\widehat{\mathcal{O}}}=\widehat{\mathcal{O}}$ and $\overline{{\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right)}={\mathcal{H}}_{\overline{A},\overline{B}}\left(\overline{F}\right).$

Thus ${\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right)$ and ${\mathcal{H}}_{\overline{A},\overline{B}}\left(\overline{F}\right)$ are called the equipped hyperhomographies in $F^2$ and ${\overline{F}}^2$, respectively. Besides, if we admit that $\overline{A}{•}_{{}_{ab}}x=x=x{•}_{{}_{ab}}\overline{A}$ for all $a\in \overline{A},b\in \overline{B}$ and $(x,y)\in H_{a,b}\left(F\right)$, then the bijective map $\mathsf{\Pi }:H_{a,b}\left(F\right)⟶{\mathcal{H}}_{a,b}\left(F\right)$ defined by $\mathsf{\Pi }(x,y)={\displaystyle \frac{(x,y)}{\sim }}$, where ${\displaystyle \frac{(x,y)}{\sim }}=\left\{\begin{array}{cc}(x,y),\hfill & \mathrm{if}x\ne a\hfill \\ \mathcal{O},\hfill & \mathrm{if}x=a\hfill \end{array}\right.,$ equip the quotient ${\mathcal{H}}_{{}_{a,b}}\left(F\right)$ with a group structure and gives us a group isomorphism $(H_{a,b}\left(F\right),{•}_{{}_{ab}})\stackrel{\mathsf{\Pi }}{\cong }({\mathcal{H}}_{a,b}\left(F\right),{•}_{{}_{ab}}).$

In addition, the concepts in Definition (8) can be similarly defined on ${\mathcal{H}}_{a,b}\left(F\right)$, only by substituting a with $\mathcal{O}$.

Definition 9.

Let ${\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right)$ be an equipped hyperhomography. We define the hyperoperation "∘" on ${\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right)$ as follows.

Let $(x,y),(x^{\prime },y^{\prime })\in {\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right)$. If $(x,y)\in {\mathcal{H}}_{a,b}\left(F\right)$ and $(x^{\prime },y^{\prime })\in {\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right)$ for some $a,a^{\prime }\in \overline{A}$ and $b,b^{\prime }\in \overline{B}$, then

$$(x,y)\circ (x^{\prime },y^{\prime })=\left\{\begin{array}{cc}\left\{\widehat{x_i{•}_{{}_{ab}}{x}_j}\right|(x_i,x_j)\in {\mathcal{G}}_{a,b}^x\times {\mathcal{G}}_{a^{\prime },b^{\prime }}^{x^{\prime }}\},& \mathit{if}{\mathcal{H}}_{a,b}\left(F\right)={\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right)\hfill \\ ({\mathcal{H}}_{a,b}\left(F\right)\cup {\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right))\setminus \left\{\widehat{\mathcal{O}}\right\},& \mathit{otherwise}.\hfill \end{array}\right.$$

Theorem 3.

If ${\mathcal{H}}_{\overline{A},\overline{B}}\left(\overline{F}\right)$ is an equipped hyperhomography, then $\left({\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right),\circ \right)$ has a hypergroup structure.

Proof. 

Suppose that $\{X,Y,Z\}\subseteq {\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right)$ such that $X=(x,y)\in {\mathcal{H}}_{a,b}\left(F\right),Y=(x^{\prime },y^{\prime })\in {\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right)$ and $Z=(x^{″},y^{″})\in {\mathcal{H}}_{a^{″},b^{″}}\left(F\right)$ where, $J=\{(a,b),(a^{\prime },b^{\prime }),(a^{″},b^{″})\}\subseteq \overline{A}\times \overline{B}$. First we notice that $(x,y)\circ (x^{\prime },y^{\prime })\subseteq {\mathcal{P}}^{\ast }\left({\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right)\right),$ because $(x,x^{\prime })\in {\mathcal{G}}_{a,b}^x\times {\mathcal{G}}_{a^{\prime },b^{\prime }}^{x^{\prime }}$ implies that $\widehat{x{•}_{{}_{ab}}{x}^{\prime }}\in (x,y)\circ (x^{\prime },y^{\prime })$, i.e $(x,y)\circ (x^{\prime },y^{\prime })$ is a non-empty set and belongs to ${\mathcal{P}}^{\ast }\left({\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right)\right).$ Besides, if $(x,y)=(x_1,y_1)$ and $(x^{\prime },y^{\prime })=(x_1^{\prime },y_1^{\prime })$, then $x=x_1$ and $x^{\prime }=x_1^{\prime }$, meaning that ${\mathcal{G}}_{a,b}^x={\mathcal{G}}_{a,b}^{x_1}$ and ${\mathcal{G}}_{a,b}^{x^{\prime }}={\mathcal{G}}_{a,b}^{x_1^{\prime }}$. Hence we have ${\mathcal{G}}_{a,b}^x\times {\mathcal{G}}_{a,b}^{x^{\prime }}={\mathcal{G}}_{a,b}^{x_1}\times {\mathcal{G}}_{a,b}^{x_1^{\prime }}$ and therefore $\left\{\widehat{z{•}_{{}_{ab}}w}\right|(z,w)\in {\mathcal{G}}_{a,b}^x\times {\mathcal{G}}_{a,b}^{x^{\prime }}\}=\left\{\widehat{z{•}_{{}_{ab}}w}\right|(z,w)\in {\mathcal{G}}_{a,b}^{x_1}\left(f_{a,b}\right)\times {\mathcal{G}}_{a,b}^{x_1^{\prime }}\}$, equivalently with $(x,y)\circ (x^{\prime },y^{\prime })=(x_1,y_1)\circ (x_1^{\prime },y_1^{\prime })$. By consequence, the hyperoperation “∘” is well defined.

If $X=(a,\infty )$ or $Y=(a,\infty )$ or $Z=(a,\infty ),$ then the associativity is obvious. If not, we have the following cases.

Case 1: $\left|J\right|=1$.

This means that ${\mathcal{H}}_{a,b}\left(F\right)={\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right)={\mathcal{H}}_{a^{″},b^{″}}\left(F\right)$ and we have

$$\begin{array}{cc}\hfill [(x,y)\circ (x^{\prime },y^{\prime })]\circ (x^{″},y^{″})& =\left\{\widehat{\left(x_i{•}_{{}_{ab}}{x}_j^{\prime }\right)}|(x_i,x_j^{\prime })\in {\mathcal{G}}_{a,b}^x\times {\mathcal{G}}_{a,b}^{x^{\prime }}\right\}\circ (x^{″},y^{″})\hfill \\ \hfill & =\left\{\widehat{\left(x_i{•}_{{}_{ab}}{x}_j^{\prime }\right){•}_{{}_{ab}}{x}_k^{″}}|(x_i,x_j^{\prime },x_k^{″})\in {\mathcal{G}}_{a,b}^x\times {\mathcal{G}}_{a,b}^{x^{\prime }}\times {\mathcal{G}}_{a,b}^{x^{″}}\right\}.\hfill \end{array}$$

Similarly, it holds that

$$(x,y)\circ [(x^{\prime },y^{\prime })\circ (x^{″},y^{″})]=\left\{\widehat{x_i{•}_{{}_{ab}}\left(x_j^{\prime }{•}_{{}_{ab}}{x}_k^{″}\right)}|(x_i,x_j^{\prime },x_k^{″})\in {\mathcal{G}}_{a,b}^x\times {\mathcal{G}}_{a,b}^{x^{\prime }}\times {\mathcal{G}}_{a,b}^{x^{″}}\right\}.$$

On the other hand we have

$$\begin{array}{c}\hfill L_{a,b}(\widehat{x_i},\widehat{x_j^{\prime }})\cap L_{a,b}(\widehat{x_i{•}_{{}_{ab}}{x}_j^{\prime }},\widehat{\mathcal{O}})=\left\{(x_i{•}_{{}_{ab}}{x}_j^{\prime },0)\right\}\subseteq L_0,\\ \hfill L_{a,b}(\widehat{x_j^{\prime }},\widehat{x_k^{″}})\cap L_{a,b}(\widehat{\mathcal{O}},\widehat{x_j^{\prime }{•}_{{}_{ab}}{x}_k^{″}})=\left\{(x_j^{\prime }{•}_{{}_{ab}}{x}_k^{″},0)\right\}\subseteq L_0.\end{array}$$

In other words, for the six points $p_1=\widehat{x_i}$, $p_2=\widehat{x_j^{\prime }}$, $p_3=\widehat{x_k^{″}}$, $p_4=\widehat{x_i{•}_{{}_{ab}}{x}_j^{\prime }}$, $p_5=\widehat{\mathcal{O}}$ and $p_6=\widehat{x_j^{\prime }{•}_{{}_{ab}}{x}_k^{″}}$ on the curve we have $L_{a,b}(p_1,p_2)\cap L_{a,b}(p_4,p_5)\subseteq L_0$ and $L_{a,b}(p_2,p_3)\cap L_{a,b}(p_5,p_6)\subseteq L_0$ and therefore, by Pascal’s theorem (see Theorem 1), it follows also that $L_{a,b}(p_3,p_4)\cap L_{a,b}(p_6,p_1)\subseteq L_0$, equivalently with

$$L_{a,b}(\widehat{x_k^{″}},\widehat{x_i{•}_{{}_{ab}}{x}_j^{\prime }})\cap L_{a,b}(\widehat{x_j^{\prime }}{•}_{{}_{ab}}\widehat{x_k^{″}},\widehat{x_i})\subseteq L_0.$$

By Definition 8 we know that

$$\left\{(\left(x_i{•}_{{}_{ab}}{x}_j^{\prime }\right){•}_{{}_{ab}}{x}_k^{″},0)\right\}=L_0\cap L_{a,b}(\widehat{x_i{•}_{{}_{ab}}{x}_j^{\prime }},\widehat{x_k^{″}}),$$

$$\left\{(x_i{•}_{{}_{ab}}\left(x_j^{\prime }{•}_{{}_{ab}}{x}_k^{″}\right),0)\right\}=L_0\cap L_{a,b}(\widehat{x_i},\widehat{x_j^{\prime }{•}_{{}_{ab}}{x}_k^{″}})$$

where, by the associativity of the group operation "${•}_{{}_{ab}}$", it holds $\left(x_i{•}_{{}_{ab}}{x}_j^{\prime }\right){•}_{{}_{ab}}{x}_k^{″}=x_i{•}_{{}_{ab}}\left(x_j^{\prime }{•}_{{}_{ab}}{x}_k^{″}\right).$ This leads to the equality

$$L_0\cap L_{a,b}(\widehat{x_i{•}_{{}_{ab}}{x}_j^{\prime }},\widehat{x_k^{″}})=L_{a,b}(\widehat{x_k^{″}},\widehat{x_i{•}_{{}_{ab}}{x}_j^{\prime }})\cap L_{a,b}(\widehat{x_j^{\prime }{•}_{{}_{ab}}{x}_k^{″}},\widehat{x_i})=L_0\cap L_{a,b}(\widehat{x_i},\widehat{x_j^{\prime }{•}_{{}_{ab}}{x}_k^{″}}),$$

implying that

$$\widehat{\left(\left(x_i{•}_{{}_{ab}}{x}_j^{\prime }\right){•}_{{}_{ab}}{x}_k^{″}\right)}=\widehat{\left(x_i{•}_{{}_{ab}}\left(x_j^{\prime }{•}_{{}_{ab}}{x}_k^{″}\right)\right)}\mathrm{for}\mathrm{all}(x_i,x_j^{\prime },x_k^{″})\in {\mathcal{G}}_{a,b}^x\times {\mathcal{G}}_{a,b}^{x^{\prime }}\times {\mathcal{G}}_{a,b}^{x^{″}}.$$

Case 2: $\left|J\right|=2$.

(i) If ${\mathcal{H}}_{a,b}\left(F\right)={\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right)\ne {\mathcal{H}}_{a^{″},b^{″}}\left(F\right)$, then we have

$$\begin{array}{ll}[(x,y)\circ (x^{\prime },y^{\prime })]\circ (x^{″},y^{″})& =\left\{\widehat{z{•}_{{}_{ab}}w}|(z,w)\in {\mathcal{G}}_{a,b}^x\times {\mathcal{G}}_{a,b}^{x^{\prime }}\right\}\circ (x^{″},y^{″})\\ & ={\displaystyle \bigcup _{(u,v)\in (x,y)\circ (x^{\prime },y^{\prime })}}(u,v)\circ (x^{″},y^{″})\\ & ={\mathcal{H}}_{a,b}\left(F\right)\cup {\mathcal{H}}_{a^{″},b^{″}}\left(F\right).\end{array}$$

On the other hand

$$\begin{array}{cc}\hfill (x,y)\circ [(x^{\prime },y^{\prime })\circ (x^{″},y^{″})]& =(x,y)\circ \left({\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right)\cup {\mathcal{H}}_{a^{″},b^{″}}\left(F\right)\right)\hfill \\ \hfill & =(x,y)\circ {\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right)\cup (x,y)\circ {\mathcal{H}}_{a^{″},b^{″}}\left(F\right)\hfill \\ \hfill & ={\mathcal{H}}_{a,b}\left(F\right)\cup {\mathcal{H}}_{a^{″},b^{″}}\left(F\right).\hfill \end{array}$$

(ii) If ${\mathcal{H}}_{a,b}\left(F\right)\ne {\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right)={\mathcal{H}}_{a^{″},b^{″}}\left(F\right)$, then the associativity holds, similarly as in the case (i).

(iii) If ${\mathcal{H}}_{a,b}\left(F\right)={\mathcal{H}}_{a^{″},b^{″}}\left(F\right)\ne {\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right)$, then we have

$$\begin{array}{cc}\hfill [(x,y)\circ (x^{\prime },y^{\prime })]\circ (x^{″},y^{″})& =\left({\mathcal{H}}_{a,b}\left(F\right)\cup {\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right)\right)\circ (x^{″},y^{″})\hfill \\ \hfill & ={\mathcal{H}}_{a,b}\left(F\right)\cup {\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right)\cup {\mathcal{H}}_{a^{″},b^{″}}\left(F\right)\hfill \\ \hfill & ={\mathcal{H}}_{a,b}\left(F\right)\cup {\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right)\hfill \end{array}$$

and similarly

$$\begin{array}{ll}(x,y)\circ [(x^{\prime },y^{\prime })\circ (x^{″},y^{″})]& =(x,y)\circ ({\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right)\cup {\mathcal{H}}_{a^{″},b^{″}}\left(F\right))\\ & ={\mathcal{H}}_{a,b}\left(F\right)\cup {\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right)\cup {\mathcal{H}}_{a^{″},b^{″}}\left(F\right)\\ & ={\mathcal{H}}_{a,b}\left(F\right)\cup {\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right).\end{array}$$

Case 3: $\left|J\right|=3$.

In this case we have

$$\begin{array}{ll}[(x,y)\circ (x^{\prime },y^{\prime })]\circ (x^{″},y^{″})& =\left({\mathcal{H}}_{a,b}\left(F\right)\cup {\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right)\right)\circ (x^{″},y^{″})\\ & ={\mathcal{H}}_{a,b}\left(F\right)\cup {\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right)\cup {\mathcal{H}}_{a^{″},b^{″}}\left(F\right).\end{array}$$

On the other hand

$$\begin{array}{ll}(x,y)\circ [(x^{\prime },y^{\prime })\circ (x^{″},y^{″})]& =(x,y)\circ \left({\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right)\cup {\mathcal{H}}_{a^{″},b^{″}}\left(F\right)\right)\\ & ={\mathcal{H}}_{a,b}\left(F\right)\cup {\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right)\cup H_{a^{″},b^{″}}\left(F\right).\end{array}$$

Therefore the hyperoperation "∘" is associative.

In order to prove the reproduction axiom, we consider two cases as below:

Case 1. If $|\overline{A}\times \overline{B}|=1$, then $\overline{F}=F$ and ${\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right)={\mathcal{H}}_{a,b}\left(F\right),$ where $a\in \overline{A},b\in \overline{B}$. It follows that $({\mathcal{H}}_{a,b}\left(F\right),\circ )$ is a homography group, so the reproduction axiom holds.

Case 2. If $|\overline{A}\times \overline{B}|>1,$ consider an arbitrary element $\widehat{x}\in {\mathcal{H}}_{a,b}\left(F\right)\subseteq {\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right)$. Then

$$\begin{array}{ll}\widehat{x}\circ {\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right)& =(\widehat{x}\circ {\displaystyle \bigcup _{a\ne i\in \overline{A},b\ne j\in \overline{B}}}{\mathcal{H}}_{i,j}\left(F\right))\cup (\widehat{x}\circ {\mathcal{H}}_{a,b}\left(F\right)),\\ & =({\displaystyle \bigcup _{a\ne i\in \overline{A},b\ne j\in \overline{B}}}\widehat{x}\circ {\mathcal{H}}_{i,j}\left(F\right))\cup {\mathcal{H}}_{a,b}\left(F\right),\\ & =\left({\displaystyle \bigcup _{i\in \overline{A},j\in \overline{B}}}{\mathcal{H}}_{i,j}\left(F\right)\right)\cup {\mathcal{H}}_{a,b}\left(F\right),\\ & ={\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right).\end{array}$$

Similarly, $\left({\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right)\right)\circ \widehat{x}={\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right)$ and thus the reproduction axiom is proved. Therefore, $\left({\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right),\circ \right)$ is a hypergroup. □

Remark 2.

If $G=\left\{1\right\}$, then the hyperhomography and the associated hypergroup are the classical homography and the homography group, respectively.

Example 5.

Let us consider again Example 3, where we deal with the nondegenerate hyperhomography $H_{\overline{0},\overline{1}}\left(F\right)$ as a subset of $F^2$, having the form $H_{\overline{0},\overline{1}}\left(F\right)=H_{0,1}\left(F\right)\cup H_{0,4}\left(F\right)$ where, $H_{0,1}\left(F\right)=\{(0,\infty ),(1,2),(2,4),(3,3)\}$ and $H_{0,4}\left(F\right)=\{(0,\infty ),(2,2),(3,1),(4,3)\}$, while the associated equipped hyperhomography is ${\mathcal{H}}_{\overline{0},\overline{1}}\left(F\right)={\mathcal{H}}_{0,1}\left(F\right)\cup {\mathcal{H}}_{0,4}\left(F\right)$ where,

$${\mathcal{H}}_{0,1}\left(F\right)=\{\widehat{\mathcal{O}},(1,2),(2,4),(3,3)\},{\mathcal{H}}_{0,4}\left(F\right)=\{\widehat{\mathcal{O}},(2,2),(3,1),(4,3)\},$$

for $\widehat{\mathcal{O}}=(\mathcal{O},f_{a,b}\left(\mathcal{O}\right))=(\overline{0},f_{a,b}\left(\overline{0}\right))=(\overline{0},\infty )=(0,\infty ).$

Now let $T={\mathcal{H}}_{0,1}\left(F\right)$ and $K={\mathcal{H}}_{0,4}\left(F\right).$ Then $(T,\circ )$ and $(K,\circ )$ are reversible subhypergroups of $({\mathcal{H}}_{\overline{0},\overline{1}}\left(F\right),\circ )$, which are defined by the following Cayley tables, respectively

For a better understanding, we will explain all details in computing, for example, in the table of T the hyperproduct $(1,2)\circ (2,4)$. For doing this, since $T={\mathcal{H}}_{0,1}\left(F\right)$, we use the function $f_{0,1}\left(x\right)=1+\frac{1}{x}$ and the field $F={\mathbb{Z}}_5$. Based on Corollary 1, we obtain

$${\mathcal{G}}_{0,1}^1=\{1,\frac{-1}{1+1}\}=\{1,-2^{-1}\}=\{1,-3\}=\{1,2\},$$

$${\mathcal{G}}_{0,1}^2=\{2,\frac{-2}{2+1}\}=\{2,-2·3^{-1}\}=\{2,-4\}=\{2,1\},$$

and therefore,

$$(1,2)\circ (2,4)=\{\widehat{x_i{•}_{{}_{01}}{x}_j}\mid x_i\in {\mathcal{G}}_{0,1}^1,x_j\in {\mathcal{G}}_{0,1}^2\}=\{\widehat{1{•}_{{}_{01}}1},\widehat{1{•}_{{}_{01}}2},\widehat{2{•}_{{}_{01}}1},\widehat{2{•}_{{}_{01}}2}\}.$$

Based on Proposition 1, we have

$$\begin{array}{ccc}1{•}_{{}_{01}}1\hfill & =\hfill & 1·1·1-(-1)·(1+1-0)=3\hfill \\ 1{•}_{{}_{01}}2\hfill & =\hfill & 1·1·2-(-1)·(1+2-0)=5=0\hfill \\ 2{•}_{{}_{01}}1\hfill & =\hfill & 1·2·1-(-1)·(2+1-0)=5=0\hfill \\ 2{•}_{{}_{01}}2\hfill & =\hfill & 1·2·2-(-1)·(2+2-0)=8=3\hfill \end{array}$$

which imply that

$$(1,2)\circ (2,4)=\{(3,f_{0,1}\left(3\right)),(0,f_{0,1}\left(0\right)\}=\{(3,1+\frac{1}{3}),(0,\infty )\}=\{(3,3),(0,\infty )\}.$$

Similarly, all the other hyperproducts in both tables can be obtained.

The next result gives a characterization of the subhypergroups of the equipped hyperhomographies in $F^2$.

Theorem 4.

Let H be a non-empty subset of the hypergroup ${\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right)$. Then H is a subhypergroup of the equipped hyperhomography ${\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right)$ if and only if it can be written as $H={\displaystyle \bigcup _{(i,j)\in I\subseteq \overline{A}\times \overline{B}}}{\mathcal{H}}_{i,j}\left(F\right)$, where $I=\{(i,j)\in \overline{A}\times \overline{B}\mid H\cap {\mathcal{H}}_{i,j}\left(F\right)\ne \varnothing \}$, or H is a subhypergroup of ${\mathcal{H}}_{i,j}\left(F\right)$, for some $(i,j)\in \overline{A}\times \overline{B}$.

Proof. 

$(\Rightarrow )$. Suppose that H is a subhypergroup of ${\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right)$ and $H\nleqq {\mathcal{H}}_{i,j}\left(F\right)$, for every $(i,j)$ in $\overline{A}\times \overline{B}$. There exist $(i^{\prime },j^{\prime })\ne (s^{\prime },t^{\prime })$ in $\overline{A}\times \overline{B}$ such that $H\cap {\mathcal{H}}_{i^{\prime },j^{\prime }}\left(F\right)\ne \varnothing \ne H\cap {\mathcal{H}}_{s^{\prime },t^{\prime }}\left(F\right)$. Now let $I=\{(i,j)\in \overline{A}\times \overline{B}\mid H\cap {\mathcal{H}}_{i,j}\left(F\right)\ne \varnothing \}$. Thus we have $H\subseteq {\displaystyle \bigcup _{(i,j)\in I}}{\mathcal{H}}_{i,j}\left(F\right)\subseteq {\displaystyle \bigcup _{(i^{\prime },j^{\prime }),(s^{\prime },t^{\prime })\in I}}({\mathcal{H}}_{i^{\prime },j^{\prime }}\left(F\right)\cap H)\circ ({\mathcal{H}}_{s^{\prime },t^{\prime }}\left(F\right)\cap H)\subseteq H$. Hence $H={\displaystyle \bigcup _{(i,j)\in I}}{\mathcal{H}}_{i,j}\left(F\right)$.

$(\Leftarrow )$. It is obvious. □

Theorem 5.

Let H be a subhypergroup of the hypergroup ${\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right)$. Then H is reversible if and only if H is a subhypergroup of ${\mathcal{H}}_{a,b}\left(F\right)$, for some $(a,b)\in \overline{A}\times \overline{B}$.

Proof. 

$(\Leftarrow )$. First we prove that any subhypergroup H of ${\mathcal{H}}_{a,b}\left(F\right)$ is a regular reversible hypergroup, for any $(a,b)\in \overline{A}\times \overline{B}$. The regularity is clear, because $\widehat{\mathcal{O}}$ is an identity and each element is an inverse for itself. In order to prove the reversibility, let $\widehat{x}=(x,y)$ and $\widehat{x^{\prime }}=(x^{\prime },y^{\prime })$ be arbitrary elements in ${\mathcal{H}}_{a,b}\left(F\right)$. We distinguish three different situations.

Case 1. If $x^{\prime }\notin {\mathcal{G}}_{a,b}^x=\{x,\alpha \}$, where $x{•}_{ab}\alpha =a$, then

$$\begin{array}{ll}\widehat{x^{″}}=(x^{″},y^{″})\in (x,y)\circ (x^{\prime },y^{\prime })& ⟹(x^{″},y^{″})=\widehat{z{•}_{ab}w},\mathrm{with}(z,w)\in {\mathcal{G}}_{a,b}^x\times {\mathcal{G}}_{a,b}^{x^{\prime }}\\ & ⟹x^{″}=z{•}_{ab}w,\\ & ⟹z=x^{″}{•}_{ab}h,\mathrm{where}w{•}_{ab}h=a,\\ & ⟹(z,f_{a,b}\left(z\right))=\widehat{x^{″}{•}_{ij}h}\mathrm{and}h\in {\mathcal{G}}_{a,b}^w={\mathcal{G}}_{a,b}^{x^{\prime }},z\in {\mathcal{G}}_{a,b}^x\\ & ⟹(z,f_{a,b}\left(z\right))\in (x^{″},f_{a,b}\left(x^{″}\right))\circ (h,f_{a,b}\left(h\right))\\ & ⟹(x,y)\in (x^{″},f_{a,b}\left(x^{″}\right))\circ (h,f_{a,b}\left(h\right))\end{array}$$

Case 2. If $x^{\prime }\in {\mathcal{G}}_{a,b}^x=\{x,\alpha \}$, then $\widehat{x^{″}}=(x^{″},y^{″})\in (x,y)\circ (x^{\prime },y^{\prime })⟹(x^{″},y^{″})=\widehat{z{•}_{ab}w}$, with $z,w\in {\mathcal{G}}_{a,b}^x$. Thus $(x^{″},y^{″})\in \{\widehat{x{•}_{ab}x},\widehat{\alpha {•}_{ab}\alpha },\widehat{\mathcal{O}}\}$. It follows that $\widehat{x}\in \widehat{x^{″}}\circ \widehat{\alpha }$.

Case 3. If $(x,y)=\mathcal{O}$, then $Y\in \widehat{\mathcal{O}}\circ X=X\circ \widehat{\mathcal{O}}$, implying that $\widehat{\mathcal{O}}\in Y\circ X$ and $X\in \widehat{\mathcal{O}}\circ Y$. Notice that $\widehat{\mathcal{O}}\in X\circ X$, for all $X\in {\mathcal{H}}_{i,j}\left(F\right)$ (i.e. every element is one of its inverses).

$(\Rightarrow )$. Suppose that H is a reversible subhypergroup of ${\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right)$ such that it is not a subhypergroup of any ${\mathcal{H}}_{a,b}\left(F\right)$, with $(a,b)\in \overline{A}\times \overline{B}$. Based on Theorem 4, we have $H={\displaystyle \bigcup _{(i,j)\in I\subseteq \overline{A}\times \overline{B}}}{\mathcal{H}}_{i,j}\left(F\right)$, where $I=\{(i,j)\in \overline{A}\times \overline{B}\mid H\cap {\mathcal{H}}_{i,j}\left(F\right)\ne \varnothing \}$. Let $(x,y),(x^{\prime },y^{\prime })$ be arbitrary elements in $H\cap {\mathcal{H}}_{i,j}\left(F\right)$ and $H\cap {\mathcal{H}}_{s,t}\left(F\right)$, respectively, that are not equal to $\widehat{\mathcal{O}}$, with $(i,j)\ne (s,t)$. If $(x^{″},y^{″})\in ((x,y)\circ (x^{\prime },y^{\prime }))\cap {\mathcal{H}}_{i,j}\left(F\right)$, then, based on the reversibility, we have $(x^{\prime },y^{\prime })\in (z,w)\circ (x^{″},y^{″})\subseteq {\mathcal{H}}_{i,j}\left(F\right)$, where $z\in {\mathcal{G}}_{a,b}^x$, hence $(x^{\prime },y^{\prime })\in {\mathcal{H}}_{i,j}\left(F\right)\cap {\mathcal{H}}_{s,t}\left(F\right)=\left\{\widehat{\mathcal{O}}\right\}$. Thus $(x^{\prime },y^{\prime })=\widehat{\mathcal{O}}$, which is in contradiction with the supposition that $(x^{\prime },y^{\prime })\ne \widehat{\mathcal{O}}$. Therefore $H⩽{\mathcal{H}}_{i,j}\left(F\right)$, for some $(i,j)\in \overline{A}\times \overline{B}$. □

In the following we will present two new hypergroup structures isomorphic with the equipped homography ${\mathcal{H}}_{a,b}\left(F\right)$ in the case when $b\ne 0$ and $b=0$, respectively.

Theorem 6.

Consider the field F and define on $F^{\ast }=F\setminus \left\{0\right\}$ the hyperoperation

$$\forall x,x^{\prime }\in F^{\ast },x⊚x^{\prime }=\{x{x}^{\prime },{\displaystyle \frac{x}{x^{\prime }}},{\displaystyle \frac{x^{\prime }}{x}},{\displaystyle \frac{1}{x{x}^{\prime }}}\}.$$

Then, for every $b\ne 0$, there is the homomorphism $({\mathcal{H}}_{a,b}\left(F\right),\circ )\cong (F^{\ast },⊚)$.

Proof. 

It is easy to see that $(F^{\ast },⊚)$ is a hypergroup. Now, taking $\nu =a-b^{-1}$, consider the bijective function $\phi :F\setminus \left\{\nu \right\}⟶F^{\ast }$ defined by $\phi \left(x\right)=bx+1-ab$ and the function $\xi :{\mathcal{H}}_{a,b}\left(F\right)⟶\mathsf{\Gamma }\left(\phi \right)$ defined by $\xi \left(\right(x,y\left)\right)=(x,\phi (x\left)\right)$, where $\mathsf{\Gamma }\left(\phi \right)=\left\{\right(x,\phi \left(x\right))\mid x\in F\setminus \{\nu \left\}\right\}$ and $\xi \left((a,\infty )\right)=(a,1)=\xi \left((\overline{A},\infty )\right)=\xi \left(\widehat{\mathcal{O}}\right)$. Geometrically, $\mathsf{\Gamma }\left(\phi \right)$ is the graph of the function $\phi$, thus it is the line passing through the points of $(\nu ,0)$ and $(a,1)$, while $\xi$ is the map that projects the points of the hyperhomography ${\mathcal{H}}_{a,b}\left(F\right)$ on the above mentioned line.

Thus, using Proposition 1, for all $x_i,x_j\in F\setminus \left\{\nu \right\},$ we have

$$\begin{array}{cc}\hfill \phi \left(x_i{•}_{{}_{{}_{a,b}}}{x}_j\right)& =b\left(x_i{•}_{{}_{{}_{a,b}}}{x}_j\right)+1-ab,\hfill \\ \hfill & =b(b{x}_i{x}_j-(ab-1)(x_i+x_j-a))+1-ab\hfill \\ \hfill & =(b{x}_i+1-ab)(b{x}_j+1-ab)\hfill \\ \hfill & =\phi \left(x_i\right)\phi \left(x_j\right).\hfill \end{array}$$

Now suppose that $(x,y),(x^{\prime },y^{\prime })$ are arbitrary elements in ${\mathcal{H}}_{a,b}\left(F\right)$. It follows that

$$\begin{array}{cc}\hfill \xi ((x,y)\circ (x^{\prime },y^{\prime }))& =\{\xi \widehat{\left(x_i{•}_{{}_{{}_{a,b}}}{x}_j\right)}\mid x_i\in {\mathcal{G}}_{{}_{a,b}}^x,x_j\in {\mathcal{G}}_{{}_{a,b}}^{x^{\prime }}\}\hfill \\ \hfill & =\{(x_i{•}_{{}_{{}_{a,b}}}{x}_j,\phi \left(x_i{•}_{{}_{{}_{a,b}}}{x}_j\right))\mid x_i\in {\mathcal{G}}_{{}_{a,b}}^x,x_j\in {\mathcal{G}}_{{}_{a,b}}^{x^{\prime }}\}\hfill \\ \hfill & =\{(x_i{•}_{{}_{{}_{a,b}}}{x}_j,\phi \left(x_i\right)\phi \left(x_j\right))\mid x_i\in {\mathcal{G}}_{{}_{a,b}}^x,x_j\in {\mathcal{G}}_{{}_{a,b}}^{x^{\prime }}\}.\hfill \end{array}$$

Take now $\mathsf{\Pi }:F\times F^{\ast }⟶F^{\ast }$ with $\mathsf{\Pi }\left(\right(x,y\left)\right)=y$ as the projection map on the second component and define $\psi :{\mathcal{H}}_{a,b}\left(F\right)⟶F^{\ast }$ by $\psi =\mathsf{\Pi }\circ \xi$.

We have $\psi \left(\right(x,y\left)\right)=\phi \left(x\right)$, for all $(x,y)\in {\mathcal{H}}_{a,b}\left(F\right)$, thus $\psi$ is a bijective map and also a homomorphism because

$$\begin{array}{cc}\hfill \psi ((x,y)\circ (x^{\prime },y^{\prime }))& =\mathsf{\Pi }\left(\xi ((x,y)\circ (x^{\prime },y^{\prime }))\right)\hfill \\ \hfill & =\{\phi \left(x_i\right)\phi \left(x_j\right)\mid x_i\in {\mathcal{G}}_{{}_{a,b}}^x,x_j\in {\mathcal{G}}_{{}_{a,b}}^{x^{\prime }}\}\hfill \\ \hfill & =\{\phi \left(x_i\right)\phi \left(x_j\right)\mid \phi \left(x_i\right)\in \phi \left({\mathcal{G}}_{{}_{a,b}}^x\right),\phi \left(x_j\right)\in \phi \left({\mathcal{G}}_{{}_{a,b}}^{x^{\prime }}\right)\}\left(\phi \mathrm{is}\mathrm{bijective}\mathrm{map}\right)\hfill \\ \hfill & =\{\phi \left(x_i\right)\phi \left(x_j\right)\mid \phi \left(x_i\right)\in \{\phi \left(x\right),\frac{1}{\phi \left(x\right)}\},\phi \left(x_j\right)\in \{\phi \left(x^{\prime }\right),\frac{1}{\phi \left(x^{\prime }\right)}\}\}\hfill \\ \hfill & =\phi \left(x\right)⊚\phi \left(x^{\prime }\right)\hfill \\ \hfill & =\psi \left((x,y)\right)\circ \psi \left((x^{\prime },y^{\prime })\right).\hfill \end{array}$$

Therefore $({\mathcal{H}}_{a,b}\left(F\right),\circ )$ is isomorphic to $(F^{\ast },⊚).$ □

Theorem 7.

Consider the field F and define on $F^{\ast }=F\setminus \left\{0\right\}$ the hyperoperation

$$\forall x,x^{\prime }\in F,x⊚x^{\prime }=\{x+x^{\prime },x-x^{\prime },-x+x^{\prime },-x-x^{\prime }\}.$$

Then, if $b=0$, there is the homomorphism $({\mathcal{H}}_{a,b}\left(F\right),\circ )\cong (F,⊛)$.

Proof. 

Clearly, $(F,⊛)$ is a hypergroup. Consider the bijective function $\phi :F⟶F$ defined by $\phi \left(x\right)=x-a$ and be $\mathsf{\Gamma }\left(\phi \right)=\left\{\right(x,\phi \left(x\right))\mid x\in F\}$ its graph. Besides define $\xi :{\mathcal{H}}_{a,b}\left(F\right)⟶\mathsf{\Gamma }\left(\phi \right)$ by $\xi \left(\right(x,y\left)\right)=(x,\phi (x\left)\right)$, where $\xi \left((a,\infty )\right)=(a,0)=\xi \left((\overline{A},\infty )\right)$. Therefore, for all $x_i,x_j\in F,$ we have

$$\begin{array}{cc}\hfill \phi \left(x_i{•}_{{}_{{}_{a,b}}}{x}_j\right)& =\left(x_i{•}_{{}_{{}_{a,b}}}{x}_j\right)-a,\hfill \\ \hfill & =(x_i+x_j-a)-a\hfill \\ \hfill & =(x_i-a)+(x_j-a)\hfill \\ \hfill & =\phi \left(x_i\right)+\phi \left(x_j\right)\hfill \end{array}$$

and for all $(x,y),(x^{\prime },y^{\prime })\in {\mathcal{H}}_{a,b}\left(F\right)$

$$\begin{array}{cc}\hfill \xi ((x,y)\circ (x^{\prime },y^{\prime }))& =\{\xi \widehat{\left(x_i{•}_{{}_{{}_{a,b}}}{x}_j\right)}\mid x_i\in {\mathcal{G}}_{{}_{a,b}}^x,x_j\in {\mathcal{G}}_{{}_{a,b}}^{x^{\prime }}\},\hfill \\ \hfill & =\{(x_i{•}_{{}_{{}_{a,b}}}{x}_j,\varphi \left(x_i{•}_{{}_{{}_{a,b}}}{x}_j\right))\mid x_i\in {\mathcal{G}}_{{}_{a,b}}^x,x_j\in {\mathcal{G}}_{{}_{a,b}}^{x^{\prime }}\},\hfill \\ \hfill & =\{(x_i{•}_{{}_{{}_{a,b}}}{x}_j,\phi \left(x_i\right)+\phi \left(x_j\right))\mid x_i\in {\mathcal{G}}_{{}_{a,b}}^x,x_j\in {\mathcal{G}}_{{}_{a,b}}^{x^{\prime }}\}.\hfill \end{array}$$

As in the previous theorem, let $\mathsf{\Pi }:F\times F⟶F$, $\mathsf{\Pi }\left(\right(x,y\left)\right)=y$ be the projection map on second component and define $\psi :{\mathcal{H}}_{a,b}\left(F\right)⟶F$ by $\psi =\mathsf{\Pi }\circ \xi$.

Therefore, for all $(x,y)\in {\mathcal{H}}_{a,b}\left(F\right)$, $\psi \left(\right(x,y\left)\right)=\phi \left(x\right)$ and thus $\psi$ is a bijective map. We claim that $\psi$ is a homomorphism, too, because

$$\begin{array}{cc}\hfill \psi ((x,y)\circ (x^{\prime },y^{\prime }))& =\mathsf{\Pi }\left(\xi ((x,y)\circ (x^{\prime },y^{\prime }))\right)\hfill \\ \hfill & =\{\phi \left(x_i\right)+\phi \left(x_j\right)\mid x_i\in {\mathcal{G}}_{{}_{a,b}}^x,x_j\in {\mathcal{G}}_{{}_{a,b}}^{x^{\prime }}\}\hfill \\ \hfill & =\{\phi \left(x_i\right)+\phi \left(x_j\right)\mid \phi \left(x_i\right)\in \phi \left({\mathcal{G}}_{{}_{a,b}}^x\right),\phi \left(x_j\right)\in \phi \left({\mathcal{G}}_{{}_{a,b}}^{x^{\prime }}\right)\}\left(\phi \mathrm{is}\mathrm{bijective}\mathrm{map}\right)\hfill \\ \hfill & =\{\phi \left(x_i\right)+\phi \left(x_j\right)|\phi \left(x_i\right)\in \{\phi \left(x\right),-\phi \left(x\right)\},\phi \left(x_j\right)\in \{\phi \left(x^{\prime }\right),-\phi \left(x^{\prime }\right)\}\}\hfill \\ \hfill & =\phi \left(x\right)⊚\phi \left(x^{\prime }\right)\hfill \\ \hfill & =\psi \left((x,y)\right)\circ \psi \left((x^{\prime },y^{\prime })\right).\hfill \end{array}$$

Therefore $({\mathcal{H}}_{a,b}\left(F\right),\circ )$ is isomorphic with $(F^{\ast },⊛)$. □

4. Associated ${\mathbf{H}}_{\mathbf{v}}$-Groups

Vougiouklis [13] introduced the notion of $H_v-$group as a generalization of the notion of hypergroup, substituting the associativity of the hyperoperation with the weak associativity, i.e., $a\circ (b\circ c)\cap (a\circ b)\circ c\ne \varnothing$ for all $a,b,c\in H$. The motivation of introducing this hyperstructure is the following one. We know that the quotient of a group with respect to a normal subgroup is a group, while the quotient of a group with respect to any subgroup is a hypergroup. Vougiouklis stated that the quotient of a group with respect to any partition of the group is an $H_v-$group.

In the following we equip the hyperhomography ${\mathcal{H}}_{\overline{A},\overline{B}}\left(\overline{F}\right)={\displaystyle \bigcup _{(a,b)\in \overline{A}\times \overline{B}}}{\mathcal{H}}_{a,b}\left(\overline{F}\right)$ as a subset of ${\overline{F}}^2\cup \left\{\widehat{\mathcal{O}}\right\}$ with an $H_v-$group structure, by defining the following hyperoperation

$$(\overline{x},\overline{y})\overline{\circ }(\overline{x^{\prime }},\overline{y^{\prime }})=\{(\overline{u},\overline{v})\mid (u,v)\in (\overline{x}\times \overline{y})\circ (\overline{x^{\prime }}\times \overline{y^{\prime }})\}.$$

Notice that

$$(x,y)=\widehat{\mathcal{O}}⟺(\overline{x},\overline{y})=\widehat{\mathcal{O}}⟺\overline{x}\times \overline{y}=\widehat{\mathcal{O}},$$

and

$$(c,d)\notin (\overline{x}\times \overline{y})\cap {\mathcal{H}}_{a,b}\left(F\right)\mathrm{or}(c^{\prime },d^{\prime })\notin ({\overline{x}}^{\prime }\times {\overline{y}}^{\prime })\cap {\mathcal{H}}_{a^{\prime },b^{\prime }}\left(F\right)⟹(c,d)\circ (c^{\prime },d^{\prime })=\varnothing .$$

Moreover according with Thorem 2, the hyperoperation $\overline{\circ }$ is well defined on ${\mathcal{H}}_{{}_{\overline{A},\overline{B}}}\left(\overline{F}\right)$ and in addition we have

$$\overline{(x,y)\circ (x^{\prime },y^{\prime })}\subseteq (\overline{x},\overline{y})\overline{\circ }(\overline{x^{\prime }},\overline{y^{\prime }}).$$

Proposition 2. 

$({\mathcal{H}}_{\overline{A},\overline{B}}\left(\overline{F}\right),\overline{\circ })$ is an $H_v$-group.

Proof. 

Let $(x,y)$, $(x^{\prime },y^{\prime })$ and $(x^{″},y^{″})$ be elements in ${\mathcal{H}}_{\overline{A},\overline{B}}\left(\overline{F}\right).$ Then we have

$$\overline{(x,y)\circ (x^{\prime },y^{\prime })\circ (x^{″},y^{″})}\subseteq \left[(\overline{x},\overline{y})\overline{\circ }(\overline{x^{\prime }},\overline{y^{\prime }})\right]\overline{\circ }(\overline{x^{″}},\overline{y^{″}})\cap (\overline{x},\overline{y})\overline{\circ }\left[(\overline{x^{\prime }},\overline{y^{\prime }})\overline{\circ }(\overline{x^{″}},\overline{y^{″}})\right].$$

 □

Proposition 3.

Let ${\psi }_{{}_{\overline{A},\overline{B}}}:{\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right)⟶{\mathcal{H}}_{\overline{A},\overline{B}}\left(\overline{F}\right)$, ${\psi }_{{}_{\overline{A},\overline{B}}}(x,y)=(\overline{x},\overline{y})$. Then ${\psi }_{{}_{\overline{A},\overline{B}}}$ is an epimorphism of $H_v$-groups.

Proof. 

Suppose that $(x,y)$ and $(x^{\prime },y^{\prime })$ belong to ${\mathcal{H}}_{\overline{A},\overline{B}}\left(F\right).$ We have

$$\begin{array}{ll}{\psi }_{{}_{\overline{A},\overline{B}}}((x,y)\circ (x^{\prime },y^{\prime }))& =\left\{(\overline{u},\overline{v})\right|(u,v)\in (x,y)\circ (x^{\prime },y^{\prime })\}\\ & \subseteq (\overline{x},\overline{y})\overline{\circ }({\overline{x}}^{\prime },{\overline{y}}^{\prime })\\ & ={\psi }_{{}_{\overline{A},\overline{B}}}(x,y)\overline{\circ }{\psi }_{{}_{\overline{A},\overline{B}}}(x^{\prime },y^{\prime }).\end{array}$$

 □

Example 6.

If we consider the hyperhomography ${\mathcal{H}}_{\overline{0},\overline{1}}\left(\overline{F}\right)=\{\widehat{\mathcal{O}},(\overline{1},\overline{2}),(\overline{2},\overline{1}),(\overline{2},\overline{2})\}$, then after long calculations similarly s those in Example 5, we get the following $H_v$-group table.

Proposition 4.

On ${\mathcal{H}}_{a,a}\left(F\right)$, as a subset of ${\mathcal{H}}_{\overline{A},\overline{A}}\left(F\right)$, define the hyperoperation

$$(x,y)\cdot (x^{\prime },y^{\prime })=\left\{\begin{array}{cc}\{\widehat{x{•}_{{}_{aa}}{x}^{\prime }},\widehat{y{•}_{{}_{aa}}{y}^{\prime }}\},\hfill & \mathit{if}\mathcal{O}\notin \{(x,y),(x^{\prime },y^{\prime })\}\hfill \\ (x,y),\hfill & \mathit{if}(x^{\prime },y^{\prime })=\mathcal{O}\hfill \\ (x^{\prime },y^{\prime }),\hfill & \mathit{if}(x,y)=\mathcal{O}.\hfill \end{array}\right.$$

Then $({\mathcal{H}}_{a,a}\left(F\right),\cdot )$ is an $H_v-group$.

Proof. 

First we prove that, if $\mathcal{O}\ne \widehat{x}$ and $\widehat{x}\in {\mathcal{H}}_{a,a}\left(F\right)$, then $\widehat{f_{a,a}\left(x\right)}\in {\mathcal{H}}_{a,a}\left(F\right).$ To this aim, consider an arbitrary element $\widehat{x}\in {\mathcal{H}}_{a,a}\left(F\right)$ not equal to $\mathcal{O}$ and notice that $f_{a,a}^2=i{d}_F$. Then

$$\begin{array}{cc}\hfill \widehat{x}\in {\mathcal{H}}_{a,a}\left(F\right)& ⟹(x,y)\in {\mathcal{H}}_{a,a}\left(F\right),y=f_{a,a}\left(x\right)\hfill \\ \hfill & ⟹f_{a,a}\left(y\right)=f_{a,a}\left(f_{a,a}\left(x\right)\right)\hfill \\ \hfill & ⟹f_{a,a}\left(y\right)=(f_{a,a}\circ f_{a,a})\left(x\right)\hfill \\ \hfill & ⟹f_{a,a}\left(y\right)=x\hfill \\ \hfill & ⟹(y,x)\in {\mathcal{H}}_{a,a}\left(F\right),x=f_{a,a}\left(y\right)\hfill \\ \hfill & ⟹\widehat{y}\in {\mathcal{H}}_{a,a}\left(F\right)\hfill \\ \hfill & ⟹\widehat{f_{a,a}\left(x\right)}\in {\mathcal{H}}_{a,a}\left(F\right).\hfill \end{array}$$

Consequently, $(x,y)\cdot (x^{\prime },y^{\prime })\subseteq {\mathcal{H}}_{a,a}\left(F\right),$ for all $(x,y),(x^{\prime },y^{\prime })\in {\mathcal{H}}_{a,a}\left(F\right)$ and “⋅” is well defined. Now, let $(x,y),(x^{\prime },y^{\prime }),(x^{″},y^{″})$ belong to ${\mathcal{H}}_{a,a}\left(F\right)$. We get

$$\{\widehat{x{•}_{{}_{aa}}{x}^{\prime }{•}_{{}_{aa}}{x}^{″}},\widehat{y{•}_{{}_{aa}}{y}^{\prime }{•}_{{}_{aa}}{y}^{″}}\}\subseteq ([(x,y)\cdot (x^{\prime },y^{\prime })]\cdot (x^{″},y^{″}))\cap ((x,y)\cdot [(x^{\prime },y^{\prime })\cdot (x^{″},y^{″})])\ne \varnothing ,$$

thus the weak associativity condition holds. It can easily be seen that the reproduction axiom is valid, too. □

Example 7.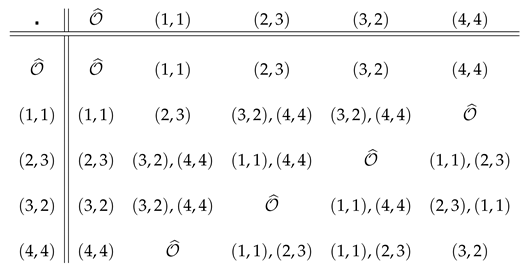

The Cayley table of the $H_v-$group $({\mathcal{H}}_{0,0}\left(F\right),\cdot )$ where, $F={\mathbb{Z}}_5$ is again the field of order 5, is as follows:

In this table, we have $\widehat{\mathcal{O}}\cdot (x,y)=(x,y)=(x,y)\cdot \widehat{\mathcal{O}}$, for all $(x,y)\in {\mathcal{H}}_{0,0}\left(F\right)$ and

$$(x,y)\cdot (x^{\prime },y^{\prime })=\{(x+x^{\prime },{(x+x^{\prime })}^{-1}),(y+y^{\prime },{(y+y^{\prime })}^{-1})\},$$

for all $(x,y),(x^{\prime },y^{\prime })\in {\mathcal{H}}_{0,0}\left(F\right)\setminus \left\{\widehat{\mathcal{O}}\right\}.$ The hyperoperation is not associative, but only weak associative, as we can notice here below:

$$\widehat{\mathcal{O}}=[[(1,1)\cdot (1,1)]\cdot (3,2)]\ne [(1,1)\cdot [(1,1)\cdot (3,2)]]=\{\widehat{\mathcal{O}},(3,2),(4,4)\}.$$

5. Conclusions

In the last few years, researchers in the hypercompositional structure theory have investigated, principally from a theoretical point of view, all types of hyperrings: general hyperrings [20], multiplicative hyperrings [15], additive hyperrings [21], superrings [22], but till now, only the Krasner hyperrings have found interesting and useful applications in number theory, algebraic geometry, scheme theory, as mentioned in the introductory part of this article. Here the authors continue the study on the research topic started in [1] about elliptic hypercurves defined on quotient Krasner hyperfield, with applications in cryptography [8]. In a similar way, the notion of a homography on a field is extended to hyperhomography over Krasner hyperfields. More exactly, considering an arbitrary field F and a normal subgroup G of its multiplicative group, we get a Krasner hyperfield $\overline{F}=F/G$. Then the homography $H_{a,b}\left(F\right)=\{(x,y)\in F^2\mid y=f_{a,b}\left(x\right)=b+\frac{1}{x-a}\}$, where $a,b\in F$ is naturally extended to the hyperhomography $H_{\overline{A},\overline{B}}\left(\overline{F}\right)=\{(\overline{x},\overline{y})\in {\overline{F}}^2\mid \overline{1}\in (\overline{x}⊝\overline{A})\odot (\overline{y}⊝\overline{B})\}$ over the hyperfield $(\overline{F},\oplus ,\odot )$. Besides, the group operation on a homography leads to a hyperoperation on the associated equipped hyperhomography ${\mathcal{H}}_{\overline{A},\overline{B}}\left(\overline{F}\right)$, that becomes a hypergroup. Then, all reversible subhypergroups of an equipped hyperhomography are characterized. In the last part of the paper, other hyperoperations are defined on hyperhomographies and their properties are investigated in connection with weak associativity.