Feature Selection Based on Swallow Swarm Optimization for Fuzzy Classification
Abstract
:1. Introduction and Literature Review
- The original swallow swarm algorithm is designed for continuous optimization; for the first time we offer a new binary version of swallow swarm optimization for solving binary optimization problems.
- A novel feature selection method based on binary swallow swarm optimization is proposed. This is the first work applying the binary swallow swarm optimization to feature selection.
- As an example of building fuzzy rule-based classifiers, the proposed method is compared with wrapper feature selections based on other metaheuristics, feature selection algorithm based on mutual information, and algorithm without feature selection.
- The Wilcoxon signed-rank test is used to evaluate the proposed method.
- A multiple regression equation is found that reflects the relationship between the BSSO runtime and the number of features, the number of instances, and the number of classes.
1.1. Literature Review
1.1.1. Quantum Methods
1.1.2. Modified Algebraic Operations
1.1.3. Transfer Functions
2. Fuzzy Rule-Based Classifier
3. Fuzzy Rule Base Generation
| Algorithm 1 Fuzzy rule base generation algorithm. |
| 1: Input: m, Tr. 2: Output: fuzzy rule base Ri (where i = 1, 2…, m). 3: begin 4: for i←1 to m do 5: for k←1 to D do 6: : 7: ; 8: : 9: ; 10: Calculate a center of : 11: b ← a + (c – a)/2; 12: Create a symmetric triangular membership function with borders a and c, and center b for fuzzy term Aki; 13: end 14: membership functions (where k = 1, 2, …, D) and output ck ← k; 15: end 16: end |
4. Wrapper-Based Feature Selection Algorithm
4.1. Swallow Swarm Optimization
- Head leader is a particle with the best value of the objective function;
- Local leaders are l particles that follow the head leader in accordance with the value of the objective function;
- Aimless particles are k particles with the worst value of the objective function;
- Explorers are all other particles.
4.2. Binary Swallow Swarm Optimization Algorithm
| Algorithm 2 Binary Swallow Swarm Optimization. |
| 1: Input: train data. 2: Output: SHL – position of the head leader. 3: Parameters: iterations – maximum number of cycles, N – population size, D – dimension, pvs, pvhl, phe, pher, ple, pler, l – local leaders, k – aimless particles. 4: begin 5: for i ← to N do 6: Initialize each solution Si in the population: Si ← rand{0,1}D; 7: Select j-th (j = 1,2,…,D) feature for subset Sub where Sij = 1; 8: Build reduced dataset (subtra) based on Sub; 9: Evaluate fitness value (fitnessi) of Sub: fitnessi ← errorrate; Evaluate fitness value (fitnessi) of Sub: fitnessi ← errorrate; 10: end 11: SHL ← Sk, where ; 12: for iter←1 to iterations do 13: for i ← to N do 14: Find nearest local leader SLL among population {S1, S2, …, SN}; 15: Evolve a new solution Se={f1, f2, …, fD} using Equation (2); 16: Select j-th feature (j = 1,2,…,D) for subset Sub, where Sej = 1; 17: Build reduced dataset (subtra) based on Sub; 18: Evaluate fitness value (fitnessi) of Sub: fitnessi ← errorrate; 19: if fitnessSe< fitnessi then 20: Si ← Se; 21: fitnessi ← fitnessSe; 22: end 23: end 24: ; 25: end 26: end |
5. Experiment
5.1. Datasets and Parameter Setting
5.2. Comparison with the Other Approaches
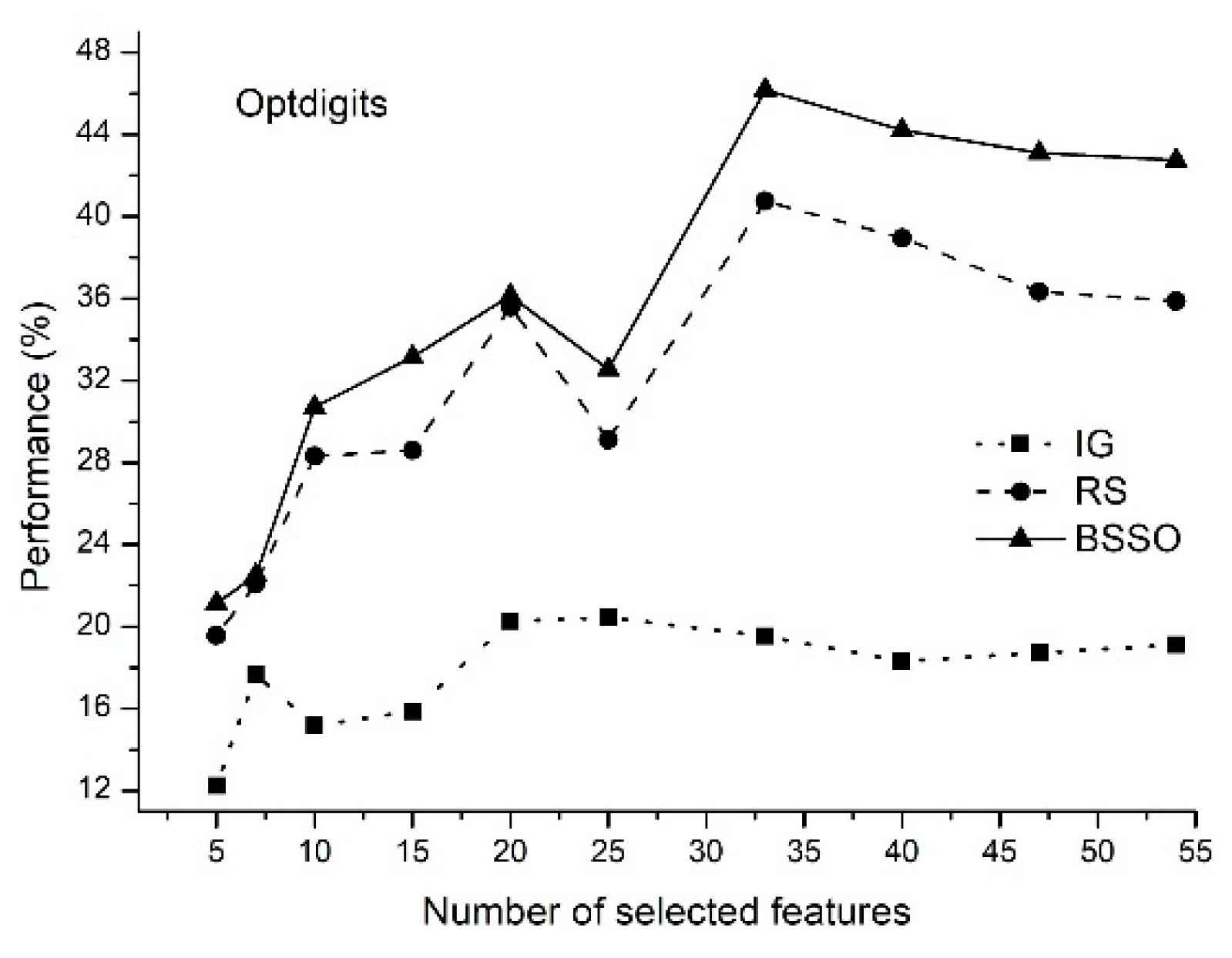
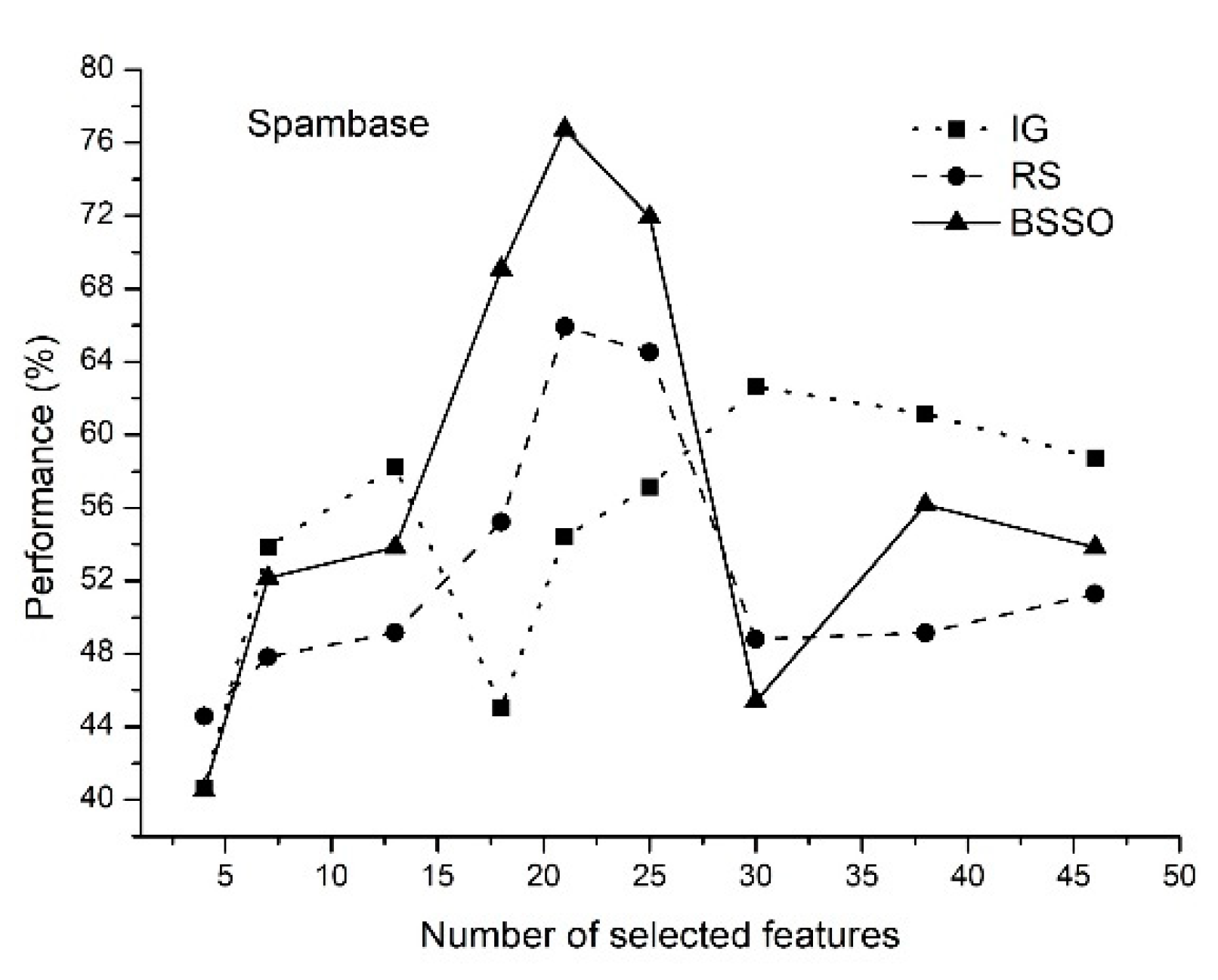
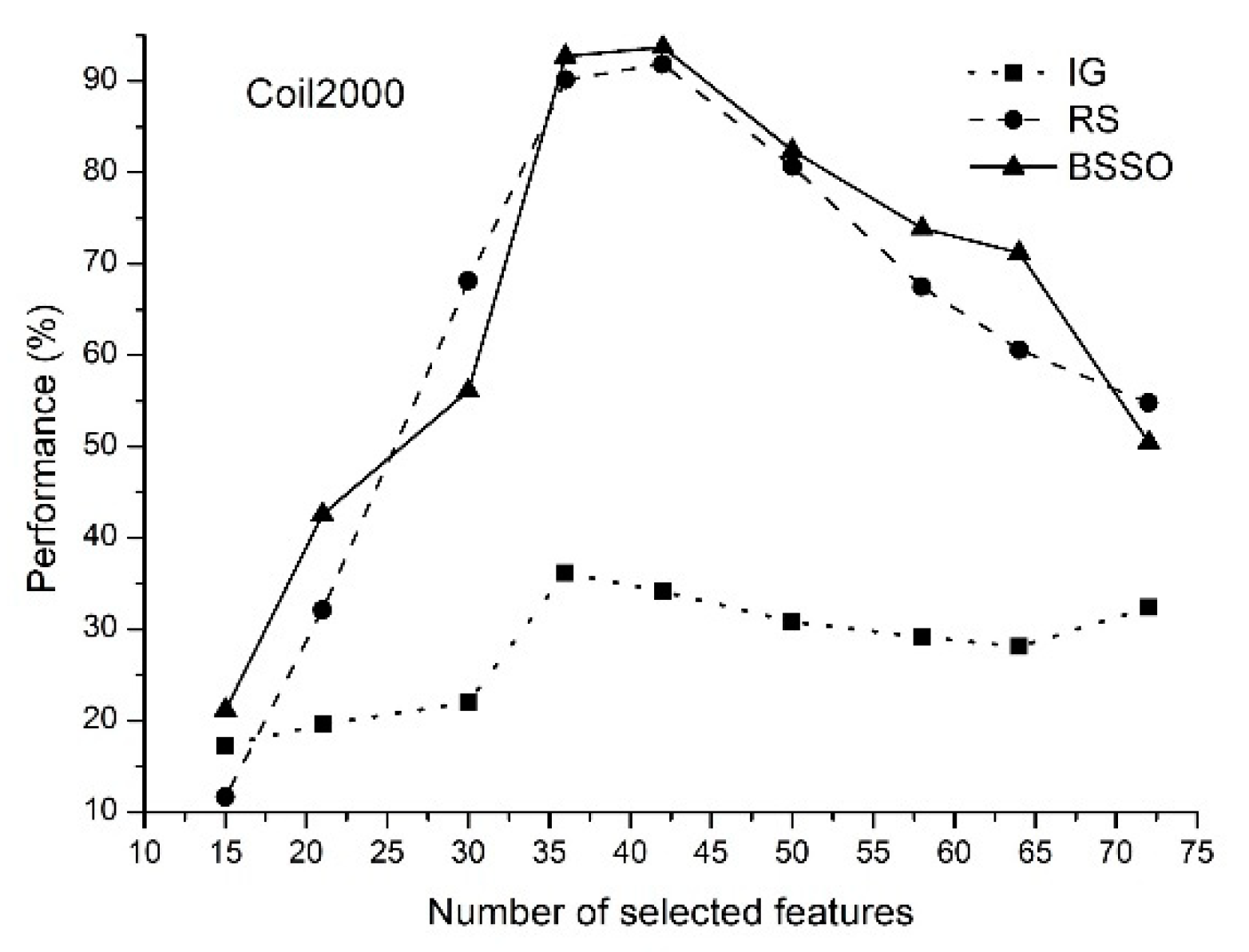
- The proposed method of feature selection on some data sets allows to obtain a classification rate exceeding 90%, which indicates that the feature selection method is effective by reducing the amount of data processing.
- The classification rate of the increases with an increase in the number of features selected. When the number of selected features reaches a certain value, the classification rate decreases.
- The proposed method allows selecting the optimal features.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Garcia, S.; Luengo, J.; Herrera, F. Data Preprocessing in Data Mining; Intelligent Systems Reference Library; Springer International Publishing: Cham, Switzerland; New York, NJ, USA; Berlin, Germany, 2015; Volume 72, pp. 59–139. ISBN 978-3-319-10246-7. [Google Scholar]
- Alkuhlani, A.; Nassef, M.; Farag, I. Multistage Feature Selection Approach for High-Dimensional Cancer Data. Soft Comput. 2017, 21, 6895–6906. [Google Scholar] [CrossRef]
- Jalalirad, A.; Tjalkens, T. Using Feature-Based Models with Complexity Penalization for Selecting Features. J. Signal Process. Syst. 2018, 90, 201–210. [Google Scholar] [CrossRef]
- Kohavi, R.; John, G.H. Wrappers for Feature Subset Selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Ramirez-Gallego, S.; Mourino-Talin, H.; Martinez-Rego, D.; Bolon-Canedo, V.; Benitez, J.M.; Alonso-Betanzos, A.; Herrera, F. An Information Theory-Based Feature Selection Framework for Big Data Under Apache Spark. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1441–1453. [Google Scholar] [CrossRef]
- Bolon-Canedo, V.; Sanchez-Marono, N.; Alonso-Betanzos, A. Feature Selection for High-Dimensional Data; Springer: Heidelberg, Germany, 2015; ISBN 978-3-319-21857-1. [Google Scholar]
- Singh, D.; Singh, B. Hybridization of Feature Selection and Feature Weighting for High Dimensional Data. Appl. Intell. 2019, 49, 1580–1596. [Google Scholar] [CrossRef]
- Hamedmoghadam, H.; Jalili, M.; Yu, X. An Opinion Formation Based Binary Optimization Approach for Feature Selection. Phys. A Stat. Mech. Its Appl. 2018, 491, 142–152. [Google Scholar] [CrossRef]
- Banitalebi, A.; Aziz, M.I.A.; Aziz, Z.A. A Self-Adaptive Binary Differential Evolution Algorithm for Large Scale Binary Optimization Problems. Inf. Sci. 2016, 367, 487–511. [Google Scholar] [CrossRef]
- Yang, J.; Honavar, V. Feature Subset Selection Using a Genetic Algorithm. IEEE Intell. Syst. 1998, 13, 44–49. [Google Scholar] [CrossRef]
- Raymer, M.L.; Punch, W.F.; Goodman, E.D.; Kuhn, L.A.; Jain, A.K. Dimensionality Reduction Using Genetic Algorithms. IEEE Trans. Evol. Comput. 2000, 4, 164–171. [Google Scholar] [CrossRef]
- Wu, K.; Yap, K. Feature Extraction; Guyon, I., Nikravesh, M., Gunn, S., Zadeh, L.A., Eds.; Studies in Fuzziness and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2006; Volume 207, ISBN 978-3-540-35488-8. [Google Scholar]
- Kabir, M.M.; Shahjahan, M.; Murase, K. A New Local Search Based Hybrid Genetic Algorithm for Feature Selection. Neurocomputing 2011, 74, 2914–2928. [Google Scholar] [CrossRef]
- Hodashinsky, I.A.; Mekh, M.A. Fuzzy Classifier Design Using Harmonic Search Methods. Program. Comput. Softw. 2017, 43, 37–46. [Google Scholar] [CrossRef]
- Moayedikia, A.; Ong, K.L.; Boo, Y.L.; Yeoh, W.G.; Jensen, R. Feature Selection for High Dimensional Imbalanced Class Data Using Harmony Search. Eng. Appl. Artif. Intell. 2017, 57, 38–49. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. The Ant System: Optimization by a Colony of Cooperating Agents. IEEE Trans. Syst. Man Cybern. Part B 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Vieira, S.M.; Sousa, J.M.C.; Runkler, T.A. Ant Colony Optimization Applied to Feature Selection in Fuzzy Classifiers. Lect. Notes Comput. Sci. 2007, 4529, 778–788. [Google Scholar]
- Erguzel, T.T.; Ozekes, S.; Gultekin, S.; Tarhan, N. Ant Colony Optimization Based Feature Selection Method for QEEG Data Classification. Psychiatry Investig. 2014, 11, 243. [Google Scholar] [CrossRef] [PubMed]
- Saraç, E.; Ozel, S.A. An Ant Colony Optimization Based Feature Selection for Web Page Classification. Sci. World J. 2014, 16, 649260. [Google Scholar] [CrossRef]
- Ghimatgar, H.; Kazemi, K.; Helfroush, M.S.; Aarabi, A. An Improved Feature Selection Algorithm Based on Graph Clustering and Ant Colony Optimization. Knowl. Based Syst. 2018, 159, 270–285. [Google Scholar] [CrossRef]
- Abdull Hamed, H.N.; Kasabov, N.K.; Shamsuddin, S.M. Quantum-Inspired Particle Swarm Optimization for Feature Selection and Parameter Optimization in Evolving Spiking Neural Networks for Classification Tasks. In Evolutionary Algorithms; InTech: Rijeka, Croatia, 2011; pp. 133–148. [Google Scholar]
- Zouache, D.; Ben Abdelaziz, F. A Cooperative Swarm Intelligence Algorithm Based on Quantum-Inspired and Rough Sets for Feature Selection. Comput. Ind. Eng. 2018, 115, 26–36. [Google Scholar] [CrossRef]
- Han, K.H.; Kim, J.H. Quantum-Inspired Evolutionary Algorithms with a New Termination Criterion, He Gate, and Two-Phase Scheme. IEEE Trans. Evol. Comput. 2004, 8, 164–171. [Google Scholar] [CrossRef]
- Nezamabadi-Pour, H. A Quantum-Inspired Gravitational Search Algorithm for Binary Encoded Optimization Problems. Eng. Appl. Artif. Intell. 2015, 40, 62–75. [Google Scholar] [CrossRef]
- Yuan, X.; Nie, H.; Su, A.; Wang, L.; Yuan, Y. An Improved Binary Particle Swarm Optimization for Unit Commitment Problem. Expert Syst. Appl. 2009, 36, 8049–8055. [Google Scholar] [CrossRef]
- Bouzidi, S.; Riffi, M.E. Discrete Swallow Swarm Optimization Algorithm for Travelling Salesman Problem. In Proceedings of the ACM International Conference Proceeding Series, Rabat, Morocco, 21–23 July 2017; ACM Press: New York, NY, USA, 2017; Volume F1305, pp. 80–84. [Google Scholar]
- Kiran, M.S.; Gunduz, M. XOR-Based Artificial Bee Colony Algorithm for Binary Optimization. Turk. J. Electr. Eng. Comput. Sci. 2013, 21, 2307–2328. [Google Scholar] [CrossRef]
- Korkmaz, S.; Kiran, M.S. An Artificial Algae Algorithm with Stigmergic Behavior for Binary Optimization. Appl. Soft Comput. J. 2018, 64, 627–640. [Google Scholar] [CrossRef]
- Singh, U.; Salgotra, R.; Rattan, M. A Novel Binary Spider Monkey Optimization Algorithm for Thinning of Concentric Circular Antenna Arrays. IETE J. Res. 2016, 62, 736–744. [Google Scholar] [CrossRef]
- Hodashinsky, I.A.; Nemirovich-Danchenko, M.M.; Samsonov, S.S. Feature Selection for Fuzzy Classifier Using the Spider Monkey Algorithm. Bus. Inform. 2019, 13, 29–42. [Google Scholar] [CrossRef]
- Kashan, M.H.; Nahavandi, N.; Kashan, A.H. DisABC: A new artificial bee colony algorithm for binary optimization. Appl. Soft Comput. J. 2012, 12, 342–352. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. A Discrete Binary Version of the Particle Swarm Algorithm. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; IEEE: Piscataway, NJ, USA, 1997; Volume 5, pp. 4104–4108. [Google Scholar]
- Mirjalili, S.; Lewis, A. S-Shaped Versus V-Shaped Transfer Functions for Binary Particle Swarm Optimization. Swarm Evol. Comput. 2013, 9, 1–14. [Google Scholar] [CrossRef]
- Crawford, B.; Soto, R.; Astorga, G.; Garcia, J.; Castro, C.; Paredes, F. Putting Continuous Metaheuristics to Work in Binary Search Spaces. Complexity 2017, 2017, 8404231. [Google Scholar] [CrossRef]
- Islam, M.J.; Li, X.; Mei, Y. A Time-Varying Transfer Function for Balancing the Exploration and Exploitation Ability of a Binary PSO. Appl. Soft Comput. J. 2017, 59, 182–196. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. BGSA: Binary Gravitational Search Algorithm. Nat. Comput. 2010, 9, 727–745. [Google Scholar] [CrossRef]
- Bardamova, M.; Konev, A.; Hodashinsky, I.; Shelupanov, A. A Fuzzy Classifier with Feature Selection Based on the Gravitational Search Algorithm. Symmetry 2018, 10, 609. [Google Scholar] [CrossRef]
- Xiang, J.; Han, X.; Duan, F.; Qiang, Y.; Xiong, X.; Lan, Y.; Chai, H. A Novel Hybrid System for Feature Selection Based on an Improved Gravitational Search Algorithm and k-NN Method. Appl. Soft Comput. J. 2015, 31, 293–307. [Google Scholar] [CrossRef]
- Arora, S.; Anand, P. Binary Butterfly Optimization Approaches for Feature Selection. Expert Syst. Appl. 2019, 116, 147–160. [Google Scholar] [CrossRef]
- Mafarja, M.; Aljarah, I.; Faris, H.; Hammouri, A.I.; Al-Zoubi, A.M.; Mirjalili, S. Binary Grasshopper Optimisation Algorithm Approaches for Feature Selection Problems. Expert Syst. Appl. 2019, 117, 267–286. [Google Scholar] [CrossRef]
- Mafarja, M.; Aljarah, I.; Heidari, A.A.; Faris, H.; Fournier-Viger, P.; Li, X.; Mirjalili, S. Binary Dragonfly Optimization for Feature Selection Using Time-Varying Transfer Functions. Knowl. Based Syst. 2018, 161, 185–204. [Google Scholar] [CrossRef]
- Panwar, L.K.; Reddy, K.; Verma, A.; Panigrahi, B.K.; Kumar, R. Binary Grey Wolf Optimizer for Large Scale Unit Commitment Problem. Swarm Evol. Comput. 2018, 38, 251–266. [Google Scholar] [CrossRef]
- Faris, H.; Mafarja, M.M.; Heidari, A.A.; Aljarah, I.; Al-Zoubi, A.M.; Mirjalili, S.; Fujita, H. An Efficient Binary Salp Swarm Algorithm with Crossover Scheme for Feature Selection Problems. Knowl. Based Syst. 2018, 154, 43–67. [Google Scholar] [CrossRef]
- Papa, J.P.; Rosa, G.H.; De Souza, A.N.; Afonso, L.C.S. Feature Selection Through Binary Brain Storm Optimization. Comput. Electr. Eng. 2018, 72, 468–481. [Google Scholar] [CrossRef]
- Mirjalili, S.; Wang, G.G.; Coelho, L.; Dos, S. Binary Optimization Using Hybrid Particle Swarm Optimization and Gravitational Search Algorithm. Neural Comput. Appl. 2014, 25, 1423–1435. [Google Scholar] [CrossRef]
- Garcia, J.; Crawford, B.; Soto, R.; Astorga, G. A Clustering Algorithm Applied to the Binarization of Swarm Intelligence Continuous Metaheuristics. Swarm Evol. Comput. 2019, 44, 646–664. [Google Scholar] [CrossRef]
- Hu, X.; Pedrycz, W.; Wang, X. Fuzzy Classifiers with Information Granules in Feature Space and Logic-Based Computing. Pattern Recognit. 2018, 80, 156–167. [Google Scholar] [CrossRef]
- Ganesh Kumar, P.; Devaraj, D. Fuzzy Classifier Design Using Modified Genetic Algorithm. Int. J. Comput. Intell. Syst. 2010, 3, 334–342. [Google Scholar] [CrossRef]
- Mekh, M.A.; Hodashinsky, I.A. Comparative Analysis of Differential Evolution Methods to Optimize Parameters of Fuzzy Classifiers. J. Comput. Syst. Sci. Int. 2017, 56, 616–626. [Google Scholar] [CrossRef]
- Neshat, M.; Sepidnam, G.; Sargolzaei, M. Swallow Swarm Optimization Algorithm: A New Method to Optimization. Neural Comput. Appl. 2013, 23, 429–454. [Google Scholar] [CrossRef]
- Alcala-Fdez, J.; Fernandez, A.; Luengo, J.; Derrac, J.; Garcia, S.; Sanchez, L.; Herrera, F. KEEL Data-Mining Software Tool: Data Set Repository, Integration of Algorithms and Experimental Analysis Framework. J. Mult. Log. Soft Comput. 2011, 17, 255–287. [Google Scholar]
- Cheng, S. Brain Storm Optimization Algorithm, Concepts, Principles and Applications; Cheng, S., Shi, Y., Eds.; Springer: Cham, Switzerland, 2019; ISBN 978-3-030-15070-9. [Google Scholar]
- Cai, J.; Luo, J.; Wang, S.; Yang, S. Feature Selection in Machine Learning: A New Perspective. Neurocomputing 2018, 300, 70–79. [Google Scholar] [CrossRef]
- Wolpert, D.H. The Existence of a Priori Distinctions Between Learning Algorithms. Neural Comput. 1996, 8, 1341–1420. [Google Scholar] [CrossRef]
| Dataset | Number of Classes | Number of Features | Number of Examples |
|---|---|---|---|
| apendicitis | 2 | 7 | 106 |
| balance | 3 | 4 | 625 |
| banana | 2 | 2 | 5300 |
| bupa | 2 | 6 | 345 |
| cleveland | 5 | 13 | 297 |
| coil2000 | 2 | 85 | 9822 |
| contraceptive | 3 | 9 | 1473 |
| dermatology | 6 | 34 | 358 |
| ecoli | 8 | 7 | 336 |
| glass | 7 | 9 | 214 |
| haberman | 2 | 3 | 306 |
| heart | 2 | 13 | 270 |
| hepatitis | 2 | 19 | 80 |
| ionosphere | 2 | 33 | 351 |
| iris | 3 | 4 | 150 |
| magic | 2 | 10 | 19020 |
| newthyroid | 3 | 5 | 215 |
| optdigits | 10 | 64 | 5620 |
| ring | 2 | 20 | 7400 |
| segment | 7 | 19 | 2310 |
| spambase | 2 | 57 | 4597 |
| tae | 3 | 5 | 151 |
| texture | 11 | 40 | 5500 |
| thyroid | 3 | 21 | 7200 |
| titanic | 2 | 3 | 2201 |
| twonorm | 2 | 20 | 7400 |
| vehicle | 4 | 18 | 846 |
| wdbc | 2 | 30 | 569 |
| wine | 3 | 13 | 178 |
| wisconsin | 2 | 9 | 683 |
| Parameter | Setting |
|---|---|
| N—Population of particles | 40 |
| l—local leaders | 3 |
| k—aimless particles | 6 |
| Iterations | 300 |
| pve | 0.7 |
| pvhl | 0.7 |
| phe | 0.9 |
| pher | 0.9 |
| ple | 0.8 |
| pler | 0.8 |
| Dataset | All features | IG | BSSO | RS | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Learn | Test | F‘ | Learn | Test | F‘ | Learn | Test | F‘ | Learn | Test | |
| apendicitis | 72.15 | 66.77 | 4.90 | 79.05 | 78.40 | 3.30 | 83.03 | 79.32 | 3.40 | 83.03 | 80.23 |
| balance | 46.24 | 46.25 | 2.00 | 38.88 | 38.90 | 3.60 | 46.26 | 45.93 | 3.50 | 46.26 | 45.77 |
| banana | 44.45 | 44.41 | 1.00 | 59.42 | 59.40 | 1.00 | 59.42 | 59.40 | 1.00 | 59.42 | 59.40 |
| bupa | 49.47 | 46.92 | 1.70 | 46.60 | 46.89 | 2.90 | 60.48 | 61.15 | 2.90 | 60.48 | 59.98 |
| cleveland | 54.07 | 54.04 | 5.00 | 53.58 | 53.05 | 7.70 | 57.02 | 51.63 | 7.20 | 56.95 | 51.28 |
| coil2000 | 9.75 | 9.67 | 33.70 | 37.91 | 37.99 | 37.60 | 93.84 | 93.75 | 39.60 | 92.87 | 92.74 |
| contraceptive | 42.63 | 42.71 | 5.40 | 42.33 | 42.30 | 2.20 | 44.65 | 44.54 | 2.30 | 44.65 | 44.47 |
| dermatology | 93.95 | 89.68 | 13.00 | 41.14 | 38.09 | 20.80 | 97.73 | 92.46 | 19.20 | 97.30 | 92.46 |
| ecoli | 32.79 | 32.89 | 3.50 | 50.49 | 51.40 | 3.90 | 53.57 | 53.32 | 3.90 | 53.57 | 53.32 |
| glass | 55.81 | 52.65 | 3.30 | 25.31 | 21.62 | 6.00 | 61.00 | 54.02 | 6.30 | 63.54 | 52.71 |
| haberman | 45.43 | 45.47 | 2.00 | 44.73 | 44.83 | 1.10 | 70.15 | 70.61 | 1.10 | 70.15 | 70.61 |
| heart | 56.87 | 55.93 | 5.10 | 58.26 | 55.92 | 3.60 | 70.41 | 64.07 | 3.50 | 70.04 | 64.07 |
| hepatitis | 64.36 | 60.08 | 9.20 | 51.14 | 41.65 | 8.10 | 94.31 | 85.16 | 8.10 | 93.20 | 84.98 |
| ionosphere | 87.94 | 87.45 | 9.40 | 67.14 | 67.00 | 7.00 | 85.41 | 81.28 | 8.90 | 78.92 | 74.36 |
| iris | 93.85 | 94.00 | 2.00 | 96.74 | 96.67 | 2.10 | 96.89 | 94.67 | 2.00 | 96.89 | 94.67 |
| magic | 56.70 | 56.75 | 6.00 | 60.15 | 60.16 | 3.90 | 71.39 | 71.44 | 3.90 | 71.39 | 71.44 |
| newthyroid | 96.54 | 95.39 | 3.00 | 94.89 | 94.39 | 3.40 | 97.88 | 95.84 | 3.50 | 97.88 | 95.37 |
| optdigits | 23.41 | 23.12 | 22.30 | 24.46 | 24.10 | 37.80 | 47.32 | 46.00 | 35.60 | 42.93 | 41.72 |
| ring | 49.51 | 49.52 | 10.20 | 49.17 | 49.19 | 1.00 | 58.50 | 58.44 | 4.60 | 54.52 | 53.20 |
| segment | 72.20 | 71.48 | 6.00 | 20.31 | 20.09 | 8.30 | 88.26 | 86.02 | 8.80 | 87.78 | 85.46 |
| spambase | 56.81 | 56.73 | 27.90 | 63.84 | 64.29 | 22.60 | 73.57 | 73.45 | 25.10 | 70.93 | 70.74 |
| tae | 35.17 | 36.41 | 3.50 | 34.66 | 34.41 | 2.80 | 41.80 | 41.07 | 3.00 | 41.80 | 40.40 |
| texture | 64.48 | 68.55 | 19.10 | 27.88 | 27.84 | 13.00 | 68.49 | 68.31 | 16.00 | 66.85 | 66.09 |
| thyroid | 22.50 | 22.50 | 17.30 | 92.31 | 92.36 | 1.50 | 93.33 | 93.24 | 1.80 | 88.38 | 89.14 |
| titanic | 68.53 | 66.52 | 1.00 | 77.61 | 77.87 | 1.50 | 77.61 | 77.87 | 1.50 | 77.61 | 77.87 |
| twonorm | 96.87 | 96.91 | 10.10 | 88.32 | 88.20 | 19.70 | 96.89 | 96.91 | 19.90 | 96.67 | 95.68 |
| vehicle | 25.40 | 24.83 | 8.00 | 21.93 | 21.75 | 8.10 | 49.24 | 43.74 | 7.70 | 47.47 | 45.88 |
| wdbc | 90.43 | 90.17 | 18.50 | 93.40 | 92.97 | 10.90 | 97.34 | 96.12 | 11.70 | 96.09 | 95.78 |
| wine | 89.82 | 87.57 | 6.10 | 50.01 | 45.36 | 6.50 | 96.57 | 94.41 | 7.00 | 95.86 | 94.31 |
| wisconsin | 92.81 | 92.25 | 6.30 | 75.68 | 74.98 | 5.60 | 94.42 | 93.85 | 7.10 | 94.63 | 92.75 |
| Average | 59.70 | 58.92 | 8.88 | 55.58 | 54.74 | 8.58 | 74.23 | 72.27 | 9.00 | 73.27 | 71.23 |
| Dataset | BMA | BGA(S) | BGA(V) | BBA(S) | BBA(V) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Test | F‘ | Test | F‘ | Test | F‘ | Test | F‘ | Test | F‘ | |
| apendicitis | 76.36 | 2.90 | Nr 1 | nr | nr | nr | 78.76 | 3.10 | 77.11 | 3.40 |
| balance | 46.24 | 4.00 | nr | nr | nr | nr | 46.08 | 3.04 | 46.08 | 3.04 |
| banana | 59.36 | 1.00 | nr | nr | nr | nr | nr | nr | nr | nr |
| bupa | 58.17 | 2.70 | 59.80 | 2.80 | 60.00 | 2.70 | 57.30 | 2.74 | 56.56 | 2.66 |
| cleveland | 54.15 | 8.20 | 52.50 | 7.30 | 54.40 | 2.80 | 53.30 | 6.40 | 52.00 | 8.36 |
| coil2000 | 74.96 | 31.3 | 90.60 | 38.5 | 94.00 | 1.00 | nr | nr | nr | nr |
| contraceptive | 44.06 | 2.80 | nr | nr | nr | nr | nr | nr | nr | nr |
| dermatology | 90.99 | 21.6 | nr | nr | nr | nr | nr | nr | nr | nr |
| ecoli | 51.22 | 3.90 | nr | nr | nr | nr | 50.30 | 3.34 | 50.90 | 3.48 |
| glass | 56.12 | 6.20 | 56.00 | 5.10 | 53.20 | 5.90 | 57.60 | 5.30 | 55.40 | 5.73 |
| haberman | 67.96 | 1.10 | nr | nr | nr | nr | 57.50 | 1.90 | 57.60 | 1.90 |
| heart | 74.21 | 5.40 | 67.00 | 2.80 | 67.70 | 3.00 | 66.60 | 3.36 | 66.70 | 4.20 |
| hepatitis | 85.51 | 8.10 | 87.20 | 7.90 | 82.50 | 5.30 | 84.52 | 9.40 | 81.22 | 9.17 |
| ionosphere | 91.58 | 16.8 | nr | nr | nr | nr | 89.29 | 16.4 | 89.81 | 18.2 |
| iris | 94.67 | 1.80 | nr | nr | nr | nr | 95.07 | 1.92 | 94.80 | 1.90 |
| magic | nr | nr | 70.70 | 4.10 | 70.70 | 4.10 | 71.41 | 3.90 | 70.41 | 4.32 |
| newthyroid | 96.77 | 3.50 | 96.50 | 3.70 | 96.50 | 3.30 | 93.67 | 4.15 | 94.02 | 4.20 |
| optdigits | nr | nr | nr | nr | nr | nr | nr | nr | nr | nr |
| ring | 58.39 | 1.00 | 58.60 | 1.00 | 57.90 | 1.00 | nr | nr | nr | nr |
| segment | 81.90 | 9.00 | 85.70 | 9.10 | 84.10 | 8.80 | nr | nr | nr | nr |
| spambase | 74.27 | 23.7 | 65.40 | 27.0 | 70.00 | 2.70 | nr | nr | nr | nr |
| tae | nr | nr | nr | nr | nr | nr | nr | nr | nr | nr |
| texture | 73.69 | 12.1 | nr | nr | nr | nr | nr | nr | nr | nr |
| thyroid | 90.93 | 1.80 | 99.30 | 20.0 | 99.30 | 16.9 | nr | nr | nr | nr |
| titanic | 77.60 | 1.40 | nr | nr | nr | nr | nr | nr | nr | nr |
| twonorm | 96.74 | 19.7 | 96.80 | 19.9 | 96.10 | 17.8 | nr | nr | nr | nr |
| vehicle | 47.87 | 5.90 | 45.60 | 7.80 | 40.00 | 4.80 | 43.05 | 6.16 | 40.55 | 6.56 |
| wdbc | 95.18 | 10.4 | nr | nr | nr | nr | nr | nr | nr | nr |
| wine | 96.08 | 6.20 | 94.80 | 5.80 | 92.20 | 6.80 | 92.39 | 6.28 | 93.56 | 6.74 |
| wisconsin | 93.59 | 5.30 | 94.00 | 5.70 | 93.60 | 3.50 | nr | nr | nr | nr |
| Median of Differences | Standardized Test Statistic | p-Value | Null Hypothesis |
|---|---|---|---|
| BSSO_Learn—All_Learn | 4.659 | <0.001 | Reject |
| BSSO_Learn—IG_Learn | 4.623 | <0.001 | Reject |
| BSSO_Learn—RS_Learn | 3.070 | 0.002 | Reject |
| BSSO_Test—All_Test | 4.206 | <0.000 | Reject |
| BSSO_Test—IG_Test | 4.418 | <0.000 | Reject |
| BSSO_Test—RS_Test | 3.263 | 0.001 | Reject |
| BSSO_Test—BSMA_Test | 0.127 | 0.899 | Retain |
| BSSO_Test—BGSA(S)_Test | −0.379 | 0.879 | Retain |
| BSSO_Test—BGSA(V)_Test | 1.060 | 0.299 | Retain |
| BSSO_Test—BBSO(S)_Test | 0.682 | 0.496 | Retain |
| BSSO_Test—BBSO(V)_Test | 1.363 | 0.173 | Retain |
| BSSO_F‘—IG_F‘ | −0.389 | 0.697 | Retain |
| BSSO_F‘—RS_F‘ | −2.027 | 0.043 | Reject |
| BSSO_F‘—BSMA_F‘ | −0.522 | 0.602 | Retain |
| BSSO_F‘—BGSA(S)_F‘ | −0.455 | 0.649 | Retain |
| BSSO_F‘—BGSA(V)_F‘ | 1.847 | 0.065 | Retain |
| BSSO_F‘—BBSO(S) _F | −0.502 | 0.615 | Retain |
| BSSO_F‘—BBSO(V) _F | −1.193 | 0.233 | Retain |
| Dataset | BSSO | RS | IG |
|---|---|---|---|
| apendicitis | 2.4969 | 1.7509 | 0.0690 |
| balance | 8.6825 | 7.2545 | 0.0909 |
| banana | 28.8653 | 26.7955 | 0.1769 |
| bupa | 4.3853 | 4.0395 | 0.0807 |
| cleveland | 13.7823 | 10.5905 | 0.1189 |
| coil2000 | 649.0763 | 502.0300 | 115.3146 |
| contraceptive | 25.6143 | 23.5633 | 0.2409 |
| dermatology | 34.5858 | 30.0775 | 0.2775 |
| ecoli | 12.4913 | 12.1631 | 0.1179 |
| glass | 7.7928 | 7.5788 | 0.1019 |
| haberman | 2.7073 | 2.3386 | 0.0730 |
| heart | 5.3957 | 3.7275 | 0.0929 |
| hepatitis | 2.5654 | 2.1653 | 0.0760 |
| ionosphere | 11.6846 | 11.0012 | 0.1689 |
| iris | 2.2396 | 2.0328 | 0.0700 |
| magic | 210.2207 | 186.0533 | 6.4670 |
| newthyroid | 3.9593 | 3.8287 | 0.0780 |
| optdigits | 1355.8079 | 1300.9188 | 26.0010 |
| ring | 135.9984 | 75.0970 | 2.5237 |
| segment | 134.1489 | 124.1207 | 1.0419 |
| spambase | 213.8056 | 145.8274 | 11.2431 |
| tae | 2.4275 | 2.4025 | 0.0710 |
| texture | 980.7259 | 679.4120 | 12.0827 |
| thyroid | 200.5548 | 113.6152 | 4.5406 |
| titanic | 10.3387 | 9.7130 | 0.1179 |
| twonorm | 200.8571 | 141.2837 | 4.1145 |
| vehicle | 29.2830 | 26.9224 | 0.2696 |
| wdbc | 16.3909 | 14.0634 | 0.2389 |
| wine | 4.9080 | 4.8560 | 0.0879 |
| wisconsin | 8.6997 | 8.2846 | 0.1189 |
| Model | Unstandardized Coefficients | t | Sig. Level | 95.0% Confidence Interval for B | ||||
|---|---|---|---|---|---|---|---|---|
| B | Std. Error | Lower Bound | Upper Bound | |||||
| (Constant) | −285.890 | 54.884 | −5.209 | 0.000 | −398.707 | −173.074 | ||
| NoCl | 60.487 | 11.764 | 5.142 | 0.000 | 36.306 | 84.667 | ||
| NoFe | 7.682 | 1.607 | 4.780 | 0.000 | 4.378 | 10.985 | ||
| NoEx | 0.022 | 0.007 | 2.975 | 0.006 | 0.007 | 0.037 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hodashinsky, I.; Sarin, K.; Shelupanov, A.; Slezkin, A. Feature Selection Based on Swallow Swarm Optimization for Fuzzy Classification. Symmetry 2019, 11, 1423. https://doi.org/10.3390/sym11111423
Hodashinsky I, Sarin K, Shelupanov A, Slezkin A. Feature Selection Based on Swallow Swarm Optimization for Fuzzy Classification. Symmetry. 2019; 11(11):1423. https://doi.org/10.3390/sym11111423
Chicago/Turabian StyleHodashinsky, Ilya, Konstantin Sarin, Alexander Shelupanov, and Artem Slezkin. 2019. "Feature Selection Based on Swallow Swarm Optimization for Fuzzy Classification" Symmetry 11, no. 11: 1423. https://doi.org/10.3390/sym11111423
APA StyleHodashinsky, I., Sarin, K., Shelupanov, A., & Slezkin, A. (2019). Feature Selection Based on Swallow Swarm Optimization for Fuzzy Classification. Symmetry, 11(11), 1423. https://doi.org/10.3390/sym11111423






