Makeup Interpolation Based on Color and Shape Parametrization

Abstract

In this paper, we address the problem of synthesizing continuous variations with the appearance of makeup by taking a linear combination of the examples. Makeup usually shows a vague boundary and does not form a clear shape, which makes this problem unique from the existing image interpolation problems. We approach this problem as an interpolation between semi-transparent image layers and tackle this by presenting new parametrization schemes for the color and for the shape separately in order to achieve an effective interpolation. For the color parametrization, our main idea is based on the observation of the symmetric relation between the color and transparency of the makeup; we provide an optimization framework for extracting a representative palette of colors associated with the transparent values, which enables us to easily set up the color correspondence among the multiple makeup samples. For the shape parametrization, we exploit a polar coordinate system, that creates the in-between shapes effectively, without ghosting artifacts.

1. Introduction

Digital makeup has become more important in recent years, and a great deal of effort has been devoted to the study of believably transferring a example makeup to a new subject [1,2]. Furthermore, an automated makeup suggestion system has been presented based on a makeup database [3], which helps the users to find several candidate makeup styles that are suitable for their own faces. Previous research, however, does not allow modifications to the examples during transferring, which may limit the usability when the users want to adjust the suggested example makeup to fit to their faces in their own ways. Here, we present a method for modifying the existing makeup examples by taking a linear combination of them. For the modification purpose, this linear combination of the examples can be more intuitive than conventional image manipulation techniques; this can be especially prevalent for the novice users who do not know what they want exactly, and it also expands the possibilities for the makeup suggestion systems to enable continuous variation of the output makeup.

We approach this problem as an interpolation between semi-transparent images because the conventional digital makeup process ends up with adding a semi-transparent makeup image layer over a given target no-makeup facial image. A naive per-pixel interpolation between the makeup image layers would suffer from well-known ghosting artifacts in the synthesized result. Applying the conventional image interpolation methods based on feature matching also would not be trivial when explicit corresponding features do not exist between the transparent alpha mattes. In fact, makeup usually does not form a clear shape. Instead, it tends to be blended naturally with the skin and has a vague boundary. To the best of our knowledge, there has been no attempt to interpolate the images with such alpha mattes yet.

We tackle this problem by presenting new parametrization schemes for the color and for the shape separately in order to achieve an effective interpolation. For the color parametrization, we provide an optimization framework for extracting a representative palette of colors associated with the transparent values for each given makeup image layer. This enables us to easily set up the color correspondence among the multiple makeup examples. Based on the observation of the examples, we also suggest parameterizing the shape in a polar coordinate system, which is turned out to create the in-between shapes effectively without the ghosting artifacts. Please note, however, that our method is not a general-purpose image interpolation method. It is specialized and customized for semi-transparent images without clear shapes, such as makeup layers. Here, we also mainly focus on the makeup around the eye region because it is often one of the most complicated and interesting regions for facial makeup.

The paper consists of the following sections. First we introduce several related works in Section 2. Then, we provide a detailed description about the method in Section 3. We demonstrate the effectiveness of our interpolation method with the experimental results in Section 4. Finally, we conclude the paper and discuss the limitations and the future work in Section 5.

2. Related Work

The analysis and the synthesis of human skin have attracted many researchers in the field of image processing and they have made a good deal of improvement. This is especially true with skin color spectrum analysis [4,5,6]. Since cosmetic makeup over a person’s skin is an ordinary activity in daily life, the analysis of its resulting color spectrum has also drawn attention from researchers [7,8]. Based on those results, Huang et al. presented a physics-based method for a realistic rendering of synthetic makeup [9]. For digital makeup, the transference of a makeup sample to a new subject has been an active research area. Ojima et al. proposed a method to extract a makeup mask from a pair of before and after makeup face images and then transferred the mask map to other faces [10]. Since their method is only applicable to skin-colored foundation makeup, there have been several succeeding research results extending the makeup transfer to be suitable for color makeup as well. Tong et al. measured the quotient of the after divided by the before makeup face images to represent the spatially-varying intensity of the makeup and used it for transferring the extracted makeup component [1]. Guo et al. proposed a new method for extracting the makeup from a single after-makeup image. They decomposed the makeup into several layers and applied them over different faces [2]. To preserve the personal features and lighting conditions while transferring, Li et al. proposed separating the facial image into intrinsic image layers and physics-based reflectance models [11].

While these previous works related to makeup are mainly focused on transferring, Scherbaum et al. proposed a method to suggest the best makeup by analyzing the input face images. For this purpose, they constructed a database of example makeup related to different facial shapes and skin tones. Then, given an input face image, they found the face shape that is the most similar in the database and suggest its corresponding cosmetic map as the best suitable makeup for the input [3].

During the digital makeup, the existing methods do not allow modifications of the example makeup. This, however, may restrict their usage when the user wants to adjust the resulting digital makeup. In fact, unlike those makeup transfer methods from academia, many commercial makeup systems provide the users with the flexibility of choosing colors, densities, and textures through graphical user interfaces such as the color palettes and virtual brushes [12,13]. However, these interactive systems heavily depend on the user’s manual work, which makes it hard to achieve a good makeup result from scratch, especially for novice users. Recently, more advanced makeup simulation systems have been developed to help users get useful information at each makeup step and to quickly learn how to use the systems [14,15]. However, the controllability of these systems is still restricted to a few primitive methods, such as changing the colors or the textures of predefined shapes.

Our work is also closely related to the conventional image morphing methods. Most of the methods, however, require an explicit registration of the features from the input images [16,17,18,19]. For images without clear feature correspondences, methods based on optimal mass transport have been presented [20,21,22]. As these methods assume mass conservation during the morphing process, the methods work well mainly for shapes of a similar size. Recently, based on an implicit shape representation, Sanchez et al. generated a morphing sequence of a volumetric object from one shape to another [23]. Although the method basically deals with a 3D object, it can be applied to the implicit images without much modification. However, the method still aims at objects with clear boundaries.

Recently, in the graphics community, there has been progress in applying deep neural networks to synthesize images satisfying user given conditions. Given a single reference makeup image, Liu et al. proposed a deep transfer network for transferring the input makeup to a target face image [24], where the shape and the color of the input makeup are preserved during the process. In various image synthesis applications, conditional generative adversarial networks (GAN) have drawn much attention and have been widely used to learn mappings between a set of two image pairs [25]. However, it is practically hard to apply this approach to makeup applications due to the many makeup and no-makeup image pairs required for training. Later, inspired by GAN, CycleGAN was introduced, which can be applied to the unpaired training image sets [26,27]. Chang et al. adopted this approach and presented a method for transferring the makeup style of an input image to new facial images [28].

In comparison to the related work, this paper addresses the novel problem of synthesizing continuous variations of the makeup. Our approach lies between the transfer and the simulation of the makeup. We model the makeup layer with tailored parameterizations, which enables the users to make manipulations intuitively.

3. Makeup Interpolation

3.1. Preparation of Examples

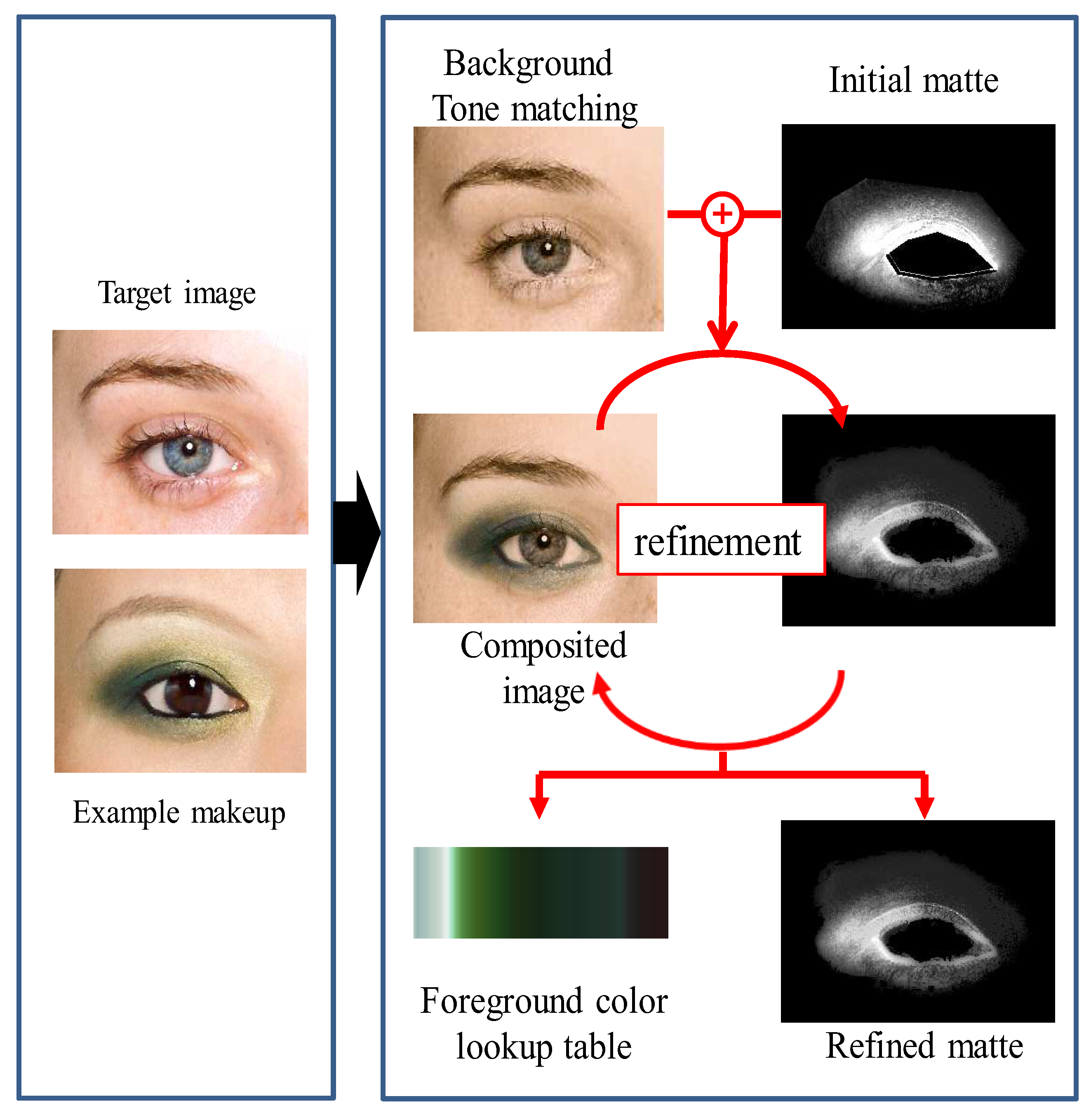
By taking multiple makeup facial image examples as inputs and an additional no-makeup facial image as a target, our method synthesizes a makeup image of the target subject. Figure 1 shows the input image examples and the target image.

The input makeup images are preprocessed to be aligned with the target image. For this purpose, we first find 88 facial feature points from each image by applying the active shape model [30]. During this process, we manually adjust, if necessary, the positions of a few erroneous points. Then, we apply the thin plate spline-based image warping technique [31] to deform the example images, so they match with the target image as shown in Figure 2. We choose this method due to its simplicity in implementation, and it works sufficiently well for our purposes. Please note, however, that there have been many alternative methods recently presented for this registration process [32] if a more precise alignment is required.

3.2. Initial Makeup Matting

Facial makeup usually consists of two layers: One is for the skin-colored foundation to reduce blemishes and wrinkles, and the other is for the colorization of specific facial regions, such as the eyes and the lips. The foundation is applied on the whole face relatively uniformly while the colorization is put on locally. Here, we are more interested in the local colorization, especially around the eyes, such as the eyeshadow, and extract the makeup from each example image to form a semi-transparent makeup layer.

We consider the process of this layer separation as the matting problem, in which the example makeup image $\mathbf{I}(x,y)$ is the composition of the background no-makeup facial image $\mathbf{B}(x,y)$ and the foreground makeup image layer $\mathbf{F}(x,y)$ with the transparency matte $\alpha (x,y)$, where $\alpha \in [0,1]$. This matting is formulated as:

$$\mathbf{I}=(1-\alpha )\mathbf{B}+\alpha \mathbf{F},$$

(1)

where position $(x,y)$ is omitted in the equation for the simplicity of the notation. Matting is a problem of estimating $\mathbf{B}$, $\mathbf{F}$, and $\alpha$ with only given $\mathbf{I}$, which is a severely under-constrained problem. Thus, to make the problem solvable, it requires additional assumptions about the background and the foreground or about the alpha matte. A typical minimal assumption is given by the user as the trimap which denotes the definitely backgroundregion and the definitely foreground region in the image. Then, a matting algorithm solves the remaining undecided region. Figure 3b shows the example of the input trimap, where black, white, and gray define the definitely background, the definitely foreground, and the undecided region respectively.

As the matting is a under-constrained problem, virtually any arbitrary $\mathbf{F}$ or matte $\alpha$ can still be the solution to reconstruct the input $\mathbf{I}$ by computing the according $\mathbf{B}$ from Equation (1) as long as the values of alpha and the resulting images do not violate the range conditions, such as being non-negative and not exceeding the maximum intensity value. Thus, it requires more assumptions about the solutions, and these assumptions are different from the application domains. With various assumptions, there are many matting algorithms available with their own pros and cons [33].

Here, we are not aiming at inventing a new general-purpose matting algorithm. Instead, our method takes the matting result from any matting algorithm as an initial input, and refines it to be suitable for the interpolation while reflecting the specific characteristics of the makeup. We choose to use the matting method of Shahrian and his colleagues [34] and its resulting mattes are treated as the initial input for our refinement process described in the following subsection. Figure 3c shows the initial matting result.

3.3. Matte Refinement

We refine the initial input matte to be more suitable for the makeup interpolation in consideration of the following two criteria:

• Accuracy: Resembles the original example makeup image well when applied to the new target no-makeup image.
• Controllability: Is easy to be modified and blended with other mattes.

For accuracy, we take advantage of the characteristics of the makeup layer. In the conventional matting problem, the main difficulty lies in the fact that there is seldom a general measure available to quantify the quality of the resulting matte. In our case, however, we know beforehand that the resulting matte is going to be applied to the target no-makeup image, and afterward, its composited result should resemble the example makeup image well. In other words, the target no-makeup image can be used to approximate the background of the source example makeup image, which makes our matting problem more solvable.

For controllability, we reduce the number of controllable parameters by abstracting the $\alpha$ and $\mathbf{F}$ to be as concise as possible. In the color makeup, such as the eyeshadow, we observed a certain tendency in the change of color roughly correlated with that of density of the makeup in many cases. Figure 4 demonstrates this tendency, in which the tone of the color changes gradually and generates a gradation effect along with the direction approximately coinciding with the gradient direction of the alpha value. Based on this observation, we formulate the foreground color embedded into the alpha matte, which is:

$$\mathbf{F}=f\left(\alpha \right).$$

(2)

This parametrization of $\mathbf{F}$ eventually allows us to simplify the process of the makeup interpolation; the color correspondences between the makeups are given by the transparent values.

Our refining process consists of two steps. First, we adjust the overall tone of the target image as close to the input example makeup images as possible (Section 3.3.1). Then, we apply the initial makeup matte to the target image and iteratively optimize the alpha and the foreground color parametrization under the above criteria (Section 3.3.2). This two-step process is illustrated in Figure 5.

3.3.1. Background Color Tone Matching

Our basic strategy for measuring the matting quality is to apply the matte to the target no-makeup image and evaluate it by comparing it with the source example makeup image. However, the subjects in both images are generally different in their skin colors. Even if the subject is the same, the foundation makeup results in the difference in the overall skin tone. Thus, we first adjust the overall skin tone of the target no-makeup image to match with that of the source makeup image.

To match the skin colors apart from the localized effect, such as the eyeshadow, we only consider the definitely background region defined in the user given trimap. To match the color tone between the images, one of the popular candidates is to use the histogram matching algorithm [35]. However, the usual facial images do not contain enough intensity variations with less dark area, which causes overfitting. Instead, we suggest using a linear regression model to match the colors of the images, which is:

$$\left(\begin{array}{c}{\widehat{\mathbf{B}}}_r^t\\ {\widehat{\mathbf{B}}}_g^t\\ {\widehat{\mathbf{B}}}_b^t\end{array}\right)=\mathbf{A}\left(\begin{array}{c}{\mathbf{B}}_r^t\\ {\mathbf{B}}_g^t\\ {\mathbf{B}}_b^t\\ 1\end{array}\right),$$

(3)

where ${\mathbf{B}}_r^t$, ${\mathbf{B}}_g^t$ and ${\mathbf{B}}_b^t$ are the red, green and blue components of the background region of the target image, and $\mathbf{A}$ is the $3\times 4$ linear regression matrix. ${\widehat{\mathbf{B}}}^t$ is the resulting adjusted background image. Note that the regression matrix has four columns in order to incorporate a constant addition term. We applied the least squares to compute the regression matrix as follows:

$$arg\underset{\mathbf{A}}{min}{\left({\mathbf{B}}^e-{\widehat{\mathbf{B}}}^t\right)}^2$$

(4)

where ${\mathbf{B}}^e$ is the portion of the example makeup image belonging to the definitely background region. Figure 6 shows the matching results, where the overall color tone of the leftmost target no-makeup image becomes similar to those of the example makeup images.

3.3.2. Foreground Color Parametrization

We explain how to parameterize the foreground color with respect to the transparency $\alpha$ as shown in Equation (2) while maintaining the quality of the matte. As we store the transparent value in 8 bits in a discrete manner for the implementation, rather than deriving an analytic, continuous function, we realize this parametrization as a look-up table that relates each discrete alpha value to its corresponding foreground color.

Because the foreground color and the alpha are coupled in the matting process as shown in Equation (1), we adopt an expectation maximization (EM) framework for the optimization. First, we fix the alpha and find the best foreground color for each alpha value. Then, we fix the foreground color and adjust the alpha value at each pixel to generate the best result. We repeat the process until it converges. We describe the details of each step below.

Expectation step: For each alpha value, we compute a representative single foreground color value. We reformulate the matting Equation (1) to compute the foreground color given with the alpha and the background color:

$$\mathbf{F}=\frac{{\mathbf{I}}^e-(1-\alpha ){\widehat{\mathbf{B}}}^t}{\alpha },$$

(5)

where ${\mathbf{I}}^e$ is the example makeup image and ${\widehat{\mathbf{B}}}^t$ is the adjusted target image obtained from Equation (3). We choose the representative foreground color for each alpha value by averaging the computed foreground colors of all the pixels with the same alpha. Performing this process for every alpha value, which includes 256 discrete alpha values in our implementation, completes the foreground color look-up table, which is $\mathbf{F}=\mathrm{lookup}\left[\alpha \right]$.

Maximization step: For each pixel, we adjust the alpha value while fixing the foreground lookup table such that the composited target image is as close as possible to the example source makeup image. Given the alpha value ${\alpha }_p$ from the previous iteration, we simply try each of the possible alpha values in the range of $[{\alpha }_p-k,{\alpha }_p+k]$ and choose the best one, that is:

$$arg\underset{\alpha }{min}\parallel {\mathbf{I}}^e-(1-\alpha ){\widehat{\mathbf{B}}}^t-\alpha ·\mathrm{lookup}\left[\alpha \right]\parallel .$$

(6)

In our experiments, we set the searching range k to be $0.1$.

To enforce the spatial consistency of the alpha values, we apply the Gaussian smoothing to the alpha before performing each expectation step. As we only adjust the alpha values in the undecided region, applying the Gaussian smoothing to the whole region results in a diffusion effect near the boundary region, so that the alpha value of the pixels near to the definitely background region becomes closer to 0 while those near to the definitely foreground region get closer to 1. This also prevents the alpha values from the divergence during the optimization. Likewise we apply the Gaussian smoothing to the foreground color lookup table before each maximization step to enforce the consistency along with the alpha value. In our experiments, this EM process converges in less than 30 iterations for all examples. 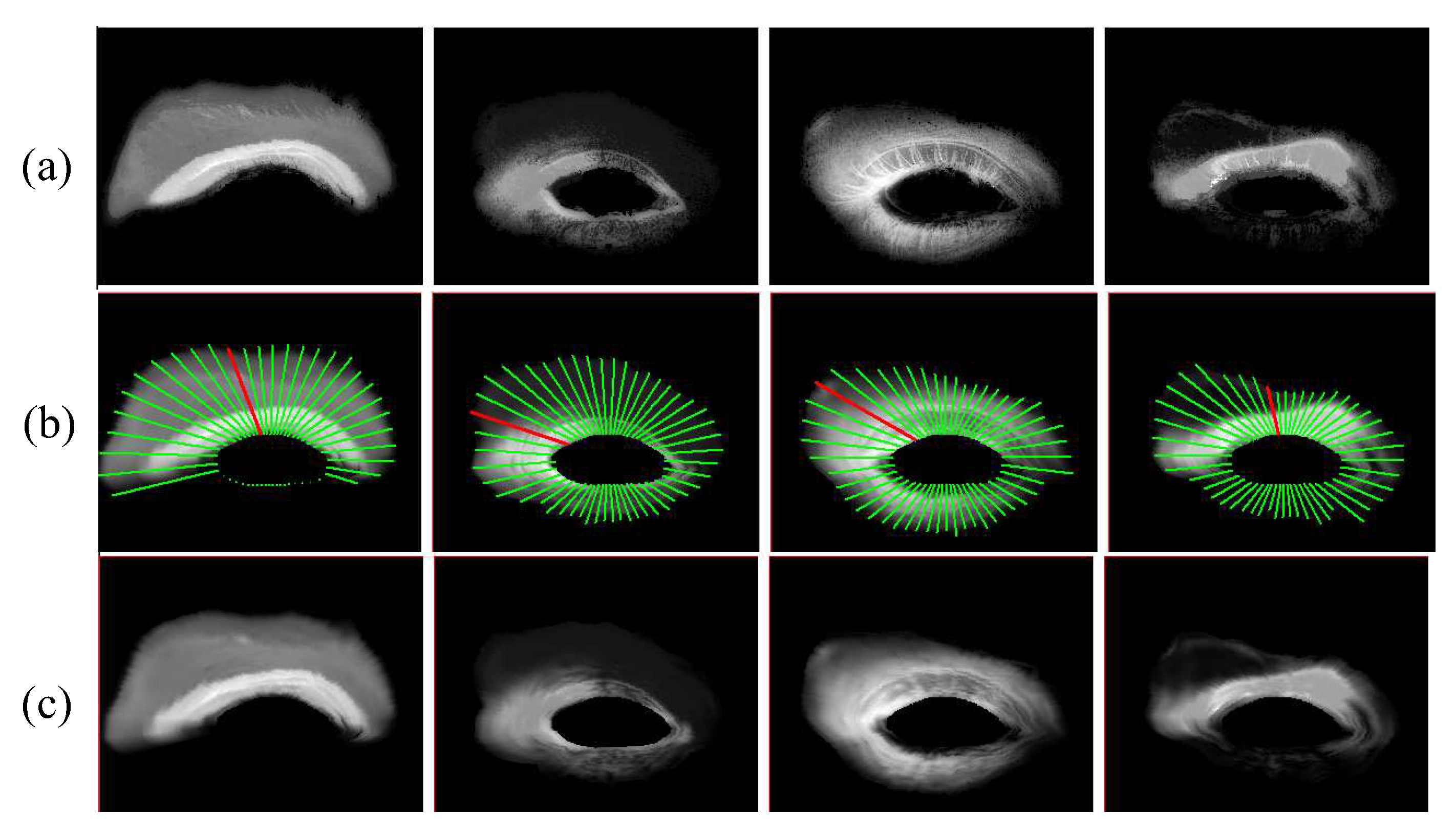Figure 7 shows the refinement results compared to the initial mattes. It also shows the resulting color parametrization in the bottom row.

3.4. Shape Parametrization

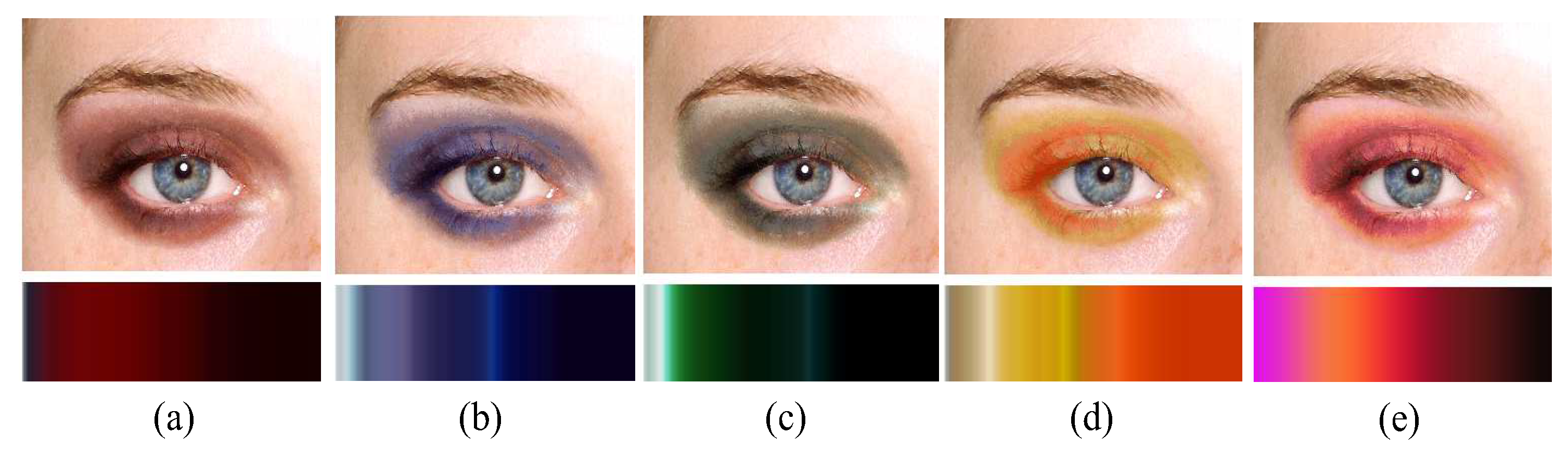
The purpose of our shape parameterization of the alpha matte is to facilitate an effective interpolation by reflecting the intrinsic characteristics of makeup. From observing many real makeup examples, we found that the shapes of the makeup usually form similar shapes to an elliptical that is aligned to a certain orientation. The eyeshadows, which are shown in Figure 4, are the typical examples of this type. Inspired by this observation, we represent the makeup shape in a polar coordinate system.

The polar coordinate system is defined by its origin and the reference radial direction of zero degrees. We choose to locate the origin at the center of the eyeball region. For the reference radial direction, one of the possible candidates would be the principal direction from the principal component analysis (PCA) [35]. However, our origin does not coincide with the centroid of the alpha matte, which makes it hard to apply the principal direction. Instead, we compute the centroid of the matte from the image moment [36] and take the offset direction from the origin to the centroid as the reference radial direction, by which we reflect the bias direction of the alpha distribution.

With the given polar coordinate system, we model the alpha distribution. In a conventional image interpolation, creating believable boundary shapes of the inbetweens is important for a convincing result. On the other hand, in our case, creating the convincing inner patterns of the matte is more important because the makeup matte usually does not show a clear boundary. For this purpose, we represent the alpha distribution by sampling the values along a radial direction and approximate them with the cubic B-splines. We build 48 B-spline approximations that are evenly spaced along the angular direction to represent the shape, as shown in Figure 8b, where the red lines in the figure denote the reference zero-degrees direction.

For each B-spline approximation, we place the knots in a non-uniform manner to reflect the distribution of the alpha. Our knot placing strategy is as follows: we first place two knots $n_1$ and $n_2$ at both the beginning and the end of the sample range with non-zero alpha values. Then, we compute the centroid of the alpha values between these two knots and place a new knot $n_3$ at the centroid position, which divides the region into two sub-regions of $[n_1,n_3]$ and $[n_3,n_2]$. For each sub-region, we place a new knot at the centroid of the alpha values. We continue this process until the total number of the knots reaches a user specific number. In our experiments, we place 32 knots for each B-spline approximation and Figure 8c shows the approximation results.

3.5. Makeup Synthesis

Through the parameterization, the makeup matte is converted into a pair of foreground color $\mathrm{lookup}\left[\alpha \right]$ and a set of B-spline approximations $\mathbf{S}$ with their own polar coordinate system. Then, we synthesize a new makeup matte (${\mathrm{lookup}}_{new}\left[\alpha \right],{\mathbf{S}}_{new}\left[\alpha \right]$) by taking a weighted average of the multiple example makeup mattes as follows:

$$\begin{array}{cc}\hfill {\mathrm{lookup}}_{new}\left[\alpha \right]& =\sum _i^N{w}_i·{\mathrm{lookup}}_i\left[\alpha \right]\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\mathbf{S}}_{new}\left[\alpha \right]& =\sum _i^N{w}_i·{\mathbf{S}}_i,\hfill \end{array}$$

(8)

where the subscript i means the i-th example, the $w_i$ is the weight value, and N is the total number of the examples. For averaging the foreground color lookup tables, we represent the color in the CIELAB color space as it results in a perceptually smooth transition of the lightness during the interpolation [37].

The generated alpha matte from the B-spline approximation smoothens out the fine details from the example alpha mattes. We recover the lost details by applying the method of texture-by-numbers from the image analogies from Herzmann et al. [38]. The texture-by-numbers method requires a pair of input images. The first one is a photograph, and the other is its simple abstraction. Then, a new synthetic photograph can be generated by providing only a new guiding abstract image. In our case, the B-spline approximation is considered as the abstraction, and the details are synthesized by pasting the best-matching small patches that are found in the example mattes. We accelerate this process by using the patch match method [39].

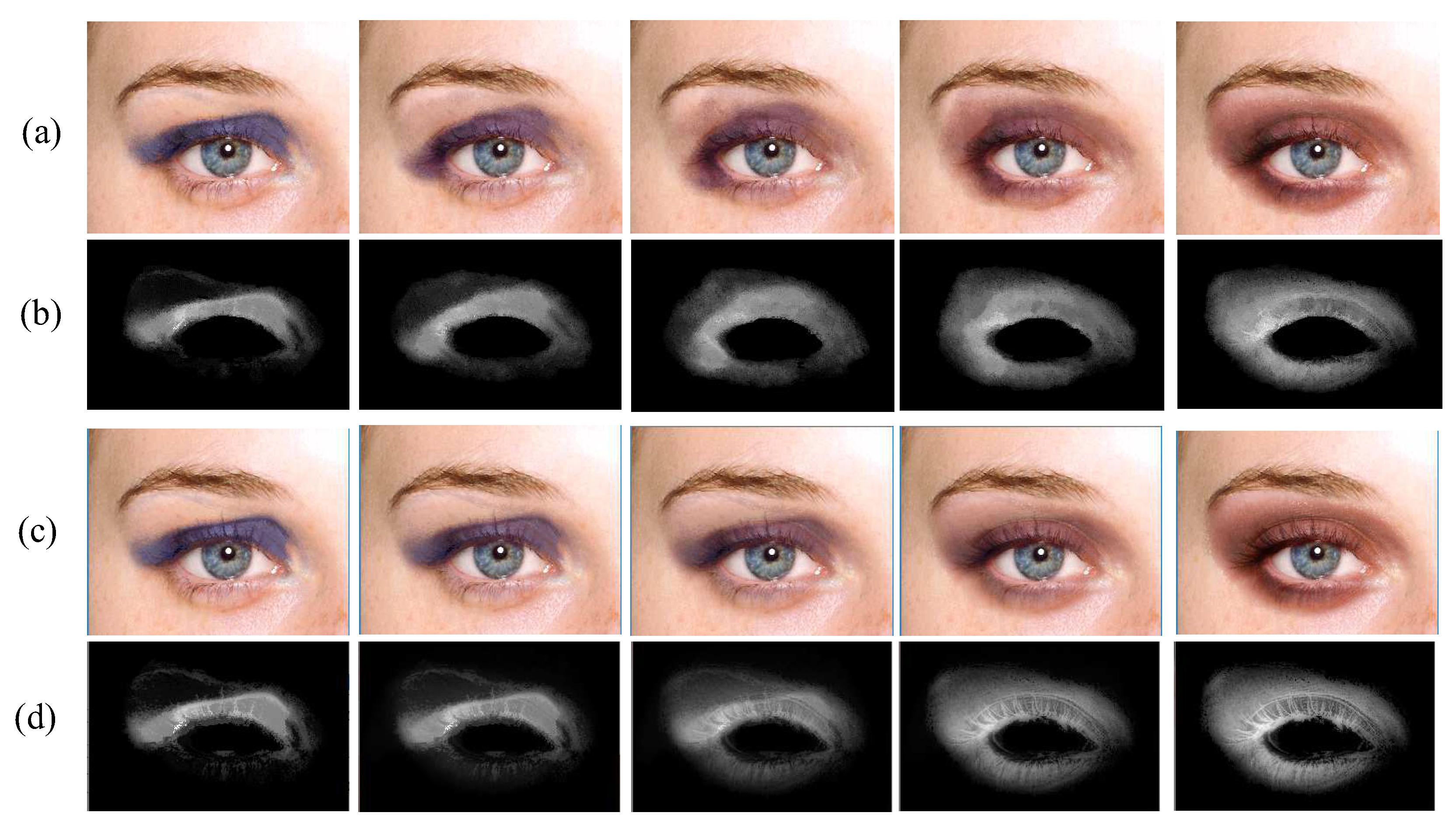
The upper row images of Figure 10 shows the synthesis results by interpolating between two example makeups. The second row is the resulting matte by interpolating between the B-splines, and the third row is the results after adding the details using the patch match method. We also obtain the inbetween foreground color lookup tables shown in the bottom row.

4. Experimental Results

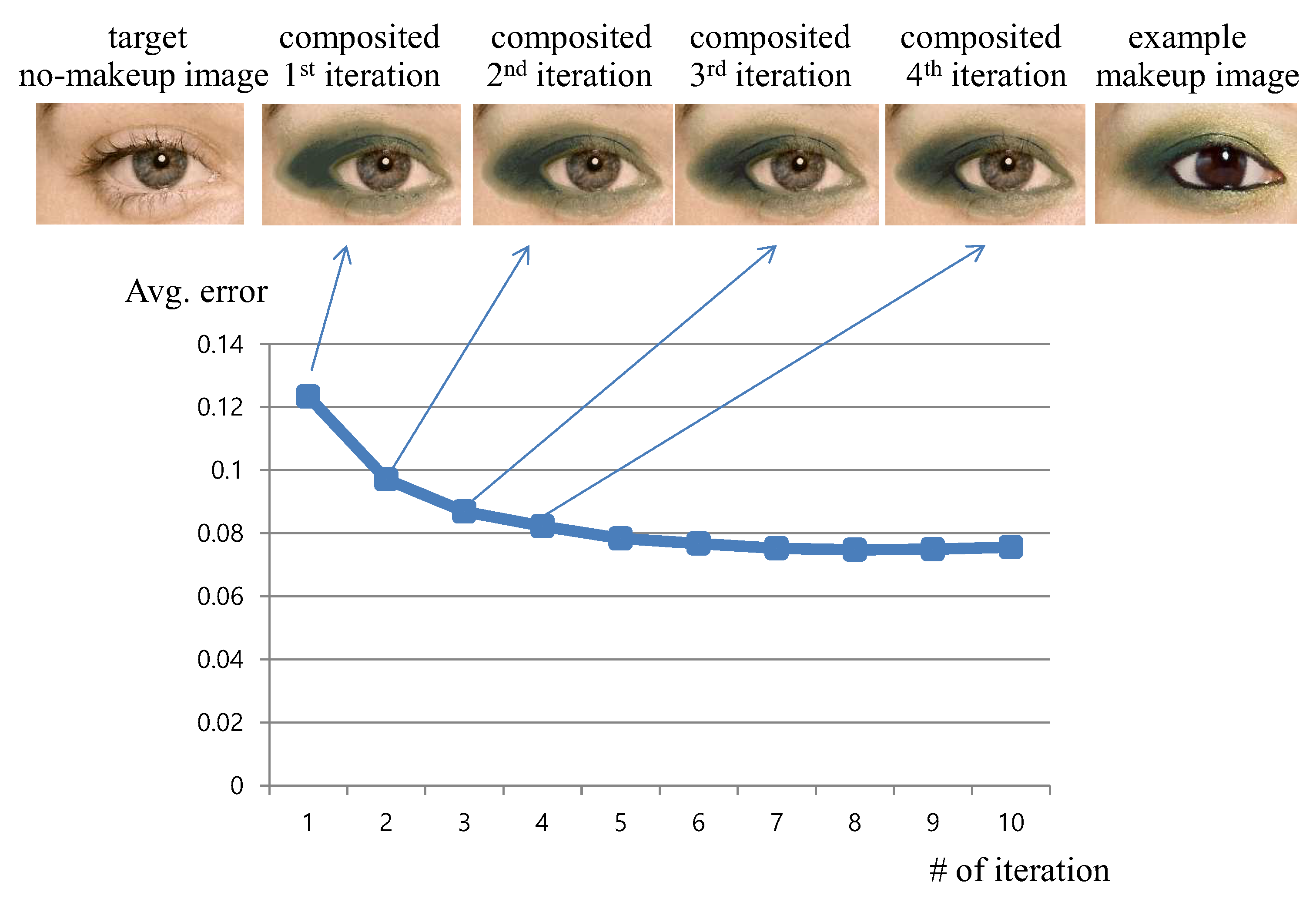
We first show the convergence of our foreground color parametrization in Figure 9. The upper images are the composited makeup images that are applied to the target no-makeup image. The errors are measured by comparing them with the example makeup image. The process converges quickly, which is shown in the graph. Along with the iteration, the composited makeup improves to resemble the example. Please watch the supplementary video showing the refinement process and the convergence of the parametrization.

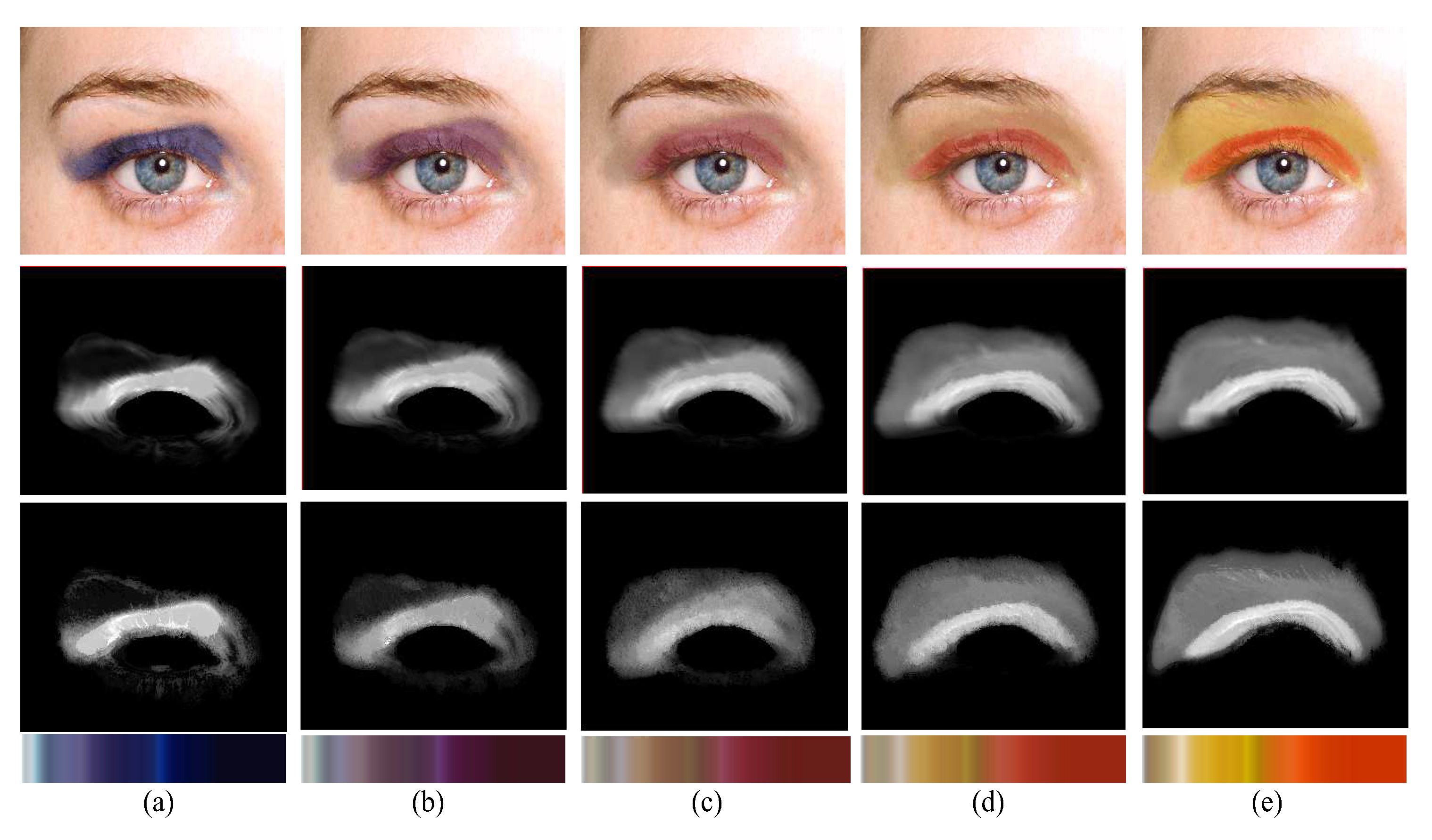
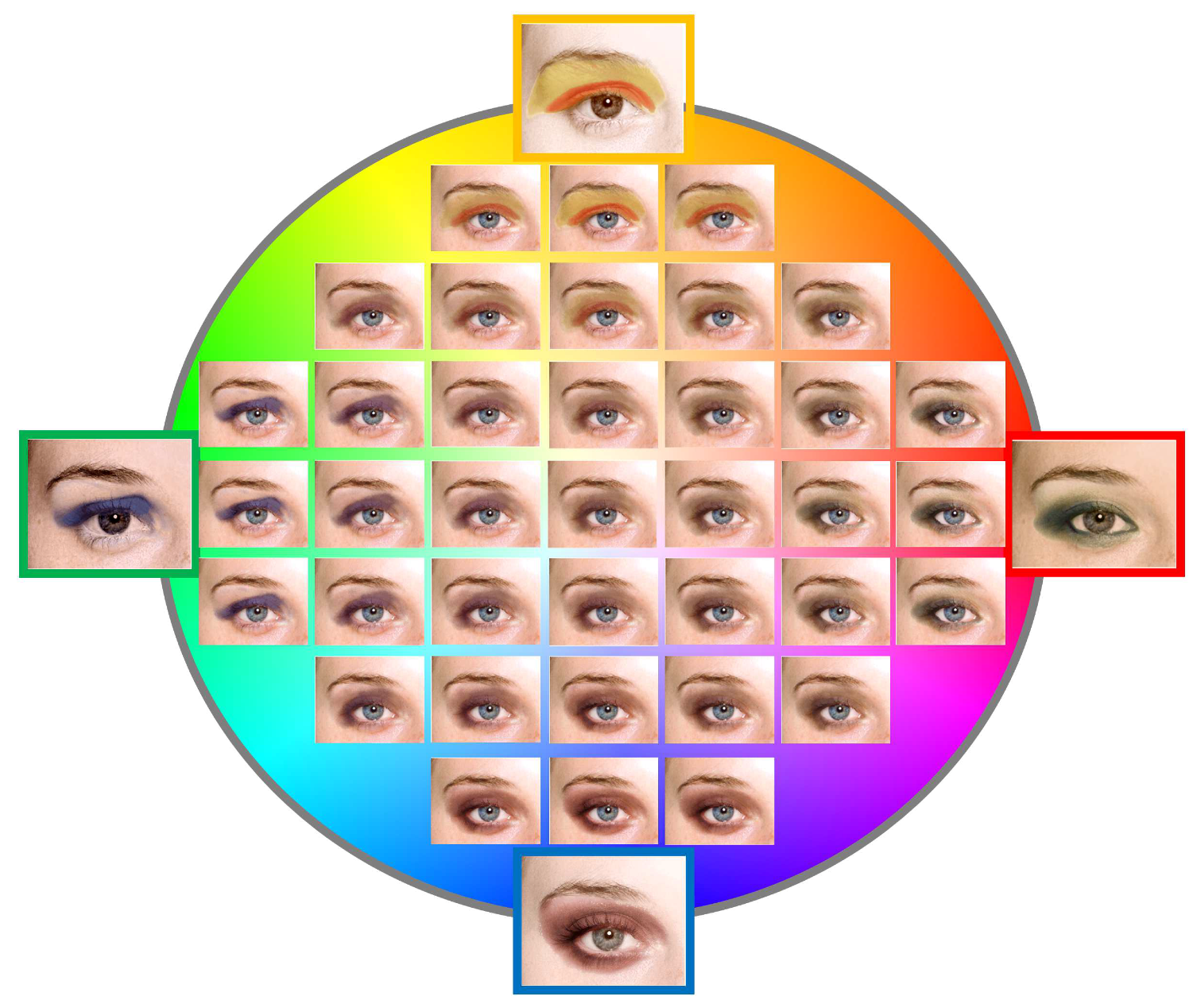
Figure 10 and Figure 11 show the in-between results by interpolating between the two makeup examples. Both the shape and the color change in an intuitive way without suffering from any ghosting artifacts. Figure 12 shows the various linear combination results of the four different makeup examples. We can see the continuous variations in the appearance of the synthesized makeup. Please watch the supplementary video for the morphing sequences.

As illustrated in Figure 13, our color parametrization facilitates the user to easily edit the makeup color by simply changing the foreground color lookup table. This is as intuitive as using a color palette for painting.

Figure 14 shows the comparison results between the presented method and the simple image blending method, in which the colors and the transparencies of each pixel pair of the same position from two different mattes are interpolated. As demonstrated in the figure, the shape change is more noticeable in our results.

5. Conclusions and Discussion

In this paper, we present a method for makeup interpolation based on the color and the shape parametrization. Our method generates interesting continuous variations in the appearance of the makeup. To the best of our knowledge, it is the first attempt to create a morphing sequence from the example alpha mattes. Our main technical contribution is to present a new customized parametrization method that is suitable for makeup mattes. By correlating the foreground color with the alpha, we obtain a smooth, intuitive transition of color. The B-spline approximation in a radial direction enables us to capture the characteristics of the makeup shapes.

Our method has some limitations though. First of all, as we focused on color makeup, such as eyeshadows, the method would not be applicable for interpolating between complicated patterns, such as graffiti on a wall. However, we believe that cloud-like shapes can still be a possible application of our method without much modification. While interpolating between the foreground color lookup tables, we simply mix the colors of the same alpha value. However, if we find a correspondence between the lookup tables by matching the color patterns, it would generate a more interesting transition. Although we applied our method only to eyeshadow in our experiments, we believe that our method can be applied to other makeup, for instance blush makeup on the cheek or to lipstick as well. Finally, for future work, we would like to exploit current deep learning techniques to our problem. Recently developed generative adversarial networks (GAN) have been successfully applied to various user guided image synthesis tasks [26,40,41]. Thus, instead of relying on the interpolation or the transfer of the existing makeup, professional and proper makeup can be generated from rough sketches of novice users, from which they can benefit by learning how to do makeup more effectively.