Algorithm for Detecting Communities in Complex Networks Based on Hadoop
Abstract
:1. Introduction
- Based on the idea of the maximum modularity, and combining the distributed characteristics of the Hadoop platform, a new modularity matrix update method is proposed and a corresponding community merging strategy is constructed to implement a fast and accurate detection and discovery of complex network community structures;
- We theoretically analyze our proposed CDOH algorithm, and show the computational cost of our algorithm can achieve computational cost when we use enough parallel nodes;
- Experimental results on 3 real datasets demonstrate that CDOH significantly outperforms the traditional complex network community detection algorithm in terms of both the efficiency and accuracy of the community detection of complex networks.
2. Related Works
3. Complex Network Community Detecting Algorithm Based on Hadoop
3.1. Definitions
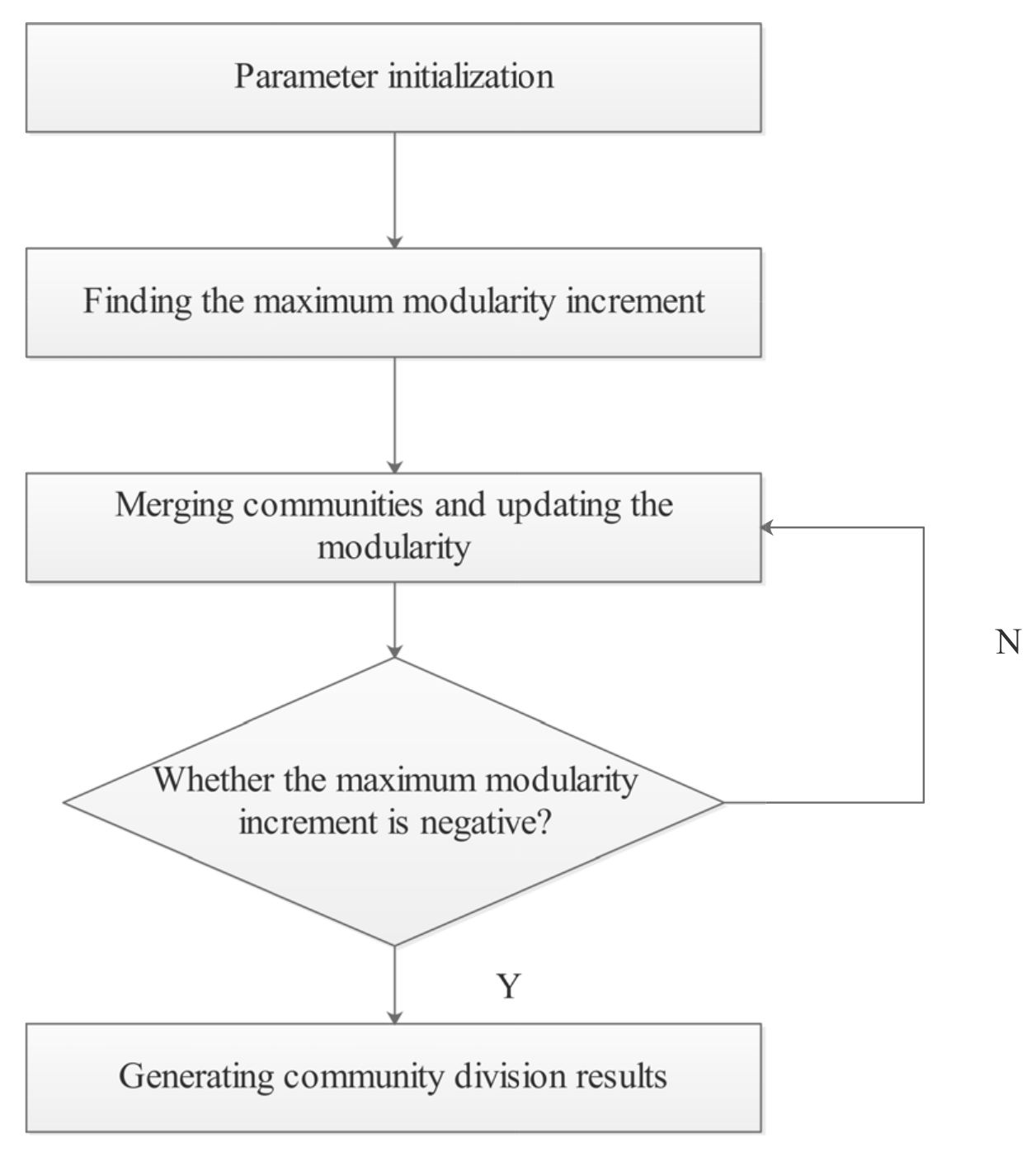
3.2. The CDOH Algorithm
3.2.1. Parameter Initialization
- First, we load the complex network data from the input file, then calculate the number of nodes n and edges m of the complex network, and broadcast the number of edges (m) to all nodes;
- Finally, we use Equation (4) to calculate the modularity increment between each pair of nodes, and construct a new network N using this modularity increment.
| Algorithm 1 Initialization of CDOH Parameters |
| Input: D: Preprocessed network data; Output: : Modularity increment; N: Network; 1: N = networkLoad(D); 2: n = getVertices(N); 3: m = getEdges(N); 4: Broadcast the number of edges m to all nodes in the cluster; 5: for each Node i in N do 6: = getDegree(i); 7: ; 8: for each Edge e in N do 9: ; |
3.2.2. Find the Maximum Modularity Increment
- First, we compare the value of each edge e in network N, find the maximum modularity increment , and broadcast it to all nodes in the cluster;
- Second, we get the cartesian product T of the edge set E and node set V, , s denotes the number of the source node, d denotes the number of destination node, and denote the community numbers of the source node and destination node respectively, and denotes the modularity increment between the source node and destination node;
- Third, we find the sub-set in the set T, where equals to ;
- Finally, to organize the merged communities, we obtain the community number (i) of the source node and the community number (j) of the destination node, which represent the current communities to be merged. If i or j already belongs to a new community in C, we will get the new community to merge i and j into it, or merge i and j into another new community, whose number is . The final output is the community C after merging.
| Algorithm 2 Find the Maximum Modularity Increment and Communities that need to be Merged |
| Input: : Modularity increment; : Network; Output: : Communities; : Maximum Modularity increment; 1: ; 2: Broadcasting to all nodes in the cluster; 3: ; 4: for each quintuple t in T do 5: if then 6: ; 7: for each quintuple t in do 8: ; 9: if or then 10: k = Get the new number of community i or j from C; 11: = insert(i,j); 12: else 13: n = n + 1; 14: = insert(i, j); |
3.2.3. Merging and Updating Communities
- First, we obtain the Cartesian product T of the node set V and edge set E. Then, we look for the new community number corresponding to and in . Let X to be the set of community numbers to be merged in this round contained by the new community of the community and Y to be the set of community numbers to be merged in this round contained by the new community of the community ;
- Second, using Equation (5), we will merge and update community i in X and community j in Y. If there is an edge connecting communities i and j, then the modularity increment between new communities X and Y should include the modularity increment between communities i and j. However, if there is no edge connecting communities i and j, the modularity increment between new communities X and Y should be reduced by the doubled product of vector value of community i and vector value of community j.
| Algorithm 3 Merging and Updating Communities |
| Input: : Communities; N(E,V): Network; Output: : Updated Network; 1: Update the number of the communities that need to be merged and the community number of the corresponding nodes to their corresponding new community number; 2: ; 3: for each quintuple t in T do 4: ; 5: ; 6: if ( or ) and then 7: X = a set of community numbers to be merged in this round contained by the new community corresponding to ; 8: Y = a set of community numbers to be merged in this round contained by the new community corresponding to ; 9: for each community i in X and each community j in Y do 10: if there exists at least an edge connecting i and j then 11: 12: else 13: |
3.2.4. Generating Community Discovery Results
- We will first traverse all nodes and keep the nodes with the same community number together. If is already in C, it means that the corresponding community of has already appeared. The node in the community that have been stored in C need to be taken out, merged with the current node , and then stored in C; otherwise they are stored in C directly;
- Then we store the community and community’s node set on the Hadoop distributed file system (HDFS) one by one. Thus, CDOH stores the final results of community discovery with a set of the tuple , and finishes the detection and discovery of complex network communities on Hadoop platform.
| Algorithm 4 Generating Community Discovery Results |
| Input: : Network; Output: : Communities; 1: for each in N do 2: if then 3: g = getNodeId(); 4: c = insert(); 5: C = insert(); 6: else 7: C = add(); 8: for each community c in C do 9: output c; |
3.3. Computational Complexity Analysis of the CDOH Algorithm
4. Experimental Results
4.1. Datasets and Evaluation Algorithms
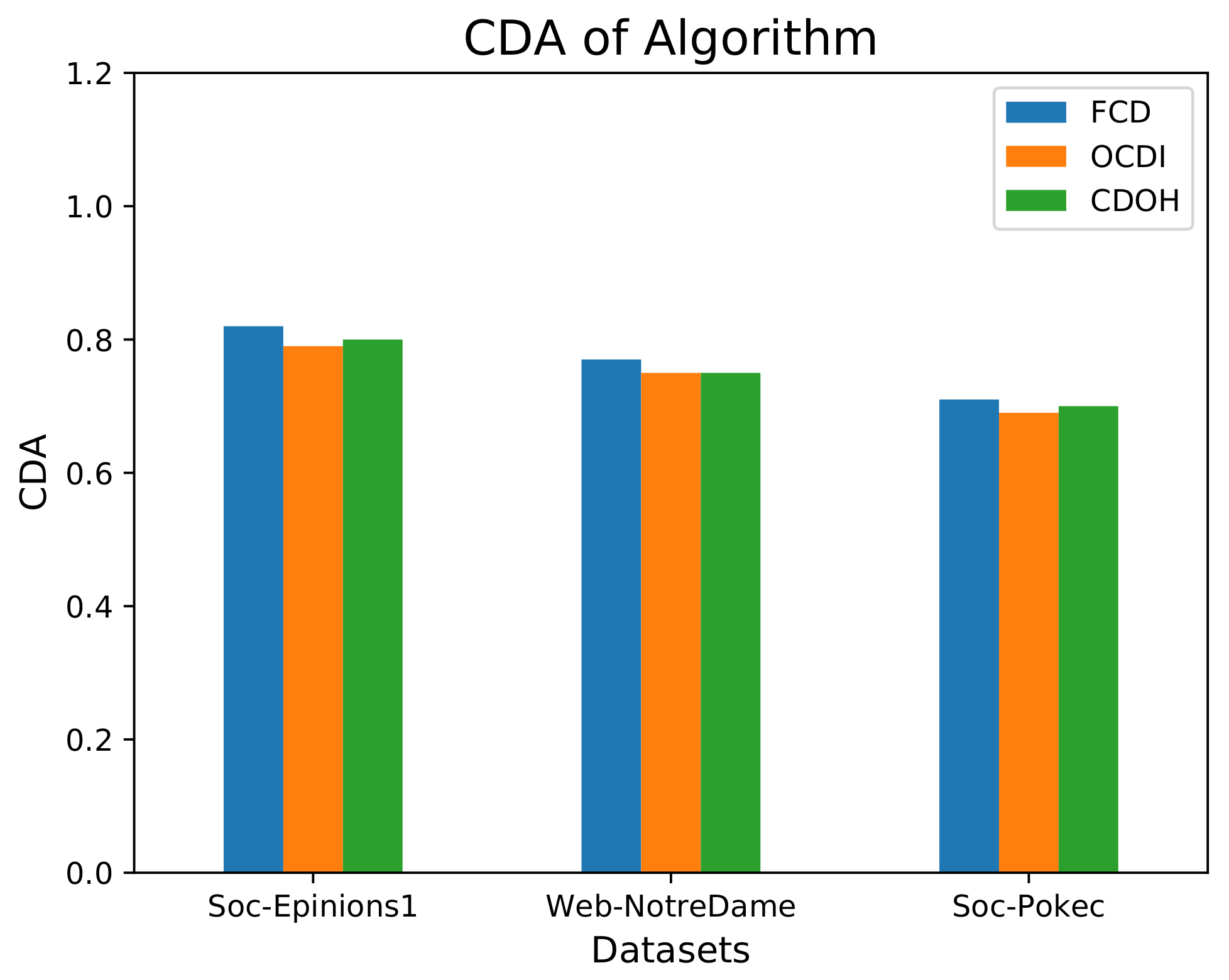
4.2. Analysis of Community Detection Accuracy
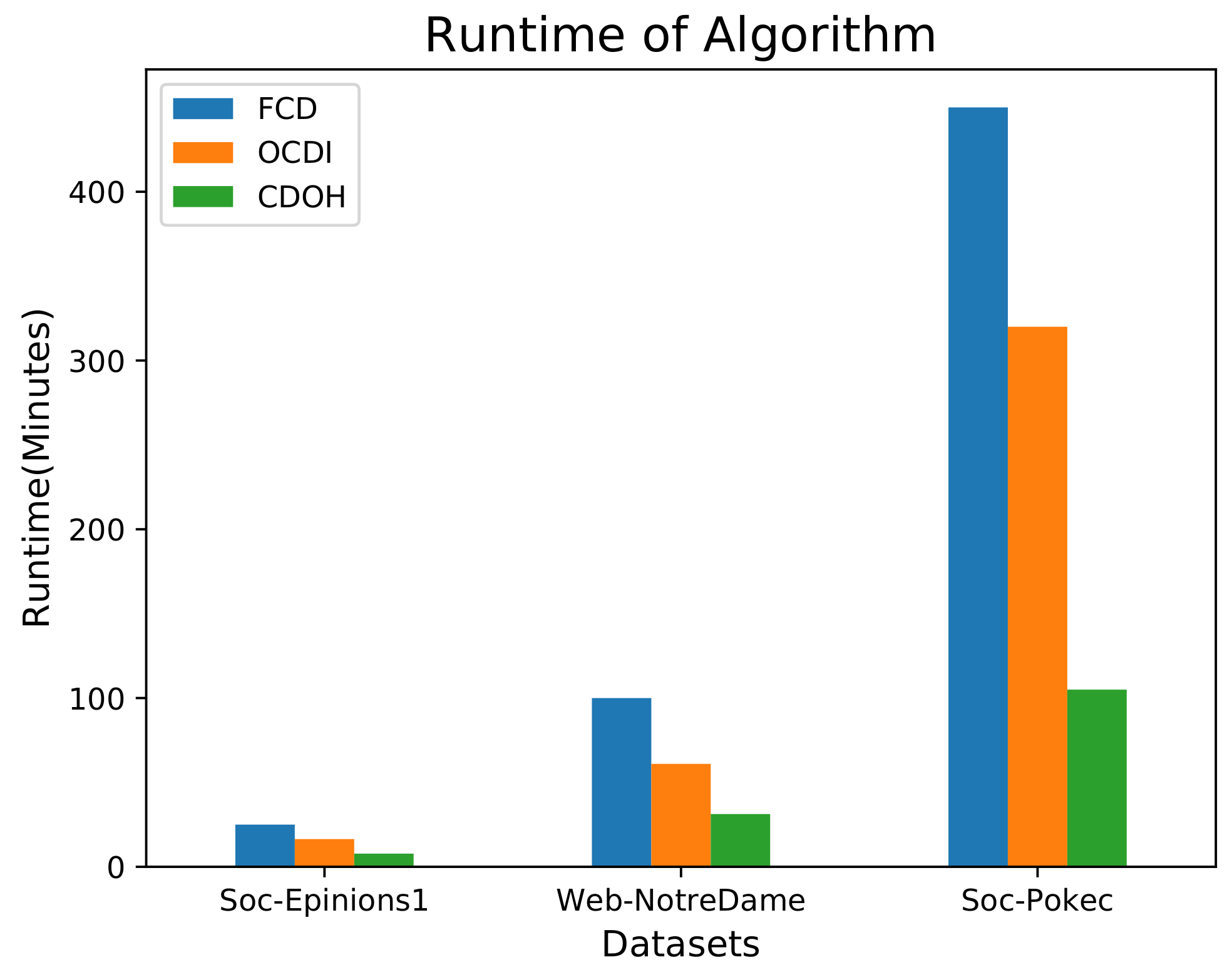
4.3. Analysis of Community Detection Efficiency
5. Conclusions and Future Works
5.1. Conclusions
5.2. Future Works
Author Contributions
Funding
Conflicts of Interest
References
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Faloutsos, M.; Faloutsos, P.; Faloutsos, C. On power-law relationships of the Internet topology. ACM SIGCOMM Comput. Commun. Rev. 1999, 29, 251–262. [Google Scholar] [CrossRef]
- Sen, P.; Manna, S.S. Clustering properties of a generalized critical Euclidean network. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2003, 68, 026104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zheng, X.; Chen, J.; Shao, J.; Bie, L. Topological properties analysis of Beijing public transport network based on complex network theory. J. Phys. 2012, 61, 95–105. [Google Scholar]
- Fan, R. Cooperative Innovation of Social Governance under the Paradigm of Complex Network Structure. Soc. Sci. China 2014, 4, 98–120. [Google Scholar]
- Newman, M.E.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2003, 69, 17–32. [Google Scholar] [CrossRef]
- Yang, J.; Leskovec, J. Defining and evaluating network communities based on ground-truth. Knowl. Inf. Syst. 2015, 42, 181–213. [Google Scholar] [CrossRef]
- Xin, S.; Giancarlo, S.; Vincenzo, M.; Antonio, P.; Christian, E.; Chang, C. An Edge Intelligence Empowered Recommender System Enabling Cultural Heritage Applications. IEEE Trans. Ind. Inf. 2019, 15, 4266–4275. [Google Scholar]
- Newman, M.E. Fast algorithm for detecting community structure in networks. Phys. Rev. E 2003, 69, 066133. [Google Scholar] [CrossRef]
- Clauset, A.; Newman, M.E.; Moore, C. Finding community structure in very large networks. Phys. Rev. E 2004, 70, 066111. [Google Scholar] [CrossRef] [Green Version]
- Pan, L.; Jin, J.; Wang, C.; Xie, J. Edge Community Mining Based on Local Information in Social Networks. J. Electron. 2012, 40, 2255–2263. [Google Scholar]
- Xiong, Z. Community Discovery Technology and Its Application in Online Social Networks; Central South University: Changsha, China, 2012. [Google Scholar]
- Huang, W. Research on Web Community Discovery Algorithms; Beijing University of Posts and Telecommunications: Beijing, China, 2013. [Google Scholar]
- Leng, Z. Research on network community discovery algorithm based on greedy optimization technology. J. Electron. 2014, 42, 723–729. [Google Scholar]
- Zhang, X.; You, H.; Zhu, W.; Quiao, S.; Li, J.; Gutierrez, L.A.; Zhang, Z.; Fan, X. Overlapping community identification approach in online social networks. Physica A Stat. Mech. Appl. 2015, 421, 233–248. [Google Scholar] [CrossRef]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of community hierarchies in large networks. Comput. Res. Repos. 2008, abs/0803.0476. [Google Scholar]
- Parsa, M.G.; Mozayani, N.; Esmaeili, A. An EDA-based community detection in complex networks. In Proceedings of the International Symposium on Telecommunications, Tehran, Iran, 9–11 September 2014; pp. 476–480. [Google Scholar]
- Oliveira, J.E.M.D.; Quiles, M.G. Community Detection in Complex Networks Using Coupled Kuramoto Oscillators. In Proceedings of the International Conference on Computational Science and ITS Applications, Guimaraes, Portugal, 30 June–3 July 2014; pp. 85–90. [Google Scholar]
- Jing-Ya, X.; Tao, L.; Lin-Tao, Y.; Davison, M. Finding College Student Social Networks by Mining the Records of Student ID Transactions. Symmetry 2019, 11, 307. [Google Scholar] [Green Version]
- Yuhui, G.; Qian, Y. Evolution of Conformity Dynamics in Complex Social Networks. Symmetry 2019, 11, 299. [Google Scholar] [Green Version]
- Giuseppe, A.; Domenico, C.; Antonio, M.; Antonio, P. Mobile Encrypted Traffic classification Using Deep Learning. In Proceedings of the 2018 Network Traffic Measurement and Analysis Conference (TMA), Vienna, Austria, 26–29 June 2018. [Google Scholar]
- Giuseppe, A.; Domenico, C.; Antonio, M.; Pescapé, A. Mobile encrypted traffic classification using deep learning: Experimental evaluation, lessons learned, and challenges. IEEE Trans. Netw. Serv. Manag. 2019, 16, 445–458. [Google Scholar]
- Ruoyu, W.; Zhen, L.; Yongming, C.; Deyu, T.; Jin, Y.; Zhao, Y. Benchmark Data for Mobile App Traffic Research. In Proceedings of the 15th EAI International Conference on Mobile and Ubiquitous Systems: Computing, Networking and Services, New York, NY, USA, 5–7 November 2018. [Google Scholar]
- Clauset, A. Finding local community structure in networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2005, 72, 026132. [Google Scholar] [CrossRef] [Green Version]
- Li, J. Research on Overlapping Community Discovery Algorithm Based on Hadoop Platform; Jilin University: Changchun, China, 2014. [Google Scholar]
- Riedy, J.; Bader, D.A.; Meyerhenke, H. Scalable Multi-threaded Community Detection in Social Networks. In Proceedings of the IEEE International Parallel and Distributed Processing Symposium Workshops & Phd Forum, Shanghai, China, 21–25 May 2012; pp. 1619–1628. [Google Scholar]
- Moon, S.; Lee, J.G.; Kang, M. Scalable community detection from networks by computing edge betweenness on MapReduce. In Proceedings of the 2014 International Conference on Big Data and Smart Computing (BIGCOMP), Bangkok, Thailand, 15–17 January 2014; pp. 145–148. [Google Scholar]
- Wu, W.; Li, M.; Li, G. A Parallelization of Louvain algorithm. Comput. Digit. Eng. 2016, 44, 1402–1406. [Google Scholar]
- Blondel, V.D.; Guillaume, J.L.; Lambiotee, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 10, P10008. [Google Scholar] [CrossRef]
- Lai, B. Research on Parallelization of Community Discovery Algorithm Based on Hadoop; Jiangxi University of Science and Technology: Ganzhou, China, 2017. [Google Scholar]
- Alessio, C.; Tiziano, D.M.; Daniele, D.S.; Grossi, R.; Marion, A.; Versari, L. D2k: Scalable Community Detection in Massive Networks via Small-Diameter k-Plexes; KDD 2018; ACM: New York, NY, USA, 2018; pp. 1272–1281. [Google Scholar]
- Vincenzo, M.; Antonio, P.; Giancarlo, S. Community detection based on Game Theory. Eng. Appl. Artif. Intell. 2019, 85, 773–782. [Google Scholar]
- Mcdaid, A.F.; Greene, D.; Hurley, N. Normalized Mutual Information to evaluate overlapping community finding algorithms. CoRR 2011, abs/1110.2515. [Google Scholar]


| Symbols | Meanings |
|---|---|
| N | A complex network |
| V | a set of nodes |
| node i | |
| E | a set of edges |
| Denotes the connection between node and node , if they are connected, is 1; Otherwise is 0. | |
| the node degree of node | |
| M | the modularity of a network |
| C | the set of detected network communities |
| a community i | |
| the total number of edges interconnected between nodes within the community c | |
| m | the total number of edges in the network |
| the sum of the node degrees of all nodes in the community c | |
| The ratio of the sum of degrees of all nodes in the community c to the sum of degrees of all nodes in N | |
| the modularity increment | |
| the number of connection edges between communities and |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.000 | 0.033 | 0.025 | −0.012 | 0.033 | 0.029 | −0.012 | −0.017 | −0.021 | −0.017 | −0.012 | −0.012 |
| 2 | 0.033 | 0.000 | −0.015 | 0.036 | 0.036 | −0.012 | −0.009 | −0.012 | −0.015 | −0.012 | −0.009 | −0.009 |
| 3 | 0.025 | −0.015 | 0.000 | 0.030 | −0.015 | 0.025 | −0.015 | 0.025 | −0.026 | 0.025 | −0.015 | −0.015 |
| 4 | −0.012 | 0.036 | 0.030 | 0.000 | −0.009 | 0.033 | −0.009 | −0.012 | −0.015 | −0.012 | −0.009 | −0.009 |
| 5 | 0.033 | 0.036 | −0.015 | −0.009 | 0.000 | 0.033 | −0.009 | −0.012 | −0.015 | −0.012 | −0.009 | −0.009 |
| 6 | 0.029 | −0.012 | 0.025 | 0.033 | 0.033 | 0.000 | −0.012 | −0.017 | −0.021 | −0.017 | −0.012 | −0.012 |
| 7 | −0.012 | −0.009 | −0.015 | −0.009 | −0.009 | −0.012 | 0.000 | 0.033 | 0.030 | −0.012 | −0.009 | 0.036 |
| 8 | −0.017 | −0.012 | 0.025 | −0.012 | −0.012 | −0.017 | 0.033 | 0.000 | 0.025 | 0.029 | −0.012 | −0.012 |
| 9 | −0.021 | −0.015 | −0.026 | −0.015 | −0.015 | −0.021 | 0.030 | 0.025 | 0.000 | 0.025 | 0.030 | 0.030 |
| 10 | −0.017 | −0.012 | 0.025 | −0.012 | −0.012 | −0.017 | −0.012 | 0.029 | 0.025 | 0.000 | 0.033 | −0.012 |
| 11 | −0.012 | −0.009 | −0.015 | −0.009 | −0.009 | −0.012 | −0.009 | −0.012 | 0.030 | 0.033 | 0.000 | 0.036 |
| 12 | −0.012 | −0.009 | −0.015 | −0.009 | −0.009 | −0.012 | 0.036 | −0.012 | 0.030 | −0.012 | 0.036 | 0.000 |
| 1 | 3 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0.025 | 0.033 | 0.029 | −0.012 | −0.017 | −0.021 | −0.017 | −0.012 | −0.012 | 0.021 |
| 3 | 0.025 | 0 | −0.015 | 0.025 | −0.015 | 0.025 | −0.026 | 0.025 | −0.015 | −0.015 | 0.015 |
| 5 | 0.033 | −0.015 | 0 | 0.033 | −0.009 | −0.012 | −0.015 | −0.012 | −0.009 | −0.009 | 0.027 |
| 6 | 0.029 | 0.025 | 0.033 | 0 | −0.012 | −0.017 | −0.021 | −0.017 | −0.012 | −0.012 | 0.021 |
| 7 | −0.012 | −0.015 | −0.009 | −0.012 | 0 | 0.033 | 0.03 | −0.012 | −0.009 | 0.036 | −0.019 |
| 8 | −0.017 | 0.025 | −0.012 | −0.017 | 0.033 | 0 | 0.025 | 0.029 | −0.012 | −0.012 | −0.025 |
| 9 | −0.021 | −0.026 | −0.015 | −0.021 | 0.03 | 0.025 | 0 | 0.025 | 0.03 | 0.03 | −0.031 |
| 10 | −0.017 | 0.025 | −0.012 | −0.017 | −0.012 | 0.029 | 0.025 | 0 | 0.033 | −0.012 | −0.025 |
| 11 | −0.012 | −0.015 | −0.009 | −0.012 | −0.009 | −0.012 | 0.03 | 0.033 | 0 | 0.036 | −0.019 |
| 12 | −0.012 | −0.015 | −0.009 | −0.012 | 0.036 | −0.012 | 0.03 | −0.012 | 0.036 | 0 | −0.019 |
| 13 | 0.021 | 0.015 | 0.027 | 0.021 | −0.019 | −0.025 | −0.031 | −0.025 | −0.019 | −0.019 | 0 |
| Dataset | No. of Nodes | No. of Edges | Node Average Degree | Description |
|---|---|---|---|---|
| Soc-Epinions | 75,879 | 508,837 | 13.4118 | Epinions.com Date Set |
| Web-NotreDame | 325,729 | 1,497,134 | 9.1925 | Web Graph Data Set |
| Soc-Pokec | 1,632,803 | 30,622,564 | 37.5092 | Poke Social Data Set |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hai, M.; Li, H.; Ma, Z.; Gao, X. Algorithm for Detecting Communities in Complex Networks Based on Hadoop. Symmetry 2019, 11, 1382. https://doi.org/10.3390/sym11111382
Hai M, Li H, Ma Z, Gao X. Algorithm for Detecting Communities in Complex Networks Based on Hadoop. Symmetry. 2019; 11(11):1382. https://doi.org/10.3390/sym11111382
Chicago/Turabian StyleHai, Mo, Haifeng Li, Zhekun Ma, and Xiaomei Gao. 2019. "Algorithm for Detecting Communities in Complex Networks Based on Hadoop" Symmetry 11, no. 11: 1382. https://doi.org/10.3390/sym11111382
APA StyleHai, M., Li, H., Ma, Z., & Gao, X. (2019). Algorithm for Detecting Communities in Complex Networks Based on Hadoop. Symmetry, 11(11), 1382. https://doi.org/10.3390/sym11111382





