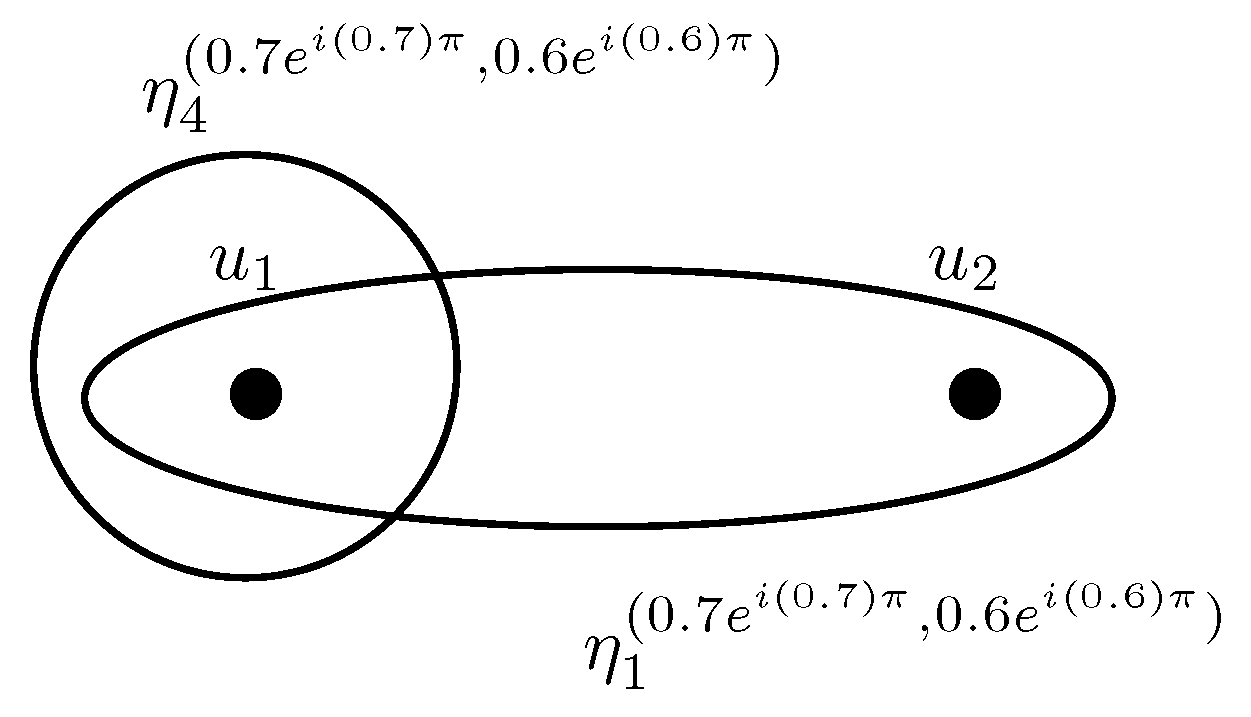1. Introduction
In 1965, fuzzy sets (FSs) were originally defined by Zadeh [
1] as a novel approach to represent uncertainty arising in various fields. The idea of “partial membership” was questioned by many researchers at that time. The extension of crisp sets to FSs, i.e., the extension of membership function
from
to
, bears comparison to the generalization of
to
. Just like
was extended to
with the incorporation of imaginary quantities, FSs have been extended to complex fuzzy sets (CFSs) by Ramot et al. [
2]. A CFS is characterized by a membership function
whose range is not limited to [0,1] but extends to the unit circle in the complex plane. Hence,
is a complex-valued function that assigns a grade of membership of the form
,
to any element
x in the universe of discourse. The membership function
of CFS consists of two terms, namely, an amplitude term
which lies in the unit interval
and a phase term (periodic term)
which lies in the interval
. During the last few years, many researchers have paid special attention to CFSs. Yazdanbakhsh and Dick [
3] gives an updated review of the development of CFSs.
Atanassov [
4] had proposed a different extension of FSs by intuitionistic fuzzy sets (IFSs). Fuzzy sets give the degree of membership of an element in a given set (the non-membership of degree equals one minus the degree of membership), while IFSs give both a degree of membership and a degree of non-membership, which are to some extent independent from each other. The truth (T) and falsity (F) membership functions are used to characterize an IFS in such a way that the sum of truth and falsity degrees should not be greater than one at any point. These figures allow for some indeterminacy in the expression of memberships. Progress on the investigation of IFSs and related extensions of the FS concept continues to be made. Liu et al. [
5] introduced different types of centroid transformations of IF values. Feng et al. [
6] defined various new operations for generalized IF soft sets. Recently, Shumaiza et al. [
7] have proposed group decision-making based on the VIKOR method with trapezoidal bipolar fuzzy information. Akram and Arshad [
8] proposed a novel trapezoidal bipolar fuzzy TOPSIS method for group decision-making. Alcantud et al [
9] proposed a novel modelization of the party formation process, in which citizens’ private opinions are described by means of continuous fuzzy profiles. A novel hesitant fuzzy model for group decision-making was proposed by Alcantud and Giarlotta [
10].
Of particular importance are two extensions of IFSs proposed by Yager [
11,
12,
13]. In these papers he introduced Pythagorean fuzzy sets (PFSs) and
q-rung orthopair fuzzy sets (
q-ROFSs). A
q-ROFS is characterized by means of truth and falsity degrees satisfying the constraint that the sum of the
qth powers of both degrees should be less than one. PFSs consist of the case where
. Thus,
q-ROFSs generalize both the notions of IFSs and PFSs so that the uncertain information can be dealt with in a more widened range. After that, Liu and Wang [
14] applied certain simple weighted operators to aggregate
q-ROFSs in decision-making. Intertemporal choice problems have been investigated with the help of fuzzy soft sets [
15]. These problems appear in the analysis of environmental issues and sustainable development with an infinitely long horizon, project evaluations, or health care [
16,
17]. In multi-attribute decision making,
q-ROF Heronian mean operators were defined by Wei et al. [
18]. For further applications of
q-ROFSs, we refer the readers to the work presented in [
19,
20]. Complex intuitionistic fuzzy sets (CIFSs) were introduced by Alkouri and Salleh [
21] in order to generalize IFSs in the spirit of [
2] by adding non-membership degree
to the CFSs subjected to the constraint
. The CIFSs are used to handle information about uncertainty and periodicity simultaneously. As an extension of both PFSs and CIFSs, Ullah et al. [
22] proposed complex Pythagorean fuzzy sets (CPFSs) and discussed some applications.
The vagueness in the representation of various objects and the uncertain interactions between them originated the necessity of fuzzy graphs (FGs), that were first defined by Rosenfeld [
23] (see also the remarks made by Bhattacharya [
24]). The notion of FGs was extended to complex fuzzy graphs (CFGs) by Thirunavukarasu et al. [
25]. Intuitionistic fuzzy graphs (IFGs) were defined by Parvathi and Karunambigai [
26]. The energy of Pythagorean fuzzy graphs (PFGs) was discussed by Akram and Naz [
27]. Akram and Habib [
28] defined
q-ROF competition graphs and discussed their applications. Akram et al. [
29] proposed a novel description on edge-regular
q-ROFGs. Yaqoob et al. [
30] defined complex intuitionistic fuzzy graphs (CIFGs) and discussed an application of CIFGs in cellular networks to test the proposed model. Later on, complex neutrosophic graphs were studied by Yaqoob and Akram [
31]. Recently, complex Pythagorean fuzzy graphs (CPFGs) and their applications in decision making have been put forward by Akram and Naz [
32].
A hypergraph, as an extension of a crisp graph, is a powerful tool to model different practical problems in various fields, including biological sciences, computer science, sustainable development and social networks [
33,
34,
35]. Co-authorship networks, an important type of social network, have been studied extensively from various angles such as degree distribution analysis, social community extraction and social entity ranking. Most of the previous studies consider the co-authorship relation between two or more authors as a collaboration using crisp hypergraphs. Han et al. [
36] proposed a hypergraph analysis approach to understand the importance of collaborations in co-authorship networks. Zhang and Liu [
37] proposed a hypergraph model of social tagging networks. Ouvrard et al. [
38] studied the hypergraph modeling and visualization of collaboration networks.
In order to allow for uncertainty in crisp hypergraphs, fuzzy hypergraphs (FHGs) were defined by Kaufmann [
39] as an extension of FGs. Lee-Kwang and Lee [
40] discussed fuzzy partitions using FHGs. A valuable contribution to FGs and FHGs has been proposed by Mordeson and Nair [
41]. Fuzzy transversals of FHGs were studied by Goetschel et al. [
42]. Intuitionistic fuzzy hypergraphs (IFHGs) were defined by Parvathi et al. [
43]. Further discussion on IFHGs can be seen in [
44,
45]. Akram and Luqman [
46] defined bipolar neutrosophic hypergraphs with applications. Transversals and minimal transversals of
m-polar FHGs were studied by Akram and Sarwar [
47]. Luqman et al. [
48] presented
q-ROFHGs and their applications. Further, Luqman et al. [
49,
50] have proposed
m-polar and
q-rung picture fuzzy hypergraph models of granular computing.
The proposed research generalizes the concepts of CIFGs and CPFGs. These existing models can only depict the uncertainty having periodic nature occurring in pairwise relationships. The existence of various complex network models in which the relationships are more generalized rather than the pairwise relationships motivates the extension of CIFGs and CPFGs to complex intuitionistic fuzzy and complex Pythagorean fuzzy hypergraphs. Let us consider the modeling of research collaborations through CIFGs and CPFGs. The uncertainty and periodicity of the given data are dealt with with the help of phase terms and amplitude terms, respectively. Two research articles are connected through an edge if both have the same author but if more than two articles are written by the same author then CIFGs and CPFGs fail to model this situation. Thus the main objective of this study is to generalize the concepts of CIFGS and CPFGs to complex q-rung orthopair fuzzy hypergraphs. As argued above, complex q-ROF models provide more flexibility than IFSs and FSs. Therefore a complex q-rung orthopair fuzzy hypergraph model proves to be a very general framework to deal with vagueness in complex hypernetworks when the symmetrical relationships go beyond pairwise interactions. The generality of the proposed model can be observed from the reduction of complex q-rung orthopair fuzzy models to CIF and CPF models for and , respectively. Moreover, most of the previous studies consider the co-authorship relation between two or more authors as a collaboration using crisp hypergraphs. Here we consider a complex q-rung orthopair fuzzy hypergraph model of co-authorship network to represent the collaboration relations between authors having uncertainty and vagueness of periodic nature simultaneously.
The contents of this paper are as follows. In
Section 2 and
Section 3, we define complex intuitionistic fuzzy hypergraphs and complex Pythagorean fuzzy hypergraphs, respectively. In
Section 4, complex
q-ROF hypergraphs are discussed. In
Section 5, we define the
q-ROF transversals and minimal transversals of
q-ROF hypergraphs.
Section 6 illustrates an application of
q-ROF hypergraphs in research collaboration networks. We also present an algorithm to select an author with powerful collaboration characteristics using the score and choice values of
q-rung orthopair fuzzy hypergraphs and give a brief comparison of our proposed model with CIF and CPF models. The final
Section 7 contains conclusions and future research directions.
2. Complex Intuitionistic Fuzzy Hypergraphs
In this section, we define the notion of complex intuitionistic fuzzy hypergraphs. A complex intuitionistic fuzzy hypergraph extends the concept of CIFGs. The proposed hypergraph model is used to handle the uncertain and periodic real-life situations when the relationships are analyzed between more than two objects. The main model that we use in our research design is given in the next definition:
Definition 1. [21] A complex intuitionistic fuzzy set (CIFS) I on the universal set Y is defined as,where , , , and for every . For every , and are the amplitude terms for membership and non-membership of u, and and are the phase terms for membership and non-membership of u. CIFSs where the phase terms equal zero (for all u) reduce to ordinary IFSs. When in addition, the amplitude terms for non-membership of all elements equal zero, we obtain a FS.
The application of this concept to graphs was produced in [
30]. We represent definition of complex intuitionistic fuzzy graphs as follows:
Definition 2. A complex intuitionistic fuzzy graph (CIFG) on Y is an ordered pair , where A is a complex intuitionistic fuzzy set on Y and B is complex intuitionistic fuzzy relation on Y such that,, and , for all . When we apply Definition 1 to hypergraphs we obtain the following structure that generalizes Definition 2:
Definition 3. Let Y be a non-trivial set of universe. A complex intuitionistic fuzzy hypergraph (CIFHG) is defined as an ordered pair , where is a finite family of complex intuitionistic fuzzy sets on Y and is a complex intuitionistic fuzzy relation on complex intuitionistic fuzzy sets ’s such that the following conditions hold:
- (i)
, and , for all - (ii)
for all
Notice that is the crisp hyperedge of .
Note that the above formula reduces to Definition 2 if we consider only two vertices in an hyperedge.
We illustrate the previous definition with a graphical example.
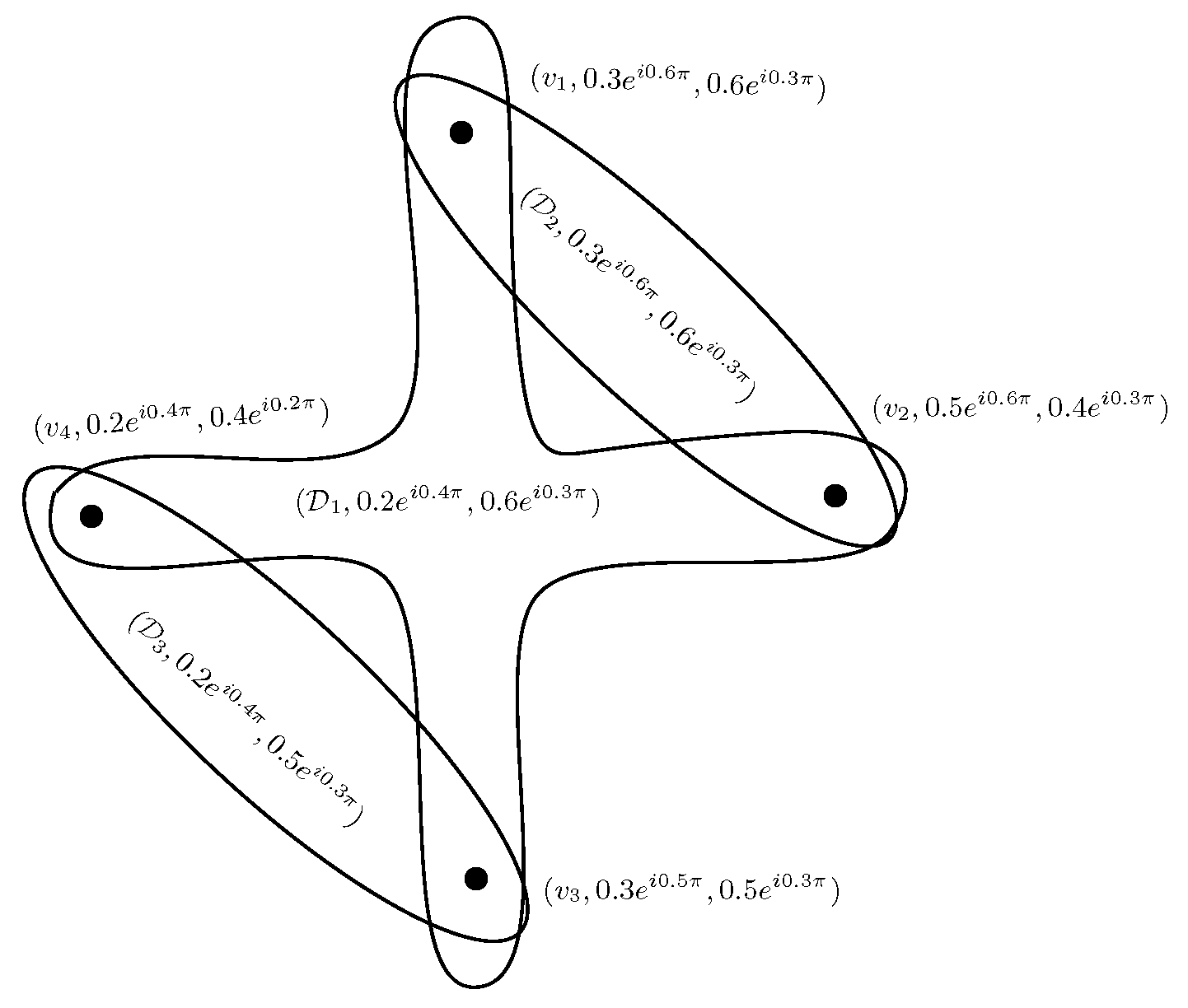
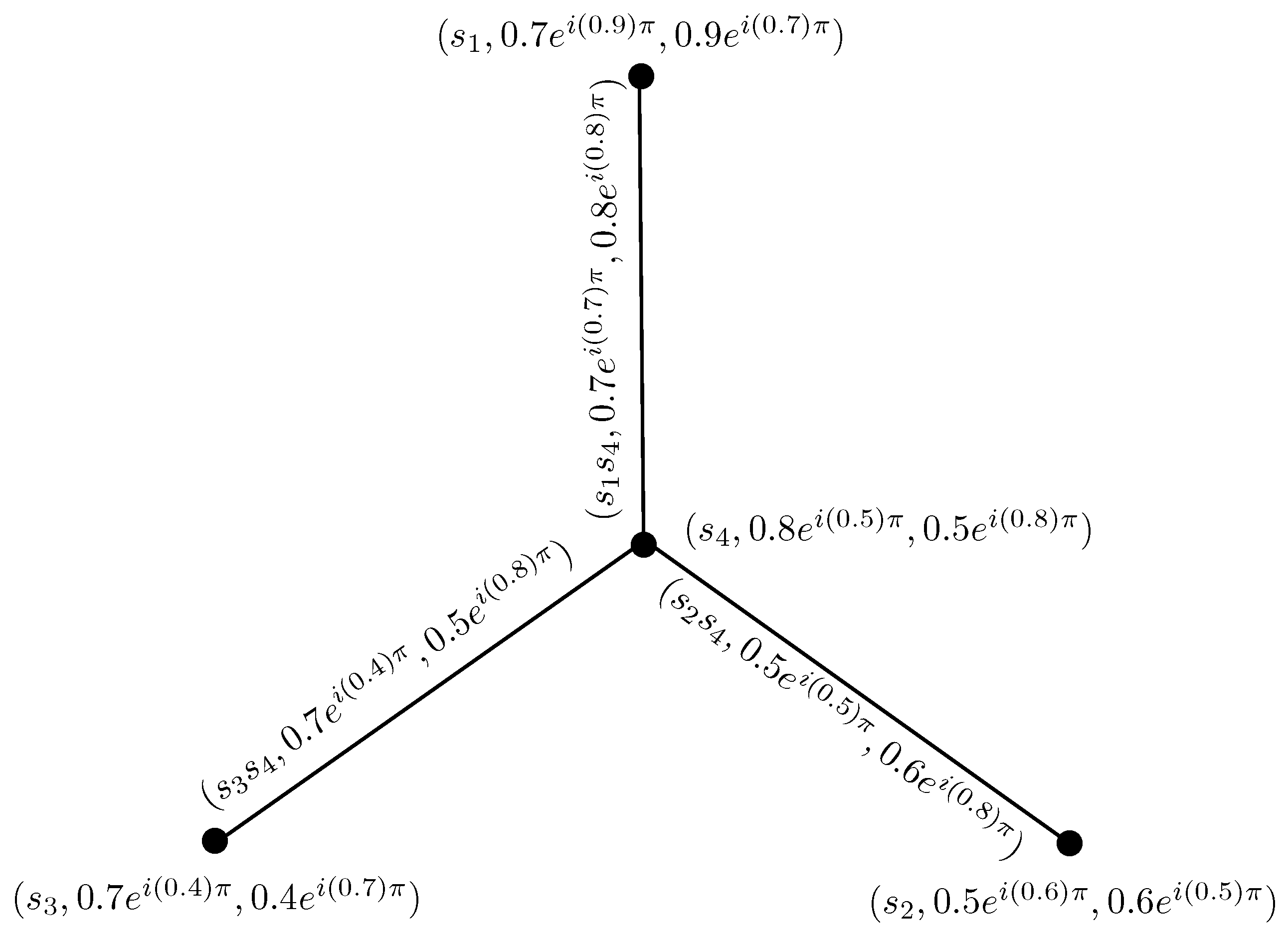
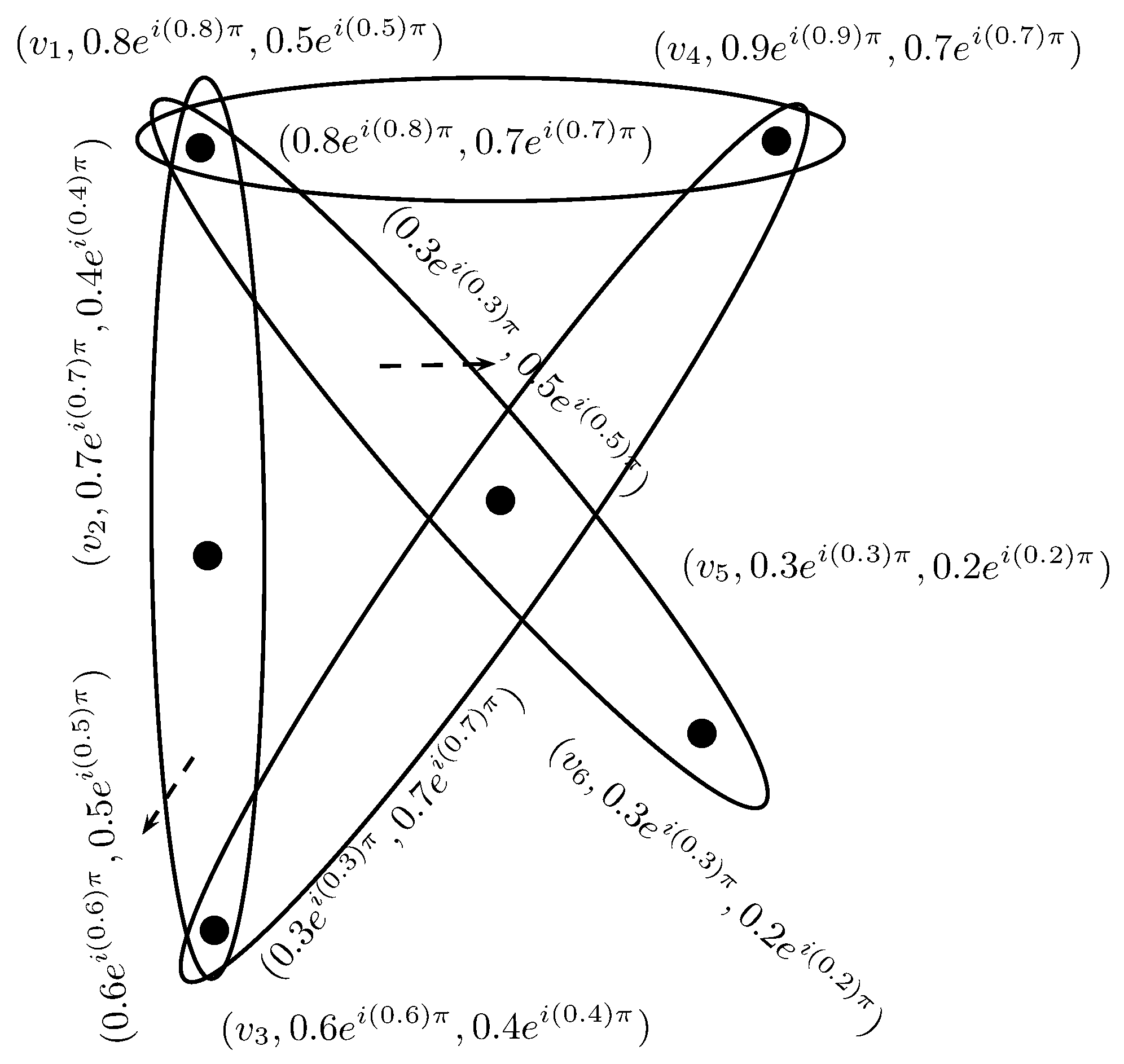
Example 1. Consider a CIFHG on . The CIFR is defined as, , , and . The corresponding CIFHG is shown in Figure 1. Simple CIFHGs are the following special types of CIFHGs:
Definition 4. A CIFHG is simple if whenever and , then .
A CIFHG is support simple if whenever , , and , then .
Our next notion produces a link between CIFHGs and crisp hypergraphs. The subsequent example illustrates this construction.
Definition 5. Let be a CIFHG. Suppose that and such that . The level hypergraph of H is defined as an ordered pair , where
- (i)
and ,
- (ii)
.
Note that the level hypergraph of H is a crisp hypergraph.
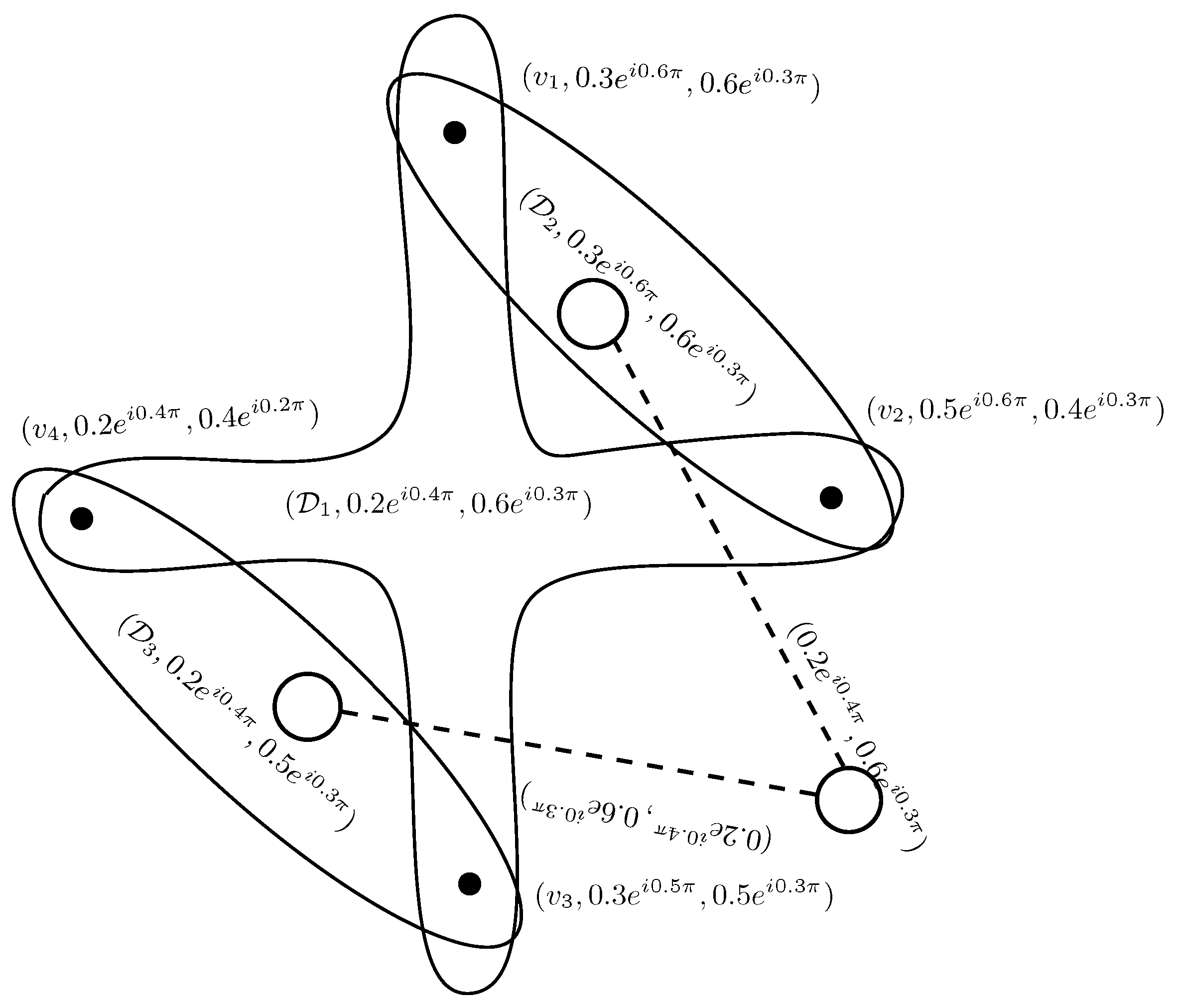
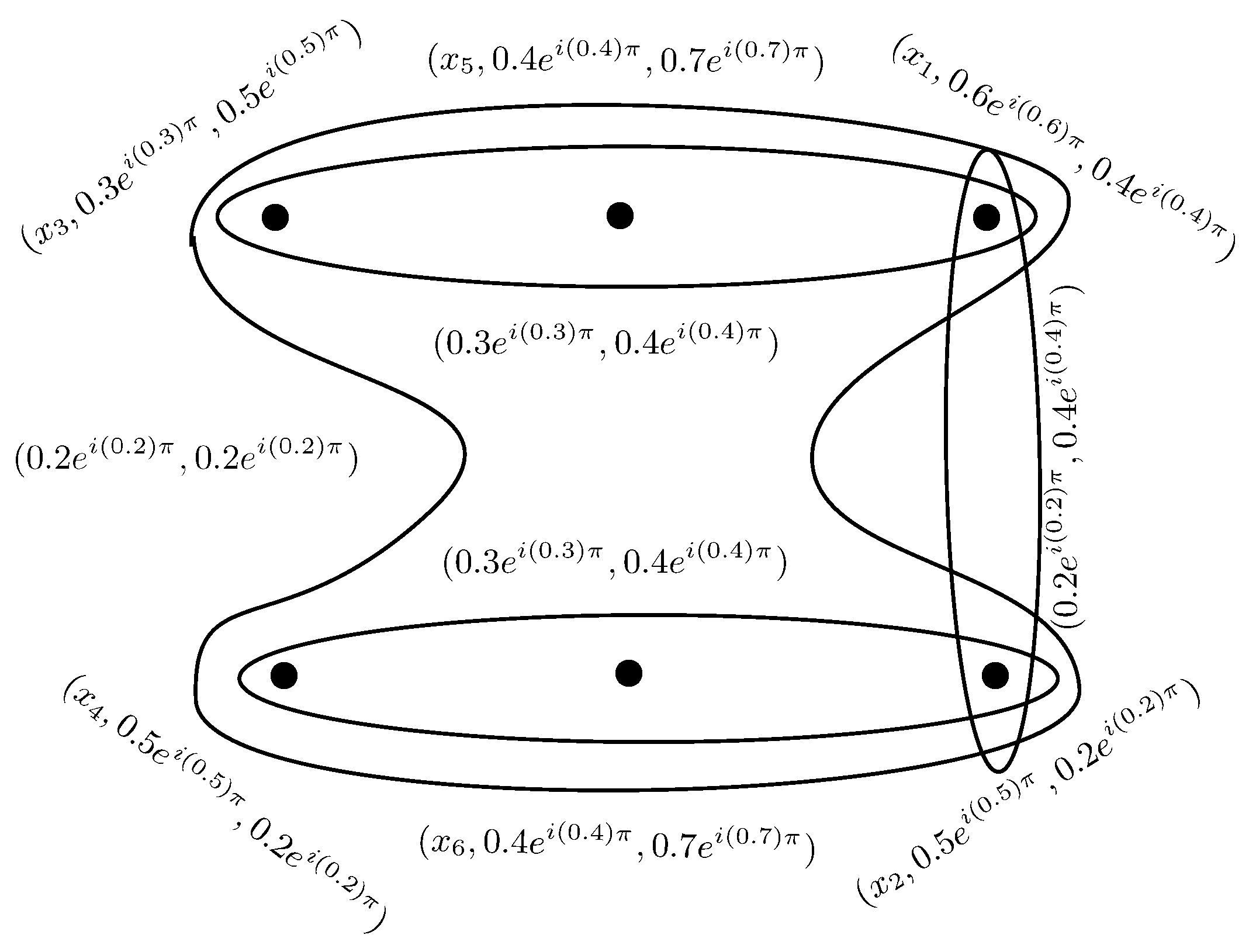
Example 2. Consider a CIFHG as shown in Figure 1. Let , , , and . The level hypergraph of H is shown in Figure 2. Definition 6. Let be a CIFHG. The complex intuitionistic fuzzy line graph of H is defined as an ordered pair , where and there exists an edge between two vertices in if . The membership degrees of are given as,
- (i)
,
- (ii)
.
Definition 7. A CIFHG is said to be linear if for every ,
- (i)
,
- (ii)
.
Example 3. Consider a CIFHG as shown in Figure 1. By direct calculations, we have Note that, and . Hence, CIFHG is not linear. The corresponding CIFHG and its line graph is shown in Figure 3. Theorem 1. A simple strong CIFG is the complex intuitionistic line graph of a linear CIFHG.
Definition 8. The 2-section of a CIFHG is a CIFG having same set of vertices as that of H, is a CIFS on , and such that .
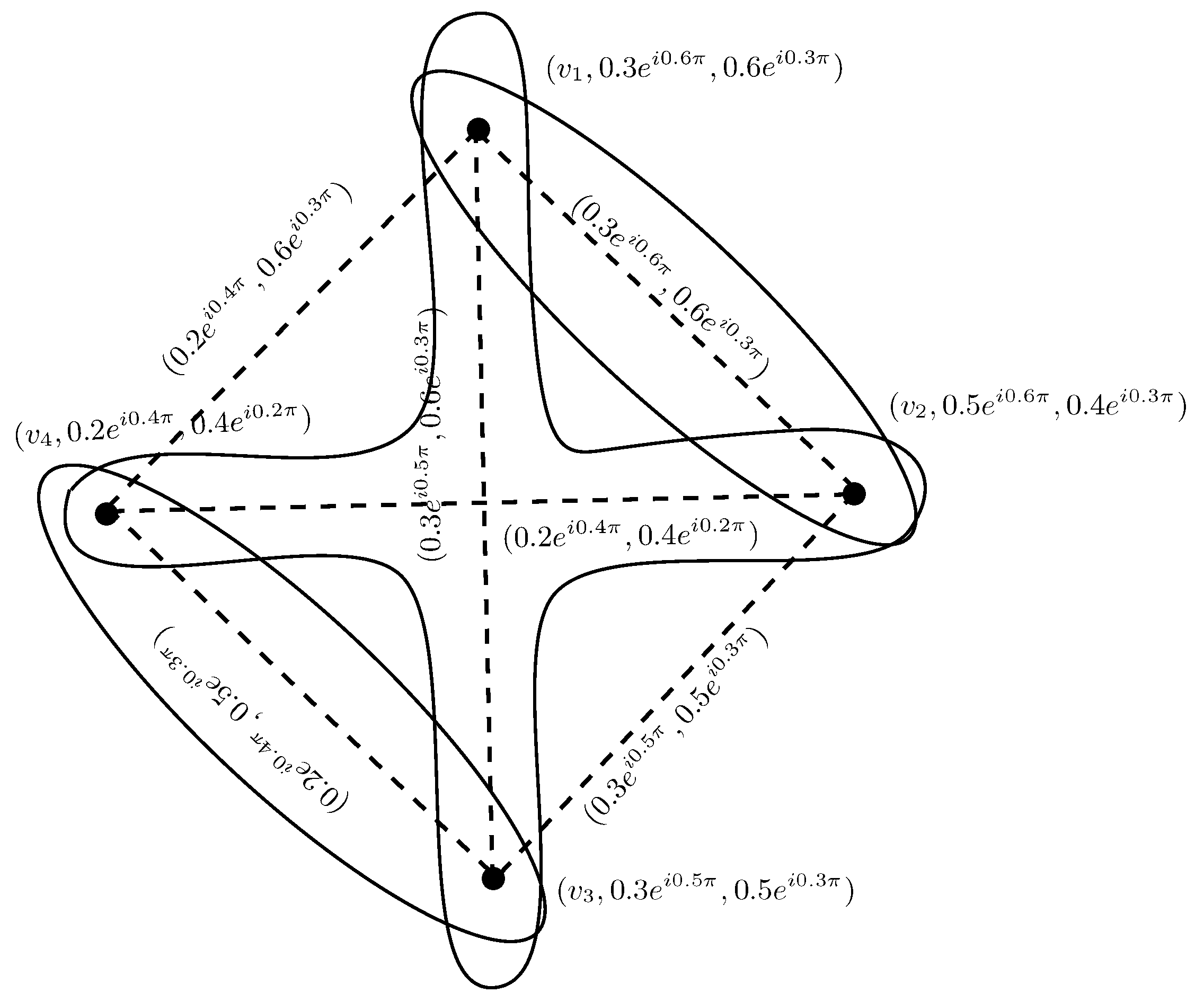
Example 4. An example of a CIFHG is given in Figure 4. The 2-section of H is presented with dashed lines. Definition 9. Let be a CIFHG. A complex intuitionistic fuzzy transversal (CIFT) τ is a CIFs of Y satisfying the condition for all , where is the height of ρ.
A minimal complex intuitionistic fuzzy transversal t is the CIFT of H having the property that if , then τ is not a CIFT of H.
3. Complex Pythagorean Fuzzy Hypergraphs
We now turn our attention to the next class of hypergraphs called complex Pythagorean fuzzy hypergraphs. A complex Pythagorean fuzzy hypergraph is the generalization of CPFGs and CIFHGs. The occurrence of truth and falsity degrees whose sum is not less than one but the sum of squares does not exceed one in complex hypernetworks motivates the necessity of this proposed model.
Definition 10. [32] A complex Pythagorean fuzzy graph (CPFG) on Y is an ordered pair , where C is a CPFS on Y and D is CPFR on Y such that, , and , for all .
Definition 11. A complex Pythagorean fuzzy hypergraph (CPFHG) on Y is defined as an ordered pair , where is a finite family of CPFSs on Y and is a CPFR on CPFSs ’s such that,
- (i)
, and for all - (ii)
for all
Note that, is the crisp hyperedge of .
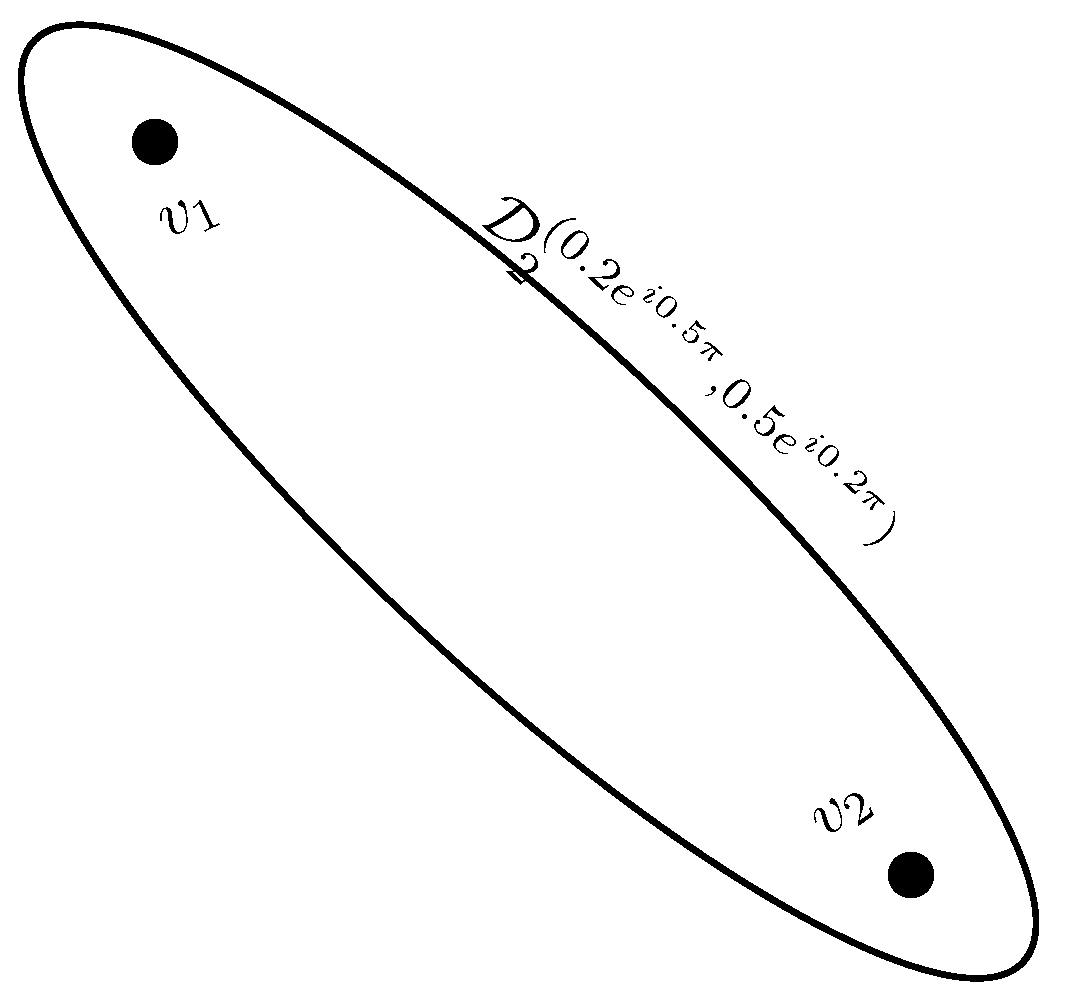
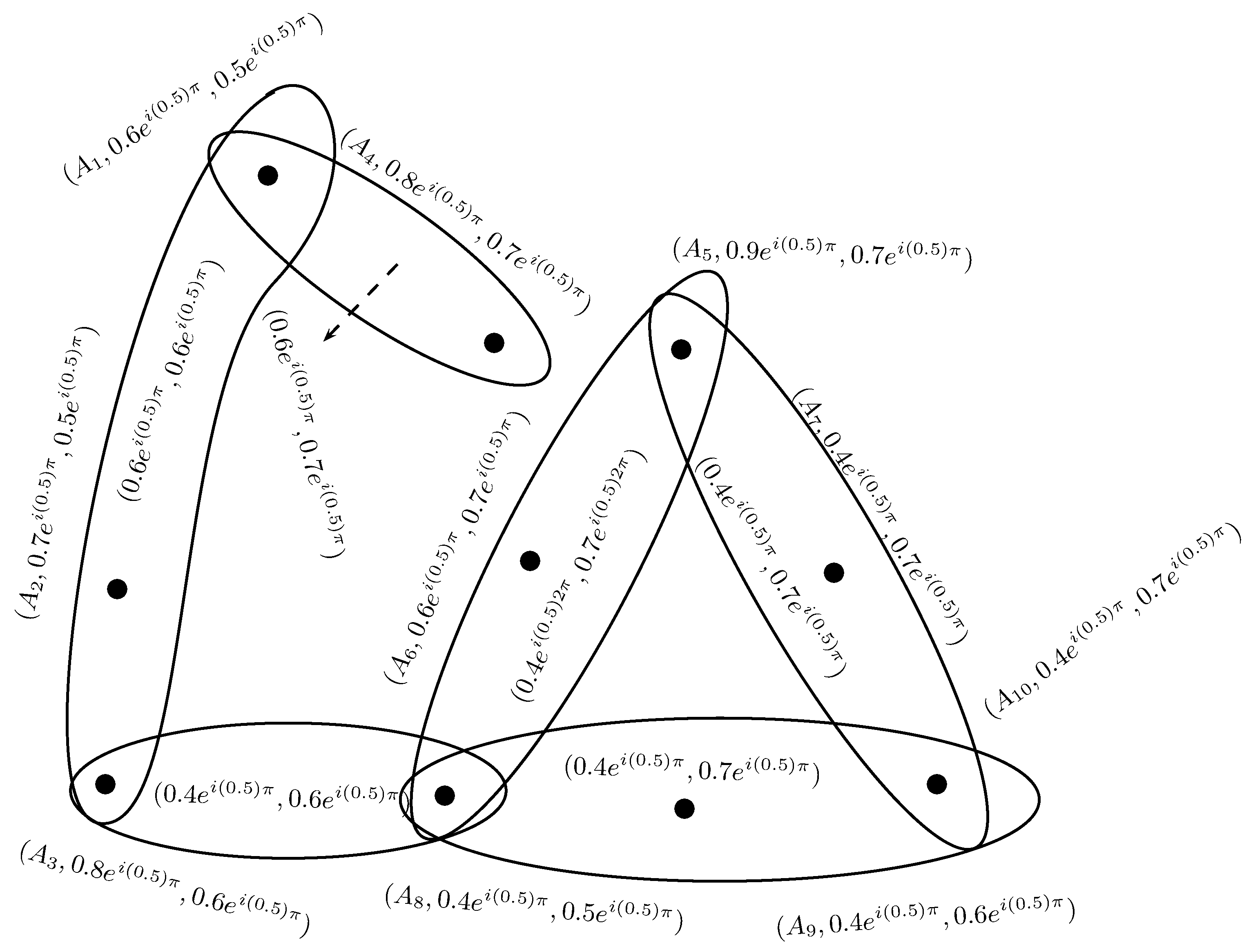
Example 5. Consider a CPFHG on . The CPFR is defined as, , , , , and . The corresponding CPFHG is shown in Figure 5. Definition 12. A CPFHG is simple if whenever and , then .
A CPFHG is support simple if whenever , , and , then .
Definition 13. Let be a CPFHG. Suppose that and such that . The level hypergraph of is defined as an ordered pair , where
- (i)
and ,
- (ii)
.
Note that, level hypergraph of is a crisp hypergraph.
Example 6. Consider a CPFHG as shown in Figure 5. Let , , , and . Then, level hypergraph of is shown in Figure 6. Definition 14. Let be a CPFHG. The complex Pythagorean fuzzy line graph of is defined as an ordered pair , where and there exists an edge between two vertices in if , for all . The membership degrees of are given as,
- (i)
,
- (ii)
.
Definition 15. A CPFHG is said to be linear if for every ,
- (i)
,
- (ii)
.
Example 7. Consider a CPFHG as shown in Figure 5. By direct calculations, we haveNote that, and . Hence, CPFHG is linear. The corresponding CPFHG and its line graph is shown in Figure 7. Theorem 2. A simple strong CPFG is the complex Pythagorean fuzzy line graph of a linear CPFHG.
Definition 16. The 2-section of a CPFHG is a CPFG having same set of vertices as that of , is a CPFS on , and such that .
Example 8. An example of a CPFHG is given in Figure 8. The 2-section of is presented with dashed lines. Definition 17. Let be a CPFHG. A complex Pythagorean fuzzy transversal (CPFT) τ is a CPFS of Y satisfying the condition for all , where is the height of ρ.
A minimal complex Pythagorean fuzzy transversal t is the CPFT of having the property that if , then τ is not a CPFT of .
4. Complex q-Rung Orthopair Fuzzy Hypergraphs
This section explores the class of complex q-rung orthopair fuzzy graphs and complex q-rung orthopair fuzzy hypergraphs. Complex q-rung orthopair fuzzy hypergraphs generalize the notions of CIFHGs and CPFHGs. The class of Cq-ROFSs extends the classes of CIFSs and CPFSs. The space of Cq-ROFSs increases as the value of parameter q increases. Based on these advantages of Cq-ROFSs, we combine the theories of Cq-ROFSs and graphs to define complex q-rung orthopair fuzzy graphs and complex q-rung orthopair fuzzy hypergraphs.
Definition 18. [13] A q-rung orthopair fuzzy set (q-ROFS) Q in the universal set Y is defined as, , where the function defines the truth-membership and defines the falsity-membership of the element and for every , . Furthermore, is called the indeterminacy degree or q-ROF index of u to the set Q. Definition 19. A complex q-rung orthopair fuzzy set (Cq-ROFS) S in the universal set Y is given as,where , , , and for every , . Remark 1.
When , C1-ROFS is called a CIFS.
When , C2-ROFS is called a CPFS.
Definition 20. Let and , be two Cq-ROFSs in Y, then
- (i)
, , and , for amplitudes and phase terms, respectively, for all .
- (ii)
, , and , for amplitudes and phase terms, respectively, for all .
Definition 21. Let and , be two Cq-ROFSs in Y, then
- (i)
- (ii)
Definition 22. A complex q-rung orthopair fuzzy relation (Cq-ROFR) is a Cq-ROFS in given as,where , , characterize the truth and falsity degrees of R, and such that for all , . Example 9. Let be the universal set and be the subset of . Then, the C5-ROFR R is given as, Note that, , for all Hence, R is a C5-ROFR on Y.
Definition 23. A complex q-rung orthopair fuzzy graph(Cq-ROFG) on Y is an ordered pair , where is a complex q-rung orthopair fuzzy set on Y and is complex q-rung orthopair fuzzy relation on Y such that, , for all .
Remark 2. Note that,
When , C1-ROFG is called a CIFG.
When , C2-ROFG is called a CPFG.
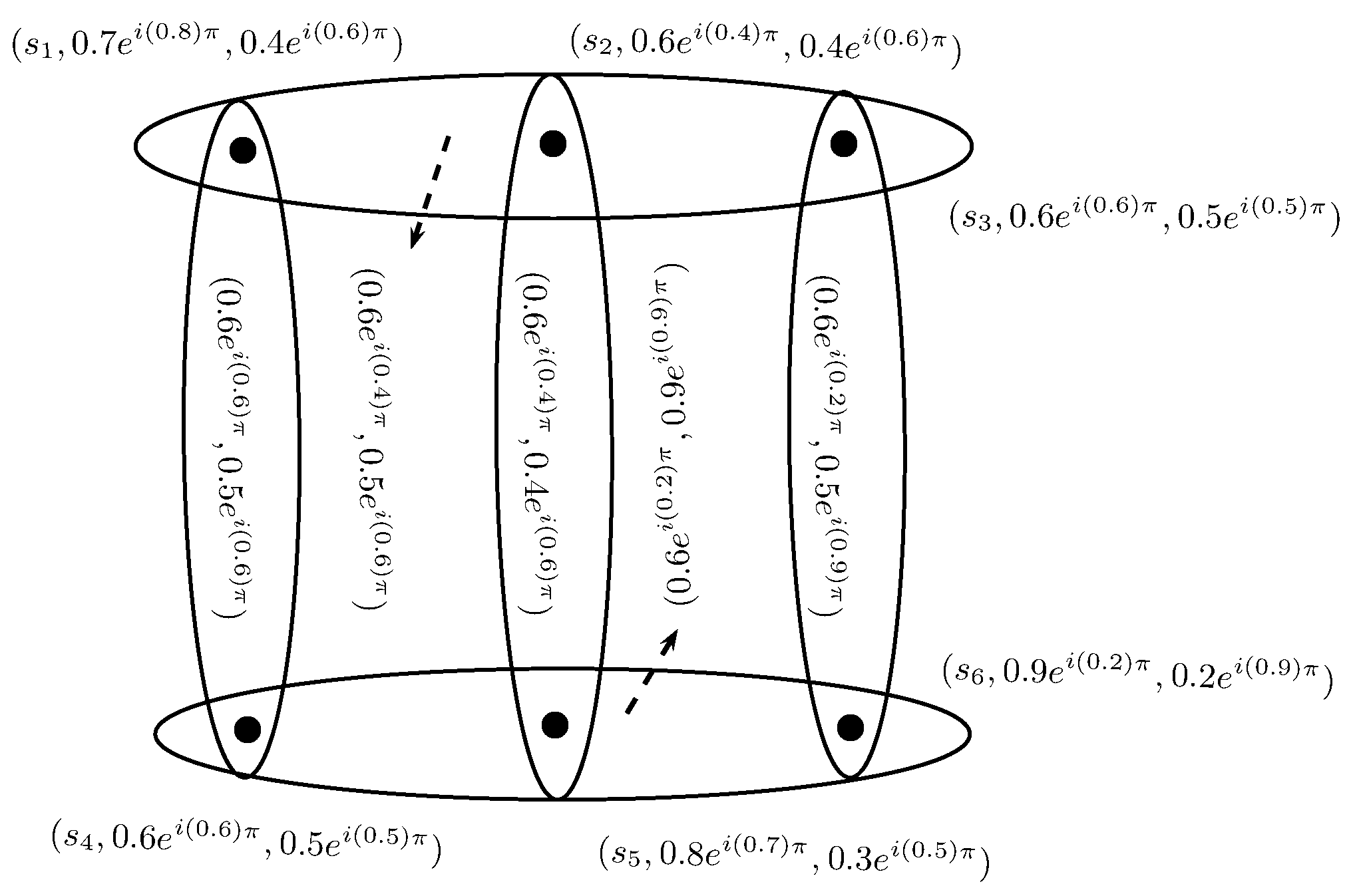
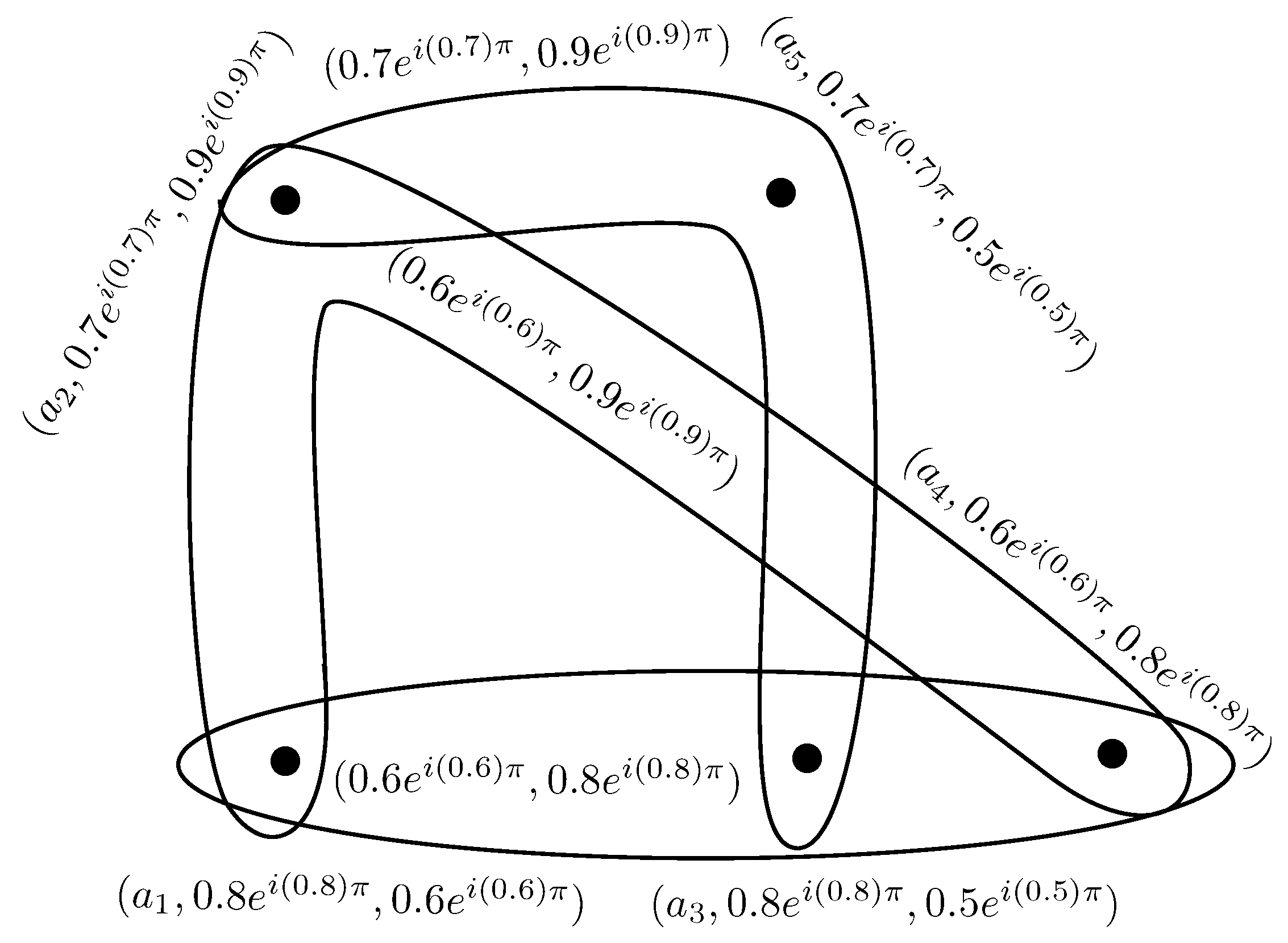
Example 10. Let be a C6-ROFG on , , , where , , , , , , , and , , , , , , , , are C6-ROFS and C6-ROFR on Y, respectively. The corresponding C6-ROFG is shown in Figure 9. We now define the more extended concept of complex q-ROF hypergraphs.
Definition 24. The support of a Cq-ROFS is defined as . The height of a Cq-ROFS is defined as If , then S is called normal.
Definition 25. Let Y be a non-trivial set of universe. A complex q-rung orthopair fuzzy hypergraph (Cq-ROFHG) is defined as an ordered pair , where is a finite family of complex q-rung orthopair fuzzy sets on Y and η is a complex q-rung orthopair fuzzy relation on complex q-rung orthopair fuzzy sets ’s such that,
- (i)
, , for all - (ii)
for all
Note that, is the crisp hyperedge of .
Remark 3. Note that,
When , C1-ROFHG is a CIFHG.
When , C2-ROFHG is a CPFHG.
Definition 26. Let be a Cq-ROFHG. The height of , given as , is defined as , where , , , . Here, and denote the truth and falsity degrees of vertex to hyperedge , respectively.
Definition 27. Let be a Cq-ROFHG. Suppose that and such that . The level hypergraph of is defined as an ordered pair , where
- (i)
and ,
- (ii)
.
Note that, level hypergraph of is a crisp hypergraph.
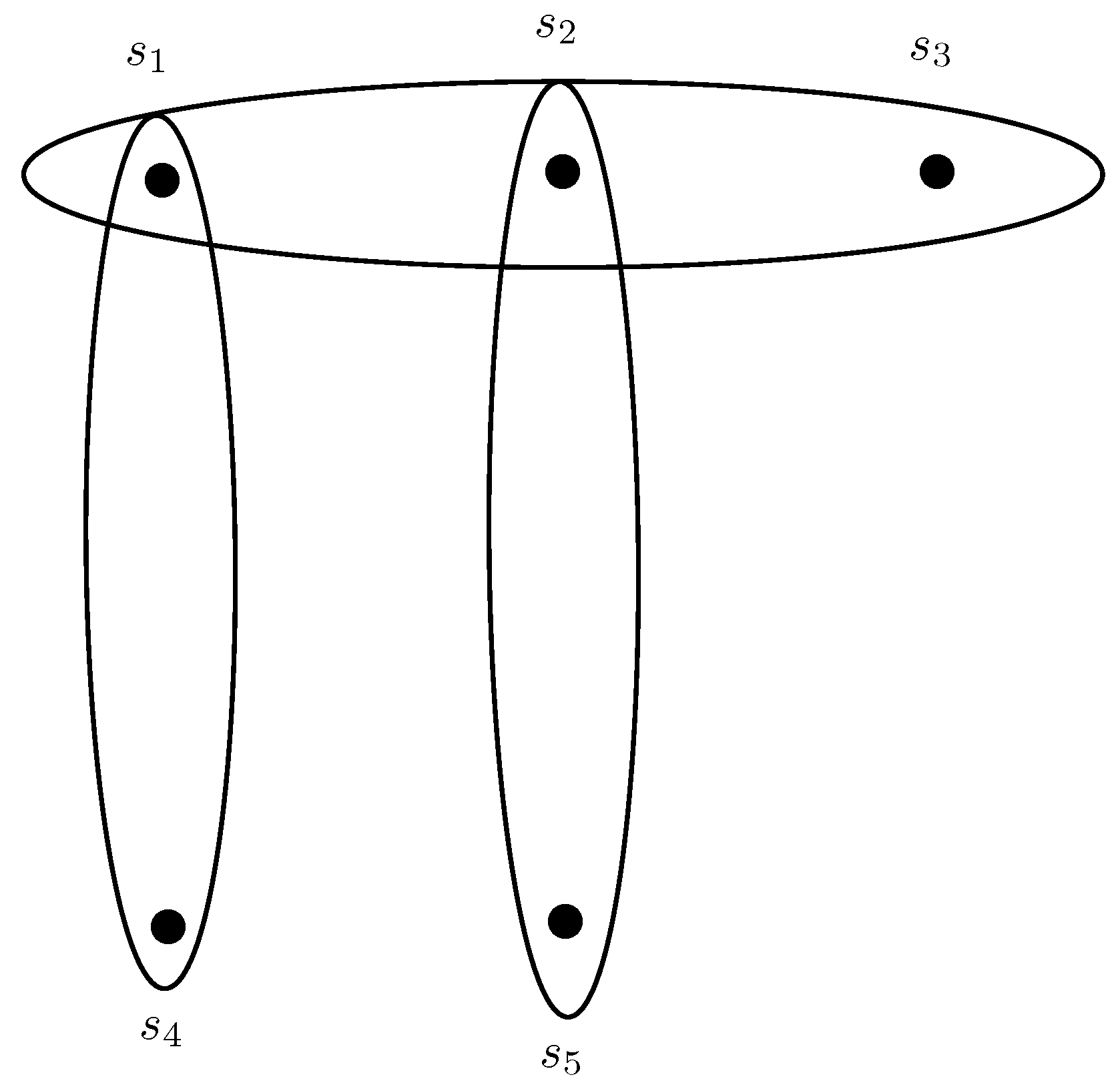
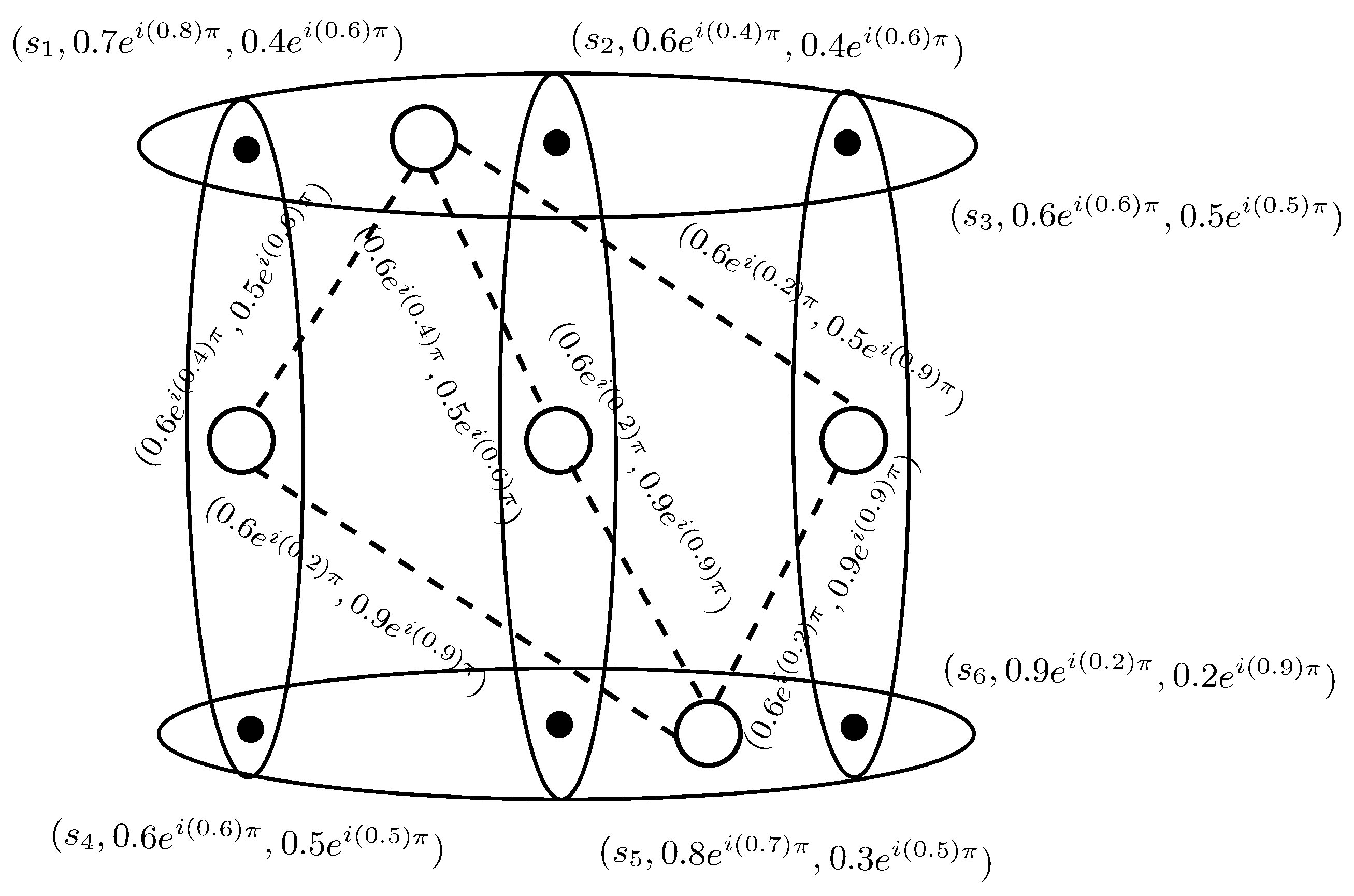
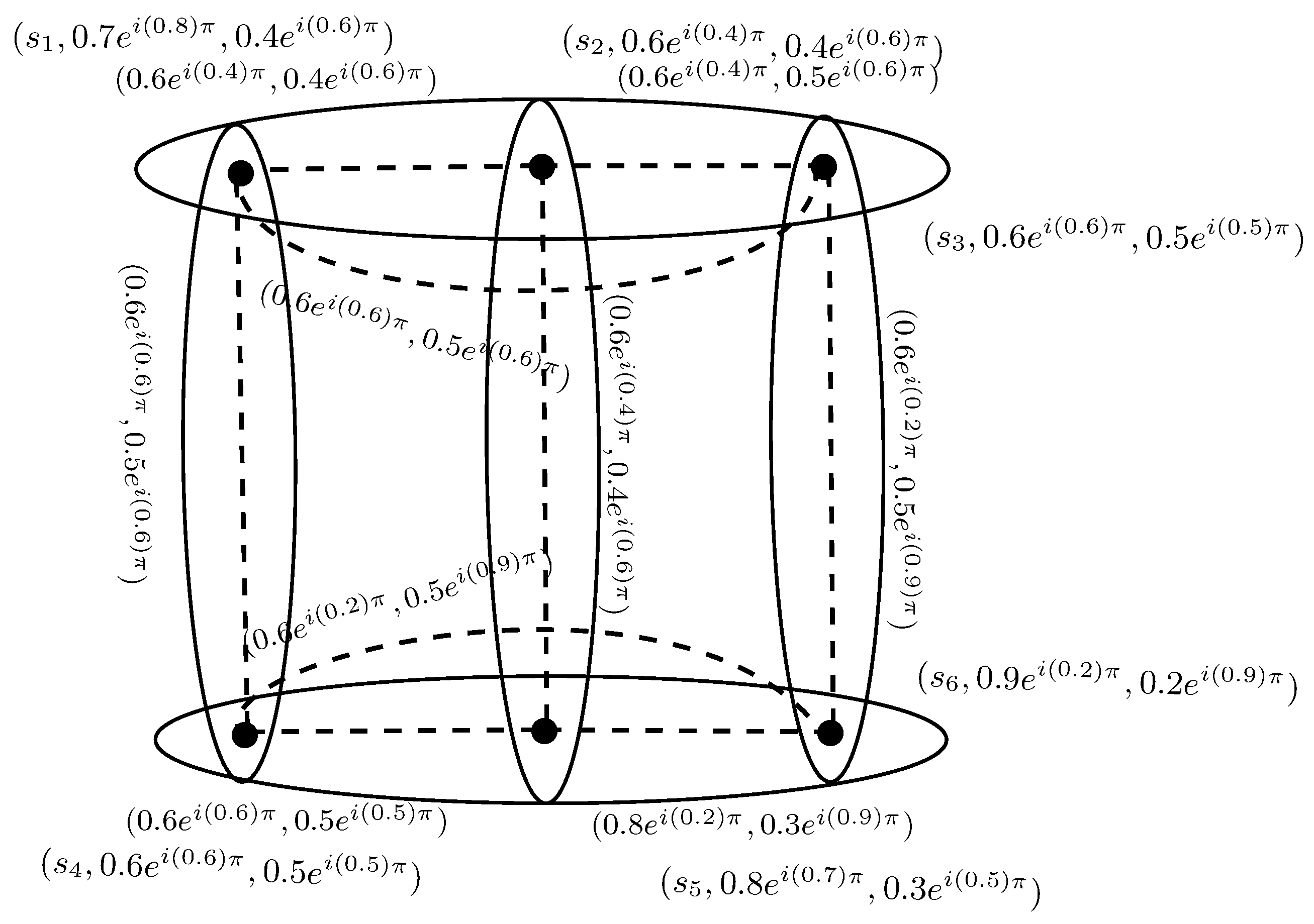
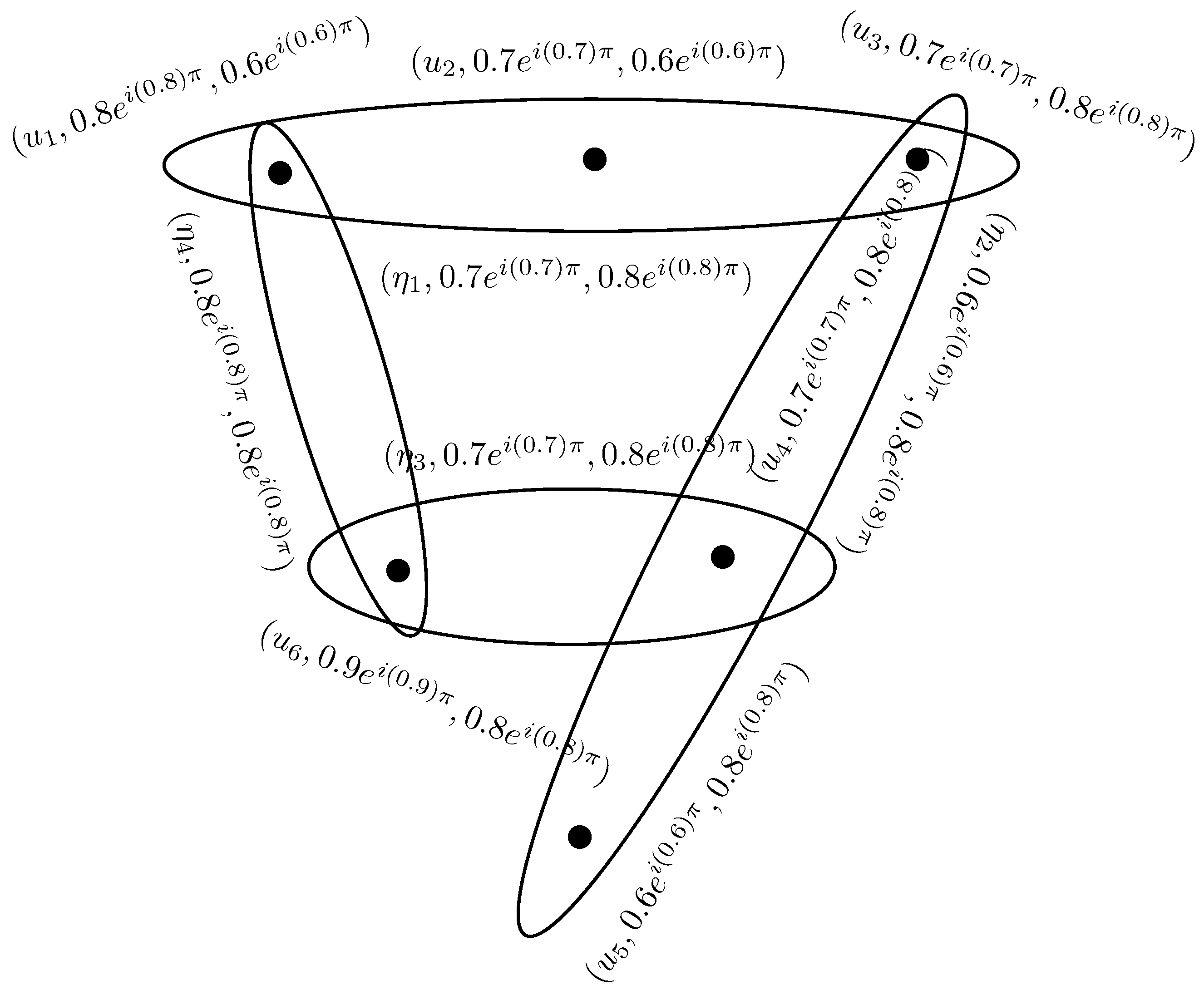
Example 11. Consider a C6-ROFHG on . The C6-ROFR η is given as, , , and The incidence matrix of is given in Table 1. The corresponding C6-ROFHG is shown in Figure 10. Let , , , and , then level hypergraph of is shown in Figure 11. 5. Transversals of Complex q-Rung Orthopair Fuzzy Hypergraphs
In this section we study transversality. Prior to the main definition we need the following auxiliary concept:
Definition 28. Let be a Cq-ROFHG and for , , , and let be the level hypergraph of . The sequence of complex numbers such that , , , and satisfying the conditions,
- (i)
if , , , , then , and
- (ii)
,
is called the fundamental sequence of , denoted by . The set of level hypergraphs is called the set of core hypergraphs or the core set of , denoted by .
Now we are ready to define:
Definition 29. Let be a Cq-ROFHG. A complex q-rung orthopair fuzzy transversal (Cq-ROFT) τ is a Cq-ROFs of Y satisfying the condition for all , where is the height of ρ.
A minimal complex q-rung orthopair fuzzy transversal t is the Cq-ROFT of having the property that if , then τ is not a Cq-ROFT of .
Let us denote the family of minimal Cq-ROFTs of by .
Example 12. Consider a C5-ROFHG on . The C5-ROFR η is given as, , , and . The incidence matrix of is given in Table 2. The corresponding C5-ROFHG is shown in Figure 12. By routine calculations, we have , , and . Consider a C5-ROFS of Y such that , , . Note that, Thus, we have for all Hence, is a C5-ROFT of . Similarly,are C5-ROFTs of Definition 30. A Cq-ROFHG is a partial Cq-ROFHG of if , denoted by . A Cq-ROFHG is ordered if the core set , , ⋯, is ordered, i.e., . is simply ordered if is ordered and
Definition 31. A Cq-ROFS S on Y is elementary if S is single-valued on . A Cq-ROFHG is elementary if every and η are elementary.
Proposition 1. If τ is a Cq-ROFT of , then , for all . Furthermore, if τ is minimal Cq-ROFT of , then .
Lemma 1. Let be a partial Cq-ROFHG of . If is minimal Cq-ROFT of , then there is a minimal Cq-ROFT of such that
Proof. Let be a Cq-ROFS on Y, which is defined as . Then, is a Cq-ROFT of . Thus, there exists a minimal Cq-ROFT of such that □
Lemma 2. Let be a Cq-ROFHG then
Proof. Let
and
Suppose that for
,
,
, and
Define a function
by
From definition of , we have . Definition 28 implies that for every , Thus, is a Cq-ROFT of . Since, is minimal Cq-ROFT and for all This implies that is also a Cq-ROFT and but the minimality of implies that . Hence, which implies that for every Cq-ROFT and for each , and so we have □
We now illustrate a recursive procedure to find in Algorithm 1.
| Algorithm 1: To find the family of minimal Cq-ROFTs . |
Let be a Cq-ROFHG having the fundamental sequence , , ⋯, and core set , , ⋯, . The minimal transversal of is determined as follows,
Determine a crisp minimal transversal of . Determine a crisp minimal transversal of satisfying the condition , i.e., obtain an hypergraph having the hyperedges and a loop at every vertex . Thus, we have Let be the minimal transversal of Obtain a sequence of minimal transversals such that is the minimal transversal of satisfying the condition . Define an elementary Cq-ROFS having the support and , . Determine a minimal Cq-ROFT of as .
|
Example 13. Consider a C5-ROFHG on as shown in Figure 13. Let , , , and . Clearly, the sequence satisfies all the conditions of Definition 28. Hence, it is the fundamental sequence of . Note that, is the minimal transversal of and , is the minimal transversal of , and is the minimal transversal of . Consider Hence, is a C5-ROFT of .
Lemma 3. Let be a Cq-ROFHG with . If τ is a Cq-ROFT of , then , for every . If then
Proof. Since is a Cq-ROFT of , implies that Let , then , , , and . This shows that . If , i.e., is minimal Cq-ROFT then . Thus, we have □
Lemma 4. Let β be a Cq-ROFT of a Cq-ROFHG . Then, there exists such that .
Proof. Let . Suppose that is a transversal of and , for such that Let be an elementary Cq-ROFS having support and be an elementary Cq-ROFS having support , for . Then, Algorithm 1 implies that is a Cq-ROFT of and is minimal Cq-ROFT of such that . □
Theorem 3. Let and be Cq-ROFHGs. Then, is simple, , , for every , and for every Cq-ROFS , exactly one of the conditions must satisfy,
- (i)
, for some or
- (ii)
there is and , where , , such that , i.e., ξ is not a Cq-ROFT of .
Proof. Let . Since, the family of all minimal Cq-ROFTs form a simple Cq-ROFHG on . Lemma 3 implies that every edge of has height . Let be an arbitrary Cq-ROFS.
- Case(i)
If is a Cq-ROFT of , then Lemma 4 implies the existence of a minimal Cq-ROFT such that . Thus, the condition (i) holds and (ii) violates.
- Case(ii)
If is not a Cq-ROFT of , then there is an edge such that . If condition (i) holds, implies that , which is the contradiction against the fact that is Cq-ROFT. Hence, condition (i) does not hold and (ii) is satisfied.
Conversely, suppose that satisfies all properties as mentioned above and . Let , then we obtain and conditions (ii) is not satisfied, so is Cq-ROFT of . If t is minimal Cq-ROFT of and , t does not satisfy (ii), this implies the existence of such that , hence . Since, t is minimal Cq-ROF which implies that , and t were chosen arbitrarily therefore, we have . □
The construction of fundamental subsequence and subcore of Cq-ROFHG is discussed in Algorithm 2.
| Algorithm 2: Construction of fundamental subsequence and subcore. |
Let be a Cq-ROFHG and be a partial Cq-ROFHG of . The fundamental subsequence is constructed as follows:
Let and . Construct , a partial hypergraph of , by removing all hyperedges of , which contain properly any other hyperedge of . In the same way, a partial hypergraph of is constructed by removing all hyperedges of , which contain properly any other hyperedge of or any other hyperedge of . is non-trivial iff there exists a Cq-ROFT and a vertex such that . Continuing the same procedure, construct , a partial hypergraph of , by removing all hyperedges of , which contain properly any other hyperedge of or contain any other hyperedge of . is non-trivial iff there exists a Cq-ROFT and an element such that . Let be the set of complex numbers such that the corresponding partial hypergraphs are non-empty. Then, and are subsequence and subcore set of , respectively.
|
Definition 32. Let be a Cq-ROFHG having fundamental subsequence and subcore of . The Cq-ROFT core of is defined as an elementary Cq-ROFHG such that,
- (i)
, i.e., is also a fundamental subsequence of ,
- (ii)
height of every is iff is an hyperedge of .
Theorem 4. For every Cq-ROFHG, we have .
Proof. Let and . Definition 32 implies that and is an hyperedge of . Since and is a transversal of therefore Thus, is a Cq-ROFT of .
Let and . Definition 28 implies that , for . Definition of subcore implies the existence of an hyperedge
of such that and . For , we have . Hence, is a Cq-ROFT of .
Let is a Cq-ROFT of . This implies that there is such that . But is a Cq-ROFT of and implies that . Thus, . Also implies that . □
Although can be taken as a minimal transversal of , it is not necessary for to be the minimal transversal of , for all , and . Furthermore, it is not necessary for the family of minimal Cq-ROFTs to form a hypergraph on Y. For those Cq-ROFTs that satisfy the above property, we have:
Definition 33. A Cq-ROFT τ having the property that , for all , and is called the locally minimal Cq-ROFT of . The collection of all locally minimal Cq-ROFTs of is represented by .
Note that, , but the converse is not generally true.
Example 14. Consider a C6-ROFHG as shown in Figure 14. The C6-ROFSis a locally minimal C6-ROFT of . Theorem 5. Let be an ordered Cq-ROFHG with . If is a minimal transversal of , then there exists such that and is a minimal transversal of , for all . In particular, if , then there exists a locally minimal Cq-ROFT and
Proof. Let . Since, is an ordered Cq-ROFHG, therefore . Also, there exists such that . Following this iterative procedure, we have a nested sequence of minimal transversals, where every . Let be an elementary Cq-ROFS having height and support . Let us define such that , that generates the required minimal Cq-ROFT of . If , is locally minimal Cq-ROFT of . Hence, □
Theorem 6. Let be a simply ordered Cq-ROFHG with . If , then there exists such that .
Proof. Let and is a simply ordered Cq-ROFHG. Theorem 5 implies that a nested sequence of minimal transversals can be constructed. Let Let be an elementary Cq-ROFS having height and support such that generates the locally minimal Cq-ROFT of with . □