Enhanced Membrane Computing Algorithm for SAT Problems Based on the Splitting Rule
Abstract
:1. Introduction
2. Preliminaries
2.1. Membrane Computing System (P System)
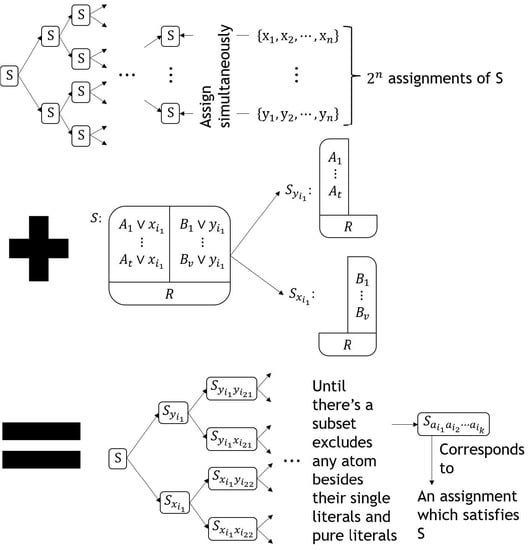
2.2. Tradtional Membrane Computing Algorithm of SAT Problems
2.3. Simplification Rules
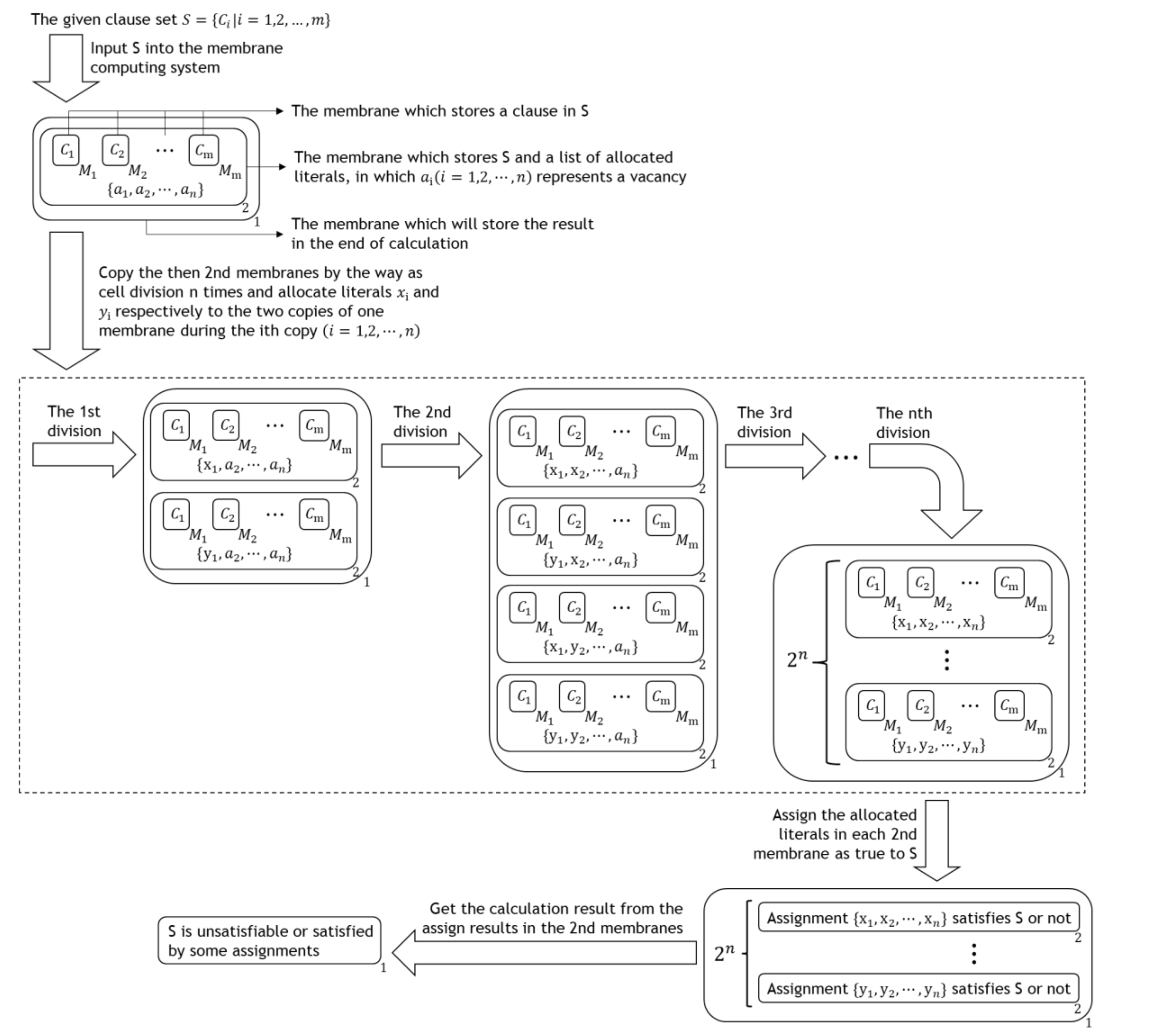
3. Proposed New Algorithm
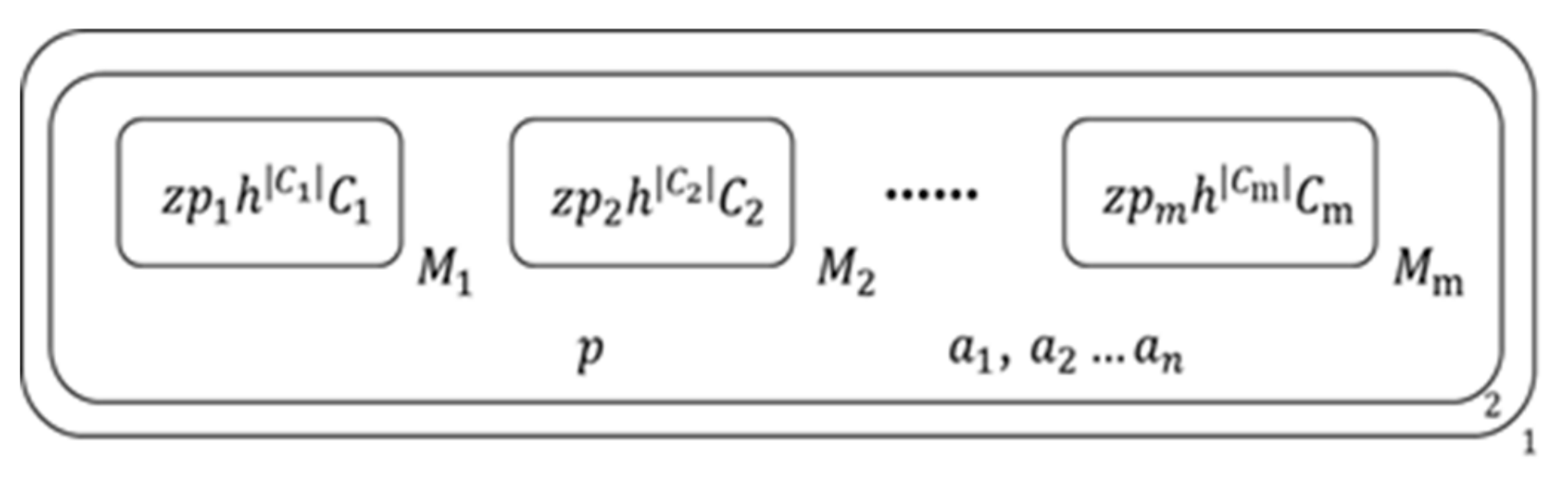
3.1. Definition
- (1)
- O: {, denote the literals of given clause set;, denotes the number of literals in a clause;, are the literal symbols of and ;, denotes the number of literals’ symbols;, denote the atoms of the given formulae;, are objects in the literal list of 2nd membrane;are the transitive symbols of and ;, denote the transport sign of membrane ;, denotes the number of membranes ;, denote the assignments of literals and ;, are the melting symbol of objects and membrane;, are aided symbols}.
- (2)
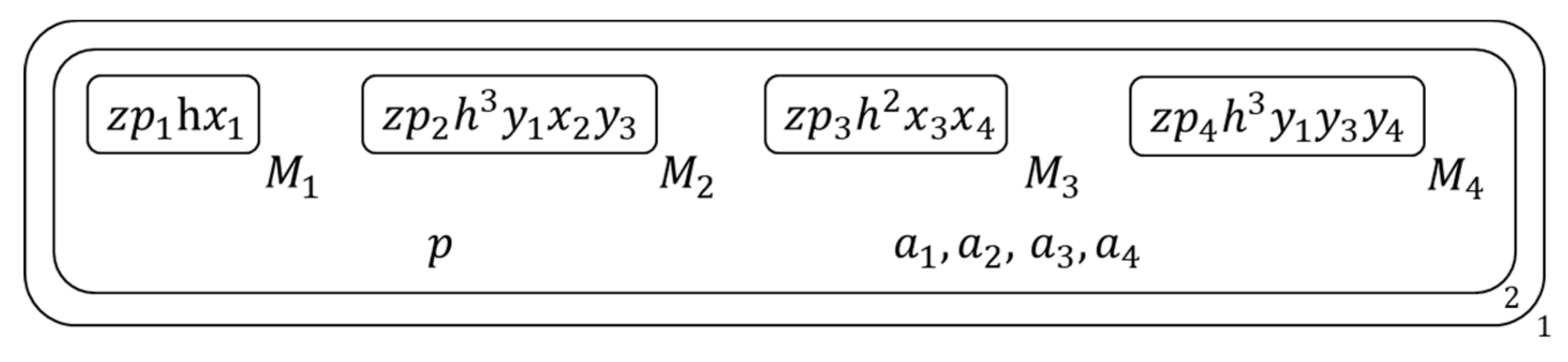
- the initial membrane structure is as Figure 2:denote the jth clause in the given clause set, represents the number of literals in .
- (3)
- ;;.
- (4)
- ) specific as described in the part of algorithm, and they are made up by three types of evolutionary rules:
- (a)
- , copy the membrane i into two copies when it or them contains object a, turn a in two copies into b and c respectively;
- (b)
- , turn a into b when c is existent or inexistent;
- (c)
- , turn a into b and c, meanwhile, send c into the membrane i or out the membrane which a was inside.
- (5)
- = 1.
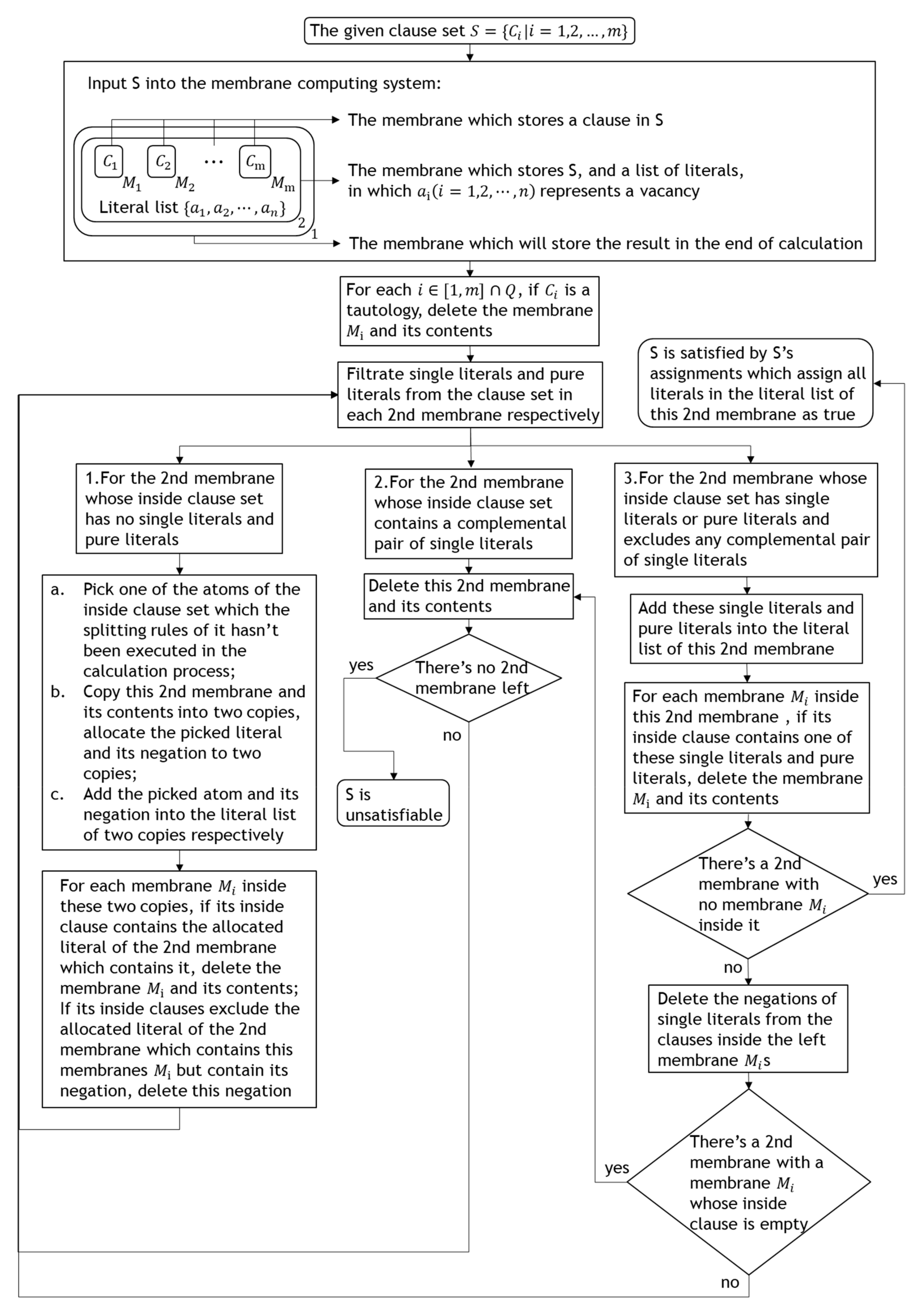
3.2. Compiling
- (1)
- Tautology rule:This rule is executed on the only 2nd membrane at the beginning of the calculation.Pick tautologies from the clauses inside membrane s, and mark the membrane s which contain tautologies with a delete symbol, ;Delete all contents inside the membrane s which are marked with a delete symbol:Delete the membrane s which are marked with a delete symbol,
- (2)
- One-literal rule:This rule is executed on each 2nd membrane.
- (3)
- Pure-literal rule:This rule is executed on each 2nd membrane as follows:Send all literals in the inside clause set outside from their original membranes: , then delete the repetitive literals: , finally delete the complemental pairs of literals:
- (4)
- Splitting rule:
- (a)
- For the 2nd membrane whose inside clause set has no single literals and pure literals, pick one of the atoms of the inside clause set which the splitting rules of it hasn’t been executed in the calculation process, and copy this 2nd membrane and its contents into two copies, allocate the picked literal and its negation to two copies, then add the picked atom and its negation into the literal list of two copies respectively, , then for each membrane inside these two copies, judge the type of its inside clause: , if its inside clause contains the allocated literal of the 2nd membrane which contains it, delete the membrane and its contents, if its inside clauses exclude the allocated literal of the 2nd membrane which contains this membranes , but contain its negation, delete this negation: ;
- (b)
- For the 2nd membrane whose inside clause set contains a complemental pair of single literals, delete this 2nd membrane and its contents with a unsatisfiable symbol N: , this is how unsatisfiable symbol N works in this algorithm: , if all 2nd membranes have been deleted, there’s no rule can be executed, the membrane structure has only the membrane which stores the final result left and this membrane is empty at this point, it means that S is unsatisfiable;
- (c)
- For the 2nd membrane whose inside clause set has single literals or pure literals and excludes any complemental pair of single literals, first add these single literals and pure literals into the literal list of this 2nd membrane: , then for each membrane inside this 2nd membrane, judge the type of its inside clause: , if its inside clause contains one of these single literals and pure literals, delete the membrane and its contents: , or else delete the negations of single literals from the clauses inside the left membrane s: , if there’s a membrane whose inside clause is empty at this point, delete this 2nd membrane and its contents: .
4. Example Illustration
- Copy each membrane and its contents into two copies , Figure 5 shows the membrane structure of this time.
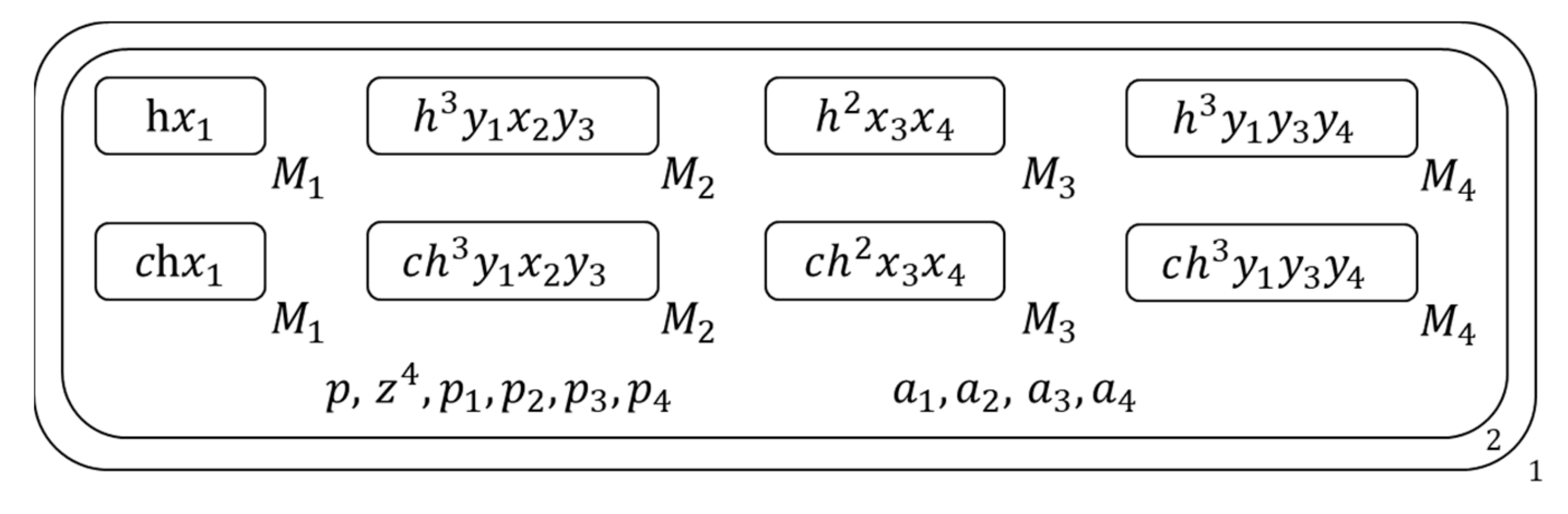
- Then for copy with mark c, release all literals of its inside clause to the 2nd membrane which contains it and generate literal symbols of all pure literals of this 2nd membrane’s inside clause set with these released literals , and for the copy without mark c, if its inside clause is a one-literal clause, mark the literal of this inside clause with one-literal symbol and send the one-literal symbol outside , Figure 6 shows the membrane structure of this time.
- 3.
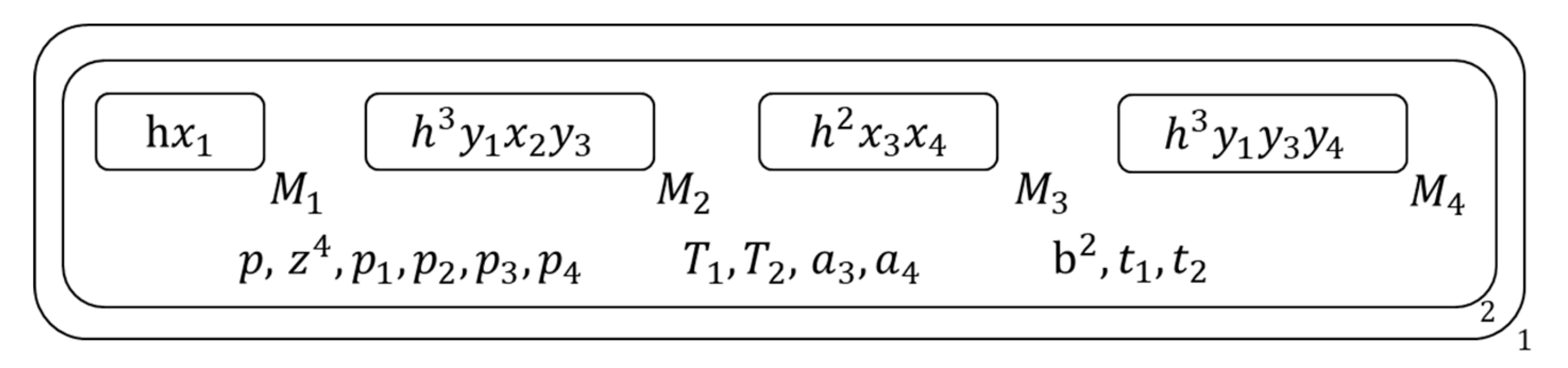
- Next execute following three operations respectively on the membrane s which contain different types of clauses , Figure 10 shows the membrane structure of this time.
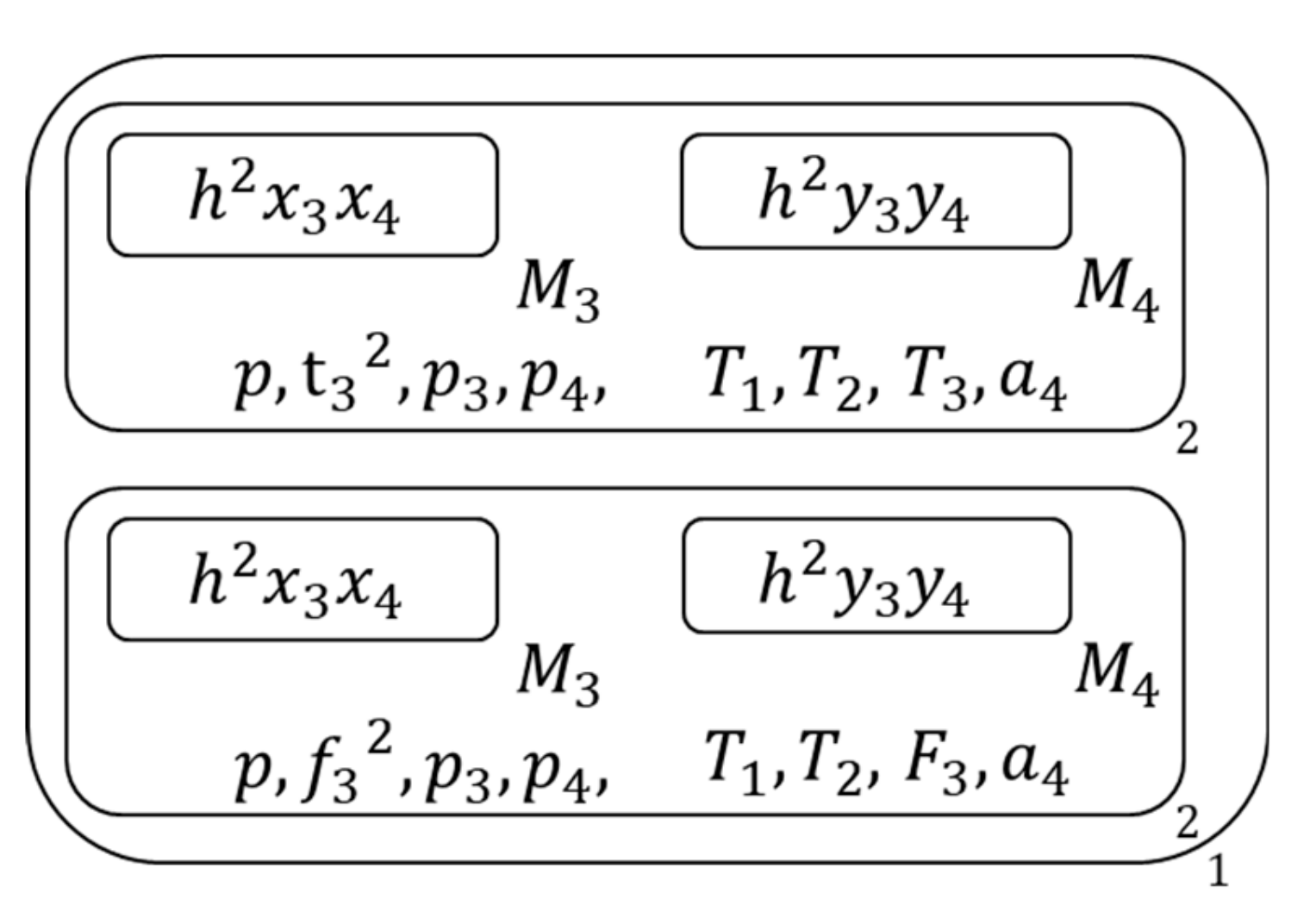
- Copy each membrane and its contents into two copies , Figure 11 shows the membrane structure of this time.
- Then for the copy with mark c, release all literals of its inside clause to the 2nd membrane which contains it and generate literal symbols of all pure literals of this 2nd membrane’s inside clause set with these released literals , and for the copy without mark c, if its inside clause is a one-literal clause, mark the literal of this inside clause with one-literal symbol and send the one-literal symbol outside , Figure 12 shows the membrane structure of this time.
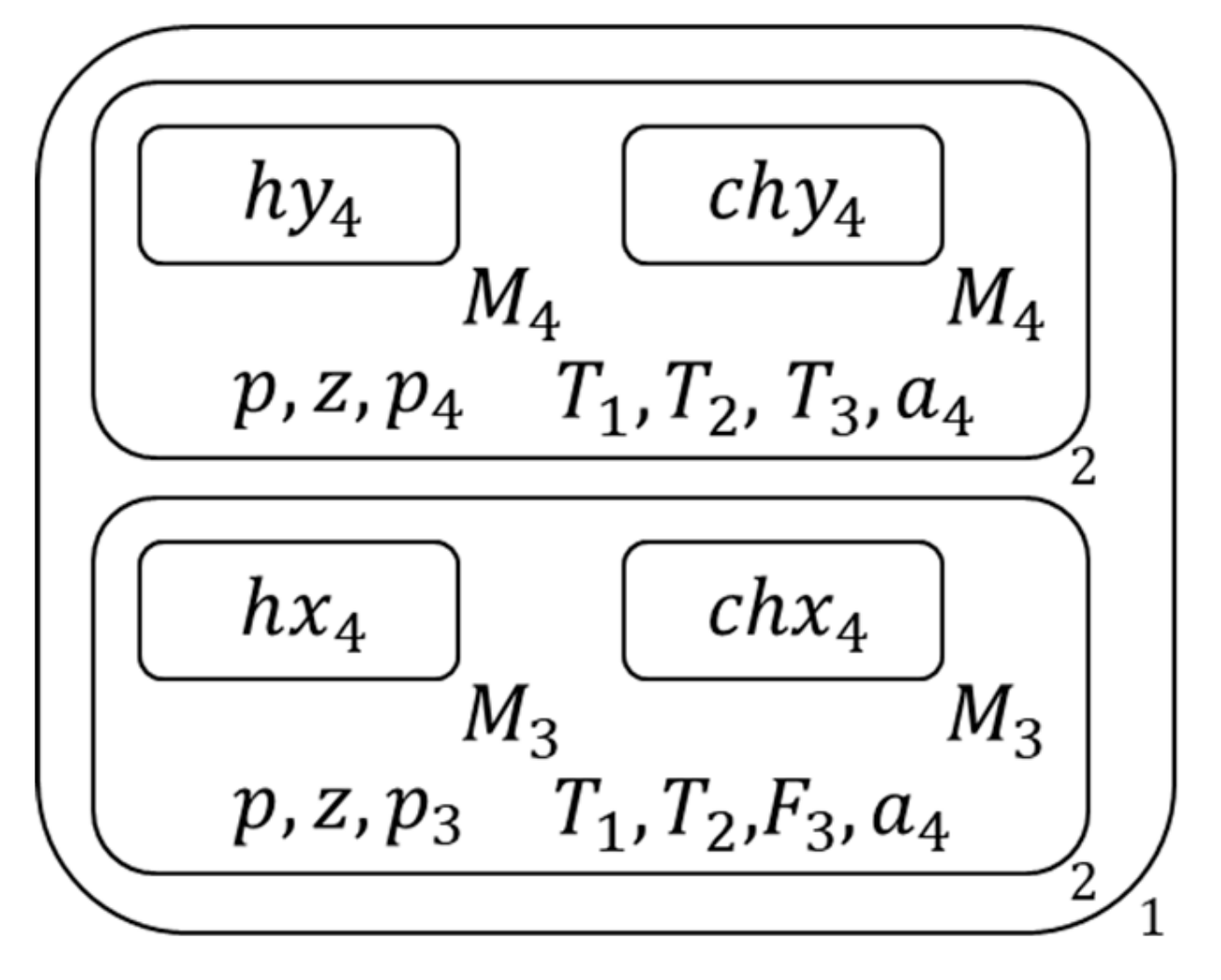
- Pick one of the atoms of the inside clause set which the splitting rules of it hasn’t been executed in the calculation process, and copy this 2nd membrane and its contents into two copies, allocate the picked literal and its negation to two copies, then add the picked atom and its negation into the literal list of two copies respectively , Figure 13 shows the membrane structure of this time.
- 2.
- Then for each membrane inside these two copies, judge the type of its inside clause , Figure 15 shows the membrane structure of this time.
- 3.
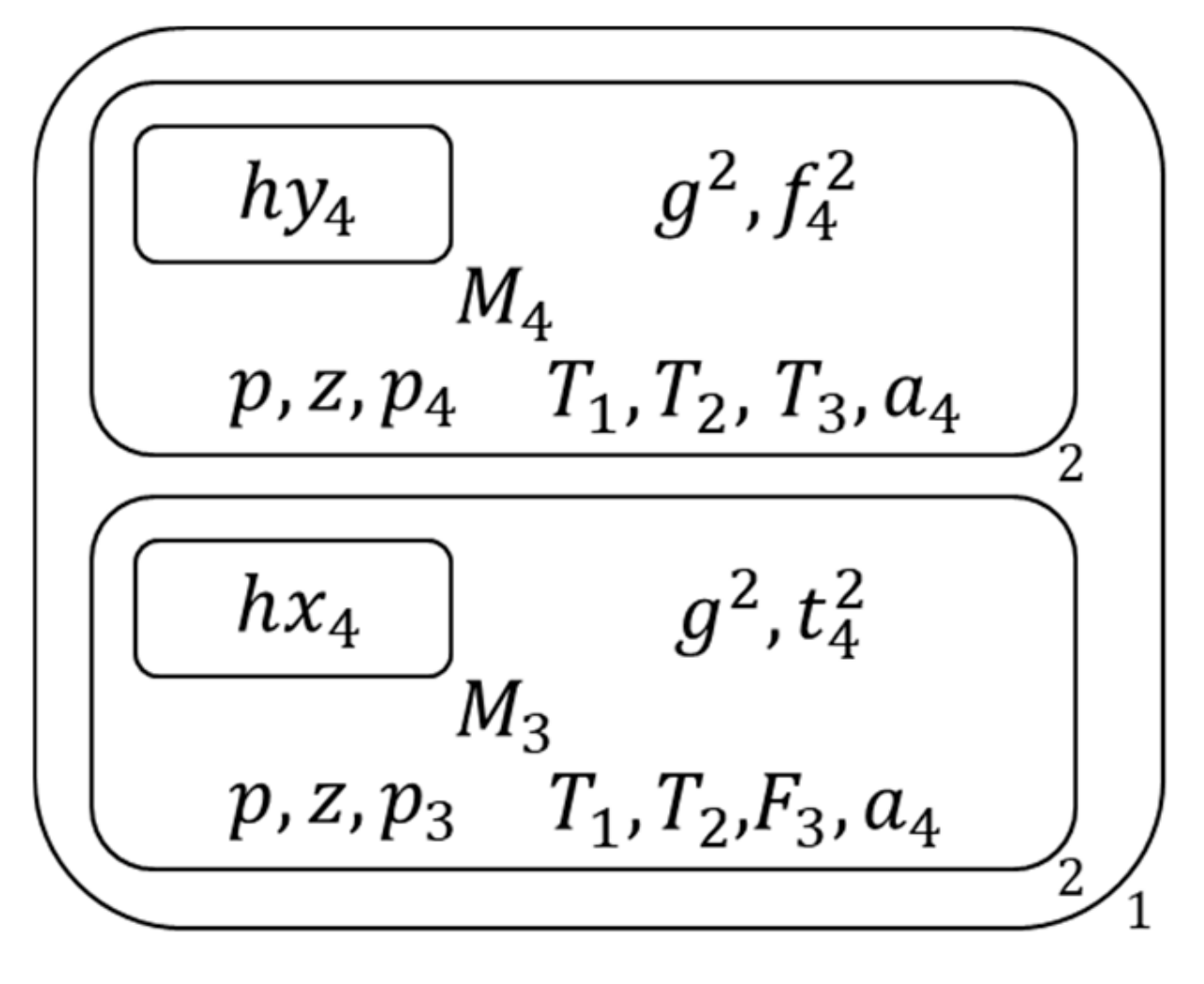
- Next execute following three operations respectively on the membrane s which contain different types of clauses , Figure 16 shows the membrane structure of this time.
- Copy each membrane and its contents into two copies , Figure 17 shows the membrane structure of this time.
- Then for the copy with mark c, release all literals of its inside clause to the 2nd membrane which contains it and generate literal symbols of all pure literals of this 2nd membrane’s inside clause set with these released literals , and for the copy without mark c, if its inside clause is a one-literal clause, mark the literal of this inside clause with one-literal symbol and send the one-literal symbol outside , Figure 18 shows the membrane structure of this time.
- Add these single literals and pure literals into the literal list of this 2nd membrane , then for each membrane inside this 2nd membrane, judge the type of its inside clause , Figure 19 shows the membrane structure of this time.
- 2.
- Next execute following three operations respectively on the membrane s which contain different types of clauses , Figure 21 shows the membrane structure of this time.
- 3.
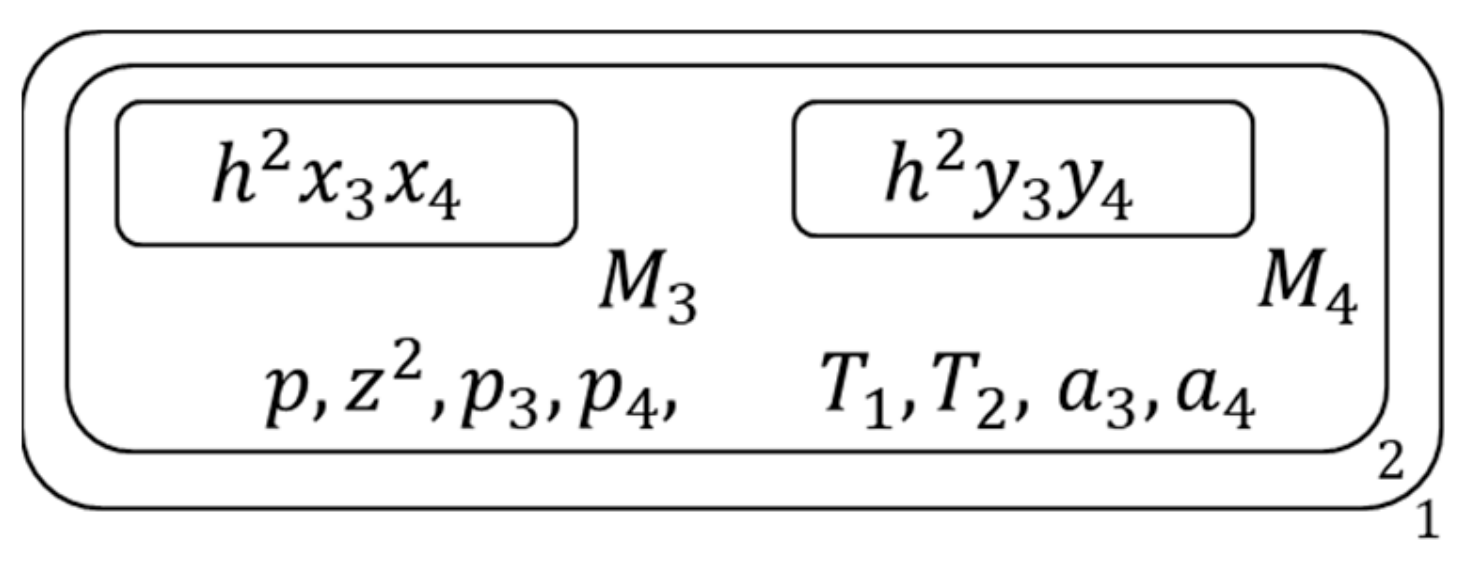
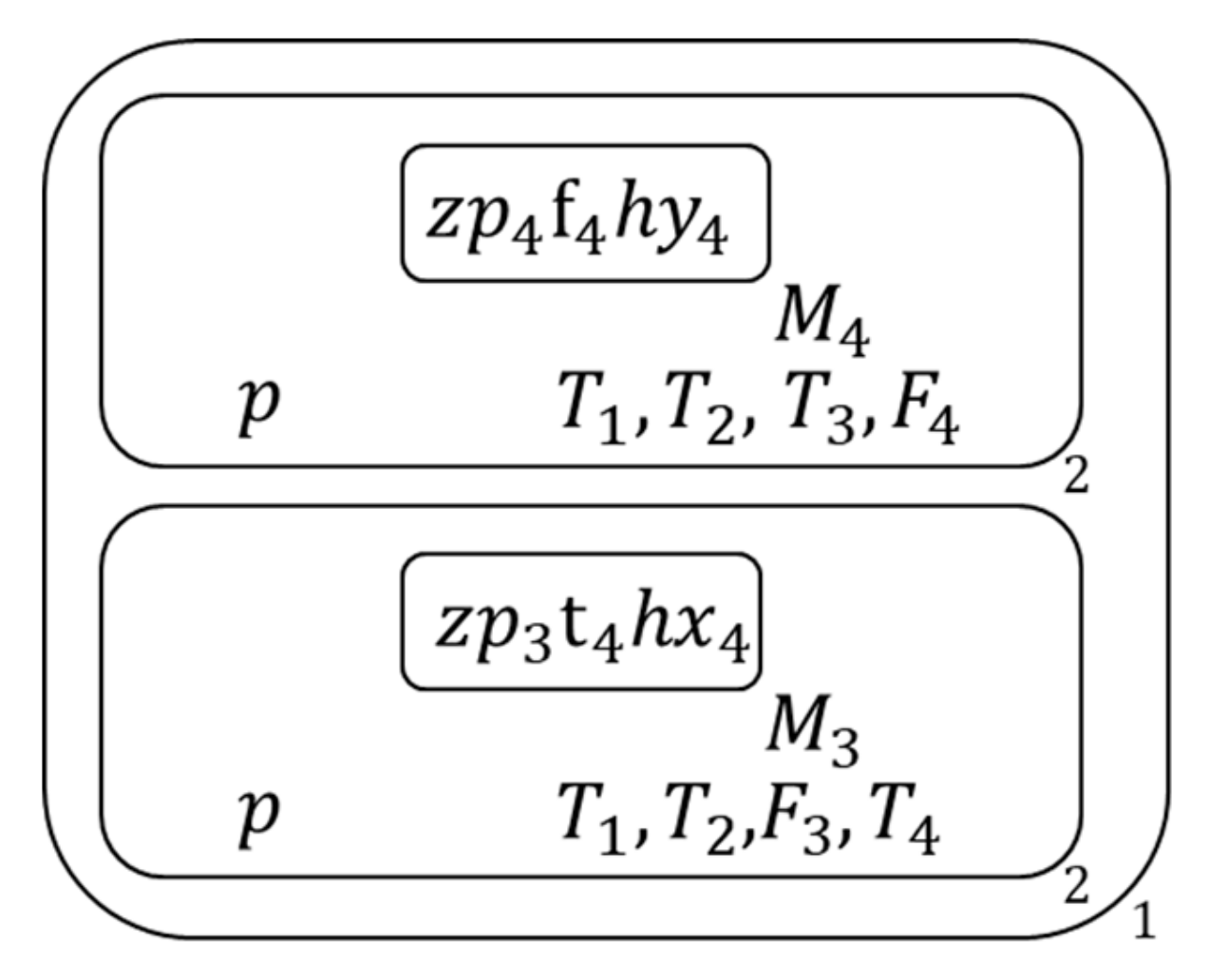
- Pick a 2nd membrane like this, and delete all 2nd membrane and their contents except the literal list of the picked 2nd membrane , Figure 22 shows the membrane structure of this time.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kautz, H.; Selman, B. The State of SAT. Discrete Appl. Math. 2007, 155, 1514–1524. [Google Scholar] [CrossRef]
- Marques-Silva, J.; Lynce, I.; Malik, S. Conflict-driven clause learning SAT solvers. In Handbook of Satisfiability; Biere, A., Heule, M., Van Maaren, H., Walsh, T., Eds.; IOS Press: Amsterdam, The Netherlands, 2009; Volume 185, pp. 131–153. [Google Scholar]
- Davis, M.; Putnam, H. A Computing Procedure for Quantification Theory. J. ACM 1960, 7, 201–215. [Google Scholar] [CrossRef]
- Sorensson, N.; Een, N. MiniSat—A SAT solver with conflict-clause minimization. In Proceedings of the SAT-05 8th International Conference on Theory and Applications of Satisfiability Testing, St Andrews, UK, 19–23 June 2005. [Google Scholar]
- Biere, A. MiniSat, cadical, lingeling, plingeling, treengeling and yalsat Entering the SAT Competition 2018. In Proceedings of the SAT Competition 2018: Solver and Benchmark Descriptions; 2018. [Google Scholar]
- Moskewicz, M.W.; Madigan, C.F.; Zhao, Y.; Zhang, L.; Malik, S. Chaff: Engineering an efficient SAT solver. In Proceedings of the 38th annual Design Automation Conference, Las Vegas, NV, USA, 22 June 2001. [Google Scholar]
- Simon, L.; Audemard, G. Predicting Learnt Clauses Quality in Modern SAT Solver. In Proceedings of the 21th International Joint Conference on Artificial Intelligence, Pasadena, CA, USA, 11–17 July 2009. [Google Scholar]
- Juretus, K.; Savidis, I. Importance of Multi-parameter SAT Attack Exploration for Integrated Circuit Security. In Proceedings of the 2018 IEEE Asia Pacific Conference on Circuits and Systems, Chengdu, China, 26–30 October 2018. [Google Scholar]
- Liu, C.; Zhang, L.; He, X.; Guo, Y. Analysis of SET Reconvergence and Hardening in the Combinational Circuit Using a SAT-Based Method. IEEE Access 2018, 6, 48740–48746. [Google Scholar] [CrossRef]
- Efficient Methods for Conversion and Solution of Sparse Systems of Low-Degree Multivariate Polynomials over GF(2) Via Sat-Solvers. Available online: http://eprint.iacr.org/2007/024 (accessed on 25 January 2007).
- Cook, S.A. The complexity of theorem-proving procedures. In Proceedings of the Third ACM Symposium on Theory of Computing, Shaker Heights, OH, USA, 3–5 May 1971. [Google Scholar]
- Martins, R.; Manquinho, V.; Lynce, I. An overview of parallel SAT solving. Constraints 2012, 17, 304–347. [Google Scholar] [CrossRef]
- Păun, G. Computing with Membranes. J. Comput. Syst. Sci. 2000, 61, 108–143. [Google Scholar] [CrossRef]
- Gutiérrez-Naranjo, M.A.; Pérez-Jiménez, M.J.; Riscos-Núñez, A.; Romero-Campero, F.J. On the efficiency of cell-like and tissue-like recognizing membrane systems. Int. J. Intell. Syst. 2009, 24, 747–765. [Google Scholar] [CrossRef]
- Gutiérrez-Naranjo, M.A.; Pérez-Jiménez, M.J.; Riscos-Núñez, A.; Romero-Campero, F.J. On the power of dissolution in P systems with active membranes. In Proceedings of the International Workshop on Membrane Computing, Vienna, Austria, 18–21 July 2005; pp. 224–240. [Google Scholar]
- Macías-Ramos, L.F.; Pérez-Jiménez, M.J.; Riscos-Núñez, A.; Rius-Font, M. The efficiency of tissue P systems with cell separation relies on the environment. In Proceedings of the International Conference on Membrane Computing, Budapest, Hungary, 28–31 August 2012; pp. 243–256. [Google Scholar]
- Pan, L.; Pérez-Jiménez, M.J. Computational complexity of tissue–like P systems. J. Complex. 2010, 26, 296–315. [Google Scholar] [CrossRef]
- Pérez-Jiménez, M.J.; Riscos-Núñez, A.; Rius-Font, M.; Valencia-Cabrera, L. The relevance of the environment on the efficiency of tissue P systems. In Proceedings of the International Conference on Membrane Computing Chisinau, Chisinau, Moldova, 20–23 August 2013; pp. 308–321. [Google Scholar]
- Manca, V. DNA and membrane algorithms for SAT. Fund. Inform. 2002, 49, 205–221. [Google Scholar]
- Ciobanu, G.; Păun, G.; Pérez-Jiménez, M.J. Applications of Membrane Computing; Springer: Berlin, Germany, 2006. [Google Scholar]
- Ishii, K.; Fujiwara, A.; Tagawa, H. Asynchronous P systems for SAT and Hamiltonian cycle problem. In Proceedings of the 2010 Second World Congress on Nature and Biologically Inspired Computing, Fukuoka, Japan, 15–17 December 2010. [Google Scholar]
- Song, T.; Macías-Ramosb, L.F.; Pan, L.; Pérez-Jiménez, M.J. Time-free solution to SAT problem using P systems with active membranes. Theor. Comput. Sci. 2014, 529, 61–68. [Google Scholar] [CrossRef]
- Adorna, H.N.; Pan, L.; Song, B. On Distributed Solution to SAT by Membrane Computing. Int. J. Comp. Commun. 2018, 13, 303–322. [Google Scholar] [CrossRef]
- Păun, G. Membrane Computing: An Introduction; Springer: Berlin, Germany, 2002. [Google Scholar]
- Liu, X.H. Automatic Reasoning Based on The Resolution Method; Science Press: Beijing, Chinese, 1994. [Google Scholar]










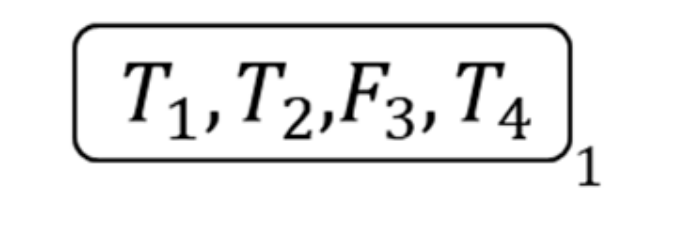
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, L.; Liu, J. Enhanced Membrane Computing Algorithm for SAT Problems Based on the Splitting Rule. Symmetry 2019, 11, 1412. https://doi.org/10.3390/sym11111412
Hao L, Liu J. Enhanced Membrane Computing Algorithm for SAT Problems Based on the Splitting Rule. Symmetry. 2019; 11(11):1412. https://doi.org/10.3390/sym11111412
Chicago/Turabian StyleHao, Le, and Jun Liu. 2019. "Enhanced Membrane Computing Algorithm for SAT Problems Based on the Splitting Rule" Symmetry 11, no. 11: 1412. https://doi.org/10.3390/sym11111412
APA StyleHao, L., & Liu, J. (2019). Enhanced Membrane Computing Algorithm for SAT Problems Based on the Splitting Rule. Symmetry, 11(11), 1412. https://doi.org/10.3390/sym11111412