2. Preliminaries and Definitions
Throughout this paper, stands for the n-dimensional Euclidean space and for its non-negative orthant. Consider the following vector minimization problem:
(MP) Minimize
Subject to
where and are differentiable functions defined on
Definition 1. A point is said to be an efficient solution of (MP) if there exists no other such that for some and for all
Definition 2. The positive polar cone of a cone is defined by Let and be closed convex cones with non-empty interiors and and be non-empty open sets in and , respectively, such that . Suppose is a vector- valued differentiable function.
Definition 3. The function f is said to be invex at (with respect to where ), if and for fixed , we have If the above inequality sign changes to ≤, then f is called incave at with respect to
Definition 4. The function f is said to be pseudoinvex at (with respect to where ), if and for fixed , we have If the above inequality sign changes to then f is called pseudoincave at with respect to
Definition 5. The function f is said to be -invex at (with respect to η), if there exists a differentiable function such that each component , where is the range of , is strictly increasing on its domain and , so that , for fixed we have If the above inequality sign changes to ≤, then f is called -incave at with respect to
Definition 6. The function f is said to be -pseudoinvex at (with respect to η), if there exists a differentiable function such that each component , where is the range of , is strictly increasing on its domain and , so that , for fixed we have If the above inequality sign changes to then f is called -pseudoincave at with respect to
Definition 7. The function f is said to be -bonvex at (with respect to η), if there exists a differentiable function such that each component , where is the range of , is strictly increasing on its domain and , so that , for fixed and we have
If the above inequality sign changes to then f is called -boncave at with respect to
Definition 8. The function f is said to be -pseudobonvex at (with respect to η), if there exists a differentiable function such that each component , where is the range of , is strictly increasing on its domain and , so that , for fixed and
If the above inequality sign changes to then f is called -pseudoboncave at with respect to
We now give an example of -bonvexity with respect to but not -bonvex.
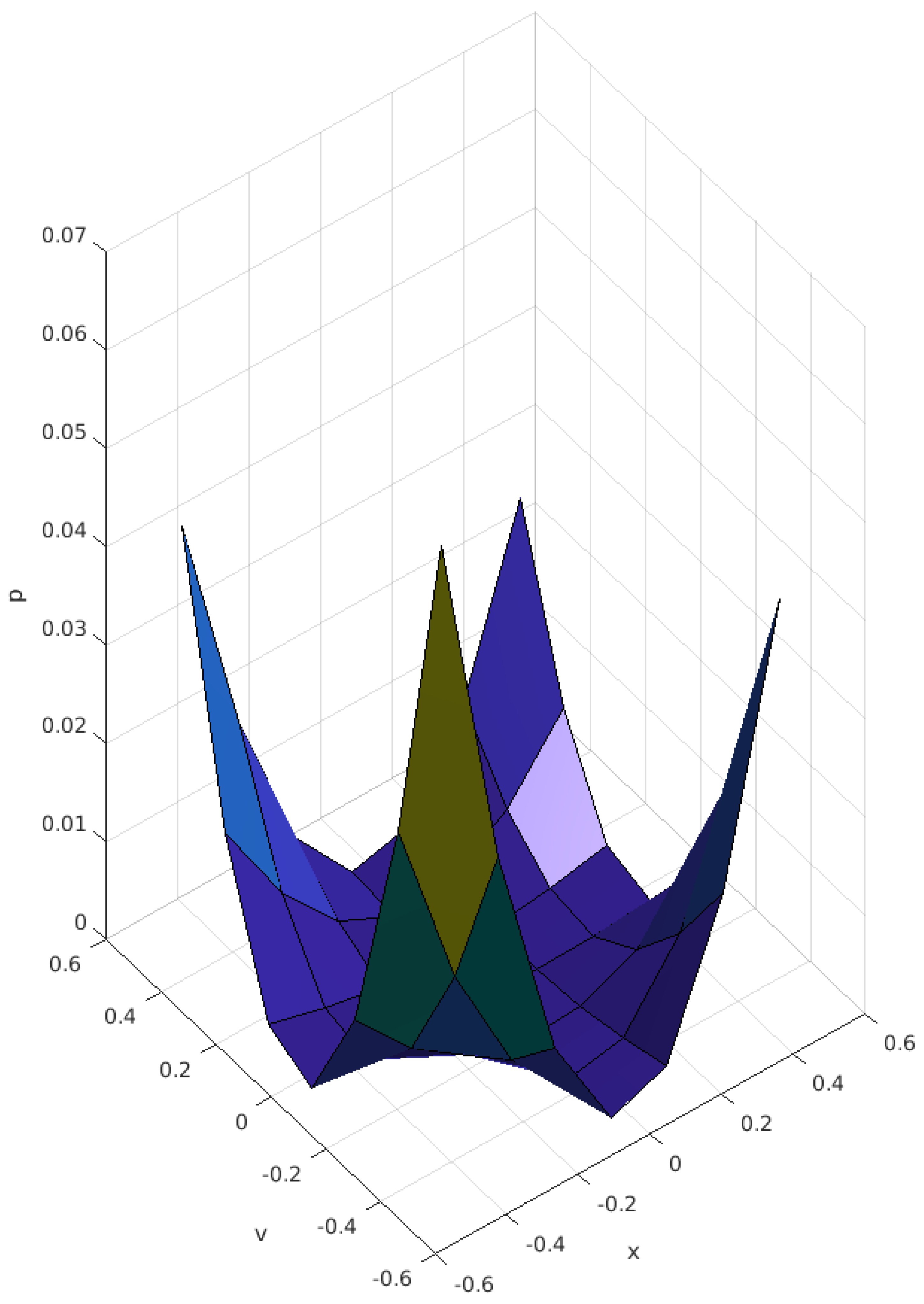
Example 1. Let .
Let be defined aswhere and be defined as: Let
be given as:
To show that f is -bonvex at with respect to , we have to claim that
Putting the values of
and
in the above expressions, we have
and
Hence,
(from
Figure 1),
(in
Figure 2) and
and
Therefore, f is -bonvex at with respect to and
Next, we claim that function f is not -bonvex. For this, it is sufficient to prove that at least one is not -bonvex.
It follows that
and
(in
Figure 3). Therefore,
is not
-bonvex at
with respect to
. Hence,
is not
-bonvex at
with respect to
Definition 9. Let C be a compact convex set in . The support function of C is defined by The subdifferential of is given by For any convex set , the normal cone to S at a point is defined by It is readily verified that for a compact convex set S, y is in if and only if Suppose that and are open sets such that
3. Second-Order Nondifferentiable Multiobjective Symmetric Fractional Programming Problem Over Arbitrary Cones
Now, we consider the following pair of a nondifferentiable multiobjective second-order fractional symmetric dual program over arbitrary cones
(GMFP) Minimize
subject to
(GMFD) Maximize
subject to
where
and
and
and ; and are arbitrary cones in and , respectively, such that ; and are differentiable functions; and are differentiable strictly increasing functions on their domains; , are compact convex sets in ; and are compact convex sets in ,. and are positive polar cones of and , respectively. It is assumed that in the feasible regions, the numerators are nonnegative and denominators are positive. and are vectors in and respectively, .
Equivalently, the above problem is reduced in the given form:
(EGMFP) Min
subject to
(EGMFD) Maximize
subject to
Let and be the sets of feasible solutions of (EGMFP) and (EGMFD), respectively. Next, we prove duality theorems for (EGMFP) and (EGMFD), which equally apply to (GMFP) and (GMFD), respectively. Let and .
Theorem 1. (Weak Duality). Let and . Assume that for :
- (i)
is - bonvex and is invex at u for fixed v with respective to .
- (ii)
is a - boncave and is invex at u for fixed v with respective to .
- (iii)
is a - boncave and is invex at y for fixed x with respective to .
- (iv)
is a - bonvex and is invex at y for fixed x with respective to .
- (v)
and .
- (vi)
Then, the following can not hold simultaneously:
, for all and , for some .
Proof. From Assumption (v) and Equation (
6), we get
Using Equations (
7) and (
9), we obtain,
From Assumption (i), we have
and
Since and combining above inequalities, it follows that
Similarly, from Assumption (ii), we get
and
Multiplying by in above inequalities and taking summation over , it follows that
Adding the inequalities in Equations (
13) and (
16), we get
Since
from Equations (
17) and (
5), we get
Similarly, using Hypotheses (iii)–(v) and the primal constraints in Equations (
1)–(
4), we have
On adding the inequalities in Equations (
18) and (
19), we get
Since
it yields
From Assumption (vi), we have, . Since , it follows that , hence the result. □
Remark 1. Since every convex function is pseudoconvex, the above weak duality theorem for the symmetric dual pair (EGMFP) and (EGMFD) can also be obtained under pseudobonvexity assumptions.
Theorem 2. (Weak Duality). Let and . Assume that for :
- (i)
is - pseudobonvex and is pseudoinvex at u for fixed v with respective to .
- (ii)
is a - pseudoboncave and is pseudoinvex at u for fixed v with respective to .
- (iii)
is a - pseudoboncave and is pseudoinvex at y for fixed x with respective to .
- (iv)
is a - pseudobonvex and is pseudoinvex at y for fixed x with respective to .
- (v)
and .
- (vi)
Then, the following cannot hold simultaneously:
, for all and , for some .
Proof. The proof follows on the lines of Theorem 1. □
Theorem 3. (Strong Duality). Let be an efficient solution to (EGMFP), fix in (EGMFD). Further, assume that
- (i)
is positive definite
and
for all .
- (ii)
The matrix
is positive definite for .
- (iii)
For and implies that
- (iv)
is linearly independent.
- (v)
Then, there exist and such that is feasible for (EGMFD). Furthermore, if the assumptions of Theorem 1 or Theorem 2 are satisfied, then is an efficient solution to (EGMFD).
Proof. Since
is an efficient solution of (EMFP), by Fritz John necessary conditions [
14], there exists
and
such that
From Assumption (i) and Equation (
24), we have
We claim that
The proof is by contradiction. Let
for some
Since
, the relation in Equation (
33) yields
From the relation in Equations (
22), (
33) and (
34), we obtain
On using Asumption (iv), this gives
Since
we obtain
but
and thus the relation in Equation (
36) implies
. Thus, from the relation in Equations (
25), (
34) and (
36), we get
In addition, from the relation in Equation (
34), we get
which is a contradiction, since
Hence, we get
Since
, using Equations (
22) and (
33), we get
Hence, from Assumption (iii), we get
From the relation in Equation (
33),
and
we have
, from Equations (
21) and (
22), we have
By Assumptions (i) and (iii), we have
Since
and
, the relation in Equation (
40) implies that
, and the relation in Equation (
38) reduces to
Let
. Then,
as
is a closed convex cone. On substituting
into the place of
x in Equation (
41), we get
In addition, by letting
and
simultaneously in Equation (
41), we have
Since
and
, we have
From Equations (
26) and (
34) and using
, we get
,
This implies
Similarly, by Equation (
27) and Assumption (iii),
, we obtain
Combining Equations (
31), (
45), (
46) and (
31), it follows that
This together with Equations (
42), (
43) and (
47) shows that
. Now, let
be not an efficient solution of (EGMFD). Then, there exists other
such that
,
and
, for some
. This contradicts the result of the Theorems 1 and 2. Hence, the proof is complete. □
Remark 2. In the case of symmetric programming problem, the proof of converse duality theorem remains same as Theorem 3.
Theorem 4. (Converse duality theorem). Let be an efficient solution to (EGMFD), fix in (EGMFP). Further, assume that
- (i)
is positive definite and
for all .
- (ii)
The matrix
is positive definite for .
- (iii)
For and implies that
- (iv)
is linearly independent.
- (v)
Then, there exist and such that is feasible for (EGMFP). Furthermore, if the assumptions of Theorem 1 or Theorem 2 are satisfied, then is an efficient solution to (EGMFP).
Proof. The results can be obtained on the lines of Theorem 3. □