A Satellite Task Planning Algorithm Based on a Symmetric Recurrent Neural Network
Abstract
:1. Introduction
1.1. Proposal of the Intelligent Satellite
1.2. Task Planning for Satellite Earth Observation
2. Related Research
2.1. Overview of Satellite Task Planning Algorithms
2.2. Overview of the Application of Neural Networks in Task Planning Algorithms
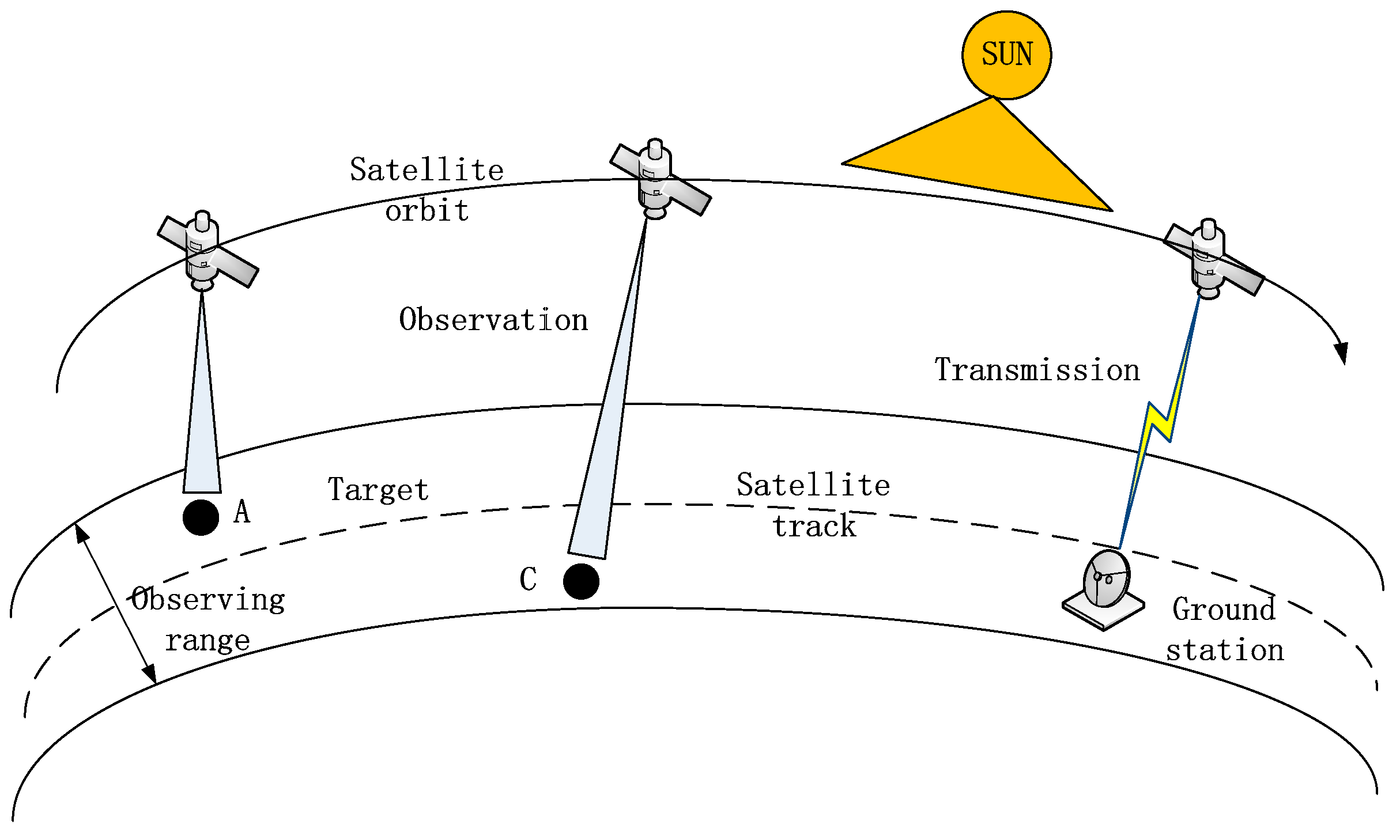
3. Problem Description
3.1. Problem Description
- When the iSAT satellite detects natural disasters, such as floods, mudslides, forest fires or ground targets that are covered by clouds, new observation requests are autonomously generated;
- The iSAT satellite receives cooperative observation requests, sent by other iSAT satellites, such as the joint observation of multiple types of sensors;
- The iSAT satellite receives a user observation request, uploaded by the ground control center or the ground user terminal.
3.2. Assumptions and Constraints
3.2.1. Assumptions
- (1)
- The scheduling range is defined as the interval between two consecutive satellite-ground communication links. In terms of time, geographically, we only plan observation tasks within a given range of observation tasks.
- (2)
- Intelligent satellites operate well throughout the entire dispatch range and will not be affected by space radiation effects.
- (3)
- Intelligent satellites have certain autonomic capabilities, allowing them to analyze the collected image information. If an event of interest is detected, a new task can be generated in-orbit.
- (4)
- Smart satellites can only be charged when idle (for example, without performing a task) and in the sun. The iSAT satellite can be charged while performing tasks and in the sun, but the energy obtained is much less than the energy consumed to observe the payload or transmit the payload, so the energy obtained is negligible.
- (5)
- When a smart satellite processes a task at any time, the task is not replaced by other tasks. That is, the observation task or the transmission task cannot be interrupted or deleted, once it is executed.
- (6)
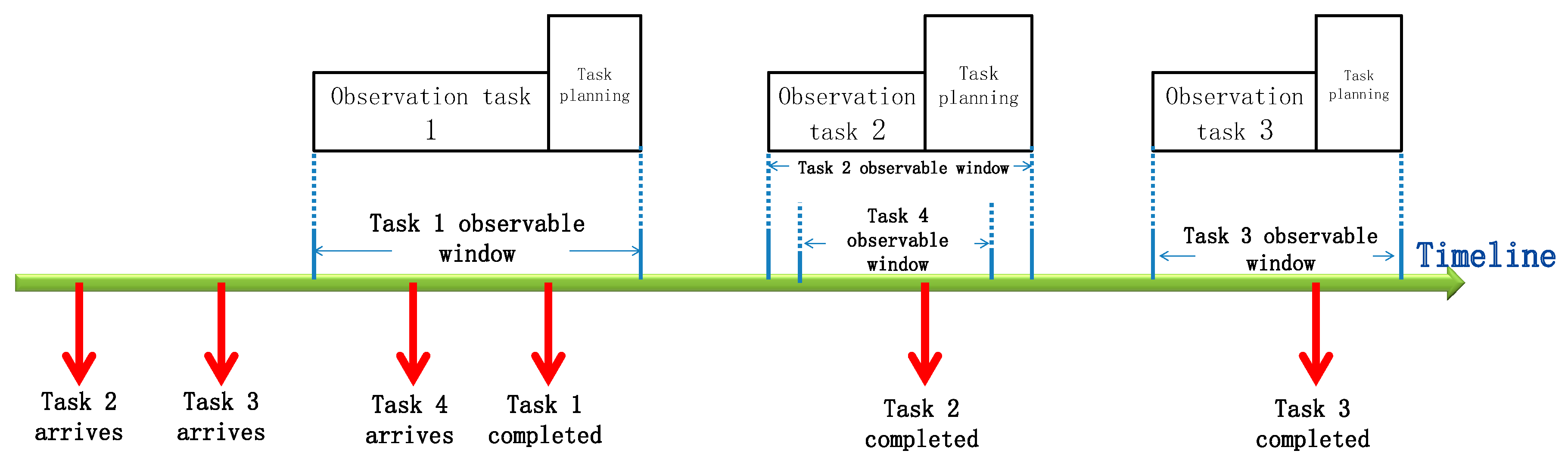
- There is no priority constraint between the tasks, but each task has a constraint on the observation time window. All tasks have one and only one corresponding observation time window.
3.2.2. Constraints
Task Switching Time Constraint
Energy Constraint
Data Storage Constraint
4. Mixed Integer Programming Model

5. Heuristic Search Algorithm Based on a Symmetric Recurrent Neural Network
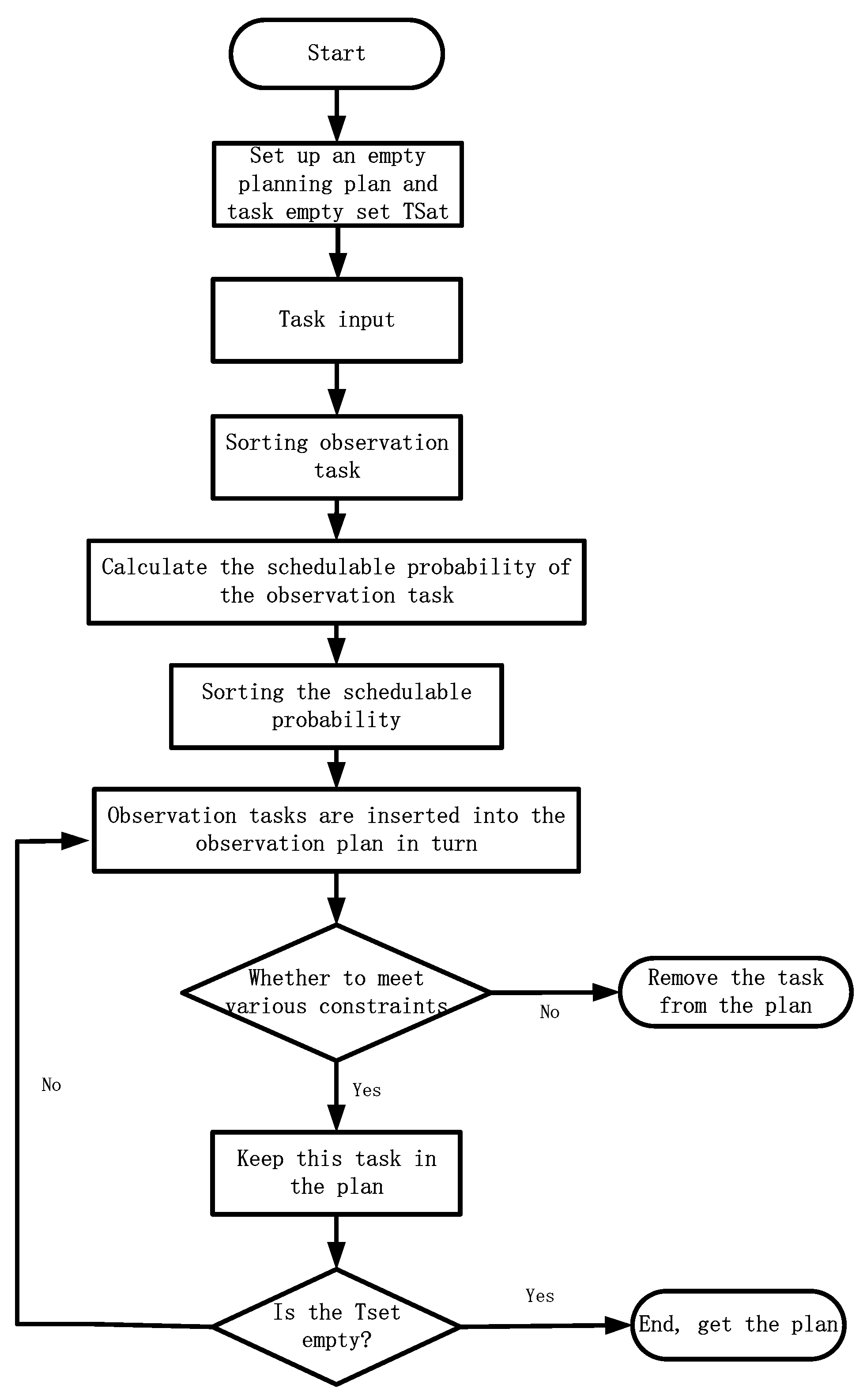
5.1. Algorithm Design
| Algorithm 1 Heuristic Search Algorithm Based on a Symmetric Structure Neural Network |
| 1: Algorithm initialization: set empty planning scheme and task empty set TSet; 2: Input all observation tasks within the planning into TSet; 3: Separate the observation tasks in the TSet in chronological order; 4: Calculate the schedulable probability of each observation task in the TSet; 5: Sort the observation tasks in the TSet; 6: Insert the best FTask into the observation scheme to perform constraint checking; 7: Repeat step 5 to output the observation plan. |
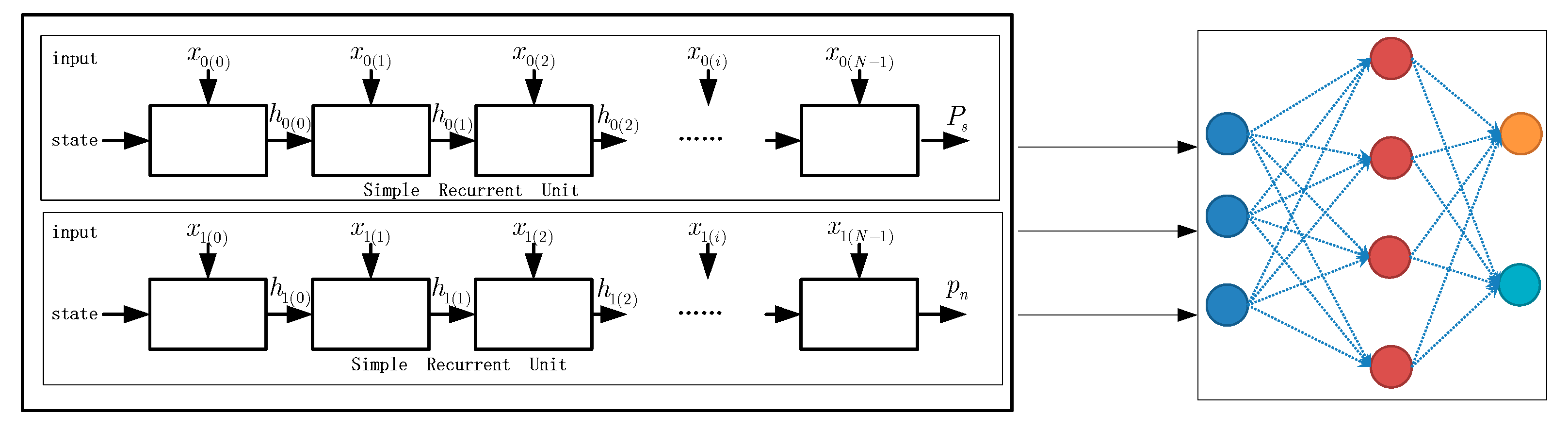
5.2. Model Input
5.3. Optimization Algorithm and Loss Function
6. Experiment
6.1. Experiment Setting
6.1.1. Track Parameter Setting
6.1.2. Experiment Setting
6.1.3. Indicator Setting
6.2. Analysis of Results
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Min, S. China’s intelligent space-based integrated information network concept. In Proceedings of the 2018 Software Definition Satellite Summit, Beijing, China, 4 April 2018. [Google Scholar]
- Zhao, J.; Wu, F.; Liu, G. Development and Prospect of software definition satellite technology. Satell. Netw. 2017, 12, 46–50. [Google Scholar]
- Ulversoy, T. Software Defined Radio: Challenges and Opportunities. IEEE Commun. Surv. Tutor. 2010, 12, 531–550. [Google Scholar] [CrossRef]
- NASA. Space Telecommunication Radio System STRS Architecture Standard. Revion 1.02.1. 2010. [Google Scholar]
- Reinhart, R.C. Space Communication and Navigation SDR Testbed, Overview and Opportunity for Experiments. In Proceedings of the SDR WinnComm Technical Conference, Washington, DC, USA, 8 January 2013. [Google Scholar]
- Feng, Y. The fully softwareized “quantum” satellite is of great significance. Def. Perspect. 2015, 9, 17–18. [Google Scholar]
- Lockheed Martin’s First Smart Satellites Are Tiny with Big Missions. Available online: https://news.lockheedmartin.com (accessed on 20 March 2019).
- Yang, X. Integrated Integrated Spatial Information System Based on “Software Star”. J. China Acad. Electron. Inf. Technol. 2004, 5, 15–22. [Google Scholar]
- Li, L. Software-defined satellite intelligence leads the space flight. China Sci. Technol. Awards 2019, 235, 26–28. [Google Scholar]
- Yang, Z. Research on Low-Cost Digital Signal Processing Technology of Space-Based Network Intelligent Satellite; National University of Defense Technology: Changsha, China, 2016. [Google Scholar]
- Qin, H. Research on Key Technologies of Intelligent Satellite (iSAT) for Space-Based Network; National University of Defense Technology: Changsha, China, 2017. [Google Scholar]
- Jin, P.; Yu, K. Simulation Study on Integrated Scheduling of Satellite Target Resources. Comput. Simul. 2018, 35, 16–21. [Google Scholar]
- Berger, J.; Giasson, E.; Florea, M.; Harb, M.; Teske, A.; Petriu, E.; Abielmona, R.; Falcon, R.; Lo, N. A Graph-based Genetic Algorithm to Solve the Virtual Constellation Multi-Satellite Collection Scheduling Problem. IEEE Congr. Evoluti. Comput. 2018, 1–8. [Google Scholar] [CrossRef]
- Mouw, C.B.; Greb, S.; Aurin, D.; DiGiacomo, P.M.; Lee, Z.; Twardowski, M.; Binding, C.; Hu, C.; Ma, R.; Moore, T.; et al. Aquatic Color Radiometry Remote Sensing of Coastal and Inland Waters: Challenges and Recommendations for Future Satellite Mission. Remte Sens. Environ. 2015, 160, 15–30. [Google Scholar] [CrossRef]
- Xhafa, F.; Sun, J.; Barolli, A.; Biberaj, A.; Barolli, L. Genetic Algorithms for Satellite Scheduling Problems. Mob. Inf. Syst. 2012, 8, 351–377. [Google Scholar] [CrossRef] [Green Version]
- Sarkheyli, A.; Bagheri, A.; Ghorbani-Vaghei, B.; Askari-Moghadam, R. Using an Effective Tabu Search in Interactive Resources Scheduling Problem for Leo Satellites Missions. Aerosp. Sci. Technol. 2013, 29, 287–295. [Google Scholar] [CrossRef]
- Qi, M.R. Using Constraint Satisfaction to Cooperate Satellites’ Activities for the Mission of Area Target Observation. J. Astronaut. 2007, 28, 238–242. [Google Scholar]
- Globus, A.; Wu, G.; Liu, J. A Two-phase Scheduling Method with the Consideration of Task Clustering for Earth Observing Satellites. Comput. Op. Res. 2013, 40, 1884–1894. [Google Scholar]
- He, R.; Gao, P.; Bai, B. Models, algorithms and applications to the task planning system of imaging satellites. Syst. Eng. Theor. Pract. 2011, 31, 411–422. [Google Scholar]
- Gao, P.; Tan, Y.J.; Li, J.F.; He, R.J. An Ant Colony Algorithm for Remote Satellite and Groud Integration Scheduling Problem in Parallel Environment. Adv. Mater. Res. 2013, 791, 1341–1346. [Google Scholar] [CrossRef]
- Jiang, W.; Pang, X. The group scheduling method for the tasks of imaging satellite network. Syst. Eng. Theor. Pract. 2014, 34, 2154–2162. [Google Scholar]
- Zheng, Z.; Guo, J.; Gill, E. Onboard autonomous mission re-planning for multi-satellite system. Acta Astronaut. 2018, 145, 28–43. [Google Scholar] [CrossRef] [Green Version]
- Niu, X. Dynamically Scheduling of Multiple Satellites for Response to Natural Disasters Using Genetic Algorithms. Geogr. Geo-Inf. Sci. 2018, 34, 126–130. [Google Scholar]
- Marinelli, F.; Nocella, S.; Rossi, F.; Smriglio, S. A Lagrangian Heuristic for Satellite Range Scheduling with Resource Constraints. Comput. Oper. Res. 2011, 38, 1572–1583. [Google Scholar] [CrossRef]
- Bina, C.; Straub, J.; Marsh, R. Scheduling Algorithm Development for an Open Source Software Spacecraft. In Universisty of North Dakota School of Graduate Studies Scholarly Forum; University of North Dakota: North Dakota, ND, USA, 2015; pp. 212–223. [Google Scholar]
- Tangpattanakul, P.; Jozefowiez, N.; Lopez, P.A. A multi-objective local search heuristic for scheduling Earth observations taken by an agile satellite. Eur. J. Op. Res. 2015, 245, 542–554. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Sun, K. Muti-image Satellites Cooperative Observing Scheduling on GRASP. Control Eng. China 2012, 19, 691–694, 698. [Google Scholar]
- Xue, J. Research on Autonomous Task Planning of Earth Observation Satellite; Nanjing Aerospace University: Nanjing, China, 2015; pp. 47–68. [Google Scholar]
- Si, X. Autonomous Task Planning Method of Spacecraft Based on The Constraint Satisfaction; Beijing Institute of Technology: Beijing, China, 2015; pp. 34–58. [Google Scholar]
- Liu, S.; Chen, Y.; Xing, L.; Sun, K. Method of agile imaging satellites autonomous task planning. Comput. Integr. Manuf. Syst. 2016, 22, 928–934. [Google Scholar]
- Wang, Z.; Wang, Y.l. New Multi-satellite Scheduling Method. Chin. Space Sci. Technol. 2012, 32, 8–14. [Google Scholar]
- Haijiao, W.A.; Zhen, Y.A.; Wugen, Z.H.; Dalin, L.I. Online scheduling of image satellites based on neural network and deep reinforcement learning. Chin. J. Aeronaut. 2019, 32, 1011–1019. [Google Scholar]
- Li, C.; Chen, Y. Date-Driven Onboard Scheduling for an Autonomous Observation Satellite. In Proceedings of the 27th International Joint Conference on Artificial Intelligence, Beijing, China, 7 July2018; pp. 5773–5774. [Google Scholar]
- Chen, H.; Zhou, Y.; Du, C.; Li, J. A Satellite Cluster Date Transmission Scheduling Method based on Genetic Algorithm with Rote Learning Operator. In Proceedings of the IEEE Congress on Evolutionary Computation, Vancouver, BC, Canada, 24–29 July 2016; pp. 5076–5083. [Google Scholar]
- Wang, C.; Chen, H.; Zhai, B.; Li, J.; Chen, L. Satellite Observing Mission Scheduling Method base on Case-Based Learning and a Genetic Algorithm. In Proceedings of the IEEE International Conference on Tools with Artificial Intelligence, San Jose, CA, USA, 6–8 November 2017; pp. 627–634. [Google Scholar]
- Wang, C.; Jing, N.; Li, J.; Wang, J.; Chen, H. An Algorithm of Cooperative Multiple Satellites Task planning Based on Multi-agent Reinforcement Learning. J. Univ. Def. Technol. 2011, 33, 53–58. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. Comput. Sci. 2014, 27–43. [Google Scholar]
- Li, G.; Xing, L.; Chen, Y. A hybrid online scheduling mechanism with revision and progressive techniques for autonomous Earth observation satellite. Acta Astronaut. 2017, 140, 308–321. [Google Scholar] [CrossRef]
- Li, G. Models and Algorithms for Distributed Earth Observation Satellite System Online Coordination Scheduling under Communication Constraints; National University of Defense Technology: Changsha, China, 2017. [Google Scholar]
- Haykin, S. Neural Networks and Machine Learning; Mechanical Industry Press: Beijing, China, 2011. [Google Scholar]
| Parameter Name | Parameter Value |
|---|---|
| Semimajor axis | 7065 km |
| Semimajor axis | 0.0000923 km |
| Orbital inclination | 98.7359 |
| Right ascension point | 183.922 |
| Perigee amplitude | 114.442 km |
| Angle of approach | 354.784 |
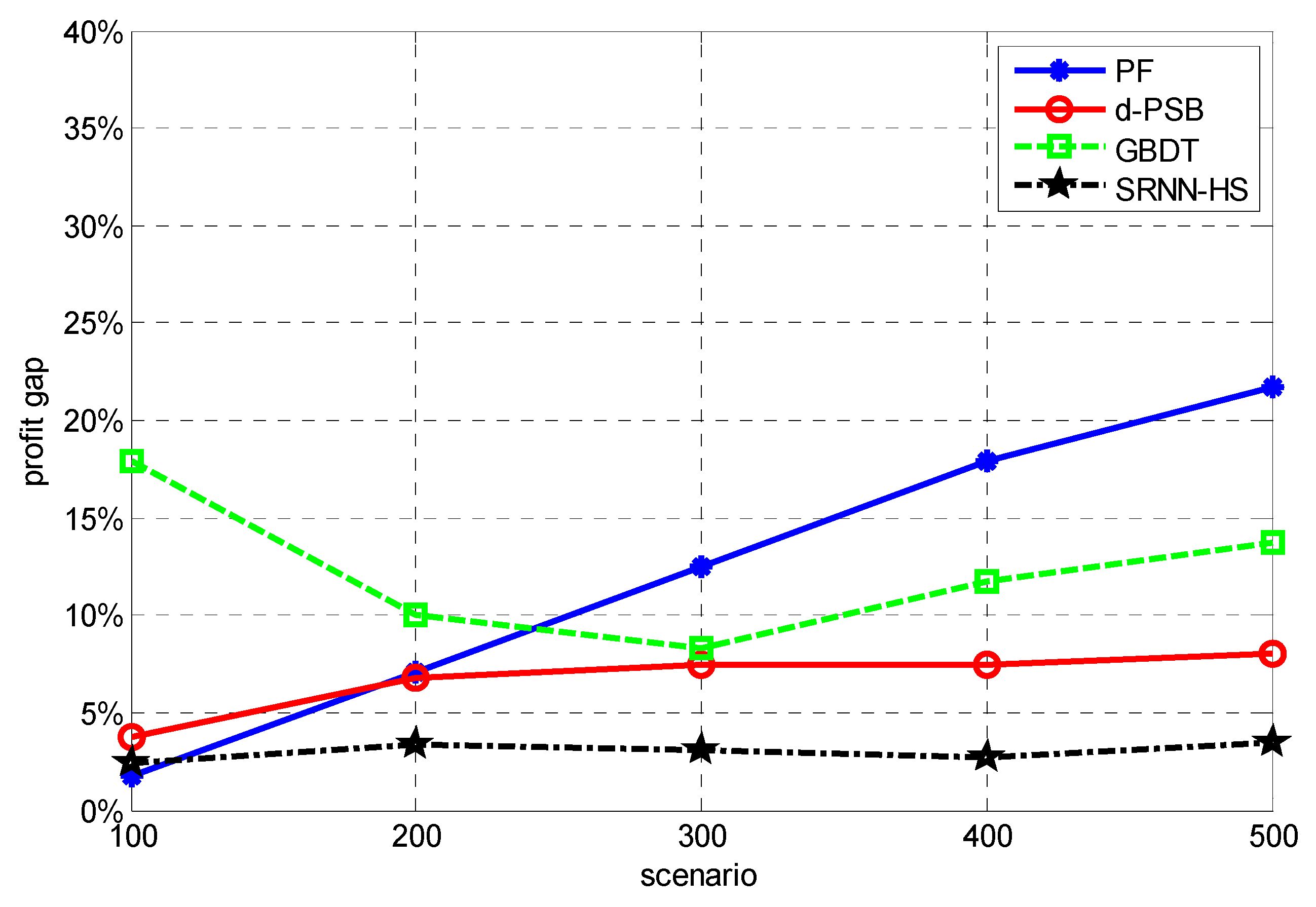
| Scenario | Indicator | CPLEX | PF | d-PSB | GBDT | SRNN-HS |
|---|---|---|---|---|---|---|
| 100 | profit | 1577.90 | 1559.17 | 1518.50 | 1295.70 | 1540.0 |
| profit gap | 1.73% | 3.76% | 17.91% | 2.40% | ||
| 200 | profit | 2303.20 | 2126.83 | 2148.80 | 2072.90 | 2225.50 |
| profit gap | 7.1% | 6.76% | 10.00% | 3.36% | ||
| 300 | profit | 2756.30 | 2391.77 | 2551.40 | 2526.60 | 2672.10 |
| profit gap | 12.46% | 7.46% | 08.32% | 3.06% | ||
| 400 | profit | 3096.50 | 2521.13 | 2866.50 | 2732.70 | 3012.40 |
| profit gap | 17.87% | 7.43% | 11.73% | 2.72% | ||
| 500 | profit | 3378.70 | 2610.70 | 3105.80 | 2915.00 | 3262.60 |
| profit gap | 21.70% | 8.06% | 13.72% | 3.43% |
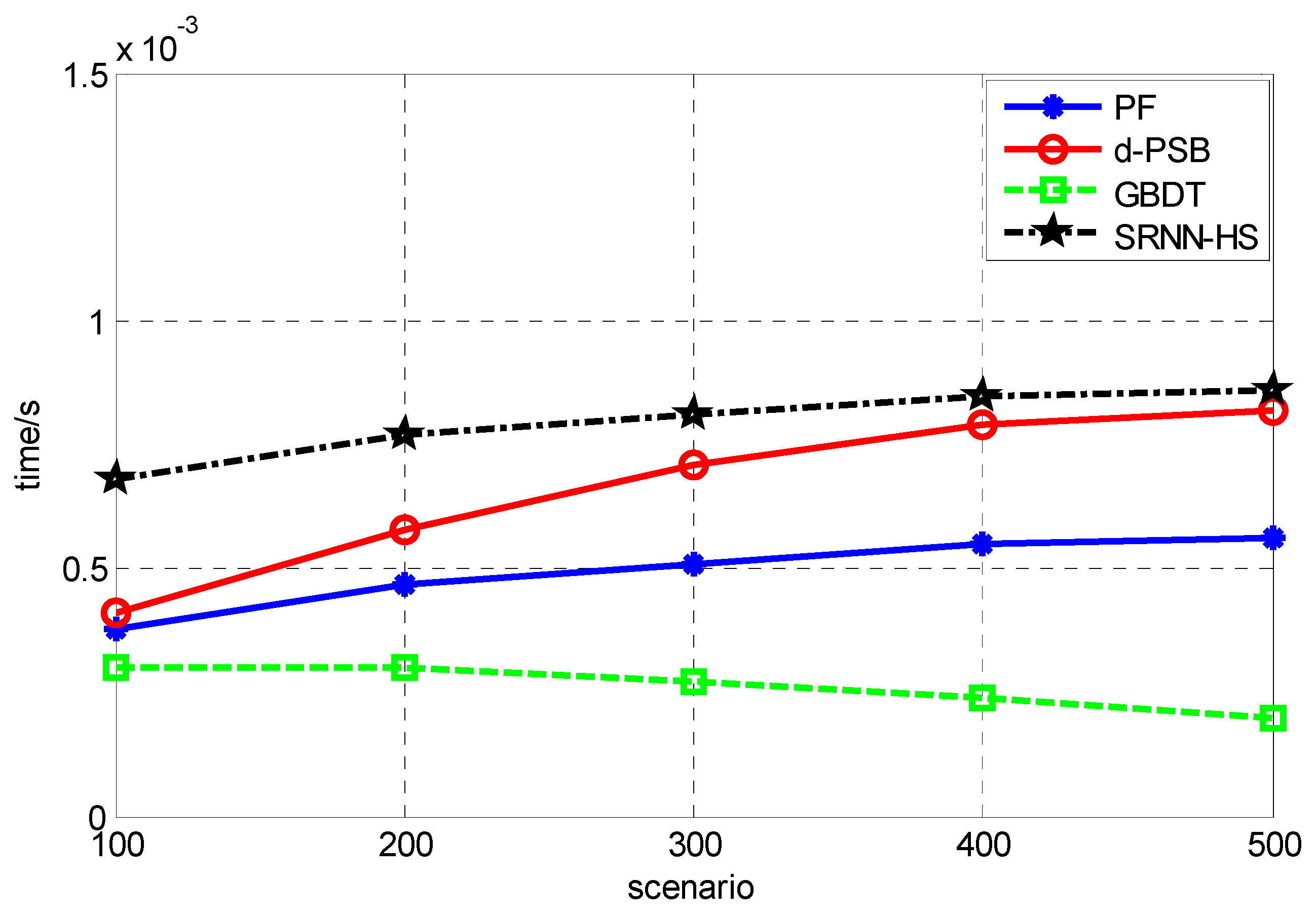
| Scenario | PF | d-PSB | GBDT | SRNN-HS |
|---|---|---|---|---|
| 100 | 0.00038 s | 0.00041 s | 0.00030 s | 0.00068 s |
| 200 | 0.00047 s | 0.00058 s | 0.00030 s | 0.00077 s |
| 300 | 0.00051 s | 0.00071 s | 0.00027 s | 0.00081 s |
| 400 | 0.00055 s | 0.00079 s | 0.00024 s | 0.00085 s |
| 500 | 0.00056 s | 0.00082 s | 0.00020 s | 0.00086 s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Yang, J. A Satellite Task Planning Algorithm Based on a Symmetric Recurrent Neural Network. Symmetry 2019, 11, 1373. https://doi.org/10.3390/sym11111373
Liu S, Yang J. A Satellite Task Planning Algorithm Based on a Symmetric Recurrent Neural Network. Symmetry. 2019; 11(11):1373. https://doi.org/10.3390/sym11111373
Chicago/Turabian StyleLiu, Sikai, and Jun Yang. 2019. "A Satellite Task Planning Algorithm Based on a Symmetric Recurrent Neural Network" Symmetry 11, no. 11: 1373. https://doi.org/10.3390/sym11111373




