About the Orbit Structure of Sequences of Maps of Integers

Abstract

Motivated by connections to the study of sequences of integers, we study, from a dynamical systems point of view, the orbit structure for certain sequences of maps of integers. We find sequences of maps for which all individual orbits are bounded and periodic and for which the number of periodic orbits of fixed period is finite. This allows the introduction of a formal $\zeta$-function for the maps in these sequences, which are actually polynomials. We also find sequences of maps for which the orbit structure is more complicated, as they have both bounded and unbounded orbits, both individual and global. Most of our results are valid in a general numeration base.

1. Introduction

In this paper, motivated by their intrinsic interest and by applications to the study of certain sequences of integers and Diophantine equations, we investigate from a dynamical systems point of view certain sequences of maps of integerss. We are mostly interested in understanding the space of orbits. We find sequences of maps for which all individual orbits are bounded and periodic and for which the number of periodic orbits of fixed period is finite. This allows one to introduce a formal $\zeta$-function for all functions in these sequences. We also find sequences for which the orbit structure is more complicated, as they have both bounded and unbounded orbits, both individual and global.

In what follows, let $b\ge 2$ be a numeration base. We let $\mathbb{N}$ denote the set of integers $\{1,2,3,4,5,\cdots \}$. If $N\in \mathbb{N}$, we let $s_b\left(N\right)$ denote the sum of base-b digits of N. If x is a string of digits, let ${\left(x\right)}^{\wedge k}$ denote the base 10 integer obtained by repeating xk-times. Let ${\left[x\right]}_b$ denote the value of the string x in base b.

The starting point of this investigation was the observation that certain sequences of integers, recently introduced on OEIS [1], such as A305130, A305131, A306830, A323190, have dynamical stems interpretation in terms of sequences of maps of integers. Dynamical interpretations for sequences of integers were studied before. For example, references [2,3,4] call a sequence of integers realizable if there exists a dynamical system for which the sequence counts the periodic orbits of certain period. Here we will realize certain sequences of integers as sets of fixed points for certain sequences of functions of integers. Then we study the overall orbit structure of these sequences of functions.

Definition 1.

Let ${\left(f_m\right)}_m=\{f_m:\mathbb{N}\to \mathbb{N}|m\in \mathbb{N}\}$ be a sequence of functions of integers.

A point $N\in \mathbb{N}$ is called individual fixed point for ${\left(f_m\right)}_m$ if there exists at least one $m\in \mathbb{N}$ such that $f_m\left(N\right)=N$.

A point $N\in \mathbb{N}$ is called global fixed point for ${\left(f_m\right)}_m$ if $f_m\left(N\right)=N$$\forall m\in \mathbb{N}.$

Definition 2.

Let $f:\mathbb{N}\to \mathbb{N}$ be a function. A sequence of integers ${\left(N_k\right)}_{k\ge 1}$ is called individual orbit for f if $f\left(N_k\right)=N_{k+1},\forall k\ge 1.$

Let ${\left(f_m\right)}_m=\{f_m:\mathbb{N}\to \mathbb{N}|m\in \mathbb{N}\}$ be a sequence of functions. A sequence of integers ${\left(N_k\right)}_{k\ge 1}$ is called global orbit for ${\left(f_m\right)}_m$ if for all $k\ge 1$ there exists $m_k$ such that $f_{m_k}\left(N_k\right)=N_{k+1}.$

An orbit ${\left(N_k\right)}_{k\ge 1}$ is called bounded if there exists $M\ge 1$ such that $N_k\le M,\forall k\ge 1$. An orbit ${\left(N_k\right)}_{k\ge 1}$ is called periodic if there exist $1\le k_1<k_2$ such that $N_{k_1}=N_{k_2}.$ Then $k_2-k_1$ is called the period of the periodic orbit.

Remark 1.

It is clear that all bounded orbits of a sequence of maps of integersare periodic.

Motivated by some properties of the taxicab number 1729 [5], one of us introduced in [6] the class of b-additive Ramanujan–Hardy or (bARH-numbers) and the class of b-multiplicative Ramanujan–Hardy or (bMRH-numbers. The first class consists of all integers N for which there exists an integer M, called additive multiplier, such that the sum of base b digits of N times M added to the reversal of the product gives N. The second class consists of all integers N for which there exists an integer M, called multiplicative multiplier, such that the sum of base b digits of N times M multiplied by the reversal of the sum gives N. In [7] we change the definitions above. We replace the product between the sum of digits and the multiplier by the sum of the sum of base b digits of N and a positive extra term which we call additive respectively multiplicative extra term. This gives two new classes of numbers, b-wARH and b-wMRH. These are strictly larger than those above. Another motivation for the study of these new classes of numbers is the study of numerical palindromes. All palindromes that either have an even number of digits or an odd number of digits and the middle digit even belong to the first class, and all squares of palindromes with al least two digits belong to the second class.

The following sequences of functions of integers are naturally related to the sequences of numbers introduced above and will be studied in the paper from a dynamical systems point of view.

Definition 3.

We let weak b-Additive Ramanujan–Hardy sequence (or b-wARH) be the sequence:

$$f_M:\mathbb{N}\to \mathbb{N},f_M\left(N\right)=(S_b\left(N\right)+M)+{(S_b\left(N\right)+M)}^R,M\in \mathbb{N},$$

(1)

We let Dual weak b-Additive Ramanujan–Hardy sequence (or Dual b-wARH) be the sequence:

$$f_M:\mathbb{N}\to \mathbb{N},f_M\left(N\right)=(S_b\left(M\right)+N)+{(S_b\left(M\right)+N)}^R,M\in \mathbb{N},$$

(2)

We let weak b-Multiplicative Ramanujan–Hardy sequence (or b-wMRH) be the sequence:

$$f_M:\mathbb{N}\to \mathbb{N},f_M\left(N\right)=(S_b\left(N\right)+M).{(S_b\left(N\right)+M)}^R,M\in \mathbb{N},$$

(3)

We let Dual weak b-Multiplicative Ramanujan–Hardy sequence (or Dual b-wMRH) be the sequence:

$$f_M:\mathbb{N}\to \mathbb{N},f_M\left(N\right)=(S_b\left(M\right)+N).{(S_b\left(M\right)+N)}^R,M\in \mathbb{N},$$

(4)

We let b-Additive Ramanujan–Hardy Sequence (or b-ARH) be the sequence:

$$f_M:\mathbb{N}\to \mathbb{N},f_M\left(N\right)=(S_b\left(N\right).M)+{(S_b\left(N\right).M)}^R,M\in \mathbb{N},$$

(5)

We let dual b-Additive Ramanujan–Hardy Sequence (or dual b-ARH) be the sequence:

$$f_M:\mathbb{N}\to \mathbb{N},f_M\left(N\right)=(S_b\left(M\right).N)+{(S_b\left(M\right).N)}^R,M\in \mathbb{N},$$

(6)

We let b-Multiplicative Ramanujan–Hardy Sequence (or b-MRH) be the sequence:

$$f_M:\mathbb{N}\to \mathbb{N},f_M\left(N\right)=(S_b\left(N\right).M).{(S_b\left(N\right).M)}^R,M\in \mathbb{N},$$

(7)

We let Dual b-Multiplicative Ramanujan–Hardy Sequence (or dual b-MRH) be the sequence:

$$f_M:\mathbb{N}\to \mathbb{N},f_M\left(N\right)=(S_b\left(M\right).N).{(S_b\left(M\right).N)}^R,M\in \mathbb{N},$$

(8)

We observe that the operations of addition and multiplication are independent of the base, but the operation of taking the reversal is not. In order to have a match with what was done in [6,7,8], in Formulas (1)–(8), the notation ${\left(N\right)}^R$ means the reversal of the base b-representation of the operand N.

2. Statements of the Main Results

The following proposition shows the relationship between the sequences of integers introduced in [6,7,8] and the sequences of functions of integers introduced in Definition 3.

Proposition 1.

(a) The individual fixed points of the b-ARH sequence are the b-ARH-numbers.

(b) The individual fixed points of the b-MRH sequence are the b-MRH-numbers.

(c) The individual fixed points of b-the wARH sequence are the b-wARH-numbers.

(d) The individual fixed points of the b-wMRH sequence are the b-wMRH-numbers.

(e) The indices M for which the maps $f_M$ in the dual b-ARH sequence have individual fixed points are those for which $s_b\left(M\right)$ are additive multipliers of b-ARH-numbers.

(f) The indices M for which the maps $f_M$ in the dual b-MRH sequence have individual fixed points are those for which $s_b\left(M\right)$ are multiplicative multipliers of b-MRH-numbers.

(g) The indices M for which the maps $f_M$ in the dual b-wARH sequence have individual fixed points are those for which $s_b\left(M\right)$ are additive extra terms of b-wARH-numbers.

(h) The indices M for which the maps $f_M$ in the dual b-wMRH sequence have individual fixed points are those for which $s_b\left(M\right)$ are multiplicative extra terms of b-wMRH-numbers.

The proof of Proposition 1 is straighforward and follows from the basic definitions.

Proposition 2.

Neither of the sequences of functions introduced in Definition 3 has a global fixed point.

Proof. 

Let $N\in \mathbb{N}$.

If $f_M$ belongs to one of the b-ARH, b-MRH, b-wARH, or b-wMRH sequences, choose $M>N$. Then it follows from (1), (3), (5), and (7) that $f_M\left(N\right)>N$. Therefore, N is not an individual fixed point for $f_M$ and, consequently, N is not a global fixed point for any of the sequences of functions above.

Assume now that $f_M$ belongs to one of the dual b-ARH, dual b-MRH, dual b-wARH, or dual b-wMRH sequences, and M satisfies $s_b\left(M\right)>N$. Then it follows from (2), (4), (6), and (8) that $f_M\left(N\right)>N$, so N is not an individual fixed point for $f_M$ and, consequently, N is not a global fixed point for any of the sequences of functions above. □

Proposition 3.

All the sequences of functions introduced in Definition 3 have unbounded global orbits for all points in the domain.

The proof of Proposition 3 is done in Section 3.

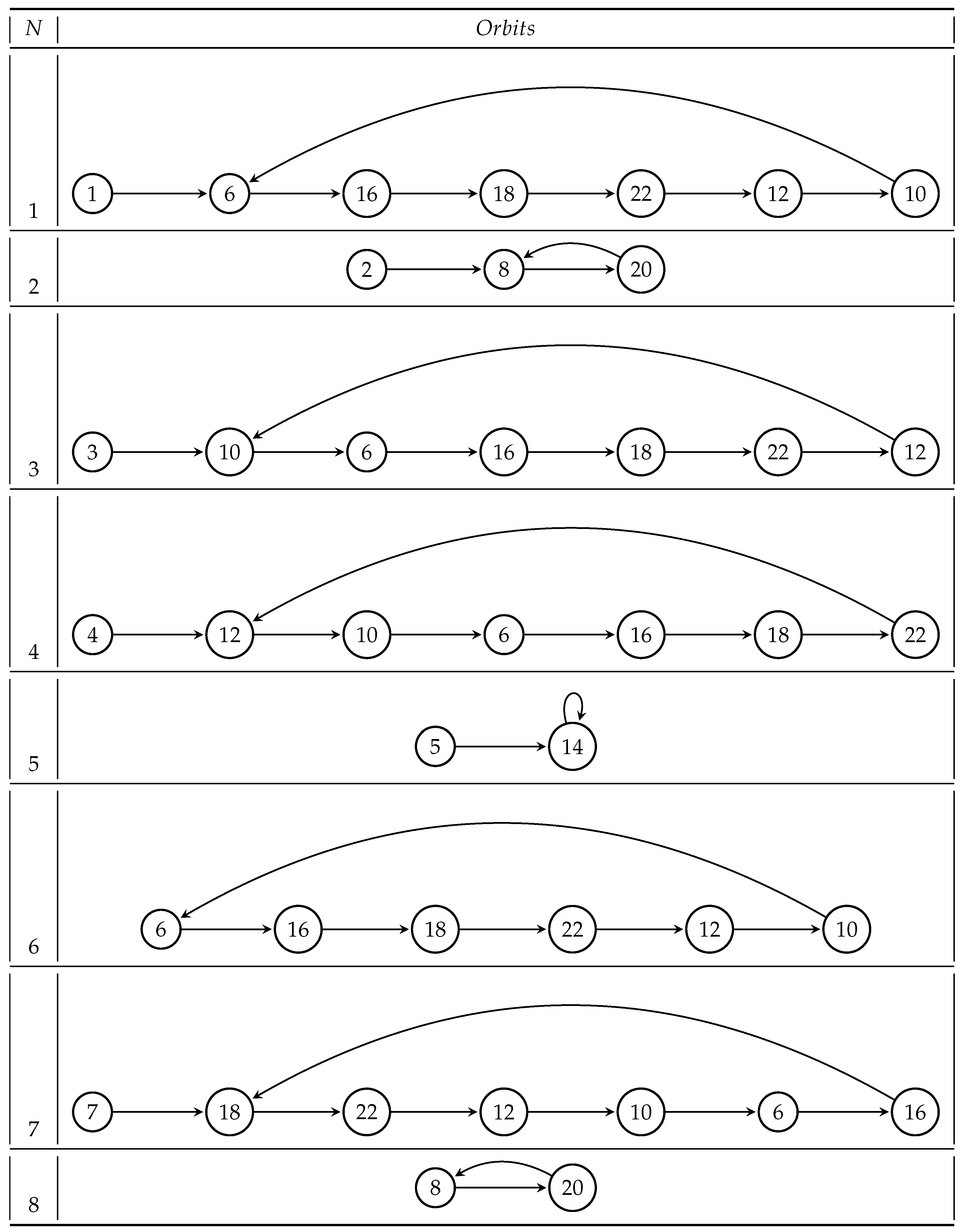
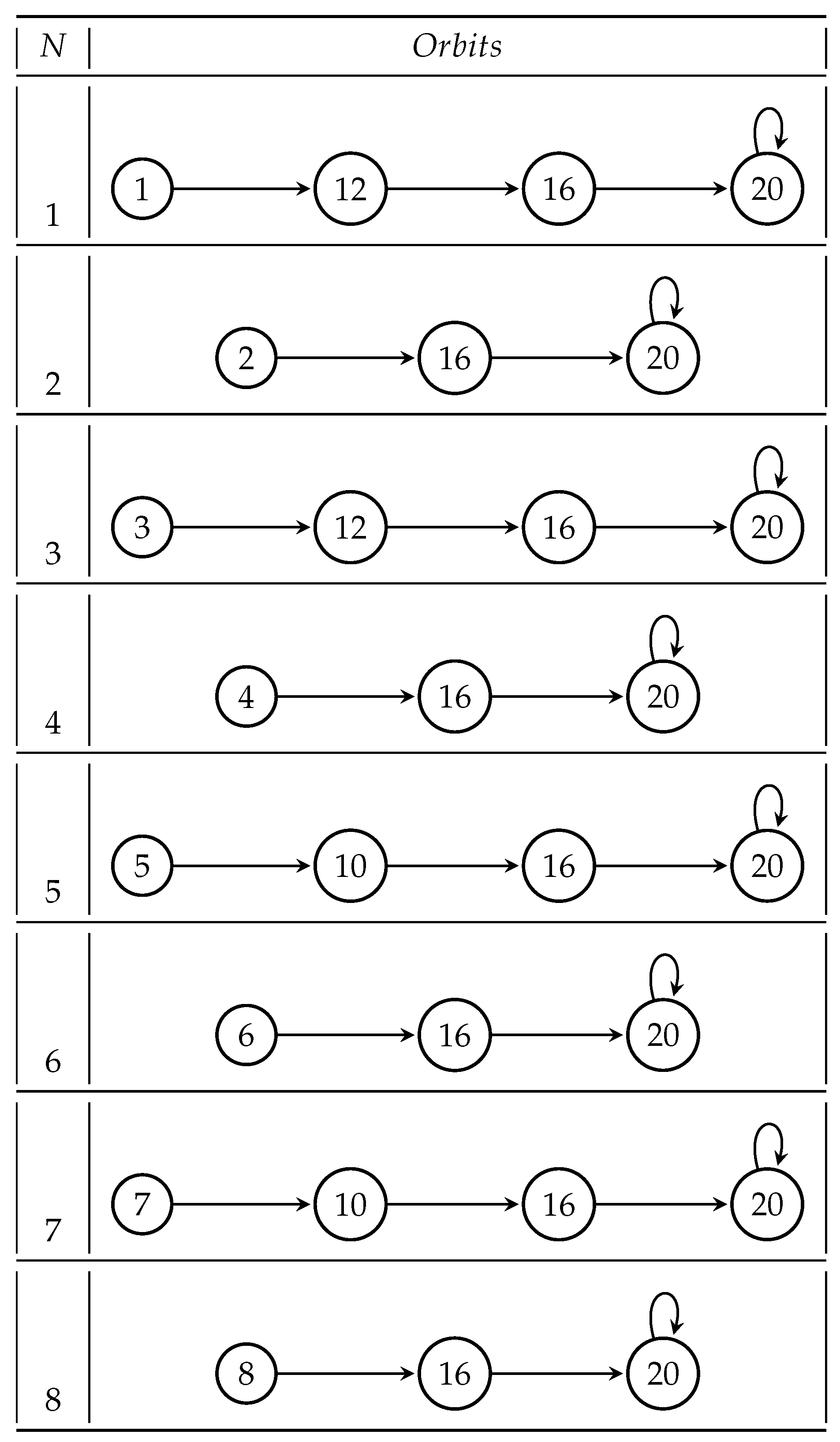
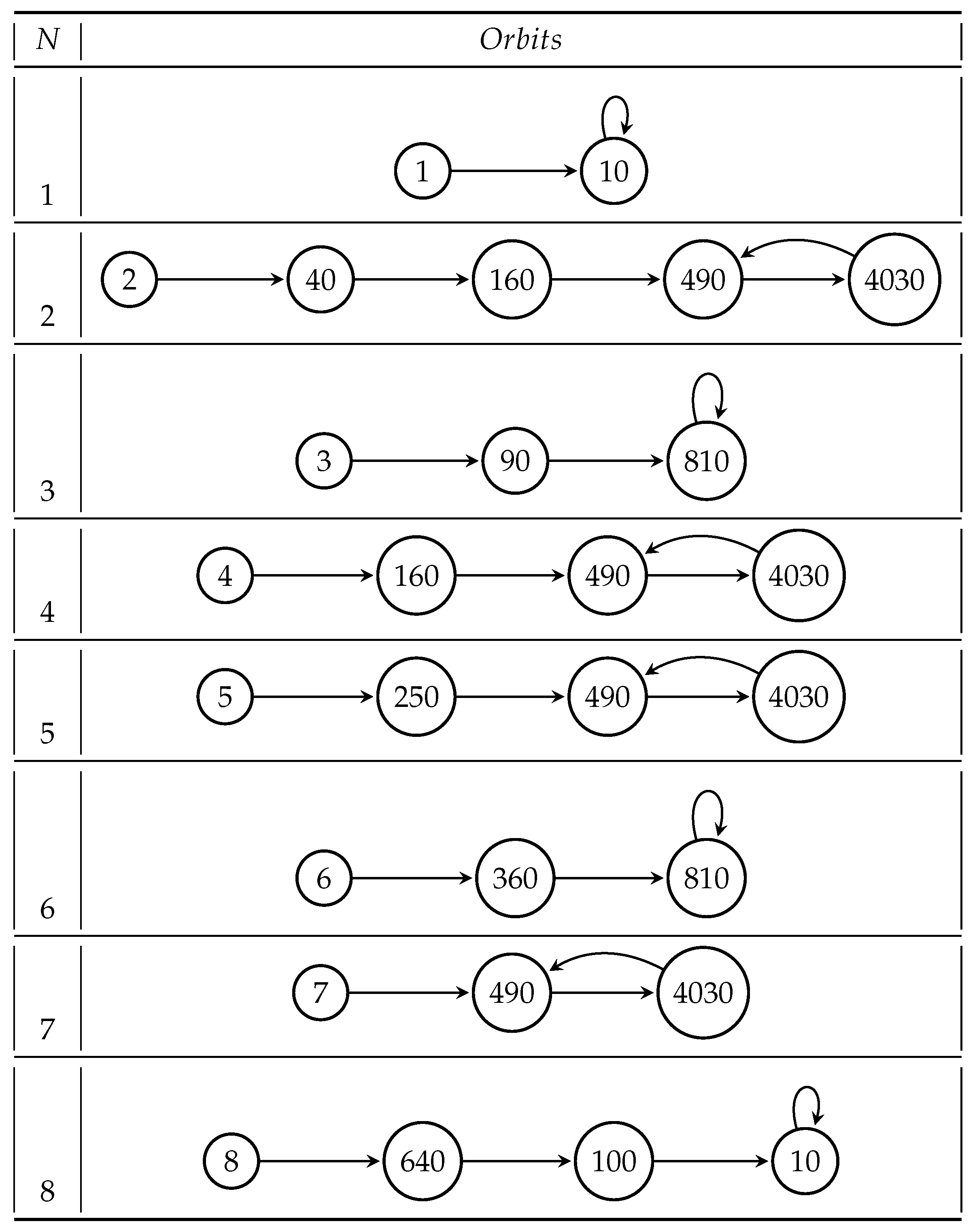
We show in Figure 1, Figure 2 and Figure 3 individual orbits for several functions of integers introduced in Definition 3. We observe that all of them are bounded. Moreover, all orbits are attracted to a finite number of periodic cycles. The following proposition shows that this is a general fact.

Proposition 4.

All the sequences of functions b-ARH, b-wARH, b-MRH, b-wMRH have all individual orbits bounded, and are consequently periodic. Moreover, all orbits are attracted to a finite number of periodic cycles.

The proof of Proposition 4 is done in Section 4.

The orbit structure of the dual sequences of functions is quite different.

Proposition 5.

(1) The sequences of functions dual b-ARH, dual b-wARH, dual b-MRH, and dual b-wMRH have all individual orbits starting with an integer N such that $N>b$ unbounded.

The proof of Proposition 5 is done in Section 5.

Proposition 6.

All functions in the sequences of functions b-ARH, b-wARH, b-MRH, b-wMRH have a finite number of periodic orbits of fixed period.

Proof. 

The proofs for all sequences are similar and follow the idea of some of the proofs from [6,7], where we prove that all functions in the sequences b-ARH, b-wARH, b-MRH, b-wMRH have a finite number of fixed points. Assume that f is a function and k is a fixed period. A number $N\in \mathbb{N}$ has an orbit of period k if

$$f^k\left(N\right)=N.$$

(9)

By writing what this means explicitely one observes that the left hand side of (9) grows polynomially in terms of the number of digits of N, because $s_b\left(N\right)$ grows polynomially in terms of of the number of digits of N. In contrast, the right hand side of (9), N itself, grows exponentially in terms of the number of digits. This discrepancy allows to bound the number of digits of N in terms of k, which allows to bound the number of periodic orbits of period k. □

Remark 2.

Proposition 6 allows to define a ζ function for all functions in the sequences b-ARH, b-wARH, b-MRH, b-wMRH. If $f:\mathbb{N}\to \mathbb{N}$ is a function, we denote by $p_n\left(f\right)$ the number of periodic orbits of f of length n. Then the following function is well defined.

$$\zeta \left(f\right)=\sum _{n=1}^{\infty }{p}_n\left(f\right)x^n.$$

(10)

The computation of the coefficients $p_n\left(f\right)$ can be numerically challenging. For example we show in [6] that for the function $f_1$ from the 10-MRH sequence one has $p_1\left(f_1\right)$ = 4. This is a restatement of the fact that the only $MRH$ numbers with multiplier $M=1$ are 1, 18, 1729, 1458. We show below that all ζ functions associated with the functions in the sequences b-ARH, b-wARH, b-MRH, b-wMRH are polynomials. For each function f the sequence ${\left\{p_n\right\}}_n$ has only a finite number of nonzero terms. This is true because all functions in the sequences b-ARH, b-wARH, b-MRH, b-wMRH cannot have periodic orbits of arbitrary large period. Indeed, as we proved in Proposition 4 all orbits are attracted by a finite number of periodic cycles.

The following propositions are of independent interest and will be used in the proof of Proposition 4.

Proposition 7.

If N is a positive integer with at least two digits, then $s_b\left(N\right)\le N.$

Proof. 

If N has at least two digits the statement follows from ([8], Proposition 5a). If N has one digit, the statement is obvious. □

Proposition 8.

All individual functions f in the sequences of functions b-ARH, b-wARH, b-MRH, b-wMRH have the following property: there exists an integer $N_0,$ depending on f, such that $f\left(N\right)<N,\forall N\ge N_0$.

Proof. 

• We show the proof for the b-wARH-sequence. Let $f_A$ be an element of the sequence. Let k be a positive integer that satisfies $\frac{k(b-1)}{b^{k-2}}<\frac{1}{2}$. Choose $N_0=max\{2(b-1)A,{\left(b\right)}^{k-1}\}$. Let $N>N_0$. Then N has at least k digits and

  $$s_b\left(N\right)\le k(b-1).$$

  (11)

The assumption $b^{k-1}\le N$ implies

$$b\le \frac{N}{b^{k-2}}.$$

(12)

From (11) and (12) it follows that

$$s_b\left(N\right)\le k(b-1)\le kb\le \frac{Nk}{b^{k-2}}.$$

(13)

We use now that the base b-reversal of an integer can increase it by at most b times and (11) to conclude that

$$f_A\left(N\right)=s_b\left(N\right)+A+{(s_b\left(N\right)+A)}^R\le \frac{Nk}{b^{k-2}}(1+b)+A(1+b).$$

(14)

Using now that $N>2A(1+b)$ and that $\frac{k(b-1)}{b^{k-2}}<\frac{1}{2}$, Equation (14) becomes

$$f_A\left(N\right)<\frac{N}{2}+\frac{N}{2}<N.$$

(15)

• We show the proof for the b-ARH-sequence. Let $f_M$ be an element of the sequence.

Let k be a positive integer that satisfies

$$\frac{{(b-1)}^2{k}^2{M}^2}{b^{k-2}}<1.$$

(16)

Choose $N_0={\left(b\right)}^{k-1}$. Let $N>N_0$. Then N has at least k digits and (11) and (12) holds.

Using now that the base b-reversal of an integer can increase it by at most b times, and (16), we conclude that:

$$\begin{array}{c}{f}_M\left(N\right)=(s_b\left(N\right)·M)·{(s_b\left(N\right)·M)}^R\le (b-1)kM(b-1)kMb\\ \le {(b-1)}^2{k}^2{M}^2\frac{N}{b^{k-2}}<N.\end{array}$$

• We show the proof for the b-MRH-sequence. Let $f_M$ be an element of the sequence. Let k be a positive integer that satisfies

  $$\frac{{(b-1)}^2{k}^2{M}^2}{b^{k-2}}<1.$$

  (17)

Choose $N_0={\left(b\right)}^{k-1}$. Let $N>N_0$. Then N has at least k digits and (11) and (12) holds.

Using now that the base b-reversal of an integer can increase it by at most b times, and (17), we conclude that:

$$\begin{array}{c}{f}_M\left(N\right)=(s_b\left(N\right)·M)·{(s_b\left(N\right)·M)}^R\le (b-1)kM(b-1)kMb\\ \le {(b-1)}^2{k}^2{M}^2\frac{N}{b^{k-2}}<N.\end{array}$$

• We show the proof for the b-wMRH-sequence. Let $f_M$ be an element of the sequence. Let k be a positive integer that satisfies

  $$\frac{{[M(b-1)k+M]}^2}{b^{k-2}}<1.$$

  (18)

Choose $N_0={\left(b\right)}^{k-1}$. Let $N>N_0$. Then N has at least k digits and (11) and (12) holds.

Using now that the base b-reversal of an integer can increase it by at most b times, and (18), we conclude that:

$$\begin{array}{c}{f}_M\left(N\right)=(s_b\left(N\right)+M)·{(s_b\left(N\right)+M)}^R\le b{[M(b-1)k+M]}^2\\ \le {[M(b-1)k+M]}^2\frac{N}{b^{k-2}}<N.\end{array}$$

(19)

 □

3. Proof of Proposition 3

Proof. 

Let $N\in \mathbb{N}$.

• We show the proof for the b-wARH sequence. Choose $k_0$ such that $b^{k_0}-s_b\left(N\right)>0.$

We construct by induction on k a sequence of integers ${\left(A_k\right)}_{k\ge k_0}$ such that

$$f_{A_k}\circ f_{A_{k-1}}\circ \cdots \circ f_{A_2}\circ f_{A_{k_0}}\left(N\right)=b^k+1,\forall k\ge k_0.$$

(20)

If $k=k_0$ choose $A_{k_0}=b^{k_0}-s_b\left(N\right)(>0).$ Then

$$f_{A_{k_0}}\left(N\right)=b^{k_0}+{\left(b^{k_0}\right)}^R=b^{k_0}+1.$$

Assume (20) true for $k>k_o$ and prove it for $k+1$. Define $N_k=b^k+1$. Define $A_{k+1}=b^{k+1}-s_b\left(N_k\right)=b^{k+1}-2$. Then

$$\begin{array}{c}{f}_{A_{k+1}}\circ f_{A_k}\circ f_{A_{k-1}}\circ \cdots \circ f_{A_2}\circ f_{A_{k_0}}\left(N\right)\\ =f_{A_{k+1}}\left(f_{A_k}\circ \cdots \circ f_{A_2}\circ f_{A_{k_0}}\left(N\right)\right)\\ =f_{A_{k+1}}\left(N_k\right)=s_b\left(N_k\right)+A_{k+1}+{\left(s_b\left(N_k\right)+A_k\right)}^R=b^{k+1}+1\end{array}$$

and (20) holds true for $k+1$.

• We show the proof for the b-wMRH sequence. Choose $k_0$ such that $b^{k_0}-s_b\left(N\right)>0.$

We construct by induction on k a sequence of integers ${\left(A_k\right)}_{k\ge k_0}$ such that

$$f_{A_k}\circ f_{A_{k-1}}\circ \cdots \circ f_{A_2}\circ f_{A_{k_o}}\left(N\right)=b^k,\forall k\ge k_0.$$

(21)

If $k=k_0$ choose $A_{k_0}=b^{k_0}-s_b\left(N\right)(>0).$ Then

$$f_{A_{k_0}}\left(N\right)=b^{k_0}·{\left(b^{k_0}\right)}^R=b^{k_0}·1=b^{k_0}.$$

Assume (21) to be true for $k>k_0$ and prove it for $k+1$. Define $N_k=b^k$. Define $A_{k+1}=b^{k+1}-s_b\left(N_k\right)=b^{k+1}-1$. Then

$$\begin{array}{c}{f}_{A_{k+1}}\circ f_{A_k}\circ f_{A_{k-1}}\circ \cdots \circ f_{A_2}\circ f_{A_{k_0}}\left(N\right)\\ =f_{A_{k+1}}\left(f_{A_k}\circ \cdots \circ f_{A_2}\circ f_{A_{k_0}}\left(N\right)\right)\\ =f_{A_{k+1}}\left(N_k\right)=(s_b\left(N_k\right)+A_{k+1})·{\left(s_b\left(N_k\right)+A_k\right)}^R=b^{k+1}·1=b^{k+1}.\end{array}$$

and (21) holds true for $k+1$.

• We show the proof for the b-MRH sequence. Choose $k_0$ such that $\frac{b^{k_0}}{s_b\left(N\right)}\ge 1.$

We construct by induction on k a sequence of integers ${\left(A_k\right)}_k$ such that

$$f_{A_k}\circ f_{A_{k-1}}\circ \cdots \circ f_{A_2}\circ f_{A_{k_0}}\left(N\right)\ge b^k,\forall k\ge k_0.$$

(22)

If $k=k_0$ choose an integer $A_{k_0}\ge \frac{b^{k_0}}{s_b\left(N\right)}\ge 1.$ Then

$$f_{A_{k_0}}\left(N\right)\ge b^{k_0}·{(s_b\left(N\right)·A_{k_0})}^R\ge {10}^{k_0}·1=b^{k_0}.$$

Assume now (22) true for $k>k_o$ and prove it for $k+1$. Define $N_k=f_{A_k}\cdots \circ f_{A_2}\circ f_{A_{k_0}}\left(N\right).$ Choose an integer $A_{k+1}\ge \frac{b^{k+1}}{s_b\left(N_k\right)}>1.$ Then

$$f_{A_{k+1}}\circ f_{A_k}\circ \cdots \circ f_{A_2}\circ f_{A_{k_0}}\left(N\right)=f_{A_k}\left(f_{A_{k-1}}\cdots \circ f_{A_2}\circ f_{A_{k_0}}\left(N\right)\right)$$

$$=f_{A_{k+1}}\left(N_k\right)=(s_b\left(N_k\right)·A_{k+1})·{(s_b\left(N_k\right)·A_{k+1})}^R\ge b^{k+1}.$$

and (22) holds true for $k+1$.

• We show the proof for the b-ARH sequence. Choose $k_0$ such that ${10}^{k_0}-s_b\left(N\right)>0.$

We construct by induction on k a sequence ${\left(A_k\right)}_k$ such that

$$f_{A_k}\circ f_{A_{k-1}}\cdots \circ f_{A_2}\circ f_{A_{k_0}}\left(N\right)=b^k+1,\forall k\ge k_0.$$

(23)

If $k=k_0$ choose $A_{k_0}=b^{k_0}-s_b\left(N\right)(>0).$ Then

$$f_{A_{k_0}}\left(N\right)=b^{k_0}+{\left({10}^{k_0}\right)}^R=b^{k_0}+1.$$

Assume now (23) is true for $k>k_0$ and prove it for $k+1$. Define $N_k=b^{k_0}+1$. Define $A_{k+1}=b^{k+1}-s_b\left(N_k\right)=b^k-2$. Then

$$f_{A_k}\circ f_{A_{k-1}}\cdots \circ f_{A_2}\circ f_{A_{k_o}}\left(N\right)=f_{A_k}\left(N_k\right)=s_b\left(N_k\right)+A_k={(s_b\left(N_k\right)+A_k)}^R=b^k+1$$

and (23) holds true for $k+1$.

• We show the proof for the dual b-wARH sequence. Choose integers $k_0$ and $A_{k_0}\ge 1$ such that $s_b\left(A_{k_0}\right)+N=b^{k_0}.$

We construct by induction on k a sequence ${\left(A_k\right)}_{k\ge k_0}$ such that

$$f_{A_k}\circ f_{A_{k-1}}\circ \cdots \circ f_{A_{k_0+1}}\circ f_{A_{k_0}}\left(N\right)=b^k+1,\forall k\ge k_0.$$

(24)

If $k=k_0$ then

$$f_{A_{k_0}}\left(N\right)=s_b\left(A_{k_0}\right)+N+{\left(s_b\left(A_{k_0}\right)+N\right)}^R=b^{k_0}+{\left(b^{k_0}\right)}^R=b^{k_0}+1.$$

Assume now (24) is true for $k>k_0$ and prove it for $k+1$. Define $N_k=b^k+1$. Choose $A_{k+1}$ such that $s_b\left(A_{k+1}\right)+N_k=b^{k+1}.$ Then

$$f_{A_{k+1}}\circ f_{A_k}\circ \cdots \circ f_{A_2}\circ f_{A_{k_0}}\left(N\right)=f_{A_{k+1}}\left(f_{A_k}\cdots \circ f_{A_2}\circ f_{A_{k_0}}\left(N\right)\right)$$

$$=f_{A_{k+1}}\left(N_k\right)=(s_b\left(A_{k+1}\right)+N_k)+{(s_b\left(A_{k+1}\right)+N_k)}^R=b^{k+1}+1,$$

and (24) holds true for $k+1$.

• We show the proof for the dual b-MRH sequence. Choose $k_0$ and $A_{k_0}\ge 1$ such that $\left(s_b\left(A_{k_0}\right)\right)·\left(N\right)=b^{k_0}.$

We construct by induction on k a sequence of integers ${\left(A_k\right)}_k$ such that

$$f_{A_k}\circ f_{A_{k-1}}\circ \cdots \circ f_{A_{k_0+1}}\circ f_{A_{k_0}}\left(N\right)=b^k,\forall k\ge k_0.$$

(25)

If $k=k_0$. Then

$$f_{A_{k_0}}\left(N\right)=(s_b\left(A_{k_0}\right)·N)·{\left(s_b\left(A_{k_0}\right)·N\right)}^R=b^{k_0}·{\left(b^{k_0}\right)}^R=b^{k_0}.$$

Assume now (25) to be true for $k>k_o$ and prove it for $k+1$. Define $N_k=b^k$. Choose $A_{k+1}$ such that $s_b\left(A_{k+1}\right)·\left(N_k\right)=b^{k+1}.$ Then

$$f_{A_{k+1}}\circ f_{A_k}\circ \cdots \circ f_{A_2}\circ f_{A_{k_0}}\left(N\right)=f_{A_{k+1}}\left(f_{A_k}\cdots \circ f_{A_2}\circ f_{A_{k_0}}\left(N\right)\right)$$

$$=f_{A_{k+1}}\left(N_k\right)=(s_b\left(A_{k+1}\right)·N_k)·\left({(s_b\left(A_{k+1}\right)·N_k)}^R\right)=b^{k+1},$$

and (25) holds true for $k+1$.

• We show the proof for the dual b-wMRH sequence. Choose $k_0$ and $A_{k_0}\ge 1$ such that $s_b\left(A_{k_0}\right)+\left(N\right)=b^{k_0}.$

We construct by induction on k a sequence of integers ${\left(A_k\right)}_k$ such that

$$f_{A_k}\circ f_{A_{k-1}}\circ \cdots \circ f_{A_{k_0+1}}\circ f_{A_{k_0}}\left(N\right)=b^k,\forall k\ge k_0.$$

(26)

If $k=k_0$. Then

$$f_{A_{k_0}}\left(N\right)=(s_b\left(A_{k_0}\right)+N)·{\left(s_b\left(A_{k_0}\right)+N\right)}^R=b^{k_0}·{\left(b^{k_0}\right)}^R=b^{k_0}.$$

Assume now (26) is true for $k>k_o$ and prove it for $k+1$. Define $N_k=b^k$. Choose $A_{k+1}$ such that $N_k=b^k$. Define $s_b\left(A_{k+1}\right)+N_k=b^{k+1}$. Then

$$f_{A_{k+1}}\circ f_{A_k}\circ \cdots \circ f_{A_2}\circ f_{A_{k_0}}\left(N\right)=f_{A_{k+1}}\left(f_{A_k}\cdots \circ f_{A_2}\circ f_{A_{k_0}}\left(N\right)\right)$$

$$=f_{A_{k+1}}\left(N_k\right)=(s_b\left(A_{k+1}\right)+N_k)·\left((s_b\left(A_{k+1}\right)+{\left(N_k\right)}^R)\right)=b^{k+1},$$

and (26) holds true for $k+1$.

• We show the proof for the dual b-ARH sequence. Choose integers $k_0$ and $A_{k_0}\ge 1$ such that $\left(s_b\left(A_{k_0}\right)\right)·\left(N\right)=b^{k_0}.$

We construct by induction on k a sequence ${\left(A_k\right)}_{k\ge k_0}$ such that

$$f_{A_k}\circ f_{A_{k-1}}\circ \cdots \circ f_{A_{k_0+1}}\circ f_{A_{k_0}}\left(N\right)=b^k+1,\forall k\ge k_0.$$

(27)

If $k=k_0$ then

$$f_{A_{k_0}}\left(N\right)=((\left(s_b\left(A_{k_0}\right)\right)·\left(N\right))+{\left(s_b\left(A_{k_0}\right)·\left(N\right)\right)}^R=b^{k_0}·{\left(b^{k_0}\right)}^R=b^{k_0}+1.$$

Assume now (27) is true for $k>k_0$ and prove it for $k+1$. Define $N_k=b^k+1$. Choose $A_{k+1}$ such that $\left(s_b\left(A_{k+1}\right)\right)·N=b^{k+1}$. Then

$$f_{A_{k+1}}\circ f_{A_k}\circ \cdots \circ f_{A_2}\circ f_{A_{k_0}}\left(N\right)=f_{A_{k+1}}\left(f_{A_k}\cdots \circ f_{A_2}\circ f_{A_{k_0}}\left(N\right)\right)$$

$$=f_{A_{k+1}}\left(N_k\right)=(s_b\left(A_{k+1}\right)·N_k)+\left((s_b\left(A_{k+1}\right)·{\left(N_k\right)}^R)\right)=b^{k+1}+1,$$

and (27) holds true for $k+1$. □

4. Proof of Proposition 4

Proof. 

• We show the proof for the b-wARH sequence. Let $f_A$ be a map from the sequence. Let $N_0$ be the integer from Proposition 8 corresponding to $f_A$. Then

  $$f_A\left(N\right)<N\mathrm{if}N\ge N_0.$$

  (28)

It follows from Proposition 7 that

$$\begin{array}{c}{f}_A\left(N\right)=(s_b\left(N\right)+A)+{(s_b\left(N\right)+A)}^R\le (N+A)(b+1)\\ <(N_0+A)(b+1),\mathrm{if}N<N_0.\end{array}$$

(29)

Let ${\left\{N_k\right\}}_k$ be an orbit of $f_A$. Define $M=max\{N_1,(N_0+A)(b+1)\}.$ Then conditions (28), (29) imply that $|N_k|\le M,\forall k\ge 1$, so the orbit is bounded.

• We show the proof for the b-ARH sequence. Let $f_M$ be a map from the sequence. Let $N_0$ be the integer from Proposition 8 corresponding to $f_M$. Then

  $$f_M\left(N\right)<N\mathrm{if}N\ge N_0.$$

  (30)

It follows from Proposition 7 that

$$\begin{array}{c}{f}_M\left(N\right)=(s_b\left(N\right)·M)+{(s_b\left(N\right)·M)}^R\le (N+M)(b+1)\\ <(N_0+M)(b+1),\mathrm{if}N<N_0.\end{array}$$

(31)

Let ${\left\{N_k\right\}}_k$ be an orbit of $f_A$. Define $\overline{M}=max\{N_1,(N_0+M)(b+1)\}.$ Then conditions (30), (31) imply that $|N_k|\le \overline{M},\forall k\ge 1$, so the orbit is bounded.

• We show the proof for the b-wMRH sequence. Let $f_A$ be a map from the sequence. Let $N_0$ be the integer from Proposition 8 corresponding to $f_A$. Then

  $$f_A\left(N\right)<N\mathrm{if}N\ge N_0.$$

  (32)

It follows from Proposition 7 that

$$\begin{array}{c}{f}_A\left(N\right)=(s_b\left(N\right)·A)+{(s_b\left(N\right)·A)}^R\le (N+A)(b+1)\\ <(N_0+A)(b+1),\mathrm{if}N<N_0.\end{array}$$

(33)

Let ${\left\{N_k\right\}}_k$ be an orbit of $f_A$. Define $\overline{M}=max\{N_1,(N_0+A)(b+1)\}$. Then conditions (32), (33) imply that $|N_k|\le \overline{M},\forall k\ge 1$, so the orbit is bounded.

• We show the proof for the b-MRH sequence. Let $f_M$ be a map from the sequence. Let $N_0$ be the integer from Proposition 8 corresponding to $f_M$. Then

  $$f_M\left(N\right)<N\mathrm{if}N\ge N_0.$$

  (34)

It follows from Proposition 7 that

$$\begin{array}{c}{f}_M\left(N\right)=(s_b\left(N\right)·M)·{(s_b\left(N\right)·M)}^R\le {\left(NM\right)}^2(b+1)\\ <{\left(N_{0}M\right)}^2(b+1),\mathrm{if}N<N_0.\end{array}$$

(35)

Let ${\left\{N_k\right\}}_k$ be an orbit of $f_A$. Define $\overline{M}=max\{N_1,{\left(N_{0}M\right)}^2(b+1)\}.$ Then conditions (28) and (29), (34), (35) imply that $|N_k|\le \overline{M},\forall k\ge 1$, so the orbit is bounded.

To prove the last statement in Proposition 4, we observe that the pairs of Inequalities, (34) and (35), (32) and (33), (30) and (31), and (28) and (29), provide an upper and lower treshhold that will eventually contain an element from each orbit, as the interval betwen the treshholds contains only a finite number of integers we conclude that each orbit is going to colaps into a periodic cycle. □

5. Proof of Proposition 5

Proof. 

We assume throughout the proof that $N>\frac{1}{b}$.

• We show the proof for the dual b-wARH sequence. Let $f_A$ be a function in the sequence and $N\in \mathbb{N}$. We observe that the base b reversal of an integer decrease the integer by at most a factor of $\frac{1}{b}$. Therefore:

  $$f_A\left(N\right)=(s_b\left(A\right)+N)+{(s_b\left(A\right)+N)}^R\ge (1+\frac{1}{b})(s_b\left(A\right)+N)\ge (1+\frac{1}{b})N.$$

  (36)

As $1+\frac{1}{b}>1$, the iteration of (38) shows that the orbit of N is unbounded.

• We show the proof for the dual b-ARH sequence. Let $f_A$ be a function in the sequence and $N\in \mathbb{N}$. We observe that the base b reversal of an integer decrease the integer by at most a factor of $\frac{1}{b}$. Therefore:

  $$f_A\left(N\right)=(s_b\left(A\right)·N)+{(s_b\left(A\right)·N)}^R\ge (1+\frac{1}{b})(s_b\left(A\right)·N)\ge (1+\frac{1}{b})N.$$

  (37)

As $1+\frac{1}{b}>1$, the iteration of (39) shows that the orbit of N is unbounded.

• We show the proof for the dual b-MRH sequence. Let $f_M$ be a function in the sequence and $N\in \mathbb{N}$. We observe that the base b reversal of an integer decrease the integer by at most a factor of $\frac{1}{b}$. Therefore:

  $$f_M\left(N\right)=(s_b\left(M\right)\times N)\times {(s_b\left(M\right)\times N)}^R\ge \frac{1}{b}{(s_b\left(M\right)\times N)}^2\ge \frac{1}{b}{N}^2.$$

  (38)

As $\frac{N}{b}>1$, the iteration of (38) shows that the orbit of N is unbounded.

• We show the proof for the dual b-wMRH sequence. Let $f_A$ be a function in the sequence and $N\in \mathbb{N}$. We observe that the base b reversal of an integer decrease the integer by at most a factor of $\frac{1}{b}$. Therefore:

  $$f_A\left(N\right)=(s_b\left(A\right)+N)·{(s_b\left(A\right)+N)}^R\ge (1·\frac{1}{b}){(s_b\left(A\right)+N)}^2\ge \frac{1}{b}{N}^2.$$

  (39)

As $\frac{N}{b}>1$, the iteration of (39) shows that the orbit of N is unbounded. □

6. Conclusions

In this paper, motivated by their intrinsic interest and by applications to the study of certain sequences of integers, we investigate from a dynamical systems point of view certain sequences of maps of integers. We are mostly interested in understanding the space of orbits. We find sequences of maps of integers for which all individual orbits are bounded and periodic and for which the number of periodic orbits of fixed period is finite. This allows us to introduce formal $\zeta$-functions for all functions in these sequences, which are actually polynomials. We also find sequences of maps of integers for which the orbit structure is more complicated, as they have both bounded and unbounded orbits, both individual and global. We observe that the notion of a chaotic dynamical system for single maps is very well established in the literature. Nevertheless, the notion of a chaotic system for a larger group of symmetries it is not yet crystalized. We hope that our results will provide a collection of useful examples that together with further additional research may lead to a general theory of chaotic families of maps, and in particular a general theory of chaotic sequences of maps of integers.