Discrete Quantum Harmonic Oscillator
Abstract
:1. Introduction
2. Preliminaries
3. Sequence of Discrete Quantum Harmonic Oscillators
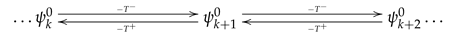
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hounkonnou, M.N.; Arjika, S.; Baloitcha, E. Pöschl-Teller Hamiltonian: Gazeau-Klauder type coherent states, related statistics and geometry. J. Math. Phys. 2014, 55, 123502. [Google Scholar] [CrossRef]
- Lorente, M. Continuous vs. discrete models for the quantum harmonic oscillator and the hydrogen atom. Phys. Lett. A 2001, 285, 119–126. [Google Scholar] [CrossRef] [Green Version]
- Novikov, S.P.; Veselov, P. Exactly solvable two-dimensional Schrödinger operators and Laplace transformations. In Solitons, Geometry, and Topology: On the Crossroad; American Mathematical Society Translations: Series 2; American Mathematical Society: Providence, RI, USA, 1997; Volume 179, pp. 109–132. [Google Scholar]
- Boykin, T.B.; Klimeck, G. The discretized Schrödinger equation and simple models for semiconductor quantum wells. Eur. J. Phys. 2004, 25, 503–514. [Google Scholar] [CrossRef]
- Bruckstein, A.M.; Kailath, T. On discrete Schrödinger equations and their two-component wave equation equivalents. J. Math. Phys. 1987, 28, 2914–2924. [Google Scholar] [CrossRef]
- Fernández, D.J.; Fernández-García, N. Higher-order supersymmetric quantum mechanics. AIP Conf. Proc. 2005, 744, 236–273. [Google Scholar]
- Fernández, D.J. Trends in supersymmetric quantum mechanics. In Integrability, Supersymmetry and Coherent States; CRM Series in Mathematical Physics; Springer: Cham, Switzerland, 2019; pp. 37–68. [Google Scholar]
- Goliński, T. Factorization method on time scales. Appl. Math. Comput. 2019, 347, 354–359. [Google Scholar] [CrossRef]
- Tarasov, V.E. Exact discretization of Schrödinger equation. Phys. Lett. A 2016, 380, 68–75. [Google Scholar] [CrossRef]
- Dobrogowska, A.; Fernández, D.J. Darboux transformations and second order difference equations. arXiv 2018, arXiv:1807.06895. [Google Scholar]
- Elaydi, S. An Introduction to Difference Equations; Springer: New York, NY, USA, 1999. [Google Scholar]
- Álvarez-Nodarse, R.; Atakishiyev, N.M.; Costas-Santos, R.S. Factorization of the hypergeometric-type difference equation on the uniform lattice. ETNA Electron. Trans. Numer. Anal. 2007, 27, 34–50. [Google Scholar]
- Nikiforov, A.F.; Suslov, S.K.; Uvarov, V.B. Classical orthogonal polynomials of a discrete variable. In Springer Series in Computational Physices; Springer: Berlin, Germany, 1991. [Google Scholar]
- Bavinck, H.; Vanhaeringen, H. Difference Equations for Generalized Meixner Polynomials. J. Math. An. App. 1994, 184, 453–463. [Google Scholar] [CrossRef] [Green Version]
- Kruchinin, V.D.; Shablya, Y.V. Explicit Formulas for Meixner Polynomials. Int. J. Math. Math. Sci. 2015, 2015, 620569. [Google Scholar] [CrossRef]
- Dobrogowska, A. New classes of second order difference equations solvable by factorization method. Appl. Math. Lett. 2019, 98, 300–305. [Google Scholar] [CrossRef]
- Dobrogowska, A.; Hounkonnou, M.N. Factorization Method and General Second Order Linear Difference Equation. In Differential and Difference Equations with Applications; Pinelas, S., Caraballo, T., Kloeden, P., Graef, J., Eds.; ICDDEA 2017, Springer Proceedings in Mathematics & Statistics vol 230; Springer: Cham, Switzerland, 2018; pp. 67–77. [Google Scholar] [Green Version]
- Dobrogowska, A.; Jakimowicz, G. Factorization method applied to the second order difference equations. Appl. Math. Lett. 2017, 74, 161–166. [Google Scholar] [CrossRef]
- Dobrogowska, A.; Odzijewicz, A. Second order q-difference equations solvable by factorization method. J. Comput. Appl. Math. 2006, 193, 319–346. [Google Scholar] [CrossRef] [Green Version]
- Dobrogowska, A.; Odzijewicz, A. Solutions of the q-deformed Schrödinger equation for special potentials. J. Phys. A Math. Theor. 2007, 40, 2023–2036. [Google Scholar] [CrossRef]
- Goliński, T.; Odzijewicz, A. Factorization method for second order functional equations. J. Comput. Appl. Math. 2005, 176, 331–355. [Google Scholar] [CrossRef] [Green Version]
- Schrödinger, E. A method of determining quantum-mechanical eigenvalues and eigenfunctions. Proc. R. Ir. Acad. Sect. A 1940, 46, 9–16. [Google Scholar]
- Infeld, L.; Hull, T.E. The Factorization Method. Rev. Mod. Phys. 1951, 23, 21–68. [Google Scholar] [CrossRef]
- de Lange, O.L.; Raab, R.E. Operator Methods in Quantum Mechanics; Claredon Press: Oxford, UK, 1991. [Google Scholar]
- Mielnik, B. Factorization method and new potentials with the oscillator spectrum. J. Math. Phys. 1984, 25, 3387. [Google Scholar] [CrossRef]
- Koekoek, R.; Lesky, P.A.; Swarttouw, R.F. Hypergeometric Orthogonal Polynomials and Their q-Analogues; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dobrogowska, A.; Fernández C., D.J. Discrete Quantum Harmonic Oscillator. Symmetry 2019, 11, 1362. https://doi.org/10.3390/sym11111362
Dobrogowska A, Fernández C. DJ. Discrete Quantum Harmonic Oscillator. Symmetry. 2019; 11(11):1362. https://doi.org/10.3390/sym11111362
Chicago/Turabian StyleDobrogowska, Alina, and David J. Fernández C. 2019. "Discrete Quantum Harmonic Oscillator" Symmetry 11, no. 11: 1362. https://doi.org/10.3390/sym11111362
APA StyleDobrogowska, A., & Fernández C., D. J. (2019). Discrete Quantum Harmonic Oscillator. Symmetry, 11(11), 1362. https://doi.org/10.3390/sym11111362



