Metal–Insulator Transition in Three-Dimensional Semiconductors
Abstract
:1. Introduction
2. Model and Symmetries
3. Self-Consistent Approximation
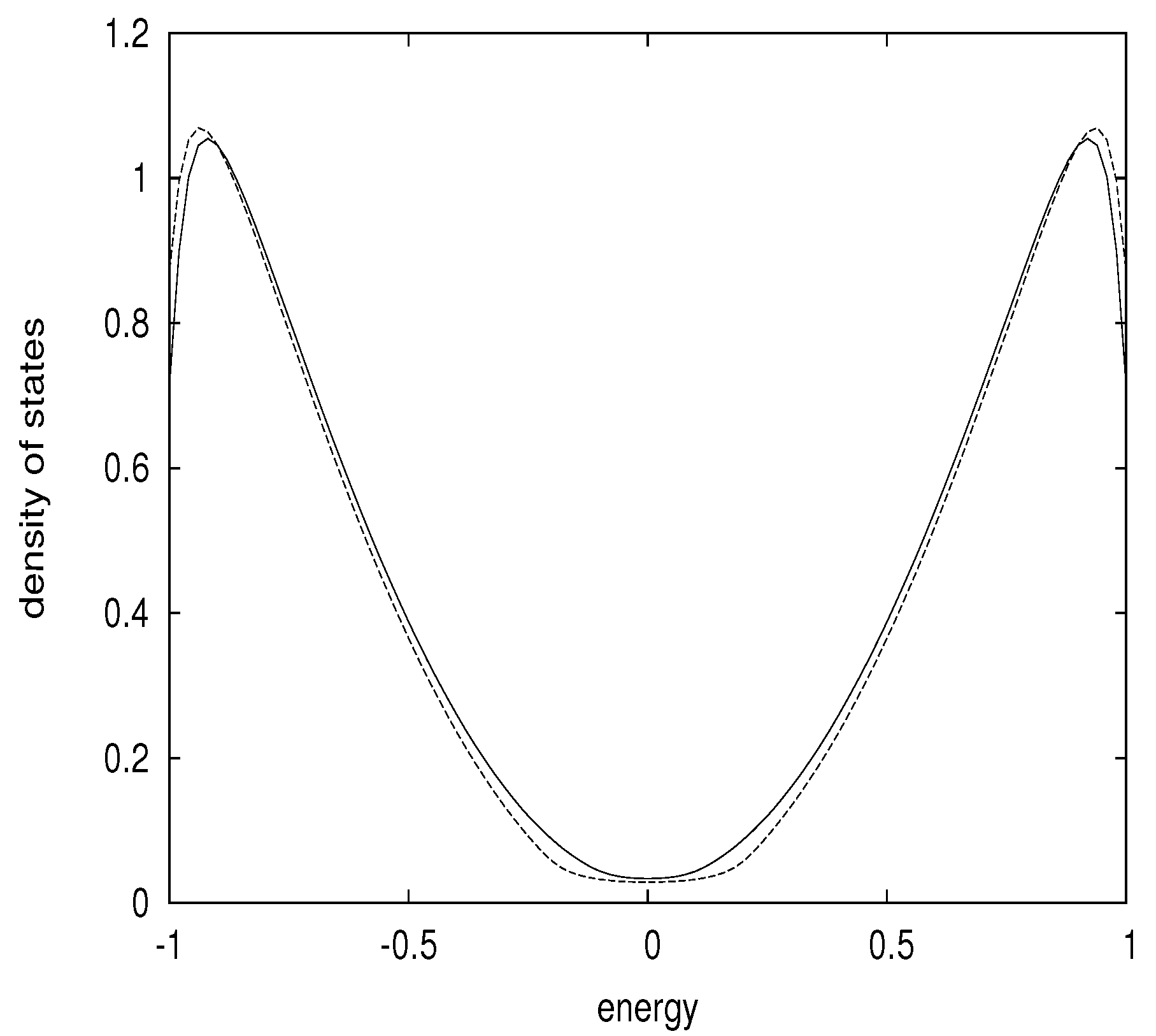
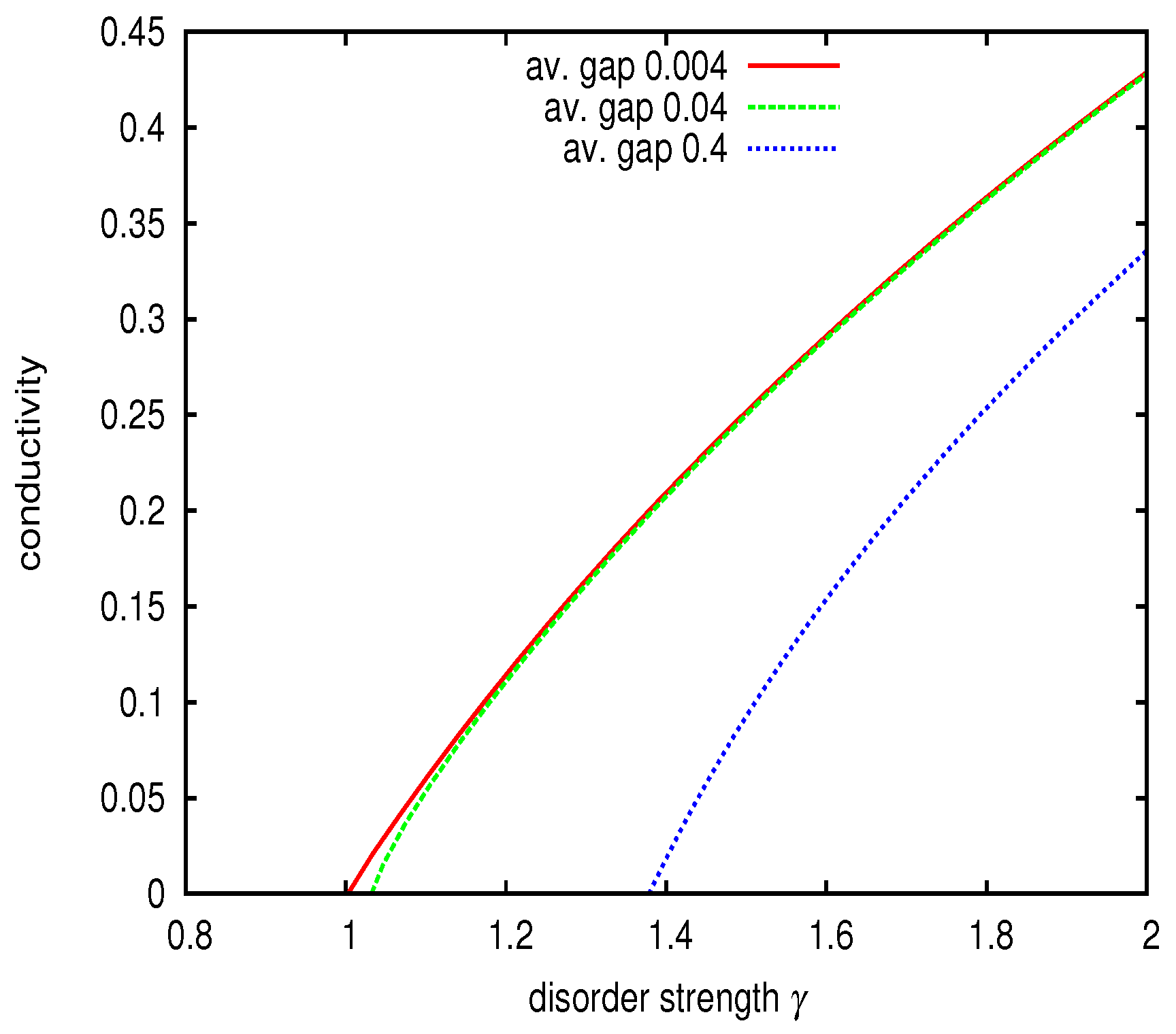
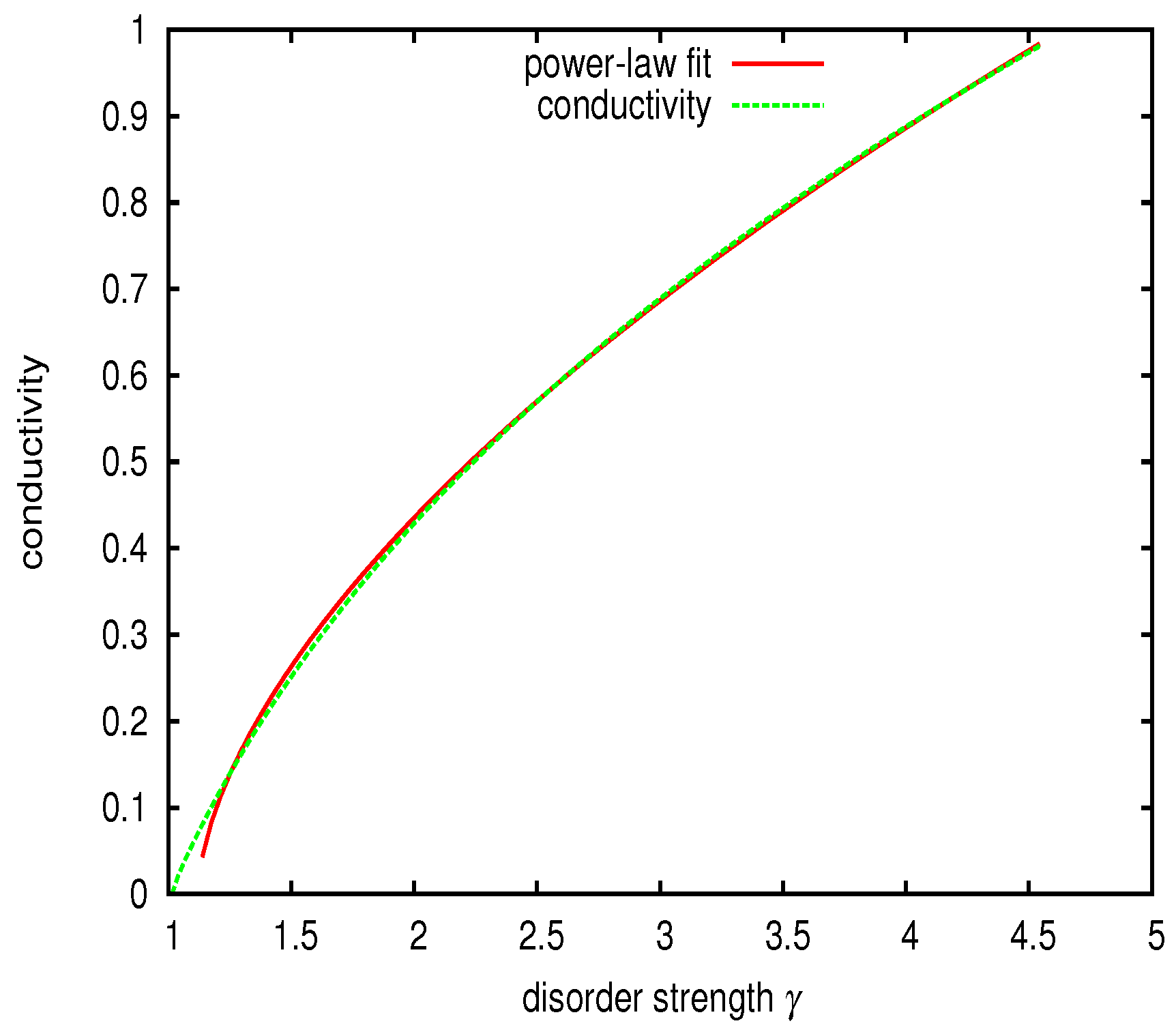
4. Scaling Relation of the Average Two-Particle Green’s Function
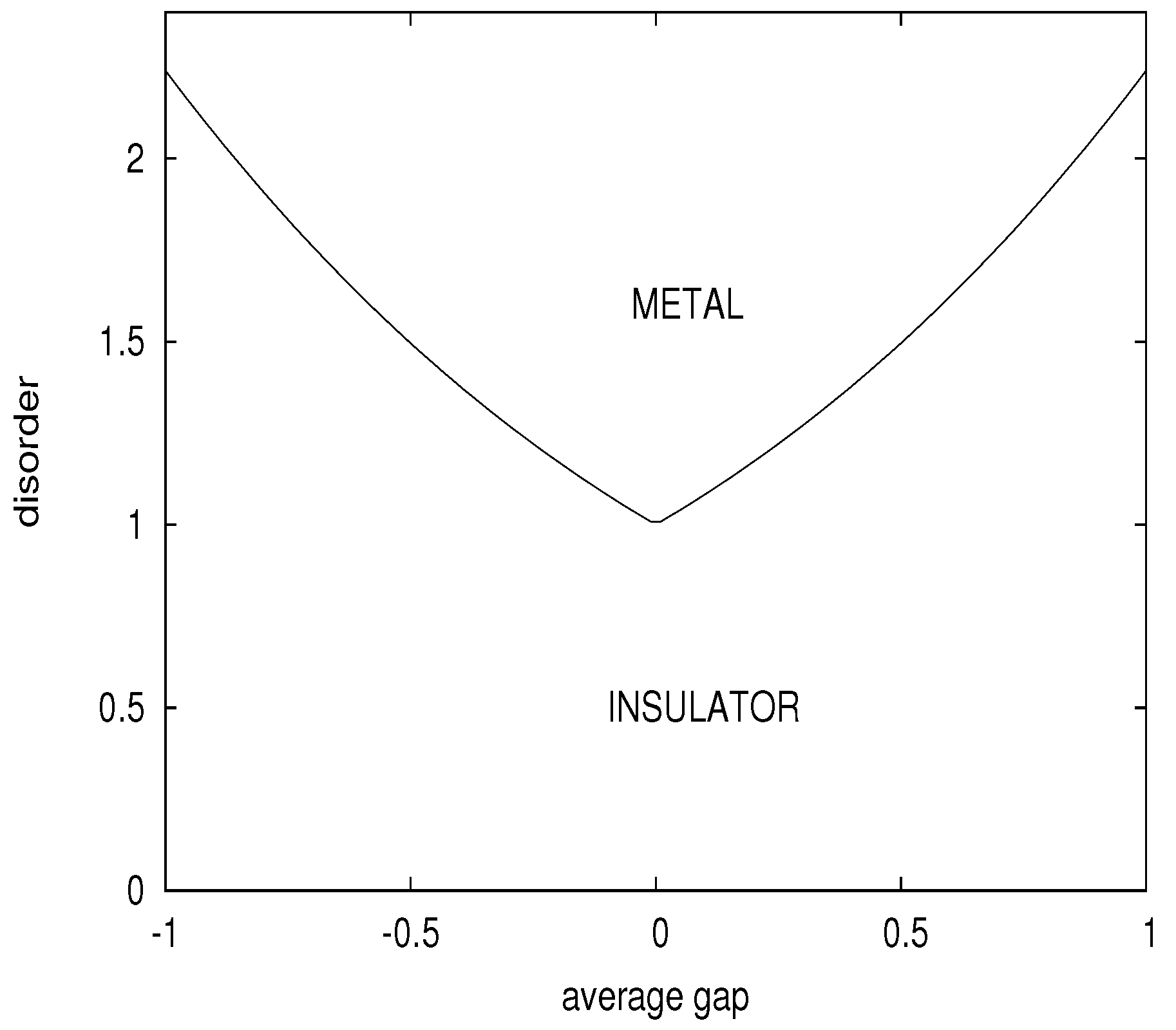
5. Discussion and Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Saunders College: Rochester, NY, USA, 1976. [Google Scholar]
- Fradkin, E. Critical behavior of disordered degenerate semiconductors. I. Models, symmetries, and formalism. Phys. Rev. B 1986, 33, 3257–3262. [Google Scholar] [CrossRef]
- Fradkin, E. Critical behavior of disordered degenerate semiconductors. II. Spectrum and transport properties in mean-field theory. Phys. Rev. B 1986, 33, 3263–3268. [Google Scholar] [CrossRef]
- Wan, X.; Turner, A.M.; Vishwanath, A.; Savrasov, S.Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 2011, 83, 205101. [Google Scholar] [CrossRef]
- Smith, J.; Banerjee, S.; Pardo, V.; Pickett, W.E. Dirac Point Degenerate with Massive Bands at a Topological Quantum Critical Point. Phys. Rev. Lett. 2011, 106, 056401. [Google Scholar] [CrossRef]
- Burkov, A.A.; Balents, L. Weyl Semimetal in a Topological Insulator Multilayer. Phys. Rev. Lett. 2011, 107, 127205. [Google Scholar] [CrossRef] [Green Version]
- Burkov, A.A.; Hook, M.D.; Balents, L. Topological nodal semimetals. Phys. Rev. B 2011, 84, 235126. [Google Scholar] [CrossRef]
- Xu, G.; Weng, H.; Wang, Z.; Dai, X.; Fang, Z. Chern Semimetal and the Quantized Anomalous Hall Effect in HgCr2Se4. Phys. Rev. Lett. 2011, 107, 186806. [Google Scholar] [CrossRef] [PubMed]
- Witczak-Krempa, W.; Kim, Y.B. Topological and magnetic phases of interacting electrons in the pyrochlore iridates. Phys. Rev. B 2012, 85, 045124. [Google Scholar] [CrossRef]
- Young, S.M.; Zaheer, S.; Teo, J.C.Y.; Kane, C.L.; Mele, E.J.; Rappe, A.M. Dirac Semimetal in Three Dimensions. Phys. Rev. Lett. 2012, 108, 140405. [Google Scholar] [CrossRef] [PubMed]
- Hosur, P.; Parameswaran, S.A.; Vishwanath, A. Charge Transport in Weyl Semimetals. Phys. Rev. Lett. 2012, 108, 046602. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Sun, Y.; Chen, X.-Q.; Franchini, C.; Xu, G.; Weng, H.; Dai, X.; Fang, Z. Dirac semimetal and topological phase transitions in A3Bi (A = Na, K, Rb). Phys. Rev. B 2012, 85, 195320. [Google Scholar] [CrossRef]
- Singh, B.; Sharma, A.; Lin, H.; Hasan, M.Z.; Prasad, R.; Bansil, A. Topological electronic structure and Weyl semimetal in the TlBiSe2 class of semiconductors. Phys. Rev. B 2012, 86, 115208. [Google Scholar] [CrossRef]
- Cho, G.Y. Possible topological phases of bulk magnetically doped Bi2Se3: Turning a topological band insulator into the Weyl semimetal. arXiv 2012, arXiv:1110.1939v2. [Google Scholar]
- Halász, G.B.; Balents, L. Time-reversal invariant realization of the Weyl semimetal phase. Phys. Rev. B 2012, 85, 035103. [Google Scholar] [CrossRef]
- Nandkishore, R.; Huse, D.A.; Sondhi, S. Rare region effects dominate weakly disordered three-dimensional Dirac points. Phys. Rev. B 2014, 89, 245110. [Google Scholar] [CrossRef]
- Liu, C.-X.; Ye, P.; Qi, X.-L. Chiral gauge field and axial anomaly in a Weyl semimetal. Phys. Rev. B 2013, 87, 235306. [Google Scholar] [CrossRef]
- Biswas, R.R.; Ryu, S. Diffusive transport in Weyl semimetals. Phys. Rev. B 2014, 89, 014205. [Google Scholar] [CrossRef]
- Kobayashi, K.; Ohtsuki, T.; Imura, K.-I. Disordered Weak and Strong Topological Insulators. Phys. Rev. Lett. 2013, 110, 236803. [Google Scholar] [CrossRef] [Green Version]
- Huang, Z.; Das, T.; Balatsky, A.V.; Arovas, D.P. Stability of Weyl metals under impurity scattering. Phys. Rev. B 2013, 87, 155123. [Google Scholar] [CrossRef]
- Kobayashi, K.; Ohtsuki, T.; Imura, K.-I.; Herbut, I.F. Density of States Scaling at the Semimetal to Metal Transition in Three Dimensional Topological Insulators. Phys. Rev. Lett. 2014, 112, 016402. [Google Scholar] [CrossRef] [Green Version]
- Ominato, Y.; Koshino, M. Quantum transport in a three-dimensional Weyl electron system. Phys. Rev. B 2014, 89, 054202. [Google Scholar] [CrossRef]
- Roy, B.; Das Sarma, S. Diffusive quantum criticality in three-dimensional disordered Dirac semimetals. Phys. Rev. B 2014, 90, 241112(R). [Google Scholar] [CrossRef]
- Sbierski, B.; Pohl, G.; Bergholtz, E.J.; Brouwer, P.W. Quantum Transport of Disordered Weyl Semimetals at the Nodal Point. Phys. Rev. Lett. 2014, 113, 026602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Syzranov, S.V.; Gurarie, V.; Radzihovy, L. Critical Transport in Weakly Disordered Semiconductors and Semimetals. Phys. Rev. Lett. 2015, 114, 166601. [Google Scholar] [CrossRef] [Green Version]
- Ziegler, K. Quantum transport in 3D Weyl semimetals: Is there a metal-insulator transition? Eur. Phys. J. B 2016, 89, 268. [Google Scholar] [CrossRef] [Green Version]
- Ziegler, K. Quantum transport with strong scattering: beyond the nonlinear sigma model. J. Phys. A Math. Theor. 2015, 48, 055102. [Google Scholar] [CrossRef]
- Ziegler, K. Zero mode protection at particle-hole symmetry: A geometric interpretation. J. Phys. A Math. Theor. 2019, 52, 455101. [Google Scholar] [CrossRef]
- Rosenbaum, T.F.; Andres, K.; Thomas, G.A.; Bhatt, R.N. Sharp Metal-Insulator Transition in a Random Solid. Phys. Rev. Lett. 1980, 45, 1723–1726. [Google Scholar] [CrossRef]
- Rosenbaum, T.F.; Milligan, R.F.; Paalanen, M.A.; Thomas, G.A.; Bhatt, R.N.; Lin, W. Metal-insulator transition in a doped semiconductor. Phys. Rev. B 1983, 27, 7509–7523. [Google Scholar] [CrossRef] [Green Version]
- Roy, A.; Sarachik, M.P. Susceptibility of Si:P across the metal-insulator transition. II. Evidence for local moments in the metallic phase. Phys. Rev. B 1988, 37, 5531–5534. [Google Scholar] [CrossRef]
- Rosenbaum, T.F.; Thomas, G.A.; Paalanen, M.A. Critical behavior of Si:P at the metal-insulator transition. Phys. Rev. Lett. 1994, 72, 2121. [Google Scholar] [CrossRef] [PubMed]
- Löhneysen, H. Current issues in the physics of heavily doped semiconductors at the metal-insulator transition. Philos. Trans. R. Soc. Lond. A 1998, 356, 139–156. [Google Scholar] [CrossRef]
- Ziegler, K. Scaling behavior and universality near the quantum Hall transition. Phys. Rev. B 1997, 55, 10661–10670. [Google Scholar] [CrossRef] [Green Version]
- Ziegler, K. Random-Gap Model for Graphene and Graphene Bilayers. Phys. Rev. Lett. 2009, 102, 126802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Altshuler, B.L.; Simons, B.D. Mesoscopic Quantum Physics; Akkermans, E., Montambaux, G., Pichard, J.-L., Zinn-Justin, J., Eds.; North-Holland: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Altland, A.; Simons, B.D. Condensed Matter Field Theory; Cambridge University Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Schäfer, L.; Wegner, F. Disordered system with n orbitals per site: Lagrange formulation, hyperbolic symmetry, and goldstone modes. Z. Phys. B 1980, 38, 113–126. [Google Scholar] [CrossRef]
- Stupp, H.; Hornung, M.; Lakner, M.; Madel, O.; Löhneysen, H. Possible solution of the conductivity exponent puzzle for the metal-insulator transition in heavily doped uncompensated semiconductors. Phys. Rev. Lett. 1993, 71, 2634–2637. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ziegler, K. Metal–Insulator Transition in Three-Dimensional Semiconductors. Symmetry 2019, 11, 1345. https://doi.org/10.3390/sym11111345
Ziegler K. Metal–Insulator Transition in Three-Dimensional Semiconductors. Symmetry. 2019; 11(11):1345. https://doi.org/10.3390/sym11111345
Chicago/Turabian StyleZiegler, Klaus. 2019. "Metal–Insulator Transition in Three-Dimensional Semiconductors" Symmetry 11, no. 11: 1345. https://doi.org/10.3390/sym11111345




