Analysis of a Trapped Bose–Einstein Condensate in Terms of Position, Momentum, and Angular-Momentum Variance
Abstract
1. Introduction
2. The Anisotropic Harmonic-Interaction Model
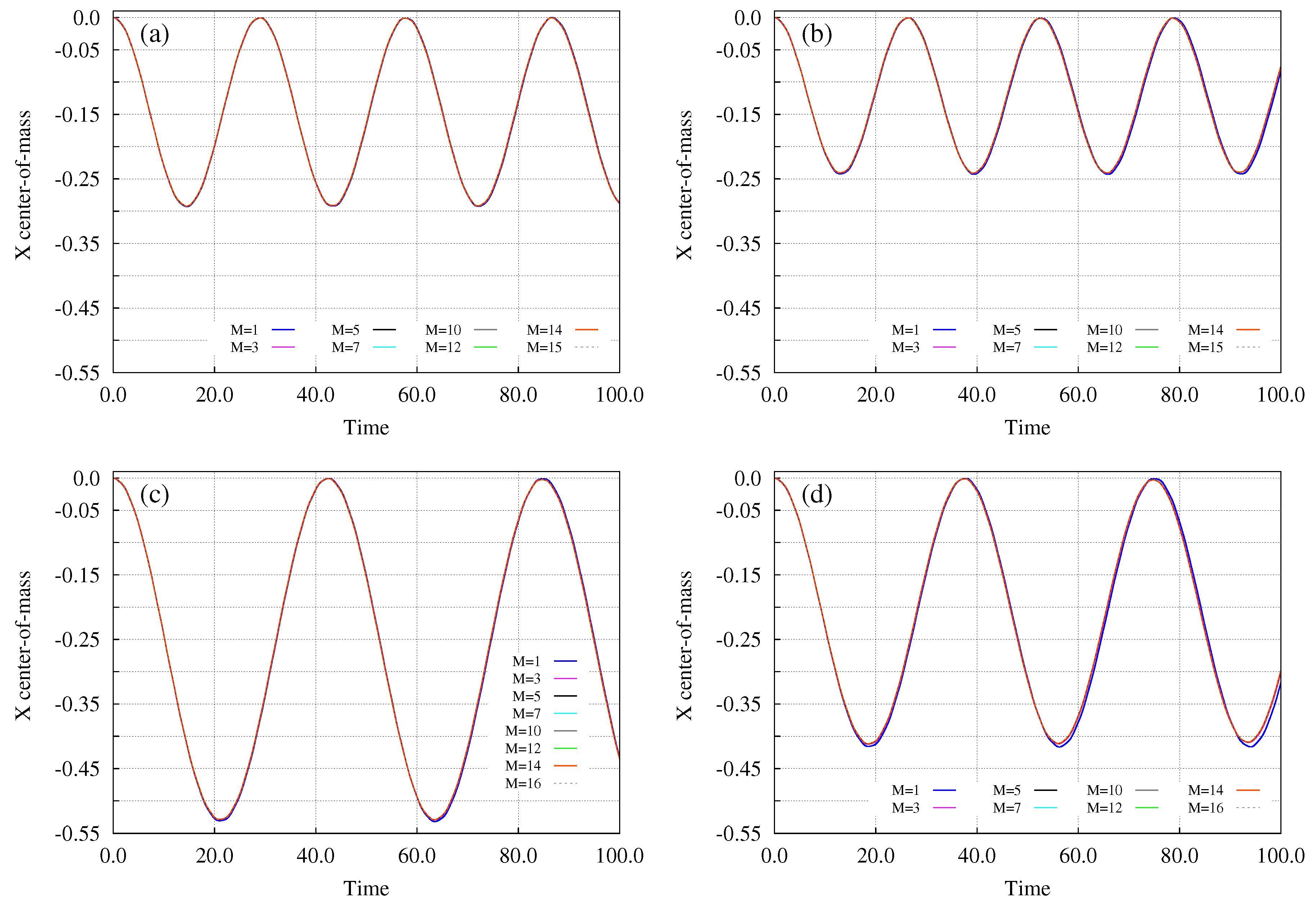
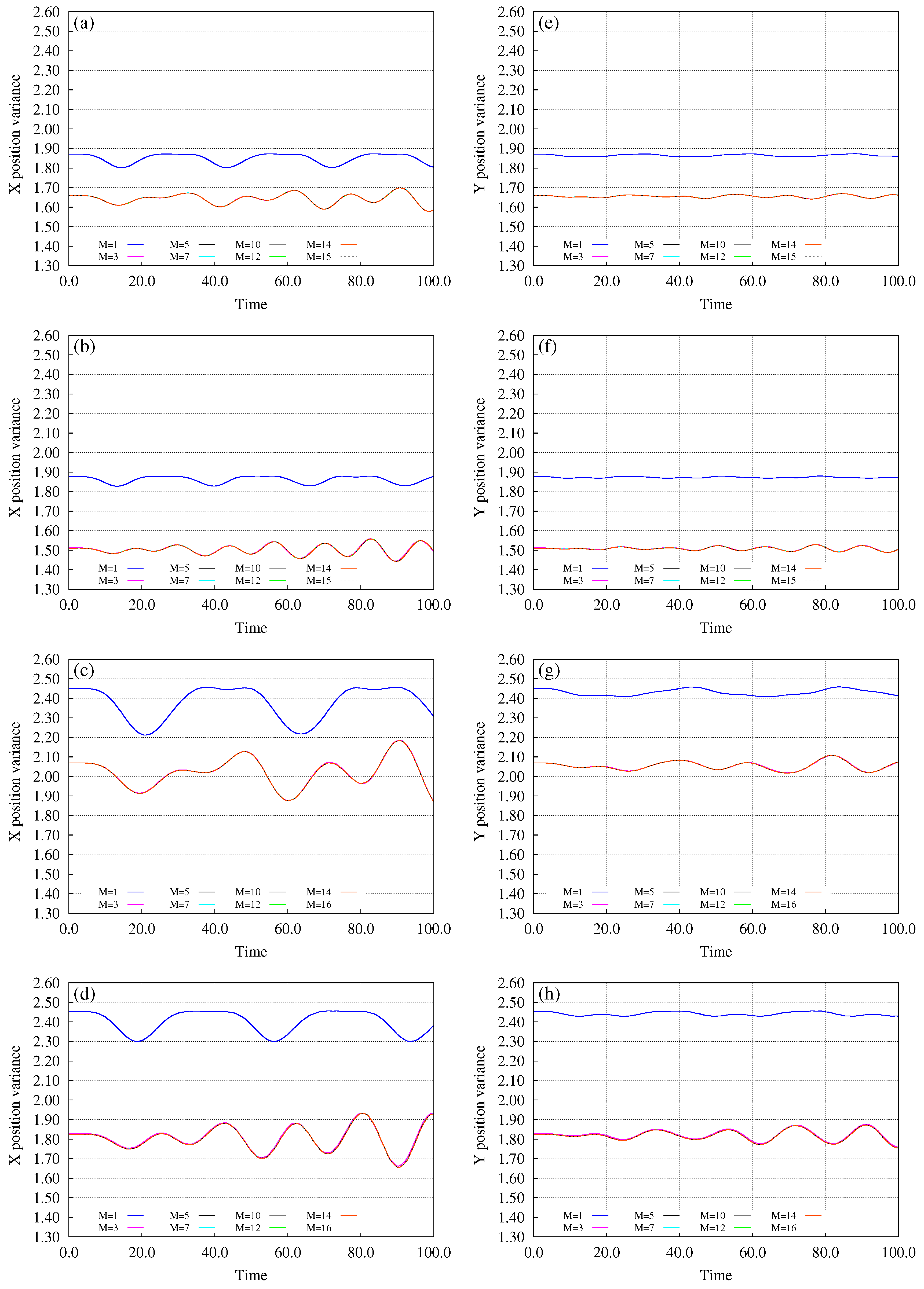
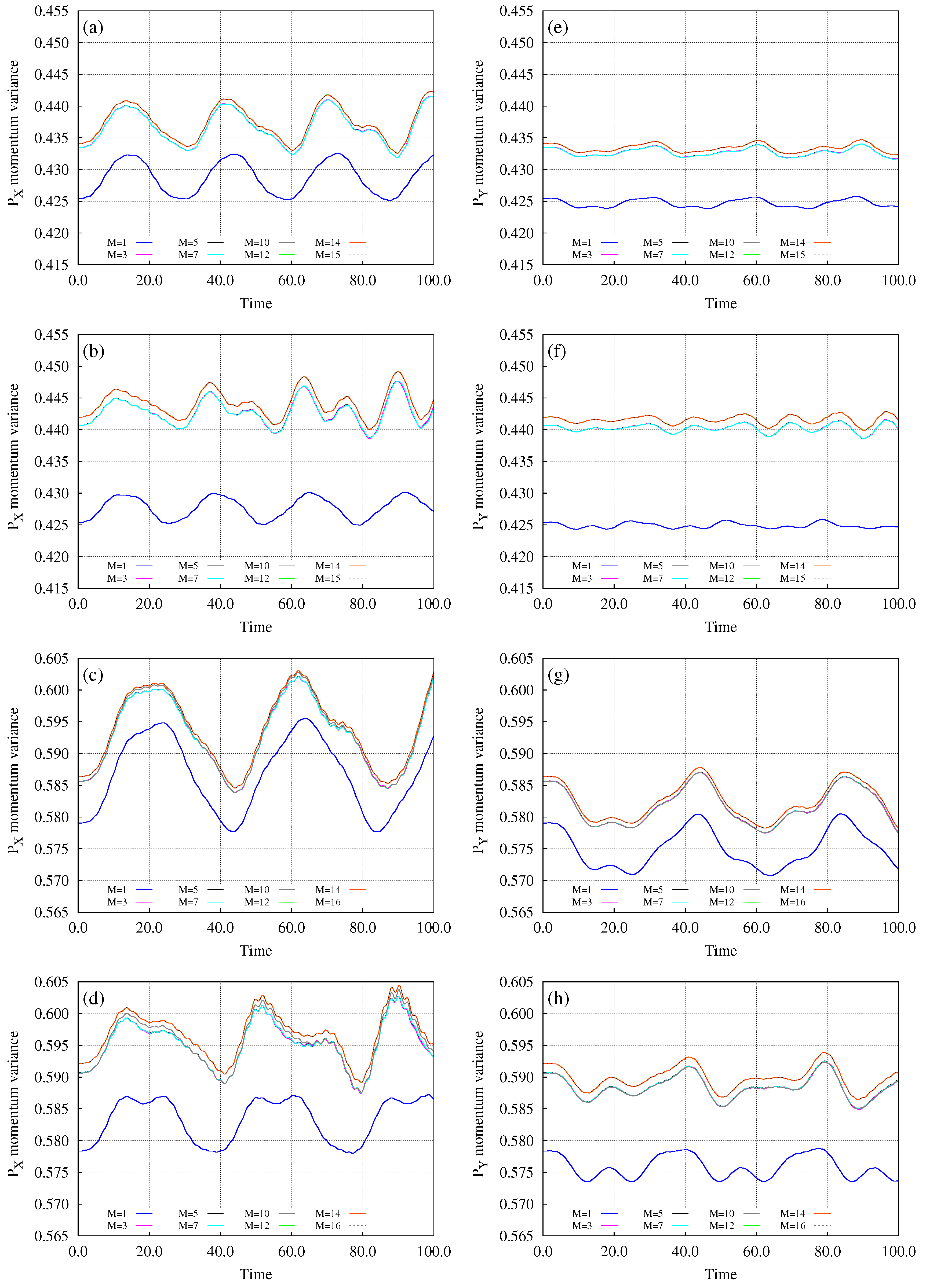
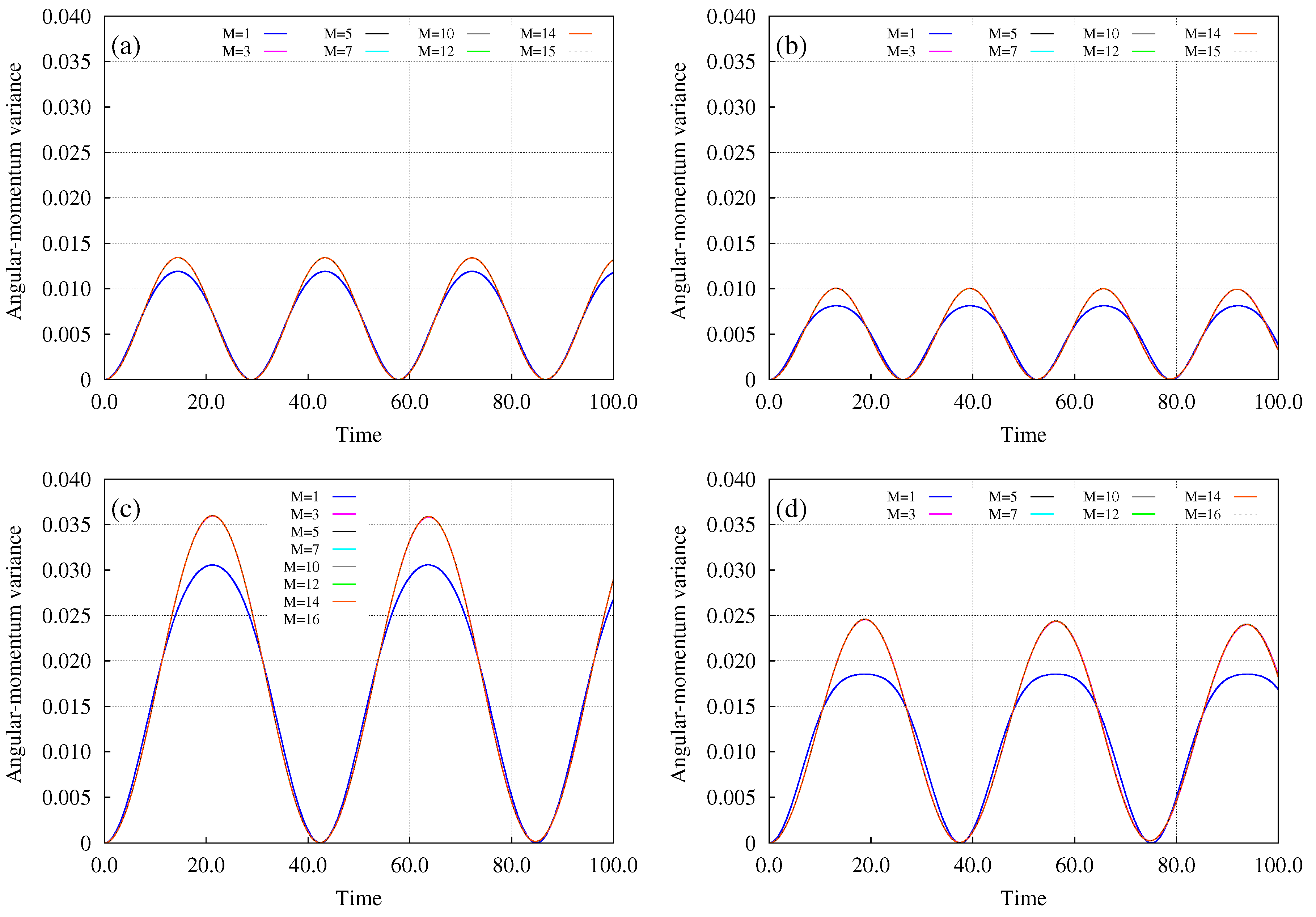
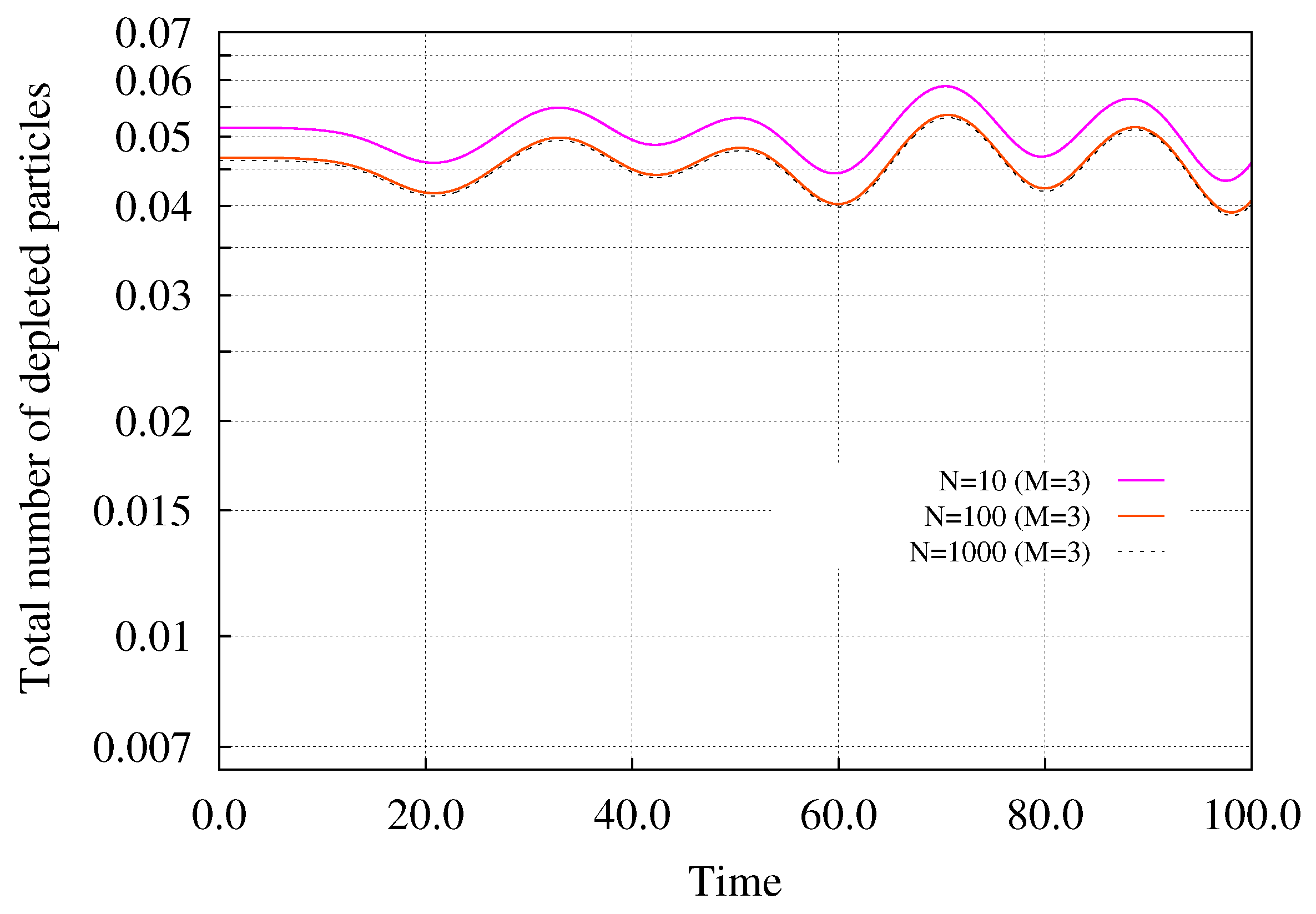
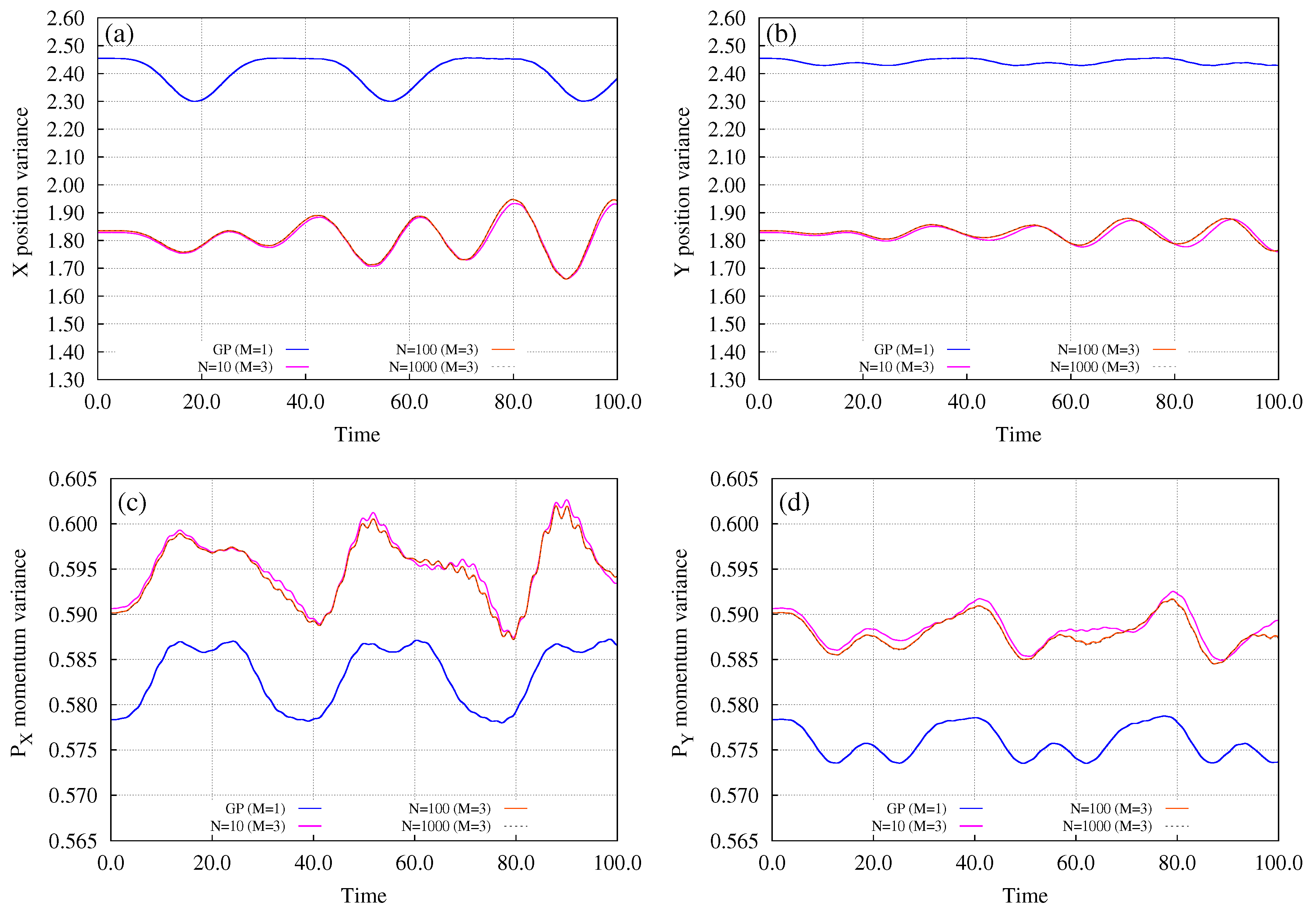
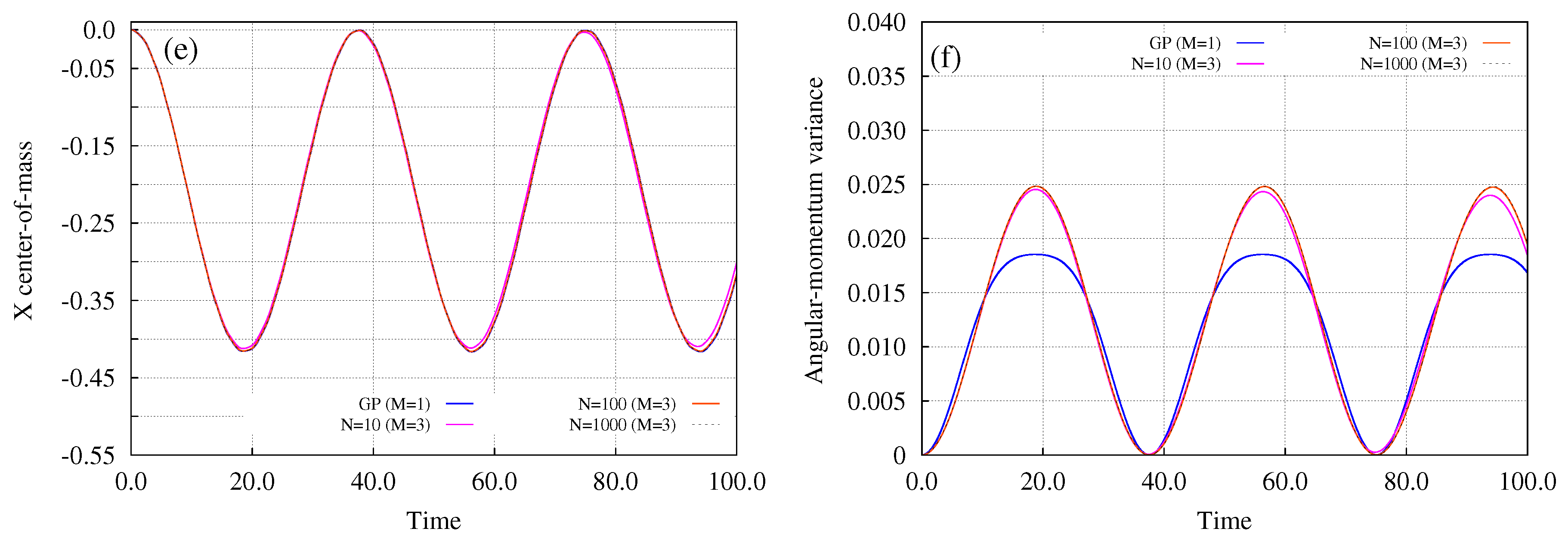
3. Bosons in an Annulus Subject to a Tilt
4. Summary and Outlook
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Variances and Translations
References
- Cornell, E.A.; Wieman, C.E. Nobel Lecture: Bose–Einstein condensation in a dilute gas, the first 70 years and some recent experiments. Rev. Mod. Phys. 2002, 74, 875. [Google Scholar] [CrossRef]
- Ketterle, W. Nobel lecture: When atoms behave as waves: Bose–Einstein condensation and the atom laser. Rev. Mod. Phys. 2002, 74, 1131. [Google Scholar] [CrossRef]
- Dalfovo, F.; Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of Bose–Einstein condensation in trapped gases. Rev. Mod. Phys. 1999, 71, 463. [Google Scholar] [CrossRef]
- Leggett, A.J. Bose–Einstein condensation in the alkali gases: Some fundamental concepts. Rev. Mod. Phys. 2001, 73, 307. [Google Scholar] [CrossRef]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 885. [Google Scholar] [CrossRef]
- Castin, Y.; Dum, R. Low-temperature Bose–Einstein condensates in time-dependent traps: Beyond the U(1) symmetry breaking approach. Phys. Rev. A 1998, 57, 3008. [Google Scholar] [CrossRef]
- Lieb, E.H.; Seiringer, R.; Yngvason, J. Bosons in a trap: A rigorous derivation of the Gross-Pitaevskii energy functional. Phys. Rev. A 2000, 61, 043602. [Google Scholar] [CrossRef]
- Lieb, E.H.; Seiringer, R. Proof of Bose–Einstein Condensation for Dilute Trapped Gases. Phys. Rev. Lett. 2002, 88, 170409. [Google Scholar] [CrossRef]
- Erdos, L.; Schlein, B.; Yau, H.-T. Rigorous Derivation of the Gross-Pitaevskii Equation. Phys. Rev. Lett. 2007, 98, 040404. [Google Scholar] [CrossRef]
- Erdos, L.; Schlein, B.; Yau, H.-T. Derivation of the cubic non-linear Schrödinger equation from quantum dynamics of many-body systems. Invent. Math. 2007, 167, 515. [Google Scholar] [CrossRef]
- Klaiman, S.; Alon, O.E. Variance as a sensitive probe of correlations. Phys. Rev. A 2015, 91, 063613. [Google Scholar] [CrossRef]
- Klaiman, S.; Streltsov, A.I.; Alon, O.E. Uncertainty product of an out-of-equilibrium many-particle system. Phys. Rev. A 2016, 93, 023605. [Google Scholar] [CrossRef]
- Klaiman, S.; Cederbaum, L.S. Overlap of exact and Gross-Pitaevskii wave functions in Bose–Einstein condensates of dilute gases. Phys. Rev. A 2016, 94, 063648. [Google Scholar] [CrossRef]
- Michelangeli, A.; Olgiati, A. Mean-field quantum dynamics for a mixture of Bose–Einstein condensates. Anal. Math. Phys. 2017, 7, 377. [Google Scholar] [CrossRef]
- Cederbaum, L.S. Exact many-body wave function and properties of trapped bosons in the particle limit. Phys. Rev. A 2017, 96, 013615. [Google Scholar] [CrossRef]
- Alon, O.E. Solvable model of a generic trapped mixture of interacting bosons: reduced density matrices and proof of Bose–Einstein condensation. J. Phys. A 2017, 50, 295002. [Google Scholar] [CrossRef]
- Coleman, A.J.; Yukalov, V.I. Reduced Density Matrices: Coulson’s Challenge; Lectures Notes in Chemistry; Springer: Berlin, Germany, 2000; Volume 72. [Google Scholar]
- Klaiman, S.; Beinke, R.; Cederbaum, L.S.; Streltsov, A.I.; Alon, O.E. Variance of an anisotropic Bose–Einstein condensate. Chem. Phys. 2018, 509, 45. [Google Scholar] [CrossRef]
- Alon, O.E. Condensates in annuli: Dimensionality of the variance. Mol. Phys. 2019, 117, 2108. [Google Scholar] [CrossRef]
- Theisen, M.; Streltsov, A.I. Many-body excitations and deexcitations in trapped ultracold bosonic clouds. Phys. Rev. A 2016, 94, 053622. [Google Scholar] [CrossRef]
- Haldar, S.K.; Alon, O.E. Impact of the range of the interaction on the quantum dynamics of a bosonic Josephson junction. Chem. Phys. 2018, 509, 72. [Google Scholar] [CrossRef]
- Haldar, S.K.; Alon, O.E. Many-body quantum dynamics of an asymmetric bosonic Josephson junction. New J. Phys. 2019, 21, 103037. [Google Scholar] [CrossRef]
- Cosme, J.G.; Weiss, C.; Brand, J. Center-of-mass motion as a sensitive convergence test for variational multimode quantum dynamics. Phys. Rev. A 2016, 94, 043603. [Google Scholar] [CrossRef]
- Alon, O.E.; Cederbaum, L.S. Attractive Bose–Einstein condensates in anharmonic traps: Accurate numerical treatment and the intriguing physics of the variance. Chem. Phys. 2018, 515, 287. [Google Scholar] [CrossRef]
- Sakmann, K.; Schmiedmayer, J. Conserving symmetries in Bose–Einstein condensate dynamics requires many-body theory. arXiv 2018, arXiv:1802.03746v2. [Google Scholar]
- Klaiman, S.; Streltsov, A.I.; Alon, O.E. Solvable Model of a Generic Trapped Mixture of Interacting Bosons: Many-Body and Mean-Field Properties. J. Phys. Conf. Ser. 2018, 999, 012013. [Google Scholar] [CrossRef]
- Hall, R.L. Some exact solutions to the translation-invariant N-body problem. J. Phys. A 1978, 11, 1227. [Google Scholar] [CrossRef]
- Hall, R.L. Exact solutions of Schrödinger’s equation for translation-invariant harmonic matter. J. Phys. A 1978, 11, 1235. [Google Scholar] [CrossRef]
- Cohen, L.; Lee, C. Exact reduced density matrices for a model problem. J. Math. Phys. 1985, 26, 3105. [Google Scholar] [CrossRef]
- Osadchii, M.S.; Muraktanov, V.V. The System of Harmonically Interacting Particles: An Exact Solution of the Quantum-Mechanical Problem. Int. J. Quant. Chem. 1991, 39, 173. [Google Scholar] [CrossRef]
- Załuska-Kotur, M.A.; Gajda, M.; Orłowski, A.; Mostowski, J. Soluble model of many interacting quantum particles in a trap. Phys. Rev. A 2000, 61, 033613. [Google Scholar] [CrossRef]
- Yan, J. Harmonic Interaction Model and Its Applications in Bose–Einstein Condensation. J. Stat. Phys. 2003, 113, 623. [Google Scholar] [CrossRef]
- Gajda, M. Criterion for Bose–Einstein condensation in a harmonic trap in the case with attractive interactions. Phys. Rev. A 2006, 73, 023603. [Google Scholar] [CrossRef]
- Armstrong, J.R.; Zinner, N.T.; Fedorov, D.V.; Jensen, A.S. Analytic harmonic approach to the N-body problem. J. Phys. B 2011, 44, 055303. [Google Scholar] [CrossRef]
- Armstrong, J.R.; Zinner, N.T.; Fedorov, D.V.; Jensen, A.S. Virial expansion coefficients in the harmonic approximation. Phys. Rev. E 2012, 86, 021115. [Google Scholar] [CrossRef]
- Schilling, C. Natural orbitals and occupation numbers for harmonium: Fermions versus bosons. Phys. Rev. A 2013, 88, 042105. [Google Scholar] [CrossRef]
- Benavides-Riveros, C.L.; Toranzo, I.V.; Dehesa, J.S. Entanglement in N-harmonium: Bosons and fermions. J. Phys. B 2014, 47, 195503. [Google Scholar] [CrossRef]
- Bouvrie, P.A.; Majtey, A.P.; Tichy, M.C.; Dehesa, J.S.; Plastino, A.R. Entanglement and the Born-Oppenheimer approximation in an exactly solvable quantum many-body system. Eur. Phys. J. D 2014, 68, 346. [Google Scholar] [CrossRef]
- Armstrong, J.R.; Volosniev, A.G.; Fedorov, D.V.; Jensen, A.S.; Zinner, N.T. Analytic solutions of topologically disjoint systems. J. Phys. A 2015, 48, 085301. [Google Scholar] [CrossRef]
- Schilling, C.; Schilling, R. Number-parity effect for confined fermions in one dimension. Phys. Rev. 2016, 93, 021601. [Google Scholar] [CrossRef]
- Klaiman, S.; Streltsov, A.I.; Alon, O.E. Solvable model of a trapped mixture of Bose–Einstein condensates. Chem. Phys. 2017, 482, 362. [Google Scholar] [CrossRef]
- Sakmann, K.; Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Exact ground state of finite Bose–Einstein condensates on a ring. Phys. Rev. A 2005, 72, 033613. [Google Scholar] [CrossRef]
- Gupta, S.; Murch, K.W.; Moore, K.L.; Purdy, T.P.; Stamper-Kurn, D.M. Bose–Einstein Condensation in a Circular Waveguide. Phys. Rev. Lett. 2005, 95, 143201. [Google Scholar] [CrossRef] [PubMed]
- Cozzini, M.; Jackson, B.; Stringari, S. Vortex signatures in annular Bose–Einstein condensates. Phys. Rev. A 2006, 73, 013603. [Google Scholar] [CrossRef]
- Bao, C.G. Oscillation bands of Bose–Einstein condensates on a ring: Beyond the mean-field theory. Phys. Rev. A 2007, 75, 063626. [Google Scholar] [CrossRef]
- Smyrnakis, J.; Bargi, S.; Kavoulakis, G.M.; Magiropoulos, M.; Kärkkäinen, K.; Reimann, S.M. Mixtures of Bose Gases Confined in a Ring Potential. Phys. Rev. Lett. 2009, 103, 100404. [Google Scholar] [CrossRef] [PubMed]
- Halkyard, P.L.; Jones, M.P.A.; Gardiner, S.A. Rotational response of two-component Bose–Einstein condensates in ring traps. Phys. Rev. A 2010, 81, 061602. [Google Scholar] [CrossRef]
- Mathey, L.; Ramanathan, A.; Wright, K.C.; Muniz, S.R.; Phillips, W.D.; Clark, C.W. Phase fluctuations in anisotropic Bose–Einstein condensates: From cigars to rings. Phys. Rev. A 2010, 82, 033607. [Google Scholar] [CrossRef]
- Sherlock, B.E.; Gildemeister, M.; Owen, E.; Nugent, E.; Foot, C.J. Time-averaged adiabatic ring potential for ultracold atoms. Phys. Rev. A 2011, 83, 043408. [Google Scholar] [CrossRef]
- Zöllner, S.; Bruun, G.M.; Pethick, C.J.; Reimann, S.M. Bosonic and Fermionic Dipoles on a Ring. Phys. Rev. Lett. 2011, 107, 035301. [Google Scholar] [CrossRef]
- Adhikari, S.K. Dipolar Bose–Einstein condensate in a ring or in a shell. Phys. Rev. A 2012, 85, 053631. [Google Scholar] [CrossRef]
- Dubessy, R.; Liennard, T.; Pedri, P.; Perrin, H. Critical rotation of an annular superfluid Bose–Einstein condensate. Phys. Rev. A 2012, 86, 011602. [Google Scholar] [CrossRef]
- Woo, S.J.; Son, Y.-W. Vortex dynamics in an annular Bose–Einstein condensate. Phys. Rev. A 2012, 86, 011604. [Google Scholar] [CrossRef]
- Moulder, S.; Beattie, S.; Smith, R.P.; Tammuz, N.; Hadzibabic, Z. Quantized supercurrent decay in an annular Bose–Einstein condensate. Phys. Rev. A 2012, 86, 013629. [Google Scholar] [CrossRef]
- Toikka, L.A.; Suominen, K.-A. Snake instability of ring dark solitons in toroidally trapped Bose–Einstein condensates. Phys. Rev. A 2013, 87, 043601. [Google Scholar] [CrossRef]
- Eckel, S.; Lee, J.G.; Jendrzejewski, F.; Murray, N.; Clark, C.W.; Lobb, C.J.; Phillips, W.D.; Edwards, M.; Campbell, G.K. Hysteresis in a quantized superfluid ‘atomtronic’ circuit. Nature 2014, 506, 200. [Google Scholar] [CrossRef]
- Mateo, A.M.; Gallemí, A.; Guilleumas, M.; Mayol, R. Persistent currents supported by solitary waves in toroidal Bose–Einstein condensates. Phys. Rev. A 2015, 91, 063625. [Google Scholar] [CrossRef]
- Kolář, M.; Opatrný, T.; Das, K.K. Criticality and spin squeezing in the rotational dynamics of a Bose–Einstein condensate on a ring lattice. Phys. Rev. A 2015, 92, 043630. [Google Scholar] [CrossRef]
- Roy, A.; Angom, D. Geometry-induced modification of fluctuation spectrum in quasi-two-dimensional condensates. New J. Phys. 2016, 18, 083007. [Google Scholar] [CrossRef][Green Version]
- Roussou, A.; Smyrnakis, J.; Magiropoulos, M.; Efremidis, N.K.; Kavoulakis, G.M. Rotating Bose–Einstein condensates with a finite number of atoms confined in a ring potential: Spontaneous symmetry breaking beyond the mean-field approximation. Phys. Rev. A 2017, 95, 033606. [Google Scholar] [CrossRef]
- Wang, J.-G.; Xu, L.-L.; Yang, S.-J. Ground-state phases of the spin-orbit-coupled spin-1 Bose gas in a toroidal trap. Phys. Rev. A 2017, 96, 033629. [Google Scholar] [CrossRef]
- Guenther, N.-E.; Massignan, P.; Fetter, A.L. Quantized superfluid vortex dynamics on cylindrical surfaces and planar annuli. Phys. Rev. A 2017, 96, 063608. [Google Scholar] [CrossRef]
- Roy, A.; Angom, D. Ramifications of topology and thermal fluctuations in quasi-2D condensates. J. Phys. B 2017, 50, 225301. [Google Scholar] [CrossRef]
- Padavić, K.; Sun, K.; Lannert, C.; Vishveshwara, S. Physics of hollow Bose–Einstein condensates. Europhys. Lett. 2017, 120, 20004. [Google Scholar] [CrossRef]
- Eckel, S.; Kumar, A.; Jacobson, T.; Spielman, I.B.; Campbell, G.K. A Rapidly Expanding Bose–Einstein Condensate: An Expanding Universe in the Lab. Phys. Rev. X 2018, 8, 021021. [Google Scholar] [CrossRef] [PubMed]
- Sun, K.; Padavić, K.; Yang, F.; Vishveshwara, S.; Lannert, C. Static and dynamic properties of shell-shaped condensates. Phys. Rev. A 2018, 98, 013609. [Google Scholar] [CrossRef]
- Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Role of Excited States in the Splitting of a Trapped Interacting Bose–Einstein Condensate by a Time-Dependent Barrier. Phys. Rev. Lett. 2007, 99, 030402. [Google Scholar] [CrossRef] [PubMed]
- Alon, O.E.; Streltsov, A.I.; Cederbaum, L.S. Multiconfigurational time-dependent Hartree method for bosons: Many-body dynamics of bosonic systems. Phys. Rev. A 2008, 77, 033613. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Lévêque, C.; Madsen, L.B.; Streltsov, A.I.; Alon, O.E. Multiconfigurational time-dependent Hartree approaches for indistinguishable particles. arXiv 2019, arXiv:1908.03578v1. [Google Scholar]
- Alon, O.E.; Streltsov, A.I.; Cederbaum, L.S. Multiconfigurational time-dependent Hartree method for mixtures consisting of two types of identical particles. Phys. Rev. A. 2007, 76, 062501. [Google Scholar] [CrossRef]
- Sakmann, K.; Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Exact Quantum Dynamics of a Bosonic Josephson Junction. Phys. Rev. Lett. 2009, 103, 220601. [Google Scholar] [CrossRef]
- Grond, J.; Schmiedmayer, J.; Hohenester, U. Optimizing number squeezing when splitting a mesoscopic condensate. Phys. Rev. A 2009, 79, 021603. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Sakmann, K.; Alon, O.E.; Cederbaum, L.S.; Streltsov, A.I. Numerically exact quantum dynamics of bosons with time-dependent interactions of harmonic type. Phys. Rev. A 2012, 86, 063606. [Google Scholar] [CrossRef]
- Krönke, S.; Cao, L.; Vendrell, O.; Schmelcher, P. Non-equilibrium quantum dynamics of ultra-cold atomic mixtures: the multi-layer multi-configuration time-dependent Hartree method for bosons. New J. Phys. 2013, 15, 063018. [Google Scholar] [CrossRef]
- Cao, L.; Krönke, S.; Vendrell, O.; Schmelcher, P. The multi-layer multi-configuration time-dependent Hartree method for bosons: Theory, implementation, and applications. J. Chem. Phys. 2013, 139, 134103. [Google Scholar] [CrossRef]
- Streltsov, A.I. Quantum systems of ultracold bosons with customized interparticle interactions. Phys. Rev. A 2012, 88, 041602. [Google Scholar] [CrossRef]
- Streltsova, O.I.; Alon, O.E.; Cederbaum, L.S.; Streltsov, A.I. Generic regimes of quantum many-body dynamics of trapped bosonic systems with strong repulsive interactions. Phys. Rev. A 2014, 89, 061602. [Google Scholar] [CrossRef]
- Fischer, U.R.; Lode, A.U.J.; Chatterjee, B. Condensate fragmentation as a sensitive measure of the quantum many-body behavior of bosons with long-range interactions. Phys. Rev. A 2015, 91, 063621. [Google Scholar] [CrossRef]
- Fasshauer, E.; Lode, A.U.J. Multiconfigurational time-dependent Hartree method for fermions: Implementation, exactness, and few-fermion tunneling to open space. Phys. Rev. A 2016, 93, 033635. [Google Scholar] [CrossRef]
- Lode, A.U.J. Multiconfigurational time-dependent Hartree method for bosons with internal degrees of freedom: Theory and composite fragmentation of multicomponent Bose–Einstein condensates. Phys. Rev. A 2016, 93, 063601. [Google Scholar] [CrossRef]
- Sakmann, K.; Kasevich, M. Single-shot simulations of dynamic quantum many-body systems. Nat. Phys. 2016, 12, 451. [Google Scholar] [CrossRef]
- Cao, L.; Bolsinger, V.; Mistakidis, S.I.; Koutentakis, G.M.; Krönke, S.; Schurer, J.M.; Schmelcher, P. A unified ab initio approach to the correlated quantum dynamics of ultracold fermionic and bosonic mixtures. J. Chem. Phys. 2017, 147, 044106. [Google Scholar] [CrossRef] [PubMed]
- Bolsinger, V.J.; Krönke, S.; Schmelcher, P. Beyond mean-field dynamics of ultra-cold bosonic atoms in higher dimensions: facing the challenges with a multi-configurational approach. J. Phys. B 2017, 50, 034003. [Google Scholar] [CrossRef]
- Lévêque, C.; Madsen, L.B. Time-dependent restricted-active-space self-consistent-field theory for bosonic many-body systems. New J. Phys. 2017, 19, 043007. [Google Scholar] [CrossRef]
- Weiner, S.E.; Tsatsos, M.C.; Cederbaum, L.S.; Lode, A.U.J. Phantom vortices: Hidden angular momentum in ultracold dilute Bose–Einstein condensates. Sci Rep. 2017, 7, 40122. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Bruder, C. Fragmented Superradiance of a Bose–Einstein Condensate in an Optical Cavity. Phys. Rev. Lett. 2017, 118, 013603. [Google Scholar] [CrossRef]
- Bolsinger, V.J.; Krönke, S.; Schmelcher, P. Ultracold bosonic scattering dynamics off a repulsive barrier: Coherence loss at the dimensional crossover. Phys. Rev. A 2017, 96, 013618. [Google Scholar] [CrossRef]
- Katsimiga, G.C.; Mistakidis, S.I.; Koutentakis, G.M.; Kevrekidis, P.G.; Schmelcher, P. Many-body quantum dynamics in the decay of bent dark solitons of Bose–Einstein condensates. New J. Phys. 2017, 19, 123012. [Google Scholar] [CrossRef]
- Schurer, J.M.; Negretti, A.; Schmelcher, P. Unraveling the Structure of Ultracold Mesoscopic Collinear Molecular Ions. Phys. Rev. Lett. 2017, 119, 063001. [Google Scholar] [CrossRef]
- Chen, J.; Schurer, J.M.; Schmelcher, P. Entanglement Induced Interactions in Binary Mixtures. Phys. Rev. Lett. 2018, 121, 043401. [Google Scholar] [CrossRef]
- Lévêque, C.; Madsen, L.B. Multispecies time-dependent restricted-active-space self-consistent-field-theory for ultracold atomic and molecular gases. J. Phys. B 2018, 51, 155302. [Google Scholar] [CrossRef]
- Roy, R.; Gammal, A.; Tsatsos, M.C.; Chatterjee, B.; Chakrabarti, B.; Lode, A.U.J. Phases, many-body entropy measures, and coherence of interacting bosons in optical lattices. Phys. Rev. A 2018, 97, 043625. [Google Scholar] [CrossRef]
- Elsayed, T.A.; Streltsov, A.I. Probing quantum states with momentum boosts. Phys. Rev. A 2018, 98, 013618. [Google Scholar] [CrossRef]
- Nguyen, J.H.V.; Tsatsos, M.C.; Luo, D.; Lode, A.U.J.; Telles, G.D.; Bagnato, V.S.; Hulet, R.G. Parametric Excitation of a Bose–Einstein Condensate: From Faraday Waves to Granulation. Phys. Rev. X 2019, 9, 011052. [Google Scholar] [CrossRef]
- Marchukov, O.V.; Fischer, U.R. Self-consistent determination of the many-body state of ultracold bosonic atoms in a one-dimensional harmonic trap. Ann. Phys. 2019, 405, 274. [Google Scholar] [CrossRef]
- Streltsov, A.I.; Streltsova, O.I. MCTDHB-Lab, Version 1.5. 2015. Available online: http://www.mctdhb-lab.com (accessed on 29 September 2019).
- Streltsov, A.I.; Cederbaum, L.S.; Alon, O.E.; Sakmann, K.; Lode, A.U.J.; Grond, J.; Streltsova, O.I.; Klaiman, S.; Beinke, R. The Multiconfigurational Time-Dependent Hartree for Bosons Package, Version 3.x. Available online: http://mctdhb.org (accessed on 29 September 2019).
- Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. General variational many-body theory with complete self-consistency for trapped bosonic systems. Phys. Rev. A 2006, 73, 063626. [Google Scholar] [CrossRef]
- Meyer, H.-D.; Manthe, U.; Cederbaum, L.S. The multi-configurational time-dependent Hartree approach. Chem. Phys. Lett. 1990, 165, 73. [Google Scholar] [CrossRef]
- Manthe, U.; Meyer, H.-D.; Cederbaum, L.S. Wave-packet dynamics within the multiconfiguration Hartree framework: General aspects and application to NOCl. J. Chem. Phys. 1992, 97, 3199. [Google Scholar] [CrossRef]
- Beck, M.H.; Jäckle, A.; Worth, G.A.; Meyer, H.D. The multiconfiguration time-dependent Hartree (MCTDH) method: A highly efficient algorithm for propagating wavepackets. Phys. Rep. 2000, 324, 1. [Google Scholar] [CrossRef]
- Meyer, H.-D.; Gatti, F.; Worth, G.A. (Eds.) Multidimensional Quantum Dynamics: MCTDH Theory and Applications; Wiley-VCH: Weinheim, Germany, 2009. [Google Scholar]
- Wang, H.; Thoss, M. Multilayer formulation of the multiconfiguration time-dependent Hartree theory. J. Chem. Phys. 2003, 119, 1289. [Google Scholar] [CrossRef]
- Manthe, U. A multilayer multiconfigurational time-dependent Hartree approach for quantum dynamics on general potential energy surfaces. J. Chem. Phys. 2008, 128, 164116. [Google Scholar] [CrossRef]
- Vendrell, O.; Meyer, H.-D. Multilayer multiconfiguration time-dependent Hartree method: Implementation and applications to a Henon-Heiles Hamiltonian and to pyrazine. J. Chem. Phys. 2011, 134, 044135. [Google Scholar] [CrossRef] [PubMed]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alon, O.E. Analysis of a Trapped Bose–Einstein Condensate in Terms of Position, Momentum, and Angular-Momentum Variance. Symmetry 2019, 11, 1344. https://doi.org/10.3390/sym11111344
Alon OE. Analysis of a Trapped Bose–Einstein Condensate in Terms of Position, Momentum, and Angular-Momentum Variance. Symmetry. 2019; 11(11):1344. https://doi.org/10.3390/sym11111344
Chicago/Turabian StyleAlon, Ofir E. 2019. "Analysis of a Trapped Bose–Einstein Condensate in Terms of Position, Momentum, and Angular-Momentum Variance" Symmetry 11, no. 11: 1344. https://doi.org/10.3390/sym11111344
APA StyleAlon, O. E. (2019). Analysis of a Trapped Bose–Einstein Condensate in Terms of Position, Momentum, and Angular-Momentum Variance. Symmetry, 11(11), 1344. https://doi.org/10.3390/sym11111344




